初二5-3-1解一元一次不等式组
- 格式:doc
- 大小:568.74 KB
- 文档页数:12


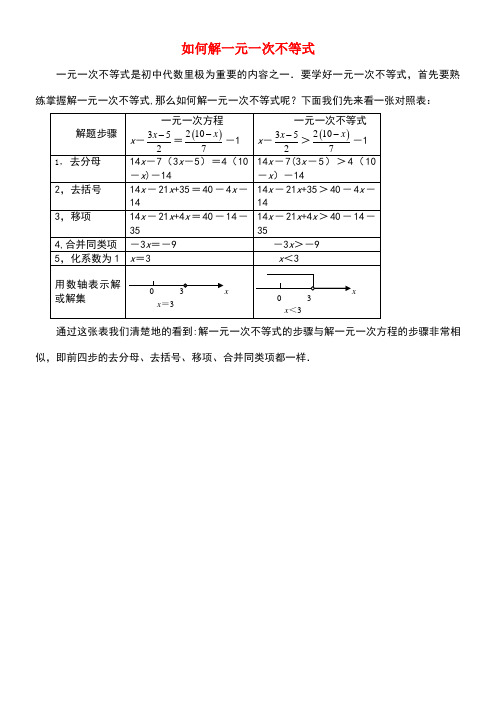
如何解一元一次不等式一元一次不等式是初中代数里极为重要的内容之一.要学好一元一次不等式,首先要熟练掌握解一元一次不等式,那么如何解一元一次不等式呢?下面我们先来看一张对照表:通过这张表我们清楚地的看到:解一元一次不等式的步骤与解一元一次方程的步骤非常相似,即前四步的去分母、去括号、移项、合并同类项都一样.从这张表中,我们还可以看到解一元一次不等式和解一元一次方程的不同之处,主要表现在:(1)一元一次不等式的左右两边是用不等号连联系的,而一元一次方程的左右两边则是有等号联系的;(2)在第五步化系数为1时稍微有一点变化,即在整个解题过程中,解一元一次方程是用的等式的性质,而解一元一次不等式则是用的不等式的基本性质.就是说解一元一次不等式的化系数为1时,要特别注意负号和不等号的方向问题;(3)一元一次不等式的解集合里有无限多个数.为了能说明解一元一次不等式的一般步骤,下面再举两例:例1 解不等式:3-5(15x -2)-4(-1+5 x )<10.解 去括号,得3-x +10+4-20x <10, 移项、合并同类项,得7<21x ,即21x >7,化系数为1,得x >13.说明 由本题的解题过程可知,解不等式和解一元一次方程一样,也不一定按部就班地利用其一般步骤,而灵活运用,另外这里观察“5(15x -2)”,也不一定急于去分母,而直接去括号,既省去去分母的麻烦,又快速准确,在移项时,也不一定非得让含未知数的项移到左边,我们这里把含未知数的项到右边可以避免“-"号的干扰.例2 解不等式:4-521262x x-+≤,并把解集在数轴上表示出来. 解 去分母,得24-(5-2x )≤3(去括号,得24-5+2x ≤3+6x , 移项、合并同类项,得4x ≥16, 化系数为1,得x ≥4. 解集在数轴表示如图:说明 去分母时,分数线具有括号的作用,所以去掉分母不要忘记添上括号,特别是括号前面是“-",同时不能漏乘不含分母的整式项,在数轴上表示解集时应注意原点是空心还是实心等等.练习题41,解下列不等式:(1)3(1-x)<2(x+9).(2)2(4x+3)≤3(2x+5).(3)22213+≥-x x.(4)x x+-<+521322.2,求不等式3(x+1)≥5x-1的正整数解.参考答案:1,(1)x>-3、(2)x≤92、(3)x≤8、(4)x>12;2,由不等式解得x≤2,所以正整数解是1、2;尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。


5-3-1 基本方法概述
对于“双元变量不等式问题”,如果两个变量是有等量关系的,那么这种问题一般都会颇有难度。
我们需要联系前几章的知识点进行分析,比如说洛必达法则。
5-3-1主要起一个总括的作用,解决这种变量之间有关系的问题,方法有以下几种:
1、变形
变形技巧①:两变量直接变形
变形技巧②:设t变形
2、强行作差
不管是哪一种方法,其核心目的都是一样的:把双变量转换为单变量。
同样,每一种方法都不是万能的,都有各自的缺陷,因此每一种方法都要掌握。

巧解一元一次不等式怎样才能正确而迅速地解一元一次不等式?现结合实例介绍一些技巧,供参考.1.巧用乘法例1 解不等式0.25x>10.5.分析因为0.25×4=1,所以两边同乘以4要比两边同除以0.25来得简便.解两边同乘以4,得x>42.2.巧用对消法例2 解不等式解原不等式变为3.巧用分数加减法法则故 y<-1.4.逆用分数加减法法则解原不等式化为,5.巧用分数基本性质例5 解不等式约去公因数2后,两边的分母相同;②两个常数项移项合并得整数.例6 解不等式分析由分数基本性质,将分母化为整数和去分母一次到位可避免繁琐的运算.解原不等式为整理,得8x-3-25x+4<12-10x,思考:例5可这样解吗?请不妨试一试.6.巧去括号去括号一般是内到外,即按小、中、大括号的顺序进行,但有时反其道而行之即由外到内去括号往往能另辟捷径.7.逆用乘法分配律例8 解不等式278(x-3)+351(6-2x)-463(3-x)>0.分析直接去括号较繁,注意到左边各项均含有因式x-3而逆用分配律可速解此题.解原不等式化为(x-3)(278-351×2+463)>0,即 39(x-3)>0,故x>3.8.巧用整体合并例9 解不等式3{2x-1-[3(2x-1)+3]}>5.解视2x-1为一整体,去大、中括号,得3(2x-1)-9(2x-1)-9>5,整体合并,得-6(2x-1)>14,9.巧拆项例10 解不等式分析将-3拆为三个负1,再分别与另三项结合可巧解本题.解原不等式变形为得x-1≥0,故x≥1.练习题解下列一元一次不等式③3{3x+2-[2(3x+2)-1]}≥3x+1.答案。
一元一次不等式组的解法•一元一次不等式组解集:一元一次不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集。
注:当任何数x都不能使各个不等式同时成立,我们就说这个一元一次不等式组无解或其解集为空集。
例如:不等式x-5≤-1的解集为x≤4;不等式x﹥0的解集是所有非零实数。
•复习本考点时主要主要集中在解不等式(组)、求不等式(组)的整数解、确定不等式中字母的取值范围及不等式(组)的应用.• 1.搞清不等号与一些词语含义的对应关系,如:“>”表示大于、高出、多于、超过;“<”表示小于、低于、不足、合算;“≥”表示大于或等于、不少于、不低于、至少;“≤”表示小于或等于、不大于、不超过、至多.• 2.弄清“或”与“且”的用法:“或”表示两者居其一即可;而“且”表示两者必须同时符合,缺一不可.• 3.在数轴上表示解集时注意:(1)方向:向左、向右表示小于、大于;(2)空心圈与实心点问题:空心圈表示不包含该点;实心点表示包含该点.• 4.解不等式(组)要注意:•(1)迁移错误(由解方程迁移来的错误);(2)性质使用不当;•(3)概念理解不清;(4)移项不变号;(5)不等方向问题等.• 5.遇到含参数时要注意分类讨论.• 6.特别要注意不等式的性质3的应用.•解法:求不等式组的解集的过程,叫做解不等式组。
•求几个一元一次不等式的解集的公共部分,通常是利用数轴来确定的,公共部分是指数轴上被两条不等式解集的区域都覆盖的部分;一般由两个一元一次不等式组成的不等式组由四种基本类型确定,它们的解集、数轴表示如下表:(设a<b)•一元一次不等式组的解答步骤:(1)分别求出不等式组中各个不等式的解集;(2)将这些不等式的解集在同一个数轴上表示出来,找出它们的的公共部分;(3)根据找出的公共部分写出不等式组的解集,若没有公共部分,说明不等式组无解。
解法诀窍:同大取大;例如:X>-1X>2不等式组的解集是X>2同小取小;例如:X<-4X<-6不等式组的解集是X<-6大小小大中间找;例如,x<2,x>1,不等式组的解集是1<x<2大大小小不用找例如,x<2,x>3,不等式组无解•一元一次不等式组的整数解:一元一次不等式组的整数解是指在不等式组中各个不等式的解集中满足整数条件的解的公共部分。
【考纲说明】1、根据具体问题中数量关系列出不等式组,解决简单问题。
2、了解一元一次不等式组解、解集的意义,在数轴上表示或判定其解集。
3、灵活运用一元一次不等式组,并解不等式组。
4、本部分在中考中占3-10分。
【趣味链接】一个长方形足球场的长为X米,宽为70米,如果它的周长大于350米,面积小于7650平方米,求X的取值范围,并判断这个球场是否可以作为国际足球比赛(注:用于国际比赛的足球场的长在100至110米之间,宽在64至75米之间。
)【知识梳理】一元一次不等式组1、一元一次不等式组的概念:几个一元一次不等式合在一起,就组成了一个一元一次不等式组。
2、几个一元一次不等式的解集的公共部分,叫做它们所组成的一元一次不等式组的解集。
3、求不等式组的解集的过程,叫做解不等式组。
4、当任何数x都不能使不等式同时成立,我们就说这个不等式组无解或其解为空集。
5、一元一次不等式组的解法(1)分别求出不等式组中各个不等式的解集(2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集。
6、不等式与不等式组不等式:①用符号〉,=,〈号连接的式子叫不等式。
②不等式的两边都加上或减去同一个整式,不等号的方向不变。
③不等式的两边都乘以或者除以一个正数,不等号方向不变。
④不等式的两边都乘以或除以同一个负数,不等号方向相反。
7、不等式的解集:①能使不等式成立的未知数的值,叫做不等式的解。
②一个含有未知数的不等式的所有解,组成这个不等式的解集。
③求不等式解集的过程叫做解不等式。
【经典例题】【例1】下列不等式组中,解集是2<x <3的不等式组是( )A 、⎩⎨⎧>>23x xB 、⎩⎨⎧<>23x xC 、⎩⎨⎧><23x xD 、⎩⎨⎧<<23x x【例2】在数轴上从左至右的三个数为a ,1+a ,-a ,则a 的取值范围是( ) A 、a <12 B 、a <0 C 、a >0 D 、a <-12【例3】(2007年湘潭市)不等式组10235x x +⎧⎨+<⎩≤,的解集在数轴上表示为( )【例4】不等式组31025x x +>⎧⎨<⎩的整数解的个数是( )A 、1个B 、2个C 、3个D 、4个【例5】在平面直角坐标系内,P (2x -6,x -5)在第四象限,则x 的取值范围为( ) A 、3<x <5 B 、-3<x <5 C 、-5<x <3 D 、-5<x <-3【例6】(2007年南昌市)已知不等式:①1x >,②4x >,③2x <,④21x ->-,从这四个不等式中取两个,构成正整数解是2的不等式组是( ) A 、①与②B 、②与③C 、③与④D 、①与④【例7】若y 同时满足y +1>0与y -2<0,则y 的取值范围是______________.【例8】(2007年遵义市)不等式组3010x x -<⎧⎨+⎩≥的解集是 .【例9】不等式组20.53 2.52x x x -⎧⎨---⎩≥≥的解集是 .【例10】若不等式组⎩⎨⎧->+<121m x m x 无解,则m 的取值范围是 .ABCD【例11】不等式组15x x x >-⎧⎪⎨⎪<⎩≥2的解集是_________________【例12】不等式组2x x a>⎧⎨>⎩的解集为x >2,则a 的取值范围是_____________.【例13】解下列不等式组(1)328212x x -<⎧⎨->⎩ (2)572431(1)0.54x x x -≥-⎧⎪⎨--<⎪⎩(3)2x <1-x ≤x +5 (4)3(1)2(9)34140.50.2x x x x -<+⎧⎪-+⎨-≤-⎪⎩【例14】(2007年滨州)解不等式组3(21)42132 1.2x x x x ⎧--⎪⎪⎨+⎪>-⎪⎩≤,把解集表示在数轴上,并求出不等式组的整数解.【例15】求同时满足不等式6x-2≥3x-4和2112132x x+--<的整数x的值.【例16】若关于x、y的二元一次方程组533x y mx y m-=-⎧⎨+=+⎩中,x的值为负数,y的值为正数,求m的取值范围.【课堂练习】1.下列不等式组中,是一元一次不等式组的是()A.2,3xx>⎧⎨<-⎩B.10,20xy+>⎧⎨-<⎩C.320,(2)(3)0xx x->⎧⎨-+>⎩D.320,11xxx->⎧⎪⎨+>⎪⎩2.下列说法正确的是()A.不等式组3,5xx>⎧⎨>⎩的解集是5<x<3 B.2,3xx>-⎧⎨<-⎩的解集是-3<x<-2C .2,2x x ≥⎧⎨≤⎩的解集是x=2 D .3,3x x <-⎧⎨>-⎩的解集是x ≠33.不等式组2,3482x x x⎧>-⎪⎨⎪-≤-⎩的最小整数解为( ) A .-1 B .0 C .1 D .44.在平面直角坐标系中,点P (2x -6,x -5)在第四象限,则x 的取值范围是( ) A .3<x<5 B .-3<x<5 C .-5<x<3 D .-5<x<-35.若不等式组2,x x m<⎧⎨>⎩有解,则m 的取值范围是______.6.已知三角形三边的长分别为2,3和a ,则a 的取值范围是_____.7.将一筐橘子分给若干个儿童,如果每人分4个橘子,则剩下9个橘子;•如果每人分6个橘子,则最后一个儿童分得的橘子数将少于3个,由以上可推出,共有_____个儿童,分_____个橘子. 8.若不等式组2,20x a b x ->⎧⎨->⎩的解集是-1<x<1,则(a+b )2006=______.9.解不等式组2(2)4,(1)10(2)32x x x x -≤-⎧⎪+⎨-<⎪⎩10.若不等式组1,21x m x m <+⎧⎨>-⎩无解,求m 的取值范围.11、(一题多变题)如果关于x 的不等式(a -1)x<a+5和2x<4的解集相同,则a•的值为______.(1)一变:如果(1)5,24a x a x -<+⎧⎨<⎩的解集是x<2,则a 的取值范围是_____;(2)二变:如果24,1,51x x a x a ⎧⎪<⎪≥⎨⎪+⎪<-⎩的解集是1≤x<2,则a 的取值范围是____12.(科内交叉题)在关于x 1,x 2,x 3的方程组121232133,,x x a x x a x x a+=⎧⎪+=⎨⎪+=⎩中,已知a 1>a 2>a 3,请将x 1,x 2,x 3按从大到小的顺序排列起来.13.(科外交叉题)设“○”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图1-6-1所示,那么每个“○”、“□”、•“△”这样的物体,按质量从小到大的顺序排列为( ) A .○□△ B .○△□ C .□○△ D .△□○14.(结论开放题)有甲,乙,丙三个人在一起讨论一个一元一次不等式组,•他们各说出该不等式组的一个性质. 甲:它的所有解为非负数.乙:其中一个不等式的解集为x ≤8.丙:其中一个不等式在解的过程中需改变不等号的方向.请试着写出符合上述条件的一个不等式组,并解答.15.(阅读理解题)先阅读不等式x2+5x-6<0的解题过程,然后完成练习.解:因为x2+5x-6<0,所以(x-1)(x+6)<0.因为两式相乘,异号得负.所以10,60xx->⎧⎨+<⎩或10,60xx-<⎧⎨+>⎩即1,6xx>⎧⎨<-⎩(舍去)或1,6xx<⎧⎨>-⎩所以不等式x2+5x-6<0的解集为-6<x<1.练习:利用上面的信息解不等式228xx-+<0.16.(方案设计题)为了保护环境,某企业决定购买10台污水处理设备,现有A,B•两种型号的设备,其中每台的价格,月处理污水量如下表:经预算,•该企业购买设备的资金不高于105•万元,•若企业每月产生的污水量为2040t,为了节约资金,请你为企业设计购买方案.【课后作业】1、如果不等式组x ax b>⎧⎨<⎩无解,那么不等式组的解集是()A.2-b<x<2-aB.b-2<x<a-2C.2-a<x<2-bD.无解2、方程组43283x mx y m+=⎧⎨-=⎩的解x、y满足x>y,则m的取值范围是()A.910m> B.109m> C.1910m> D.1019m>3、若不等式组2123x ax b-<⎧⎨->⎩的解集为-1<x<1,那么(a+1)(b-1)的值等于________.4、若不等式组4050a xx a->⎧⎨+->⎩无解,则a的取值范围是_______________.5、某宾馆底层客房比二楼少5间,某旅游团有48人,若全安排在底层,每间4人,则房间不够;若每间5人,则有房间没有住满5人;若全安排在二楼,每间住3人,房间不够;每间住4人,则有房间没有住满4人,求该宾馆底层有客房多少间?6、(2007,厦门,3分)小宝和爸爸,妈妈三人在操场上玩跷跷板,爸爸体重为69•千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,•这时爸爸的一端仍然着地.后来小宝借来一副质量为6千克的哑铃,•加在他和妈妈坐的一端,结果爸爸被跷起,那么小宝的体重可能是()A.23.2千克 B.23千克 C.21.1千克 D.19.9千克7、(2008,天津,3分)不等式组322(1),841x xx x+>-⎧⎨+>-⎩的解集为______.8、(2007,青岛,8分),某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,•每瓶饮料中甲,乙的含量如下表所示,现用甲原料和乙原料各2800克进行试生产,•计划生产A,B两种饮料共100瓶.设生产A种饮料x瓶,解答下列问题.(1)有几种符合题意的生产方案?写出解答过程;(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,•这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低.【课后反馈】本次______________同学课堂状态:_________________________________________________________________本次课后作业:___________________________________________________________________________________需要家长协助:____________________________________________________________________________________家长意见:________________________________________________________________________________________经典例题1、C2、D3、C4、B5、A6、D7、1<y<28、-1≤x<39、-14≤x≤4 10、m>2 11、2≤x<5 12、a<2 13、(1)31023x<<(2)无解(3)-2<x<13(4)x>-3 14、2,1,0,-115、不等式组的解集是27310x≤<-,所以整数x为016、-2<m<0.5课堂练习1.A 点拨:B中含有两个未知数x,y.C中x的最高次数是2,D中分母中含有未知数.2.C 点拨:A中不等式组的解集是x>5,B,D中不等式组的解集是空集.3.B 点拨:不等式组的解集为-23<x≤4,所以最小整数解为0.4.A 点拨:由题意得260,50,xx->⎧⎨-<⎩,解得3<x<5.5.m<26.1<a<5 点拨:由题意知3-2<a<3+2,即1<a<5.本题考查三角形三边之间的关系.7.7;37 点拨:设有x个儿童,则橘子的个数为4x+9,依题意得0<4x+9-6(x-1)<3,解之得6<x<7.5,因为x 为正整数,所以x=7,所以4x+9=4×7+9=37(个).8.19.解:不等式(1)的解集为x≤0.不等式(2)的解集为x>-3.所以原不等式组的解集为-3<x≤0.点拨:先求每一个不等式的解集,然后找出它们的公共部分.10.错解:由不等式组无解可知2m-1>m+1,所以m>2.正确解法:由题意得2m-1≥m+1时,因为原不等式组无解,所以m≥2.点拨:此题错误原因在于忽略了m+1与2m-1可以相等,即类似,x ax a>⎧⎨<⎩的形式也是1 1.7 (1)1<a≤7 (2)1<a≤7点拨:由题意得(a-1)x<a+5的解集为x<2,所以52110.aaa+⎧=⎪-⎨⎪->⎩,所以a=7.(1)由题意得a-1>0,即a>1时,512axax+⎧<⎪-⎨⎪<⎩的解集为x<2.所以51aa+-≥2,所以a≤7,所以1<a≤7.(2)由一变可知51aa+-≥2,当a-1>0,即a>1时,1<a≤7;当a-1<0,即a<1时,a+5≤2(a-1),所以a≥7,此时a的值不存在.综上所述,1<a≤7.去分母时,要根据分母是正是负两种情况进行讨论.12.解:将方程组的三式相加得2(x1+x2+x3)=a1+a2+a3.所以x1+x2+x3=12(a1+a2+a3),因为x1+x2=a1,所以a1+x3=12(a1+a2+a3),所以x3=12(a2+a3-a1).同理x1=12(a1+a3-a2),x2=12(a1+a2-a3).因为a1>a2>a3.所以x1-x2=12(a1+a3-a2)-12(a1+a2-a3)=a3-a2<0,所以x1<x2,同理x1>x3,所以x3<x1<x2.13.D 点拨:由第一个天平知○>□,由第二个天平知□=2△,即□>△,所以○>□>△.本题主要考查了数形结合的数学思想和观察识别图形的能力.14.解:可以写出不同的不等式组,如3325(1), 221(2). x xx x-≤+⎧⎨-<-⎩,不等式(1)的解集为x≤8,•不等式(2)的解集为x>1,所以原不等式组的解集为1<x≤8.点拨:此题为结论开放性试题,答案不唯一,只要符合题意即可.15.解:因为两式相除,异号得负,由228xx-+<0,得220,80xx->⎧⎨+<⎩或220,80xx-<⎧⎨+>⎩,即1,8xx>⎧⎨<-⎩(舍去)或1,8xx<⎧⎨>-⎩所以不等式228xx-+<0的解集是-8<x<1.点拨:认真阅读所给材料,从中获取相关信息,由两式相乘,异号得负,•得到两式相除,异号得负,由此解不等式228xx-+<0.16.解:设购买污水处理设备A型号x台,则购买B型号(10-x)台,根据题意,得1210(10)105,240200(10)2040.x xx x+-≤⎧⎨+-≥⎩,解这个不等式组,得1≤x≤2.5.因为x是整数,所以x=1或2.当x=1时,购买资金为12×1+10×9=102(万元),当x=2时,购买资金为12×2+10×8=104(万元).因此,为了节约资金,应购污水处理设备A型号1台,B型号9台.点拨:本题是“方案设计”问题,•一般可把它转化为求不等式组的整数解问题.通过表格获取相关信息,在实际问题中抽象出不等式组是解决这类问题的关键.课后作业1、A2、D3、-64、a≤15、解:设该宾馆底层有客房x间,则二楼有客房(x+5)间,根据题意得4848,5448485,43xx⎧<<⎪⎪⎨⎪<+<⎪⎩,•解得485<x<11,因为x为整数,所以x=10.答:宾馆底层有客房10间.6、C 点拨:设小宝的体重为x千克,根据题意,得269,2669. x xx x+<⎧⎨++>⎩解这个不等式组得21<•x<23,故选C.7、-4<x<3 点拨:由①得:x>-4;由②得:x<3,分别解完不等式后可以利用数轴或口诀“比大的小,比小的大,中间找”得到最终结果.此题考查利用数形结合解不等式组,是对学生基本运算方法、运算法则、基本性质的动用能力的考查.8、解:(1)设生产A种饮料x瓶,根据题意,得2030(100)2800, 4020(100)2800.x xx x+-≤⎧⎨+-≤⎩解这个不等式组,得20≤x≤40,因为其中正整数解共有21个,所以符合题意的生产方案有21种.(2)根据题意,得y=2.6x+2.8(100-x),整理,得y=-0.2x+280.因为k=-0.2<0,所以y随x的增大而减小,所以当x=40时成本总额最低.。