当前位置：文档之家 › 模糊控制第三章解析答案课堂

模糊控制第三章解析答案课堂

  • 格式：ppt
  • 大小：1.77 MB
  • 文档页数：89

下载文档原格式

  / 89

合集下载

第三章(2) 模糊控制系统的设计

第三章(2) 模糊控制系统的设计

假设中等小费是15%，高是25%，小费低是5%。 小费函数大致形状如下。明显地，曲线形状受 当地传统、文化喜好影响，但三条规则通用。
0.25
0.15
0.05
服务差或食品差 服务好或食品好
3.3 模糊控制器的设计举例 31
μ μ A(e) μ B(e)
0
e
3.2模糊控制系统的设计 12
二、模糊控制器的设计原则 b). α 较小，控制灵敏度高； α 较大，鲁棒性好； 一般取α = 0.5。
μ μ A(e) μ B(e) μ μ A(e) μ B(e)
0
e
0
e
3.2模糊控制系统的设计
13
二、模糊控制器的设计原则 3、设计规则库 规则数： N=nout*(nin(nlevel-1)+1)。 4、设计模糊推理 可由软、硬件实现。
20
3.3 模糊控制器的设计举例
3.3 模糊控制器的设计举例 4、模糊控制规则的确定 为使系统输出的动态特性最佳，根据操作经验而 总结的一条条模糊条件语句。
3
4 5 2 1
Td
0
t
3.3 模糊控制器的设计举例
21
3.3 模糊控制器的设计举例 （1）误差e = T – Td 为负大时，全功率加热。
5、精确化方法 一定要选取有代表性的值。
3.2模糊控制系统的设计
14
3.3 模糊控制器的设计举例 以加热炉温度控制系统为例： 由于模糊关系矩阵是一个高阶矩阵，多次合成计 算使输出使系统实时性变差，在实际应用中通 常采用查表法。
DE
Td
_
e
Δ
KΔe Ke E
模糊 控制表
U
Ku
u
被控对象

控制工程第3章习题解答

控制工程第3章习题解答

3.5 使用温度计对水温进行测量，若水温为恒定值，该温度计能在1分钟时指示出实际温度值的98%。

假定温度计为一个一阶系统，求该系统的时间常数T 。

解：恒定的水温可以视为一个阶跃输入信号，温度计的测量输出可以视为对该阶跃输入信号的响应。

一阶系统的单位阶跃响应的时间函数为：)0(1)(/>-=-t e t x T t o （P82，3.3.2） 根据题意可知：98.01)(/11=-=-=Tt o e t x→02.0/1=-T e →256.050ln 1==T (min)若测量开始后，实际水温从零度起，以10°C/min 的速度线性升温，求温度计在1分钟时的示值与实际水温的误差是多大？（帮助公式：11111222++-=+⋅Ts T s T sTs s ） 根据题意，实际的温度输入信号为：t t x i ⋅=10)(其拉氏变换为：210)(ss X i =测量误差的时间函数为：]1110[)()]()([)()]([)()()()(2111+⋅⋅-=⋅-=-=-=---s T sL t x s G s X L t x s X L t x t x t x t e i i i o i o i其中：)(10]11[10]111[10]1110[/2212121T t e T T t Ts T s T s L Ts s L s T s L ----⋅+-=++-=+⋅=+⋅⋅所以：)1(56.2)1(10)(1010)(256.0///t T t T t e e T e T T t t t e ----=-=⋅+--=当t=1时，测量误差为：5.2)1(56.2)(256.0/11=-=-=e t e t3.7已知控制系统的微分方程为)(20)()(5.2t x t y t y =+'，试用拉氏变换法求该系统的单位脉冲响应)(t w 和单位阶跃响应)(t x ou ，并讨论二者之间的关系解：由传递函数的定义和系统的微分方程（P34，2.2.2~2.2.3），可得系统的传递函数为4.0815.220)()()(+=+==s s s X s Y s G 系统的单位脉冲响应为（P81）t e s L s X s G L t w 4.0118]14.08[)]()([)(---=⋅+==系统的单位阶跃响应为（P82）：)1(20]4.011[4.08]14.08[)]()([)(4.0111t ou e s s L s s L s X s G L t x -----=+-=⋅+==比较)(t x ou 和)(t w ，有)(t w =)(t x ou' 即系统的单位脉冲响应等于系统的单位阶跃响应的微分。

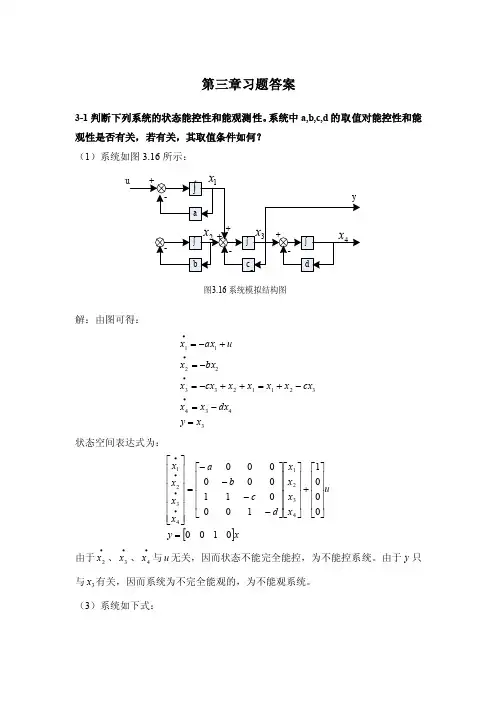
现代控制理论第三章习题解答

现代控制理论第三章习题解答

第三章习题答案3-1判断下列系统的状态能控性和能观测性。

系统中a,b,c,d 的取值对能控性和能观性是否有关，若有关，其取值条件如何？ （1）系统如图3.16所示：图3.16 系统模拟结构图解：由图可得：343432112332211x y dx x x cx x x x x cx x bx x u ax x =-=-+=++-=-=+-=∙∙∙∙状态空间表达式为：[]xy ux x x x d c b a x x x x 0100000110001100000043214321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙由于∙2x 、∙3x 、∙4x 与u 无关，因而状态不能完全能控，为不能控系统。

由于y 只与3x 有关，因而系统为不完全能观的，为不能观系统。

（3）系统如下式：x d c y ub a x x x x x x ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∙∙∙00000012200010011321321 解：如状态方程与输出方程所示，A 为约旦标准形。

要使系统能控，控制矩阵b 中相对于约旦块的最后一行元素不能为0，故有0,0≠≠b a 。

要使系统能观，则C 中对应于约旦块的第一列元素不全为0，故有0,0≠≠d c 。

3-2时不变系统X y u X X ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=∙111111113113试用两种方法判别其能控性和能观性。

解：方法一：[]⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=2-2-112-2-11AB B M 1111,1111,3113C B A系统不能控。

,21<=rankM ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎦⎤⎢⎣⎡=44221111CA C N 系统能观。

第3章 模糊控制

第3章 模糊控制

期望值
＋ － y
e
ec
ke d/dt kec
E
EC
ห้องสมุดไป่ตู้
模糊
控制器
U
u
ku
图中ke、kec为量化因子，ku为比例因子
量化： 将一个论域离散成确定数目的几小段(量化 级)。每一段用某一个特定术语作为标记，这 样就形成一个离散域。
假设在实际中，误差的连续取值范围是 e=[eL,eH]，eL表示低限值，eH表示高限值。 将离散语言变量E的论域定义为{-m,„,-1, 0,1, „,m}。则有量化因子： 2m ke eH eL 量化因子实际上类似于增益的概念，在这 个意义上称量化因子为量化增益更为合适。
i Ri : IF x1 IS A1i AND x2 IS A2 AND xp IS Aip
i i THEN vi a0 a1 x aip x p i 1 , , N
(3 1)
vi 是模糊语言值; xi是一个输入变量；是输 i 出变量；系数集{a j }是待辨识的参数。模型的辨 i i ( N , p ) { A , a 识分两步。即结构参数 的辨识和系数 j j } 的确定。
1、最大隶属度函数法 简单地取所有规则推理结果的模糊集合中隶属 度最大的那个元素作为输出值。即： 当论域 V 中，其最大隶属度函数对应的输出 值多于一个时，简单取最大隶属度输出的平均即 可： U 0 max v (v) v V 为具有相同最大隶属度输出的总数。 此方法计算简单，但丢失信息，控制性能不高。
式中，<>代表取整运算。 模糊控制器的输出U可以通过下式转换为 实际的输出值u：
uH uL u ku U 2
问题的提出 变量量化会导致一定的量化误差。 解决方法 在量化级之间，加入插值运算。对于任意一 个连续的测量值可以通过相邻两个离散值的加 权运算得到模糊度的值。

第3章 模糊控制理论的基础讲解

第3章 模糊控制理论的基础讲解

（3）模糊控制易于被人们接受。模糊控 制的核心是控制规则，模糊规则是用语言 来表示的，如“今天气温高，则今天天气 暖和”，易于被一般人所接受。 （4）构造容易。模糊控制规则易于软件 实现。 （5）鲁棒性和适应性好。通过专家经验 设计的模糊规则可以对复杂的对象进行有 效的控制。
第二节 模糊集合
一、模糊集合 模糊集合是模糊控制的数学基础。
c (x) Min A (x), B (x)
② 代数积算子
c (x) A (x) B (x)
③ 有界积算子
c (x) Max0, A (x) B (x) 1
（2）并运算算子 设C=A∪B，有三种模糊算子： ① 模糊并算子
c (x) Max A (x), B (x)
c (x) A (x) B ( x) 1 1 (1 A (x)) (1 B (x))
γ取值为[0，1]。
当γ=0时， c (x) A (x) ，B相(x当) 于A∩B
时的算子。
当γ=1时，c (x) A(x) B (x) A(，x)相.B (x)
（3）等集
两个模糊集A和B，若对所有元素u，
它们的隶属函数相等，则A和B也相等。
即
A B A (u) B (u)
（4）补集 若 A 为A的补集，则
A A (u) 1 A (u)
例如，设A为“成绩好”的模糊集， 某学生 u0 属于“成绩好”的隶属度为：
A (u0 ) 0.8 则u0 属于“成绩差”的隶属度
第三章 模糊控制的理论基础
第一节 概 述 一、 模糊控制的提出
以往的各种传统控制方法均是建立在 被控对象精确数学模型基础上的，然而， 随着系统复杂程度的提高，将难以建立 系统的精确数学模型。

第三章、模糊控制系统

第三章、模糊控制系统
0.1 0.6 0.7 0.2 V= 例： % 3 + 4 + 5 + 6
精确量(V0)
∴V0 = 5
当论域V中，其最大隶属度函数对应的输出值多于一个时， 简单取最大隶属度输出的平均即可：
即：当有（v1） µ 2）= L =µc (vJ ) 最大时 µ = （v
1 J 取v0 = ∑ v j J j =1
U 1 , U 2 , L ,U n ：输出论域上模糊子集
总的模糊关系： R( 其中：
e , de , u ) = U Ri
n
当ki 取µv (vi )时
重心法
模糊化计算的其它方法：左取大、右取大等。
第二节：模糊控制系统的设计 一、模糊控制器的结构设计 模糊控制器的结构设计包括：输入输出变量选择、模糊化 算法、模糊推理规则和精确化计算方法。 一维模糊控制器 被控对象 输入输出 (按模糊控制器输入变量个数) 变量 多输入多输出 单输入单输出 二维模糊控制器 多维模糊控制器
例：x分成三档(NB、ZE、PB)； y y分成两档(NB、PB)； 模糊分区形式：
PB NB 0 NB ZE
R1
R2 R4
R3
PB 24
问：在此分档情况下，最大规则数为多少？
x
2 规则库 用一系列模糊条件描述的模糊控制规则就构成模糊控制规则库。 建立 规则库 选择输入变量和输出变量 建立规则（完备性、交叉性、一致性）
完备性：对于任意给定的输入均有相应的控制规则起作用。 交叉性：控制器的输出值总由数条规则来决定。 一致性：规则中不存在相互矛盾的规则。
模糊控制规则建立方法 1）专家经验法： 通过对专家控制经验的咨询形成控制规则库。 实质：通过语言条件语句来模拟人类的控制行为。

自动控制原理第三章课后习题 答案(最新)要点

自动控制原理第三章课后习题 答案(最新)要点

3-1（1） )(2)(2.0t r t c= （2） )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。

已知全部初始条件为零。

解：（1） 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应：s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c（2）)()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应：124.004.01)(2++=s s s C t e t g t 4s i n 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ，用其测量容器内的水温，1min 才能显示出该温度的98%的数值。

若加热容器使水温按10ºC/min 的速度匀速上升，问温度计的稳态指示误差有多大？解法一 依题意，温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知：o o T c 98)4(=，因此有 min 14=T ，得出 min 25.0=T 。

视温度计为单位反馈系统，则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法，当t t r ⋅=10)( 时，C T Ke ss ︒===5.21010。

解法二 依题意，系统误差定义为 )()()(t c t r t e -=，应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T s Ts Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 23-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ％、峰值时间ｔp 和调节时间ｔs 。

自动控制原理第三章课后习题答案解析（最新）

自动控制原理第三章课后习题答案解析（最新）

完美WORD 格式格式专业整理专业整理 知识分享知识分享3-1（1） )(2)(2.0t r t c =（2） )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。

已知全部初始条件为零。

解：（1） 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==F 单位脉冲响应：s s C /10)(= 010)(³=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(³=t tt c（2）)()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s f单位脉冲响应：124.004.01)(2++=s s s C t et g t4sin 325)(3-=单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s C t et et c tt4sin 434cos 1)(33----=3-2温度计的传递函数为11+Ts ，用其测量容器内的水温，1min 才能显示出该温度的98%的数值。

若加热容器使水温按10ºC/min 的速度匀速上升，问温度计的稳态指示误差有多大？解法一 依题意，温度计闭环传递函数11)(+=F Ts s 由一阶系统阶跃响应特性可知：o o T c 98)4(=，因此有 min 14=T ，得出 min 25.0=T 。

视温度计为单位反馈系统，则开环传递函数为Ts s s s G 1)(1)()(=F -F =îíì==11vT K用静态误差系数法，当t t r ×=10)( 时，C T Ke ss°===5.21010。

模糊控制系统

模糊控制系统

二、模糊控制器设计

一般有：

单变量模糊控制器

一维模糊控制器 二维模糊控制器 多维模糊控制器

多变量模糊控制器
二、模糊控制器设计


单输入-单输出模糊控制器
一维模糊控制器：输入输出变量只有一个。假设输入 变量为e、输出控制量为u，可以用以下规则表示：
R1： R2： ： Rn: 如果 否则如果 否则如果 e 是 E1， 则 u 是 U1； e 是 E2， 则 u 是 U2； e 是 En， 则 u 是 Un。


Yn+1=PB Yn+1=PS Yn+1=ZE Yn+1=ZE Yn+1=NS Yn+1=NB

一、模糊控制系统的组成


这个控制对象而言 比如：当Yn-1=ZE 且Yn=PS，这时要求Yn+1=ZE。 参照对象规则3，可以导出此时的控制U应该满足NS为 佳，即： 如果 Yn-1=ZE, 且Yn=PS 那么， U=PS 其目的是使输出Y趋向零， 这就是一条控制规则。

2、Larsen模糊推理算法
一、模糊控制系统的组成
3、Takagi-Sugeno模糊推理算法 IF x is Ai and y is Bi then z=fi (x,y) 推理输出为：
4、Tsukamoto模糊推理算法
这是一种当Ai、Bi、Ci的隶属度函数为单调函数时的 特例。对于该方法，首先根据第1条规则求出α 1=C1(z1) 而求得z1；再根据α 2=C2(z2)求得z2，准确的输出量可表 示为z1和z2的加权组合，即


规则库的建立 用一系列模糊条件描述的模糊控制规则就构成 模糊控制规则库 模糊控制规则相关的主要有：

模糊控制(matlab)(4)

模糊控制(matlab)(4)

解模糊后，还要经过尺度变换，求出实际输出。
y y u u man min max min y k ( u ) u 1 2 2
u1 ：为精确量； ymax，ymin：为控制量的变化范围；4～20mA 或 1～5V。 y：为计算机输出的控制量； ku：比例因子。
小结：
模糊控制系统的基本构成以及模糊控制器各部分的功能。 模糊化 知识库 决策逻辑
1）确定输入量 2）对输入量进行尺度变换，使其在各自的论域范围。 3）对输入量进行模糊处理，用相应的模糊集合表示。 1、最大隶属度函数法 反模糊化 作业： P66 2、加权平均法（重心法） 3、取中位数法 3-1 3-2
第二节 模糊控制系统的设计
模糊逻辑控制器的工作过程：
每采集一组数（data）(ei，dei)，经模糊化 （Fuzzy）→ E，DE→ Fuzzy推理（inference）合成运算得Ui →精确化（defuzzification） 得ui →尺度变换得yi 。 上述所有工作为在线(on-line)运算 速度慢，实时性差 能否先(off-line)制出表格数据（模糊查询表）looking up table 在线时，只要有一组(ei，dei)，即可从表中查出u。
0 . 3 0 . 7 1 0 . 7 0 . 3 PM 2 3 4 5 6
这样就将一个精确数转变成了模糊数。
二、模糊控制规则
有四种方法：专家经验法、观察法、基于模糊模型、自组织法 专家经验法：通过对专家控制经验的咨询形成控制规则库。 采用“if-then”规则语言来表达经验。
规则库：用语言值表示的控制规则。反映控制专家的经验 和知识。
▲模糊化
▲决策逻辑
模糊控制系统的核心，对模糊量由给定的规则进 行模糊推理 ▲反模糊化 将模糊输出量转化为精确量 1）将模糊量变换成精确量 2）精确量经尺度变换成实际的控制量。

智能控制技术-第三章

智能控制技术-第三章
量化的特点：1、测量变量的量化会带来误 差；2、同时减少了系统对小的扰动的敏感 性。
一个简单的求中间隶属度值的求取。
在模糊控制系统中，变量的量化给出了控 制器计算的简化和控制值的平滑之间的一 个折衷，为了消除大的误差，在量化级之 间的一些插值运算是必要的。
一个简单的方法是引入一个权系数w(.)：对 于一个连续的测量值可以通过相邻两个离 散值的加权运算得到模糊度的值。
模糊控制器结构指的是输入输出变 量、模糊化算法、模糊推理规则和精确 化计算方法。
控制器的设计第一步首先确定控制器的输 入输出变量。
1、控制器输入输出变量
主要讲单输入-单输出模糊控制结构。
单输入-单输出模糊控制结构指的是系 统控制量只有一个，系统输出量只有一个。
单输入-单输出模糊控制结构又分一维模糊 控制器、二维模糊控制器和多维模糊控制 器。
m
vik i
v0
i1 m
ki
i1
ki视情况而定。如果，那么加权平均法就变为重 心法。
面积重心法对于不同的隶属度函数形状会
有不同的推理输出结果。最大隶属度函数 法对隶属度函数的形状要求不高。
第二节 模糊控制系统设计
一、模糊控制器的结构设计 在设计模糊控制器前，首先根据被
控对象的具体情况来确定模糊控制器的 结构。
设被控对象用以下三个控制规律描述：
规律1： 如果Yn=PM 且Un=PM 那么Yn+1=PB； 规律2： 如果Yn=PS 且Un=NS 那么Yn+1=ZE； 规律3： 如果Yn=NS 且Un=PS 那么Yn+1=ZE； 规律4： 如果Yn=NM 且Un=NM 那么Yn+1=NB； 其中Y是输出，U是控制，n是离散时间。
例如：两个输出变量A、B下的一个模糊空 间划分示意图。

第三章模糊控制(习题)

第三章模糊控制(习题)

如果衣服不很脏,那么洗涤时间应该为： 如果衣服不很脏,那么洗涤时间应该为：
1 1 0.91 0.5 0.5 B = + + + + 1 2 3 4 5
'
1 − 1 1 − 0.25 1 − 0.01 1 − 0 1 − 0 A = + + + + 1 2 3 4 5 0 0.75 0.99 1 1 = + + + + 1 2 3 4 5
'
B ' = A' R 0 0.3 0.8 1 0 0.5 0.5 0.5 0.5 0.5 = [0 0.75 0.99 1 1]0.9 0.9 0.9 0.36 0.1 1 0.91 0.36 0#39; R 0 0 .3 0 .8 1 0 0.5 0.5 0.5 0.5 0.5 = [0 0.75 0.99 1 1]0.9 0.9 0.9 0.36 0.1 1 0.91 0.36 0 1 1 1 0.91 0.36 0 = [1 1 0.91 0.5 0.5]
解：由于“很”是集中化算子。因此 由于“ 是集中化算子。 C=【不很长】=1- 很长】=1C=【不很长】=1-【很长】=1-【长】2 即：
1 1 0.91 0.36 0 C= + + + + 1 2 3 4 5
“如果衣服脏,那么洗涤时间应长,否则洗涤时 如果衣服脏,那么洗涤时间应长, 间不必很长”的模糊推理关系可表示为： 间不必很长”的模糊推理关系可表示为：
R = ( A × B) ∪ ( A × C )
C
1 0 0 .5 0 A × B = 0.1[0 0 0.3 0.8 1] = 0 0 0 0 0

《控制工程基础》第三章习题解题过程和参考答案 (2)

《控制工程基础》第三章习题解题过程和参考答案 (2)
，其中
以下求各指标：
由 ，其中 ，
故：
（也可查图3-16而得）
（2）由式（3-46），单位脉冲响应：
代入各参数：
3-7某二阶系统的结构框图如题3-7图所示，试画出 ， 和 时的单位阶跃响应曲线。
题3-7图控制系统框图
解：
系统闭环传递函数为：
系统的参数为： 。
(1)
此时， ，为欠阻尼，可求得：
(2)
此时，由 ，可知 ，仍为欠阻尼。由于阻尼比增大，因此超调量减小。
而调节时间 ，所以：
由此得联立方程：
解得：
3-10典型二阶系统的单位阶跃响应为
试求系统的最大超调 、峰值时间 、调节时间 。
解：
由式（3-46），典型二阶系统的单位阶跃响应表达式为：
，其中
将上式与给定响应式比较，可计算系统的二个参数 。
由 ，求得阻尼比：
或者也可这样求：
由 ，求得阻尼比：
由 ，得
二个参数求出后，求各指标就很方便了。
综合有：
开环增益K在上述范围内，则闭环系统不但稳定，且所有闭环极点的实部均小于-1。
3-19已知单位反馈系统的开环传递函数为
试根据下述条件确定 的取值范围。
（1）使闭环系统稳定；
（2）当 时，其稳态误差 。
解：
（1）关于闭环稳定性
求解本题当然可以用普通方法，如在习题3-12至3-18中所应用的。
但我们换一种思路，设计利用一些规律性的结果。在习题3-17中已经求出，对于单位反馈系统若具有下列形式的开环传递函数：
①特征方程的系数均大于0且无缺项。
②列劳斯表如下
1
10
21
10
10
结论：劳斯表第—列均为正值，系统闭环稳定。

(完整word版)智能控制技术(第三章)答案

(完整word版)智能控制技术(第三章)答案

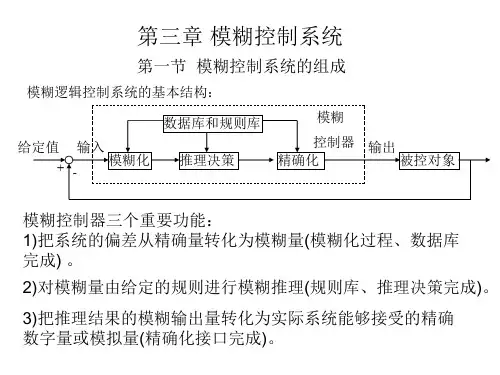
3—1 模糊逻辑控制器由哪几部分组成？各完成什么功能？答：模糊控制系统的主要部件是模糊化过程、知识库(数据库和规则库）、推理决策和精确化计算.1、模糊化过程 模糊化过程主要完成：测量输入变量的值，并将数字表示形式的输入量转化为通常用语言值表示的某一限定码的序数.2、知识库 知识库包括数据库和规则库。

1）、数据库 数据库提供必要的定义，包含了语言控制规则论域的离散化、量化和正规化以及输入空间的分区、隶属度函数的定义等。

2）、规则库 规则库根据控制目的和控制策略给出了一套由语言变量描述的并由专家或自学习产生的控制规则的集合。

它包括：过程状态输入变量和控制输出变量的选择，模糊控制系统的建立。

3、推理决策逻辑 推理决策逻辑是利用知识库的信息模拟人类的推理决策过程，给出适合的控制量。

（它是模糊控制的核心）.4、精确化过程 在推理得到的模糊集合中取一个能最佳代表这个模糊推理结果可能性的精确值的过程称为精确化过程。

｛模糊控制器采用数字计算机。

它具有三个重要功能:1） 把系统的偏差从数字量转化为模糊量(模糊化过程、数据库两块）； 2） 对模糊量由给定的规则进行模糊推理（规则库、推理决策完成）;3）把推理结果的模糊输出量转化为实际系统能够接受的精确数字量或模拟量（精确化接口）。

3—2 模糊逻辑控制器常规设计的步骤怎样？应该注意哪些问题？ 答：常规设计方法设计步骤如下：1、 确定模糊控制器的输入、输出变量2、 确定各输入、输出变量的变化范围、量化等级和量化因子3、 在各输入和输出语言变量的量化域内定义模糊子集。

4、 模糊控制规则的确定5、 求模糊控制表3-3 已知由极大极小推理法得到输出模糊集为：0.30.810.50.112345C =++++-----。

试用重心法计算出此推理结果的精确值z. 重心法重心法 是取模糊隶属度函数的曲线与横坐标围城面积的重心为模糊推理最终输出值。

连续：0()()v VvVv v dvv v dvμμ=⎰⎰ 离散：101()()mkvkk mvkk v v v v μμ===∑∑采用离散重心法：101()()0.3(1)0.8(2)1(3)0.5(4)0.1(5)0.30.810.50.10.3(1)0.8(2)1(3)0.5(4)0.1(5)2.7=-2.7407mkvkk mvkk v v v v μμ===⨯-+⨯-+⨯-+⨯-+⨯-=++++⨯-+⨯-+⨯-+⨯-+⨯-=∑∑ 3—5 设在论域(){42024}e =--误差，，，，和控制电压{024,6,8}u =，，上定义的模糊子集的隶属度函数分别如图3—21、图3—22所示。

模糊控制第三章解析答案课堂

模糊控制第三章解析答案课堂
12
? 模糊集合一般由论域和隶属函数构成。因此， 模糊化的实质就是求取相应概念对应数值域 的模糊集合隶属函数。
? 为了便于工程实现，通常把输入变量范围人 为地定义成离散的若干级，所定义级数的多 少取决于所需输入量的分辨率。定义输入量 的隶属函数可选用吊钟型、梯形和三角形。
? 理论上吊钟型最为理想，但计算复杂。实践 证明：用三角形和梯形函数其性能并没有十 分明显的差别。
36
? 用于描述人们控制经验的基本语句结构有 三种形式，它们分别反映了三种基本的推 理。这三种基本结构和形式如下：
? 这种推理是一种最简单的蕴涵关系，在语
言表达时表示为“如果 A，那么B ”，即
有：if A then B
~
~
37
② ( A? B) ? ( AC ? C)结构
~
~
~
~
? 这种推理较之前一种复杂，这种蕴涵关系在 用语言表达时叙述为“如果 A，那么B；否则 C ”，即有：
38
? 这种推理的前件有两个，这种蕴涵关系在 用语言表述时为“如果 A而且 B那么C ”， 即有：
? 模糊控制规则应具备如下特性： 1. 完备性 ? 通过设计经验和工程知识，使模糊控制规
则具有完备性。所谓完备性，是指对于任 意给定的输入，均有相应的控制作用。要
39
求控制规则的完备性是保证系统能被控制的 必要条件之一。 2. 一致性 ? 控制规则的一致性是指控制规则中不存在 相互矛盾的规则。如果两条规则的条件部 分相同，但结论部分相差很大，则称两条 规则相互矛盾。 3. 交互作用性 ? 如果控制器的输出值总由数条控制规则来 决定，说明控制规则之间是相互联系、相
方法，其基本思想是：首先定义一基础概念 （Genic concept）及其相应的隶属函数， 然后通过语义算子的作用，产生具有相关语 义的新概念及其隶属函数。 ? 常用的语义算子主要有：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
20
4. 训练法 ? 训练算法的原理：根据不同的测量结构和应
用场合，由专家选定具体的论域上表述概念 的个数，然后通过经验算法自动生成相应概 念的隶属函数特性曲线，最后，专家依据经 验对其中的一个或几个概念进行训练，以适 合不同的测量要求。
21
? 其基本思想：对于训练样本 (包括论域内若干 个测量点上的状态数据以及相应隶属于人类 经验的被测量，用自然语言符号描述的状态 符号)，在当前概念模式下，根据最大隶属度 准则判定，若数据状态与概念状态相一致， 则训练结束；若不相符，则将相应概念隶属 函数曲线的修正率加以改变，以实现符合专 家经验的被测量数据状态与符号状态的一致。
13
? 目前在实际中常用的处理方法是 Mamdani提 出的方法。就是把偏差 e的变化范围设定为 [6，+6]区间内的连续变化量，并使之离散化， 构成含13个整数元素的离散集合：
{-6，-5，-4，-3，-2，-1，0，+1，+2， +3，+4，+5，+6}
? 如果是非对称型的，也可用1～13取代-6～ +6。
方法，其基本思想是：首先定义一基础概念 （Genic concept）及其相应的隶属函数， 然后通过语义算子的作用，产生具有相关语 义的新概念及其隶属函数。 ? 常用的语义算子主要有：
18
19
? 式中，C为基础概念，CI为是加了一定语义关系 作用后的新概念，只要知道基础概念“C”的隶 属函数，通过上述语义算子的作用，可以自动生 成相关语义概念的隶属函数。
12
? 模糊集合一般由论域和隶属函数构成。因此， 模糊化的实质就是求取相应概念对应数值域 的模糊集合隶属函数。
? 为了便于工程实现，通常把输入变量范围人 为地定义成离散的若干级，所定义级数的多 少取决于所需输入量的分辨率。定义输入量 的隶属函数可选用吊钟型、梯形和三角形。
? 理论上吊钟型最为理想，但计算复杂。实践 证明：用三角形和梯形函数其性能并没有十 分明显的差别。
模糊控制技术
第3章 模糊控制技术基础
1
第3章 模糊控制技术基础
3.1 模糊控制基本原理
3.1.1 模糊控制的引入及实现 3.1.2 模糊控制过程 1. 模糊控制基本思想 ? 一般选偏差信号e作为模糊控制器的一个输
入量，把偏差信号e的精确量进行模糊化变 成模糊量，偏差e的模糊量可以用相应的模 糊语言表示，得到了偏差e的模糊语言集合
温控制时，控制系统的工作原理及工作过程可简述 如下：
5
1) 确定模糊控制器的输入变量和输出变量 ? 在此将炉温800 ℃作为给定值t0，测量得到
的炉温记为t(K)，则误差 e(K)=t0-t(K) (3.2)
作为模糊控制器的输入变量。 2) 输入变量及输出变量的模糊语言描述 ? 设描述输入变量及输出变量的语言值的模糊
? 设执行控制量 u的论域为 Y，并同X一样也把 控制量的大小划分为 7个等级 (也可以多于 7 个)，即：
7
Y＝{-3，-2，-1，0，+1，+2，+3} 3) 模糊控制规则的语言描述 ? 根据手动控制策略，模糊控制规则可归纳如
下：
8
4) 模糊控制规则的矩阵形式 ? 模糊控制规则实际上是一组多重条件语句，
11
3.2 模糊化方法
? 把测量值（数值量）转换为主观量值（模糊量） 的过程称为模糊化，也即把物理量的精确值转 换成语言变量值。由此，它可以定义为在确定 的输入论域中将所观测的输入空间转换为模糊 集的映射，以便实现模糊控制算法。
? 模糊化的基本思想是定义一个模糊语言映射作 为从数值域至语言域（符号域）的模糊关系， 从而在数值测量的基础上，将数值域中的数值 信号映射到语言域上，为实现模糊推理奠定基 础。
2. 非线性划分法 ? 这种方法主要应用于采用了非线性敏感元件
(如热敏电阻等)的模糊控制系统的模糊化。
16
图3.3 模糊化的非线性划分法
17
3. 语义关系生成法 ? 模糊量的语义值(如“热”与“很热”之间的
语义关系)是根据相应的数值关系来确定的。 ? E.Benoit等人提出了基于语义关系的模糊化
照模糊推理合成规则推理计算输出控制量 (模 糊量)； ④ 由上述得到的控制量 (模糊量 )计算精确的输 出控制量，并作用于执行机构。
4
2. 模糊控制系统的工作原理
? 该温度控制系统基本控制规则可以用语言描述为： ① 若炉温低于800 ℃，则升压，低得越多，升压越高； ② 若炉温高于800 ℃，则降压，高得越多，降压越低； ③ 若炉温等于800 ℃，则保持电压不变。 ? 对于上述温度控制系统，采用模糊控制方法进行炉
它可以表示为从误差论域X到控制量论域Y的 模糊关系R。 5) 模糊决策
9
? 模糊控制器的控制作用取决于控制量，而控 制量通过式(3.1)进行计算，即
? 控制量 实际上等于误差的模糊向量 和 模糊关系 的合成。
6) 控制量的模糊量转化为精确量 ? 上面求得的控制量 为一模糊向量，设为：
10
? 对于控制量的模糊子集按照最大隶属度原则， 应选取控制量为“ -1”级。即当误差为 PS时， 控制量为NS，为“-1”级。具体地说，当炉 温偏高时，应降低一点电压。
14
? 如果精确量 x的实际变化范围为 [ a，b]，将 [ a，b]区间的精确变量转换为[-6 ，+6]区间 变化的变量y，采用如下公式：
(3.3)
1. 线性划分法 ? 这是最为简单的一种方法，根据研究对象的
具体情况，选定相应的自然语言描述符号后， 将研究对象的论域均匀划分。
15
图3.2 模糊化的线性划分法
2
的一个子集。再由模糊子集和模糊控制规则 (模糊关系)根据模糊推理的合成规则进行模 糊决策，得到模糊控制量为：
(3.1)
图3.1 模糊控制原理框图
3
? 模糊控制过程可概括为下述4个步骤：
① 根据本次采样得到的系统的输出值，计算所 选择系统的输入变量；
② 将输入变量的精确值变为模糊量； ③ 根据输入变量 (模糊量 )及模糊控制规则，按
子集为： {负大，负小，零，正小，正大}
6
? 采用如下简记形式： NB＝负大，NS＝负小，Z＝零，PS＝正小， PB＝正大。
? 设误差 e的论域为 X，并将误差大小量化为 7 个等级，分别表示为 -3， -2， -1，0，+1， +2，+3，则有： X＝{-3，-2， -1，0，+1，+2，+3}