芜湖市张镇中学新人教版八年级下复习试卷(四)及答案

八年级数学（答题时间120分钟，满分150分）温馨提示：本卷共八大题，计23小题，满分150分，考试时间120分钟。

一、选择题（本题共10小题，每小题4分，共40分）1．下列各式中，计算正确的是（）．A．B．C．D．2．下列各式中属于最简二次根式的是（）．A．B．C．D．3．估计的值应在（）．A．4和5之间B．5和6之间C．6和7之间D．7和8之间4．如图，一架靠墙摆放的梯子长5米，底端离墙脚的距离为3米，则梯子顶端离地面的距离为（）．A．5米B．4米C．3米D．2米5．勾股定理从被发现到现在已有五千年的历史，人们对这个定理的证明找到了很多方法．我国数学家刘徽利用“出入相补”原理（一个平面图形从一处移到另一处，面积不变；又若图形分成若干块，则各部分的面积和等于原来图形的面积）也证明了勾股定理，如图所示，这种证法体现的数学思想是（）．A．数形结合思想B．分类思想C．函数思想D．归纳思想6．在一个三角形地块中分出一块（阴影部分）种植花草，尺寸如图，则PQ的长度是（）．A．1m B．2m C．3m D．4m7．如图，在四边形ABCD中，对角线AC和BD交于点O，下列条件能判定四边形ABCD为平行四边形的是（）．A．，B．，C．，D．，8．如图，在“V”字形图形中，，，，，，若要求出这个图形的周长，则需添加的一个条件是（）．A．BE的长B．DE的长C．AB的长D．AB与BE的和9．如图所示，有一块直角三角形纸片，，，，将斜边AB翻折，使得点B 恰好落在直角边AC的延长线上的点E处，折痕为AD，则BD的长为（）．A．2cm B．C．D．5cm10．如图，在中，，，，D为AB边上一动点（不与点A重合），为等边三角形，过点D作DE的垂线，F为垂线上任意一点，连接EF，G为EF的中点，连接BG、CG，则的最小值是（）．A．B．C．D．10二、填空题（本大题共4小题，每小题5分，满分20分）11．请写出一组勾股数______．12．已知：，，则=______．13．我国南宋著名的数学家秦九韶，曾提出利用三角形的三边求面积的“秦九韶公式”（三斜求积术）：若一个三角形的三边长分别为a，b，c，则这个三角形的面积．若一个三角形的三边长a，b，c分别为，，，则这个三角形的面积为______．14．如图，C为平行四边形ABDG外一点，连接BC，DC，分别交边AG于点F，E，使，，，若，，则（1）CE的长为______；（2）AB的长为______．三、（本大题共2小题，每小题8分，满分16分）15．已知实数a在数轴上的对应点位置如图，化简．16．在平面直角坐标系中，按要求完成下列各题：（1）描出下列各点，，，将这些点依次用线段连接，并写出点C关于y轴对称的点的坐标为______；（2）在y轴上有点D，则的最小值为______；（3）证明：是直角三角形．四、（本大题共2小题，每小题8分，满分16分）17．请观察式子：，．仿照上面的方法解决下列问题：（1）化简：①=______；②=______；③=______．（2）把中根号外的因式移到根号内，化简的结果是______．18．如图，在平行四边形ABCD中，∠ABC、∠BCD的角平分线交于边AB上一点E，且．（1）求证：；（2）求线段CE的长．五、（本大题共2小题，每小题10分，满分20分）19．如图，在平行四边形ABCD中，点E在BA的延长线上，点F在DC的延长线上，连接BF、DE、EF，EF交AD于点G，交BC于点H，．求证：四边形EBFD是平行四边形．20．定义：若一个三角形一边上的中线、高线与这条边均有交点，则这两个交点之间的距离称为这条边上的“中高距”．如图，中，AD为BC边上的中线，AE为BC边上的高线，则DE的长称为BC边上的“中高距”．（1）若BC边上的“中高距”为0，则的形状是______三角形；（2）若∠B=30°，∠C=45°，AB=4，求BC边上的“中高距”．六、（本题满分12分）21．高空抛物是一种不文明的危险行为，据研究，从高处坠落的物品，其下落的时间t（s）和高度h（m）近似满足公式（不考虑空气阻力的影响）．（1）求物体从40m的高空落到地面的时间；（2）已知从高空坠落的物体所带能量（单位：J）E=10×物体质量（kg）×高度（m），某质量为0.05kg的鸡蛋经过6s落在地上，这个鸡蛋在下落过程中所带能量有多大？你能得到什么启示？（注：65J的能量就可以杀伤无防护的人体）七、（本题满分12分）22．如图，在中，，延长AC到点D，在BC边上取一点H，连接HD，设E和F 分别是AB和HD的中点，连接EF，若EF恰好与BC垂直，垂足为K．已知，试求EF的长．八、（本题满分14分）23．在和中，点D在BC边上，，．（1）若．①如图1，当时，连接EC，证明：；②如图2，当时，过点A作DE的垂线，交BC边于点F，若，，求线段CF的长；（2）如图3，已知，作∠DAE的角平分线交BC边于点H，若，，当时，请直接写出线段BD的长．八年级数学参考答案一、选择题（本大题共10小题，每小题4分，共40分）题号12345678910答案C D D B A B B C B A第10题解析取的中点，连接，则三点共线，进而得到点在直线上运动，作点关于的对称点，连接，得到，进而得到三点共线时，的值最小，作，∵，，∴．即的最小值是．二、填空题（本大题共4小题，每小题5分，满分20分）11．3，4，5（不唯一）；12．4；13．；14．（1）2（2分）；（2）（3分）三、（本大题共2小题，每小题8分，满分16分）15．解：由图知：，，．（4分）原式．（8分）16．（1）解：如下左图（2分）点关于轴对称的点的坐标为（4分）（2）解：如上右图，点D即为所求（5分）此时．（6分）（3）解：，，，∴，∴是直角三角形．（8分）四、（本大题共2小题，每小题8分，满分16分）17．（1）解：①，②，③．（6分）（2）．（8分）（注：只写最后结果不扣分）18．（1）证明：四边形是平行四边形，，，，，，、的角平分线交于边上一点，，，．．即．（4分）（2）解：∵，，，，，，由（1）可知．（8分）五、（本大题共2小题，每小题10分，满分20分）19．证明：在平行四边形ABCD中，，，∴，∵∴，即．在和中，∴．（8分）∴，又，∴四边形是平行四边形．（10分）20．解：（1）等腰（4分）（2）在中，，，∴，∴．在中，，，∴，∴．（8分）∵点D为的中点，∴，∴．（10分）六、（本题满分12分）21．解：（1）∵，，∴．（4分）（2）∵，，∴，∴（8分）∴，∴．（10分）严禁高空抛物．（12分）七、（本题满分12分）22．解：如图，分别取AC，CD的中点P、Q，连接PE，FQ，作垂足为M．（2分）∵点、F分别为、的中点，∴分别是、的中位线，∴，．∴，．∵，∴．∵P、Q分别为的中点，∴．∴．∴．∴．（10分）∵，，∴，∵，∴，又∵，∴四边形为平行四边形，∴．（12分）八、（本题满分14分）23．（1）①证明：，，在和中，，．（2分），，，，．（4分）②解：如图2，连接，作交的延长线于点G，，，，，、都是等边三角形，在和中，，．（6分），，，，，，，，，，是的垂直平分线，．（8分）设，则，在中，，即，解得，即线段的长为．（10分）线段的长为5.6．（14分）具体过程如下：如图3，延长至N，使，连接，交的延长线于点M，连接，作于P，，．，，，，在和中，，，，，，，．中，，，，即，．，，．，是的角平分线，，是线段的垂直平分线，．设，则，，在中，，即，解得，．（说明：以上解答方法不唯一，只要合理，均要赋分）。

芜湖市张镇中学新人教版八年级下复习试卷及答案Document number：PBGCG-0857-BTDO-0089-PTT1998芜湖市张镇中学八年级数学下学期复习（一）姓名 班级 学号 得分一、选择题（每小题３分，共2４分）1.在式子,1a πxy 2，4332c b a ，x +65，87y x +，9x+y 10中，分式的个数是（ ） （A ） 2 ( B ) 3 ( C ) 4 ( D ) 52．如果把分式yx x +10中的x 、y 都扩大10倍，则分式的值（ ） （A ）扩大100倍 （B ）扩大10倍 （C ）不变 （D ）缩小到原来的1013.下列等式成立的是（ ）( A )()23- ＝-9 ( B )()23--＝91 ( C )()212a ＝14a ( D )＝×710-4.某厂去年的产值是m 万元，今年的产值是n 万元（m ﹤n ）,则今年的产值比去年的产值增加的百分比是（ ） ( A )n n m -×100％（ B ）m m n -×100％（ C ）（mn +1）×100％ （ D ）m m n 10-×100％ 5.已知总电阻R 与1R 、2R 关系式是R 1＝11R +21R ，若R ＝6欧姆，1R ＝32R ，则1R 、2R 的值分别是（ ）（A ）R ＝45欧姆,R ＝15欧姆,( B )R ＝24欧姆, R ＝8欧姆( C ) 1R ＝29欧姆, 2R ＝23欧姆,( D ) 1R ＝32欧姆, 2R ＝92欧姆 6、若分式6922-+-x x x 的值为0，则x 的值为（ ） （Ａ）±３ （Ｂ）－３或２ （ C ）３ （Ｄ）－３７、若关于ｘ的分式方程42-x ＝３＋xm -4有增根，则ｍ的值是（ ） （Ａ）－２ （Ｂ）２ （３）４ （Ｄ）－４８、计算a －ｂ＋ba b +22 （ ） （Ａ）b a b b a ++-22 （Ｂ）ａ＋ｂ （Ｃ）ba b a ++22 （Ｄ）ａ－ｂ二、填空题（每小题３分，共１８分）９、ｘ、ｙ满足关系 时，分式yx y x +-无意义 １０、22222n m mn n m +＝mn 2 １１、2361a -÷aa 612-的结果是 １２、已知a 1－b 1＝５，则bab a b ab a ---+2232的值是１３、我国是一个水资源贫乏的国家，每一个公民都应自觉养成节约用水的意识的习惯。

新人教版八年级下学期数学复习试卷八年级下学期数学复习试卷已经新鲜出炉，想把数学考好的同学请看下文。

下面是店铺分享给大家的八年级下学期数学复习试卷，希望大家喜欢!八年级下学期数学复习试卷一一、选择题：1. 如果代数式有意义，那么x的取值范围是( )A.x≥0B.x≠1C.x>0D.x≥0且x≠12. 下列各组数中，以a、b、c为边的三角形不是直角三角形的是( )A BC D3.如图，直线上有三个正方形，若的面积分别为5和11，则的面积为( )A.4B.6C. 16D.554. 如图，在平行四边形ABCD中，下列结论中错误的是( )A. ∠1=∠2B. ∠BAD=∠BCDC. AB=CDD. AC⊥BD5. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是边AD，AB的中点，EF交AC于点H，则的值为( )A. 1B.C.D.6. 的图象如图所示，当时，的取值范围是( )A. B. C. D.7. 体育课上，20人一组进行足球比赛，每人射点球5次，已知某一组的进球总数为49个，进球情况记录如下表，其中进2个球的有x 人，进3个球的有y人，若(x，y)恰好是两条直线的交点坐标，则这两条直线的解析式是进球数 0 1 2 3 4 5人数 1 5 x y 3 2A.y=x+9与y= x+B. y=-x+9与y= x+C. y=-x+9与y=- x+D. y=x+9与y=- x+8. 已知一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(0，﹣2)和点B(1，0)，则k= ，b=9.已知:ΔABC中,AB=4,AC=3,BC= ,则ΔABC的面积是( )A.6B.5C.1.5D.210. 如图，已知一条直线经过点A(0，2)、点B(1，0)，将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC，则直线CD 的函数解析式为.11.四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是( )A. AB∥DC，AD∥BCB. AB=DC，AD=BCC. AO=CO，BO=DOD. AB∥DC，AD=BC12.有一块直角三角形纸片，如图1所示，两直角边AC=6cm,BC=8cm ，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于( )A.2cmB.3cmC.4cmD.5cm二、填空题:13. 计算：14. 已知，则 =_________。

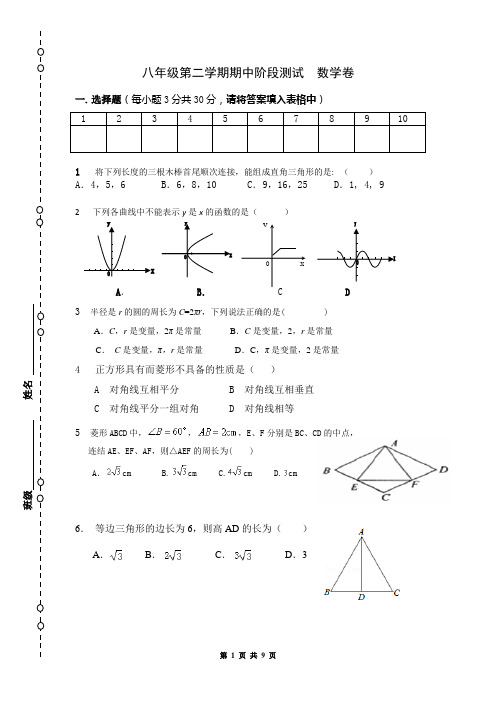
八年级第二学期期中阶段测试 数学卷2 下列各曲线中不能表示y 是x 的函数的是（ ）A ．B ．D3 半径是r 的圆的周长为C =2πr ，下列说法正确的是( )A ．C ，r 是变量，2π 是常量B ．C 是变量，2，r 是常量 C ． C 是变量，π，r 是常量D ．C ，π是变量，2是常量4 正方形具有而菱形不具备的性质是（ ）A 对角线互相平分B 对角线互相垂直C 对角线平分一组对角D 对角线相等 5 菱形ABCD 中，，，E 、F 分别是BC 、CD 的中点，连结AE 、EF 、AF ，则△AEF 的周长为( )A ．cm B.cm C.cm D.cm6． 等边三角形的边长为6，则高AD 的长为（ ）A ．B ．C ．D ．37 下列变量之间的关系不是函数关系的是（ ）班级 姓名A 长方形的宽一定，其长与面积B 正方形的周长与面积C 等腰三角形的底边与面积D 速度一定时行驶的路程与时间A 是一条直线B 过二、四象限C y 随x 的增大而增大D 过点1,k k ⎛⎫⎪⎝⎭9 △ABC 中，∠ABC=90°，AB=BC ，三角形的顶点在相互平行的三条直线l 1、l 2、l 3上，且相邻两平行线之间的距离均为1，则AC 的长是（ ）B10 中点，当点P 在BC 上从点B 向点C 移动，而点R 不动时，下列结论正确的是（ ）二. 填空题（每题3分共24分，将答案直接填在横线上） 11 如图，数轴上点A 所表示的数为a ，则a 的值12．有一个三角形, 其两边长为4和5, 要使三角形为直角三角形, 则第三边长为13 点E 是正方形ABCD 的边BC 延长线上的一点，且CE=AC ，若AE 交CD 于点F ， 则∠AFC = _______ °14 当m= 时，函数2(m 3)xm y -=-是正比例函数15 等腰三角形的周长是20，将底边长y 表示成腰长x 的函数．请写出函数解析式 ；腰长x 的取值范围 ．当x =7时，相对应的函数值y = 16 菱形两条对角线长分别为6cm , 8cm 则菱形周长为 ，面积为 17 如图，平行四边形ABCD 的对角线AC 、BD 交于点O ，DE ∥AC ，CE ∥BD ，要使四边形OCED 是矩形，则还须添加的条件是 （填一个即可）．18 网格中的小正方形边长均为1，△ABC 的三个顶点在格点上，则△ABC 中AB 边上的高为 _________ ．三 解答题（共46分，写出解题过程和证明过程，只写结果不得分） 19 (8分) 正方形ABCD 中，E 是BC 的中点，F 为CD 上一点，且，请证明△AEF 是直角三角形（提示：可以设正方形边长为4a ，∵E 是BC 的中点， ，∴CF=a ，DF=3a ，CE=BE=2a ．借助勾股定理和勾股逆定理解决）20 （6分） 一列快车、一列慢车同时从相距300km 的两地出发，相向而行．如图分别表示两车到目的地的距离s （km ）与行驶时间t （h ）的关系． （1）快车的速度为 km/h ，慢车的速度为 km/h ； （2）经过多久两车相遇？ ( 第一问直接写结果, 第二问需写过程 )21 （6分） 点（2，-4）在正比例函数 y kx = 的图像上 （1） 求k 的值（2） 若点（-0.5，m ）在函数y kx =的图象上，求m 的值 （3） 若123(0.5,)(2,)(1,y )A y B y C -都在此函数图像上，求123,,y y y 值22 （6分） D 、E 分别是不等边三角形ABC 的边AB 、AC 的中点．O 是△ABC所在平面上的动点，连接OB 、OC ，G 、F 分别是OB 、OC 的中点，顺次连接点D 、G 、F 、E ．（1）点O 在△ABC 的内部时，求证四边形DGFE 是平行四边形；（2）若四边形DGFE 是菱形，则OA 与BC 应满足怎样的数量关系？（第二问直接写出答案，不需说明理由．）23 (6分) △ABC 中，D 是BC 边上的一点，E 是AD 的中点，过点A 作BC 的平 行线交BE 的延长线于F ，且AF=DC ，连结CF ． （1）求证：D 是BC 的中点；（2）如果AB=AC ，先猜测四边形ADCF 的形状，再证明你的猜测．班级 姓名24 （6分）△ABC中，AB=AC，D是BC的中点，∠A＝90°，DE⊥AB，DF⊥AC，垂足分别为E、F．（1）证明BDE CDF∆≅∆（2）求证：四边形AEDF是正方形．25 如图1，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF 交正方形外角∠DCG的平分线CF于点F，（1）若取AB的中点M并连接EM，可通过全等证出AE=EF，请写出证明过程．（2）如图2，若点E是BC的延长线上（除C点外）的任意一点，其他条件不变，那么结论“AE=EF”是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由；（25题如地方不够可写在反面）（8分）第二学期期中阶段测试八年级数学参考答案填空11 如果两个实数的平方相等,那么这两个实数也相等 假 12 3 13 14 -3 15 2205106y x x =-+<<16 周长为 20cm 面积为 242cm 17 90oE ∠=(答案不唯一) 18 解答19 解：设正方形的边长为4a ， ∵E 是BC 的中点，，∴CF=a ，DF=3a ，CE=BE=2a ．由勾股定理得：AF 2=AD 2+DF 2=16a 2+9a 2=25a 2，EF 2=CE 2+CF 2=4a 2+a 2=5a 2，AE 2=AB 2+BE 2=16a 2+4a 2=20a 2，∴由勾股定理逆定理：AF 2=EF 2+AE 2， ∴△AEF 为直角三角形．20 解：（1）快车的速度为300÷=45km/h ，慢车的速度为300÷10=30km/h ，故答案为：45，30； （2）=4h答：经过4h 两车第一次相遇；21 （1） 把（2，-4）代入 y kx =中，得 24,2k k =-=- （2） 把点（-0.5，m ）代入2y x =-，得 2(0.5)1m =-⨯-=（3）123213A B C 220.512(2)4212,y x y y y y y y =-∴=-⨯=-=-⨯-==-⨯=-∴>> ，，三点都在上，22 （1）证明：∵D 、E 分别是AB 、AC 边的中点，∴DE∥BC，且DE=BC，同理，GF∥BC，且GF=BC，∴DE∥GF且DE=GF，∴四边形DEFG是平行四边形；（2）OA=BC时，平行四边形DEFG是菱形．23 （1）证明：∵四边形ABDE是平行四边形，∴AE∥BD，AE=BD，∵在△ABC中，AB=AC，D为BC中点，∴AD⊥BC，CD=BD，∴∠ADC=90°，CD=AE，CD∥AE，∴四边形ADCE是平行四边形，∴四边形ADCE是矩形；中，根据30°所对的直角边（2）若∠AOE=120°，则∠DEA=30°在Rt ADE是斜边的一半，所以DE=2DA=224 解：连接BD，在Rt△ABD中，BD2=AB2+AD2=32+42=52，在△CBD中，CD2=132，BC2=122，而122+52=132，即BC2+BD2=CD2，∴根据勾股定理的逆定理∠DBC=90°，S四边形ABCD=S△BAD+S△DBC=•AD•AB+DB•BC，=×4×3+×12×5=36．所以需费用36×100=3600（元）．25 解：（1）∵四边形ABCD是正方形∴AB=BC，∠B=∠BCD=∠DCG=90°，∵取AB的中点M，点E是边BC的中点，∴AM=EC=BE，∴∠BME=∠BEM=45°，∴∠AME=135°，∵CF平分∠DCG，∴∠DCF=∠FCG=45°，∴∠ECF=180°﹣∠FCG=135°，∴∠AME=∠ECF，∵∠AEF=90°，∴∠AEB+∠CEF=90°，又∠AEB+∠MAE=90°，∴∠MAE=∠CEF，即∴△AME≌△ECF（ASA），∴AE=EF，（2）AE=EF仍然成立，理由如下：在BA延长线上截取AP=CE，连接PE，则BP=BE，∵∠B=90°，BP=BE，∴∠P=45°，又∠FCE=45°，∴∠P=∠FCE，∵∠PAE=90°+∠DAE，∠CEF=90°+∠BEA，∵AD∥CB，∴∠DAE=∠BEA，∴∠PAE=∠CEF，∴在△APE与△ECF中，，∴△APE≌△ECF（ASA），∴AE=EF．。

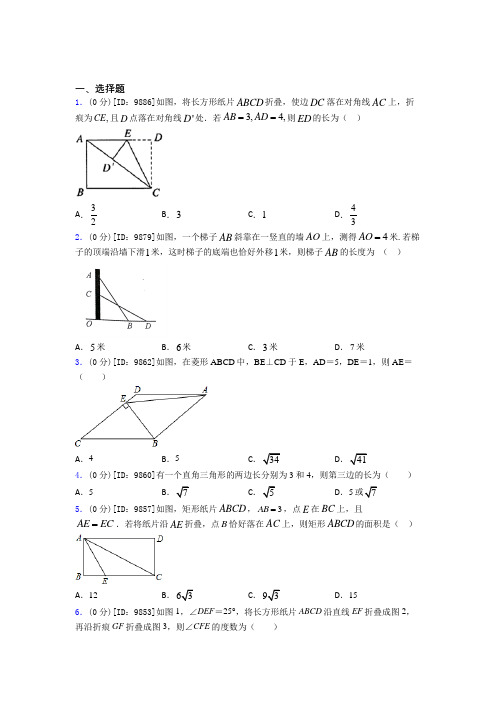
一、选择题1．(0分)[ID ：9886]如图，将长方形纸片ABCD 折叠，使边DC 落在对角线AC 上，折痕为,CE 且D 点落在对角线'D 处．若3,4,AB AD ==则ED 的长为（ ）A ．32B ．3C ．1D ．432．(0分)[ID ：9879]如图，一个梯子AB 斜靠在一竖直的墙AO 上，测得4AO =米.若梯子的顶端沿墙下滑1米，这时梯子的底端也恰好外移1米，则梯子AB 的长度为 （ ）A ．5米B ．6米C ．3米D ．7米 3．(0分)[ID ：9862]如图，在菱形ABCD 中，BE ⊥CD 于E ，AD ＝5，DE ＝1，则AE ＝（ ）A ．4B ．5C ．34D ．414．(0分)[ID ：9860]有一个直角三角形的两边长分别为3和4，则第三边的长为（ ） A ．5 B ．7 C ．5D ．5或7 5．(0分)[ID ：9857]如图，矩形纸片ABCD ，3AB =，点E 在BC 上，且AE EC =．若将纸片沿AE 折叠，点B 恰好落在AC 上，则矩形ABCD 的面积是（ ）A ．12B ．3C ．3D ．156．(0分)[ID ：9853]如图1，∠DEF ＝25°，将长方形纸片ABCD 沿直线EF 折叠成图2，再沿折痕GF 折叠成图3，则∠CFE 的度数为（ ）A．105°B．115°C．130°D．155°7．(0分)[ID：9852]在矩形ABCD中,AB=2,AD=4,E为CD的中点,连接AE交BC的延长线于F点,P为BC上一点,当∠PAE=∠DAE时,AP的长为()A．4B．174C．92D．58．(0分)[ID：9922]《九章算术》勾股章有一问题，其意思是：现有一竖立着的木柱，在木柱上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺，牵着绳索退行，在离木柱根部8尺处时绳索用尽，请问绳索有多长？若设绳索长度为x尺，根据题意，可列方程为（）A．82﹢x2 = (x﹣3)2B．82﹢(x+3)2= x2C．82﹢(x﹣3)2= x2D．x2﹢(x﹣3)2= 829．(0分)[ID：9921]已知直角三角形中30°角所对的直角边长是23cm，则另一条直角边的长是（）A．4cm B．43 cm C．6cm D．63 cm10．(0分)[ID：9833]下列各式中一定是二次根式的是( )A．23-B．2(0.3)-C．2-D．x11．(0分)[ID：9910]小明搬来一架 3.5 米长的木梯，准备把拉花挂在 2.8 米高的墙上，则梯脚与墙脚的距离为( )A．2.7 米B．2.5 米C．2.1 米D．1.5 米12．(0分)[ID：9898]下列结论中，矩形具有而菱形不一定具有的性质是（）A．内角和为360°B．对角线互相平分C．对角线相等D．对角线互相垂直13．(0分)[ID：9885]如图，ABC中，CD AB⊥于,D E是AC的中点．若6,5,AD DE==则CD的长等于（）A．5B．6C．8D．1014．(0分)[ID ：9869]如图，菱形ABCD 的对角线AC ，BD 相交于点O ，E ，F 分别是AB ，BC 边上的中点，连接EF.若3EF =，BD=4，则菱形ABCD 的周长为（ ）A ．4B ．46C ．47D ．28 15．(0分)[ID ：9915]菱形周长为40cm ，它的条对角线长12cm ， 则该菱形的面积为（ ）A ．24B ．48C ．96D ．36二、填空题16．(0分)[ID ：10028]使二次根式1x -有意义的x 的取值范围是 _____．17．(0分)[ID ：10010]若由你选择一个喜欢的数值m ，使一次函数()2y m x m =-+的图象经过第一、二、四象限，则m 的值可以是___________．18．(0分)[ID ：10008]已知菱形ABCD 的边长为5cm ，对角线AC ＝6cm ，则其面积为_____cm 2．19．(0分)[ID ：9999]化简()2-2的结果是________；3.14π-的相反数是________；364-的绝对值是_________.20．(0分)[ID ：9994]在Rt ABC ∆中，a ，b ，c 分别为A ∠，B ，C ∠的对边，90C ∠=︒，若:2:3a b =，52c =，则a 的长为_______．21．(0分)[ID ：9993]在函数y=1x x -中，自变量x 的取值范围是_____． 22．(0分)[ID ：9991]函数126x y x +=+的自变量x 的取值范围是_________． 23．(0分)[ID ：9978]在矩形ABCD 中，对角线AC 、BD 交于点O ，AB ＝1，∠AOB ＝60°，则AD ＝________．24．(0分)[ID ：9946]如图，在平行四边形ABCD 中，P 是CD 边上一点，且AP 和BP 分别平分∠DAB 和∠CBA ，若AD=5，AP=8，则△APB 的周长是 ．25．(0分)[ID ：9934]如图，已知▱ABCO 的顶点A 、C 分别在直线x ＝2和x ＝7上，O 是坐标原点，则对角线OB长的最小值为_____．三、解答题26．(0分)[ID：10126]某单位计划在新年期间组织员工到某地旅游，参加旅游的人数估计为10到25人，甲乙两家旅行社的服务质量相同，且报价都是每人200元，经过协商，甲旅行社表示可以给每位游客七五折优惠，乙旅行社表示可以先免去一位游客的旅游费用，然后给予其余游客八折优惠．若单位参加旅游的人数为x人，甲乙两家旅行社所需的费用分别为y1和y2．（1）写出y1，y2与x的函数关系式并在所给的坐标系中画出y1，y2的草图；（2）根据图像回答，该单位选择哪家旅行社所需的费用最少？27．(0分)[ID：10118]如图，已知一次函数y kx b=+的图象经过A(-2，-1)，B(1，3)两点，并且交x轴于点C，交y轴于点D．（1）求该一次函数的解析式；（2）△ABC的面积．28．(0分)[ID：10087]已知：在ABC中，1BC=．（1）若点D为AB的中点，且112CD AB==，求AC的长；（2）若30BAC ∠=︒，且12BC AB =，求AC 的长． 29．(0分)[ID ：10077]在社会主义新农村建设中，衢州某乡镇决定对A 、B 两村之间的公路进行改造，并有甲工程队从A 村向B 村方向修筑，乙工程队从B 村向A 村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务有甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y （米）与施工时间x （天）之间的函数图象，请根据图象所提供的信息解答下列问题：（1）乙工程队每天修公路多少米？（2）分别求甲、乙工程队修公路的长度y （米）与施工时间x （天）之间的函数关系式． （3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？30．(0分)[ID ：10051]已知，如图，BD 平分ABC ∠交AC 于点D ，点E 、F 分别是AB 、BC 的中点，连接DE ，且// DE BC .(1) 求证:BE CF =；(2)连接DF ，若5AB BC ==，6AC =，求四边形BEDF 的面积.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1．A2．A3．C4．D5．C6．A7．B8．C9．C10．B11．C12．C13．C14．C15．C二、填空题16．x≤1【解析】由题意得：1－x≥0解得x≤1故答案为x≤1点睛：二次根式有意义的条件是：a≥017．（答案不唯一满足均可）【解析】【分析】一次函数的图象经过第一二四象限列出不等式组求解即可【详解】解：一次函数的图象经过第一二四象限解得：m的值可以是1故答案为：1（答案不唯一满足均可）【点睛】此题主18．24【解析】【分析】根据菱形的性质求出另一条对角线BD的长然后再求面积即可【详解】如图所示：∵菱形ABCD的边长为5cm对角线AC＝6cm∴AC⊥BDAO＝CO＝3cmBD=2BO∴BO＝＝4(cm19．4【解析】分析：根据二次根式的性质相反数的定义绝对值的意义解答即可详解：==2314﹣π的相反数为π﹣31=4故答案为2π﹣3144点睛：本题考查了二次根式的性质相反数的定义绝对值的意义是基础题熟记20．4【解析】【分析】设每份为x则根据勾股定理即可求出x的值然后求出a的长【详解】解：根据题意设每份为x∵∴在中由勾股定理得解得：（负值已舍去）∴；故答案为：4【点睛】本题考查了勾股定理解直角三角形解题21．x＜1【解析】【分析】根据被开方数大于等于0分母不等于0列式进行计算即可求解【详解】解：根据题意得1-x≥0且1−x≠0解得x＜1故答案为x＜1【点睛】本题考查了函数自变量的取值范围函数自变量的范围22．x＞-3【解析】【分析】根据被开方数大于等于0分母不等于0列式计算即可得解【详解】解：由题意得2x+6＞0解得x＞-3故答案为x＞-3【点睛】本题考查了函数自变量的范围一般从三个方面考虑：（1）当函23．【解析】【分析】【详解】解：∵四边形ABCD是矩形∴AC=2OABD=2BOAC=BD∴OB=OA∵∴是等边三角形故答案为【点睛】本题考查矩形的对角线相等24．【解析】试题分析：∵四边形ABCD是平行四边形∴AD∥CBAB∥CD∴∠DAB+∠CBA=180°又∵AP和BP分别平分∠DAB和∠CBA∴∠PAB=∠DAB∠PBA=∠ABC∴∠PAB+∠PBA=25．9【解析】【分析】过点B作BD⊥直线x＝7交直线x＝7于点D过点B作BE⊥x轴交x轴于点E则OB＝由于四边形OABC是平行四边形所以OA＝BC又由平行四边形的性质可推得∠OAF＝∠BCD则可证明△O三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．A解析：A【解析】【分析】首先利用勾股定理计算出AC 的长，再根据折叠可得DEC ≌'D EC ，设ED x =，则'=D E x ，''2=-=AD AC CD ，4AE x =-，再根据勾股定理可得方程2222(4)x x +=-，解方程即可求得结果．【详解】解：∵四边形ABCD 是长方形，3,4AB AD ==，∴3,4====AB CD AD BC ，90ABC ADC ∠=∠=︒，∴ABC 为直角三角形，∴5AC ===，根据折叠可得：DEC ≌'D EC ，∴'3==CD CD ，'DE D E =，'90∠=∠=︒CD E ADC ，∴'90∠=︒AD E ，则AD'E △为直角三角形，设ED x =，则'=D E x ，''2=-=AD AC CD ，4AE x =-，在'Rt AD E 中，由勾股定理得：222''+=AD D E AE ，即2222(4)x x +=-， 解得：32x =， 故选：A ．【点睛】 此题主要考查了轴对称的折叠问题，以及勾股定理的应用，关键是掌握折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．2．A解析：A【解析】【分析】设BO xm =，利用勾股定理依据AB 和CD 的长相等列方程，进而求出x 的值，即可求出AB 的长度．【详解】解：设BO xm =，依题意，得1AC =，1BD =，4AO =．在Rt AOB 中，根据勾股定理得222224AB AO OB x =+=+，在Rt COD 中，根据勾股定理22222(41)(1)CD CO OD x =+=-++，22224(41)(1)x x ∴+=-++，解得3x =，5AB ∴==，答：梯子AB 的长为5m ．故选：A ．【点睛】本题考查了勾股定理在实际生活中的应用，本题中找到AB CD =利用勾股定理列方程是解题的关键．3．C解析：C【解析】【分析】根据菱形的性质得出CD=AD=5，进而得出CE=4，利用勾股定理得出BE ，进而利用勾股定理得出AE 即可．【详解】∵菱形ABCD ，∴CD ＝AD ＝5，CD ∥AB ，∴CE ＝CD ﹣DE ＝5﹣1＝4，∵BE ⊥CD ，∴∠CEB ＝90°，∴∠EBA ＝90°，在Rt △CBE 中，BE 3==，在Rt △AEB 中，AE ==故选C ．【点睛】此题考查菱形的性质，关键是根据菱形的性质得出CD=AD ． 4．D解析：D【解析】【分析】分4是直角边、4是斜边，根据勾股定理计算即可．【详解】当4是直角边时，斜边，当4是斜边时，另一条直角边=故选：D．【点睛】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．5．C解析：C【解析】【分析】证明30BAE EAC ACE，求出BC即可解决问题．【详解】解：四边形ABCD是矩形，∴∠=︒，90BEA=EC，∴∠=∠，EAC ECAEAC BAE，又∵将纸片沿AE折叠，点B恰好落在AC上，30BAE EAC ACE，AB=，3BC AB，333∴矩形ABCD的面积是33393AB BC．故选：C．【点睛】本题考查矩形的性质，翻折变换，直角三角形30角性质等知识，解题的关键是灵活运用所学知识解决问题．6．A解析：A【解析】【分析】由矩形的性质可知AD∥BC，由此可得出∠BFE=∠DEF=25°，再根据翻折的性质可知每翻折一次减少一个∠BFE的度数，由此即可算出∠CFE度数．【详解】解：∵四边形ABCD为长方形，∴AD∥BC，∴∠BFE=∠DEF=25°．由翻折的性质可知：图2中，∠EFC=180°-∠BFE=155°，∠BFC=∠EFC-∠BFE=130°，图3中，∠CFE=∠BFC-∠BFE=105°．故选：A．【点睛】本题考查翻折变换以及矩形的性质，解题的关键是找出∠CFE=180°-3∠BFE．解决该题型题目时，根据翻折变换找出相等的边角关系是关键．7．B解析：B【解析】【分析】根据矩形的性质结合等角对等边，进而得出CF的长，再利用勾股定理得出AP的长．【详解】∵∠PAE=∠DAE,∠DAE=∠F∴∠PAE=∠F∴PA=PF∵E是CD的中点∴BF=8设AP=x，则BP=8−x在RtΔABP中，4+(8−x)2=x2得x =174故选：B点睛：此题主要考查了矩形的性质以及勾股定理等知识，正确得出FC的长是解题关键．8．C解析：C【解析】【分析】设绳索长为x尺，根据勾股定理列出方程解答即可．【详解】解：设绳索长为x尺，可列方程为（x-3）2+82=x2，故选：C．【点睛】本题考查了勾股定理的应用，找准等量关系，正确列出一元二次方程是解题的关键. 9．C解析：C【解析】如图，∵∠C=90°，∠B=30°，，∴cm，由勾股定理得：，故选C．10．B解析：B【解析】二次根式要求被开方数为非负数，易得B为二次根式.故选B.11．C解析：C【解析】【分析】仔细分析题意得：梯子、地面、墙刚好形成一直角三角形，梯高为斜边，利用勾股定理解此直角三角形即可．【详解】=2.1（米）．故选C．【点睛】本题考查了勾股定理的应用．善于提取题目的信息是解题以及学好数学的关键．12．C解析：C【解析】【分析】矩形与菱形相比，菱形的四条边相等、对角线互相垂直；矩形四个角是直角，对角线相等，由此结合选项即可得出答案．【详解】A、菱形、矩形的内角和都为360°，故本选项错误；B、对角互相平分，菱形、矩形都具有，故本选项错误；C、对角线相等菱形不具有，而矩形具有，故本选项正确D、对角线互相垂直，菱形具有而矩形不具有，故本选项错误，故选C．【点睛】本题考查了菱形的性质及矩形的性质，熟练掌握矩形的性质与菱形的性质是解题的关键. 13．C解析：C【解析】【分析】先根据直角三角形的性质求出AC 的长，再根据勾股定理即可得出结论．【详解】解：∵ABC 中，CD AB ⊥于D ，∴∠ADC =90°，则ADC 为直角三角形，∵E 是AC 的中点，DE =5，∴AC =2DE =10，在Rt ADC 中，AD =6，AC =10，∴8CD =， 故选：C ．【点睛】本题考查的是直角三角形斜边上的中线，熟知在直角三角形中，斜边上的中线等于斜边的一半是解答此题的关键． 14．C解析：C【解析】【分析】首先利用三角形的中位线定理得出AC ，进一步利用菱形的性质和勾股定理求得边长，得出周长即可．【详解】解：∵E ，F 分别是AB ，BC 边上的中点，∴∵四边形ABCD 是菱形，∴AC ⊥BD ，OA=12OB=12BD=2，∴，∴菱形ABCD 的周长为．故选C ．15．C解析：C【解析】【分析】根据菱形的性质，四条边相等且对角线互相平分且互相垂直，由勾股定理得出BO 的长，进而得其对角线BD 的长，再根据菱形的面积等于对角线乘积的一半计算即可.【详解】解：如图：四边形ABCD 是菱形，对角线AC 与BD 相交于点O ，∵菱形的周长为40，∴AB=BC=CD=AD=10，∵一条对角线的长为12，当AC=12，∴AO=CO=6，在Rt △AOB 中，根据勾股定理，得BO=8，∴BD=2BO=16，∴菱形的面积=12AC•BD=96， 故选：C ．【点睛】此题主要考查了菱形的性质、菱形的面积公式以及勾股定理等知识，根据题意得出BO 的长是解题关键．二、填空题16．x≤1【解析】由题意得：1－x≥0解得x≤1故答案为x≤1点睛：二次根式有意义的条件是：a≥0解析：x ≤1【解析】由题意得：1－x ≥0，解得x ≤1.故答案为x ≤1. a a ≥0. 17．（答案不唯一满足均可）【解析】【分析】一次函数的图象经过第一二四象限列出不等式组求解即可【详解】解：一次函数的图象经过第一二四象限解得：m 的值可以是1故答案为：1（答案不唯一满足均可）【点睛】此题主 解析：（答案不唯一，满足02m <<均可）【解析】【分析】一次函数()2y m x m =-+的图象经过第一、二、四象限，列出不等式组200,m m -<⎧⎨>⎩求解即可．【详解】解：一次函数()2y m x m =-+的图象经过第一、二、四象限，200m m -<⎧⎨>⎩解得：02m <<m 的值可以是1．故答案为：1（答案不唯一，满足02m <<均可）．【点睛】此题主要考查了一次函数图象，一次函数y kx b =+的图象有四种情况：①当0,0k b >>时，函数y kx b =+的图象经过第一、二、三象限；②当0,0k b ><时，函数y kx b =+的图象经过第一、三、四象限；③当0,0k b <>时，函数y kx b =+的图象经过第一、二、四象限；④当0,0k b <<时，函数y kx b =+的图象经过第二、三、四象限．18．24【解析】【分析】根据菱形的性质求出另一条对角线BD 的长然后再求面积即可【详解】如图所示：∵菱形ABCD 的边长为5cm 对角线AC ＝6cm ∴AC ⊥BD AO ＝CO ＝3cmBD=2BO ∴BO ＝＝4(cm解析：24【解析】【分析】根据菱形的性质求出另一条对角线BD 的长，然后再求面积即可.【详解】如图所示：∵菱形ABCD 的边长为5cm ，对角线AC ＝6cm ，∴AC ⊥BD ，AO ＝CO ＝3cm ，BD=2BO ，∴BO ＝22AB AO -＝4(cm)，∴BD ＝8cm ，∴S 菱形ABCD =12×6×8＝24(cm 2)， 故答案为24．【点睛】本题考查了菱形的性质，熟练掌握菱形的对角线互相垂直平分以及菱形的面积等于对角线积的一半是解题的关键.19．4【解析】分析：根据二次根式的性质相反数的定义绝对值的意义解答即可详解：==2314﹣π的相反数为π﹣31=4故答案为2π﹣3144点睛：本题考查了二次根式的性质相反数的定义绝对值的意义是基础题熟记解析： 3.14π-4【解析】分析：根据二次根式的性质，相反数的定义，绝对值的意义解答即可．=2，3.14﹣π的相反数为π﹣3.14=-=4．故答案为2，π﹣3.14，4．点睛：本题考查了二次根式的性质，相反数的定义，绝对值的意义，是基础题，熟记概念是解题的关键．20．4【解析】【分析】设每份为x 则根据勾股定理即可求出x 的值然后求出a 的长【详解】解：根据题意设每份为x∵∴在中由勾股定理得解得：（负值已舍去）∴；故答案为：4【点睛】本题考查了勾股定理解直角三角形解题 解析：4【解析】【分析】设每份为x ，则2a x =，3=b x ，根据勾股定理，即可求出x 的值，然后求出a 的长．【详解】解：根据题意，设每份为x ，∵:2:3a b =，∴2a x =，3=b x ，在Rt ABC ∆中，由勾股定理，得222(2)(3)x x +=，解得：2x =（负值已舍去），∴4a =；故答案为：4．【点睛】本题考查了勾股定理解直角三角形，解题的关键是熟练掌握勾股定理求出三角形的边长．21．x ＜1【解析】【分析】根据被开方数大于等于0分母不等于0列式进行计算即可求解【详解】解：根据题意得1-x≥0且1−x≠0解得x ＜1故答案为x ＜1【点睛】本题考查了函数自变量的取值范围函数自变量的范围解析：x ＜1【解析】【分析】根据被开方数大于等于0，分母不等于0列式进行计算即可求解．【详解】解：根据题意得，1-x≥0且1−x≠0，解得x ＜1．故答案为x ＜1．【点睛】本题考查了函数自变量的取值范围，函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．22．x ＞-3【解析】【分析】根据被开方数大于等于0分母不等于0列式计算即可得解【详解】解：由题意得2x+6＞0解得x ＞-3故答案为x ＞-3【点睛】本题考查了函数自变量的范围一般从三个方面考虑：（1）当函解析：x ＞-3．【解析】【分析】根据被开方数大于等于0，分母不等于0列式计算即可得解．【详解】解：由题意得，2x+6＞0，解得x ＞-3．故答案为x ＞-3．【点睛】本题考查了函数自变量的范围，一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．23．【解析】【分析】【详解】解：∵四边形ABCD 是矩形∴AC=2OABD=2BOAC=BD∴OB=OA∵∴是等边三角形故答案为【点睛】本题考查矩形的对角线相等 解析：3 【解析】【分析】【详解】解：∵四边形ABCD 是矩形，∴AC=2OA ，BD=2BO ，AC=BD ，∴OB=OA ，∵60∠=，AOB ∴OAB 是等边三角形，1OB AB ∴==22BD OB ==223AD BD AB =-=故答案为3．【点睛】本题考查矩形的对角线相等．24．【解析】试题分析：∵四边形ABCD是平行四边形∴AD∥CBAB∥CD∴∠DAB+∠CBA=180°又∵AP和BP分别平分∠DAB和∠CBA∴∠PAB=∠DAB∠PBA=∠ABC∴∠PAB+∠PBA=解析：【解析】试题分析：∵四边形ABCD是平行四边形，∴AD∥CB，AB∥CD，∴∠DAB+∠CBA=180°，又∵AP和BP分别平分∠DAB和∠CBA，∴∠PAB=∠DAB，∠PBA=∠ABC，∴∠PAB+∠PBA=（∠DAB+∠CBA）=90°，∴∠APB=180°﹣（∠PAB+∠PBA）=90°；∵AB∥CD，∴∠PAB=∠DPA，∴∠DAP=∠DPA，∴AD=DP=5，同理：PC=CB=5，即AB=DC=DP+PC=10，在Rt△APB中，AB=10，AP=8，∴BP==6，∴△APB的周长=6+8+10=24.考点：1平行四边形；2角平分线性质；3勾股定理；4等腰三角形.25．9【解析】【分析】过点B作BD⊥直线x＝7交直线x＝7于点D过点B作BE⊥x轴交x轴于点E则OB＝由于四边形OABC是平行四边形所以OA＝BC又由平行四边形的性质可推得∠OAF＝∠BCD则可证明△O解析：9【解析】【分析】过点B作BD⊥直线x＝7，交直线x＝7于点D，过点B作BE⊥x轴，交x轴于点E．则OB22．由于四边形OABC是平行四边形，所以OA＝BC，又由平行四边形OE BE的性质可推得∠OAF＝∠BCD，则可证明△OAF≌△BCD，所以OE的长固定不变，当BE 最小时，OB取得最小值，即可得出答案．【详解】解：过点B作BD⊥直线x＝7，交直线x＝7于点D，过点B作BE⊥x轴，交x轴于点E，直线x＝2与OC交于点M，与x轴交于点F，直线x＝7与AB交于点N，如图：∵四边形OABC是平行四边形，∴∠OAB＝∠BCO，OC∥AB，OA＝BC，∵直线x＝2与直线x＝7均垂直于x轴，∴AM∥CN，∴四边形ANCM是平行四边形，∴∠MAN＝∠NCM，∴∠OAF＝∠BCD，∵∠OFA＝∠BDC＝90°，∴∠FOA＝∠DBC，在△OAF 和△BCD 中，FOA DBC OA BC OAF BCD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△OAF ≌△BCD （ASA ）．∴BD ＝OF ＝2，∴OE ＝7+2＝9，∴OB ＝22OE BE +．∵OE 的长不变，∴当BE 最小时（即B 点在x 轴上），OB 取得最小值，最小值为OB ＝OE ＝9． 故答案为：9．【点睛】本题考查了平行四边形的性质、坐标与图形性质、全等三角形的判定与性质；熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．三、解答题26．（1）1150y x =，2160160y x =-，图象见解析；（2）当人数为16人时，两家均可选择，当人数在1016x ≤<之间时选择乙旅行社，当人数1625x <时，选择甲旅行社．【解析】【分析】（1）根据题意可以直接写出甲乙旅行社收费1y 、2y （元)与参加旅游的人数x （人)之间的关系式，再画出图象；（2）根据题意，可以列出相应的不等式，从而可以得到该单位选择哪一家旅行社支付的旅游费用较少．【详解】解：（1）由题意可得，12000.75150y x x =⨯=，即甲旅行社收费1y （元)与参加旅游的人数x （人)之间的关系式是1150y x =； 22000.80(1)160160y x x =⨯-=-，即乙旅行社收费2y （元)与参加旅游的人数x （人)之间的关系式是2160160y x =-；（2）当150160(1)x x =-时，解得，16x =，即当16x =时，两家费用一样；当150160(1)x x >-时，解得，16x <，即当1016x ≤<时，乙社费用较低；当150160(1)x x <-时，解得，16x >，即当1625x <时，甲社费用较低；答：当人数为16人时，两家均可选择，当人数在1016x ≤<之间时选择乙旅行社，当人数1625x <时，选择甲旅行社．【点睛】本题考查了一次函数的应用、一元一次不等式的应用，解答本题的关键是明确题意，利用一次函数的性质和不等式的性质解答．27．（1）4533y x =+；（2）52． 【解析】【分析】（1）利用待定系数法即可求出一次函数解析式；（2）求出点D 坐标，根据ABC AOD BOD SS S =+即可求解．【详解】（1）把A (-2，-1)，B (1，3)代入y =kx +b 得 213k b k b -+=-⎧⎨+=⎩，解得 4353k b ⎧=⎪⎪⎨⎪=⎪⎩， 所以一次函数解析式为4533y x =+； （2）把x =0代入4533y x =+得y =53， ∴D 点坐标为(0，53)， ∴15155=21=23232ABC AOD BOD S S S =+⨯⨯+⨯⨯． 【点睛】（1）待定系数法是求函数解析式的一种常用方法，要深刻领会，其实质是根据题意设出函数关系式，把点的坐标代入解析式构造方程，求解，回代，最后确定解析式； （2）平面直角坐标系中如果图形的面积不易直接求，则一般采用割补法求解． 28．（1）3AC =；（2）3【解析】【分析】（1）如图1，根据已知条件得到∠ACB ＝90°，AB ＝2，BD ＝AD ＝1，推出△ACD 是等边三角形，得到∠B ＝60°，根据直角三角形的性质即可得到结论；（2）如图2，过B 作BC′⊥AC 于C′，根据直角三角形的性质得到BC′＝12AB ，推出点C 与C′重合，于是得到结论．【详解】（1）如图，D 为AB 中点，112CD BD AD AB ====， B BCD A ACD ∴∠=∠∠=∠,， 180A B BCD ACD ∠+∠+∠+∠=，90ACB BCD ACD ∴∠=∠+∠=，12BC AB ==,， 3AC ∴=； （2）过B 作'BC AC ⊥于'C ，BC ＝12AB ，BC ＝1 AB=2 在Rt ABC 中30A ∠=︒，1'12BC AB ∴==， ','1BC AC BC BC ⊥==，垂线段最短，且过直线外一点有且只有一条直线与已知直线垂直，C ∴与'C 重合，BC AC ∴⊥，223AC AB BC ∴=-【点睛】本题考查了解直角三角形，等腰三角形的判定和性质，含30°直角三角形的性质，正确的作出图形是解题的关键．29．（1）120米（2）y 乙=120x ﹣360，y 甲=60x （3）9【解析】【分析】【详解】解：（1）由图得：720÷（9﹣3）=120（米），答：乙工程队每天修公路120米．（2）设y 乙=kx+b ，则3k+b=0{9k+b=720，解得：k=120{b=360-．∴y 乙=120x ﹣360． 当x=6时，y 乙=360．设y 甲=kx ，则360=6k ，k=60，∴y 甲=60x ．（3）当x=15时，y 甲=900，∴该公路总长为：720+900=1620（米）．设需x 天完成，由题意得：（120+60）x=1620，解得：x=9．答：该项工程由甲、乙两工程队一直合作施工，需9天完成（1）根据图形用乙工程队修公路的总路程除以天数，即可得出乙工程队每天修公路的米数．（2）根据函数的图象运用待定系数法即可求出y与x之间的函数关系式．（3）先求出该公路总长，再设出需要x天完成，根据题意列出方程组，求出x，即可得出该项工程由甲、乙两工程队一直合作施工，需要的天数．30．（1）见解析；（2）6【解析】【分析】（1）由平行线的性质和角平分线的概念可得BE=DE，易证四边形DEFC是平行四边形，可得DE=CF，等量代换即可得出结论；（2）易证四边形BEDF是平行四边形，再由BE=DE证得四边形BEDF是菱形，由等腰三角形“三线合一”可得BD⊥EF，根据勾股定理求得BD，根据三角形中位线定理求得EF，根据菱形的面积公式即可得出答案.【详解】（1）证明：∵DE∥BC，∴∠DBC=∠BDE，∵BD平分∠ABC，∴∠EBD=∠DBC，∴∠BDE=∠EBD，∴BE=DE，∵E、F是AB、BC的中点，∴EF∥AC，∵DE∥BC，∴四边形DEFC是平行四边形，∴DE=CF，∴BE=CF；（2）∵AB=BC=5，BD平分∠ABC，∴BD⊥AC，CD=12AC=3.在Rt△BDC中，BD∵E、F是AB、BC的中点，∴EF=12AC=3.∵F是BC中点，∴BF=CF，∴DE=BF，DE∥BF，∴四边形BEDF是平行四边形，又∵BE=DE，∴四边形BEDF是菱形，∴S菱形BEDF=12 BD·EF=12×4×3=6.【点睛】本题主要考查了等腰三角形的判定和性质，平行四边形的判定和性质，菱形的判定和性质，三角形中位线定理，根据三角形中位线定理和平行四边形的判定证出平行四边形是解决（1）的关键，证出四边形BEDF是菱形是解决（2）的关键.。

芜湖市张镇中学八年级数学下学期复习（四）班级 姓名 学号 得分一、选择题（每小题3分，共24分）1.下列命题中正确的是（ ）A.对角线互相平分的四边形是菱形B.对角线互相平分且相等的四边形是菱形C.对角线互相垂直的四边形是菱形D.对角线互相垂直平分的四边形是菱形2.某花木场有一块等腰梯形ABCD 的空地，其各边的中点分别是E 、F 、G 、H 测量得对角线AC=10米，现想用篱笆围成四边形EFGH 场地，则需篱笆总长度是（ ） A. 40米 B. 30米 C.20米 D.10米3.在梯形ABCD 中，AD ∥BC,对角线AC ⊥BD,且AC=10,BD=6,则该梯形的面积是（ ）A. 30B. 15C.2154.如图，已知矩形ABCD,R 、P 分别是DC 、BC 上 的点，E、F分别是AP 、RP 的中点，当P 在BC 上从B 向C 移动而R 不动时，那么下列结论成立 的是（ ）A. 线段Ef 的长逐渐增大.B.线段Ef 的长逐渐减少C.线段EF 的长不改变.D.线段EF 的长不能确定.5.在平行四边形、矩形、正方形、等腰梯形、直角 梯形中，不是轴对称图形的有（ ）A. 1个B.2个C.3个D.4个6.中的两条对角线相交于O 平移后，图中能重合的三角形共有（ ）A.2对B.3对C.4对D.5对7.菱形的周长为高的8倍，则它的一组邻角是（ ）A.30°和150°B.45°和135°C.60°和120°D.80°和100°8.在矩形ABCD 中，AB=3,BC=4,则点A 到对角线BD 的距离为（ ） A.512 B.2 C.25 D.513二、填空题（每小题3分，共18分）9.在平行四边形ABCD 中，DB=DC,∠C=70°,AE ⊥BD 于E,则∠DAE= 度10.如图，BD 是平行四边形ABCD 的对角线，点E 、F 在BD 上，要使四边形AECF11.如图，一个平行四边形被分成面积为1S 、2S 、3S 、4S 四个小平行四边形，当CD沿AB 自左向右在平行四边形内平行滑动时，则1S 4S 与2S 3S 的大小关系为 .12．若梯形的面积为12c 2m ,高为3cm,则此中位线长为 .13.对角线 的四边形是菱形.14.在梯形ABCD 中，DC ∥AB,DC+CB=AB,且∠A=51°,则∠B 的度数是 .三.解答题15.(10分)已知：如图，在平行四边形E 、F 是对角线AC 上的两点，且AE=CF.求证：16．(18分)已知：如图，D是△ABC的BC边上的中点，DE⊥AC,DF⊥AB,求证：（1）△ABC是等腰三角形；（2）当∠A=90°时，试判断四边形AFDE是怎样的四边形，证明你的判断结论.17.(10分)如图，已知直线m∥n,A、B为直线n上的两点，C、P为直线m上的两与△ABC的面积相等；理由是： .18.（10分）如图，在菱形ABCD 中，EEF ⊥AC 交CB 的延长线于F.求证：AB 与EF 互相平分19.(14分)如图，以△ABC 三边为边在BC 同侧作三个等边△ABD 、△BCE 、△ACF,请回答下列问题：（1） 求证：四边形ADEF 是平行四边形；（2） 当△ABC 满足什么条件时，四边形ADEF 是矩形.测试题参考答案1～8 D C A CB C A A9～14 20 BE=DF(不唯一) 1S 4S =2S 3S 4 互相垂直平分 78°15. 略16. (1) 略(2)AFDE 是正方形17．(1)△ABC 和△ABP, △AOC 和△BOP,△CPA 和△CPB; (2) △ABP, (3)同底等高18.略19. (1)略 (2)150°。

芜湖市张镇中学八年级数学下学期复习（三）班级姓名学号得分一、选择题（每小题3分，共24分）1、在下列以线段a,b,c的长为三边的三角形中，不能构成直角三角形的是（）A.a=9,b=41,c=40B.a=b=5,c=52C.a：b：c=3：4：5D.a=11,b=12,c=152、若△ABC中，AB=13,AC=15,高AD=12,则BC的长是（）A.14B.4C.14或4D.以上都不对3.2002年8月在北京召开的国际数学家大会会徽取材于古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a,较长直角边为b,那么()2ba+（3题图）（4（5题图）4．如图，四边形ABCD中，AB=3,BC=4,CD=12,DA=13,且∠ABC=90°,则四边形ABCD 的面积是（）A．84 B.36 C.251D.无法确定5.如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，B C'交AD于E,AD=8,AB=4,则DE的长为（）A.3B.4C.5D.66、如果△ABC中，∠A：∠B：∠C=1：2：3，那么BC：AC：AB的值是（）A.1：2：3B. 3：2：1C. 1：3：2D. 1：2：37.若三角形的三边长分别等于2，6，2，则此三角形的面积为（ ） A.22 B. 2 C.23 D. 38.如图，以t R △ABC 为直径分别向外作半圆，若 1S =10，3S =8，则2S =（ ） A.2 B.6 C.2 D.6二、填空题（每小题4分,共24分）9、已知一个直角三角形的两条直角边分别为6㎝，8㎝，那么这个直角三角形斜边上的高为 。

10、三角形的两边长分别为3和5，要使这个三角形是直角三角形，则第三边长是 。

11、△ABC 中，AB=10,BC=16,BC 边上的中线AD=6，则AC= 。

2024年芜湖市重点中学八年级下册物理期末复习检测试题注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、单选题1．如图所示，两只容器分别盛有相同高度的酒精和水，在A、B、C三点中，液体产生的压强分别为p A、p B、p C，则下列有关p A、p B、p C的大小的关系，正确的A．p A＞p B＞p C B．p A＜p B＜p C C．p A＝p B＞p C D．p A＝p B＜p C2．如图的实例中，属于增大大压强的是A．双肩包的背带做得很宽B．大型载重车装有很多车轮C．切蛋使用很细的钢丝D．挖掘机装有宽大的履带3．如图是一支新的签字笔，下列表述中符合生活实际的是（）A．它的重力是1NB．它平放时对桌面的压强是1.25×103PaC．用它写字时，与纸面间的摩擦是滚动摩擦D．将它放入水中时下沉4．如果地球上物体所受的重力消失，下列现象不正确的是（）A．水壶里的水很容易倒入人的口中B．河水不会自动向低处流动C．人轻轻一跳就可能离开地球D．地球上的物体将浮在空中不会自动落下来5．潜水艇在水中可以自由的上浮和下沉，是靠潜水艇内水舱的充水和排水来实现的。

潜水艇在水中能够浮沉，你认为它主要是靠改变A．所受浮力B．自身重力C．水的压强D．水的密度6．如图所示，盛有水的薄壁杯子静止在水平桌面上，杯子重1N，高10cm，底面积30cm2；杯内水重2N，水深6cm，水的密度为1.0×10kg/m2，g取10N/kg．下列选项中正确的是（）A．水对杯底的压强为800Pa B．水对杯底的压力为1.8NC．水杯对桌面的压强为1050Pa D．水杯对桌面的压力为3.2N7．为保证行车安全，汽车中安装了多个光学仪器，下列说法中错误的是A．车头灯照明利用了凹面镜反射原理B．夜间行驶时车内不开灯是防止车内物品在前挡风玻璃上成像影响安全驾驶C．行车记录仪相当于一台数码相机，其摄像头相当于一个凸透镜D．后视镜利用了凸面镜对光线的发散和成正立、缩小实像的特点8．用力拍打衣服，衣服上的灰尘就掉下来，其原因是A．拍打衣服，灰尘振动而掉落B．拍打衣服，灰尘受力运动而掉下来C．拍打衣服，衣服受力运动，灰尘由于惯性保持静止，从而脱离衣服而掉下来D．拍打衣服，因为惯性，衣服保持静止，而灰尘运动，从而将灰尘从衣服中分离二、多选题9．一支密度计分别放入两种液体中，静止时位置如图所示．若密度计在甲、乙液体中受到的浮力分别是F甲、F乙，甲、乙两种液体的密度分别为ρ甲、ρ乙．下列说法正确的是（）A．F甲= F乙B．F甲> F乙C．ρ甲< ρ乙D．ρ甲> ρ乙10．如图所示为冬奥会的一些运动项目，关于这些项目中的情景，下列说法中正确的是（）A．跳台雪运动员在空中下落的过程中，重力势能不变B．短道速滑运动员在转弯滑行的过程中，运动状态不变C．冰壶运动员掷出去的冰壶能继续向前运动，是由于冰壶具有惯性D．冰球运动员用球杆推着冰球使其水平滑动的过程中，冰球所受重力没有做功三、填空题11．“蛟龙”号载人潜水器（如图所示）于2016年5月18日在西北太平洋完成该海域的第三次科学应用下潜．“蛟龙”号潜水器漂浮在海面上时，其受到的重力_______（选填“大于”“等于”或“小于”）浮力；当“蛟龙”号下潜至5000 m深处时，受到海水的压强是__________pa．（ρ海水=1.0×10 3 kg/m3）12．小明两次水平拉动同一物体在同一水平面上做匀速直线运动，两次物体运动的路程(s)﹣时间(t)图象如图所示，由图像可知：两次物体运动的速度：v1____________v2；两次物体所受的拉力F1____________F2；0～6s两次拉力对物体做功的功率：P1____________P2(均选填“＞”、“＝”或“＜”)。

芜湖市张镇中学新人教版八年级下复习试卷及答案Prepared on 22 November 2020芜湖市张镇中学八年级数学下学期复习（一）姓名 班级 学号 得分一、选择题（每小题３分，共2４分）1.在式子,1a πxy 2，4332c b a ，x +65，87y x +，9x+y 10中，分式的个数是（ ） （A ） 2 ( B ) 3 ( C ) 4 ( D ) 52．如果把分式yx x +10中的x 、y 都扩大10倍，则分式的值（ ） （A ）扩大100倍 （B ）扩大10倍 （C ）不变 （D ）缩小到原来的1013.下列等式成立的是（ ）( A )()23- ＝-9 ( B )()23--＝91 ( C )()212a ＝14a ( D )＝×710-4.某厂去年的产值是m 万元，今年的产值是n 万元（m ﹤n ）,则今年的产值比去年的产值增加的百分比是（ ） ( A )n n m -×100％（ B ）m m n -×100％（ C ）（mn +1）×100％ （ D ）m m n 10-×100％ 5.已知总电阻R 与1R 、2R 关系式是R 1＝11R +21R ，若R ＝6欧姆，1R ＝32R ，则1R 、2R 的值分别是（ ）（A ）R ＝45欧姆,R ＝15欧姆,( B )R ＝24欧姆, R ＝8欧姆( C ) 1R ＝29欧姆, 2R ＝23欧姆,( D ) 1R ＝32欧姆, 2R ＝92欧姆 6、若分式6922-+-x x x 的值为0，则x 的值为（ ） （Ａ）±３ （Ｂ）－３或２ （ C ）３ （Ｄ）－３７、若关于ｘ的分式方程42-x ＝３＋xm -4有增根，则ｍ的值是（ ） （Ａ）－２ （Ｂ）２ （３）４ （Ｄ）－４８、计算a －ｂ＋ba b +22 （ ） （Ａ）b a b b a ++-22 （Ｂ）ａ＋ｂ （Ｃ）ba b a ++22 （Ｄ）ａ－ｂ二、填空题（每小题３分，共１８分）９、ｘ、ｙ满足关系 时，分式yx y x +-无意义 １０、22222n m mn n m +＝mn 2 １１、2361a -÷aa 612-的结果是 １２、已知a 1－b 1＝５，则bab a b ab a ---+2232的值是１３、我国是一个水资源贫乏的国家，每一个公民都应自觉养成节约用水的意识的习惯。