惠州市2009届高三第一次调研考试(数学理)

2009年惠州市高三年级理科数学命题考卷(32)一、选择题（本大题共10小题，每小题5分，共50分）1. 设集合A={x|0≤x≤2}，集合B={x|x²3x+2=0}，则A∩B的结果是（）A. {1, 2}B. {1}C. {2}D. ∅2. 若复数z满足|z1|=|z+i|，则z在复平面内对应的点位于（）A. 第一象限B. 第二象限C. 直线y=x上D. 直线y=x上3. 函数f(x)=x²2x+3的对称轴是（）A. x=1B. x=1C. x=2D. x=24. 已知数列{an}是等差数列，a1=1，a3=3，则a5的值为（）A. 5B. 6C. 7D. 85. 若向量a=(2, 3)，向量b=(1, 2)，则2a3b的模长为（）A. 5B. 10C. 15D. 206. 已知函数f(x)=|x1|，则f(x)在区间（0, 2）上的最小值为（）A. 0B. 1C. 2D. 37. 设等比数列{an}的公比为q，若a1+a3=6，a2+a4=18，则q的值为（）A. 2B. 3C. 4D. 58. 若直线y=kx+b与圆(x1)²+(y2)²=4相切，则k的取值范围是（）A. [3, 3]B. (3, 3)C. [2, 2]D. (2, 2)9. 已知函数f(x)=ln(x+1)，则f'(x)在区间（0, 1）上的符号为（）A. 正B. 负C. 零D. 无法确定10. 设三角形ABC的三边长分别为a、b、c，若a²+b²=3c²，则三角形ABC的形状为（）A. 锐角三角形B. 钝角三角形C. 直角三角形D. 等边三角形二、填空题（本大题共5小题，每小题5分，共25分）11. 已知数列{an}是等差数列，a1=1，a3=3，则an=______。

12. 若函数f(x)=x²2x+3，则f(x)的最小值为______。

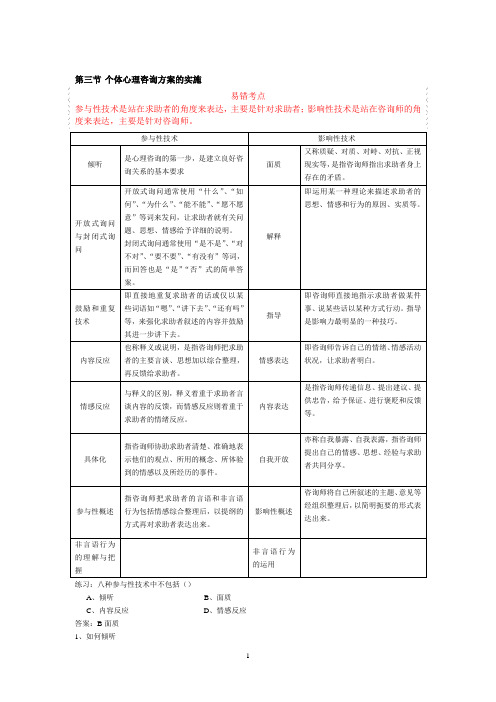
第三节个体心理咨询方案的实施易错考点参与性技术是站在求助者的角度来表达，主要是针对求助者；影响性技术是站在咨询师的角度来表达，主要是针对咨询师。

参与性技术影响性技术倾听是心理咨询的第一步，是建立良好咨询关系的基本要求面质又称质疑、对质、对峙、对抗、正视现实等，是指咨询师指出求助者身上存在的矛盾。

开放式询问与封闭式询问开放式询问通常使用“什么”、“如何”、“为什么”、“能不能”、“愿不愿意”等词来发问，让求助者就有关问题、思想、情感给予详细的说明。

封闭式询问通常使用“是不是”、“对不对”、“要不要”、“有没有”等词，而回答也是“是”“否”式的简单答案。

解释即运用某一种理论来描述求助者的思想、情感和行为的原因、实质等。

鼓励和重复技术即直接地重复求助者的话或仅以某些词语如“嗯”、“讲下去”、“还有吗”等，来强化求助者叙述的内容并鼓励其进一步讲下去。

指导即咨询师直接地指示求助者做某件事、说某些话以某种方式行动。

指导是影响力最明显的一种技巧。

内容反应也称释义或说明，是指咨询师把求助者的主要言谈、思想加以综合整理，再反馈给求助者。

情感表达即咨询师告诉自己的情绪、情感活动状况，让求助者明白。

情感反应与释义的区别，释义着重于求助者言谈内容的反馈，而情感反应则着重于求助者的情绪反应。

内容表达是指咨询师传递信息、提出建议、提供忠告，给予保证、进行褒贬和反馈等。

具体化指咨询师协助求助者清楚、准确地表示他们的观点、所用的概念、所体验到的情感以及所经历的事件。

自我开放亦称自我暴露、自我表露，指咨询师提出自己的情感、思想、经验与求助者共同分享。

参与性概述指咨询师把求助者的言语和非言语行为包括情感综合整理后，以提纲的方式再对求助者表达出来。

影响性概述咨询师将自己所叙述的主题、意见等经组织整理后，以简明扼要的形式表达出来。

非言语行为的理解与把握非言语行为的运用练习：八种参与性技术中不包括（）A、倾听B、面质C、内容反应D、情感反应答案：B面质1、如何倾听1）倾听是心理咨询的第一步，是建立良好咨询关系的基本要求。

2009届六校第一次联考高三数学（理科）试卷命题人：深圳实验学校本试卷共4页，21小题，满分150分，考试用时120分钟．第I 卷一、选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有—项是符合题目要求的．1．复数z 1=a+2i ，z 2=-2+i ，如果||||21z z <，则实数a 的取值范围是 ( ) A ．-1<a<1 B ．a>1 C. a>0 D.a<-1或a>12．设全集U={1，2，3，4，5，7}，集合A={1，3，5，7}，集合B={3，5}，则 ( )A ．U=A ∪B B ．B A U U ⋃=)(C ．)()(B A U U U ⋃=D ．)(B A U U⋃= 3．函数y=1+cos2x 的图象 ( )A ．关于x 轴对称B ．对称关于原点对称C ．关于直线2π=x 对称 D ．关于直线4π=x4．若a 、b 为空间两条不同的直线，α、β为空间两个不同的平面，则a ⊥α的一个充分条件是( )A ．a//β且α⊥βB ．β⊂a 且α⊥βC. a ⊥b 且b ∥αD. a ⊥β且α∥β 5．已知命题p ：“若1sin |=α，则2ππα+=k ，k ∈Z ”：命题q:“若1||||>+b a ，则1||>+b a ”则 ( )A.p 真q 假B.p 假q 真 C ．“p 或q ”假 D ．“p 且q ”真6．用1，2，3这三个数字组成四位数，规定这三个数字必须都使用，但相同的数字不能相邻，以这样的方式组成的四位数共有 ( )A ．9个B ．18个C ．12个D ．36个7．设=OM )21,1(，)1,0(=ON ，则满足条件10≤⋅≤OM OP ，10≤⋅≤ON OP 的动点P 的 化范围（图中阴影部分含边界）是( )8．一个算法的程序框图如下图所示，若该程序输出的结果为1110，则判断框中应填入的条件是( )A. i<9B. i<10C.i>11D. i<11第Ⅱ卷二、填空题：本大题共7小题，每小题5分，满分30分．本大题分为必做题和选做题两部分．（一）必做题：第9、10、11、12题是必做题，每道试题考生都必须做答． 9．若函数)sin(2)(φω+=x x f ，x ∈R （其中ω>0，2||πφ<)的最小正周期是π，且2)0(-=f ，则其解析式f （x)=________．10.函数y=f(x ）的图象是两条直线的一部分，如图所示，其定义域为[-1，0）∪（0,1]，则不等式f （x)-f （-x)>-1的解集为_____．11.如图，是2007年在广州举行的全国少数民族运动会上，七位评委为某民族舞蹈打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数为______，方差为____．12.若直线2ax-by+2=0（a,b ∈R ）始终平分圆014.222=+-++y x y x 的周长，则ab 的最大值是____．（二）选做题；第13、14、15题是选做题，考生只能选做二题，三题全答的，只计算前两题的得分． 13．（坐标系与参数方程选做题）在极坐标系中，点(1，0)到直线ρ(cos θ+sin θ)=2的距离为____．14.（不等式选讲选做题）已知|1|||)(-+=x x x f ，则)21(f =_______，f （x)<2的取值范围为____．15．（几何证明选讲选做题）如图，已知：△ABC 内接于eO ，点D 在OC 的延长线上，AD 是eO 的切线,若∠B=300，AC=1，则AD 的长为______.三、解答题:本大题共6小题，满分80分，解答须写出文字说明、证明过程和演算步骤． 16．（本题满分12分）已知向量a=（sin θ,1），b=（1，cos θ）,22πθπ<<-.(I)若a ⊥b ，求θ：(Ⅱ)求||b a +的最大值．17．（本题满分14分）在三棱柱ABC-A 1B 1C 1中，已知：CC 1⊥底面ABC ，AC ⊥BC ，且AB=4，AC=AA 1=2． (I)证明：A 1C ⊥BC ：(Ⅱ)求二面角C 1-A 1B-C 的余弦值．18．（本题满分14分）在某次乒乓球比赛中，甲、乙、丙三名选手进行单循环赛（即每两个比赛一场），共比赛三场，若这三人在以往的相互比赛中，甲胜乙的概率为31，甲胜丙的概率为41，乙胜丙的概率为31.(I)求甲获第一、丙获第二、乙获第三的概率；(Ⅱ)若每场比赛胜者得1分，负者得0分，设在此次比赛中甲得分数为X ，求EX ．19．（本题满分14分）已知点F(-1，0)和直线l:x=-2，动点M 到点F 的距离与到直线l 的距离之比为22.(I)求动点M 的轨迹方程：(Ⅱ)设过点F 的直线交动点M 的轨迹于A 、B 两点，并且线段AB 的中点在直线x+y=0上，求 直线AB 的方程．20．（本题满分14分） 已知数列}{n a 的首项211=a ，前n 项和)1(2≥=n a n S n n . (I)求数列}{n a 的通项公式：(Ⅱ)设b 1=0，)2(1≥=-n S S b nn n ，T n 为数列}{n b 的前n 项和，求证:12+<n nT n .21．（本题满分12分）已知函数)0(ln )(2>+=x x ax x f (I)求f(x ）的单调区间：(Ⅱ)当a=0时，设斜率为k 的直线与曲线y=f （x)交于),(11y x A 、))(,(2122x x y x B <两点， 求证：211x k x <<.参考答案一、选择题：本大题共8小题，每小题5分，满分40分．二、填空题：本大题共7小题，每小题5分，满分30分． 9、=)(x f )42sin(2π-x 10、-<≤-x x 1{21或0<x ≤1} 11.85,1.612、41 13、2214、1，2321<<-x 15.3三、解答题；本大题共6小题，满分80分，解答须写出文字说明、证明过程和演算步骤． 16．（本题满分12分）解：(1)若a ⊥b ，则sin θ+cos θ=0, 2分 由此得tanθ=-1)22(πθπ<<-， 所以4πθ-=； 6分(Ⅱ)由a=（sin θ,1），b=（1，cos θ)，得=+||b a 22)cos 1()1(sinθθ-++)cos (sin 23θθ++=,)4sin(223πθ++= 10分 当1)4sin(=+πθ时，b a +取得最大值， 即当4πθ=时，b a +最大值为12+ ……12分17．（本题满分14分）解:(I)∵因为C 1C ⊥平面ABC ，∴BC ⊥CC 1， 2分又∵AC ⊥BC ，且AC ∩C 1C=C ，所以BC ⊥ 平面A 1ACC 1，因为⊆C A1平面A 1ACC 1，所以A 1C ⊥BC. 6分(Ⅱ)建立如图直角坐标系，则)2,0,2(1A ，)0,32,0(B ，)2,32,0(1B ， 易知，平面A 1BC 的一个法向量m=（1，0,-1）． 8分 设平面A 1BC 1的一个法向量为n=（x,y,z ）， 由⎩⎨⎧=⋅=⋅⋅00111B C n A C n ．得)3,1,0(=n 10分>=<n m ,cos =⋅⋅nm nm ||46-. 所以二面角C 1-A 1B-C 的余弦值是46 14分18．（本题满分14分）解：(I)设甲获第一、丙获第二、乙获第三为事件A ， 则P （A ）=181324131=⨯⨯ …………6分(Ⅱ)X 可能的取值为0,1,2． P(X=0)=214332=⨯， P(X=1)=32414331⨯+⨯125=，P(X=2)=1214131=⨯……………12分EX +⨯=210⨯+⨯21251127121= …………14分19．（本题满分14分）解：(I)设动点M 的坐标为(x,y ），由于动点M 到点F 的距离与到直线l 的距离之比为22,故2)1(22+++x yx 22=,……2分 化简得：1222=+y x ，这就是动点M 的轨迹方程……6分(Ⅱ)设直线AB 的方程为y=k(x+1)(k ≠0)，代入1222=+y x ，整理得22)21(x k +022422=-++k x k ∵直线AB 过椭圆的左焦点F ，∴方程有两个不等实根， 8分 记),(11y x A ，),(22y x B ，AB 中点),(00y x P ， 则=+21x x 12422+-k k，)(21210x x x +=12222+-=k k，)1(00+=x k y 122+=kk ，∵线段AB 的中点P 在直线x+y=0上，=+∴00y x 12222+-k k0122=++k k ,∴k=0,或21=k …10分当直线AB 与x 轴垂直时，线段AB 的中点F 不在直线x+y=0上，∴直线AB 的方程是y=0或x-2y+1=0. 14分 20．（本题满分14分） 解：(I)由211=a ，n n a n S 2=， ①∴121)1(---=n n a n S ， ② ①-②得：1--=n n n S S a 122)1(---=n n a n a n ．即 1-n n aa )2(11≥+-=n n n ， 4分=1a a nL a a a a n n n 2.11---⋅1223a a a a ⋅L nn n n 211-⋅+-=)1(23142+=⋅n n ， )1(1+=∴n n a n 8分第(Ⅱ)答案改为：1+=n n S n ，==∴-nn n S S b 1)2(112≥-=n n， 10分∴L b b T n ++≡=2-=+n b n )12111(222nL +++-<n L +⨯+⨯321211())1(1+⨯+n n )111(+--=n n 12+=n n,故12+<n n T n 14分 21．（本题满分12分）解：(I)xax x ax x f 1212)('2+=+=)0(>x ， 2分 当a>0时，f'(x)>0，f （x ）在(0，+∞)上是增函数； 当a<0时，由f'（x)=0，得a ax 221--=（取正根）， 在区间)221,0(a a--内．f'（x)>0，f(x)是增函数：在区间),221(+∞--a a内，f'（x)<0，f （x)是减函数．综上，当a ≥O 时，f(x ）的增区间为(0,+∞)，没有减区间； 当a<0时，f(x ）的减区间是),221(+∞--a a ，增区间是)221,0(a a--． 6分(Ⅱ)当a=0时，f(x)=lnx(x>0），1212ln ln 1x x x x k --=，今证明<1x 21212ln ln x x x x x <--, 8分 先证明)ln (ln 121x x x -0)(12<--x x 设 h(x)=x 1(lnx-lnx 1)-(x-x 1),(x>x 1>0） 则1)('1-=xxx h ， ∵x>x 1>0，∴h'(x)<0，h(x)在[x 1，+∞)上是减函数． 10分∵x 2>x 1,∴h(x 2)<h （x 1）=0， 即 x 1(lnx 2-lnx 1）-（x 2-x 1）<0<∴1x 1212ln ln x x x x --,同理可证21212ln ln x x x x x <--.211x kx <<∴ 12分。

图1图2惠州市2024届高三第一次调研考试试题数学全卷满分150分，时间120分钟．注意事项：1．答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上。

2．作答单项及多项选择题时，选出每个小题答案后，用2B 铅笔把答题卡上对应题目的答案信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效。

3．非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上，写在本试卷上无效。

一、单项选择题：本题共8小题，每小题满分5分，共40分。

在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分。

1.已知集合{}*|,6U x x x =∈≤N ，{}1,2,3A =，{}3,5B =，求()U A B = ð（）团用数学软件制作“蚊香”模型，画法如下：在水平直线上取长度为1的线段AB ，作一个等边三角形ABC ，然后以点B 为圆心，AB 为半径逆时针画圆弧交线段CB 的延长线于点D ，由此得到第1段圆弧 AD ，再以点C 为圆心，CD 为半径逆时针画圆弧交线段AC 的延长线于点E ，再以点A 为圆心，AE 为半径逆时针画圆弧……以此类推，当得到如图2所示的“蚊香”恰好有11段圆弧时，则该“蚊香”的长度为（）A ．14πB ．18πC ．30πD ．44π多项符合题目要求。

全部选对得5分，部分选对得2分，有选错的得0分。

三、填空题：本题共4小题，每题5分，共20分。

四、解答题：本题共6小题，共70分。

解答应写出文字说明、证明过程或演算步骤。

18.（本小题满分12分）设等差数列{}n a 的公差为d ，且12d a =，59a =．（1）求数列{}n a 的通项公式；（2）设数列{}n b 满足11222332n n nn a b a b a b ++++=-，求{}n b 的前n 项和n S ．19．（本小题满分12分）如图，在五面体ABCDE 中，AD ⊥平面ABC ，//AD BE ，2AD BE =，AB BC =.（1）问：在线段CD 上是否存在点P ，使得PE ⊥平面ACD ？若存在，请指出点P 的位置，并证明；若不存在，请说明理由．（2）若AB =，2AC =，2AD =，求平面ECD 与平面ABC 夹角的余弦值．21．（本小题满分12分）已知椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ，上顶点为B ，右焦点为()0,1F ，O 为坐标原点，线段OA 的中点为D ，且BD DF =．（1）求C 的方程；（2）已知点M N 、均在直线2=x 上，以MN 为直径的圆经过O 点，圆心为点T ，直线AM AN 、分别交椭圆C 于另一点P Q 、，证明直线PQ 与直线OT 垂直．22．（本小题满分12分）惠州市2024届高三第一次调研考试数学试题参考答案与评分细则一、单项选择题：本题共8小题，每小题满分5分，共40分题号12345678答案BCACDBDA1.【解析】由已知可得{}1,2,3,5A B ⋃=，{}1,2,3,4,5,6U =，所以(){}6,4=B A C U ，故选：B ．5.【解析】由弧长公式r l ⋅=α得：r l ⋅=31，r l 232⋅=，r l 333⋅=，...，r l 11311⋅=，其中1==AB r ，()ππ44113213211321=+⋅⋅⋅+++=+⋅⋅⋅+++=∴l l l l L 蚊香的长度故选：D.二、多项选择题：本题共4小题，每小题满分5分，共20分。

2009年普通高等学校招生全国统一考试理科数学（全国I 卷）本试卷分第卷（选择题）和第卷（非选择题）两部分．第卷1至2页，第卷3至4页．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷考生注意： 1．答题前，考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ，并贴好条形码．请认真核准条形码上的准考证号、姓名和科目． 2．每小题选出答案后，用2Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．在试题卷上作答无效．．．．．．．．．． 3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．参考公式： 如果事件A B ，互斥，那么 球的表面积公式()()()P A B P A P B +=+24πS R = 如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B ∙=∙球的体积公式 如果事件A 在一次试验中发生的概率是P ，那么 34π3V R =n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径一、选择题(1)设集合A=｛4，5，7，9｝，B=｛3，4，7，8，9｝，全集U=A B ，则集合[()u A B I中的元素共有（A ）（A ）3个 （B ）4个 （C ）5个 （D ）6个解：{3,4,5,7,8,9}A B = ，{4,7,9}(){3,5,8}U A B C A B =∴= 故选A 。

也可用摩根律：()()()U U U C A B C A C B =（2）已知1iZ＋=2+i,则复数z=（B ） （A ）-1+3i (B)1-3i (C)3+i (D)3-i 解：(1)(2)13,13z i i i z i =+⋅+=+∴=- 故选B 。

(3) 不等式11X X +-＜1的解集为（ D ）（A ）｛x }{}011x x x 〈〈〉 (B){}01x x 〈〈（C ）{}10x x -〈〈 (D){}0x x 〈 解：验x=-1即可。

惠州市届高三第一次调研考试数学试题(理科〕〔本试卷共4页，21小题，总分值150分。

考试用时120分钟〕本卷须知：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

2．选择题每题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

一、选择题：本大题共8小题，每题5分，共40分. 在每题给出的四个选项中，只有一项符合题目要求.1.集合{}{}1,2,3,14M N x Z x ==∈<<，那么 〔 〕A.N M ⊆B.N M =C.}3,2{=N MD.)4,1(=N M 2.复数1iz i=-在复平面上对应的点位于 〔 〕 A.第一象限3.平面向量a ()1,2=-，b ()4,m =，且⊥a b ，那么向量53-a b =( ) A. (7,16)-- B.(7,34)-- C.(7,4)-- D.(7,14)-4.直线1l 与直线2:l 3460x y +-=平行且与圆：2220x y y ++=相切,那么直线1l 的方程是( )A. 3410x y +-=B. 3410x y ++=或3490x y +-=C. 3490x y ++=D. 3410x y +-=或3490x y ++= 5.对于平面α、β、γ和直线a 、b 、m 、n ,以下命题中真命题是( ),,,,a m a n m n αα⊥⊥⊂⊂,那么a α⊥//,a b b α⊂,那么//a α//,,,a b αβαγβγ==那么//a b ,,//,//a b a b ββαα⊂⊂,那么//βα6.不等式组201x y y x ≤⎧⎪≥⎨⎪≤-⎩表示的平面区域的面积是( )A.12 B. 0 C. 1 D. 327.函数x x x f 3)(3-=，假设过点()0,16A 且与曲线()y f x =相切的切线方程为16y ax =+，那么实数a 的值是( )A.3-B.38.对于任意两个正整数,m n ,定义某种运算“※〞如下:当,m n 都为正偶数或正奇数时,m ※n =m n +;当,m n 中一个为正偶数,另一个为正奇数时,m ※n =mn .那么在此定义下,集合{(,)M a b a =※12,,}b a b **=∈∈N N 中的元素个数是( )二、填空题：本大题共7小题，每题5分，总分值30分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．〔一〕必做题：第9至13题为必做题，每道试题考生都必须作答． 9.右图是某高三学生进入高中三年来第1次到14次的数学考试成绩 茎叶图, 根据茎叶图计算数据的中位数为 . 10.等差数列{n a },满足381,6a a ==,那么此数列的前10项 的和10S = .11.直线l 与直线01=--y x 垂直，那么直线l 的倾斜角=α .12.设()f x 是(,)-∞+∞上的奇函数,(3)()f x f x +=. 当01x ≤≤时有()2f x x =, 那么(8.5)f = .13.一物体在力5, 02,()34, 2x F x x x ≤≤⎧=⎨+>⎩(单位：N )的作用下沿与力F 相同的方向,从0x =处运动到4x = (单位：m )处,那么力()F x 做的功为 焦. 14.〔坐标系与参数方程选做题〕在极坐标系中,圆4sin ρθ=的圆心到直线()6R πθρ=∈的距离是 .15.〔几何证明选讲选做题〕如图,AD 为圆O 直径,BC 切圆O 于点E ,,AB BC DC BC ⊥⊥ , 4,1AB DC ==,那么AD 等于 .7 98 6 3 89 3 9 8 8 4 1 5 10 3 1 11 4三、解答题：本大题共6小题，总分值80分．解答须写出文字说明、证明过程和演算步骤． 16.〔本小题总分值12分〕函数()2,f x x x x R =∈.(1)求()f x 的最大值和最小正周期；(2)假设28f απ⎛⎫-=⎪⎝⎭，α是第二象限的角，求sin 2α. 17.〔本小题总分值12分〕某社团组织50名志愿者利用周末和节假日参加社会公益活动,活动内容是：1、到各社区宣传慰问,倡导文明新风；2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活开工程,相关的数据如下表所示：(1) 分层抽样方法在做义工的志愿者中随机抽取6名,年龄大于40岁的应该抽取几名? (2) 上述抽取的6名志愿者中任取2名,求选到的志愿者年龄大于40岁的人数的数学期望.18.〔本小题总分值14分〕如图,三棱锥O ABC -的侧棱,,OA OB OC 两两垂直,且1OA =,2OB OC ==,E 是OC 的中点.(1)求O 点到面ABC 的距离；(2)求二面角E AB C --的正弦值. 19.〔本小题总分值14分〕等差数列{}n a 的公差0d ≠，它的前n 项和为ns ，假设570s=，且2722,,a a a 成等比数列.〔1〕 求数列{}n a 的通项公式；〔2〕设数列1n s ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，求证：1368n T ≤<. 20.〔本小题总分值14分〕在平面直角坐标系x o y 中，点(,)(0)P a b a b >>为动点，12,F F 分别为椭圆22221x y a b+=的左右焦点．△12F P F 为等腰三角形．〔1〕求椭圆的离心率e ；〔2〕设直线2P F 与椭圆相交于,A B 两点，M 是直线2P F 上的点，满足2A MB M =-， ABCEO求点M 的轨迹方程．21.〔本小题总分值14分〕二次函数2(),(0)f x ax bx c a =++≠,且不等式()2f x x <的解集为(12)-，.(1) 方程()30f x a +=有两个相等的实根,求()f x 的解析式. (2) ()f x 的最小值不大于3a -,求实数a 的取值范围.(3) a 如何取值时,函数2()()y f x x ax m =--+(||1m >)存在零点,并求出零点.惠州市届高三第一次调研考试 数学 (理科〕参考答案与评分标准一．选择题：共8小题，每题5分，总分值40分题号 1 2 3 4 5 6 7 8 答案CBADCADB1.【解析】{}{}3,241=<<∈=x Z x N ，故}3,2{=N M ，应选C. 2.【解析】1i i -(1)11222i i i +==-+，所以点〔11,)22-. 3.【解析】∵⊥a b ,∴4-202m m ⋅==⇒=a b ,∴53(7,16)-=--a b .应选A. 4.【解析】圆2220x y y ++=的圆心为(0,1)-,半径为1r =,因为直线12//l l ,所以,设直线1l 的方程为340x y c ++=,由题意得221134c =⇒=-+或9c =.所以,直线1l 的方程3410x y +-=或3490x y ++=.应选D.(二）【解析】对于平面α、β、γ和直线a 、b ,真命题是“假设//,,,a b αβαγβγ==,那么//a b 〞.应选C6.【解析】不等式组表示的可行域如以以下图， 故面积为211121=⋅⋅.应选A. 7.【解析】设切点为00(,)M x y ，那么03003x x y -= ①，∵33)(200-='=x x f k ，又切线l 过A 、M 两点，∴0016x y k -=那么00201633x y x -=- ②联立①、②可解得2,200-=-=y x ，从而实数a 的值为21692a k --===-应选D. 8.【解析】从定义出发,抓住,a b 的奇偶性对12实行分拆是解决此题的关键,当,a b 同奇偶时,根据m ※n =m n +将12分拆两个同奇偶数的和,当,a b 一奇一偶时,根据m ※n =mn 将12分拆一个奇数与一个偶数的积,再算其组数即可.假设,a b 同奇偶,有1211121039485766=+=+=+=+=+=+,前面的每种可以交换位置,最后一种只有1个点(6,6),这时有25111⨯+=;假设,a b 一奇一偶,有1211234=⨯=⨯,每种可以交换位置,这时有224⨯=; ∴共有11415+=个.应选B二．填空题：共7小题，每题5分，总分值30分．其中14~15题是选做题，考生只能选做一题．9．94.5 10．35 11．34π 〔或135︒〕 12．1- 13．36 14． 3 15． 5 9.【解析】从茎叶图中可知14个数据排序为：79 83 86 88 91 93 94 95 98 98 99 101 103 114中位数为94与95的平均数94.5 . 10.【解析】1103810()10()1071035222a a a a S +⨯+⨯⨯====.11.【解析】直线l 与直线10x y --=垂直得1tan l k α=-=，∴34απ=. 12.【解析】(8.5)(5.53)(5.5)(2.53)(2.5)(0.53)f f f f f f =+==+==-+(0.5)(0.5)20.51f f =-=-=-⨯=-.13.【解析】42402()5(34)W F x dx dx x dx ==++=⎰⎰⎰205x +42234362x x ⎛⎫+= ⎪⎝⎭14.【解析】由4sin ρθ=得圆O 为22(2)4x y +-=,圆O 的圆心(0,2)C 直线()6R πθρ=∈的直角坐标方程为30x y =，所以点(0,2)C 到直线()6R πθρ=∈的315.【解析】连接OE ,BC 切圆O 于点E ,OE BC ∴⊥.又,AB BC DC BC ⊥⊥，O是AD 中点，1()2OE AB DC ∴=+.25AD OE ∴== 三、解答题：16.解(1)∵()2222cos sin 2sin cos 244f x x x x x ππ⎫⎛⎫=+=+⎪ ⎪⎪⎝⎭⎝⎭2sin 24x π⎛⎫=+ ⎪⎝⎭ ………………………4分∴()f x 的最大值为2,……5分，最小正周期为22T ππ== ………6分 (2)由(1)知,()2sin 24f x x π⎛⎫=+⎪⎝⎭所以2sin 282f απα⎛⎫-==⎪⎝⎭,即sin α=………………………8分 又α是第二象限的角,所以cos 4α===-……10分所以sin 22sin cos 2ααα⎛=== ⎝⎭ ………12分 17解：(1)假设在做义工的志愿者中随机抽取6名,那么抽取比例为61244=……………2分 ∴ 年龄大于40岁的应该抽取1824⨯=人. ………………………4分 (2)在上述抽取的6名志愿者中任取2名,假设选到年龄大于40岁的人数为ξ, ∵ 6名志愿者中有2人的年龄大于40岁,其余4人的年龄在20到40岁之间, ∴ ξ可能的取值为0,1,2. ………………………5分那么0224262(0)5C C p C ξ===,1124268(1)15C C p C ξ===,22261(2)15C p C ξ=== ………8分 ∴ξ的分布列为………10分∴ ξ的数学期望为2812012515153E ξ=⨯+⨯+⨯= ………12分 18〔本小题总分值14分〕解: (1)取BC 的中点D ,连AD 、OD,OB OC OD BC =⊥则、,AD BC ⊥.,BC OAD O OH AD H ∴⊥⊥面过点作于那么OH ⊥面ABC ,OH 的长就是所要求的距离.2222, 2.BC OD OC CD ==-= ………………………3分OA OB ⊥、OA OC ⊥,,.OA OBC OA OD ∴⊥⊥平面则223AD OA OD =+=,在直角三角形OAD 中,有26.3OA OD OH AD⋅===…6分〔另解:由1126,.)363ABC V S OH OA OB OC OH ∆=⋅=⋅⋅==知(2)连结CH 并延长交AB 于F ,连结OF 、EF .,.,,,OC OAB OC AB OH ABC CF AB EF AB ⊥∴⊥⊥∴⊥⊥面又面那么EFC ∠就是所求二面角的平面角. ……………9分 作EG CF ⊥于G ,那么16.26EG OH == 在直角三角形OAB 中,,5OA OB OF AB ⋅== 在直角三角形OEF 中,2241,55EF OE OF =+=+=……………12分 63030766sin ,arcsin .(arccos )318185EG EFG EFG EF ∠===∠=或表示为故所求的正弦值是1830 ……………14分 方法二: (1)以O 为原点,OB 、OC 、OA 分别为x 、y 、z 轴建立空间直角坐标系. 那么有(0,0,1)A 、(2,0,0)B 、(0,2,0)C 、(0,1,0).E ……2分 设平面ABC 的法向量为1(,,),n x y z = 那么由11:20;n AB n AB x z ⊥⋅=-=知由11:20.n AC n AC y z ⊥⋅=-=知取1(1,1,2)n =,……4分 那么点O 到面ABC的距离为111n OA d n ⋅===……6分 (2) (2,0,0)(0,1,0)(2,1,0),(2,0,0)(0,0,1)(2,0,1)EB AB =-=-=-=- ……8分 设平面EAB 的法向量为(,,),n x y z =那么由n AB ⊥知:20;n AB x z ⋅=-= 由n EB ⊥知:20.n EB x y ⋅=-=取(1,2,2).n =……………10分 由(1)知平面ABC 的法向量为1(1,1,2).n = ……………11分 那么cos <1,n n >119n n n n ⋅====⋅. ……………13分 结合图形可知,二面角E ABC --的正弦值是1830……………14分 19.〔此题总分值14分〕解：〔1〕数列{}n a 是等差数列且570s =，∴151070a d +=. ①…2分2722,,a a a 成等比数列，∴27222a a a =即2111(6)()(21).a d a d a d +=++②………4分由①，②解得16,4a d ==或114,0(a d ==舍去）…………5分∴42n a n =+ ………6分〔2〕证明;由〔1〕可得224n s n n =+， …………7分 所以211111()2442ns n n n n ==-++. …………8分所以123111111n n nT s s s s s -=+++++111111*********()()()()()41342443541142n n n n =-+-+-++-+--++ 3111()8412n n=-+++. …………10分 3111()08412n T n n -=-+<++，∴38nT <. …………11分 1111()0413n n T T n n +-=->++，∴数列{}n T 是递增数列，∴116n T T ≥=.………13分∴1368nT≤<. …………14分20解：〔1〕设12(,0),(,0)(0)F c F c c ->，由题意,可得212PF F F =,2c =， ……………2分 整理得22()10c c aa++=，得1ca=-(舍)或12c a =，所以12e =. ……………4分〔2〕由〔1〕知2,a c b ==,可得椭圆方程为2223412x y c +=.直线2PF方程为),y x c =- ……………………………………………5分,A B两点的坐标满足方程组2223412)x y c y x c ⎧+=⎪⎨=-⎪⎩,消去y 并整理得2580,x cx -=……6分解得1280,,5x x c ==得方程组的解110,x y =⎧⎪⎨=⎪⎩2285x c y ⎧=⎪⎪⎨⎪⎪⎩……………………8分不妨设8((0,)5A cB ,设M 的坐标为(,)x y 那么8(,5AM x c y =-(,)BM x y =， …………10分由),y x c =-得3c x y =-.于是8338(,),55AM x y =-()BM x= …………11分由2AM BM =-得38)(255y x x y -⋅+=-，化简得218150x --=， ………………………………13分将2y =c x y =得210516x c x+=，由0c >得0x >.因此,点M 的轨迹方程是218150(0)x x --=>. …14分21解：∵()2f x x <的解集为(12)-，, ∴220ax b x c +-+<（）的解集为(12)-，, ……………………1分 ∴0a >,且方程220ax b x c +-+=（）的两根为12-和 即202a 4402a b c b a b c c a-++==-⎧⎧⇒⎨⎨+-+==-⎩⎩2，∴2()(2)2,(0)f x ax a x a a =+--> ……2分 〔1〕∵方程()30f x a +=有两个相等的实根,即2(2)0ax a x a +-+=有两个相等的实根∴222(2)403440a a a a ∆=--=⇒+-=, ∴2a =-或23a =…………3分 ∵0a >,∴23a =, ∴2244()333f x x x =+- …………4分〔2〕222228(2)()(2)224a a a f x ax a x a a x aa----=+--=++（） ∵0a >,∴()f x 的最小值为228(2)4a a a ---, ……………………5分那么228(2)34a a a a---≤-,23440a a +-≤,解得223a -≤≤, …………7分∵0a >,∴203a <≤………………………………8分 〔3〕由2()()0,(0,1)y f x x ax m a m =--+=>>,得2(1)2(2)0a x x a m -+-+= (※)①当1a =时,方程(※) 有一解12mx =+, 函数2()()y f x x ax m =--+有一零点12mx =+； ……………………9分 ②当1a ≠时, 242(2)(1)a m a m ⎡⎤∆=+-+-⎣⎦方程(※)有一解242(2)(1)0a m a m ⎡⎤⇔∆=+-+-=⎣⎦, 令214440m m ∆=+-≥得22m m ≥≤-或, ||1m >11m m ><-即或，∴ i)当1m >，a a 2()()y f x x ax m =--+有一零点11x a=-. ……………10分ii) 当2m ≤-时，a 的两根都为正数，∴当aa 2()()y f x x ax m =--+有一零点11x a=-.11分ⅲ) 当21m -<<-时，214440m m ∆=+-<，0∴∆> ③方程(※)有二解242(2)(1)0a m a m ⎡⎤⇔∆=+-+->⎣⎦,i)假设1m >,214440m m ∆=+->，a ,〔a 〕，函数2()()y f x x ax m =--+有两个零点1,2x …12分ii) 当2m <-时，214440m m ∆=+->，a 的两根都为正数，∴当a 0a <时，函数2()()y f x x ax m =--+有两个零点1,2x 13分ⅲ) 当21m -≤<-时，214440m m ∆=+-≤，0∴∆>恒成立， ∴a 取大于0(1a ≠)的任意数，函数2()()y f x x ax m =--+有两个零点1,2x…14分。

2009年惠州市普通高中毕业班综合测试数学（理科）（24）2009.10本试卷共6页，21小题，满分150分。

考试用时120分钟。

参考公式：如果事件A B 、互斥，那么()()()P A B P A P B +=+． 如果事件A B 、相互独立，那么()()()P AB P A P B =．如果事件A 在1次实验中发生的概率是p ，那么n 次独立重复实验中恰好发生k 次的概率k n kk n n p p C k P --=)1()(．一、选择题：本大题共8个小题；每小题5分，共40分．在每小题给出的四个选项中，有且只有一项是符合题目要求的．1．复数2(2)(1)12i i i+--的值是( ).A ．2 B. 2- C. 2i D. 2i - 2．已知命题:,sin p x R x x ∀∈>，则A ．:,sin p x R x x ⌝∃∈<B ．:,sin p x R x x ⌝∀∈≤C ．:,sin p x R x x ⌝∃∈≤D ．:,sin p x R x x ⌝∀∈<3．把函数sin y x =的图象按向量(,)k a b = 平移后得到函数sin()13y x π=-+的图象，则向量(,)k a b =为A ．(,1)3πB.(,1)3π-C. (,1)3π- D.(,1)3π--4． 已知函数c bx ax x f ++=23)(，其导数)('x f 的图象如右图，则函数)(x f 的极小值是 A ．c b a ++ B ．c b a ++48 C ．b a 23+ D ．c5．设O 为坐标原点，)1,1(A ，若点),(y x B 满足⎪⎩⎪⎨⎧≤≤≤≤≥+--+.21,21,012222y x y x y x 则⋅取得最小值时，点B 的个数是 A ．1B ．2C ．3D ．无数个6．右面框图表示的程序所输出的结果是_______A ．12B ．132C ．1320D ．118807．有6个座位连成一排，现有3人就坐，则恰有两个空座位相邻的不同坐法有 （ ）A ．36种B ．48种C ．72种D ．96种 8．某校对高三年级的学生进行体检，现将高三男生的体重(单位：kg )数据进行整理后分成六组，并绘制频率分布直方图(如图所示)．已知图中从左到右第一、第六小组的频率分别为16.0、07.0，第一、第二、第三小组的频率成等比数列，第三、第四、第五、第六小组的频率成等差数列，且第三小组的频数为100，则该校高三年级的男生总数为 A ．480 B ．440 C ．420 D ．400二、填空题：本大题共7个小题，每小题5分，满分30分．其中13～15题是选做题，考生在这三题中选做两题，三题全答的只计算前两题得分． 9．计算：22(sin 2)x dx -+⎰= ．10．设n S 为等差数列}{n a 的前n 项和，若41a =，105=S ，则n S 取得最大值时，n 的值为 ．图4P11．已知正实数b a ,满足等式b a 32log log =，给出下列五个等式①1>>b a ，②1>>a b ，③1<<b a ，④1<<a b ，⑤b a =，其中可能成立的关系式是 （填序号）12．已知抛物线x y 42=的准线与双曲线2221x y a-=交于A 、B 两点，点F 为抛物线的焦点，若FAB ∆为直角三角形，则双曲线的离心率是 ． 考生在13～15题中选做两题，三题全答的只计算前两题得分．13．（坐标系与参数方程选做题）.在直角坐标系xoy 中，已知点C )3,3(--，若以o 为极点，x 轴的正半轴为极轴，则点C 的极坐标)0,0)(,(<<->θπρθρ可写为______14．（不等式选讲选做题）设函数()|4||1|f x x x =-+-，则()f x 的最小值是 ，若()5f x ≤，则x 的取值范围是 ．15．（几何证明选讲选做题）如图，P 是圆O 外一点， 过P 引圆O 的两条割线P AB 、PCD ，P A = AB =5，CD = 3，则PC =____________．三、解答题：本大题共6小题，共80分．解答须写出文字说明、证明过程或演算步骤． 16．（本小题满分12分）已知向量)sin ,(cos αα=a, )sin ,(cos ββ=b, 552||=-b a. （Ⅰ）求cos()αβ-的值; （Ⅱ）若02πα<<, 02πβ-<<, 且5sin 13β=-, 求sin α． 17．（本小题满分12分）某电视台举行电视奥运知识大奖赛，比赛分初赛和决赛两部分．为了增加节目的趣味性，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰．已知选手甲答题的正确率为32． （Ⅰ）求选手甲可进入决赛的概率；（Ⅱ）设选手甲在初赛中答题的个数为ξ，试写出ξ的分布列，并求ξ的数学期望． 18．（本小题满分14分）如图，在三棱锥P-ABC 中， PA=3，AC=AB=4，PB=PC=BC=5，D 、E 分别是BC 、AC 的中点，F 为PC 上的一点，且PF:FC=3:1． （1）求证：PA ⊥BC ；（2）试在PC 上确定一点G ，使平面ABG ∥平面DEF ； （3）在满足（2）的情况下，求二面角G-AB-C 的平面 角的正切值．19．（本小题满分14分）若存在实常数k 和b ，使得函数()f x 和()g x 对其定义域上的任意实数x 分别满足：()f x kx b ≥+和()g x kx b ≤+，则称直线:l y kx b =+为()f x 和()g x 的“隔离直线”．已知2()h x x =，()2ln (x e x e ϕ=为自然对数的底数)．（Ⅰ）求()()()F x h x x ϕ=-的极值；（Ⅱ）函数()h x 和()x ϕ是否存在隔离直线？若存在，求出此隔离直线方程；若不存在，请说明理由． 20．（本小题满分14分）已知O 为C B A ,,三点所在直线外一点，且OC B OA μλ+=O 。

一、选择题（共8小题，每小题5分，满分40分）1、（2008•湖南）复数（﹣）等于（）A、8B、﹣8C、8iD、﹣8i2、（2008•江西）定义集合运算：A*B={z|z=xy，x∈A，y∈B}．设A={1，2}，B={0，2}，则集合A*B的所有元素之和为（）A、0B、2C、3D、63、（2008•陕西）已知{a n}是等差数列，a1+a2=4，a7+a8=28，则该数列前10项和S10等于（）A、64B、100C、110D、1204、（2009•浙江）在二项式（﹣）的展开式中，含x4的项的系数是（）A、﹣10B、10C、﹣5D、55、为得到函数（）的图象，只需将函数y=sin2x的图象（）A、向左平移个长度单位B、向右平移个长度单位C、向左平移个长度单位D、向右平移个长度单位6、（2009•安徽）设a＜b，函数y=（a﹣x）（x﹣b）2的图象可能是（）A、B、C、D、7、（2008•辽宁）4张卡片上分别写有数字1，2，3，4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为（）A、B、C、D、8、已知﹣，则=（）A、﹣2008B、2008C、2010D、﹣2010二、填空题（共7小题，满分30分）9、设向量a=（1，2），b=（2，3），若向量λa+b与向量c=（﹣4，﹣7）共线，则λ=_________．10、设曲线y=e ax在点（0，1）处的切线与直线x+2y+1=0垂直，则a=_________．11、（2009•北京）若实数x，y满足﹣则s=y﹣x的最小值为_________．12、（2008•山东）执行下边的程序框图，若p=0.8，则输出的n=_________．13、某几何体的俯视图是如右图所示的矩形，正视图（或称主视图）是一个底边长为8、高为5的等腰三角形，侧视图（或称左视图）是一个底边长为6、高为5的等腰三角形．则该儿何体的体积为_________．14、已知圆的极坐标方程为ρ=2cosθ，则该圆的圆心到直线ρsinθ+2ρcosθ=1的距离是_________．15、如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为6，sinB=，则线段AC的长是_________．三、解答题（共6小题，满分80分）16、（2006•辽宁）已知函数f（x）=sin2x+2sinxcosx+3cos2x，x∈R，求：（1）函数f（x）的最大值及取得最大值的自变量x的集合；（2）函数f（x）的单调增区间．17、（2008•辽宁）某批发市场对某种商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：周销售量 2 3 4频数20 50 30（1）根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；（2）已知每吨该商品的销售利润为2千元，ξ表示该种商品两周销售利润的和（单位：千元），若以上述频率作为概率，且各周的销售量相互独立，求ξ的分布列和数学期望．18、（2010•重庆）如图，三棱锥P﹣ABC中，PC⊥平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD⊥平面PAB．（1）求证：AB⊥平面PCB；（2）求二面角C﹣PA﹣B的大小的余弦值．19、设函数f（x）=2ln（x﹣1）﹣（x﹣1）2．（1）求函数f（x）的单调递增区间；（2）若关于x的方程f（x）+x2﹣3x﹣a=0在区间[2，4]内恰有两个相异的实根，求实数a 的取值范围．20、已知直线x﹣2y+2=0经过椭圆：（＞＞）的左顶点A和上顶点D，椭圆C的右顶点为B，点S是椭圆C上位于x轴上方的动点，直线AB，BS与直线：分别交于M，N两点．（1）求椭圆C的方程；（2）求线段MN的长度的最小值．21、（2007•四川）已知函数f（x）=x2﹣4，设曲线y=f（x）在点（x n，f（x n））处的切线与x 轴的交点为（x n+1，0）（n∈N*），其中x1为正实数．（Ⅰ）用x n表示x n+1；（Ⅱ）若x1=4，记﹣，证明数列{a n}成等比数列，并求数列{x n}的通项公式；（Ⅲ）若x1=4，b n=x n﹣2，T n是数列{b n}的前n项和，证明T n＜3．答案与评分标准一、选择题（共8小题，每小题5分，满分40分）1、（2008•湖南）复数（﹣）等于（）A、8B、﹣8C、8iD、﹣8i考点：复数代数形式的混合运算。

惠州市高三第一次调研考试数学试题(理科）参考答案题号 1 2 3 4 5 6 7 8 答案DDBBABCA1、【解析】由33412()()88ii i i i i--==-⋅=-,易知D 正确.2、【解析】因*{0,2,4}A B =，所以易知选D.3、【解析】设公差为d ，则有112421328a d a d +=⎧⎨+=⎩1101109101210022a S d =⎧⨯⇒⇒=⨯+⨯=⎨=⎩4、【解析】对于()251031551()()1r r r r r rr T C x C x x--+=-=-，对于1034,2r r -=∴=，则4x 的项的系数是225(1)10C -=5、【解析】55cos 2sin 2sin 2,3612y x x x πππ⎛⎫⎛⎫⎛⎫=+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭只需将函数sin 2y x =的图象向左平移5π12个单位得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图象。

6、【解析】可得22()()()()y a x x b x a x b =--=--- ,a b 是函数的两个零点当x a <时，则()0f x >；当a x b <<时, 则()0,f x <当x b >时，则()0,f x <故选B 。

7、【解析】要使取出的2张卡片上的数字之和为奇数，则取出的2张卡片上的数字必须一奇一偶，∴取出的2张卡片上的数字之和为奇数的概率11222442.63C C P C ⋅=== 8、【解析】8482(84)(82)(82)(8)8882n n n n n n nn --=-+--=-+数列共有251项，∴结果为(8)2512008-⋅=-，故选A.二、填空题：9、2 10、2 11、－6 12、4 13、80 14、5515、2 9、【解析】λ+a b ＝(2,23)λλ++，则λ+a b 与(47)=--，c 共线242237λλλ+-⇔=⇒=+-10、【解析】'axy ae =，∴切线的斜率0'x k y a ===，∴由1()12a ⋅-=-得2a = 11、【解析】画出可行域知，当4,2x y ==-时，246z y x =---=-为最小值.12、【解析】1110.8248++>，因此输出 4.n =13、【解析】结合题意知该几何体是四棱锥，棱锥的的底面是边长为8和6的长方形，棱锥的高是5， ∴由棱锥的体积公式得1865803V =⨯⨯⨯= 14、【解析】直线sin 2cos 1ρθρθ+=化为直角坐标方程是210x y +-=；圆2cos ρθ=的圆心()1,0到直线210x y +-=的距离是5515、【解析】∵45BNA ∠=︒，∴90BOA ∠=，∵2OM =,23BO =，∴4BM =，∵()()2322328BM MN CM MA ⋅=⋅=+-=，∴2MN =． 三、解答题16、解：（1）解法一：()1cos 23(1cos 2)sin 222x x f x x -+=++2sin 2cos2x x =++22sin(2)4x π=++……………4分∴当2242x k πππ+=+，即()8x k k Z ππ=+∈时，()f x 取得最大值22+.因此，()f x 取得最大值的自变量x 的集合是,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. ……8分解法二：222()(sin cos )sin 22cos f x x x x x =+++1sin 21cos2x x =+++22)4x π=++…………4分∴当2242x k πππ+=+，即()8x k k Z ππ=+∈时，()f x 取得最大值22+因此，()f x 取得最大值的自变量x 的集合是,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭……8分（2）解：()22)4f x x π=++由题意得222()242k x k k Z πππππ-≤+≤+∈，即3()88k x k k Z ππππ-≤≤+∈.因此，()f x 的单调增区间是()3,88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. …………12分 17、解：（1）周销售量为2吨，3吨和4吨的频率分别为0.2，0.5和0.3 ··················· 3分 （2）该商品两周可能销售4、5、6、7、8吨，所以 ξ的可能值为8、10、12、14、16，且P （ξ=8）=0.22=0.04， P （ξ=10）=2×0.2×0.5=0.2， P （ξ=12）=0.52+2×0.2×0.3=0.37， P （ξ=14）=2×0.5×0.3=0.3， P （ξ=16）=0.32=0.09．ξ的分布列为ξ8 10 12 14 16 P0.040.20.370.30.09·········· 9分E ξ=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4（千元） ·····························12分ABC DPE F18、解：（1）∵PC ⊥平面ABC ，AB ⊂平面ABC ，∴PC ⊥AB ．…………………2分∵CD ⊥平面PAB ，AB ⊂平面PAB ，∴CD ⊥AB ． …………………………4分 又PCCD C =，∴AB ⊥平面PCB ． …………………………6分（2）取AP 的中点E ，连结CE 、DE ．∵PC=AC=2， ∴CE ⊥PA ，2．………8分∵CD ⊥平面PAB ， 由三垂线定理的逆定理，得DE ⊥PA ．∴CED ∠为二面角C-PA-B 的平面角． …………………………………10分由（1）AB ⊥平面PCB ，又∵AB=BC ，可求得2． 在Rt PCB ∆中，22PC BC 6+=，PC BC 2CD PB 63⋅===………………12分 在Rt CDE ∆中，cos CED ∠=42DE 33CE 32-==．…13分∴二面角C-PA-B 大小的余弦值为33……………………………14分19、解：（1）函数()f x 的定义域为()1,+∞，……………………………………………1分∵()()221()2111x x f x x x x -⎡⎤'=--=-⎢⎥--⎣⎦，………………………………………2分 ∵1x >，则使()0f x '>的x 的取值范围为()1,2，故函数()f x 的单调递增区间为()1,2． ……………………………………………4分 （2）方法1：∵()()2()2ln 11f x x x =---，∴()2()3012ln 10f x x x a x a x +--=⇔++--=．…………………………6分令()()12ln 1g x x a x =++--， ∵23()111x g x x x -'=-=--，且1x >， 由()03()03g x x g x x ''>><<<得，得1．∴()g x 在区间[2,3]内单调递减，在区间[3,4]内单调递增，……………………9分故2()30f x x x a +--=在区间[]2,4内恰有两个相异实根(2)0,(3)0,(4)0.g g g ≥⎧⎪⇔<⎨⎪≥⎩……12分即30,42ln 20,52ln 30.a a a +≥⎧⎪+-<⎨⎪+-≥⎩解得：2ln352ln 24a -≤<-． 综上所述，a 的取值范围是[)2ln35,2ln 24--．………………………………14分 方法2：∵()()2()2ln 11f x x x =---，∴()2()3012ln 10f x x x a x a x +--=⇔++--=．…………………………6分 即()2ln 11a x x =---，令()()2ln 11h x x x =---， ∵23()111xh x x x -'=-=--，且1x >， 由()03,()03h x x h x x ''><<<>得1得．∴()h x 在区间[2,3]内单调递增，在区间[3,4]内单调递减． ……………………9分 ∵()23h =-，()32ln 24h =-，()42ln35h =-，又()()24h h <，故2()30f x x x a +--=在区间[]2,4内恰有两个相异实根()()43h a h ⇔≤<．即2ln352ln 24a -≤<-． ……………………………………12分 综上所述，a 的取值范围是[)2ln35,2ln 24--． ……………………………14分 20、解法一：（1）由已知得，椭圆C 的左顶点为(2,0),A -上顶点为(0,1),2,1D a b ∴==故椭圆C 的方程为2214x y +=……………………………4分 （2）直线AS 的斜率k 显然存在，且0k >，故可设直线AS 的方程为(2)y k x =+， 从而1016(,)33kM……………………… 5分 由22(2)14y k x x y =+⎧⎪⎨+=⎪⎩得2222(14)16164k x k x k +++-=0 ……………………… 7分 设11(,),S x y 则21228(2)14k x k --⋅=+得2122814k x k -=+，从而12414ky k =+……… 9分即222284(,),1414k kS k k -++又(2,0)B由1(2)4103y x k x ⎧=--⎪⎪⎨⎪=⎪⎩得10313x y k ⎧=⎪⎪⎨⎪=-⎪⎩101(,)33N k ∴-…………………………………… 11分故161||33k MN k =+…………………………………………… 12分 又16116180,||233333k k k MN k k >∴=+≥⋅=当且仅当16133k k =，即14k =时等号成立 14k ∴=时，线段MN 的长度取最小值83……………………………………………14分 21、解：（1）由题可得'()2f x x =． ……………………1分所以曲线()y f x =在点(,())n n x f x 处的切线方程是：()'()()n n n y f x f x x x -=-．即2(4)2()nn n y x x x x --=-．………2分 令0y =，得21(4)2()n n n n x x x x +--=-．即2142n n n x x x ++=．显然0n x ≠，∴122n n nx x x +=+．………………………………………4分 （2）由122n n n x x x +=+，知21(2)22222n n n n nx x x x x +++=++=， ……………………5分 同理21(2)22n n nx x x +--=． 故21122()22n n n n x x x x ++++=--． …………………………6分 从而1122lg2lg 22n n n n x x x x ++++=--，即12n n a a +=．所以，数列{}n a 成等比数列．……7分故111111222lg2lg 32n n n n x a a x ---+===-．即12lg 2lg 32n n n x x -+=-． ……………8分 从而12232n n n x x -+=- 所以11222(31)31n n n x --+=- ……………………………9分 （3）由（2）知11222(31)31n n n x --+=-，∴1242031n n n b x -=-=>- ……………………10分∴111112122223111113313133n n n n n n b b ----+-==<≤=-+ ………………………………11分当1n =时，显然1123T b ==<． …………………………………………12分当1n >时，21121111()()333n n n n b b b b ---<<<< ∴12n n T b b b =+++111111()33n b b b -<+++11[1()]3113n b -=-133()33n =-⋅<…13分 综上，3n T <． ………………14分。