第三章 实验 探究弹力与弹簧伸长量的关系
- 格式:docx
- 大小:35.75 KB
- 文档页数:13


实验专题:探究弹簧弹力和弹簧伸长量的关系答案解析答案解析1.【答案】(1)C(2)等于【解析】(1)因为弹簧是被放在水平桌面上测得的原长,然后把弹簧竖直悬挂起来后,由于重力的作用,弹簧的长度会增大,所以图线应出现x轴上有截距,C正确,A、B、D错误.(2)如果将指针固定在A点的下方P处,在正确测出弹簧原长的情况下,再作出x随F变化的图象,则在图象上x的变化量不变,得出弹簧的劲度系数与实际值相等.2.【解析】(1)F-L图线如图所示:(2)弹簧的原长L0即弹力为零时弹簧的长度,由图象可知,L0=5×10-2m=5 cm.劲度系数为图象直线部分的斜率,k=20 N/m.(3)记录数据的表格如下表(4)优点:可以避免弹簧自身重力对实验的影响.缺点:弹簧与桌面及绳子与滑轮间存在的摩擦会造成实验误差.3.【解析】(1)在做实验的时候一般步骤为先组装器材,然后进行实验,最后数据处理,故顺序为CBDAEF.(2)①根据描点法,图象如图所示②、③根据图象,该直线为过原点的一条直线,即弹力与伸长量成正比,即F=kx=0.43x.式中的常数表示弹簧的劲度系数,即表示使弹簧伸长或者压缩1 cm所需的外力大小为0.43 N.4.【答案】(1)如图所示30F弹=30Δx(2)B(3)A【解析】(1)如图所示,直线的斜率的倒数表示弹簧的劲度系数,即k=,代入数据得kA =N/m≈30 N/m,所以弹簧的弹力大小F弹跟弹簧伸长量Δx的函数关系是F弹=30Δx.5.【解析】(1)描点作图,如图所示:(2)图象的斜率表示劲度系数,故有:k==N/m=50 N/m(3)图线与L轴的交点坐标表示弹簧不挂钩码时的长度,其数值大于弹簧原长,因为弹簧自身重力的影响.6.【答案】(1)6.93(2)A(3)弹簧受到的拉力超过了其弹性限度【解析】(1)弹簧伸长后的总长度为14.66 cm,则伸长量Δl=14.66 cm-7.73 cm=6.93 cm.(2)逐一增挂钩码,便于有规律地描点作图,也可避免因随意增加钩码过多超过弹簧的弹性限度而损坏弹簧.(3)AB段明显偏离直线OA,伸长量Δl不再与弹力F成正比,是超出弹簧的弹性限度造成的.7.【解析】(1)根据题意知,刻度尺的最小刻度为1毫米.读数时,应估读到毫米的十分位,故l5、l6记录有误.(2)按(1)中的读数规则,得l3=6.85 cm,l7=14.05 cm.(3)根据题中求差方法,可知d4=l7-l3=7.20 cm(4)根据l4-l0=4Δl=d1,l5-l1=4Δl=d2,l6-l2=4Δl=d3,l7-l3=4Δl=d4,有Δl==1.75 cm.(5)根据胡克定律F=kx得mg=kΔl,k==N/m=28 N/m8.【答案】(1)450(2)10【解析】(1)当F=0时,弹簧的长度即为原长,由胡克定律可知图象的斜率表示劲度系数大小.(2)弹簧秤的示数为3 N,则伸长量为3/50=0.06 m,则长度为10 cm.9.【解析】(1)描点作出图象,如下图所示.(2)图象跟坐标轴交点的物理意义表示弹簧原长.由图象可知,弹簧的劲度系数应等于直线的斜率,即k==200 N/m.10.【答案】(1)竖直(2)稳定L3 1 mm(3)Lx(4)4.910【解析】(1)为保证弹簧的形变只由砝码和砝码盘的重力产生,所以弹簧轴线和刻度尺均应在竖直方向.(2)弹簧静止稳定时,记录原长L0;表中的数据L3与其他数据有效位数不同,所以数据L3不规范,标准数据应读至cm位的后两位,最后一位应为估读值,精确至0.1 mm,所以刻度尺的最小分度为1 mm.(3)由题图知所挂砝码质量为0时,x为0,所以x=L-Lx(L为弹簧长度).(4)由胡克定律F=kΔx知,mg=k(L-Lx),即mg=kx,所以图线斜率即为弹簧的劲度系数k==N/m=4.9 N/m同理,砝码盘质量m==kg=0.01 kg=10 g11.【解析】(1)根据表格中的各组数据在坐标纸上标出相应的点,然后用平滑曲线连接这些点,作出的图象如图所示.(2)根据作出的图线可知,钩码质量在0~500 g范围内图线是直线,表明弹力大小与弹簧伸长量关系满足胡克定律.在这个范围内的曲线上找到相距较远的两点,利用这两点的坐标值计算弹簧的劲度系数k==N/m=25.00 N/m.12.【解析】(1)本题考查探究弹簧弹力与形变关系的实验,意在考查考生对实验步骤的识记、实验数据的处理方法、分析归纳能力.根据实验先后顺序可知,实验步骤排列为CBDAEF.(2)②由图象可得k==0.43 N/cm,所以F=0.43x(N).13.【答案】(1)10(2)200(3)b【解析】(1)当F=0时,弹簧长度为原长,由题图得,原长为10 cm.(2)由公式F=kx得k===N/m=200 N/m(3)当弹簧长度小于原长时,处于压缩状态,故是图线b14.【答案】(1)弹簧测力计刻度尺(2)kFL(3)控制变量法(4)12.5【解析】(1)用弹簧测力计测量力的大小,用刻度尺测量长度.(2)由题目所给数据分析可知:当力一定时,伸长量和长度成正比;当长度一定时,伸长量和力成正比,故有x=kFL(取一组数据验证,式中的k不为零).(3)研究伸长量与拉力、长度的关系时,可以先控制其中一个量不变,如长度不变,再研究伸长量和拉力的关系,这种方法称为控制变量法.这是物理实验中的一个重要研究方法.(4)代入表中数据把式中的k求出,得k=0.000 8 N-1,再代入已知数据,L=20 cm,x=0.2 cm,可求得最大拉力F=12.5 N.15.【答案】CBDAEFG【解析】根据实验的实验操作过程应先安装仪器,再挂钩码然后记录数据,分析数据,最后整理即可,排列先后顺序为CBDAEFG.。

实验:探究弹力和弹簧伸长的一、实验目的1.探究弹力与弹簧伸长的关系。
2.学会利用列表法、图像法、函数法处理实验数据。
3.验证胡克定律。
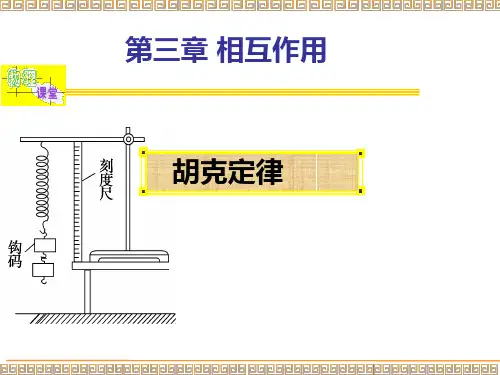
二、实验原理1.如图所示,在弹簧下端悬挂钩码时弹簧会伸长,平衡时弹簧产生的弹力与所挂钩码的重力大小相等。
2.弹簧的长度可用刻度尺直接测出,伸长量可以由拉长后的长度减去弹簧原来的长度进行计算。
这样就可以研究弹簧的弹力和弹簧伸长量之间的定量关系了。
3.求弹簧的劲度系数弹簧的弹力F 与其伸长量x 成正比,比例系数k =F x,即为弹簧的劲度系数;另外,在F x 图像中,直线的斜率也等于弹簧的劲度系数。
三、实验器材铁架台、弹簧、毫米刻度尺、钩码若干、坐标纸。
四、实验步骤1.按下图安装实验装置,记下弹簧下端不挂钩码时所对应的刻度l 0。
2.在弹簧下端悬挂一个钩码,平衡时记下弹簧的总长度并记下钩码的重力。
3.增加钩码的个数,重复上述实验过程,将数据填入表格,以F 表示弹力,l 表示弹簧的总长度,x =l -l 0表示弹簧的伸长量。
五、数据处理1.以弹力F (大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x 为横坐标,用描点法作图。
连接各点,得出弹力F 随弹簧伸长量x 变化的图线,如图所示。
2.以弹簧伸长量为自变量,写出弹力和弹簧伸长量之间的函数关系,函数表达式中常数即为弹簧的劲度系数,这个常数也可据F x 图线的斜率求解,k =ΔFΔx。
六、误差分析由于弹簧原长及伸长量的测量都不便于操作,存在较大的测量误差,另外由于弹簧自身的重力的影响,即当未放重物时,弹簧在自身重力的作用下,已经有一个伸长量,这样所作图线往往不过原点。
七、注意事项1.所挂钩码不要过重,以免弹簧被过分拉伸,超出它的弹性限度。
2.每次所挂钩码的质量差尽量大一些,从而使坐标上描的点尽可能稀一些,这样作出的图线精确。
3.测弹簧长度时,一定要在弹簧竖直悬挂且处于平衡状态时测量,刻度尺要保持竖直并靠近弹簧,以免增大误差。

实验:探究弹力和弹簧伸长的关系一、实验目的1.探究弹力和弹簧伸长量的关系.2.学会利用图象法处理实验数据,探究物理规律.二、实验原理1.如图所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧产生的弹力与所挂钩码的重力大小相等.2.用刻度尺测出弹簧在不同钩码拉力下的伸长量x,建立直角坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描出实验所测得的各组(x、F)对应的点,用平滑的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系.三、实验器材铁架台、弹簧、毫米刻度尺、钩码若干、三角板、坐标纸、重锤线.四、实验步骤1.将弹簧的一端挂在铁架台上,让其自然下垂,用刻度尺测出弹簧自然伸长状态时的长度l0,即原长.2.如图所示,在弹簧下端挂质量为m1的钩码,测出此时弹簧的长度l1,记录m1和l1,填入自己设计的表格中.3.改变所挂钩码的质量,测出对应的弹簧长度,记录m2、m3、m4、m5和相应的弹簧长度l2、l3、l4、l5,并得出每次弹簧的伸长量x1、x2、x3、x4、x5.五、数据处理1.以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线.六、误差分析1.钩码标值不准确造成系统误差.2.弹簧长度的测量和作图时造成偶然误差.七、注意事项1.所挂钩码不要过重,以免弹簧被过分拉伸,超出它的弹性限度,要注意观察,适可而止.2.每次所挂钩码的质量差适当大一些,从而使坐标点的间距尽可能大,这样作出的图线准确度更高一些.3.测弹簧长度时,一定要在弹簧竖直悬挂且处于稳定状态时测量,以免增大误差.4.描点画线时,所描的点不一定都落在一条直线上,但应注意一定要使不在直线上的点均匀分布在直线的两侧.5.记录实验数据时要注意弹力、弹簧的原长l0、总长l及弹簧伸长量的对应关系及单位.6.坐标轴的标度要适中.考点一实验原理及操作[典例1]某同学做“探究弹力和弹簧伸长量的关系”的实验.(1)图甲是不挂钩码时弹簧下端指针所指的标尺刻度,其示数为7.73 cm;图乙是在弹簧下端悬挂钩码后指针所指的标尺刻度,此时弹簧的伸长量Δl为________ cm.(2)本实验通过在弹簧下端悬挂钩码的方法来改变弹簧的弹力,关于此操作,下列选项中规范的做法是________(填选项前的字母).A.逐一增挂钩码,记下每增加一只钩码后指针所指的标尺刻度和对应的钩码的总重B.随意增减钩码,记下增减钩码后指针所指的标尺刻度和对应的钩码总重(3)图丙是该同学描绘的弹簧的伸长量Δl与弹力F的关系图线,图线的AB段明显偏离直线OA,造成这种现象的主要原因是________________.答案(1)6.93(6.92~6.94均正确)(2)A(3)超过弹簧的弹性限度考点二数据处理及误差分析[典例2]某实验小组做“探究弹力和弹簧伸长量的关系”实验,实验时,先把弹簧平放在桌面上,用直尺测出弹簧的原长L0=4.6 cm,再把弹簧竖直悬挂起来,在下端挂钩码,每增加一只钩码均记下对应的弹簧长度x,数据记录如下表所示.(1)根据表中数据作出F-x图线;(2)由此图线可得,该弹簧劲度系数k=________N/m.(3)图线与x轴的交点坐标大于L0的原因是_____________.答案(1)见图(2)50(3)未考虑弹簧自身重力的影响考点三实验改进拓展创新以本实验为背景,通过改变实验条件、实验仪器设置题目,不脱离教材而又不拘泥于教材,体现开放性、探究性等特点.1.实验器材的改进弹簧的弹力直接由力传感器测得,数据处理由计算机处理.2.实验的拓展延伸将弹簧水平放置或穿过一根水平光滑的直杆,在水平方向上做实验,消除了弹簧自重的影响.[典例3]在“探究弹力和弹簧伸长量的关系并测定弹簧的劲度系数”实验中,实验装置如图甲所示.右侧挂上钩码,相当于对弹簧提供了向右恒定的拉力.实验时先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在绳子的下端,每次测出相应的弹簧总长度L.(1)有一个同学通过以上实验测量后把6组数据在坐标纸中描点,如图乙所示.请作出F-L图线.(2)由此图线可得出该弹簧的原长L0=________ cm,劲度系数k=________ N/m.(3)试根据以上该同学的实验情况,帮助他设计一个记录实验数据的表格(不必填写其实验测得的具体数据).(4)该同学实验时,把弹簧水平放置与弹簧悬挂放置相比较,优点在于:_____________________;缺点在于:_____ ________________ _________.答案(1)见图(2)520(3)见图(4)避免弹簧自身所受重力对实验的影响弹簧与桌面及绳子与滑轮间存在的摩擦造成的实验误差增大1.(多选)如图甲所示,一个弹簧一端固定在传感器上,传感器与电脑相连.当对弹簧施加变化的作用力(拉力或压力)时,在电脑上得到了弹簧形变量与弹簧产生的弹力大小的关系图象,如图乙所示.则下列判断正确的是()A.弹簧产生的弹力和弹簧的长度成正比B.弹簧长度的增加量与对应的弹力增加量成正比C.该弹簧的劲度系数是200 N/mD.该弹簧受到反向压力时,劲度系数不变解析:选BCD.2.在“探究弹力和弹簧伸长的关系”时,某同学把两根弹簧如图甲连接起来进行探究.(1)某次测量如图乙所示,指针示数为________cm.(2)在弹性限度内,将50 g的钩码逐个挂在弹簧下端,得到指针A、B的示数L A和L B如表.用表中数据计算弹簧Ⅰ的劲度系数为________N/m(重力加速度g=10 m/s2).由表数据________(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数.答案:(1)16.00(有效数字位数正确,15.96~16.05均可) (2)12.45(12.20~12.80均可)解析:(1)刻度尺分度值为1毫米,读数应估读到毫米下一位,故指针的示数为16.00 cm.(2)当A弹簧的弹力为F A1=0.50 N、F A2=1.00 N、F A3=1.50 N、F A4=2.00 N时,弹簧长度L A1=15.71 cm、L A2=19.71 cm、L A3=23.66 cm、L A4=27.76 cm,根据ΔF=kΔx得k1=12.50 N/m、k2=12.66N/m、k3=12.20 N/m,所以弹簧Ⅰ的劲度系数k=k1+k2+k33=12.45 N/m.根据表可以计算出弹簧Ⅱ每次的伸长量Δx′,也可以根据ΔF=k′Δx′计算弹簧Ⅱ的劲度系数(劲度系数的计算也可以通过作F-x 图象处理,图象的斜率即等于弹簧的劲度系数).实验:探究弹力和弹簧伸长的关系—课后作业1.为了测量某一弹簧的劲度系数,将该弹簧竖直悬挂起来,在自由端挂上不同质量的砝码.实验测出了砝码质量m与弹簧长度l的相应数据,其对应点已在图上标出(g取9.8 m/s2)(1)作出m-l的关系图线;(2)弹簧的劲度系数为________ N/m.答案:(1)如图所示(2)0.258(0.248~0.262)2.如图甲所示,用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系.(1)为完成实验,还需要的实验器材有;________.(2)实验中需要测量的物理量有:___________________________.(3)图乙是弹簧弹力F与弹簧伸长量x的F-x图线,由此可求出弹簧的劲度系数为________ N/m.图线不过原点是由于_________________________.(4)为完成该实验,设计的实验步骤如下:A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组(x,F)对应的点,并用平滑的曲线连接起来;B.记下弹簧不挂钩码时其下端在刻度尺上的刻度l0;C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一把刻度尺;D.依次在弹簧下端挂上1个、2个、3个、4个…钩码,并分别记下钩码静止时弹簧下端所对应的刻度,并记录在表格内,然后取下钩码;E.以弹簧伸长量为自变量,写出弹力与伸长量的关系式.首先尝试写成一次函数,如果不行,则考虑二次函数;F.解释函数表达式中常数的物理意义;G.整理仪器.请将以上步骤按操作的先后顺序排列出来:_____ ___.答案:(1)刻度尺(2)弹簧原长、弹簧所受外力与对应的伸长量(或与弹簧对应的长度)(3)200弹簧自重(4)CBDAEFG3.某同学探究弹力与弹簧伸长量的关系.(1)将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在________方向(填“水平”或“竖直”).(2)弹簧自然悬挂,待弹簧________时,长度记为L0;弹簧下端挂上砝码盘时,长度记为L x;在砝码盘中每次增加10 g砝码,弹簧长度依次记为L1至L6,数据如下表:.(3)如图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与________的差值(填“L0”或“L x”).(4)由图可知弹簧的劲度系数为________ N/m;通过图和表可知砝码盘的质量为________ g(保留两位有效数字,重力加速度取9.8 m/s2).答案:(1)竖直(2)静止L3 1 mm(3)L x (4)4.9104.某同学利用如图甲所示装置做“探究弹簧弹力大小与其长度的关系”的实验.(1)在安装刻度尺时,必须使刻度尺保持________状态(填“水平”或“竖直”).(2)他通过实验得到如图乙所示的弹力大小F与弹簧长度x的关系图线.由此图线可得该弹簧的原长x0=________cm,劲度系数k=________ N/m.(3)他又利用本实验原理把该弹簧做成一把弹簧秤,当弹簧秤上的示数如图丙所示时,该弹簧的长度x=________ cm.答案:(1)竖直(2)4.0050(3)10解析:(1)刻度尺应保持竖直状态以保障与弹簧轴线平行.(2)图线在横轴上的截距等于弹簧的原长x0=4.00 cm,图线斜率等于弹簧的劲度系数k=50 N/m.(3)把该弹簧做成一把弹簧秤,当弹簧秤上的示数为3.0 N时,弹簧伸长量Δx=6 cm.此时弹簧的长度x=x0+Δx=10 cm.5.为了探究弹力F 和弹簧伸长x 的关系,某同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示图象.(1)从图象上看,该同学没能完全按照实验要求做,从而使图象上端成为曲线,图象上端成为曲线是因为________________.(2)甲、乙弹簧的劲度系数分别为________ N/m 和________ N/m(保留三位有效数字);若要制作一个精确度较高的弹簧测力计,应选弹簧________(填“甲”或“乙”).(3)从上述数据和图线中分析,请对这个研究课题提出一个有价值的建议. 建议:_______________________.答案:(1)弹簧形变量超过其弹性限度 (2)66.7 200 甲(3)建议:实验中钩码不能挂太多,以保证弹簧在弹性限度内.解析:(1)在弹性限度内弹簧的弹力与形变量成正比,超过弹簧的弹性限度,则此规律不成立,所以所给的图象上端为曲线,是因为弹簧形变量超过其弹性限度.(2)甲、乙两根弹簧的劲度系数分别为 k 甲=ΔF 甲Δx 甲=46×10-2N/m ≈66.7 N/m k 乙=ΔF 乙Δx 乙=84×10-2N/m =200 N/m要制作一个精确度较高的弹簧测力计,应选用在一定的外力作用时,弹簧的形变量大的弹簧,故选甲弹簧.(3)建议:实验中钩码不能挂太多,以保证弹簧在弹性限度内.。

弹簧弹力与伸长量的关系的实验报告在这个实验中,我们要聊聊弹簧弹力与伸长量之间的关系。
咱们得准备一根弹簧。
嘿,别小看它,这小家伙可有大用处。
你有没有想过,当你用手拉弹簧时,它的反应会是什么?我告诉你,弹簧就像一个不太愿意被拉扯的朋友,越拉越紧,但也会给你一定的回馈。
这样一来,咱们就可以用一些简单的工具来测量弹簧的伸长量,看看它到底有多能忍。
准备好几块重物,比如小砖头或书本,放在弹簧上。
每加一块重量,弹簧就会往下掉一段,嘿,这就是伸长量啦!你可能会觉得无聊,但其实这个过程就像给弹簧做体检,每次加重量,它就像在说:“哎呀,这可真沉啊!”。
通过记录下每次的重量和弹簧的伸长量,我们就能慢慢揭开它的秘密。
用个笔记本,把这些数据都记下来,简直就像在收集情报,真是有趣!然后,咱们就得好好分析一下这些数据。
你会发现,弹簧的伸长量和施加的重量之间似乎有一种神奇的联系。
每次加重,弹簧的伸长量也会随之增加。
哇,这就像是一种默契,彼此之间心有灵犀,完全不需要多说。
这种关系其实就是著名的胡克定律,简单来说,就是“拉得越多,伸得越远”。
想象一下,如果弹簧有声音,它可能会无奈地叹气:“再来一块吧,我可以承受更多!”在实验的过程中,可能会遇到一些小麻烦,比如弹簧过度伸展,甚至可能会变形。
不过没关系,这就像生活中遇到的挑战,总会有解决的办法。
只要咱们认真记录和观察,就能找到规律。
每当你看到弹簧因重物而变长时,心里是不是也有种说不出的满足感?就像看到自己的努力得到了回报,真是令人振奋。
说到这里,咱们得聊聊实验的结果。
这些数据汇总起来后,我们就能绘制出一条漂亮的图表。
想象一下,坐在桌子前,手里拿着铅笔,心里想着“我要画出一条完美的曲线”,真的是一种小小的成就感。
图表上每一个点都是我们的心血,见证了弹簧的“奋战”。
当看到这些点连成线时,那种感觉就像是看到了美妙的风景,心中满是骄傲。
咱们得总结一下这个实验的意义。
通过这个小实验,不仅能了解弹簧的性质,还能培养我们观察和分析的能力。


实验探究:弹力与弹簧伸长量的关系
班级姓名
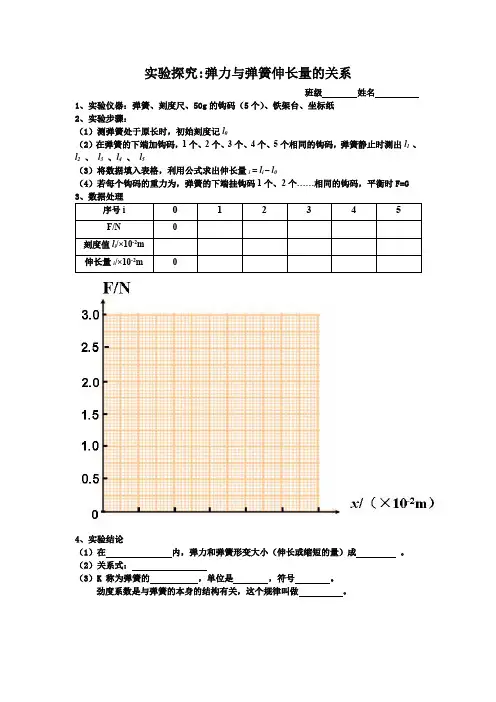
1、实验仪器:弹簧、刻度尺、50g的钩码(5个)、铁架台、坐标纸
2、实验步骤:
(1)测弹簧处于原长时,初始刻度记l0
(2)在弹簧的下端加钩码,1个、2个、3个、4个、5个相同的钩码,弹簧静止时测出l1、l2、l3、l4、l5
(3)将数据填入表格,利用公式求出伸长量i = l i– l0
(4)若每个钩码的重力为,弹簧的下端挂钩码1个、2个……相同的钩码,平衡时F=G 3、数据处理
4、实验结论
(1)在内,弹力和弹簧形变大小(伸长或缩短的量)成。
(2)关系式:
(3)K 称为弹簧的,单位是,符号。
劲度系数是与弹簧的本身的结构有关,这个规律叫做。

实验二:探究弹力和弹簧伸长量的关系实验报告一、实验背景弹力,又称内弹力,是构成物体的物质间的内部相互作用。
当物体遭受外力的刺激时,在物体内部的分子及其成分之间会产生弹力,使物体返回到原来的形状,这样形成的弹力就是弹力。
弹力能够恢复物体原来的形状,是物体具有自保能力的根本原因[1]。
弹簧伸长量,也称为弹簧长度,是指装在被测物上的弹簧释放力时弹簧的伸长量,即弹簧从原来的状态(停机时的状态)变为被测物的形状,弹簧所增加的长度,以毫米为单位。
二、实验目的、实验材料、实验程序实验目的:探究普通小弹簧的弹力与伸长量的关系,为今后的科研提供参考依据。
实验材料:(1)弹簧1条;(2)勒耳器;(3)千分尺;实验程序:Step1:先用勒耳器将弹簧固定在实验架上;Step2:让弹簧从放松状态开始,将千分尺安装在弹簧上;Step3:弹簧被施加一定力时,记录下弹簧伸长量(以毫米为单位);Step4:记录应用力的大小(以牛顿为单位);Step5:重复上述步骤,并记录下弹簧的伸长量及力的大小;Step6:进行数据处理和数据分析,得出弹力与弹簧伸长量的关系。
三、实验数据及结果表1 力与弹簧伸长量的关系应用力/N 弹簧伸长量/mm0 01 0.54 2.05 2.56 3.07 3.59 4.5从上表可知,随着力的大小增加,弹簧伸长量也在增加,当力达到9牛时,弹簧伸长量达到了4.5mm。
从上图中可以看出,随着施加的力的增大,弹簧的伸长量呈正比增大,可以解释弹力大小与弹簧伸长量之间的正比例关系。
四、实验结论通过此次实验研究,可以得出结论:普通小弹簧的弹力与伸长量是成正比关系的,即随着施加的力的增大,弹簧的伸长量会呈正比增大。
让物体返回原来的形状,这样形成的弹力就是弹力,可以用正比例模型来描述它们之间的关系。
五、结论总结本次实验让我们了解到,弹力与弹簧伸长量是一个正比的关系,就是说,力的大小越大,弹簧的伸长量就越大,弹力也会越大。
本次实验为今后的科研提供了参考,也提升了我们实践能力。

知识创新型实验。
例如设计型、开放型、探讨型实验等都有不同程度的创新,比如利用所学知识设计出很多测量重力加速度的实验方案。
其中,力学设计性实验在近年高考中有加强的趋势,应引起高度重视。
【实验目的】1.探索弹力与弹簧伸长的定量关系2.学习通过对实验数据的数学分析(列表法和图像法),探究弹簧产生的弹力与弹簧伸长之间的变化规律【实验原理】通常用悬挂钩码的方法给弹簧施加拉力,弹簧受到拉力会伸长,平衡时弹簧产生的弹力和外力大小相等.这样弹力的大小可以通过测定外力而得出;弹簧的伸长量可用直尺测出.多测几组数据,用列表或作图的方法探索出弹力和弹簧伸长的定量关系.(弹簧受到拉力会伸长,平衡时弹簧产生的弹力和外力大小相等,弹簧的伸长越大;弹力也就越大。
)【实验器材】弹簧,相同质量的砝码若干,铁架台一个(用来悬挂弹簧),刻度尺。
【实验步骤】(1)将铁架台放在实验桌上,将弹簧悬挂在铁架台上。
弹簧竖直静止时,测出弹簧的原长l0,并填入实验记录中。
(2)依次在弹簧下挂上一个砝码、两个砝码、三个砝码……。
每次,在砝码处于静止状态时,测出弹簧的总长或伸长,并填入实验记录中。
(3)根据测得的数据,以力F为纵坐标,以弹簧的伸长量Δl为横坐标,根据表中所测数据在坐标纸上描点。
(4)作弹簧的F-Δl 图像。
按照坐标图中各点的分布与走向,尝试作出一条平滑的曲线(包括直线)。
所画的点不一定正好在这条曲线上,但要注意使曲线两侧的点数大致相同。
(5)以弹簧的伸长为自变量,写出曲线所代表的函数,首先尝试一次函数,如果不行则考虑二次函数……(6)解释函数表达式中常数的物理意义。
【实验数据记录和处理】 弹簧原长l 0=_______________m弹簧F-Δl 实验图像:【实验结论】弹簧弹力大小跟弹簧伸长长度的函数表达式 。
可见,在弹簧的弹性限度内,弹簧的弹力跟弹簧的伸长量成正比(胡克定律)。
【问题与讨论】1.上述函数表达式中常数的物理意义2.如果以弹簧的总长为自变量,所写出的函数式应为 3.某同学在做实验时得到下列一组数据,他由数据计算出弹簧的劲度系数为m /N 781020.35.2l F k 2=⨯==-∆试分析他对数据处理的方法是否正确?为什么?4.根据测量数据画出F-x图象:F-x图象的斜率的物理意义为弹簧的劲度系数k.第一象限的图象表示拉伸弹簧时弹力与弹簧伸长量的关系;第三象限的图象表示压缩弹簧时弹力与弹簧压缩量的关系.5.得出实验结论:在弹性限度内,弹簧的弹力F和弹簧的形变量x成正比,即F=kx,这就是胡克定律.其中x为弹簧伸长或缩短的长度(弹簧的形变量);k为弹簧的劲度系数.注意事项:(1)给弹簧施加拉力不要太大,以免弹簧被过分拉伸,超出它的弹性限度.(2)测量弹簧长度时,不要用手拉弹簧,在弹簧自然竖直状态去测量.【基础练习】某同学在做探究弹力和弹簧伸长的关系的实验中,设计了如图所示的实验装置。
高中物理实验探究弹力和弹簧伸长的关系实验报告及实验专题强化训练【实验报告】一、实验目的1.探究弹力和弹簧伸长的定量关系(验证定律)。
2.学会利用图像研究两个物理量之间的关系的方法。
二、实验原理1.如图所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧的弹力与所挂钩码的重力。
2.用刻度尺测出弹簧在不同的钩码拉力下的伸长量x。
3.建立坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描出实验所测得的各组(x、F)对应的点,用平滑的曲线连接起来,根据实验所得的图线,就可探究弹簧的弹力和弹簧伸长量的关系。
三、实验器材轻质弹簧(一根)、钩码(一盒)、、铁架台、铅笔、重锤线、、三角板。
四、实验步骤1.如图所示,将铁架台放于桌面上固定好,将弹簧的一端固定于铁架台的横梁上,在靠近弹簧处将刻度尺(最小分度为1mm)固定于铁架台上,并用检查刻度尺是否竖直。
2.记下弹簧下端不挂钩码时所对应的刻度L0,即弹簧的原长。
3.在弹簧下端挂上一个钩码,待钩码静止后,记下弹簧下端所对应的刻度L1。
4.利用上面的方法,记下弹簧下端挂2个、3个、4个……钩码时,弹簧下端所对应的刻度L2、L3、L4……并将所得的数据记录在表格中。
5.用x n=L n-L0计算出弹簧挂1个、2个、3个……钩码时弹簧的伸长量x,并根据当地的重力加速度值g,计算出所挂钩码的总重力,这个重力就等于的大小,将所得的数据记录在表格中。
五、数据处理1.以弹力F为纵坐标,以弹簧的伸长量x为横坐标,在坐标系中描出实验所测得的各组(x、F)对应的点,用平滑的曲线连接起来,得到弹力F随弹簧伸长量x变化的图线。
2.以弹簧的伸长量为自变量,写出图线所代表的函数表达式,并解释函数表达式中常数的物理意义。
六、误差分析1.系统误差:钩码标值不准确和弹簧自身重力的影响造成的系统误差。
2.偶然误差:(1)弹簧长度的测量造成偶然误差,为了减小这种误差,要尽量多测几组数据。
(2)作图时的不规范造成的偶然误差,为了减小这种误差,画图要用铅笔作图,所描各点尽量放在一条直线上,不在直线上的点均匀地分布在直线的两侧。
实验探究弹力与弹簧伸长量的关系[学习目标]1.探究弹力与弹簧伸长量之间的关系.2.学会利用列表法、图象法、函数法处理实验数据.3.能根据F-x、F-L图象求出弹簧的劲度系数.一、实验目的1.探究弹力与弹簧伸长量之间的关系.2.学会利用列表法、图象法、函数法处理实验数据.3.能根据F-x、F-L图象求出弹簧的劲度系数.二、实验器材弹簧、刻度尺、钩码、铁架台.三、实验原理1.如图1甲所示,在弹簧下端悬挂钩码时弹簧会伸长,平衡时弹簧产生的弹力与所挂钩码受到的重力大小相等.如图乙,弹簧的原长与挂上钩码后弹簧的长度可以用刻度尺测出,其伸长量x可以用弹簧的长度减去弹簧的原长来求得.图12.建立平面直角坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描出实验所测得的各组(x,F)对应的点,用平滑曲线连接起来,根据实验所得的图象,就可探究弹力大小与弹簧伸长量之间的关系.四、实验步骤1.将弹簧的一端挂在铁架台上,让其自然下垂,用刻度尺测出弹簧自然伸长状态时的长度L0,即原长.图22.如图2所示,在弹簧下端挂质量为m1的钩码,测出此时弹簧的长度L1,记录m1和L1.3.改变所挂钩码的质量,测出对应的弹簧长度,记录m2、m3、m4、m5、…和相应的弹簧长度L2、L3、L4、L5、….4.计算出每次弹簧的伸长量x(x=L-L0)和弹簧受到的拉力F(F=mg),并将数据填入表格.五、数据处理1.建立直角坐标系,以F为纵轴、x为横轴,根据测量数据用描点法作图.连接各点得出F随弹簧伸长量x变化的图线.2.以弹簧的伸长量为自变量,写出图线所代表的函数.首先尝试一次函数,如果不行则考虑二次函数.3.得出弹力和弹簧伸长量之间的定量关系,解释函数表达式中常数的物理意义.六、误差分析1.本实验误差的主要来源为读数和作图时的偶然误差.为了减小误差,要尽量多测几组数据.2.弹簧竖直悬挂时,未考虑弹簧自身重力的影响会带来系统误差.为了减小该系统误差,实验中应使用轻质弹簧.一、实验原理及操作例1以下是某同学所进行的“探究弹力与弹簧伸长量的关系”的实验步骤:(1)将一个弹簧的上端固定在铁架台上,竖直悬挂起来,在弹簧下挂一个钩码,记下钩码的质量m1,此时弹簧平衡,弹力大小为F1=m1g,并用刻度尺测量出此时弹簧的长度L1,并记录到表格中.(2)再增加钩码,重复上述的操作,得到多组数据.(3)以力F为纵坐标,以弹簧长度L x为横坐标,根据所测的数据在坐标纸上描点.(4)按坐标纸上所描各点的分布与走向,作出一条平滑的曲线(包括直线).(5)根据图线的特点,分析弹簧的弹力F与弹簧长度L x的关系,并得出实验结论.以上步骤中至少有三个不当之处,请将不合理的地方找出来并进行修正.答案见解析解析(1)中还应该测出弹簧的原长L0,此时应在不挂钩码的情况下,让弹簧保持自然下垂状态,用刻度尺测出从悬点到弹簧下端的长度即为L0;(3)中建立坐标系时应该以弹簧的伸长量为横坐标,因为探究的是弹力与弹簧伸长量的关系;(5)中应分析弹力与弹簧伸长量的关系.1.实验中弹簧下端挂的钩码不要太多,以免超出弹簧的弹性限度.2.测量长度时,应区别弹簧原长L0、实际长度L及伸长量x三者之间的不同,明确三者之间的关系.为了减小弹簧自身重力带来的影响,测弹簧原长时应让弹簧在不挂钩码时保持自然下垂状态,而不是平放在水平面上处于自然伸长状态.3.记录数据时要注意弹力及伸长量的对应关系及单位.4.描点作图时,应使尽量多的点落在画出的线上,可允许少数点分布于线两侧,描出的线不应是折线,而应是平滑的曲线或直线.5.尽量选轻质弹簧以减小弹簧自身重力带来的影响.二、实验数据的处理例2某同学探究弹力与弹簧伸长量的关系. (1)将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧.弹簧轴线和刻度尺都应在________方向(填“水平”或“竖直”).(2)弹簧自然悬挂,待弹簧________时,长度记为L0;弹簧下端挂上砝码盘时,长度记为L x;在砝码盘中每次增加10 g砝码,弹簧长度依次记为L1至L6.数据如下表.________.(3)图3是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与________的差值(填“L0”或“L x”).图3(4)由图可知弹簧的劲度系数为________N/m;通过图和表可知砝码盘的质量为________g.(结果保留两位有效数字,重力加速度g取9.8 N/kg)答案(1)竖直(2)稳定L3 1 mm(3)L x(4)4.910解析(1)为保证弹簧的形变只由砝码和砝码盘的重力产生,弹簧轴线和刻度尺均应在竖直方向.(2)弹簧静止稳定时,记录原长L0;表中的数据L3与其他数据有效位数不同,所以数据L3不规范,标准数据应读至cm位的后两位,最后一位应为估读值,所以刻度尺的最小分度为1 mm.(3)由题图知所挂砝码质量为0时,x为0,所以x=L-L x(L为弹簧长度).(4)由胡克定律F=kx知,mg=k(L-L x),即mg=kx,所以图线斜率即为弹簧的劲度系数k =Δmg Δx =(60-10)×10-3×9.8(12-2)×10-2 N /m =4.9 N/m同理,砝码盘的质量m ′=k (L x -L 0)g =4.9×(27.35-25.35)×10-29.8 kg=0.01 kg =10 g.1.Fx 图象应是过原点的直线,直线的斜率等于弹簧的劲度系数.2.FL 图象是不过原点的直线,其与横轴的截距等于弹簧的原长,斜率仍然等于弹簧的劲度系数.三、误差分析例3 某同学做“探究弹力与弹簧伸长量的关系”的实验,他先把弹簧放在水平桌面上使其自然伸展,用直尺测出其长度L0,再把弹簧竖直悬挂起来,刻度尺的零刻度线跟弹簧上端对齐,在弹簧的下部A处固定一个指针.如图4所示.挂上钩码,平衡后测出其长度L,令x=L-L0.改变钩码个数,进行多次测量.图4(1)用F表示弹簧下端受到的钩码的拉力,则如图所示的Fx图线,你认为符合实际情况的是()(2)如果将指针固定在A点的下方P处,在正确测出弹簧原长的情况下,再作出x随F变化的图象,此时弹簧劲度系数的测量值____________实际值(填“大于”“小于”或“等于”).答案(1)C(2)等于解析(1)因为弹簧是被放在水平桌面上测得的原长,然后把弹簧竖直悬挂起来后,由于自身重力的作用,弹簧的长度会增大,所以图线应在x轴正方向上有截距,C正确,A、B、D错误.(2)如果将指针固定在A点的下方P处,在正确测出弹簧原长的情况下,再作出x随F变化的图象,则在图象上x的变化量不变,得出弹簧的劲度系数与实际值相等.四、创新实验例4在“探究弹力与弹簧伸长量的关系,并测定弹簧的劲度系数”的实验中,实验装置如图5所示.所用的每个钩码的重力相当于对弹簧提供了向右恒定的拉力.实验时先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在绳子的下端,每次测出相应的弹簧总长度.图5(1)有一个同学通过以上实验测量后把6组数据描点在图6坐标系中,请作出F—L图线.图6(2)由此图线可得出该弹簧的原长L0=________ cm,劲度系数k=________ N/m.(3)试根据该同学以上的实验情况,帮助他设计一个记录实验数据的表格(不必填写其实验测得的具体数据).(4)该同学实验时,把弹簧水平放置与弹簧悬挂放置相比较,优点在于:_______________,缺点在于:______________________.答案见解析解析(1)F—L图线如图所示:(2)弹簧的原长L0即弹力为零时弹簧的长度,由图象可知,L0=5×10-2 m=5 cm.劲度系数为图象直线部分的斜率,k=20 N/m.(3)记录实验数据的表格如下表(4)优点是:可以避免弹簧自身重力对实验的影响.缺点是:弹簧与桌面及绳子与滑轮间存在的摩擦会造成实验误差.1.(实验器材及原理)(多选)在“探究弹力与弹簧伸长量的关系”实验中,以下说法正确的是()A.弹簧被拉伸时,不能超出它的弹性限度B.用悬挂钩码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态C.用刻度尺测得弹簧的长度即为弹簧的伸长量D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等答案AB2.(实验过程及数据处理)一位同学在做“探究弹力与弹簧伸长量的关系”的实验.(1)下列的实验步骤是这位同学准备完成的,请你帮这位同学按操作的先后顺序,将这些步骤用字母排列出来是________.A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连接起来B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0C.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺D.依次在弹簧下端挂上1个、2个、3个、4个……钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式F.解释函数表达式中常数的物理意义(2)下表是这位同学所测的几组数据①根据上表的数据在图7的坐标系中作出F-x图线.图7②写出曲线的函数表达式________(x用cm作单位).③函数表达式中常数的物理意义:_______________________________________________.答案(1)CBDAEF(2)①如图所示②F=0.43x③表示弹簧的劲度系数,即表示使弹簧伸长或者压缩1 cm所需的外力大小为0.43 N解析(1)在做实验的时候一般步骤为先组装器材,然后进行实验,最后处理数据,故顺序为CBDAEF.(2)①根据描点法,图象如图所示②、③根据图象,该直线为过原点的一条直线,即弹力与伸长量成正比,即F=kx=0.43x.式中的常数表示弹簧的劲度系数,即表示使弹簧伸长或者压缩1 cm所需的外力大小为0.43 N.3.(实验误差分析)在“探究弹力与弹簧伸长量的关系”实验中,根据数据作出Fx图象如图8实线所示,可能的原因是()图8A.悬挂的钩码多,拉力超过了弹簧的弹性限度B.用直尺测量弹簧的长度时,读数小了C.有的数据不是弹簧的伸长,而是弹簧的长度D.所有数据都是用弹簧长度进行处理的答案A解析弯曲部分显示:当x达到某一值后,F与x不再成正比,前面数据呈线性分布,说明不是读数问题,而是拉力超出了弹簧的弹性限度.一、选择题1.在“探究弹力与弹簧伸长量的关系”实验中,弹簧弹力的大小为F,弹簧的形变量(伸长量或压缩量)为x,下列说法正确的是()A.实验中k的具体数值只能用逐个计算的方法求出来,而没有其他的方法B.如果没有测出弹簧原长,用弹簧长度L代替x,FL图线也是过原点的一条直线C.利用Fx图线可求出k值D.实验时要把所有点连到线上,才能探索得到真实规律答案C解析该实验中进行数据处理,可以采用图象法,并非只能用逐个计算的方法来求k,故A 错误;用弹簧长度L代替x,FL图线不过原点,故B错误;在Fx图象中图线的斜率表示弹簧劲度系数的大小,故利用Fx图线可以求出k值,故C正确;实验时并非把所有点连到线上,而是让线穿过尽量多的点,不能穿过的尽量分布在线的两侧,这样可以剔除误差比较大的点,故D错误.2.在“探究弹簧的弹力与伸长量的关系”的实验中,根据测量数据作出了弹力F和弹簧的形变量x的关系图象.下列说法正确的是()A.图线是经过坐标原点的曲线,说明F与x成正比B.图线是经过坐标原点的直线,说明F与x成正比C.弹簧的劲度系数与弹力成正比D.图线的斜率的倒数就是弹簧的劲度系数答案B解析在弹性限度内,图线是经过坐标原点的直线,说明F与x成正比,故A错误,B正确;表示弹簧的劲度系数取决于弹簧自身,故C错误;由胡克定律F=kx得:图线的斜率k=ΔFΔx弹簧的劲度系数,故D错误.3.如图1所示是“探究弹力与弹簧伸长量的关系”的实验装置,小东认真操作、正确读数后得到的数据记录如下表.由表可知()图1A.每个钩码的质量为B.实验所用刻度尺的分度值是1 mmC.每挂一个钩码,弹簧伸长12.0 cmD.实验时弹簧伸长量未超过弹性限度答案D解析每个钩码的质量m=0.989.8kg=0.1 kg,A错;由于弹簧的长度记录到整数厘米的下一位,故所用刻度尺为厘米刻度尺,最小分度为1 cm,B错;由表可以看出,每挂一个钩码,弹簧都要伸长2 cm,C错;由所给实验数据可以看出,弹簧弹力与其伸长量成正比,符合胡克定律,故弹簧伸长量未超过它的弹性限度,D对.4.(多选)一个实验小组在“探究弹力与弹簧伸长量的关系”的实验中,使用两根不同的轻质弹簧a和b,得到弹力与弹簧长度的关系的图象如图2所示.下列表述正确的是()图2A.a的截距比b的小,由此判断a的劲度系数比b的小B.a的斜率比b的大,由此判断a的劲度系数比b的大C.a的截距比b的小,由此判断a的原长比b的小D.由图象获得的信息表明弹力与弹簧的长度成正比答案BC解析题图图象中斜率表示弹簧的劲度系数k,故a的劲度系数比b的大,A错误,B正确;图象中横截距表示弹簧的原长,b的原长比a的长,C正确;测得的弹力与弹簧的伸长量成正比,而不是与弹簧的长度成正比,故D错误.二、非选择题5.某同学用如图3所示装置做“探究弹力与弹簧伸长量的关系”的实验.他先测出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上钩码,并逐个增加钩码,同时测出指针所指的标尺刻度,所得数据列表如下:(g 取9.8 m/s 2)图3(1).图4(2)根据所测得的数据和关系曲线可以判断,在______N 范围内弹力大小与弹簧伸长量关系满足胡克定律.弹簧的劲度系数为________N/m. 答案 (1)见解析图 (2)0~4.9 25.00解析 (1)根据表格中的各组数据在xm 图象上标出相应的点,然后用平滑曲线连接这些点,作出的图象如图所示.(2)根据作出的图线可知,钩码质量在0~500 g 范围内图线是直线,表明弹力大小与弹簧伸长量关系满足胡克定律.利用题给数据计算得弹簧的劲度系数k =Δmg Δx =5×102×10-3×9.8(34.60-15.00)×10-2N /m ≈25.00 N/m.6.在“探究弹力与弹簧伸长量的关系”实验中,得到轻质弹簧的弹力F 的大小和弹簧长度L 的关系图象如图5所示,则由图线可知:图5(1)弹簧的原长是________ cm ; (2)弹簧的劲度系数为________ N/m ; (3)表示弹簧处于压缩状态的是图线________. 答案 (1)10 (2)200 (3)b解析 (1)当F =0时,弹簧长度为原长,由题图得,原长为10 cm. (2)由公式F =kx 得k =F x =ΔF Δx =10(15-10)×10-2N /m =200 N/m. (3)当弹簧长度小于原长时,处于压缩状态,故是图线b .7.某同学利用如图6a 所示装置做“探究弹力与弹簧伸长量的关系”的实验.图6(1)他通过实验得到如图b 所示的弹力大小F 与弹簧长度L 的关系图线.由此图线可得该弹簧的原长L 0=________ cm ,劲度系数k =________ N/m.(2)他又利用本实验原理把该弹簧做成一把弹簧秤,当弹簧秤上的示数如图c 所示时,该弹簧的长度L =________ cm. 答案 (1)4 50 (2)10解析 (1)当F =0时,弹簧的长度即为原长,由胡克定律可知图象的斜率表示劲度系数的大小.(2)弹簧秤的示数为3.0 N ,则弹簧伸长量为x =350 m =0.06 m ,则弹簧长度为10 cm.8.某实验小组做“探究弹力与弹簧伸长量的关系”的实验,实验时,先把弹簧平放在桌面上,用直尺测出弹簧的原长L 0=4.6 cm ,再把弹簧竖直悬挂起来,在下端挂钩码,每增加一只钩码记下对应的弹簧长度L ,数据记录如下表所示:(1)图7(2)由此图线可得,该弹簧劲度系数k =________ N/cm.(3)图线与L 轴的交点坐标大于L 0的原因是________________________. 答案 见解析 解析 (1)如图所示(2)图象的斜率表示劲度系数,故有:k =ΔFΔL = 5.0-00.15-0.05N /m =50 N/m.(3)图线与L 轴的交点坐标表示弹簧不挂钩码时的长度,其数值大于弹簧原长,是因为弹簧自身重力的影响.。