∑-△模数转换器的原理及应用

(σ-δ) adc工作原理
(σ-δ) ADC是一种模数转换器，全称为Sigma-Delta模数转换器。

它的工作原理是通过对输入信号进行高速取样，并利用高速数字信号处理技术，将模拟信号转换为数字信号。

Sigma-Delta ADC 的工作原理可以从以下几个方面来解释：
1. 模拟信号输入，首先，模拟信号被输入到Sigma-Delta ADC 的输入端。

这个模拟信号可以是来自传感器、放大器、滤波器等外部电路的输出信号。

2. 量化和采样，Sigma-Delta ADC对输入信号进行高速取样和量化。

它以高速的采样率对输入信号进行采样，并将采样值转换为数字形式。

3. Sigma-Delta调制，接下来，ADC使用Sigma-Delta调制技术，将采样到的模拟信号转换为高速的1比特数据流。

这个过程涉及将模拟信号与一个高频时钟信号进行比较，生成一个1比特的数据流。

4. 数字滤波，接着，ADC使用数字滤波器对1比特数据流进行
处理，以减小高频噪声和提高信噪比。

这个数字滤波器通常是一个低通滤波器，用于去除高频噪声，并将1比特数据流转换为更高精度的数字输出。

5. 数字输出，最后，经过数字滤波器处理后的数据被输出为高精度的数字信号，代表了原始模拟信号的数值。

这个数字输出可以被用于后续的数字信号处理、存储或传输。

总的来说，Sigma-Delta ADC通过高速取样、Sigma-Delta调制和数字滤波等技术，实现了对模拟信号的高精度数字化转换。

它在音频处理、传感器接口、通信系统等领域有着广泛的应用。

sigmadeltaadc的工作原理Sigma-Delta ADC，全称为Sigma-Delta Analog-to-Digital Converter，是一种高精度的模数转换器。

它的工作原理基于Sigma-Delta调制技术，通过对输入信号进行高速采样和数字化处理，实现对模拟信号的准确量化和转换。

Sigma-Delta ADC的核心部件是一个差分运算放大器和一个数字滤波器。

首先，输入信号经过差分运算放大器进行放大，并与一个参考电压进行比较。

差分运算放大器会将输入信号转换为差分信号，并将其与参考电压进行比较，产生一个差分输出信号。

这个差分输出信号包含了输入信号与参考电压之间的差异。

接下来，差分输出信号经过一个积分器，将其进行积分运算。

积分器的作用是将输入信号中的高频成分滤除，只保留低频成分。

积分后的信号再经过一个比较器，将其与一个数字信号进行比较。

比较器会产生一个数字输出信号，表示差分输出信号与数字信号之间的差异。

然后，数字输出信号通过一个反馈回路送回到差分运算放大器的输入端，起到调节放大器增益的作用。

通过不断调节放大器增益，使得差分输出信号与数字信号之间的差异尽可能小。

这个反馈回路的作用类似于一个控制系统，通过自动调节放大器增益，使系统的稳定性和精度得到保证。

Sigma-Delta ADC的工作原理可以用一个简单的例子来说明。

假设我们要将一个模拟信号转换为一个8位的数字信号。

首先，输入信号经过差分运算放大器进行放大，并与一个参考电压进行比较。

差分运算放大器会将输入信号转换为差分信号，并将其与参考电压进行比较，产生一个差分输出信号。

如果差分输出信号大于参考电压，则比较器输出1；如果差分输出信号小于参考电压，则比较器输出0。

接下来，差分输出信号经过积分器进行积分运算。

积分器会将差分输出信号进行积分，得到一个积分后的信号。

然后，积分后的信号再经过比较器进行比较，产生一个数字输出信号。

如果积分后的信号大于数字信号，则比较器输出1；如果积分后的信号小于数字信号，则比较器输出0。

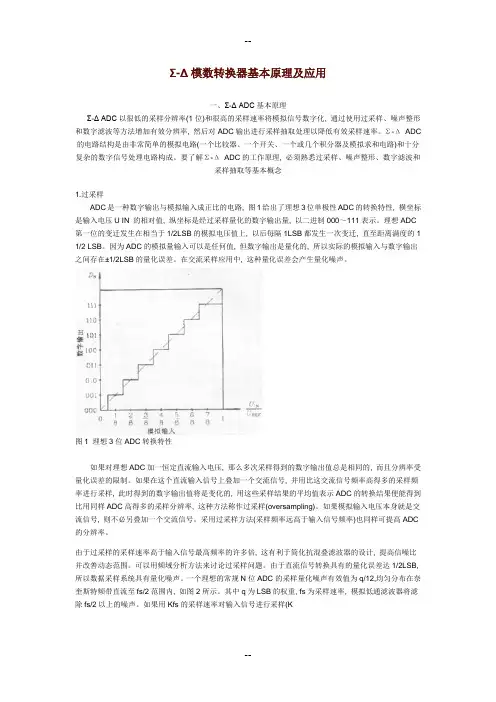
Σ-Δ模数转换器基本原理及应用一、Σ-Δ ADC基本原理Σ-Δ ADC以很低的采样分辨率(1位)和很高的采样速率将模拟信号数字化, 通过使用过采样、噪声整形和数字滤波等方法增加有效分辨率, 然后对ADC输出进行采样抽取处理以降低有效采样速率。

Σ-ΔADC 的电路结构是由非常简单的模拟电路(一个比较器、一个开关、一个或几个积分器及模拟求和电路)和十分复杂的数字信号处理电路构成。

要了解Σ-ΔADC的工作原理, 必须熟悉过采样、噪声整形、数字滤波和采样抽取等基本概念1.过采样ADC是一种数字输出与模拟输入成正比的电路, 图1给出了理想3位单极性ADC的转换特性, 横坐标是输入电压U IN 的相对值, 纵坐标是经过采样量化的数字输出量, 以二进制000～111表示。

理想ADC 第一位的变迁发生在相当于1/2LSB的模拟电压值上, 以后每隔1LSB都发生一次变迁, 直至距离满度的1 1/2 LSB。

因为ADC的模拟量输入可以是任何值, 但数字输出是量化的, 所以实际的模拟输入与数字输出之间存在±1/2LSB的量化误差。

在交流采样应用中, 这种量化误差会产生量化噪声。

图1 理想3位ADC转换特性如果对理想ADC加一恒定直流输入电压, 那么多次采样得到的数字输出值总是相同的, 而且分辨率受量化误差的限制。

如果在这个直流输入信号上叠加一个交流信号, 并用比这交流信号频率高得多的采样频率进行采样, 此时得到的数字输出值将是变化的, 用这些采样结果的平均值表示ADC的转换结果便能得到比用同样ADC高得多的采样分辨率, 这种方法称作过采样(oversampling)。

如果模拟输入电压本身就是交流信号, 则不必另叠加一个交流信号。

采用过采样方法(采样频率远高于输入信号频率)也同样可提高ADC 的分辨率。

由于过采样的采样速率高于输入信号最高频率的许多倍, 这有利于简化抗混叠滤波器的设计, 提高信噪比并改善动态范围。

sigmadeltaadc原理
Σ-Δ模数转换是一种典型的数模转换技术，它利用非线性微分模拟器（Differentiator）把模拟信号转变为进行离散采样的差分脉冲。

Σ-Δ转换技术
有很高的灵敏度，但同时也有一定的复杂性，因为需要大量的计算和设备限制。

Σ-Δ模数转换器中，Σ表示累加器（Accumulator），Δ表示微分器（Differentiator）。

它通常有两个部分，累加（Accumulation）和微分（Differentiation），一般采用了高速積分和微分技术（Sigma-Delta Topology），来完成模拟脉冲的转换。

其中累加（Accumulation）实现的是采样技术，原来的模拟信号在特定的时刻取得一个采样值；累加（Accumulation）把这些采样值累加到心跳的末端；微分（Differentiation）实现的是离散化技术，它使用如
此精密的采样技术，以在心跳的末端释放不同大小的脉冲，从而离散化地表示原始模拟信号。

Σ-Δ模数转换器使得可以使用很少的采样来代表原始模拟信号，但其本质原理却是可以植根于模拟信号的数字信息量的增加，即出现精度的提高。

Σ-Δmodulators的发展为模拟-数字转换技术提供了可靠的仪表精度以及脉冲
转换的灵活性。

2、量化噪声功率
设量化噪声是白噪声，用e(n)表示，其在以±q/2 量化单位所划分的各量化电平内的分布是一样的， 量化噪声功率用方差表示为 2
3、量化噪声的功率谱密度 由于量化噪声均等地散布于整个采样频率（ fS ）范围 内，所以量化噪声的功率谱密度可表示为：
q2 D(f ) 12f S
1 q/2 2 q E[e ] e de q q / 2 12
带模拟滤波和数字滤波的过采样
信噪比与阶数和过采样倍率之间的关系
单级调制器1~4阶与达到分辨率的最低过采样比
精度(n)
M(1阶) 2048 8192 32768 131072 524288
M(2阶) 65 129 257 514 1034
M(3阶)
M(4阶)
12 14 16 18 20
36 59 9•若输入信号的最小幅度大于量化器的量化阶梯 Q, 量化噪声的总功率是一个常数,与采样频率fs无关,
功率密度谱在0~fs/2的频带范围内均匀分布。
•量化噪声电平与采样频率成反比 ,提高采样频率 , 可以降低量化噪声电平 , 而基带是固定不变的 , 因 而减少了基带范围内的噪声功率,提高了信噪比。
1 K
设Q为量化噪声，H(S)为模拟滤波器的传递函数，输 入信号为X，输出信号为Y，有
Y ( X Y) / S Q
整理得
Y X /(S 1) QS /(S 1)
可见，当频率接近0时，（S→0），输出Y趋于X，且无噪声分量， 当频率增高时，X/(S+1)项的值减小，而噪声分量QS/(S+1)增加， 即Σ-△调制器对输入信号具有低通作用，对内部量化器产生的量 化噪声具有高通作用。换言之， Σ-△调制器具有改变噪声分布状 Σ-Δ调制器的频域线性化模型 态的功能。这种对量化噪声的频谱进行整形的特性为噪声整形特 性。

数模转换器的原理及应用数模转换器（Digital-to-Analog Converter，简称DAC）是一种电子器件，用于将数字信号转换为模拟信号。

在数字电子系统中，由于信息的数字化处理，需要将数字信号转换为模拟信号才能实现与外部环境的交互。

本文将从数模转换器的工作原理和应用两个方面进行阐述。

一、数模转换器的工作原理数模转换器的工作原理基于二进制数的电位权重加权。

简单来说，它将二进制数字输入转换为相应的电压输出。

市场上常见的数模转换器主要有两种类型：并行式和串行式。

1. 并行式数模转换器并行式数模转换器的工作原理是将各个二进制位的电平转换为相应的电压输出。

例如，一个8位的并行式数模转换器能够将8个二进制位的输入转换为对应的8个电压输出。

每一位的输入可以是0V（低电平）或5V（高电平），对应的输出电压也相应变化。

通过控制输入的二进制码，可以实现从0到255之间的电压输出。

并行式数模转换器的转换速度较快，适用于对速度要求较高的应用。

2. 串行式数模转换器串行式数模转换器的工作原理是将二进制位逐位地进行转换。

从高位开始，每个二进制位经过一定的时间间隔逐步进行转换，最终输出模拟信号。

与并行式数模转换器相比，串行式数模转换器的转换速度较慢，但由于只需要一个数据线来传输数据，所需引脚数量较少，适用于资源受限的系统设计。

二、数模转换器的应用数模转换器广泛应用于各种领域，包括通信、音频、视频、测量仪器等。

以下是一些常见的应用示例：1. 通信领域在通信领域，数模转换器用于将数字信号转换为相应的模拟信号进行传输。

例如，在数字手机中，声音信号首先被转换为数字信号，并通过数模转换器转换为模拟信号输出到扬声器，实现声音的播放。

2. 音频应用数模转换器在音频领域中扮演着重要的角色。

例如，在CD播放器中，数模转换器将数字音频信号转换为模拟音频信号，使其能够通过耳机或音箱播放出来。

同时，在音频编辑和处理中，数模转换器也可以将数字音频信号转换为模拟信号，以便进行混音、均衡等操作。

模数转换器的原理及应用模数转换器，即数模转换器和模数转换器，是一种电子器件或电路，用于将模拟信号转换为数字信号，或将数字信号转换为模拟信号。

该器件在许多领域都有广泛的应用，包括通信、音频处理、图像处理等。

一、数模转换器的原理数模转换器的原理基于采样和量化的过程。

采样是指在一段时间间隔内对连续的模拟信号进行测量，将其离散化，得到一系列的样本。

量化是指将采样得到的模拟信号样本转换为对应的数字量。

1. 采样过程：通过采样器对连续的模拟信号进行采样，即在一段时间间隔内选取一系列点，记录其幅值。

采样频率越高，采样得到的样本越多，对原始信号的还原度越高。

2. 量化过程：将采样得到的模拟信号样本转换为数字量。

量化的目的是将连续的模拟信号转换为离散的数字信号，通常使用二进制表示。

量化过程中，将采样得到的模拟信号样本确定为离散的幅值值，并用数字表示。

二、模数转换器的原理模数转换器将数字信号转换为模拟信号，其原理与数模转换器相反。

它将数字信号的离散样本重新合成为连续的模拟信号，恢复出原始的模拟信号。

1. 数字信号输入：模数转换器接收来自数字信号源的离散数字信号样本。

2. 重构模拟信号：根据输入的数字信号样本，模数转换器重构出原始的模拟信号。

这需要根据离散样本的幅值重新合成出连续变化的模拟信号。

三、模数转换器的应用模数转换器在许多领域都有广泛的应用，下面列举几个常见的应用领域：1. 通信系统：在通信系统中，模数转换器用于将数字信号转换为模拟信号进行传输。

它将数字信号编码为模拟信号，便于在传输过程中传递。

2. 音频处理：在音频处理系统中，模数转换器用于将数字音频信号转换为模拟音频信号，以便于放音或其他音频处理操作。

3. 图像处理：在数字图像处理领域，模数转换器用于将数字图像信号转换为模拟图像信号，以便于显示或其他图像处理操作。

4. 控制系统：模数转换器在控制系统中用于将数字控制信号转换为模拟控制信号，以便于控制各种设备或系统的运行。

Σ-Δ模/数转换器(ADC)的工作原理本文深入介绍-模/数转换器(ADC)的工作原理，重点关注难以理解的数字概念:过采样、噪声整形和抽样滤波等。

同时包括-转换器的多种应用。

最新的-转换器通常具有较高分辨率、高度集成、低功耗以及较低成本，使其成为过程控制、高精度温度测量以及电子称等应用的上佳ADC选择。

但由于设计者往往不太了解-类型的转换器，而选择传统的SAR ADC。

-转换器(1位ADC)的模拟侧非常简单；数字侧执行滤波和抽样，比较复杂，这部分使得- ADC的生产成本较低。

为理解转换器工作原理，您必须熟悉过采样、噪声整形、数字滤波以及抽样等概念。

本应用笔记涵盖了上述主题。

过采样首先，考虑输入信号为正弦波时传统多位ADC的频域传递函数。

以频率Fs对该输入进行采样。

根据奈奎斯特定理，Fs必须至少为输入信号带宽的两倍。

观察数字输出的FFT分析结果，我们可看到一个单音和大量随机噪声，从直流延伸至Fs/2 (图1)。

这些噪声称为量化噪声，对该结果可以按照以下考虑：ADC输入为连续信号，具有无限可能的状态，但数字输出为离散函数，其不同状态的数量取决于转换器的分辨率。

所以，从模拟到数字的转换损失了某些信息，在信号中引入了一定程度的失真。

该误差的幅值是随机的，最大为LSB。

图1. 多位ADC的FFT谱图，采样频率为FS如果我们将基频幅值除以所有噪声频率的RMS和，则得到信噪比(SNR)。

对于N位的ADC，SNR = 6.02N + 1.76dB。

为提高传统ADC的SNR(并进而提高信号复现的精度)，就必须提高位数。

仍以上例为例，但将采样频率提高，采用过采样因子k，达到kFs(图2)。

FFT分析结果表明噪底降低。

SNR与之前相同，但噪声能量已经分散至较宽的频率范围。

-转换器利用这一原理，在1位ADC之后增加了数字滤波器(图3)。

由于大多数噪声被数字滤波器滤除，所以RMS噪声较低。

这种方法使得-转换器以较低分辨率的ADC实现较宽动态范围。

∑–△型模数转换器(ADC)1.概述近年来，随着超大规模集成电路制造水平的提高，Σ-Δ型模数转换器正以其分辨率高、线性度好、成本低等特点得到越来越广泛的应用。

Σ-Δ型模数转换器方案早在20世纪60年代就已经有人提出，然而，直到不久前，在器件商品化生产方面，这种工艺还是行不通的。

今天，随着1微米技术的成熟及更小的CMOS几何尺寸，Σ-Δ结构的模数转换器将会越来越多地出现在一些特定的应用领域中。

特别是在混合信号集成电路(Mixed-signal ICs，指在单一芯片中集成有模数转换器、数模转换器以及数字信号处理器功能的集成电路芯片)中。

目前，Σ-Δ型模数转换器主要用于高分辨率的中、低频(低至直流)测量和数字音频电路。

用于低频测量的典型芯片有16位分辨的AD7701，24位分辨的AD7731等；用于高品质数字音频场合的典型芯片有18位分辨率的AD1879等。

随着设计和工艺的水平的提高，目前已经出现了高速Σ-Δ型模数转换器产品。

2. ∑–△型ADC的理论基础与一般的ADC不同，∑–△型ADC不是直接根据抽样数据的每一个样值的大小进行量化编码，而是根据前一量值与后一量值的差值即所谓的增量的大小来进行量化编码。

从某种意义上讲，它是根据信号波形的包络线进行量化编码的。

∑–△型ADC由两部分组成，第一部分为模拟∑–△调制器，第二部分为数字抽取滤波器，如下图所示。

∑–△调制器以极高的抽样频率对输入模拟信号进行抽样，并对两个抽样之间的差值进行低位量化，从而得到用低位数码表示的数字信号即∑–△码；然后将这种∑–△码送给第二部分的数字抽取滤波器进行抽取滤波，从而得到高分辨率的线性脉冲编码调制的数字信号。

因此抽取滤波器实际上相当于一个码型变换器。

由于∑–△调制器具有极高的抽样速率，通常比奈奎斯特抽样频率高出许多倍，因此∑–△调制器又称为过抽样ADC转换器。

这种类型的ADC采用了极低位的量化器，从而避免了制造高位转换器和高精度电阻网络的困难；另一方面，因为它采用了∑–△调制技术和数字抽取滤波，可以获得极高的分辨率；同时由于采用了低位量化输出的∑–△码，不会对抽样值幅度变化敏感，而且由于码位低，抽样与量化编码可以同时完成，几乎不花时间，因此不需要采样保持电路，这就使得采样系统的构成大为简化。

五、数字滤波和采样抽取 Σ-Δ调制器对量化噪声整形以后，其输出携带有输 入模拟信号的幅度信息，它的频谱特点是信号频谱。
16
在基带（ f S ）内，将量
2
化噪声移到基带（所关
心的频带）以外，所以
在Σ-Δ调制器后加一个数
字低通滤波器，对整形
后的量化噪声进行数字
滤波，可滤
除
f
S
2
Kf S 至 2 之间的无用
3. ∑-△调制器以采样速率输出1bit数据流，频率可高达MHz量级。 数字滤波和抽取的目的是从该数据流中提取出有用的信息，并将 数据速率降低到可用的水平。
4. ∑-△ADC 中的数字滤波器对1bit数据流求平均，移去带外量化 噪声并改善ADC的分辨率。数字滤波器决定了信号带宽、建立2时0 间和阻带抑制。
Σ-△模数转换器是利用过采样(Oversampling)技 术、噪声整形技术和数字滤波技术以很低的采样分 辨率和很高的采样速率将模拟信号数字化，将高分 辨率的转换问题化简为低分辨率的转换问题，增加 有效分辨率。
❖ ∑-△模数转换器的工作原理简单的讲，就是将模数转换过 后的数字量再做一次窄带低通滤波处理。当模拟量进入转换 器后，先在调制器中做求积处理，并将模拟量转为数字量， 在这个过程中会产生一定的量化噪声，这种噪声将影响到输 出结果，因此，采用将转换过的数字量以较低的频率一位一 位地传送到输出端，同时在这之间加一级低通滤波器的方法， 就可将量化噪声过滤掉，从而得到一组精确的数字量。 15
2. 其突出优点是元件匹配精度要求低，电路组成主要以数字电路为 主，能有效的用速度换取分辨率，无需微调工艺就可获得16位以 上的分辨率，制作成本低，适合于标准CMOS单片集成技术。因而， 这一技术发展迅速，已成为音频范围高分辨率(>16位)数据转换 器的主流产品，随工艺特征尺寸的进一步减少，速度和集成度还 会不断提高。

图1 ∑-△调制器∑-△调制器包含1个差分放大器、1个积分器、1个比较器以及1个由1bit DAC(1个简单的开关，可以将差分放人器的反相输入接到正或负参考电压)构成的反馈环。

反馈DAC的作用是使积分器的平均输出电压接近于比较器的参考电平。

调制器输出中“1”的密度将正比于输入信号，如果输入电压上升，比较器必须产生更多数量的“1”，反之亦然。

积分器用来对误差电压求和，对于输入信号表现为一个低通滤波器，而对于量化噪声则表现为高通滤波。

这样，大部分量化噪声就被推向更高的频段。

和前面的简单过采样相比，总的噪声功率没有改变，但噪声的分布发生了变化．现在，如果对噪声成型后的∑-△调制器输出进行数字滤波，将有可能移走比简单过采样中更多的噪声。

这种调制器(一阶)在每两倍的过采样率下可提供9dB的SNR改善。

在∑-△调制器中采用更多的积分与求和环节，可以提供更高阶数的量化噪声成形。

例如，一个二阶∑-△调制器在每两倍的过采样率可改善SNR 15dB。

图2显示了∑-△调制器的阶数、过采样率和能够获得的SNR三者之问的关系。

图2 SNR与过采样率的关系3．数字滤波和抽取∑-△调制器以采样速率输出1bit数据流，频率可高达MHz量级。

数字滤波和抽取的目的是从该数据流中提取出有用的信息，并将数据速率降低到可用的水平。

∑-△ADC 中的数字滤波器对1bit数据流求平均，移去带外量化噪声并改善ADC的分辨率。

数字滤波器决定了信号带宽、建立时间和阻带抑制。

∑-△转换器中广泛采用的滤波器拓扑是SINC3，一种具有低通特性的滤波器。

这种滤波器的一个主要优点是具有陷波特性，可以将陷波点设在和电力线相同的频率，抑制其干扰。

陷波点直接相关于输出数据速率(转换时间的倒数)。

SINC3滤波器的建立时间三倍于转换时问。

例如，陷波点设在50Hz时(60Hz数据速率)，建立时间为3／60Hz=50ms。

有些应用要求更快的建立时间，而对分辨率的要求较低。

越来越多的应用，例如过程控制、称重等，都需要高分辨率、高集成度和低价格的ADC、新型∑-△转换技术恰好可以满足这些要求。

然而，很多设计者对于这种转换技术并不十分了解，因而更愿意选用传统的逐次比较ADC。

∑-△转换器中的模拟部分非常简单(类似于一个1bit ADC)，而数字部分要复杂得多，按照功能可划分为数字滤波和抽取单元。

由于更接近于一个数字器件，∑-△ADC的制造成本非常低廉。

一、∑-△ADC工作原理要理解∑-△ADC的工作原理，首先应对以下概念有所了解：过采样、噪声成形、数字滤波和抽取。

1．过采样首先，考虑一个传统ADC的频域传输特性。

输入一个正弦信号，然后以频率fs采样－按照Nyquist定理，采样频率至少两倍于输入信号。

从FFT分析结果可以看到，一个单音和一系列频率分布于DC到fs／2间的随机噪声。

这就是所谓的量化噪声，主要是由于有限的ADC分辨率而造成的。

单音信号的幅度和所有频率噪声的RMS幅度之和的比值就是信号噪声比(SNR)。

对于一个Nbit ADC，SNR可由公式：SNR=6.02N+1.76dB得到。

为了改善SNR和更为精确地再现输入信号，对于传统ADC来讲，必须增加位数。

如果将采样频率提高一个过采样系数k，即采样频率为Kfs，再来讨论同样的问题。

FFT分析显示噪声基线降低了，SNR值未变，但噪声能量分散到一个更宽的频率范围。

∑-△转换器正是利用了这一原理，具体方法是紧接着1bit ADC之后进行数字滤波。

大部分噪声被数字滤波器滤掉，这样，RMS噪声就降低了，从而一个低分辨率ADC, ∑-△转换器也可获得宽动态范围。

那么，简单的过采样和滤波是如何改善SNR的呢?一个1bit ADC的SNR为7.78dB(6.02+1.76)，每4倍过采样将使SNR增加6dB，SNR每增加6dB等效于分辨率增加1bit。

这样，采用1bit ADC进行6?倍过采样就能获得4bit分辨率；而要获得16bit 分辨率就必须进行415倍过采样，这是不切实际的。

换 精度 。该 方法 相对 较慢 但精 确 。 由于输入 电压 在
整个测 量 周期 被平 均 ， 因此 ， 要达 到较 高 的精 度输 入
ｌ ｍｅｔ 调制器 Ｉ ｌａ
电压 ， 须在 整 个 测 量周 期 中保 持 恒 定 。该 原 理适 必
合 于许 多要 求高 分 辨 率但 变 化 缓 慢 信 号 的测 量 ， 可 应 用于 电池 充 电控 制 、 温度 传感 器 、 电表 等等 。在上 电后 第一 次转 换 开 始 时 电容 需 要 通 过 充／ 电一 直 放
在下 面的例 子 中使 用 ２ Ｍ ｚ 荡 频率 ， 个测 量周 ４ Ｈ 振 一
期 包含 ２个 基 本 时 钟 机 器 周 期
比较 器输 ｝ 士
等 于 ０ ０ ３ ｓ ．８ １ 。 ￣
目标分 辨 率 为 ２ Ｏ位 ， 为 ４ １０ 用 电 压 基 准 产 ．０ Ｖ，
生 。可 以按 照式 （ ） ６ 来选 择 Ｒ和 Ｃ：
则 以双积 分 Ａ Ｄ， ／ ∑一Ａ ／ Ａ Ｄ较 为普 及 。本文 介绍 的
Ａ Ｄ转 换 电路 则 充 分利 用 了 Ｃ Ｌ 硬 件 资 源 ， 输 ／ ＰＤ 多 入通 道 ， 有精 度 高 ， 成本 ， 具 低 测量 精 度 和 速 度 可 选 择等 突 出优 点 ， 在工业 现 场有实 际 意义 。
Ｄ Ｃ模拟输入 信号 Ａ Ｄ Ｃ反馈 环 的输 出叠加 ， Ａ ｉ 和 Ａ 叠 加的信号进行 积分并 由 比较器进行 量化 ， 比较器 的功
能就是 １ 的量 化器 。 比较 器 输 出的数 字 信 号再 通 位 过 １位的 Ｄ Ｃ转换 回模 拟信号并反馈 到输入节 点。 Ａ 调 制器 的输 出 Ｄ ｕ 处 的数 字 量 输 出与模 拟 输 ｏｔ

简述σ-δ型adc中σ-δ调制器原理1.引言在数字信号处理领域中，常常需要将连续时间信号转化成离散时间信号。

而这个过程便需要用到模数转换器（ADC），其中σ-δ型ADC是一种常用的ADC方式之一。

在本文中，我们将介绍σ-δ调制器的原理。

2.σ-δ型ADC的概述σ-δ型ADC是一种新型的ADC技术，用来将模拟信号转换成数字信号。

它采用“Σ”形结构，把输入信号转化为高频脉冲串，直接产生单比特比特流输出。

它的性能在很大程度上取决于调制器的性能。

3.σ-δ调制器的原理σ-δ调制器是σ-δ型ADC的重要组成部分，负责将模拟信号转换为脉冲序列。

它主要由两个部分组成：模拟输入电路和单比特量化器。

3.1 模拟输入电路σ-δ调制器的模拟输入电路主要作用是把模拟输入信号转化为电压。

它通常由一个变压器、一个电容、一个运算放大器和一个电阻组成。

具体原理如下：将模拟信号加到变压器的串联绕组上，使得输入电路产生一个变压比。

随后，将变压器的输出电压送到电容输入端，使得电容充放电并调制了信号频率。

对输出波形进行门限控制，将其限制在负值和正值之间。

在此过程中，用电流控制电压来调制需要转换的信号。

3.2 单比特量化器单比特量化器将包含信息的宽频信号转换成一个只有两个取值的序列：+1和-1（单比特）。

下面是较常用的三种单比特量化器：（1）单极性单比特量化器用单极性单比特量化器量化时，所有大于零的信号都被量化到+1，而所有小于零的信号都被量化到-1。

（2）双极性单比特量化器用双极性单比特量化器量化时，所有大于正门限的信号都被量化到+1，所有小于负门限的信号都被量化到-1。

（3）差分单比特量化器用差分单比特量化器量化时，将前一次量化的结果与当前输入信号进行比较，将其差异量化到+1或-1。

4.总结在本文中，我们介绍了σ-δ型ADC和其重要组成部分σ-δ调制器的原理。

我们了解到σ-δ调制器采用模拟输入电路将模拟信号转换为电压，并通过单比特量化器将宽频信号转为1和-1的信号。

查看文章标题：An Introduction to Delta Sigma Converters (Delta-Sigma 转换器 下篇)2009-07-01 22:12:19DecimationI did not mention the term "decimation" yet at all because it is neither a process nor is it mystic - it's trivial. It is required when a bitstream, e.g. the output of an analogue modulator, shall be converted to a PCM signal.The core statement is: Without losing any information in oversampled signals as many samples can be left out until the signal is not oversampled any more . (That's why it is called "oversampled"!)Figure 11 - Delta Sigma based ADC with PCM OutputDecimation takes place in delta sigma converters at the output of the digital low-pass filter. The bitstream is clocked with the sampling rate times the oversampling rate (e.g. 64 times the sample rate), and so the output of the digital low pass is clocked with the oversampling rate, too. But the sample rate clock (twice the input bandwidth) is required at the digital output only. Here decimation comes up: For an oversampling rate of e.g. 64 every 64th sample is taken, all others are discarded. This is possible because the signal is bandwidth limited by the digital low pass filter correspondingly. Quite simple - isn't it?Multi-Bit ConverterThe feedback from the 1-Bit DAC to the block "Difference" introduces a lot of noise in an analogue modulator like inFigure 2. It is possible toreduce this noise by not only using one, but several bits instead. The comparator of Figure 2, which actually operates as a 1-bit ADC, is replaced by an N-bit ADC, and the latch and the DAC must be N bit wide, too:Figure 12 - Delta-Sigma based Multi-Bit ADC with PCM OutputThe modulator's output signal will also become N bit wide and thus can no longer be called "bitstream", but it is as suitable to be converted to a PCM signal as the single bit wide bitstream is. Because less noise is introduced, the oversampling rate may be reduced or the PCM output's width can be increased. This is why in practice multi-bit modulators are normally used in ADCs. Note: The modulator's internal signal width "N" is usually a few bits only. Mathematical Operations with Bitstream SignalsDoing mathematical operations like adding two signals or multiplying a signal with a constant (or with another signal) or even other linear or nonlinear operations like filtering is easy to understand for PCM signals. But how to do this with bitstream signals? Any non-trivial mathematical jpp的空间交个朋友吧主页|博客|相册|个人档案||开心网人人网新浪微博EEPW 微博operation on quantized signals significantly affects the lower significant data bits but a bitstream has no LSBits. The input is a one-bit signal and the output has to be a one-bit signal, too!The first approach is obvious, but not very smart: Convert the bitstream to a PCM signal, do the desired operation(s) and convert the result back to a bitstream:Figure 13 - Bitstream Operations using the PCM DetourIn practice, the digital signal processor in this block diagram may be a simple adder or multplier circuit. Also, there must not necessarily be a second bitstream input.This "less smart" method takes one digital filter/decimator per input signal and one digital modulator for the output signal. Another issue of this method is the PCM clock (or sample rate resp.) which has to be introduced: A bitstream has no other sample rate than its bitstream clock, so that an arbitrary PCM sample rate ought to be chosen. This causes a loss of signal bandwidth due to the required digital filter and decimator.The second approach is a more clever way to do it: For example, what happens if you want to just add two bitstream signals (e.g., mix two audio signals) and simply add the bits of both bitstreams? You'll get a 2-bit signal (PCM, this not what you need), but its average level still represents the sum of the original input signals. We "only" need to convert this 2-bit PCM signal into a 1-bit one. Just one digital modulator is needed for that, not more, not less:Figure 14 - Adding two Bitstream SignalsTo understand this, we need a closer look on the digital modulator I explained in Figure 3. What I did not point out there is the fact that●the PCM-Signal "Digital In" has a low clock rate (the PCM sample rate) while●the output of the 1-Bit DDC has the bitstream's clock rate, e.g. 64 times the PCM signal's clock rate.Actually, the subtractor "Difference" in Figure 3 operates at the bitstream's clock rate and subtracts the 1-Bit DDC's PCM output signal from another, slowly clocked PCM signal. This subtractor is also able to subtract two PCM signals, both with the higher clock rate, of course. While the 2-bit sum of both bitstreams is not a usual PCM signal that represents the actual signal value at any time, it still can be viewed as a usable PCM signal for the digital modulator because it is sufficient when its temporal average value is correct. This, BTW, is very similar to the situation with the multi-bit signals in multi-bit converters.Because the digital modulator's signal with needs only to be as wide as its digital input, in this example the circuit diagram for the digital modulator becomes quite simple as the bitstream adder's output signal is only 2 bit wide.The general solution for mathematics with bitstreams looks like this:Figure 15 - Bitstream Operations Directly on Bitstream Signals●Take one or more bitstream(s) and convert them into PCM signals by just manifolding the single bitstream bit for each PCM data bit (that'sexactly what the 1-Bit DDC I described above does).●Do any mathematical operation (= digital signal process) you want on this PCM signal - add, multiply, filter, nonliner operations orwhatsoever. The algorithms to be applied are the same ones as in any other DSP application. You only need a sufficient signal width (number of bits for the PCM signal) in order to achieve the signal quality you aim, and for simple operations this width may be 2 bits or just1. Keep in mind that these operations take place with the bitstream's clock rate.●Use a digital modulator with the same input signal width as your mathematical operation provides to re-convert the "semi-PCM"-signal(= "multi-bit Delta Sigma modulated data stream") to a single bit bitstream.That's it. This "smart" solution takes no digital filter/decimator per input signal and only one (often quite simple) digital modulator for the output signal.Additional Thoughts and CognitionsAlias effects: Delta sigma converters must run with sampling frequencies much higher than twice the maximum signal frequency (which is the minimum sample frequency of e.g. digital outputs). This has a very welcome consequence on alias effects: Only input signal frequencies close to the sampling frequency will be folded back and can cause alias signals as you can see in the graphic below:Figure 16 - Distances of Desired and Alias Frequency BandsThus it becomes obvious that conventional ADCs need expensive low pass filters in order to obtain a bandwidth close to the theoretical Nyquist limit. Delta sigma converters require simple RC low pass filters only and with a little more expense for a 2nd order filter one will get a virtually ideal behaviour. On the other hand an output low pass filter preceeding the decimator is required, which again can be realized more precisely, easily and cheap in digital techniques. Note that in practice the proportions are much more extreme than in the graphic above as due to limited space an oversampling rate of approx. 16 only is shown there.DACs: The input signals of DACs are bandwidth limited by nature, so an input low pass filter is not necessary (it already had to be present when the digital signal was produced). An analog output filter is required anyway to suppress high frequency noise.Infinite resolution of the bitstream: In analogue modulators the bitstream is sampled, but not quantized. It still has an infinite resolution just like the analogue signal has. It is superimposed by noise of course, but the more noise you filter out (the lower the low pass filter's frequency limit is), the more of the original resolution is usable - (theoretically) without limitation. This fact is also exploited by:Direct Stream Digital (DSD) based devices: Traditionally digital devices use numerical representations of analogue samples, PCM in case of a serial signal. Delta sigma ADCs and DACs gain the PCM data out of the bitstream data (and vice versa) which is already a digital signal by means of low pass filters.Figure 17 - Complete Delta Sigma Based PCM System: 2 Delta Sigma ConvertersWhy not record the bitstream directly? Conversion in delta sigma ADCs and DACs is executed in two steps each and as always each step has negative effects on the signal quality. Leaving out half of these steps - the filter in the ADC and the modulator in the DACs - should improve the performance of the complete system. Both, the quantization noise due to the limited number of recorded PCM bits and the conversion noise of the digital modulator would be dropped.Figure 18 - Complete Delta Sigma Based DSD System: 1 Delta Sigma Converter onlyThis is actually done on super audio CDs (SACDs). The whole system from the analogue input to the analogue output now requires only one modulator and one low pass filter instead of two of both required with conventional digital recording. Please remember: The bitstream of modern, high quality ADCs and DACs use an oversampling rate of 64, e.g. the amount of data is 64 bits for each audio sample - compared to 16 or up to 20 or 24 of conventional bits required for a comparable quality. Technically, SACDs are DVDs and based on a sampling frequency of 2.8224 MHz (= 2.8224 MBits net per channel). Not much that more than on audio CDs (0.7056 MBits net per channel), and no problem at all for a DVD with its high capcity.Class-D Power Amplifiers:Figure 19 - Power Amplifiers using a Digital Output StageBoth output transistors operate in push-pull mode, i. e., alternatingly one of both is conducting while the other one is switched off. Thus the bitstream is amplified to the high level of the power supply and is available at the output with low impedance. In order to regain the bitstream's mean value a simple LC-low-pass filter is sufficient in practice. A typical representative of this kind of amplifier is the LM4670, a simple and cheap low power amplifier with an analogue input, so simple that even the LC-low-pass filter is omitted and only the speaker's parasitic inductance remains as "low-pass filter". In contrast to that the TPA3200D1 is more complex, has higher output power and includes a digital (IIS-) input.For the sake of completeness it shall be mentioned that for the operation of a class-D amplifier an analogue pulse width modulated (PWM) signal with a sufficiently high frequency can be used instead of the bitstream produced by a Delta Sigma converter. In contrast to digital pulse width modulated signals the pulse width ratios of analogue pulse width modulated signals are not quantized. With digital sources PWM operation does not suggest itself much, but with anlogue sources both techniques can be found in practice. In this case the pulse width modulator consists of a comparator comparing a triangle wave of e. g. a couple of MHz with the analogue input signal. An example is the TDA7490.Compared to a conventional analogue class-AB amplifier, which advantages and disadvantages does such a class-D amplifier show?●Advantage: Its efficiency can theoretically become 100%. In practice typical values of 90% are achieved. The efficiency of class-ABamplifiers theoretically is 50% only. Moreover, the efficieny of class-AB amplifiers decreases much more at lower output levels than that of class-D-amplifiers. E. g. for battery equipped applications the saved energy may be the decisive reason for class-D amplifiers. Butparticularly with high power amplifiers the fact of 1/5 of exhaust heat is an enomous advantage: Class-D amplifieres can be built much smaller and much more lightweight.●Disadvantage: The speaker's voltage does not only depend on the bitstream (or its mean value resp.), but in the same amount on thesupply voltage, too. (Actually it is the product of the bitstream's mean value and the supply voltage.) Thus the supply voltage has to be kept extra stable.●Disadvantage: The amplifier's output impedance results from the switching transistor's, the inductance's and the supply's resistances. Inpratice it will be distinctly higher than the output impedance of a degenerative amplifier. A low output impedance is preferred because speakers are thereby much more damped, i. e,. they can perform less uncontrolled proper motion and follow the original signal more precisely.In order to reduce both these disadvantages the supply voltage dependency as well as the output impedance can principally be lowered by degenerative feedback. But, if at all, this is by far not feasible in an amount as it is in analogue amplifieres as phase shifts inside the modulator and the low pass filter in conjunction with a degenerative feedback very soon lead to instabilities. Usually Delta Sigma amplifiers do not include degenerative feedback (as far as I experienced, at least). Once more, for the sake of completeness it shall be mentioned that PWM amplifiers do not incorporate phase shifting modulators so that degenerative feedback is much easier or much more efficient to achieve.In analogue Delta Sigma based power amplifiers another trick is possible to drastically improve the signal quality:Figure 20 - Power Output Stage as Part of the Delta Sigma ModulatorCompare to Figure 2: Instead of feeding back the bitstream via a 1-bit DAC to build the difference in this case a portion of the power transistor's output is directly fed back. Thus it is guaranteed that independent of all parasitic effects like supply voltage variations or the transistor's resistances the mean value at the low-pass input is always exactly proportional to the analogue input signal. Excellent performance is feasible by this concept. An example for that is the AD1996. Unfortunately, this trick works for amplifiers with analogue inputs only.Conclusion: Class-D power amplifiers offer a much higher efficiency and less exhaust heat at the expense of their signal quality. Thus they are favourable for generic public address systems, where high power, small size and probably portability too, are required. They are less predestinated for high-quality audio amplifiers. Constructively the most critical elements are the output transistors: The faster they switch, the less the losses are or the higher the switching frequency may be. The latter, on the other hand, allows low pass filters with higher frequencies, which due to their less phase shifts within the signal band allow stronger degenerative feedback, so that the signal quality can be improved. With the advancing semiconductor technology class-D amplifiers will be increasingly utilizable for high-quality audio amplifiers.Delta Sigma Converters or Sigma Delta Converters? Mankind does not seem to agree on one notation. Both notations are used equally often when you search via Google. I decided to stay with that guy who told he is living in the Mississippi Delta, so deltas mean something to him - and for him only the Sigma River may have a Sigma Delta... good point. Later I found out that the original name "Delta Sigma" was coined by the inventors Inose and Yasuda and "Sigma Delta" is actually not correct. I was lucky...[From Uwe Beis ,Last update: August, 12th, 2007]To Backward: An Introduction to Delta Sigma Converters (Delta-Sigma转换器 上篇)D elta-Sigma原理一般应用在ADC应用中。

∑-△模数转换器⼯作原理∑-△ADC⼯作原理越来越多的应⽤，例如过程控制、称重等，都需要⾼分辨率、⾼集成度和低价格的ADC、新型∑-△转换技术恰好可以满⾜这些要求。

然⽽，很多设计者对于这种转换技术并不⼗分了解，因⽽更愿意选⽤传统的逐次⽐较ADC。

∑-△转换器中的模拟部分⾮常简单(类似于⼀个1bit ADC)，⽽数字部分要复杂得多，按照功能可划分为数字滤波和抽取单元。

由于更接近于⼀个数字器件，∑-△ADC的制造成本⾮常低廉。

⼀、∑-△ADC⼯作原理要理解∑-△ADC的⼯作原理，⾸先应对以下概念有所了解：过采样、噪声成形、数字滤波和抽取。

1．过采样⾸先，考虑⼀个传统ADC的频域传输特性。

输⼊⼀个正弦信号，然后以频率fs采样－按照Nyquist 定理，采样频率⾄少两倍于输⼊信号。

从FFT分析结果可以看到，⼀个单⾳和⼀系列频率分布于DC到fs ／2间的随机噪声。

这就是所谓的量化噪声，主要是由于有限的ADC分辨率⽽造成的。

单⾳信号的幅度和所有频率噪声的RMS幅度之和的⽐值就是信号噪声⽐(SNR)。

对于⼀个Nbit ADC，SNR可由公式：SNR=6.02N+1.76dB得到。

为了改善SNR和更为精确地再现输⼊信号，对于传统ADC来讲，必须增加位数。

如果将采样频率提⾼⼀个过采样系数k，即采样频率为Kfs，再来讨论同样的问题。

FFT分析显⽰噪声基线降低了，SNR值未变，但噪声能量分散到⼀个更宽的频率范围。

∑-△转换器正是利⽤了这⼀原理，具体⽅法是紧接着1bit ADC之后进⾏数字滤波。

⼤部分噪声被数字滤波器滤掉，这样，RMS噪声就降低了，从⽽⼀个低分辨率ADC, ∑-△转换器也可获得宽动态范围。

那么，简单的过采样和滤波是如何改善SNR的呢?⼀个1bit ADC的SNR为7.78dB(6.02+1.76)，每4倍过采样将使SNR增加6dB，SNR每增加6dB等效于分辨率增加1bit。

这样，采⽤1bit ADC进⾏64倍过采样就能获得4bit分辨率；⽽要获得16bit分辨率就必须进⾏415倍过采样，这是不切实际的。

带辅助DAC的双路Σ-Δ转换器的原理及应用1. 内部框图AD公司新近推出的这种带辅助DAC的双路Σ-Δ模数转换器，是一个完整的15位CMOS模数转换器件。

它采样速率高，功耗低，且输入端兼有信号处理功能，接收通道上的两个带数字滤波器的Σ-Δ型ADC合用一个能隙参考基准。

控制DAC可执行AFC的功能，其它辅助功能可以从辅助串行端口获得，以满足器件多方面的性能要求。

图1所示为AD7729的内部框图。

AD7729主要有两大部分组成：模数转换器和辅助数模转换器。

模数转换器由Σ棪ば虯DC、数字滤波器、偏移调整和主串行通讯接口组成；数模转换器由10位辅助DAC、输出缓冲器和辅助串行接口组成。

1.1 模数转换器模数转换器部分有I和Q两个通道，分别由一个开关电容滤波器和一个15位的ADC组成。

片内的数字滤波器对系统的性能起着关键作用，它们的幅频和相频响应特性保证了相邻通道间的相互干扰有极好的抑制性。

a. Σ-Δ型ADC开关电容滤波器以13MHz的速率对接收的模拟量进行采样，其频率响应如2(a）所示。

接收通道上的另一个数字滤波器的时钟频率为6.5MHz，其频率响应特性如图2(b）所示。

两滤波器对应的综合频率响应如图2(c）所示。

AD7729的接收通道采用了Σ-Δ转换技术，在片内实现系统滤波，从而保证了I和Q 端15位的高精度输出。

具体工作过程是用一个充电平衡的调制器以6.5MHz的速度对开关电容滤波器的输出进行采样，并将其转化成数字脉冲串。

过高的过采样速率能分散0?.25MHz的量化噪音，并使它在所关心的频带中减小。

然后用一高阶的调制器对噪音频谱整形。

再利用数字滤波器对带外噪音进行处理，并同时把数字脉冲转化成并行的15位二进制数据。

b. 数字滤波器它有288个抽头，建立时间为44.7μs。

我们已介绍了它的两个重要功能：系统的滤波功能和消除带外量化噪音功能。

由此可以看出,它有两点优于模拟滤波器：首先，由于它位于ADC之后，消除A/D转化过程中产生的噪音；其次，它不仅消除了低通的振铃，同时还保证了线性相位响应。