第三章 习题和答案

第三章习题解答一、判断下列说法是否正确，凡对的在括号内打“√”，否则打“×”。

（1）现测得两个共射放大电路空载时的电压放大倍数均为－100，将它们连成两级放大电路，其电压放大倍数应为10000。

( )（2）阻容耦合多级放大电路各级的Q点相互独立，( )它只能放大交流信号。

( )（3）直接耦合多级放大电路各级的Q点相互影响，( )它只能放大直流信号。

( )（4）只有直接耦合放大电路中晶休管的参数才随温度而变化。

( )（5）互补输出级应采用共集或共漏接法。

( )二、现有基本放大电路：A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。

（1）要求输入电阻为1kΩ至2kΩ，电压放大倍数大于3000，第一级应采用，第二级应采用。

（2）要求输入电阻大于10MΩ，电压放大倍数大于300，第一级应采用，第二级应采用。

（3）要求输入电阻为100kΩ～200kΩ，电压放大倍数数值大于100，第一级应采用，第二级应采用。

（4）要求电压放大倍数的数值大于10，输入电阻大于10MΩ，输出电阻小于100Ω，第一级应采用，第二级应采用。

（5）设信号源为内阻很大的电压源，要求将输入电流转换成输出电压，且，输出电阻R o＜100，第一级应采用，第二级应采用。

三、选择合适答案填入空内。

（1）直接耦合放大电路存在零点漂移的原因是。

A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定（2）集成放大电路采用直接耦合方式的原因是。

A.便于设计B.放大交流信号C.不易制作大容量电容（3）选用差分放大电路的原因是。

A.克服温漂B. 提高输入电阻C.稳定放入倍数（4）差分放大电路的差模信号是两个输入端信号的，共模信号是两个输入端信号的。

A.差B.和C.平均值（5）用恒流源取代长尾式差分放大电路中的发射极电阻R e，将使电路的。

A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大（6）互补输出级采用共集形式是为了使。

第三章审计的法律责任习题一、单项选择题1、如果被审计单位的财务报表中存在重大错报，则在（）情况下很可能在诉讼中被判为重大过失。

A、注册会计师运用常规审计程序通常能够发现该错报B、审计人员确实遵守了审计准则，但却提出错误的审计意见C、注册会计师明知道存在重大错报但却虚伪的陈述，出具无保留意见的审计报告D、注册会计师基本上遵循了审计准则的相关要求2、审计人员对被审单位的应收账款进行了大量的函证，仅发现一封回函声称与被审单位记录不同：该企业表示，其仅向被审计单位发出过定货单，但随即就收回了订货要求。

对此封回函，注册会计师只看了一半，因为接一个电话而没有看完，接完电话后误以为这是一封已看完的回函，便认可了该笔应收账款的存在性。

但后来查清，该笔应收账款是被审计单位虚构的。

你认为审计人员的这种作法属于（）。

A、欺诈B、普通过失C、重大过失D、没有过失3、由于Q会计师事务所下属的各个分所均可以Q事务所的名义独立承揽业务，导致某分所为P公司出具虚假审计报告而Q所尚不知晓，给Q所带来严重影响。

为避免类似情况的再次发生，Q会计师事务所应采取的针对性措施是（）。

A、严格遵循职业道德、专业标准的要求B、建立健全会计师事务所的质量控制制度C、与委托人签订审计业务约定书D、提取风险基金或购买责任保险4、在注册会计师为避免法律诉讼而采取的以下具体措施中，（）既可以起到防患于未然的作用，又可能在出现法律纠纷后作为减轻法律责任的抗诉理由。

A、建立、健全会计师事务所的质量控制制度B、审慎地选择被审计单位C、深入了解被审计单位的业务D、严格遵循职业道德和专业标准的要求5、注册会计师在认定了以下4个账户的情况后，由于各种原因而未能作进一步的审查，致相应于该账户的财务报表项目中存在重大问题而未被发现。

其中，最有可能被判定为欺诈的是（）。

A、营业外支出账户金额不大，与以前5年情况基本一致B、应收账款账户余额异乎寻常地高，被审计单位不能加以合理解释C、累计折旧大幅度增加，但被审计单位的有关内部控制健全而有效D、实收资本大量增加，而被审计单位已出示了验资报告6、注册会计师在对ABC股份有限公司2006年度会计报表进行审计时，按照函证具体准则对有关应收账款进行了函证，并实施了其他必要的审计程序，但最终仍有应收账款业务中的错报未能查出。

习题三栈和队列一单项选择题1. 在作进栈运算时,应先判别栈是否(① ),在作退栈运算时应先判别栈是否(② )。

当栈中元素为n个,作进栈运算时发生上溢,则说明该栈的最大容量为(③ )。

①, ②: A. 空 B. 满 C. 上溢 D. 下溢③: A. n-1 B. n C. n+1 D. n/22．若已知一个栈的进栈序列是1，2，3，…，n，其输出序列为p1，p2，p3，...，pn，若p1＝3，则p2为( )。

A 可能是2B 一定是2C 可能是1D 一定是13. 有六个元素6，5，4，3，2，1 的顺序进栈，问下列哪一个不是合法的出栈序列？（）A. 5 4 3 6 1 2B. 4 5 3 1 2 6C. 3 4 6 5 2 1D. 2 3 4 1 5 64.设有一顺序栈S，元素s1,s2,s3,s4,s5,s6依次进栈，如果6个元素出栈的顺序是s2,s3,s4, s6, s5,s1,则栈的容量至少应该是（）A.2B. 3C. 5D.65. 若栈采用顺序存储方式存储，现两栈共享空间V[1..m]，top[i]代表第i个栈( i =1,2)栈顶，栈1的底在v[1]，栈2的底在V[m]，则栈满的条件是（）。

A. |top[2]-top[1]|=0B. top[1]+1=top[2]C. top[1]+top[2]=mD. top[1]=top[2]6. 执行完下列语句段后，i值为：（）int f(int x){ return ((x>0) ? x* f(x-1):2);}int i ;i =f(f(1));A．2 B. 4 C. 8 D. 无限递归7. 表达式3* 2^(4+2*2-6*3)-5求值过程中当扫描到6时，对象栈和算符栈为（），其中^为乘幂。

A. 3,2,4,1,1；(*^(+*-B. 3,2,8；(*^-C. 3,2,4,2,2；(*^(-D. 3,2,8；(*^(-8. 用链接方式存储的队列，在进行删除运算时（）。

第3章 力学基本定律与守恒律 习题及答案1．作用在质量为10 kg 的物体上的力为i t F)210(+=N ，式中t 的单位是s ，(1)求4s 后，这物体的动量和速度的变化．(2)为了使这力的冲量为200 N ·s ，该力应在这物体上作用多久，试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题．解: (1)若物体原来静止，则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向，ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速，则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理， 12v v ∆=∆,12I I=这说明，只要力函数不变，作用时间相同，则不管物体有无初动量，也不管初动量有多大，那么物体获得的动量的增量(亦即冲量)就一定相同，这就是动量定理． (2)同上理，两种情况中的作用时间相同，即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ，(s 20='t 舍去)2．一颗子弹由枪口射出时速率为10s m -⋅v ，当子弹在枪筒内被加速时，它所受的合力为 F =(bt a -)N(b a ,为常数)，其中t 以秒为单位：(1)假设子弹运行到枪口处合力刚好为零，试计算子弹走完枪筒全长所需时间；(2)求子弹所受的冲量．(3)求子弹的质量． 解: (1)由题意，子弹到枪口时，有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入，得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3．如图所示，一质量为m 的球，在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。

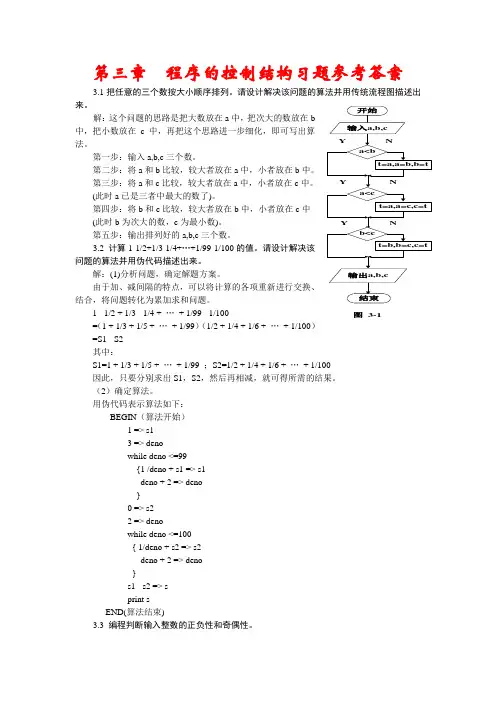
第三章 程序的控制结构习题参考答案3.1把任意的三个数按大小顺序排列。

请设计解决该问题的算法并用传统流程图描述出来。

解：这个问题的思路是把大数放在a 中，把次大的数放在b中，把小数放在c 中，再把这个思路进一步细化，即可写出算法。

第一步：输入a,b,c 三个数。

第二步：将a 和b 比较，较大者放在a 中，小者放在b 中。

第三步：将a 和c 比较，较大者放在a 中，小者放在c 中。

(此时a 已是三者中最大的数了)。

第四步：将b 和c 比较，较大者放在b 中，小者放在c 中(此时b 为次大的数，c 为最小数)。

第五步：输出排列好的a,b,c 三个数。

3.2 计算1-1/2+1/3-1/4+…+1/99-1/100的值。

请设计解决该问题的算法并用伪代码描述出来。

解：(1)分析问题，确定解题方案。

由于加、减间隔的特点，可以将计算的各项重新进行交换、结合，将问题转化为累加求和问题。

1 - 1/2 + 1/3 - 1/4 + … + 1/99 - 1/100 =（1 + 1/3 + 1/5 + … + 1/99）-（1/2 + 1/4 + 1/6 + … + 1/100）=S1 - S2其中：S1=1 + 1/3 + 1/5 + … + 1/99 ；S2=1/2 + 1/4 + 1/6 + … + 1/100因此，只要分别求出S1，S2，然后再相减，就可得所需的结果。

（2）确定算法。

用伪代码表示算法如下：BEGIN （算法开始）1 => s13 => denowhile deno <=99{1 /deno + s1 => s1deno + 2 => deno}0 => s22 => denowhile deno <=100{ 1/deno + s2 => s2deno + 2 => deno}s1 - s2 => sprint sEND(算法结束)3.3 编程判断输入整数的正负性和奇偶性。

第三章会计等式与复式记账一、单项选择题1、总分类账户与明细分类账户平行登记四要点中的“依据相同”是指（）。

A.总分类账要根据明细分类账进行登记B.明细分类账要根据总分类账进行登记C.根据同一会计凭证登记D.由同一人员进行登记2、某企业原材料总分类科目的本期借方发生额为25 000元，贷方发生额为24 000元，其所属的三个明细分类账中；甲材料本期借方发生额为8 000元，贷方发生额为6 000；乙材料借方发生额为13 000元，贷方发生额为16 000元；则丙材料的本期借、贷方发生额分别为（）。

A.借方发生额为12 000元，贷方发生额为2 000元B.借方发生额为4 000元，贷方发生额为2 000元C.借方发生额为4 000元，贷方发生额为10 000元D.借方发生额为6 000元，贷方发生额为8 000元3、甲公司月末编制的试算平衡表中，全部科目的本月贷方发生额合计为120万元，除银行存款外的本月借方发生额合计104万元，则银行存款科目（）。

A.本月借方余额为16万元B.本月贷方余额为16万元C.本月贷方发生额为16万元D.本月借方发生额为16万元4、下列记账错误中，不能通过试算平衡检查发现的是（）。

A.将某一分录的借方发生额600元，误写成6 000元B.某一分录的借贷方向写反C.借方的金额误记到贷方D.漏记了借方的发生额5、下列关于试算平衡法的说法，正确的是（）。

A.漏记某项经济业务影响试算平衡B.包括发生额试算平衡法和余额试算平衡法C.试算平衡了，账户记录一定正确D.发生额试算平衡法理论的依据是会计等式6、企业购入原材料10 000元，已开出支票支付6 000元，另4 000元暂欠。

下列会计分录正确的是（）。

A.借：原材料10 000贷：银行存款10 000B.借：原材料10 000贷：应付账款10 000C.借：原材料10 000贷：银行存款6 000应付账款4 000D.借：原材料10 000贷：应付票据6 000应付账款4 0007、企业计算应交所得税时，正确的会计分录是（）。

第三章 中值定理与导数应用§1 中值定理一、是非判定题一、假设0)('),,(,),(,],[)(=∈ξξf b a b a b a x f 使且必存在可导在有定义在 （×）二、假设0)('),,(),()(,],[)(=∈=ξξf b a b f a f b a x f 使则必存在在连续在 （×）3、假设0)('),,(),(lim )(lim ,],[)(00=∈=-→+→ξξf b a x f x f b a x f b x a x 使则存在且内可导在 （√）4、假设))((')()(),,(,],[)(a b f a f b f b a b a x f -=-∈ξξ使则必存在内可导在 （√）五、假设使内至少存在一点则在可导在上连续在与,),(,),(,],[)()(ξb a b a b a x g x f )(')(')()()()(ξξg f a g b g a f b f =-- （×）（提示：柯西中值定理，少条件0)('≠ξg ）六、假设对任意,0)('),,(=∈x f b a x 都有那么在(a,b)内f(x)恒为常数 （√）二．单项选择题 一、设1.0,(),()()'()()ab f x a x b f b f a f b a xξξ<=<<-=-则在内,使成立的有 C 。

（A ）只有一点（B ）有两个点（C ）不存在（D ）是不是存在与a,b 取值有关二、设],[)(b a x f 在上持续，(,),()(()()a b I f a f b =内可导则与 Ⅱ)0)(',),((≡x f b a 内在之间关系是 B 。

(A) (I)是（Ⅱ）的充分但非必要条件； （B ）（I ）是（Ⅱ）的必要但非充分条件；（C ）（I ）是（Ⅱ）的充分必要条件； （D ）（I ）不是（Ⅱ）的充分条件，也不是必要条件。

第三章判断题T 1 Linux操作系统的源代码是公开的，它是一种“自由软件”。

（判断）T 2 MATLAB是一种能用于数值计算的高级程序设计语言。

（判断）F 3 Windows系统中，不同文件夹中的文件不能同名（判断）F 4 Windows系统中，可以像删除子目录一样删除根目录。

（判断）F 5 Windows系统中，每一个物理硬盘只能建立一个根目录，不同的根目录在不同的物理硬盘中。

（判断）T 6 操作系统三个重要作用体现在：管理系统硬软件资源、为用户提供操作界面、为应用程序开发提供平台。

（判断）T 7 操作系统通过各种管理程序提供了“任务管理”、“存储管理”、“文件管理”、“设备管理”等多种功能。

（判断）T 8 计算机软件通常指的是用于指示计算机完成特定任务的，以电子格式存储的程序、数据和相关的文档。

（判断）T 9 软件产品是交付给用户使用的一整套程序、相关的文档和必要的数据。

（判断）T 10 软件是以二进位表示，且通常以电、磁、光等形式存储和传输的，因而很容易被复制。

T 11 为了延长软件的生命周期，常常要进行软件版本升级，其主要目的是减少错误、扩充功能、适应不断变化的环境。

（判断）T 12 在Windows系统中，按下Alt+PrintScreen键可以将桌面上当前窗口的图像复制到剪贴板中。

（判断）F [01]. 数据库管理系统是最接近计算机硬件的系统软件。

（判断）T [05]. 用Pentium4 的指令系统编写的可执行程序在PentiumⅢ中不一定能被执行；反之，用PentiumⅢ的指令系统编写的可执行程序在Pentium4 中一定能被执行。

（判断）F [07]. 所有存储在磁盘中的MP3音乐都是计算机软件。

（判断）F [09]. P3是世界著名的项目管理软件。

由于使用P3能管理一个大型工程系统的有关资源，因此，它应属于系统软件。

（判断）T [10]. 计算机软件包括软件开发和使用所涉及的资料。

第三章 缓冲溶液习题参考答案1. 在1L 1.0×10-5mol ·L -1 NaOH 溶液中，加入0.001molNaOH 或HCl ，溶液的pH 怎样改变？解：ΔpH 1≈11-9=2；ΔpH 2≈3-9=-62. 设有下列三种由乳酸和乳酸钠组成的缓冲溶液，分别计算它们的pH 值（25℃时乳酸的K a = 1.4×10-4）。

（1）1L 溶液中含有0.1mol 乳酸和0.1mol 乳酸钠。

（2）1L 溶液中含0.1mol 乳酸和0.01mol 乳酸钠。

（3）1L 溶液中含0.01mol 乳酸和0.1mol 乳酸钠。

解：（1）85.31.01.0lg )104.1lg(lg p [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n K K （2）85.21.001.0lg )104.1lg(lg [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n pK K （3）85.401.01.0lg )104.1lg(lg [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n pK K 3. 正常血浆中具有H 2PO 4-－HPO 42-缓冲系，H 2PO 4-的p K a2 = 6.8（校正后），已知正常血浆中[HPO 42-]/[H 2PO 4-]为4/1，试求血浆的pH 值；尿中[HPO 42-]/[H 2PO 4-]为1/9，试求尿的pH 值。

解：血浆的pH 值：40.714lg 8.6[HB]][B lg p pH a =+=+=-K 尿液的pH 值：84.591lg 8.6[HB]][B lg p pH a =+=+=-K 4. 将0.15mol ·L -1 NaOH 溶液0.1mL 加于10mL pH 值为4.74的缓冲溶液中，溶液的pH 值变为4.79，试求此缓冲溶液的缓冲容量。

第三章练习题一、单选1、（A）是本—量—利分析最基本的假设，是本—量—利分析的出发点。

A、相关范围假设B、模型线性假设C、产销平衡假设D、品种结构不变假设2、在各种盈亏临界图中，（B）更符合变动成本法的思路。

A、传统式Ｂ、贡献毛益式Ｃ利量式Ｄ、单位式３、在单位盈亏临界图中，产品销售单价线与（A）的交点即为盈亏临界点。

Ａ单位成本线Ｂ单位固定成本线Ｃ单位变动成本线Ｄ利润线４、已知Ａ企业为生产和销售单一产品企业，A 企业计划年度销售量为１０００件，销售单价为５０元，单位变动成本３０元，固定成本总额２５０００元，则销售量、单价、单位变动成本、固定成本各因素的敏感程度由高到低排列是（Ｃ）Ａ、单价>销售量>单位变动成本>固定成本Ｂ、单价>单位变动成本>销售量>固定成本Ｃ、单价>单位变动成本>固定成本>销售量Ｄ、单价>销售量>固定成本>单位变动成本５、在利量式盈亏临界图中，若横轴代表销售额，则利润线的斜率代表（C）Ａ、单位边际贡献B、变动成本率C、边际贡献率D、单位变动成本6、某企业只生产一种产品，单位变动成本为36元，固定成本总额4000元，产品单位售价56元，要使安全边际率达到50％，该企业的销售量应达到（A）件。

A、400B、222C、143D、5007、下列各式中，其计算结果不等于变动成本率的是（B）A 、1－边际贡献率B、1－达到盈亏临界点的作业率C、单位变动成本/单价×100％D、变动成本/销售收入×100％8、下列措施中只能提高安全边际而不能降低盈亏临界点的是（B）A、提高单价B、增加销售量C、降低单位变动成本D、压缩固定成本开支9某单位某产品的单价为40元，单位变动成本为30元，固定成本为20000元，目标净利润为26800元，所得税税率为33％，则实现目标净利润的销售量为（A）。

A、6000件B、5000件C、4680件D、5500件10、下列因素单独变动时，不会导致盈亏临界点随之变动的是（A）A、销售量B、单位变动成本C、固定成本D、单价11、下列各项指标中，其数值越小，说明企业经营的安全程度越大的是（D）A、安全边际率B、经营杠杆率C、边际贡献率D、达到盈亏临界点作业率12、某企业只经营一种销量不稳、单位边际贡献大于零、盈亏临界点销售量为1600件的产品。

第三章 多维随机向量及其概率分布(一)基本题答案1、设X 和Y 的可能取值分别为.2,1,0;3,2,1,0,==j i j i 则与因盒子里有3种球，在这3种球中任取4个，其中黑球和红球的个数之和必不超过4.另一方面，因白球只有2个，任取的4个球中，黑球和红球个数之和最小为2个，故有j i 与ٛ且,42≤+≤j i ./),(474223C C C C j Y i X p j i j i −−===因而 或0),(===j Y i X P 2).2,1,0;3,2,1,0,4(<+j i ==>+j i j i于是 ,0)0,0(1111======y Y x X P P ,0)0,0(2112======y Y x X P p.35/1/)0,0(472212033113=======C C C C y Y x X P p即 2、X 和. ⎥⎦⎤⎢⎣⎡04.032.064.0210~X ⎥⎦⎤⎢⎣⎡25.05.025.0210~Y 由独立性知，X 和Y 的联合分布为3、Y 的分布函数为显知有四个可能值：).0(0)(),0(1)(≤=>−=−y y F y e y F y ),(21X X }{{}{}11−=e ,2,10,0).1,1(),0,1(),1,0(),0,0(121−≤=≤≤===Y P Y Y P X X P 易知{}{}{}{}{},221−−−=e e 12<=P ,10,1,02,11,02121≤≤>====>≤===Y Y Y P X X P Y Y P X X P{}{}{},212,10,12121−=≤<=≤>===e e Y P Y Y P X X P {}−− {}{}.22,11,1221−=>=>>===e Y P Y Y P X X P于是，可将X 1和X 24、∑=====nm m n P n X P 0),()(ηζ∑=−−−−=nm mn m n e m n m p p 0)!(!)1(λλ()[]).,2,1,0(!1!)1()!(!!!==−+=−−=−−−=−∑n n e p p n e p p m n m n n e n n n mn m nm n λλλλλλ即X 是服从参数为λ的泊松分布.∑∑∞=−−∞=−−−−−=−−==mn mn m n mn m m mn m n m n p m e p em n m p p m Y P )!()1(!)!(!)1()(λλλλλ).,2,1,0(,!)(!)()1( ==⋅=−−−−m m ep e e m ep pmp mλλλλλλ即Y 是服从参数为λp 的泊松分布.5、由定义F （y x ,）=P {}∫∫∞−∞−=≤≤x y dxdy y x y Y x X .),(,ϕ因为ϕ（y x ,）是分段函数，要正确计算出F （y x ,;1>y ），必须对积分区域进行适当分块：等5个部分.10,10,1;1,1;10,100≤≤≤≤>>>≤≤<x y x y x y y x 或;0<≤≤x （1）对于 有 F （,00<<y x 或y x ,）=P{X ≤,x Y ≤y}=0; （2）对于 有 ;,10,10≤≤≤≤y x 2204),(y x vdudv u y x F x y ==∫∫（3）对于, 有 10,1≤≤>y x {};,1),(2y y Y X P y x F =≤≤= （4）对于, 有 10,1≤≤>x y {}21,),(x Y x X P y x F =≤≤=; （5）对于 有 ,1,1>>y x 1),(=y x F .故X 和Y 的联合分布函数⎪⎪⎪⎩⎪⎪⎪⎨⎧<<≤≤<<≤≤≤≤≤≤<<=.1,1,.1,10,1,,1,10,,10,10,,00,0),(2222y x y x y y x x y x y x y x y x F 或6、（1） ,0,0;0),(,00>>=≤≤y x y x F y x 或),(y x F =∫∫+−x y t s dsdt ze)2())(())((200202yt x s y t x se e dt e ds e−−−−−−==∫∫=)1)(1(2y x e e −−−−即⎩⎨⎧>>−−=−−.,0,0,0),1)(1(),(2其它y x e e y x F y x （2）P ()()220(),22x x y x yxy xY X f x y dxdy dx e dy e e d +∞+∞−−−−<≤===−∫∫∫∫∫x∫∫∞+−−−∞+−−=−−=03220)(2)1(2dx e e dx e e x x x x .312131(2)2131(2023=−−=−=∞+−−x x e e7、（1）时，0>x ,0)(,0;)(=≤==∫∞+−−x f x e dy e x f X Xx y X 时 即 ⎩⎨⎧≤>=−.0,0,0,)(x x e x f x X （2）{}2/111210121),(1−−≤+−−−+===≤+∫∫∫∫e e dy e dxdxdy y x f Y X P y x x xy8、（1）（i ）时,，;),()(计算根据公式∫∞+∞−=dy y x f x f X 0≤x 当10;0)(<<=x x f X 当时()();24.224.2)2(8.4)(202x x x y dy x y x f xx X −=−=−=∫0)(,1=≥x f x X 时当即⎩⎨⎧<<−=.,0;10),2(4.2)(2其它x x x x f X （ii ） 利用公式计算. 当∫∞+∞−=dx y x f y f Y ),()(;0)(,0=≤y f y Y 时,10时当<<y112)22(8.4)2(8.4)(y y Y x x y dx x y y f ∫−=−=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−−⎟⎠⎞⎜⎝⎛−=222128.42y y y );43(4.2)2223(8.422y y y y y y +−=+−=当时，1≥y .0)(=y f Y 即⎩⎨⎧<<+−=.0;10),43(4.2)(2其它y y y y y f Y 121111222211111(2)((1(,1(,)1.22222P X Y P X Y f x y dxdy dx dxdy +∞+∞⎧⎫<<=−≥≥=−=−=⎨⎬⎩⎭∫∫∫∫∪58、47809、本题先求出关于x 的边缘概率密度，再求出其在2=x 之值. 由于平面区域D 的面积为)2(X f ,2121=dx =∫x S e D 故（X,Y ）的联合概率密度为⎪⎩⎪⎨⎧∈=.,0;),(,21),其它D y x y x (f易知，X 的概率密度为∫∞+∞−⎪⎩⎪⎨⎧<<==,,0,1,21),()(2其它e x xdy y x f x f X 故.41221)2(=×=X f 10、（1）有放回抽取：当第一次抽取到第个数字时，第二次可抽取到该数字仍有十种可能机会，即为 k {}).9, ,1,0(101====i k Y i X P （2）不放回抽取：（i ）当第一次抽取第)90(≤≤k k 个数时，则第二次抽到此（第个）数是不可能的，故 k {}.)9,,1,0,; =k i k (0====i k Y i X P（ii ）当第一次抽取第个数时，而第二次抽到其他数字（非k ）的机会为，知)90(≤≤k k 9/1{}.)9,,1,0,; =k i k (9/1≠===i k Y i X P 11、（1）因∫−=−=12,)1(12)1(24)(yy y ydx x y f η.,0)(;10其它=≤≤y f y n 故在0≤y ≤1时，⎩⎨⎧≤≤−−=;1)1/()1(2)(2其它x y y x y x f ηξ因()∫−=−=x y x ydy x x f 022,)1(12124)(ξ.,0)(;10其它=≤≤x f x ξ故在0≤x ≤1时，⎩⎨⎧≤≤=.0,0/2)(2其它x y x y x y f ξη（2）因;1,121)(2/12∞≤≤==∫x x nxdy y x X f x x ξ;,0)(其它=x f ξ故在1≤x<时，∞⎪⎩⎪⎨⎧<<=.,1121)(其它x y xnxy x y f ξη因 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∞<<=≤<==∫∫∞∞,002121102121)(22/12其它y y dx y x y dx y x y f y y η 故在10≤<y 时,⎪⎩⎪⎨⎧∞<<=;011)(2其它x y y x x y f ξη 而在,1时∞<<y ⎪⎩⎪⎨⎧∞<<=.0)(2其它x y x yx y f ξη（3）在x >0,.0,0)(;0,)(≤=>==∫∞−−x x f x e dy e x f x xy ξξ⎪⎩⎪⎨⎧>=−.0,)(其它x y e x y f y x ξη ;0,)(0>==∫−−y ye dx e y f y yy η .故在y>0时，0,0)(≤=y y f η⎪⎩⎪⎨⎧<<=.0,01)(其它y x y y x f ηξ12、1(1)(2)2(),0(1)(1)X n n n n n f x dy x x y x ∞−−−−==+++∫>，故12(1)(2)0,(/1)0.n nY X n y y f y −⎧−+>=⎨⎩其它 13、X 和Y 是否独立，可用分布函数或概率密度函数验证.方法一：X 的分布函数的分布函数分别为 Y x F X 和)()(y F Y ⎩⎨⎧<≥−=+∞=−,0001),()(5.0x x e x F x F x X ⎩⎨⎧<≥−=+∞=−.0001),()(5.0y y e y F y F yY 由于独立.Y X y F x F y x F Y X 和知),()(),(={}{}{}[][]1.005.005.0)1.0(1)1.0(11.01.01.0,1.0−−−=⋅=−⋅−=>⋅>=>>=e e e F F Y P X P Y X P Y X αY X Y X x f x f y x f Y X 和分别表示和),,()()(),,(方法二：以的概率密度，可知 ⎩⎨⎧≥≥=∂∂∂=+−.00,025.0),(),()(5.02其它y x e y x y x F y x f y x ∫∞+∞−−⎩⎨⎧<≥==,0005.0),()(5.0x x e dy y x f x f x X ∫∞+∞−−⎩⎨⎧<≥==.00,05.0),()(5.0y y e dx y x f y f yY ∫∫∞+∞+−+−==>>==1.01.01.0)(5.0.25.0}1.0,1.0{.),()(),(e dxdy e Y X P a Y X y f x f y x f y x Y X 独立和知由于)()(),(j i j i y Y P x x P y Y x X P =⋅====14、因知X 与Y 相互独立，即有 . )3,2,1,2,1(==j i 首先，根据边缘分布的定义知 .2418161),(11=−===y Y x X P 又根据独立性有),(61)()(},{2411111i x X p y Y p x X p y Y x X p ===⋅===== 解得41)(==i x X P ,从而有 1218124141),(31=−−===y Y x X P 又由 )()(),(2121y Y P x X P y Y x X P =⋅====, 可得 ),(41812y Y P == 即有21)(2==y Y P , 从而 838121),(22=−===y Y x X P .类似地，由),()(),(3131y Y P x X P y Y x X P ===== 有),(411213y Y P ==得31)(3==y Y P ,从而,.111),(31=−===y Y x X P 最后=)(2x X P =1+3+1=3. 将上述数值填入表中有1x1/24 1/8 1/12 1/4 2x1/8 3/8 1/4 3/4 {}j P y X P j ⋅==1/6 1/2 1/3115、本题的关键是由题设P{X 1X 2=0}=1，可推出P{X 1X 2≠0}=0；再利用边缘分布的定义即可列出概率分布表.(1)由P{X 1X 2=0}=1,可见易见,0}1,1{}1,1{2121=====−=X X P X X P 25.0}1{}0,1{121=−===−=X P X X P 5.0}1{}1,0{221=====X P X X P 25.0}1{}0,1{121=====X P X X P 0}0,0{21===X X P121212.16、(1) ⎩⎨⎧<<=,,0,10,1)(其他x x f X ⎪⎩⎪⎨⎧≤>=−.0,0,021)(2y y ey f yY 因为X ，Y 独立，对任何y x ,都有 ).,()()y x f y f x Y =⋅(f X ⎪⎩⎪⎨⎧><<=−.,0,0,10,21),(2其他所以有y x e y x f y（2）二次方程 有实根，△ t Y Xt t 中022=++,04)2(2≥−=Y X ,02≥−Y X 即,2X Y ≤ 故=)(有实根t P dydx e dydx y x f X Y P yx y x 2122221),(}{−≤∫∫∫∫==≤∫−−=1022)(dx ex y=dx edx edx x x x 2101010222221211)21(−−∫∫−=−=−πππ21−=［∫∫∞−∞−−−−1022222121dx edx exx ππ］.1445.08555.01]5.08413.0[21)]0()1([21=−≈−−≈Φ−Φ−=ππ17、（1）因为X ，Y 独立，所以 .⎩⎨⎧>>==+−.,0,0,0,)()(),()(其他y x e y f x f y x f uy x Y X λλμ（2）根据Z 的定义，有 P{z=1}=P{Y ≥X}∫∫∫∫∞+∞−+−≥==)(),(xy x xy dydx e dydx y x f μλλμ∫∫∞+∞+−−=)(dx dy e e xy x μλμλ ),0u dx ee x x +=⋅=∫∞+−−λλλμλ{}{110=−==Z P Z P Z 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤+<=.1,1,10,,0,0)(z z z z F Z μλμ18、∵X 、Y 分别仅取0，1两个数值，∴Z 亦只取0，1两个数值. 又∵X 与Y 相互独立，∴{}{}{}{}==========00)0,0(0),max(0Y P X P Y X P Y X P Z P 1/2×1/2=1/4， 故{}{}.4/34/110111=−==−===Z P Z P 19、 X 由2×2阶行列式表示，仍是一随机变量，且X=X 1X 4--X 2X 3，根据X 1，X 2，X 3，X 4的地位是等价且相互独立的，X 1X 4与X 2X 3也是独立同分布的，因此可先求出X 1X 4和X 2X 3的分布律，再求X 的分布律. ,则X=Y 1--Y 2.随机变量Y 1和Y 2独立同分布：322411,X X Y X X Y ==记}{}{}{{}.84.016.01}0{0112121=−========Y P Y Y P Y P 16.01,132===P X X P 显见, 随机变量X=Y 1--Y 2有三个可能值--1,0,1.易见 P{X=--1}=P{Y 1=0,Y 2=1}=0.84×0.16= 0.1344， P{X=1}=P{Y 1=1,Y 2=0}=0.16×0.84=0.1344, P{X=0}=1--2×0.1344=0.7312. 于是，行列式的概率分布为 4321X X X X X =~ ⎥⎦⎤⎢⎣⎡−1344.07312.01344.010120、因为{Z=i }={X+Y=i }={X=0,Y=i }}.0,{}1,1{==−==Y i X i Y X ∪ ∪∪ 由于上述各事件互不相容，且注意到X 与Y 相与独立，则有 ∑∑==−===−====i k ik k i Y P k X P k i Y k X P i Z P 00}{}{},{}{∑=+−−−−−=−−=iik ki n ki k i nkn kk n P p pC P p c 022111()1()1∑=−−+ik k i n k n in n C Cp 02121)(,,1,0,)1(212121n n i p p C i n n i i n n+=−=−++).,(~21p n n B Y X Z ++=故注：在上述计算过程中，已约定：当r>n 时，用到了公式 并,0=rnC .12121∑=+−=ik i n n k i n k n C C C21、X 和Y 的概率分布密度为},2)(exp{21)(22σσπy x x f X −−=);(+∞<<−∞x ⎩⎨⎧≤≤−=.,0,),2/(1)(其它πππy y f Y 因X 和Y 独立，考虑到 )仅在[)(y f Y ππ,−]上才有非零值，故由卷积公式知Z 的概率密度为.221)()()(222)(dy edy y f y z f z f a y z Y X Z ∫∫−−−−∞+∞−=−=ππμσππ令σμ−−=y z t ,则上式右端等于.(2122122⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛−−Φ−−+Φ=∫−+−−−σμπσμππππσμπσμπz z dt e z z t 22、（1）由题设知 {}y X X P y M P y F n M ≤=≤=),,max()()(1),,(1y X y X P n ≤≤= )()()()()(121y F y F y X P y X P y X P Xn X n =≤≤≤=.∵),1(],0[~:,,1n i U X X X i n ≤≤θ独立且同分布 ∴⎪⎩⎪⎨⎧><<≤=,0,1,0,,0,0)(x x x x x F i X θθ∴⎪⎪⎩⎪⎪⎨⎧≥<<≤=.,1,0,,0,0)(θθθy y y y y F n n M 故⎪⎩⎪⎨⎧<<=−.,0,0,)(1其它θθy ny y f n n M（2）{}y X X P y N P y N P y F n N >−=>−=≤=),,min(1)(1)()(1()y X P y X P y X P y X y X y X P n n >>>−=>>>−= )()(1,,,12121()[])(11)(11y F y X P i X i ni −−=>Π−==故 ⎪⎩⎪⎨⎧<<−=⎪⎩⎪⎨⎧<<−−−=−−其它其它,0,00,)(,001(1()(11y y n y y n y f n n n N θθθθθ 23、由题设容易得出随机变量（X ，Y ）的概率密度，本题相当于求随机变量X 、Y 的函数S=XY 的概率密度，可用分布函数微分法求之.依题设，知二维随机变量（X ，Y ）的概率密度为()()()⎩⎨⎧∉∈=G y x Gy x y x f ,,0,2/1,若若 设为S 的分布函数,则 当{s S P s F ≤=)(}0≤s 时,()0=s F ； 当时, .2≥s ()1=s F 现设0<s<2. 曲线s xy =与矩形G 的上边交于点(s,1);位于曲线s xy =上方的点满足s xy >,位于下方的点满足s xy <. 故(){}{}{}).ln 2ln 1(2211211121s sdy dx dxdy S XY P s XY P s S P s F s x s sxy −+=−=−=>−=≤=≤=∫∫∫∫>于是,⎩⎨⎧≥≤<<−=.20,0,20,2/)ln 2(ln )(s s s s s f 或若若（二）、补充题答案1.由于即{},0)(),,min(,,max =<==Y X P Y X 故知ηξηξ{}{}{}03,23,12,1=========Y X P Y X P Y X P ；又易知{}{}{}{},9/1111,11,1==⋅=======ηξηξP P P Y X P{}{},9/12,22,2======ηξP Y X P {}{},9/13,33,3======ηξP Y X P {}{}{},9/29/19/11,22,11,2=+===+=====ηξηξP P Y X P{}{}{},9/22,33,22,3===+=====ηξηξP P Y X P {}.9/29/711,3=−===Y X P 所以2.（1）x{}.,2,1,0,0,)1( =≤≤−===n n m P P C n X m Y P m n {}（2）{}{}n X P n X m Y P m Y n X P ======,.,2,1,0,0,!)1( =≤≤⋅⋅−=−−n n m e P P C n m n mm n λλ3.22)1()1()1()0()0()1(p p Y P X P Y P X P z P +−===+====)1(2)0()1()1()0()0(p p Y P X P Y P X P z P −===+====而，由2)1,1()1,1(p Y X P Z X P ======),1()1()1,1(=====Z P X P Z X P 得. 2/1=p 5.:设随机变量ξ和η相互独立，都服从分 )1,0(N 布.则⎭⎬⎫⎩⎨⎧+−⋅=)(21exp 21),(22y x y x p π.显然， ,),(),(∫∫∫∫<SGdxdy y x p dxdy y x p,其中 G 和S 分别是如图所示的矩形ABCD 和圆.22/)21(),(2∫∫∫−−=a ax Gdx e dxdy y x p π，令,sin ,cos ϕγϕγ==y x 则 ∫∫∫∫=ππ20221),(a aSdxdy y x p 所以221212/a aaxe dx e −−−−<∫π.6.设这类电子管的寿命为ξ，则（1）三个管子均不要替换的概率为；（2）三个管子均要替换的概率为 .∫∞+==>1502.3/2)/(100)150(dx x P ξ21(−27/8)3/2(3=27/1)3/3=7.假设总体X 的密度函数为，分布函数为，第次的观察值为，独立同分布，其联合密度函数)(x f ,(1x f )(x F )()2x f i (n x )1(n i X i ≤≤i X )(),1n f x f x =.依题意，所求的概率为{}∫∫∫∫∫∫∞+∞−∞−∞−∞−−−−=−==>>><n n n nx i x x x x n n nn nn n i n n n n dx x f dx x f dx x f dx x f dx dx xx f X X X X X X P 112211111,...,2,1121)(...)()()(),,(.,...,,∫∫∞+∞−∞+∞−−−==)()()()(11n n n n n n n x dF x F dx x f x F.1)(1n x F nn n=∞−∞+=8.)(),()(21211211n P n k P n k P =+=+===+=ξξξξξξξξ)()()(2121n P k n P k P =+−===ξξξξ.由普哇松分布的可加性，知服从参数为的普哇松分布，所以 21ξξ+21λλ+)(21212112121!)()!(!)(λλλλλλλλξξξ+−−−−+−⋅==+=e n e k n ek n k P n k n k.1211211kn kk n −⎟⎟⎠⎞⎜⎜⎝⎛+−⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛=λλλλλλ9.当，0≤z (),0)(=≤=z Z P z F z ,0>z 当()z Z P z F z ≤=)(∫∫−+−=20)2(02xz y x z dy e dx∫∫−−−−−−−==202012x z z z y z x ze e dy e dxe ，所以 Y X z 2+=的分布函数为 ⎩⎨⎧>+−≤=−.0,)1(1,0,0),(z e z z y x F z10.由条件知X 和Y 的联合密度为⎪⎩⎪⎨⎧≤≤≤≤=其他若,0,31,31,41),(y x y x p以表示随机{})()(∞<<−∞≤=u u U P u F 变量U 的分布函数.显然，当0≤u 时， 0)(=u F ；当时，； 2≥u 1)(=u F 当，则20<<u []∫∫∫∫≤−uy x y x p ||,(≤−−−=−−===uy x u u dxdy dxdy u F ||2)2(411)2(44141))(2u−于是，随机变量的密度为⎪⎩⎪⎨⎧<<−=其他,0;20),2(21)(u u u p .11.记为这3个元件无故障工作的时间，则的分布函数321,,X X X ),,min(321X X X T ={}[][].)(1),,min(1(31321t X P t X X X P t F T −=>−(11)13X P t ≤−−=>)()t T P =≤=⎩⎨⎧≤>−=∴⎩⎨⎧=≤>−=−−,0,0,0,1)()3,2,1(,0,0,0,1)(~3t t e t F i t t e t F X t T t i λλ∵ 故 ⎪⎩⎪⎨⎧≤>==−.0,0,0,3)(')(3t t e t F t f t T T λλ。

第三章热力学第二定律1、在T1=750K的高温热源与T2=300K的低温热源间工作一卡诺可逆热机,当其从高温热源Q1=250kJ时,该热机对环境所做的功W= -150 Kj，放至低温热的热Q2= -100 kJ。

2、以汞为工作物质时，可逆卡诺热机效率为以理想气体为工作物质时的100% 。

（可逆热机效率与工质无关）3、液体苯在其沸点下恒温蒸发，则此过程的△U 大于零；△H 大于零；△S 大于零；△G 等于零。

4、将1mol 温度为100℃、压力为101.325kPa的液体水投入一密封真空容器中，并刚好完全蒸发为同温同压的水蒸气，则此过程的△H 大于零；△S 大于零；△G 等于零。

5、H2与O2均为理想气体，当经历如下所示的过程后，则系统的△U 等于零; △H 等于零; △S 等于零; △G 等于零。

6、732 K时，反应NH4Cl(s)==NH3(g)+HCl(g)的∆r G=－20.8 kJ·mol-1，∆r H=154 kJ·mol-1，则该反应的∆r S = 239 J·K-1·mol-1 。

7、某双原子理想气体3 mol从始态300 K，200 KPa下经过恒温可逆膨胀到150KPa ，则其过程的功W是－2152.6 J。

8、某双原子理想气体3 mol从始态350K，200 KPa下经过绝热可逆膨胀到235.5 K平衡，则其过程的功W是－7139.6 J。

9、在真空密封的容器中,1mol温度为100℃、压力为101.325 kPa的液体水完全蒸发为100℃、101.325 kPa的水蒸气, 测得此过程系统从环境吸热37.53kJ,则此过程的△H= 40.63 kJ, △S= 108.88 J·K-1, △G= 0 kJ。

判断题1、绝热过程都是等熵过程。

×2、理想气体的熵变公式∆S nC V V nC p p p V =⎛⎝ ⎫⎭⎪+⎛⎝ ⎫⎭⎪,,ln ln m m 2121只适用于可逆过程。

第三章辛亥革命与君主专制制度的终结一、单项选择题1. 1903年6月，（）在上海《苏报》发表《驳康有为论革命书》，批驳康有为所谓“中国之可立宪，不可革命”的谬论A.陈天华B.邹容C.章炳麟D.梁启超2.1903年邹容写的（）是中国近代史上第一部宣传革命和资产阶级共和国思想的著作A.《猛回头》B.《警世钟》C.《革命军》D.《驳康有为论革命书》3.中国近代第一个资产阶级革命政党是()A.强学会B.兴中会C.同盟会D.国民党4. 孙中山三民主义思想的核心是()A.驱除鞑虏B.恢复中华C.创立民国D.平均地权5.1905年11月，孙中山在《民报》发刊词中将中国同盟会的政治纲领概括为（）A.创立民国、平均地权B.驱除鞑虏、恢复中华、创立合众政府C.民族主义、民权主义、民生主义D.联俄、联共、扶助农工6.武昌起义前同盟会领导的影响最大的武装起义是()A.广州起义B.萍浏醴起义C.镇南关起义D.黄花岗起义7.中国历史上第一部具有资产阶级共和国宪法性质的法典是（）A.《钦定宪法大纲》B.《中华民国临时约法》C.《中华民国约法》D.《试训政纲领》8. 辛亥革命取得的最大成就是（）A.推翻了封建帝制B.促进了资本主义的发展C.使人民获得了一些民主自由权利D.打击了帝国主义的殖民势力9. 南京临时政府的局限性表现为（）A.承认清政府与列强所订的一切不平等条约和一切外债有效B.没有提出任何可以满足农民土地要求的政策和措施C.维护封建土地制度以及官僚、地主所占有的土地财产D.主体是资产阶级革命派10. 二次革命失败的最重要原因是()A.革命党人军队不足B.国民党力量涣散C.袁世凯军队强大D.袁世凯得到帝国主义的支持11.1915年，（）在云南率先举起反袁护国的旗帜，发动护国战争A.黄兴B.段祺瑞C.蔡锷D.孙中山12.资产阶级革命派开展护国运动的主要原因是()A.袁世凯指使刺杀宋教仁B.袁世凯强迫国会选举他为正式大总统C.袁世凯解散国会D.袁世凯复辟帝制13. 袁世凯为复辟帝制不惜出卖主权，与日本签订了卖国的（）A.中日共同防敌军事协定B.承认外蒙自治C.“二十一条”D.出让川汉、粤汉铁路14. 1917年孙中山针对（）指出“以假共和之面孔，行真专制之手段”，并举起“护法”旗帜A.黎元洪B.张勋C.张作霖D.段祺瑞15.标志着整个中国民族资产阶级领导的旧民主主义革命终结的是（）A.二次革命的失败B.护国运动的失败C.护法运动的失败D.保路风潮的失败16.20世纪初主张“实业救国”的著名实业家楷模是()A.张謇B.周学熙C.荣宗敬D.荣德生二、多项选择题1.《辛丑条约》的签订，标志着（）。

第三章习题及答案1.试确定在22H ()I (g)g+2HI(g)的平衡系统中的组分数。

（1）反应前只有HI ；（2）反应前有等物质的量的2H 和2I ；（3）反应前有任意量的2H 、2I 及HI 。

解（1）1113'=−−=−−=R R S K （2）1113=−−=K （3）2013=−−=K 4.环己烷在其正常沸点为80.75℃时的气化热为1358J g −⋅。

在此温度是液体和蒸气的密度分别为0.7199和0.00293g cm −⋅。

（1）计算在沸点时d d p/T 的近似值（仅考虑液体体积）；（2）估计在50.510Pa ×时的沸点；（3）欲使环己烷在25℃沸腾，应将压力减压到多少？解（1）根据克拉贝龙方程：6vap m,B m m 31d 358841011d [(g)(l)]353.75840.00290.71992.9510Pa K H p T T V V −⎡⎤⎢⎥∆××⎢⎥==−⎛⎞⎢⎥××−⎜⎟⎢⎥⎝⎠⎣⎦=×⋅若忽略液体体积：6vap m,B 31m d 35884102.9310Pa K 1d (g)353.75840.0029H p T TV −⎡⎤∆⎢⎥××≈==×⋅⎢⎥⎢⎥××⎣⎦(2)由克克方程：vap m,B 211255211ln R 0.5103588411ln 108.314353.75H p p T T T ∆⎛⎞=−⎜⎟⎝⎠⎛⎞××=−⎜⎟⎝⎠解得：2331.29KT =（3）将5211298K,353.75K,10Pa T T p ===代入克克方程得：42 1.4810Pa p =×。

5.溴苯Br H C 56的正常沸点为156.15℃，试计算在373K 时溴苯的蒸气压？与实验值Pa 1088.14×比较并解释这一现象。

第三章习题参考答案一、填空题1、指令格式是由操作码和操作数所组成，也可能仅由操作码组成。

2、若用传送指令访问MCS-51的程序存储器，它的操作码助记符应为MOVC 。

3、若用传送指令访问MCS-51的片内数据存储器，它的操作码助记符应为MOV 。

4、若访问MCS-51的片外数据存储器，它的操作码助记符应为MOVX 。

5、累加器（A）=80H，执行完指令ADD A，#83H后，进位位C= 1 。

6、执行ANL A，#0FH指令后，累加器A的高4位= 0000 。

7、JZ rel的操作码地址为1000H，rel=20H，它的转移目的地址为1022H 。

8、JBC 00H，rel 操作码的地址为2000H，rel=70H，它的转移目的地址为2073H 。

9、累加器（A）=7EH，（20H）= #04H，MCS-51执行完ADD A，20H指令后= 0 。

10、MOV PSW，#10H是将MCS-51的工作寄存器置为第 2 组。

11、指令LCALL 37B0H，首地址在2000H，所完成的操作是2003H 入栈，37B0H →PC。

12、MOVX A，@DPTR源操作数寻址方式为寄存器间接寻址。

13、ORL A，#0F0H是将A的高4位置1，而低4位保持不变。

14、SJMP rel的指令操作码地址为0050H，rel=65H，那么它的转移目标地址为 00B7H 。

15、设DPTR=2000H，（A）=80H，则MOVC A，@A+DPTR的操作数的实际地址为2080H 。

16、MOV C，20H源寻址方式为位寻址。

17、在直接寻址方式中，只能使用8 位二进制数作为直接地址，因此其寻址对象只限于片内RAM 。

18、在寄存器间接寻址方式中，其“间接”体现在指令中寄存器的内容不是操作数，而是操作数的地址。

19、在变址寻址方式中，以 A 作变址寄存器，以PC 或DPTR 作基址寄存器。

20、假定累加器A中的内容为30H，执行指令1000H：MOVC A,@A+PC后，把程序存储器1031H 单元的内容送入累加器A中。