部门指标分解矩阵表

思维框架：PDCA、QQTC和内容分解法在企业管理中的应用正略钧策管理咨询顾问宋炜PDCA、QQTC和内容分解这三种方法在分解绩效指标方面是卓有成效的。

但实际上，笔者发现，这些方法的应用不只是在绩效指标分解一个领域，在管理的很多方面，都有用武之地，例如，制度编写。

（二）笔者曾负责一个管理制度优化的咨询项目，对某上市公司的管理制度进行从整个体系到单个制度的全面优化。

项目组将制度首先分成法人治理制度和公司管理制度，然后在管理制度中再分三个层级，其中第二个层级的制度称“管理制度”，第三个层级的制度称“管理办法”，是对某一项工作具体的管理规定。

项目组设计了一套通用性的模板，以规范“管理制度”和“管理办法”的内部结构。

主要分为四大组成部分：第一部分，总则。

介绍编制该管理办法的目的，依据等。

第二部分，组织机构和责权划分。

第三部分，制度主要内容。

第四部分，附则。

介绍制度的实施时间以及批准部门。

在篇幅最多的第三部分，项目组提出借鉴QQTC、PDCA或内容分解的方法进行章节划分。

具体方法是：²首先按照内容分解的思路将该制度所约束的工作分解成各个子模块；²如果这些子模块在执行中有先后顺序之分，就按先后顺序编写各个模块（这体现了PDCA 的思想），如果没有先后顺序之分，就按重要性顺序编写各个模块；²如果无法按照内容分解的方式进行分解，则可以考虑将该制度所约束工作的按照类似于QQTC的方式进行分解，将各个关键要素找出来，再分章节进行单独的条款编写；²在实际的制度编写中，往往很难仅按一种思路进行结构划分，较常见的是将几种方法杂糅起来。

例如，在《物资管理办法》的第三部分中，首先是“物资计划”，对应着PDCA中的“P”，然后按先后顺序编写物资管理的各项工作，整体对应着“D”最后则是“监督与奖惩”，对应着“C”。

参见表4。

再如，在《人力资源管理制度》的第三部分，按照逻辑先后顺序分别介绍人力资源管理的各项工作：人事管理、薪酬绩效管理、培训管理、干部管理及其他专项工作等。

心之所向，所向披靡如何设计绩效考核指标体系单选题1. 组织层面绩效考核指标设计，共有四个操作步骤，其中不包括的是：√A初步收集被考核人的绩效指标B撰写指标解释表C填写绩效考核表D滚动、修定拟好的绩效考核表正确答案： D2. 人力资源规划指标的推导可量化的程度指标中，可以用计算公式表示的是：√A定量指标B定性指标C部门指标D价值指标正确答案： A3. “五因素分析法”在补充评价指标时，关于公司文件管理部门考核可量化的内容,不包括的是：√A后勤服务的时间B文件未及时传达的次数C文档抽检的符合率D重大文控泄密的次数正确答案： A4。

撰写指标解释表要尽量详尽,其中没有涉及的内容是：√A指标的编码B指标的名称C指标说明D指标类型正确答案： D5. 制定绩效考核指标涉及“五因素分析法”，其中不包括的因素是：√A时间B过程C质量D风险控制正确答案： B6. 关于指标筛选与实操性检查的原则，表述不正确的是：√A指标是否可信B指标是否可衡量C指标是否灵活D指标是否可控正确答案： C7. 关于指标赋值计分法之一的“层差法”，表述正确的是：√A设定目标值和挑战值两个指标B计算方法是用指标完成数除以目标值再乘以目标值对应分C在考核时必须结合关键事件法D在设计绩效评价体系当中最常见正确答案： A8。

在组织层面绩效考核指标战略的第一步骤中，关于目标与指标分解工具矩阵表，表述错误的是：√A用于搜集考核指标B纵列是组织的各个部门，横列是核心指标C需要区分驱动责任和结果责任D连接战略地图卡表和绩效考核表的桥梁性工具正确答案: B9。

绩效考核指标有两个常见的工具,关于“价值树分解模型”表述正确的是: √A只能运用于财务指标的分解B是对指标进行赋值的最佳方法C是部门指标的外部驱动因素D不包括分析受其他部门影响的指标正确答案： D10. 在企业中，关于重大安全生产事故、环保事故等对直接责任人的考核，通常采用的考核方法是: √A连续计分法B关键事件法C扣分法D非此即彼法正确答案: D判断题11。

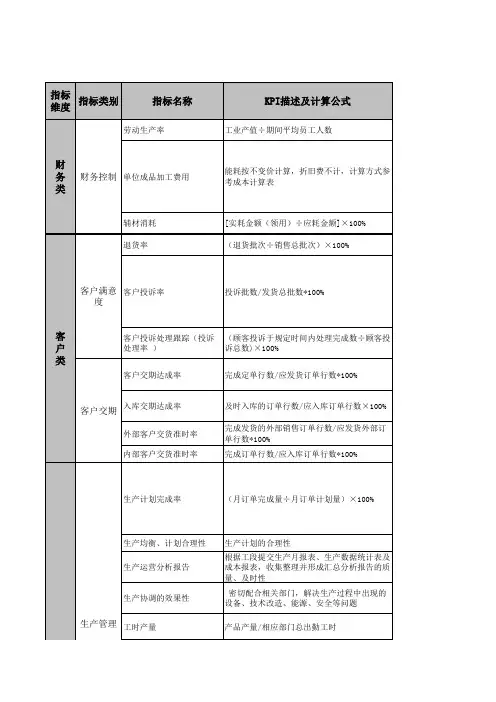
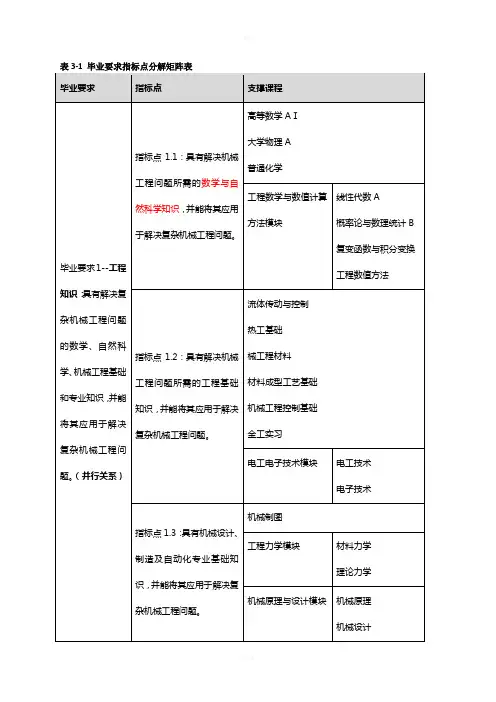
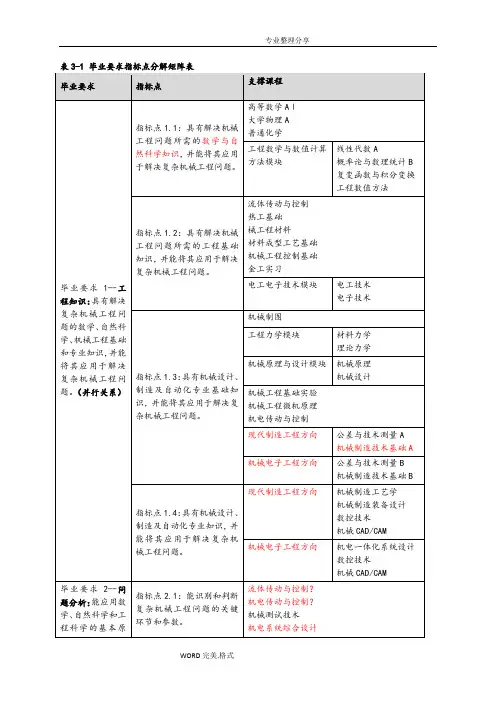
机械工程专业毕业要求及指标点分解依据工程教育认证通用标准中的12条标准和专业补充标准的要求，机械工程专业制定了明确的、公开的、可衡量的毕业要求，能够有效支撑本专业的培养目标，使得毕业生在毕业后若干年能够达到培养目标的预期，并对每项毕业要求进行了指标点分解。

本专业的毕业要求如下：1.工程知识：掌握工程领域所需的数学、自然科学、工程基础和机械工程学科专业知识，并能够用于解决机械工程领域复杂工程问题。

1-1掌握相关数学知识，并能运用于实际工程问题进行数学建模、求解与数据处理；1-2掌握相关自然科学的基础原理和思维方法，并能将其应用于解决工程科学和技术问题；1-3掌握相关机械工程知识，能将其用于解决机械工程装备研究与开发等工程问题；1-4掌握机械工程专业基础知识，并能用于解决机械产品设计、制造、技术开发、生产组织与管理、设备安装与调试等机械科学和工程技术问题；1-5掌握机械工程专业知识，并能用于解决机械工程复杂科学和工程技术问题。

2.问题分析：能够应用数学、自然科学、工程科学的基本原理，识别、表达、并通过文献研究分析机械装备设计制造、产品质量控制及设备安装与调试、生产组织与管理等复杂工程问题，以获得有效结论。

2-1能基于数学和自然科学原理识别机械工程科学和技术问题；2-2能够应用机械工程基础知识对研究对象进行正确的表达、分析机械工程问题；2-3能够综合运用机械工程专业基础理论和研究方法，借助文献寻求机械工程复杂工程问题解决方案，并获得有效结论。

3. 设计/开发解决方案：综合社会、健康、安全、法律、文化及环境等因素，设计满足机械工程需求的系统、工艺流程和装备，在设计开发环节中体现创新意识。

3-1能在机械工程设计开发中，综合考虑社会、健康、安全、法律、文化以及环境等因素，并体现创新意识；3-2能够运用相关机械工程知识，设计满足特定工程需求的系统或单元；3-3能够运用专业知识完成机械工程系统、工艺流程和装备的设计或开发。

基于平衡计分卡的绩效管理指标权重的确定在实施平衡计分卡的过程中，对于如何平衡四个层面所占权重，以及各项关键绩效指标权重的确定是公司制定和实施平衡计分卡的一个难点。

本文运用层次分析法，以实际的案例为对象，客观地确定各绩效指标的权重，避免了过去主观打分法等的随意性，以期对企业的绩效管理提供参考。

标签：平衡计分卡层次分析法绩效管理平衡计分卡(The Balanced Scorecard，BSC)起源于1990年的由哈佛大学教授Kaplan及Nolan Norton Institute最高执行长Norton两位主持一项科研计划，他们的研究发现平衡计分卡的量度必须与组织的策略紧密的结合在一起，在实务的运作上许多采用平衡计分卡的公司都不约而同的将平衡计分卡当作重要管理流程，包括个人和团队的目标、薪资制度分配资源、编列预算和规划，以及策略的反馈与学习，至此，平衡计分卡的理论和方法得到了全面的阐述和推广。

一、基于平衡计分卡的绩效管理指标体系设计1.平衡计分卡的四个维度从整体上来讲，平衡计分卡包括了两方面的内容：用财务指标反映企业过去经营行为的综合结果；用顾客、内部流程、学习与成长这三个非财务指标来反映企业未来财务绩效的动因，来补充财务指标，从而确保了企业绩效评价的全面性和科学性。

平衡计分卡的这种结构思路可以帮助企业管理者从四个重要方面来考察企业的经营情况：第一，财务维度：企业如何去面对自己的股东；第二，顾客维度：企业的顾客怎样看待自己：第三，内部流程维度：企业必须在什么方面有表现卓越：第四，学习与成长维度：企业能否持续提高和创造价值。

2.指标分解本文以某汽车制造企业为例，结合公司战略和平衡计分卡四个纬度的含义将指标分解如下：表1 平衡计分卡的四个维度的具体指标分解二、应用层次分析法确定指标权重各项关键绩效指标权重的确定也是公司制定和实施平衡计分卡的一个难点。

如果各指标的权重设置不当的话，对于员工绩效的改善是根本无益的，而且还会导致员工的逆反心理。

九宫格绩效管理体系摘要：1.九宫格绩效管理体系简介2.九宫格绩效管理体系的构成3.九宫格绩效管理体系的实施步骤4.九宫格绩效管理体系的优点与不足5.九宫格绩效管理体系的实际应用案例正文：一、九宫格绩效管理体系简介九宫格绩效管理体系是一种将企业战略目标分解为可衡量的绩效指标，并通过九宫格图进行可视化管理的高效方法。

它将企业的战略目标分解为九个方面，形成一个九宫格矩阵，从而帮助企业全面、系统地衡量和管理绩效，实现企业战略目标。

二、九宫格绩效管理体系的构成九宫格绩效管理体系主要由以下几个部分构成：1.战略目标：企业长期发展的愿景和目标，是九宫格绩效管理体系的基础和出发点。

2.绩效指标：根据战略目标分解出来的具体、可衡量的绩效指标，通常包括财务指标、客户指标、内部流程指标、学习与成长指标等。

3.九宫格矩阵：将绩效指标分别放入九个方格，形成一个九宫格矩阵，从而实现对绩效的全面管理。

4.目标值和权重：为每个绩效指标设定目标值和权重，以便更好地衡量和比较各个指标的贡献。

5.评分标准：根据绩效指标的实际完成情况，对其进行评分，以便衡量绩效达成程度。

三、九宫格绩效管理体系的实施步骤1.确定战略目标：明确企业的长期发展愿景和目标。

2.选择绩效指标：根据战略目标，选择能够衡量和反映企业战略目标实现程度的绩效指标。

3.设定目标值和权重：为每个绩效指标设定目标值和权重，以便更好地衡量和比较各个指标的贡献。

4.制定评分标准：根据绩效指标的实际完成情况，制定相应的评分标准，以便衡量绩效达成程度。

5.执行与监控：在日常工作中执行九宫格绩效管理体系，并定期监控绩效指标的完成情况。

6.绩效评估与反馈：根据绩效指标的实际完成情况进行评估，并及时给予反馈，以便调整和改进。

四、九宫格绩效管理体系的优点与不足1.优点：九宫格绩效管理体系可以帮助企业全面、系统地衡量和管理绩效，实现企业战略目标；同时，它具有可视化、易理解的特点，便于企业内部沟通和外部展示。

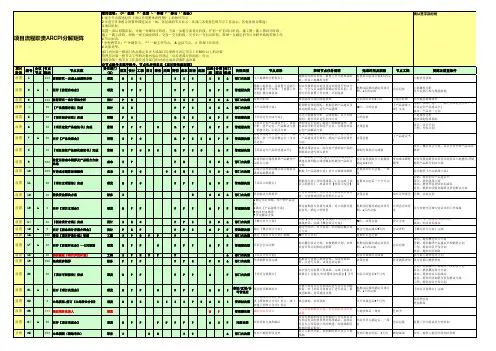
责任矩阵甘特图虽然直观地显示了项目的任务划分和进度安排，但项目需要完成的任务往往千头万绪，参与项目的部门与个人又五花八门，为此需要一种手段将任务落实到相应的人头上，确保每个任务都有相应的人员去负责和完成，这便是人员分工。

责任矩阵（responsibility matrix, RM）就是一种将工作任务分配、落实到项目执行组织的相关职能部门或个人，并明确表示出其角色、职责和工作关系的矩阵图形。

它以项目的工作任务为行，组织单元（个人）为列，用字母或特定的符号表示相关部门或个人在不同工作任务中的角色和责任职责，简洁明确地显示出项目人员的分工情况。

通过责任矩阵，项目的各项工作都能落实到具体的责任人，确保项目因岗设人，人人有事做，事事有人负责，从而避免责任不清而出现的无人负责的现象。

具体如何使用，大体有以下几个步骤：1、集项目小组成员运用工作分解结构（WBS）等工具列出需要完成的项目任务，如果已经有了项目的WBS，则可以直接用WBS中的工作包。

注意要尽可能把任务分解到可由一人单独完成，完成这项工作有且只能有一个交付结果。

任务分解不彻底难以落实到人头上，且可能导致人员分工出现混乱的情况。

2、列出参与项目管理以及负责执行项目任务的个人或职能部门的名称，并且搞清楚这些人员的教育背景、工作经验、性格特征以及能够用在项目上的工作时间情况，以便在分工时予以考虑。

3、以工作任务为行，以执行工作任务的个人或部门为列，画出相互关系矩阵图。

4、在矩阵图的行与列交叉窗口里，用字母、符号或数字显示任务与执行者在项目管理中的角色和职责——直接责任或参与，用字母表示为R——直接责任，I——参与。

5、检查个人部门或人员的任务分配是否均衡、适当，是否过度分配或者分配不当的现象，如有必要则做进一步的调整和优化。

6、将责任矩阵与项目成员沟通，让每个人都明白自己的项目中的任务和要求，确保他们明确各自的角色和承担的责任，获取他们的承诺，从而确保项目各项任务的完成。

AHP在确定指标权重中的应用AHP（层次分析法）实质上不是一个完全的定量分析法，因为在设置对比矩阵的时候，依然依靠评分者的客观评分，但是它依然在实际应用中发挥很好的作用。

AHP在人力资源绩效、薪酬、人员测评、岗位分析的确定指标权重中，同样能够很好的应用。

下面以绩效指标权重为例，看看在实际中如何使用（以excel为计算工具）。

假设某岗位已经确定有以下4个一级指标：A1工作任务指标（岗位职责内的工作）A2工作行为规范指标（公司规章制度的遵守）A3临时工作任务指标（领导、同事安排及突发事件）A4工作态度指标（工作指示服从性，与部门内外部同事协调性）现在要确定这四个指标之间的相对权重。

下面以这四个指标为例，按照AHP 计算权重的步骤，演示AHP在确定绩效指标权重中的应用。

1、构建四个指标对比矩阵。

顾名思义，就是这四个指标两两相互比较，形成一个4阶矩阵。

那么按照什么标准进行比较呢，这里有一个度量表：aij = 1，元素 i 与元素 j 对上一层次因素的重要性相同；aij = 3，元素 i 比元素 j 略重要；aij = 5，元素 i 比元素 j 重要；aij = 7，元素 i 比元素 j 重要得多；aij = 9，元素 i 比元素 j 的极其重要；aij = 2n，n=1,2,3,4，元素 i 与 j 的重要性介于aij = 2n - 1与aij = 2n + 1之间；反之则：这里稍作解释：如果第i个指标比第j个指标重要，即aij=3。

如果第j个指标比第i个指标重要，就aji=1/3。

那么现在可以按照以上的量表，对以上四个指标进行两两评判，得到一个矩阵（注：这里是按照行来进行比较，就是先A1与A2,A3,A4比较，然后A2与A3,A4比较，完成对角线以上的部分就可以了。

）2、计算矩阵的特征向量和指标权重计算出矩阵的特种向量后，就可以计算出A1,A2,A3,A4四个指标的相对权重。

1.对矩阵的各列求和（注意蓝色矩形区域）2.对每一列进行归一化处理公式如下：其中：的值为各列的和，如上图的SUM行，就是用各列的元素除以列的和。

总出口分解模型Koopman 假设包含G 国，N 行业部门从使用去想来看一国的总产出可以用用来作为本国的中间产品或者最终产品，或者用作外国的中间产品或者最终产品。

一国的总产出可以表示为：() r,s=1,2,,GGs sr r sr rX A X Y =+∑于是，国家间的投入产出模型写成矩阵形式为：1111211111212212222212221212 G G G G G G G GG G G G GG X A A A X Y Y Y X A A A X Y Y Y X A A A X Y Y Y ⎡⎤⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥⎢⎥+++⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎣⎦⎣⎦经过变化可得11111121111212212222122221212 - I- - G r r G G G G G r r G G G G GG G G GG Gr r Y X I A A A B B B X A A A B B B Y X A A I A B B B Y -⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤--⎢⎥⎢⎥⎢⎥⎢--⎢⎥⎢⎥⎢⎥⎢==⎢⎥⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎥⎢--⎣⎦⎣⎦⎣⎢⎥⎢⎥⎣⎦∑∑∑ 12G Y Y Y ⎡⎤⎥⎢⎥⎥⎢⎥⎥⎢⎥⎥⎢⎥⎥⎢⎥⎦⎣⎦111211112111121212222122221222121212 G G G G G G G G GG G G GG G G GG X X X B B B Y Y Y X X X B B B Y Y Y X X X B B B Y Y Y ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中，矩阵A 为GN*GN 直接消耗系数矩阵，Asr 表示国家r 各行业单位总产出对国家s 各行业产出的直接消耗量，B 为GN*GN 里昂惕夫逆阵，Brr 表示国家r 各行业额外生产以单位最终产品对国家s 各行业总产出的完全需求量，Xsr 为N*1矩阵，表示国家s 总产出中用于满足国家r 最终产品需求的部分， 矩阵Gs sr r X X =∑为N*1矩阵，表示国家s 各行业的总产出，矩阵Ysr 为N*1矩阵，表示国家各行业向国家r 出口的最终产品，Gs sr r Y Y =∑为N*1矩阵，表示国家s 各行业生产的最终产品总量矩阵Vs 为1*N 矩阵矩阵，表示国家s 各行业的增加值率12000 00 0G V V V V ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦将矩阵V 右乘里昂惕夫逆阵B:111112112212222212 G G G G G G G GG V B V B V B V B V B V B VB V B V B V B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦矩阵VB 每一列元素VsBsr 表示的是国家r 各行业单位最终产品中所包含的国家s 的增加值，于是，矩阵VB 每一列元素相加得到Gs sr sV B u=∑，其中u 为1*N 阶矩阵。