半导体物理第2章
- 格式:ppt
- 大小:6.99 MB
- 文档页数:70






半导体物理学简明教程答案陈志明编第二章-半导体中的载流子及其输运性质-课后习题答案半导体物理学简明教程 0第二章 半导体中的载流子及其输运性质1、对于导带底不在布里渊区中心,且电子等能面为旋转椭球面的各向异性问题,证明每个旋转椭球内所包含的动能小于(E -E C )的状态数Z 由式(2-20)给出。
证明:设导带底能量为CE ,具有类似结构的半导体在导带底附近的电子等能面为旋转椭球面,即⎪⎪⎭⎫ ⎝⎛++=-l t C m k m k k E k E 23222122)(与椭球标准方程2221122221k k k a b c++=相比较,可知其电子等能面的三个半轴a 、b 、c 分别为212])(2[ c t E E m b a -==212])(2[c l E E m c -=于是,K 空间能量为E 的等能面所包围的体积即可表示为232122)()8(3434C t l E E m m abc V -==ππ因为k 空间的量子态密度是V/(4π3),所以动能半导体物理学简明教程0半导体物理学简明教程 02/132/3*2)()2(2)(E E m V E g Vp V -= π2、完成本章从式(2-42)到(2-43)的推演,证明非简并半导体的空穴密度由式(2-43)决定。
解:非简并半导体的价带中空穴浓度p 0为 dE E g E f p VB E E VV)())(1('0-=⎰带入玻尔兹曼分布函数和状态密度函数可得dE E E TK E E m p V E E Fp VV21'0323*20)()exp()2(21--=⎰π令,)()(0T K E Ex V-=则121021)()(x T K E E V =-Tdxk E E d V 0)(=-将积分下限的E'V (价带底)改为-∞,计算可得)exp()2(202320*0TK E E T k m p FV p -=π令3230*2320*)2(2)2(2h T k m T k m N p p V ππ==则得)ex p(00Tk E E N P VF V --=半导体物理学简明教程 13、当E -E F =1.5kT 、4kT 、10kT 时,分别用费米分布函数和玻耳兹曼分布函数计算电子占据这些能级的几率,并分析计算结果说明了什么问题。




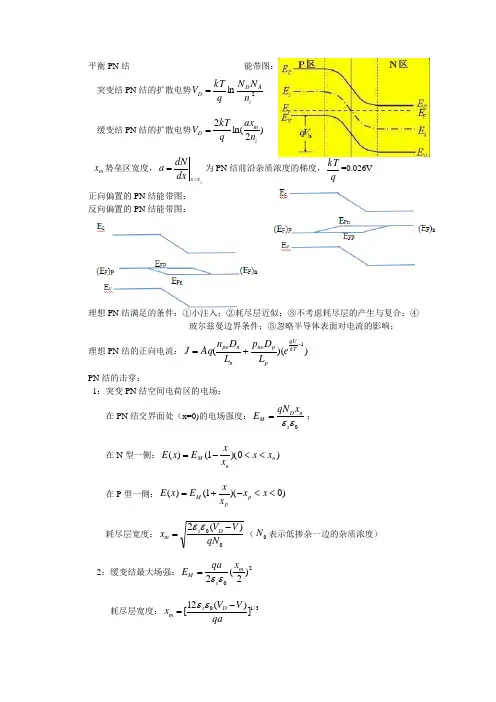
平衡PN 结 能带图:
突变结PN 结的扩散电势2ln i
A D D n N N q kT V = 缓变结PN 结的扩散电势)2ln(2i
m D n ax q kT V = m x 势垒区宽度,j
x x dx dN
a ==为PN 结前沿杂质浓度的梯度,
q kT =0.026V
正向偏置的PN 结能带图:
反向偏置的PN 结能带图:
理想PN 结满足的条件:①小注入;②耗尽层近似;③不考虑耗尽层的产生与复合;④ 玻尔兹曼边界条件;⑤忽略半导体表面对电流的影响; 理想PN 结的正向电流:))((1-+=kT qU p p no n n
po e L D p L D n Aq J
PN 结的击穿:
1:突变PN 结空间电荷区的电场:
在PN 结交界面处(x=0)的电场强度:0εεs n
D M x qN
E =;
在N 型一侧:)0)(1()(n n
M x x x x E x E <<-= 在P 型一侧:)0)(1()(<<-+=x x x x E x E p p
M 耗尽层宽度:0
0)(2qN V V x D s m -=εε(0N 表示低掺杂一边的杂质浓度) 2:缓变结最大场强:20)2(2m s M x qa
E εε=
耗尽层宽度:3/10])(12[qa
V V x D s m -=εε
3:突变结势垒电容m S T x A C 0εε=。
第二章 PN 结2-1.P N +结空间电荷区边界分别为p x -和n x ,利用TV V i e n np /2=导出一般情况下的)(n n x p 表达式。
给出N 区空穴为小注入和大注入两种情况下的)(n n x p 表达式。
2-2.热平衡时净电子电流或净空穴电流为零,用此方法推导方程20lnia d T pn nN N V =-=ψψψ。
2-3.根据修正欧姆定律和空穴扩散电流公式证明,在外加正向偏压V 作用下,PN 结N 侧空穴扩散区准费米能级的改变量为qV E FP =∆。
2-4. 硅突变结二极管的掺杂浓度为:31510-=cm N d ,320104-⨯=cm N a ,在室温下计算:(a )自建电势(b )耗尽层宽度 (c )零偏压下的最大内建电场。
2–5.若突变结两边的掺杂浓度为同一数量级,则自建电势和耗尽层宽度可用下式表示)(2)(02d a p n d a N N K x x N qN ++=εψ ⎥⎦⎤⎢⎣⎡+=)(200d a a a n N N qN N K x ψε2100)(2⎥⎦⎤⎢⎣⎡+=d a a d p N N qN N K x ψε试推导这些表示式。
2–6.推导出线性缓变P N 结的下列表示式:(a )电场(b )电势分布(c )耗尽层宽度(d )自建电势。
2-7.推导出N N +结(常称为高低结)内建电势表达式。
2-8.(a )绘出图2-6a 中31410-=cm N BC 的扩散结的杂质分布和耗尽层的草图。
解释为何耗尽层的宽度和R V 的关系曲线与单边突变结的情况相符。
(b )对于31810-=cm N m 的情况,重复(a )并证明这样的结在小R V 的行为像线性结,在大R V 时像突变结。
2-9. 对于图2-6(b )的情况,重复习题2-8。
2–10.(a )P N 结的空穴注射效率定义为在0=x 处的0/I I p ,证明此效率可写成np p n p L L II σσγ/11+==(b )在实际的二极管中怎样才能使γ接近1;2-11.长PN 结二极管处于反偏压状态,求:(1)解扩散方程求少子分布)(x n p 和)(x p n ,并画出它们的分布示意图。