基于ANSYS的裂纹应力强度因子的计算
- 格式:doc
- 大小:28.50 KB
- 文档页数:7
基于ANSYS Workbench的表面裂纹计算By Yan Fei本教程使用ANSYS Workbench17.0 进行试件表面裂纹的分析,求应力强度因子。
需要提前说明的是,本案例没有工程背景,仅为说明裂纹相的计算方法,因此参数取值比较随意,大量设置都采用了默认值。
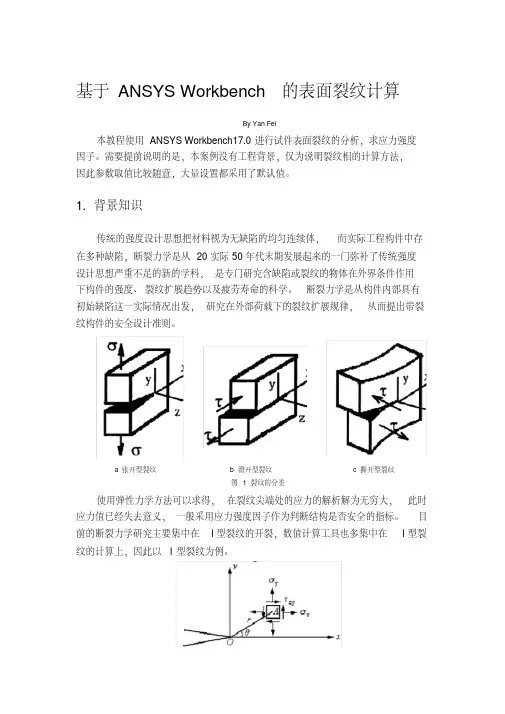
1.背景知识传统的强度设计思想把材料视为无缺陷的均匀连续体,而实际工程构件中存在多种缺陷,断裂力学是从20实际50年代末期发展起来的一门弥补了传统强度设计思想严重不足的新的学科,是专门研究含缺陷或裂纹的物体在外界条件作用下构件的强度、裂纹扩展趋势以及疲劳寿命的科学。
断裂力学是从构件内部具有初始缺陷这一实际情况出发,研究在外部荷载下的裂纹扩展规律,从而提出带裂纹构件的安全设计准则。
a 张开型裂纹b 滑开型裂纹c 撕开型裂纹图 1 裂纹的分类使用弹性力学方法可以求得,在裂纹尖端处的应力的解析解为无穷大,此时应力值已经失去意义,一般采用应力强度因子作为判断结构是否安全的指标。
目前的断裂力学研究主要集中在I型裂纹的开裂,数值计算工具也多集中在I型裂纹的计算上,因此以I型裂纹为例。
图2 裂纹尖端坐标系含有裂纹的无限大平板的I 型裂纹尖端附近的应力为:)(23cos 2sin 223sin 2sin 12cos223sin 2sin 12cos20ⅠⅠⅠr O r K r K r K xyy x +=+=-=其中,K Ⅰ叫Ⅰ型裂纹的应力强度因子。
2.ANSYS Workbench 裂纹分析2.1.分析模型的建立1 建立一个静力分析步,材料使用默认,需要说明的是,现有计算技术下,断裂力学计算一般都采用线弹性材料,考虑到断裂中塑性区一般都不大,线弹性的假设还是可以接受的。
图3 分析步设置2 建立几何模型,本案例使用spaceclaim 建立几何模型。
图4 试件平面图图5 试件立体图3 分网格,必须采用四面体网格。
本文划分单元特征尺寸1mm。
图 6 网格设置图7 分网效果4 划分网格完成以后,首先进行一次静力计算,确保所有设置正确,对ANSYS Workbench比较熟悉的同学可以省略这一步,静力计算时,试件的两个端面一个约束位移,另一个加1000N的力,方向沿试件轴向,使试件受拉。

基于ANSYS的断裂参数的计算1 引言断裂事故在重型机械中是比较常见的,我国每年因断裂造成的损失十分巨大。
一方面,由于传统的设计是以完整构件的静强度和疲劳强度为依据,并给以较大的安全系数,但是含裂纹在役设备还是常有断裂事故发生。
另一方面,对于一些关键设备,缺乏对不完整构件剩余强度的估算,让其提前退役,从而造成了不必要的浪费。
因此,有必要对含裂纹构件的断裂参量进行评定,如应力强度因了和J积分。
确定应力强度因了的方法较多,典型的有解析法、边界配位法、有限单元法等。
对于工程上常见的受复杂载荷并包含不规则裂纹的构件,数值模拟分析是解决这些复杂问题的最有效方法。
本文以某一锻件中取出的一维断裂试样为计算模型,介绍了利用有限元软件ANSYS计算应力强度因子。
2 断裂参量数值模拟的理论基础对于线弹性材料裂纹尖端的应力场和应变场可以表述为:(1)其中K是应力强度因子,r和θ是极坐标参量,可参见图1,(1)式可以应用到三个断裂模型的任意一种。
图1 裂纹尖端的极坐标系(2)应力强度因子和能量释放率的关系:G=K/E"(3)其中:G为能量释放率。
平面应变:E"=E/(1-v2)平面应力:E=E"3 求解断裂力学问题断裂分析包括应力分析和计算断裂力学的参数。
应力分析是标准的ANSYS 线弹性或非线性弹性问题分析。
因为在裂纹尖端存在高的应力梯度,所以包含裂纹的有限元模型要特别注意存在裂纹的区域。
如图2所示,图中给出了二维和三维裂纹的术语和表示方法。
图2 二维和三维裂纹的结构示意图3.1 裂纹尖端区域的建模裂纹尖端的应力和变形场通常具有很高的梯度值。
场值得精确度取决于材料,几何和其他因素。
为了捕获到迅速变化的应力和变形场,在裂纹尖端区域需要网格细化。
对于线弹性问题,裂纹尖端附近的位移场与成正比,其中r是到裂纹尖端的距离。
在裂纹尖端应力和应变是奇异的,并且随1/变化而变化。
为了产生裂纹尖端应力和应变的奇异性,裂纹尖端的划分网格应该具有以下特征:·裂纹面一定要是一致的。

⎰ ∂x ij第18卷 第2期 湖 南 城 市 学 院 学 报 (自然科学版)V ol. 18 No.2 2009 年 6 月Journal of Hunan City University ( Nat ural Science ) Jun. 2009基于ANSYS 的应力强度因子计算葛润广1,岳 烨2,毛洲明2,曹胜语3(1.中铁九局集团有限公司 第七工程有限公司,沈阳 110044;2.云南省城乡规划设计研究院,昆明 650228; 3.河北华能京张高速公路有限公司,河北 怀来 075400)摘 要:以I 型裂纹的3点弯曲试件为例,介绍和分析了运用有限元软件ANSYS 计算应力强度因子的方 法.通过对求得的应力强度因子值与解析解的比较,表明用有限元方法计算应力强度因子具有相当高的精度, 并且操作简便.关键词:ANSYS ;I 型裂纹;应力强度因子;断裂力学 中图分类号:U441.6文献标识码:A文章编号:1672–7304(2009)02–0010–03Calculate the Stress Intensity Factor by the Finite Element Software ANSYSGE Run-guang 1,YUE Ye 2,MAO Zhou-ming 2,CAO Sheng-yu 3(1. Road & Bridge Engineering Section of C hina Railway No.9, Shenyang 110044, C hina; 2. Urban & Rural Planning & Design Institute ofKunming, Yu nnan 650228, C hina; 3. Hebei Huaneng Jinzhang Expressway CO.LTD, Huailai 075400, C hina )Abstract: Taking I-type crack in three-point bending test piece as an example, this paper conducts theintroduction and analysis of the use of finite element software ANSYS calculation of stress intensity factor approach. It obtained through the stress intensity factor values with the analytic solution of the comparison, showing that the finite element method using the stress intensity factor has a very high precision, and easy to use.Key words: ANSYS; I-mode crack; stress intensity factor; fracture mechanics断裂力学是研究带裂纹材料或结构的强度以 及裂纹扩展规律的一门学科.从常规观点来看, 当结构内部一有裂纹时,其承载能力就将完全丧 失.实际则不然,在结构有裂纹时,常规强度准 则就不再使用.断裂力学提出了应力强度因子的 概念,即裂纹端部应力场强度由应力强度因子度 量,并提出新的强度准则:裂纹尖端的应力强度 因子 K I .若小于材料的断裂韧性 K cr (通过实验 获得),则构件是安全的.如何准确、有效地求得 构件裂纹尖端的应力强度因子 K I 是工程技术人 员关注的问题[1].当前已有许多种计算应力强度因子的方法, 如解析法、边界配位法、有限单元法、边界元素 法、体力法、权函数法和线弹簧模型等.常见裂 1 基本理论断裂力学可分为线弹性断裂力学与弹塑性断 裂力学.在实际工程中,裂纹端部已有很大塑性 区,线弹性断裂理论不再使用,必须采用弹塑性 断裂理论来进行分析.目前用于弹塑性断裂力学 的研究方法有很多,如 COD 法和 J 积分法等.而 J 积分法在实际中运用较为普遍[2],本文就以此为 基础.J 积分是 1 个应力、应变场参量,它的定义为J =W d - T ∂u dy s . (1)г式中的 W 为应变能密度或形变功密度,其值为εm n纹体的应力强度因子可以查阅有关的应力强度因 W = ⎰0 σij d ε .(2)子手册和计算,但对于结构或裂纹形状复杂和受 复杂载荷作用的结构,很难通过查手册计算.随 着有限单元法理论的发展和计算机技术的广泛应 用,目前一些大型的通用有限元计算软件都具有 计算各种断裂参数的功能.本文主要介绍运用有 限元方法计算应力强度因子.其中σi j 与εi j 分别为应力分量和应变分量;T 为积分回路上的应力分量; u 为力 T 作用点的位移矢 量;г 为由裂纹下自由表面上任一点开始,按逆 时针方向,环绕裂纹尖端地区而终止于裂纹自由 表面上任一点的任意积分路线,见图 1.J 积分具有与积分路径无关这一特点,可避收稿日期:2009-02-20作者简介:葛润广(1975-),男,辽宁辽阳人,工程师,主要从事高速公路工程施工管理研究.I第18 卷葛润广等:基于ANSYS的应力强度因子计算11开尖端处复杂的应力、应变场,不仅适用于线弹性,也适用于弹塑性.在线弹性状态下,Rice 证明了J 积分和应力强度因子K 之间存在如下关系[3]:用“四分之一节点”进行处理.即将于裂纹尖端相接的边中点移到距尖端1/ 4 边长位置,这样的奇异单元就可较好反映裂缝尖端对应的位移场.如图3 所示.K I =(3)其中 E = E 为平面应力状态;E =E为平面应1 1 1 - μ 2变状态.图 1 任意积分路线图2 模型建立断裂力学将各种复杂的断裂形式,分解为 3种基本类型的组合,即为I 型断裂(张开型),II型断裂(滑移型),III 型断裂(撕裂型).其中I 型裂缝在混凝土中最常见,也最为危险,极易导致构件低应力脆断,在运用断裂力学研究结构的裂缝问题时,通常以I 型裂缝做为重点.故本文以I 型裂缝为例进行分析.利用有限元软件ANSYS对3 点弯曲梁试样进行有限元分析,利用ANSYS裂缝模拟技术计算断裂强度因子KI值,将结果与理论值进行比较,以检验方法的可靠性[4].2.1 模型试件概述采用(S/W=4,W/B=2) 3 点弯曲试件,尺寸为0.05 m×0.1 m×0.4 m,裂缝和集中荷载P 位于跨中位置,见图2(厚度B=0.05 m).裂缝长度a为0.02 m,跨中荷载P 为变量.混凝土材料常数E=32.5 GP a,μ=0.2.图 3 裂缝模拟奇异单元这种单元,除了中节点位置有所变化外,其他均与正常等参单元完全相同,在裂缝分析中广泛采用.模型采用带中点20 节点的固体等参单元Solid95 单元,由于Solid95 单元具有中节点,故可利用“四分之一节点”模拟尖端应力奇异性.如图4 所示.图4 Solid95 单元由于模型的对称性,取试件的1/2 建模,跨中截面使用对称约束.裂缝尖端有限元模型如图5.图 5 裂缝尖端有限元模型3 KI计算分析J 积分与积分路径无关,选择积分路径时,2.2 裂缝模拟可避开裂缝尖端一段距离,故可对尖端网格划分精度降低,而不影响结果.在确定积分路径后,裂缝尖端附近应力场具有奇异性,即在裂缝尖端的应力分量趋于无穷大.裂缝尖端附近应力与(x 为距裂缝尖端的距离)成正比.在使用ANSYS 建立模型时,为反映这一特征,常采利用ANSYS 的后处理功能,在求解后可以通过ANSYS 通用后处理器中的单元列表功能,把各变量映射到自定义的路径中去.路径操作中提供了积分运算,被映射到路径上的变量经过运算,最x4xW W12湖 南 城 市 学 院 学 报(自然科学版) 2009年第2期后沿路径积分就得到了该种模型在特定工况下的 J 积分值.最后利用式 K I =,按平面应变问题求解K I . 为验证分析 结果的正确 性,与我国 规范 GB4161-84 中的公式所计算的数据进行比较.4 结论通过以上分析可以看出,应力强度因子在ANSYS 中的计算是可行的.与传统的利用断裂力 学中的公式直接求解相比,利用有限元软件 (ANSYS)来求解 K I 是一种简单而准确的方法. K = PS f a IBW 3/ 2 其中. (4)参考文献:[1]赵海涛, 石朝霞, 战玉宝. 基于ANSYS 的积分计算与分析[J].a 3(a /W )1/ 2ϒ1.99 -(a /W )(1- a /W )(2.15 - 3.93a /W + 2.7a 2 /W 2 )煤矿机械, 2007, 28(5): 26-27. f = ≤ƒ .2(1+ 2a /W )(1- a /W )3/ 2不同荷载下数据比较见表 1.表 1 分析结果比较P /N 200 500 800 1 100 1 400[2]吴龙平, 明斐卿, 李国成, 等.三维裂纹J 积分研究[J]. 石油化 工设备, 2006, 35(2): 14-17.[3]洪起超. 工程断裂力学基础[M]. 上海: 上海交通大学出版社,1986.[4]陈家权, 沈炜良, 徐家园, 等.应力强度因子的有限元计算[J].K I比较结果相差均在10%以内,分析结果略大 于公式结果,能满足精度及安全储备要求.究[J]. 武汉科技大学学报: 自然科学版, 2005, 28(3): 244-246. [6]邓彩艳, 张玉凤, 霍立兴. 关于J 积分测定方法的比较及相关 问题的讨论[J]. 焊接学报, 2006, 27(10): 23-25.(责任编校:陈健琼)分析结果 0.064 0.156 0.255 0.413 0.518 装备制造技术, 2003(4): 6-9.公式结果 0.059 0.149 0.238 0.327 0.416[5]龙靖宇, 王宏波. 基于有限元法的二维裂纹应力强度因子研。


在ANSYS中计算裂缝应力强度因子的技巧在ANSYS中计算裂缝应力强度因子的技巧裂缝应力强度因子用ANSYS中怎么求呀。
另外,建模时,裂纹应该怎么处理呀,难道只有画出一条线吗?首先说一下裂纹怎么画,其实裂纹很简单啊。
只要画出裂纹的上下表面(线)就可以了,即使是两个面(线)重合也一定要是两个面(线);如果考虑道对称模型就更好办了,裂纹尖点左面用一个面(线),右边用另外一个面(线),加上对称边界约束。
再说一下裂尖点附近网格的划分。
ansys提供了一个kscon的命令,主要是使得crack tip的第一层单元变成奇异单元,用来模拟断裂奇异性(singularity)。
当然这个步骤不是必须的,有的人说起用ansys算强度因子的时候就一定要用奇异单元,其实是误区(原因下面解释)好了,回到强度因子的计算。
其实只要学过一些断裂力学都知道,K的求法很多。
就拿Mode I的KI来说吧,Ansys自己提供了一个办法(displacement extrapolation),中文可能翻译作“位移外推”法,其实就是根据解析解的位移公式来对计算数据进行fitting的。
分3步走,如果你已经算完了:第一步,先定义一个crack-tip的局部坐标系,这是ansys帮助文件中说的,其实如果你的裂纹尖端就是整体坐标原点的话,而且你的x-axis就顺着裂纹,就没有什么必要了。
第二步,定义一个始于crack-tip的path,什么什么?path怎么定义??看看帮助吧,在索引里面查找fracture mechanics,找到怎么计算断裂强度因子。
(my god,我这3步全是在copy 帮助中的东东啊)。
第三步,Nodal Calcs>Stress Int Factr ,别忘了,这是在后处理postproc中啊。
办法是好,可是对于裂纹尖端的单元网格依赖性很大,所以用kscon制造尖端奇异单元很重要。
curtain的经验是path路径取的越靠近cracktip得到的强度因子就越大,所以单元最好是越fine越好啊。


裂纹尖端应力强度因子的计算图为一带有中心裂纹的长板,两端作用均布力,且p=1Pa,结构尺寸如图所示,确定裂纹尖端的应力强度因子。
已知材料的性能参数为:弹性模量E=2.06×10Pa,泊松比u=0.3应力强度因子KI=p==0.2802;现在利用有限元软件ansys对其建模求解来确定其数值解与解析解进行比较。
一、建立模型由于结构具有对称性,在利用有限元计算裂纹尖端应力强度因子时,取其四分之一的模型即可1. 输入材料的参数和选取端元FINISH/CLEAR, START/TITLE, STRESS INTENSITY-CTACK IN PLATEH=1000 !设置比例尺/TRIAD, OFF !关闭坐标系的三角符号/PREP7ET, 1, PLANE82, , , 2MP, EX, 1, 2. 06E11MP, NUXY, 1, 0.3 !输入泊松比2. 建立平面模型RECTNG,-25/H,50/H,0,100/H !生成矩形面LDIV,1,1/3,,2,0 !在1号线上生成裂纹尖端所处的位置3.划分网格为了方便裂纹尖端因子的计算,ansys软件专门提供了一个对裂纹尖端划分扇形单元的命令,即:“kscon”。
其命令流如下:LESIZE, 2,,,15,,,,,1 !对线指定单元个数LESIZE, 4,,,15,0.3,,,,1LESIZE, 3,,,12,,,,,1KSCON,5,3.5/H,1,8 !对裂纹尖端所在的位置划分扇形单元ESIZE,3/H,0,AMESH,1FINISH4.加载和求解?]痏I囚__R/SOLU !进入求解器嶊?$~菐宅鷋_'?l|錑鈑壓庢uK麡睽KK畵>Ou?__ 訽DL,4,,SYMM閼 :!痱摋铪6鸰._@ SFL,3,PRES,-1 !在3号线上施加布力倪猸 _湋繽丈\g颻湀}OUTPR,ALL}b畇__濠N鲭|FINISH 'b镫淖瑵_鲱v蠄瀯屋璅甆€_鼍_恄7]僟濢Z嵹!_価_dDO_N谶l5.后处理__貞@F茉植戮a╛__負罋在计算完成后,即可进入后处理器观察分析结果。

制造业信息化E口叠互墨墨互工盈l=臣Z墨墨互蜀墨frill/建簟,cAD,cAM,cAE,cAPPl_I___●l_llll_llllllIl_l_l___lIl_—l____lI___一基于ANSYS的裂纹尖端应力强度因子研究武小海-,回丽一。
周松1。
娄峰2(1.沈阳航空航天大学机电工程学院,沈阳110027:2.华晨汽车研究院,沈阳110136)静’。
一。
罄:摘要:通过ANSYS建立焊接接头三区域模型。
分别定义了不同的力学性能参数来模拟焊接接头各个区域力学性能的j不均匀性,分别计算裂纹处在焊接接头各个区域的应力强度因子。
计算结果表明:焊缝应力强度因子最低,母材次之,热影响区最高。
说明材料的屈服强度与裂纹尖端的应力强度因子有密切的关系。
屈服强度越高,应力强度因子越低。
:关键词:焊接接头:有限元模型:应力强度因子j&kj::、中图分类号:TG441.7文献标识码:A文章编号:1002—2333(2011)01—0042—02..,一-“。
:TheStudyinStressIntensityFactorofCrackTipBasedonANSYSWU(1.ShenyangAbstract:Inthispaper,athreemechanicalpropertiescalculatedinareXiao-hai。
HUIli,ZHOUSongandElectricalEngineering,Shenyangwas1AerospaceUniversity,InstituteofMechanical10136)regionalmodelofweldedjointstoestablishedbyANSYS.Differentparametersofthestressdefinedsimulatetheunevennatureofweldedjoints.Thecrackintensityfactorwereallregionsofweldedjointsseparately.Theresultsshowthat:theminimumfollowed,thehigheststresswasstressintensityfactorwasinatheweldingzone,basemetalinheataffectedzone.Andthematerialyieldstrengthhasintensityfactor.closerelationshipwithcracktipintensityfactor.Thehigheryieldstrength,thelowerthestressKeywords:weldedjoint;finiteelementmodel;stressintensityfactor1引言焊接结构是典型的非均质材料结构,其微观组织,力学性能都有很大区别,而且在焊接的过程中很容易形成表面裂纹和气孔、夹渣等缺陷。


基于有限元法对裂纹尖端应力强度因子的计算杨巍;张宁;许良【摘要】基于ANSYS有限元软件通过相互作用积分法建立了求解三维穿透裂纹应力强度因子的有限元模型,将有限元法和解析法求得的应力强度因子进行比较验证了模型的准确性.研究了载荷、裂纹长度、试样宽度、厚度对裂纹尖端应力强度因子的影响,在对比结果的基础上分析了裂纹尖端应力强度因子的三维效应.结果表明:在不同条件下有限元模型都可以很好的模拟出应力强度因子的值,二维状态时应力强度因子的分布规律与三维状态时的分布规律有较大差异,出于安全的考虑不应忽略应力强度因子的三维效应,对三维应力强度因子的有限元求解有一定的指导意义.【期刊名称】《沈阳航空航天大学学报》【年(卷),期】2014(031)003【总页数】5页(P19-23)【关键词】相互作用积分方法;三维穿透裂纹;应力强度因子;ANSYS【作者】杨巍;张宁;许良【作者单位】中航工业沈阳飞机工业(集团)有限公司制造工程部,沈阳110136;沈阳航空航天大学机电工程学院,沈阳110136;沈阳航空航天大学机电工程学院,沈阳110136;沈阳航空航天大学航空制造工艺数字化国防重点实验室,沈阳110136【正文语种】中文【中图分类】O346.1断裂是工程构件最危险的一种失效方式,尤其是脆性断裂,它是突然发生破坏,断裂前没有明显的征兆,这就常常引起灾难性的事故。
大量断裂事故分析中发现,断裂皆与结构中存在缺陷或裂纹有关。
由缺陷或裂纹所引起的机械、结构的断裂失效,是工程中最重要、最常见的失效模式[1]。
传统强度理论是建立在假设材料无缺陷的基础上的,但工程实际中很多按传统强度理论设计的结构由于裂纹的产生和扩展,出现大量断裂失效。
为保证含裂纹构件的安全性和可靠性,必须预测裂纹的扩展速率和构件的断裂强度,在断裂力学的工程应用中,应力强度因子K是判断含裂纹结构的断裂和计算裂纹扩展速率的重要参数。
应力强度因子的计算方法有解析法、有限元法、边界元法、权函数法等[2]。
本文使用ANSYS13.0中的互动积分法(Interaction Integrals )计算了三维贯穿裂纹的应力强度因子,计算结果表明该方法计算可靠,为计算更复杂的三维裂纹提供了一种途径。
据一些工业化国家统计,因材料和结构的破坏所造成的损失占国民经济生产总值的8% -12%多。
破坏事故所造成的人员伤亡的损失更不可估量。
我国作为一个发展中国家,在这方面的情况比西方发达国家更严重。
因此无论是为了减少破坏事故的损失还是研发满足现代工业所需要的新材料,都要求对材料的破断过程有科学的、全面的、定量化的认识。
三维裂纹作为工程中常见的裂纹形式,早在六十年代初就有不少研究者开始研究,到现在已有大量的文献资料论及这一问题,出现了一些有特点的分析方法。
工程上常见的表面裂纹的断裂分析,由于其实质是三维问题,也几乎同时开始被人们所关注。
三维裂纹问题的危害极大,断裂造成了大量的灾难性事故发生,这使得断裂力学在机械工程、海洋工程、核工程,特别是今天的航空航天工程中受到更广泛的重视和深入研究。
因此对含三维裂纹结构断裂特性尤其对三维裂纹体的应力强度因子的研究有重要的现实意义。
本文使用ANSYS成功的计算了三维贯穿裂纹的应力强度因子,为计算三维裂纹提供了一种便捷方式。
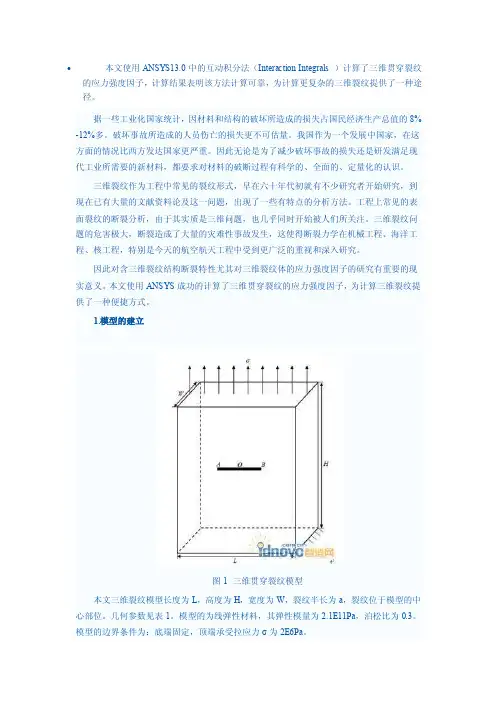
1.模型的建立图1 三维贯穿裂纹模型本文三维裂纹模型长度为L,高度为H,宽度为W,裂纹半长为a,裂纹位于模型的中心部位。
几何参数见表1。
模型的为线弹性材料,其弹性模量为2.1E11Pa,泊松比为0.3。
模型的边界条件为:底端固定,顶端承受拉应力σ为2E6Pa。
表1 模型的几何参数本文采用二维奇异单元PLANE183建立二维的裂纹模型,然后通过拉伸并使用三维奇异单元SOLID186来建立三维贯穿裂纹模型。
图2-图5给出了二维裂纹模型和三维裂纹模型。
在13.0中对应力强度因子的计算增加了一种计算方法即互动积分法(Interaction Integral s ),这种方法与计算J积分的主域积分法类似。
基于ANSYS的三维应力强度因子的计算摘要:本文在总结断裂力学各种行为研究方法的基础上,采用有限单元法思想,利用ANSYS软件建立裂纹体有限元模型。
通过计算得出I型裂纹尖端的应力强度因子,其计算结果与理论值吻合良好。
表明模型的选取和网格的划分是合理的,具有可靠的精度,其结果完全可以指导工程设计。
关键词:断裂力学;有限单元法;ANSYS;应力强度因子1 前言随着现代生产技术的高速发展,新材料、新工艺在航空、航天、压力容器、核反应堆、机械、土木等领域得到了广泛应用,结构在高速、高温、高压等环境中使用时,按照传统强度理论设计的结构在应用中却出现大量的断裂事故。
目前关于断裂力学的研究,理论上只能求解较简单的模型或做出较强的假设条件;通过实验探求其规律性的成本较高、周期较长。
因此对于断裂力学问题,尤其是三维裂纹问题目前大多借助数值方法进行研究。
裂纹问题严格来说都是三维问题,并且工程中最后发生事故的裂纹问题的物体(如机械构件,土建结构)总是有限弹性的。
因此对有限弹性裂纹问题进行三维分析在实际工程上有重要的现实意义[1]。
迄今在平面断裂力学中已形成了一整套相当成熟的计算方法,但在三维断裂问题中,尤其在表面裂纹方面,还有很多问题有待进一步探讨,本文正是在这方面进行了探索和研究。
通常板表面裂纹应力强度因子可以统一表示为:(1)只是不同的解给修正因子F赋予不同的表达式。
由Newman的研究成果可以看出,他主要考虑了拉伸或弯曲载荷下半椭圆表面裂纹的各种裂纹形状(a/c)和板宽、板厚对裂纹前缘应力强度因子的影响,而没有考虑板长的影响,也就是没有考虑平行边界对应力强度因子的影响。
2 裂纹类型与有限元法2.1 裂纹类型在断裂力学中,按裂纹受力情况和裂纹面的相对位移方向将裂纹分为三种基本类型[2]:即张开型(I型),滑移型(II型),撕裂型(III型),如图1。
两种或三种基本类型的组合称之为复合型裂纹问题。
图1中所示三种基本类型的裂纹模型的受力特点如下:I型裂纹受垂直于裂纹面的拉应力作用;II型裂纹受平行于裂纹面而垂直于裂纹前缘的剪应力作用,又称为面内剪切型;III型裂纹受既平行于裂纹面又平行于裂纹前缘的剪应力作用,对应于反平面剪切,又称为面外剪切或纵向剪切。
!----------------------------------------------------------------!---- 师访,中国矿业大学力学与建筑工程学院,江苏徐州 ----!---- SHI Fang, China University of Mining & Technology ----!---- Website: , QQ: 1549221758 ----!---- Email: fshi@ / 159********@ ----!---- Date: March 28, 2014 ----!---- 倾斜闭合裂纹应力强度因子计算实例 ----!----- /thread-1102153-1-1.html ----!----------------------------------------------------------------这里给出一个利用ANSYS计算压剪裂纹应力强度因子的APDL命令流,全参数化控制。
注意事项:(1)定义裂纹面接触关系;(2)利用KSCON定义裂尖奇异点:KSCON,关键点号,半径,1,10,0.5;(3)在裂尖建立局部坐标系,命令是:LOCAL,11,0,x,y,z,转角,转角,转角,1,1,建立的局部坐标系的x轴必须与裂纹面平行;(4)建立路径,命令:PATH和PPATH,路径上布置5个节点;(5)在后处理/POST1中激活局部坐标系,命令RSYS,11;(6)KCALC命令计算应力强度因子。
y方向应力:ANSYS输出的应力强度因子:命令流:finish/clear/Titie,SHI Fang,CUMT/PREP7/DSCALE,ALL,1.0/eshape,on!-------------------控制参数w = 2.05h = 4.05a = w/5*sqrt(2) !裂纹半长angle = 45 !裂纹与σ1方向的夹角(度)f = 100e6 !σ1COF = 0.3 !摩擦系数!-------------------theta = angle*3.1415926/180 !裂纹与σ1方向的夹角(弧度)/DSCALE,ALL,1/PNUM,KP,1/PNUM,LINE,1!-------------------et,1,183KEYOPT,1,3,2!-------------------mp,ex,1,65e9mp,prxy,1,0.25MP,MU,1,COF!-------------------k,1,0,0k,2,w,0k,3,w,hk,4,0,hk,5,0,h/2-w/2/tan(theta)k,6,w,h/2+w/2/tan(theta)k,7,w/2+a*sin(theta),h/2+a*cos(theta)k,8,w/2-a*sin(theta),h/2-a*cos(theta)k,9,w/2,h/2k,19,w/2,h/2k,21,w/2,hk,22,w/2,0!----------111和222关键点用于定义路径,以便计算应力强度因子k,111,w/2+a/2*sin(theta),h/2+a/2*cos(theta)k,222,w/2+a/2*sin(theta),h/2+a/2*cos(theta)!-------------------a,1,22,19,8,5,1a,22,2,6,7,222,19,22a,9,111,7,6,3,21,9a,5,8,9,21,4,5!-------------------dk,1,all,0DL,1, ,uy,DL,6, ,uy,!-------------------allsel,allSFL,14,PRES,f,SFL,17,PRES,f,!-------------------lesize,all,w/60KSCON,7,a/10,1,10,0.5 !定义裂纹尖端KSCON,8,a/10,1,10,0.5 !定义裂纹尖端MSHKEY,0AMESH,all !对面进行网格划分!-------------------allsel,allLSEL,S,,,3,9,6LSEL,a,,,10,,NSLL,S,1CM,lowPair,NODEallsel,allLSEL,S,,,11,12,1LSEL,a,,,16,NSLL,S,1CM,upPair,NODEallsel,all/COM, CONTACT PAIR CREATION - STARTCM,_NODECM,NODECM,_ELEMCM,ELEMCM,_LINECM,LINECM,_AREACM,AREACM,_VOLUCM,VOLU/GSAV,cwz,gsav,,tempMAT,1R,3REAL,3ET,2,169ET,3,172KEYOPT,3,9,0KEYOPT,3,10,1! Generate the target surface NSEL,S,,,LOWPAIRCM,_TARGET,NODETYPE,2ESLN,S,0ESURFCMSEL,S,_ELEMCM! Generate the contact surface NSEL,S,,,UPPAIRCM,_CONTACT,NODETYPE,3ESLN,S,0ESURFALLSELESEL,ALLESEL,S,TYPE,,2ESEL,A,TYPE,,3ESEL,R,REAL,,3/PSYMB,ESYS,1/PNUM,TYPE,1/NUM,1EPLOTESEL,ALLESEL,S,TYPE,,2ESEL,A,TYPE,,3ESEL,R,REAL,,3CMSEL,A,_NODECMCMDEL,_NODECMCMSEL,A,_ELEMCMCMDEL,_ELEMCMCMSEL,S,_KPCMCMSEL,S,_LINECMCMDEL,_LINECMCMSEL,S,_AREACMCMDEL,_AREACMCMSEL,S,_VOLUCMCMDEL,_VOLUCM/GRES,cwz,gsavCMDEL,_TARGETCMDEL,_CONTACT/COM, CONTACT PAIR CREATION - END!$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ $! 求解设置!$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ $/solutime,1nsubst,10,50,5solvefinish!$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ $! 后处理-计算应力强度因子!$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ $/post1LOCAL,11,0,w/2+a*sin(theta),h/2+a*cos(theta),,angle,,,1,1 !建立局部坐标系RSYS,11 !激活局部坐标系PLNSOL, S,Y, 0,1.0!------------------- !通过关键点获得路径上的节点号allselKSEL,S, , ,7NSLK,R*get,node1,node,0,num,maxallselKSEL,S, , ,111NSLK,R*get,node2,node,0,num,maxallselKSEL,S, , ,9NSLK,R*get,node3,node,0,num,maxallselKSEL,S, , ,222NSLK,R*get,node4,node,0,num,maxallselKSEL,S, , ,19NSLK,R*get,node5,node,0,num,maxallsel!-------------------PATH,PathSIF,5,30,20 !定义路径PPATH,1,node1 !设置路径点PPATH,2,node2PPATH,3,node3PPATH,4,node4PPATH,5,node5KCALC,0,1,3,0 !计算应力强度因子。
ANSYS计算应力强度因子APDL案例ANSYS(工程仿真软件)是一种广泛应用于工程设计和分析的计算机辅助工程(CAE)软件,它可以进行各种结构、流体、热传导和电磁场分析。
APDL(ANSYS Parametric Design Language)是ANSYS软件中的一种编程语言,可以通过编写脚本进行自动化分析和结果处理。
应力强度因子(Stress Intensity Factor,简称SIF)是一种用于描述裂纹尖端应力场的物理参数,它可以用来评估裂纹的扩展和破坏。
在实际工程中,计算应力强度因子是非常重要的,因为它可以指导材料的设计和结构的安全性评估。
下面我们将通过一个APDL案例来演示如何使用ANSYS计算应力强度因子。
案例背景:假设我们有一个受压的板材,并在板材中心位置切入一个V形裂纹,我们希望计算这个裂纹的应力强度因子。
案例步骤:1.创建几何体:使用ANSYS的几何建模工具创建一个矩形板材,然后在板材的中心位置切入一个V形裂纹。
可以使用ANSYS的前处理模块进行创建。
2.定义材料和加载:在ANSYS的主界面中,选择适当的材料模型并定义材料属性。
然后定义加载条件,例如施加恒定的压力载荷。
3.网格划分:使用网格划分功能对几何体进行离散化,生成有限元网格。
合适的网格划分是获得准确结果的关键。
可以使用ANSYS的网格生成工具进行自动划分,也可以手动划分。
4.建立约束和加载:定义边界条件和加载条件,例如将边界上的节点固定或施加位移约束。
5.装配和求解:完成模型的装配,并通过ANSYS的求解器求解应力场分布。
6.结果处理:使用后处理工具,提取裂纹尖端的应力数据。
然后使用特定方法(例如虚位移法或双奇异边界元法)计算应力强度因子。
7.计算应力强度因子:使用ANSYS的计算工具,输入裂纹尖端应力数据和几何参数,计算应力强度因子。
8.结果分析:根据计算得到的应力强度因子,评估裂纹的扩展和破坏情况。
可以根据需要进行优化设计或结构变更。
第6卷第2期2008年6月水利与建筑工程学报Journal of Water Resources and Architectural EngineeringVol.6No.2J un.,2008收稿日期:2007212225 修回日期:2008201214作者简介:祁顺彬(1976—),男(汉族),江苏赣榆人,讲师,硕士,主要从事工程结构教学方面的研究。
基于ANSYS 的Ⅰ-Ⅱ复合型裂缝应力强度因子计算祁顺彬(南京交通职业技术学院,江苏南京211188)摘 要:坝踵Ⅰ-Ⅱ复合型裂缝是否危及坝体安全,可以通过计算缝端应力强度因子用断裂判据判断裂缝稳定性来分析。
由于计算前不能确定裂缝处于压剪还是拉剪状态,可以先用ANSYS 软件算出缝端网格群奇异单元缝岸上三个结点在局部坐标下的位移分量,然后代入相应的公式算出应力强度因子。
实例计算结果较为合理,为Ⅰ-Ⅱ复合型裂缝应力强度因子计算提供了一个合理的计算方法。
关键词:Ⅰ-Ⅱ复合型;应力强度因子;ANSYS 中图分类号:TV642.3 文献标识码:A 文章编号:1672—1144(2008)02—0086—02C alculation of Stress Strength F actor for Ⅰ2ⅡComplex Crack B ased on ANSYSQ I Shun 2bin(N anjing V ocational and Technical College of Com m unication ,N anjing ,Jiangsu 211188,China )Abstract :In order to analyze whether Ⅰ2Ⅱcomplex crack of a dam heel could endanger the dam ,the stress strengthfactor may be calculated to analyze the crack stability with fracture criterion.Because the crack can not be made certain to locate in a press 2shear state or a pull 2shear state ,the local coordinate dis placement of three nodes on a singular cell bank of crack 2tip mesh group may be calculated by software ANSYS ,which is introduced to the relevant formula to calculate the stress strength factor.The example result is reasonable to provide a suitable computation method for the stress strength factor of Ⅰ2Ⅱcomplex crack.K eyw ords :Ⅰand Ⅱcomplex;stress strength factor ;ANSYS0 引 言重力坝是一种大体积混凝土结构,在浇筑过程中产生水化热,降温后上游坝踵产生较高温度应力,综合水压力作用,上游坝踵易产生拉应力集中。
Ansys断裂力学裂纹和瑕疵在很多结构和零部件中会出现,有时会导致严重的后果。
断裂力学就是研究裂纹扩散问题的学科。
12.1 断裂力学的理解断裂力学就是解决结构在外载荷作用下,裂纹和瑕疵如何扩散的问题。
它包含裂纹扩散相应的解析预报和实验结果验证。
解析预报是通过断裂参数的计算得出的,如裂纹区域的应力强度因子,它可以用来评估裂纹的生长率。
最具典型的是,裂纹的长度随着一些循环载荷的每一次作用而增长,如飞机上机舱的增压-减压。
另外,环境的情况,如温度或光线的照射等,都会影响某些材料的断裂性能。
在研究中,断裂问题需重点研究的典型参数如下:●应力强度因子(K I, K II和K III),是断裂的三个基本形式。
●J-积分,是一种不受线路影响的线积分,用来测量裂纹端点的奇异应力和应变。
●能量释放率(G),它代表裂纹开始和终止处的能量的大小。
12.2 求解断裂力学问题求解断裂力学问题包括执行线弹性或弹塑性静态分析,以及使用专用的后处理命令或宏来计算需要的断裂参数。
此处分成两个部分来介绍:●裂纹区域的建模●计算断裂参数12.2.1裂纹区域的建模断裂模型中最重要的部分就是裂纹边界的部分。
在ansys中,在二维模型和三位模型中,分别将裂纹的边界看成是裂纹端点和裂纹前端。
如图12.1所示。
r是距离裂纹端点的长度。
裂裂纹面应该是重合纹端点处的应力和应变是奇异的,的,裂纹端点(或裂纹前端)附近的单元应该是二次的,即角点之间有中间节点。
这种单元被称为奇异单元。
12.2.1.1 二维断裂模型二维断裂模型的推荐单元类型是PLANE2,6节点的三角实体单元。
裂纹端点附近的单元的第一行是奇异的,如图12.2(a)所示。
前处理模块PREP7的命令(Main Menu> Preprocessor> Meshing> Size Cntrls> Concentrat KPs> Create)可以定义某关键点附近的单元划分的大小,在断裂模型中特别有用。
基于ANSYS的裂纹应力强度因子的计算
摘要:本文分析了应力强度因子的重要性和计算应力强度因子的一般方法,以及在ANSYS中求解应力强度因子的裂纹尖端奇异性处理和具体步骤。
在二维和三维典型模型的实例应用中,对ANSYS计算结果和解析结果进行了对比分析。
关键词:裂纹应力强度因子ANSYS
Abstract:This paper analyzes the importance of the stress intensity factor and the general method of calculation. And use ANSYS to calculate the stress intensity factors of the crack tip singularity and its specific steps.In 2D and 3D models for example, the calculation results and the analytical results were compared and analyzed.
Key Words:Crack; Stress intensity factor; ANSYS
随着现代高强材料和大型结构的广泛应用,一些按传统强度理论和常规方法设计、制造的产品,发生了不少重大断裂事故。
从大量断裂事故分析中发现,断裂皆与结构中存在缺陷或裂纹有关。
裂纹的存在会降低结构系统的安全性,甚至导致整个系统的失效。
在断裂力学的工程应用中,应力强度因子是判断含裂纹结构的断裂和计算裂纹扩展速率的重要参数。
目前,确定应力强度因子的方法较多,典型的有解析法、位移外推法,等效J积分法等。
在实际工程中,解析法不能适用于受复杂载荷并包含不规则裂纹的构件,而有限元法能够建立通过建
立合理的模型,利用计算机数值模拟确定复杂条件下裂纹应力强度因子[1]。
本文分别以二维和三维断裂试样为计算模型,介绍了利用有限元软件ANSYS计算应力强度因子。
1 应力强度因子及其计算方法
在断裂力学中,应力强度因子可写成
可以看出,对于线弹性物体来说,应力强度因子与载荷呈线性关系,并依赖于物体与裂纹的几何形状和尺寸。
应力本身来表征裂纹尖端的应力强度是不适宜的,因为0时,各应力分量都无限增大。
而应力强度因子却可以有效的表征裂纹尖端附近的应力场强度,它是判断裂纹是否进入失稳状态的一个指标。
此参数的引入消除了由裂纹引起的应力奇异性所带来的数学上的困扰,它的计算依赖于裂纹前端的局部应力场。
确定应力强度因子的方法主要有三大类:解析法、数值计算法和直接测量法[2]。
解析法只适用于简单问题计算,大多数问题需要用数值方法求解。
随着计算机硬件和软件的迅猛发展,用数值方法计算就变得切实可行。
很多数值方法被尝试用来进行断裂参数计算,如有限差分法、边界元方法和无网格法等。
然而,由于缺少商业软件的支持,这些数值方法的工业应用实例相对缺乏。
在过去的半个多世纪里,有限元法效率高,成本低,成功地应用于许多工业部门。
现在有许多功能强大的商业软件可供使用,ANSYS就是其中之一。
ANSYS有限元软
件在求解精度和求解效率上经过了严格测试及广泛验证,并可直接使用多种材料模型,可以极大地减少程序编写和调试工作量。
2 应力强度因子在ANSYS中的求解
在ANSYS中求解断裂力学问题,首先要进行弹性分析或弹塑性静力分析,然后再用特殊的后处理命令,或宏命令计算所需的断裂参数。
2.1 裂纹区域的建模
因为在裂纹尖端存在高的应力梯度,所以断裂模型中最重要的区域是围绕裂纹边缘的部位,通常将二维模型的裂纹尖端作为裂纹的边缘,将三维模型的裂纹前缘作为裂纹的边缘。
在线弹性问题中,裂纹尖端或裂纹前缘附近某点的位移随的变化而变化,是裂纹尖端到该点的距离。
裂纹尖端处的应力和应变是奇异的,随变化,因此围绕裂纹尖端的有限元单元应是二项式的奇异单元,即把单元边上的中点放到1/4边上。
ANSYS能模拟二维和三维的裂纹问题,用1/4节点处理裂纹尖端奇异性的方法可以精确地计算应力强度因子(如图1)。
2.2 计算应力强度因子
在静态分析完成之后,就可以使用通用后处理器POST1来计算应力强度因子。
用POST1中的KCALC命令计算复合型断裂中的应力
强度因子KI、KII、KIII。
该命令仅适用于在裂纹区域附近具有各向同性材料的线弹性问题。
使用KCALC命令首先定义描述裂纹尖端的局部坐标系,然后定义沿裂纹面的路径,最后计算时应力强度因子需指定分析类型是平面应力或平面应变,对于薄板的分析,可定义为平面应力,对于其他分析,在裂纹尖端附近和它的渐近位置,其应力一般考虑为平面应变。
同时还需指定模型是具有对称边界条件的半裂纹模型或具有反对称边界条件的半裂纹模型,或是整体裂纹模型。
3 实例应用
3.1 二维问题
本文用一个简单二维断裂问题介绍使用ANSYS求解断裂参数的有效性。
一断裂试样厚度为5 mm,其它几何参数如图2。
其材料参数
包括弹性模量E=220 GPa,泊松比,载荷P=0.12 MPa[3]。
由于长度和宽度方向的尺寸远大于厚度方向的尺寸,且所承受的载荷位于长宽方向所构成的平面内,所以该问题满足平面应力问题的条件,可以简化为平面应力问题进行求解。
根据对称性,取整体模型的1/2建立几何模型;选择六节点三角形单元PLANE183模拟加载过程;先进行普通结构分析求解,再采用特殊的后处理命令计算断裂参数。
(如图3,图4,图5)
通过ANSYS计算,得到该问题的的应力强度因子为 1.9689 Mpa·m-2,与断裂力学中的解析解非常接近。
3.2 三维问题
有一含中心穿透裂纹的平板,其几何参数为:半裂纹长mm,半宽mm,板厚t =6.3 mm,并且,材料的弹性模量、泊松比分别为E=206 GPa,。
裂纹板承受均匀应力MPa。
(如图6)
建立三维裂纹体的有限元模型,主要是采用逐节点直接建模方法和实体建模方法。
对本例,裂纹尖端采用逐节点直接建模方法,用退化的solid95单元划分,远离裂纹采用实体建模法,采用常规solid45单元。
然后对其进行搭接布尔运算,完成带裂纹的实体模型的建立。
(图7,图8,图9)
为研究载荷、裂纹、构件几何参数对计算应力强度因子的影响,
对比分析了数值方法和解析方法的计算结果。
(如图10,图11,图12)当载荷分别为10 MPa,20 MPa,30 MPa,40 MPa,50 MPa时,数值解与手册解析公式计算值相差不大,随载荷的增大而增大。
分别改变平板的宽度和长度,随着平板尺寸的增大,的值逐渐接近断裂力学中“无限大”板裂纹应力强度因子的解析值。
4 结论
(1)通过对二维断裂问题裂纹应力强度因子的计算,发现结果与解析值非常接近,表明用ANSYS计算应力强度因子是可行的,有效的。
(2)通过对三维问题采用逐节点直接建模和实体建模相结合的方法建立模型,表明此法的可行性。
最后还研究了载荷、平板几何尺寸对裂纹应力强度因子的影响。
参考文献
[1] 赵海涛,战玉宝.基于ANSYS的应力强度因子计算[J].煤矿机械,2007,28(2):22-23.
[2] 刘明尧,柯梦龙.裂纹尖端应力强度因子的有限元计算方法分析[J].武汉理工大学学报,2011,33(6):116-121.
[3] 张朝晖.ANSYS 12.0结构分析工程应用实例解析[M].机械工业出版社,2010.。