《有限单元法》编程作业

有限单元法考试题及答案一、单项选择题（每题2分，共10分）1. 有限元法中，单元刚度矩阵的计算是基于（）。

A. 位移法B. 势能原理C. 能量守恒定律D. 牛顿第二定律答案：B2. 在有限元分析中，以下哪项不是网格划分时需要考虑的因素？（）A. 网格数量B. 网格形状C. 材料属性D. 边界条件答案：C3. 有限元分析中，以下哪项不是结构分析的基本步骤？（）A. 离散化B. 求解C. 后处理D. 优化设计答案：D4. 在有限元分析中，以下哪种类型的单元不适用于平面应力问题？（）A. 三角形单元B. 四边形单元C. 六面体单元D. 楔形单元答案：C5. 有限元分析中，以下哪种边界条件不属于几何边界条件？（）A. 固定支座B. 压力C. 温度D. 位移答案：C二、多项选择题（每题3分，共15分）6. 有限元法中，以下哪些因素会影响单元的精度？（）A. 单元形状B. 单元数量C. 材料属性D. 网格划分答案：ABD7. 在有限元分析中，以下哪些是常见的数值积分方法？（）A. 一阶积分B. 二阶积分C. 高斯积分D. 牛顿-莱布尼茨积分答案：ABC8. 有限元分析中，以下哪些是常见的单元类型？（）A. 线性单元B. 二次单元C. 三次单元D. 非线性单元答案：ABCD9. 在有限元分析中，以下哪些是常见的后处理技术？（）A. 应力云图B. 位移云图C. 模态分析D. 热分析答案：ABC10. 有限元分析中，以下哪些是常见的非线性问题？（）A. 几何非线性B. 材料非线性C. 接触非线性D. 热应力问题答案：ABCD三、填空题（每题2分，共20分）11. 有限元法中，单元刚度矩阵的计算通常基于___________原理。

答案：势能12. 在有限元分析中，网格划分的目的是将连续的___________离散化为有限数量的单元。

答案：域13. 有限元分析中，___________是将实际问题转化为数学问题的关键步骤。

-----好资料学习有限单元法中“离散”的含义是什么？有限单元法是如何将具有无限自由度的连续介1.1质问题转变成有限自由度问题的？位移有限元法的标准化程式是怎样的？）离散的含义即将结构离散化，即用假想的线或面将连续体分割成数目有限的单元，并1（数的节在其上设定有限个节点；用这些单元组成的单元集合体代替原来的连续体，而场函点值将成为问题的基本未知量。

）给每个单元选择合适的位移函数或称位移模式来近似地表示单元内位移分布规律，即2（无限自通过插值以单元节点位移表示单元内任意点的位移。

因节点位移个数是有限的，故由度问题被转变成了有限自由度问题。

）有限元法的标准化程式：结构或区域离散，单元分析，整体分析，数值求解。

（3 ?单元刚度矩阵和整体刚度矩阵各有哪些性质？各自的物理意义是什么?两者有何区别1.3整体刚度矩阵的性单元刚度矩阵的性质：对称性、奇异性（单元刚度矩阵的行列式为零）。

个自j Kij 即单元节点位移向量中第稀疏性。

单元 Kij 物理意义质：对称性、奇异性、整体刚度 j 个自由度方向引起的节点力。

由度发生单位位移而其他位移分量为零时，在第中每一列元素的物理意义是：要迫使结构的某节点位移自由度发生单位位移，而其 K 矩阵他节点位移都保持为零的变形状态，在所有个节点上需要施加的节点荷载。

什么叫应变能？什么叫外力势能？试叙述势能变分原理和最小势能原理，并回答下述2.2问题：势能变分原理代表什么控制方程和边界条件？其中附加了哪些条件？，外力所做的功将以变形能的形式储存εσ和应变(1)在外力作用下，物体内部将产生应力起来，这种能量称为应变能。

(2)外力势能就是外力功的负值。

势能变分原理可叙述如下：在所有满足边界条件的协调位移中，那些满足静力平衡条件(3) 的位移使物体势能泛函取驻值，即势能的变分为零V=0 +δp=δ Uεδ∏此即变分方程。

对于线性弹性体，势能取最小值，即02V≥ε+δδ2∏P=δ2U 此时的势能变分原理就是著名的最小势能原理。

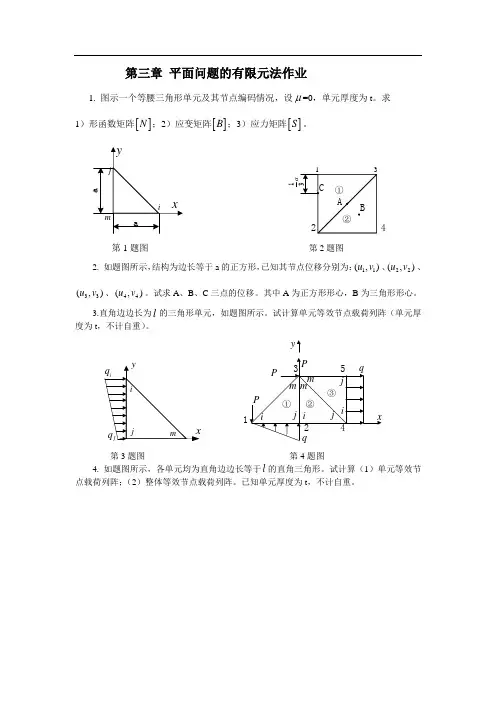
第三章 平面问题的有限元法作业1. 图示一个等腰三角形单元及其节点编码情况，设μ=0，单元厚度为t 。

求 1）形函数矩阵[]N ；2）应变矩阵[]B ；3）应力矩阵[]S 。

4第1题图 第2题图2. 如题图所示，结构为边长等于a 的正方形，已知其节点位移分别为：11(,)u v 、22(,)u v 、33(,)u v 、44(,)u v 。

试求A 、B 、C 三点的位移。

其中A 为正方形形心，B 为三角形形心。

3.直角边边长为l 的三角形单元，如题图所示。

试计算单元等效节点载荷列阵（单元厚度为t ，不计自重）。

第3题图 第4题图4. 如题图所示，各单元均为直角边边长等于l 的直角三角形。

试计算（1）单元等效节点载荷列阵；（2）整体等效节点载荷列阵。

已知单元厚度为t ，不计自重。

5．下列3个有限元模型网格，哪种节点编号更合理？为什么？934679121134612142(a) (b) (c)第5题图6.将图示结构画出有限元模型；标出单元号和节点号；给出位移边界条件；并计算半带宽（结构厚度为t ）。

2a(a) (b) 无限长圆筒 (c) 第6题图7. 结构如图所示，已知结构材料常数E 和 ，单元厚度为t 。

利用结构的对称性，采用一个单元，分别计算节点位移和单元应力。

第7题图答案：1. 1）形函数i x N a =， j y N a = ， 1m x y N a a=-- 2）应变矩阵[]1000101000101011011B a -⎡⎤⎢⎥=-⎢⎥--⎢⎥⎣⎦3）应力矩阵[]10001010001011111002222S a ⎡⎤⎢⎥-⎢⎥=-⎢⎥⎢⎥--⎢⎥⎣⎦2. A 点的位移为()2312A u u u =+ ， ()2312A v v v =+ B 点的位移为()24313B u u u u =++ ， ()24313B v v v v =++ C 点的位移为()1223C a u u u =+ ， ()C 1223av v v =+ 3. 单元等效节点载荷列阵为{}111100003663Tei ji jR q q q q ⎡⎤=++⎢⎥⎣⎦4. （2）整体等效节点载荷向量为{}111100006322TR qlt P qlt P P qlt qlt ⎡⎤=-⎢⎥⎣⎦7. （1） 减缩后的整体刚度方程22122122222221110222021102(1)22102x x b b ab R b ab b P v Etab a bab ab R v b a μμμμμμμμμ---⎡⎤--⎢⎥⎧⎫⎧⎫⎢⎥⎪⎪--⎪⎪⎢⎥⎪⎪-⎪⎪⎢⎥=⎨⎬⎨⎬---++⎢⎥⎪⎪⎪⎪⎢⎥⎪⎪⎪⎪⎩⎭-⎢⎥⎩⎭+⎢⎥⎣⎦ 节点位移22(1)Pb v Eatμ+=- ， 2212212b a v v bμ-+=单元应力为{}()2122201012bv E bv bv ab av μσμμ⎛⎫⎧⎫ ⎪⎪⎪-⎧⎫ ⎪⎪⎪⎪⎪=+-⎨⎬⎨⎬ ⎪-⎪⎪⎪⎪ ⎪-⎩⎭⎪⎪-⎪⎩⎭⎝⎭。

有限单元法习题答案有限单元法（Finite Element Method，简称FEM）是一种数值计算方法，用于求解工程和物理问题的数学模型。

它将复杂的连续体分割成许多简单的有限单元，通过对每个单元进行离散化，近似求解整个问题。

在实际应用中，有限单元法广泛应用于结构力学、流体力学、电磁学等领域。

在学习过程中，我们常常会遇到一些习题，下面将给出一些有限单元法习题的答案，希望对大家的学习有所帮助。

1. 有限单元法的基本原理是什么？答：有限单元法的基本原理是将连续体分割成有限个简单的单元，通过对每个单元进行离散化，建立局部方程，再通过组装得到整体方程。

通过求解整体方程，得到问题的近似解。

2. 如何选择合适的有限单元？答：选择合适的有限单元是保证计算精度的关键。

一般来说，有限单元的选择应该满足以下几个条件：简单性、合理性、适应性和可靠性。

常见的有限单元包括一维线元、二维三角形单元、二维四边形单元等。

3. 有限单元法的求解步骤是什么？答：有限单元法的求解步骤一般包括以下几个步骤：建立有限元模型、确定边界条件、选择适当的有限单元、建立单元刚度矩阵和载荷向量、组装单元刚度矩阵和载荷向量、施加边界条件、求解代数方程组、计算节点位移和应力、分析结果的准确性。

4. 有限单元法的优缺点是什么？答：有限单元法的优点包括：适用范围广、计算精度高、计算效率高、易于处理复杂边界条件等。

缺点包括：模型的精度受到有限单元的选择和网格划分的影响、计算结果的可信度需要通过验证、对计算机硬件要求较高等。

5. 有限单元法在结构力学中的应用有哪些？答：有限单元法在结构力学中的应用非常广泛，包括静力分析、动力分析、热力分析等。

例如，在静力分析中，可以通过有限单元法求解结构的受力状态；在动力分析中，可以通过有限单元法求解结构的振动特性；在热力分析中，可以通过有限单元法求解结构的温度分布等。

6. 有限单元法在流体力学中的应用有哪些？答：有限单元法在流体力学中的应用也非常广泛，包括流体流动、传热、质量传递等。

有限元方法编程【实用版1篇】目录（篇1）1.有限元方法概述2.有限元方法的编程步骤3.有限元方法的应用实例4.总结正文（篇1）一、有限元方法概述有限元方法是一种数值分析方法，广泛应用于固体力学、流体力学、热传导等领域。

它的基本思想是将待求解的连续体划分为有限个小的、简单的子区域，即单元，然后用有限个简单的方程组来代替原来的连续方程，通过求解这些方程组得到近似解。

这种方法既能降低问题的复杂度，又能保证解的精度，因此在工程界有着广泛的应用。

二、有限元方法的编程步骤1.几何建模：根据实际问题，创建待求解的几何模型。

这通常包括划分单元、计算节点坐标等步骤。

2.选择单元类型：根据问题类型和求解需求，选择合适的单元类型，如有限元、无限元、矩形单元、六面体单元等。

3.编写有限元方程：根据单元类型和几何模型，编写有限元方程。

这包括计算单元的刚度矩阵、质量矩阵、载荷矩阵等。

4.组装总方程：将所有单元的有限元方程组装成总方程，通常是一个大型的线性或非线性方程组。

5.求解方程组：使用数值方法（如有限元法、直接解法、迭代法等）求解总方程组，得到近似解。

6.后处理：对求解结果进行分析和处理，如计算应力、应变、位移等。

三、有限元方法的应用实例以一个简单的二维拉伸问题为例，假设有一个长方形板，在左右两端施加均匀拉力，求解板上各个点的应力和应变。

1.几何建模：将长方形板划分为矩形单元，计算节点坐标。

2.选择单元类型：此处采用矩形单元。

3.编写有限元方程：计算单元的刚度矩阵、质量矩阵、载荷矩阵，组装总方程。

4.求解方程组：使用有限元法求解总方程组，得到应力和应变。

5.后处理：分析应力和应变分布，验证解的正确性。

四、总结有限元方法作为一种数值分析方法，通过将连续体划分为有限个小的、简单的子区域，然后用有限个方程组来代替原来的连续方程，降低了问题的复杂度，同时保证了解的精度。

在实际应用中，有限元方法需要经历几何建模、单元选择、编写有限元方程、组装总方程、求解方程组和后处理等步骤。

有限单元法与程序编程实践与课程报告题目1.在三角形单元程序的基础上，增加矩形单元，完成混合单元（三角形和矩形）的有限元分析程序，并在此基础上添加热应力，并给出算例。

（难度系数0.8）2.在3结点三角形单元程序基础上，完成6结点三角形单元的有限元分析程序，并给出算例。

（难度系数0.85）3.写出由3结点三角形单元节点信息自动生成6结点三角形单元的单元节点信息的算法及fortran子程序，用算例验证程序的正确性。

4.在3结点三角形单元程序基础上，完成三角形单元的子结构有限元分析程序，并给出算例。

（难度系数1.0）5.在3结点三角形单元程序上，完成6结点三角形单元的子结构有限元分析程序，并给出算例。

（难度系数1.0）6.在3结点三角形单元程序基础上，完成空间四面体单元的有限元分析程序，并给出算例。

（难度系数0.8）7.在3结点三角形单元程序基础上，完成空间轴对称三角形截面环单元的有限元分析程序，（主要包括应变矩阵子程序、应力矩阵子程序、等效节点荷载子程序等）并给出算例。

（难度系数0.9）8.在3结点三角形单元程序基础上，完成平面四节点和八节点四边形等参数单元的有限元分析程序，并给出算例。

（难度系数1.0）9.在3结点三角形单元程序的基础上，完成空间轴对称四节点和八节点等参数单元的有限元分析程序，并给出算例。

（难度系数1.2）10.在现有程序的基础上，完成空间轴对称问题三节点截面环单元和四节点等参数单元组成混合单元的有限元分析程序，并给出算例。

（难度系数1.1）11.在现有程序的基础上，完成空间轴对称四节点和八节点等参数单元的有限元分析程序，并给出算例。

（难度系数1.1）12.在现有程序的基础上，完成空间二十节点等参数单元的有限元分析程序，并给出算例。

（难度系数1.2）（六面体）13.在3结点三角形单元程序基础上，薄板弯曲矩形单元的有限元分析程序，并给出算例。

（难度系数1.1）14.在3结点三角形单元程序基础上，薄板弯曲三角形单元的有限元分析程序，并给出算例。