南京工业大学线性代数A20082009学年第一学期
- 格式:doc
- 大小:503.50 KB
- 文档页数:7

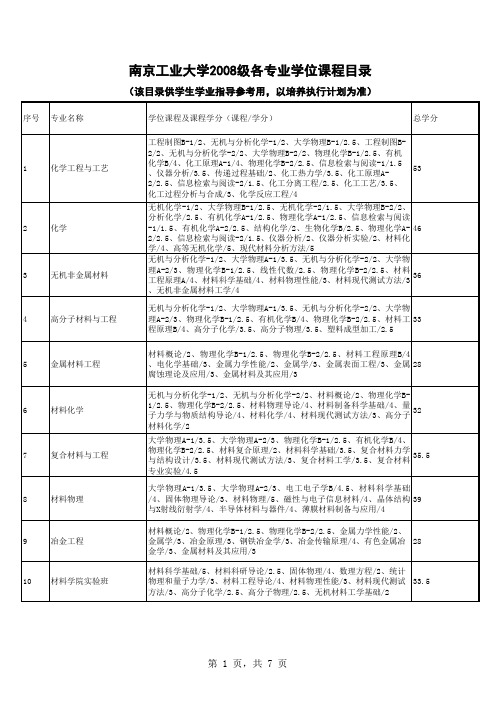


线性代数A-卷答案.一选择题(每小题3分,共24分)1. B2. D3. C4. B5. A6. C7. C8. D二、填空题(每空3分,共18分)1. ()ab a b - ;2. 10 ;3. 3 ;4. 0 ;5. ||0A ¹6. 1 或-2三、计算题(共48分)1. (8分)解:212121ni ni ni ni ni ni y a a a y a y a a D y a a y a===+++=++ååå…………………2分221211()1nnni i na a y a a y a a y a =+=++å…………………4分21100()00nni i a a y y a y==+å11()n n i i y y a -==+å (8)分2.(8分)解:因为T AA I =,所以2||||1T AA A ==,又||0A <,得||1A =- …………………3分|||||()|T T T T T I AB AA AB A A B -=-=-|||()||||()|||||T T T A A B A A B A A B =-=-=-4||(1)||4A B B A =--=--= …………………8分3.(8分)解:211det 3121110A ==-,所以A 可逆…………………2分123100(|)458010346001A I 骣÷ç÷ç÷ç÷=ç÷ç÷ç÷÷ç桫213143123100034410023301rr r r --骣÷ç÷ç÷ç÷揪井---ç÷ç÷ç÷÷ç---桫1323100201011111023301r r r r +-骣-÷ç÷ç÷ç÷揪井----ç÷ç÷ç÷÷ç---桫3222(1)100201011111001123r r r --骣-÷ç÷ç÷ç÷揪井-ç÷ç÷ç÷÷ç---桫…………………5分 233(1)100201010034001123r r r +-骣-÷ç÷ç÷ç÷揪井-ç÷ç÷ç÷÷ç-桫所以1201034123A -骣-÷ç÷ç÷ç÷=-ç÷ç÷ç÷÷ç-桫。


南京工业大学 线性代数 试题 (A )卷试题标准答案2009 --2010 学年第一学期 使用班级 江浦08级各专业一、填空题(每题3分,共15分)(1)3/212--n (2) A -(3) -1 (4) 3 (5) 0,121242363--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭二、选择题(每题3分,共15分)(1) C (2) A (3) C (4) B (5) A 三、(12分)解:n D =mx x x m x x x m x n n n ni i ---∑=2221111)(―――――――――――――――5分=mm x x m x nn i i ---∑= 00001)(21――――――――――――――――――10分=)()(11m x m ni i n --∑=-―――――――――――――――――――――――――12分四(12分)解:由矩阵方程2366AB A E B +=+可得 2636AB B E A -=- 即(6)(6)(6)A E B A E A E -=--+ (1)―――――――――6分又|6|0A E -≠,6A E -可逆,方程(1)两边左乘1(6)A E --可得――――8分70002900(6)0011015013B A E -⎛⎫ ⎪--⎪=-+= ⎪- ⎪ ⎪--⎝⎭――――――――――12分 五(12分)解:以125,,,ααα 为列构成矩阵A ,对A 施行初等行变换将其化为行最简形。
A =103211301121752421460⎛⎫ ⎪--⎪⎪⎪⎝⎭21314124r r r r r r +--10321033300111002224⎛⎫ ⎪ ⎪ ⎪ ⎪--⎝⎭ 234332r r r r --1032100000011100044⎛⎫⎪ ⎪⎪ ⎪--⎝⎭233413r r r r r ↔↔-1032101110000110000⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭23132r r r r -- 10301011010001100-⎛⎫ ⎪- ⎪ ⎪ ⎪⎝⎭――――――――――――――――――――――――――――――――――――6分 故15(,,)3,R αα= ―――――――――――――――――――――――――――8分 其一个极大线性无关组为124,,ααα且31254123,ααααααα=+=--――――――12分六、(13分)解:系数行列式)4)(1(2111111k k k k-+=--由克莱姆法则得,当,1-≠k 且4≠k 时,方程组有唯一解。
南京工业大学近些年线代期末考试卷及答案包括以下六份试卷1南京工业大学线性代数课程考试试卷(A)(江浦、浦江2005-2006学年第1学期)2南京工业大学线性代数课程考试试卷(B)(江浦、浦江2005-2006学年第1学期)3南京工业大学线性代数试题(B)卷(闭)2007--2008学年第一学期使用班级江浦各专业本科生4南京工业大学线性代数试题(A)卷(闭)2008--2009学年第一学期使用班级江浦各专业本科生5南京工业大学线性代数试题(B)卷(闭)2008--2009学年第一学期使用班级江浦各专业本科生6南京工业大学线性代数试题(A)卷(闭)2008--2009学年第二学期使用班级计软0801-3南京工业大学线性代数课程考试试卷(A)(江浦、浦江2005-2006学年第1学期)所在系(院) 班级学号姓名一. 填空题(每空3分,共15分)1、 若n 阶方阵A 满足02=+-E A A (E 为单位阵),则A 的逆矩阵=-1A ____________.2、设矩阵B 是由矩阵A 划去某一列所得, 则秩(B )________秩(A ).3、若1111320=z y x, 则=---222431111z y x ________..4、若向量⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=0112k α 与⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=110k β 正交,则=k ________.5、已知三阶矩阵A 的特征值为,2,1,1-设,223A AB -=则B 的三个特征值为________.二. 单项选择题(每题3分,共15分)1、齐次线性方程组0=x A 的一个基础解系为123212131,,100010001ααα--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则A 的秩为 ( )5)()(=A R A 4)()(=A R B 3)()(=A R C 2)()(=A R D 2、设有m 个n 维向量)(n m >,则 ( ))(A 必线性相关 )(B 必线性无关 )(C 不一定 )(D 无法确定3、设A 为n 阶方阵,则下列方阵中为对称矩阵的是 ( )()A A A '- ()B CAC ' (C 为任意n 阶方阵) ()C AA ' ()()D AA B ' (B 为任意n 阶方阵)4、设A 与B 均为n 阶方阵,若A 与B 相似,则下面论断错误的是 ( ))(A 存在M ,且0M ≠,并有AM MB = )(B A 与B 有相同的特征值B E A EC -=-λλ)( )(D A 与B 均可对角化5、若向量组321,,ααα 线性无关,向量组421,,ααα线性相关, 则 ( ))(A 4α 必不可由321,,ααα 线性表示 )(B 4α必可由321,,ααα 线性表示 )(C 2α 必不可由431,,ααα 线性表示 )(D 2α必可由431,,ααα 线性表示三. (12分) 求n 阶行列式:)1(10000220000111321------n n n n。
南京工业大学 线 性 代 数 试题(A )卷(闭)2007--2008学年第 二 学期 使用班级通信,营销 班级 学号 姓名一、填空题(每题3分,共15分) 1、设4 阶行列式A =2343αγγγ=和B =2341βγγγ=,则行列式 B A += 。
2、设A 、B 都是n 阶方阵,则222()(2)A B A AB B ---+=。
3、设0001002003004000A ⎛⎫⎪⎪= ⎪ ⎪⎝⎭,则 =-1A 。
4、设n 元线性方程组AX b =,且()R A r =,(,)R A b s =,则方程组AX b =有解的充要条件是,有唯一解的充要条件是,有无穷多解的充要条件是。
5、矩阵1551A ⎛⎫= ⎪⎝⎭的特征值为,A 能否相似于对角阵?。
二、选择题(每题3分,共15分)1、设A 为4阶方阵,则3A -为( )。
(A )34A (B )3A (C )123A (D )43A2、若向量组1(1,1,0)ε=,2(0,1,1)ε=,3(0,0,1)ε=能由向量组1123(,,)a a a α=,2123(,,)b b b α=,3123(,,)c c c α=线性表示,则向量组123,,ααα的秩为( )(A )1 (B )2(C )3(D )不能确定3、若矩阵A 的秩等于矩阵B 的秩,则( ) (A).A 与B 合同(B).B=A(C).A 与B 是相抵(或等价)矩阵(D).A ,B 是相似矩阵4、设矩阵A 是任一n (3)n ≥阶可逆方阵,*A 为A 的伴随矩阵,又k 是一常数,且0,1k ≠±,则*()kA 等于( ) (A )*kA (B )1*n kA -(C) *n k A (D)1*k A -5、设A 是3阶矩阵,特征值是0,1,2321=-==λλλ,对应的特征向量分别是123,,ααα,若321(,3,)P ααα=-,则1P AP -=( )(A )210⎛⎫ ⎪- ⎪ ⎪⎝⎭ (B )032⎛⎫ ⎪- ⎪ ⎪-⎝⎭ (C )012⎛⎫ ⎪- ⎪⎪⎝⎭(D )012⎛⎫ ⎪ ⎪ ⎪-⎝⎭ 三、(11分)计算n 阶行列式2112112112112n D =四、(12分) 设3000250004700069A ⎛⎫⎪-⎪= ⎪-⎪-⎝⎭,且有关系式222A AX E X -=-,求矩阵X . 五、(12分)设向量组1(6,4,1,1,2)T α=-,2(1,0,2,3,4)T α=-,3(1,4,9,16,22)T α=--,=4α(7,1,0,1,3)T -,求该向量组的秩及其一个极大无关组并将其余的向量用该极大无关组线性表示。
南京工业大学 线 性 代 数 试题(A )卷(闭)2008--2009学年第 一 学期 使用班级 江浦各专业本科生 班级 学号 姓名题号 一 二 三 四 五 六 七 八 总分得分(符号说明:E 表示单位矩阵,R 表示矩阵的秩,表示行列式,T 表示矩阵的转置。
)一、填空题(每题3分,共15分)1.设3阶矩阵111123012,025234006A B ⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,则AB = 。
2.设三阶矩阵A 的特征值为1,-1,3,再设325,B A A =-则B = .。
3.设n 阶矩阵A 的各行元素之和等于零,且A 的秩为1n -,则齐次线性方程组0AX =的通解为 。
4.设向量1(2,,1,0),(0,1,,1)T T k kαβ=-=-为属于实对称矩阵A 的不同特征值的特征向量,则k = 。
5.已知022=--E A A ,则=-1A。
二、选择题(每题3分,共15分)1.设齐次方程组0AX =的一个基础解系为123212131,,100010001ααα--⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则( ).5)()(=A R A 4)()(=A R B 3)()(=A R C 2)()(=A R D2.设n 阶矩阵A 有s 个不同的特征值12,,,s λλλ,而且(),i i R E A n r λ-=-1,2,,i s =。
如果A 与对角矩阵相似,则( ). (A)1s ii r n =≤∑ ()B 1s ii r n =≥∑ (C) 1s ii r n ==∑ (D) 1sii r n =≠∑3.若向量组123,,ααα线性无关,向量组124,,ααα线性相关, 则 ( ).)(A 4α必不可由123,,ααα线性表示 )(B 4α必可由123,,ααα线性表示 )(C 2α必不可由134,,ααα线性表示 )(D 2α必可由134,,ααα线性表示4. 设n m ⨯阶矩阵()R A r =, 则如下结论正确的是( ).(A )()()TR A A R A = (B)()()TR A A R A <(C) ()()TR A A R A > (D) ()()TTR A A R A ≠ 5. 对于矩阵方程AB AC =,以下结论正确的是( ).(A) B C = (B)B C ≠ (C)如A 可逆,B C =则 (D )以上均不正确. 三、(10分)计算下行列式123123123123n n n nx a a a a a x a a a D a a x a a a a a x a ++=++四、(10分)设三阶矩阵200450124A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭满足矩阵方程239AX A X E +=+,试求矩阵X .五、(14分)设向量1234(3,2,1,3),(1,3,1,4),(7,1,1,2),(1,1,3,2),αααα==---==---5(0,7,4,3)α=-,求向量组的秩和极大无关组,并把极大无关组以外的向量用极大无关组线性表示.六、(13分)当,a b 为何值时,线性非齐次方程组12341234234123402331(3)2321x x x x x x x x x a x x b x x x ax +++=⎧⎪+++=⎪⎨-+--=⎪⎪+++=-⎩无解、有唯一解、或有无穷多组解?在有无穷多解时,求出其通解.七、(15分)已知二次型22212312323(,,)2334f x x x x x x x x =+++,试回答下列问题1) 写出此二次型的矩阵A ;2) 利用正交变换QY X =该二次型化为标准型,并给出所使用的正交变换和标准型;3) 判断该二次型是否具有正定性。
八、(8分)Housesholder 矩阵是计算数学中一类重要的变换(镜面反射)方法,一般用来化矩阵为上Hesseberg 矩阵。
设实向量12(,,,)T n u u u u =且1T u u =,则其一般形式为2T H E uu =-试回答下列问题:1) 证明:Householder 矩阵是实对称正交矩阵;(3分)2) 证明:一般实对称正交矩阵的特征值只能是1或-1,并确定Householder 矩阵的特征值(3分) 3) 对于,1)T u n=,试给出此Householder 矩阵属于各特征值的特征向量.(2分)南京工业大学 线 性 代 数 试题 (A )卷试题标准答案2008--2009学年第一学期 使用班级 江浦各专业本科生一、填空题(每题3分,共15分) (1) 0 (2.) -432 (3) (1,1,,1),T k k 为任意常数.(4) 1或-1 (5)1/2()A E -.二、选择题(每题3分,共15分) (1) D (2) C (3) B (4) A (5) C 三、(10分)解:231123231123123231123231nin i nn in i n nn ini nnini x a a a a x a a a a x a x a a a a x a a a D a a x a a x a a x a a a a a x a x a a a x a ====+++++=+=+++++∑∑∑∑(从第二列至第n 列加到第1列)――――――――――――――――――――5分23232312311()11n n ni n i na a a x a a a x a a x a a a a x a =+=+++∑(提取公因子)=11000100()1001n i i x x a x x=+∑(1(2)i i c a c i -≥)――――――――――8分 =11()nn i i xx a -=+∑―――――――――――――――――――――――10分四、(10分)解:由239AX A X E +=+得(3)(3)(3)A E X A E A E -=--+―――――――6分又30A E -≠,故3A E -可逆,上式两边同时左乘1(3)A E --得500(3)480127X A E -⎛⎫ ⎪=-+=-- ⎪ ⎪--⎝⎭。
――――――――10分五、(14分)解:以122,,,T T T ααα为列生成矩阵A ,并对A 施行初等行变换将其化为行最简形.31710231171113434223A -⎛⎫⎪- ⎪= ⎪--- ⎪--⎝⎭13r r ↔ 11134231173171034223---⎛⎫⎪- ⎪⎪-⎪--⎝⎭213141233r r r r r r --- 1113401170448011715---⎛⎫⎪-- ⎪ ⎪⎪--⎝⎭14342r 111340117150112300000---⎛⎫ ⎪-- ⎪ ⎪ ⎪⎝⎭32r r +1113401171500091800000---⎛⎫ ⎪-- ⎪ ⎪ ⎪⎝⎭ 231/9r r - 111340117150001200000---⎛⎫⎪-- ⎪⎪⎪⎝⎭―6分231373r r r r ++11102011010001200000-⎛⎫⎪- ⎪⎪⎪⎝⎭12r r +10201011010001200000⎛⎫⎪- ⎪⎪⎪⎝⎭―――8分所以15(,,)3R αα=,一个极大无关组为124,,ααα,―――――――(12分)且31251242,2.ααααααα=+=-+―――――――――――――――(14分) 六、(13分)对方程组的增广矩阵进行初等行变换1111012331(|)01323211A b a b a ⎛⎫⎪⎪= ⎪---⎪-⎝⎭ 21313r r r r -- 1111001221013201231a b a ⎛⎫⎪ ⎪ ⎪---⎪----⎝⎭3242r r r r ++ 11110012210011010B a b a ⎛⎫ ⎪⎪= ⎪-+ ⎪-⎝⎭------------------------5分显然可见: 当1,1a b =≠-时方程组无解,当1a ≠时方程组有唯一解,当1,1a b ==-时方程组有无穷多组解.――――――――――――――――――――――――8分 当1,1a b ==-时继续将矩阵B 化为行最简形得B =11110012210000000000⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭ 12r r - 10111012210000000---⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭与原方程组等价的方程组为1342341122x x x x x x =-++⎧⎨=--⎩令3400x x ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,得原方程组的一个特解为1100η-⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭。
――――――――11分与原方程组对应的齐次方程组等价的方程组为 13423422x x x x x x =+⎧⎨=-⎩令3410,01x x ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭得齐次方程组的一个基础解系为121122,.1001ηη⎛⎫⎛⎫⎪ ⎪-- ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭故原方程组有无穷多组解时的通解为1122X k k ηηη=++,12,k k 为任意常数.―――13分 七、(15分)解:1)二次型的矩阵为200032023A ⎛⎫⎪= ⎪ ⎪⎝⎭―――――――――――――3分2)先计算矩阵的特征多项式200()032(2)(1)(5)023A f A E λλλλλλλλ-=-=-=----故矩阵的特征值分别为1231,2, 5.λλλ===――――――――――――6分 再计算矩阵的属于各特征值的特征向量:当11λ=时,求解方程组1()0A E x λ-=得一个特征向量为12(0,1,1)Tq =-.当22λ=时,求解方程组2()0A E x λ-=得一个特征向量为2(1,0,0)T q =.当35λ=时,求解方程组3()0A E x λ-=得一个特征向量为22(0,1,1)Tq =.令123(,,)Q q q q =,作变换X QY =,则此变换即为正交变换,该二次型在此变换下的标准型为2221,23123(,)25f y y y y y y =++。
――――――――――――12分3)因为矩阵的特征值都是正的,故该二次型为正定二次型.―――――――15分 八、1)显然H 为实矩阵,又(2)2TT TTH E uu E uu H =-=-=, 2(2)(2)TTTHH H E uu E uu E ==--=.所以H 为实对称正交矩阵.――――――――――――――――――――3分 2)设x 是实对称矩阵正交矩阵H 的属于特征值λ的特征向量,则2(,)(,)T T T T T x x x Ex x H Hx Hx Hx x x x x λλλ=====,而0T x x ≠,则必有1 1.λ=或-容易验证 Hu u =-,即1-是H 的一个特征值,设v 是和u 正交的非零向量,则有Hv v =,又R(u)=1,这种非零向量v 可以求出1n -个。