酶促反应动力学(有方程推导过程)

酶动力学综合实验实验（一）——碱性磷酸酶Km值的测定【目的要求】1.了解底物浓度对酶促反应速度的影响2.了解米氏方程、Km值的物理意义及双倒数作图求Km值的方法。

【实验原理】1、碱性磷酸酶：碱性磷酸酶是广泛分布于人体各脏器器官中，其中以肝脏为最多。

其次为肾脏、骨骼、肠和胎盘等组织。

但它不是单一的酶，而是一组同功酶。

本实验用的碱性磷酸酶是从大肠杆菌中提取的。

2、米氏方程：Michaelis-Menten 在研究底物浓度与酶促反应速度的定量关系时，导出了酶促反应动力学的基本公式，即：错误！未找到引用源。

(1) 式中：v表示酶促反应速度，错误！未找到引用源。

表示酶促反应最大速度，[S]表示底物浓度，错误！未找到引用源。

表示米氏常数。

3、错误！未找到引用源。

值的测定主要采用图解法，有以下四种：①双曲线作图法（图1-1，a）根据公式（1），以v对[s]作图，此时1/2错误！未找到引用源。

时的底物浓度[s]值即为Km值，以克分子浓度（M）表示。

这种方法实际上很少采用，因为在实验条件下的底物浓度很难使酶达到饱和。

实测错误！未找到引用源。

一个近似值，因而1/2错误！未找到引用源。

不精确。

此外由于v对[S]的关系呈双曲线，实验数据要求较多，且不易绘制。

②Lineweaver- Burk作图法双倒数作图法（图1-1，b）实际工作中，常将米氏方程（式（1））作数学变换，使之成为直线形式，测定要方便、精确得多。

其中之一即取（1）式的倒数，变换为Lineweaver- Burk方程式：错误！未找到引用源。

(2)以错误！未找到引用源。

对错误！未找到引用源。

作图，即为y=ax+b形式。

此时斜率为错误！未找到引用源。

，纵截距为错误！未找到引用源。

把直线外推与横轴相交，其截距相交，其截距即为—错误！未找到引用源。

③Hofstee作图法（略）把（2）式等号两边乘以错误！未找到引用源。

，得：错误！未找到引用源。

(3)以v对错误！未找到引用源。

酶促反应动力学米氏方程摘要：1.酶促反应动力学的基本概念2.米氏方程的推导过程3.米氏方程的应用4.酶促反应动力学的影响因素5.总结正文：一、酶促反应动力学的基本概念酶促反应动力学是研究酶促反应速度及其影响因素的科学。

在酶促反应中，酶作为催化剂，可以降低反应所需的活化能，从而加速反应速率。

酶促反应动力学主要研究酶浓度、底物浓度、温度、pH、抑制剂和激活剂等因素对反应速率的影响。

二、米氏方程的推导过程米氏方程是描述酶促反应速度与底物浓度之间关系的经典方程。

其推导过程如下：1.假设酶分子的数量为[E]，底物浓度为[S]，酶促反应速度为v。

2.酶在催化过程中会与底物结合形成酶- 底物复合物（ES），此过程为慢反应。

3.酶- 底物复合物在达到一定程度后会分解为酶和产物，此过程为快反应。

4.根据慢反应和快反应的速率常数，可以得到酶促反应速度的表达式。

5.将表达式中的慢反应和快反应速率常数用米氏常数（Km）表示，即可得到米氏方程：v = (Km * [S]) / (Km + [S])三、米氏方程的应用米氏方程可以用于分析酶促反应的动态过程，预测反应速度与底物浓度的关系，以及研究酶的结构与功能。

此外，通过比较不同底物和酶的米氏方程，可以了解酶的专一性和底物选择性。

四、酶促反应动力学的影响因素酶促反应动力学受到多种因素的影响，主要包括：1.酶浓度：在一定范围内，酶浓度的增加会提高反应速率，但当酶浓度达到饱和时，反应速率不再随酶浓度增加而提高。

2.底物浓度：底物浓度的增加会提高反应速率，但当底物浓度达到一定程度时，反应速率不再随底物浓度增加而提高。

3.温度：温度的升高会加速反应速率，但过高的温度会导致酶失活，使反应速率降低。

4.pH：酶的活性受pH 值的影响，pH 值的改变会影响酶的催化效率。

5.抑制剂和激活剂：抑制剂会降低酶的催化效率，而激活剂会提高酶的催化效率。

五、总结酶促反应动力学是研究酶促反应速度及其影响因素的科学。

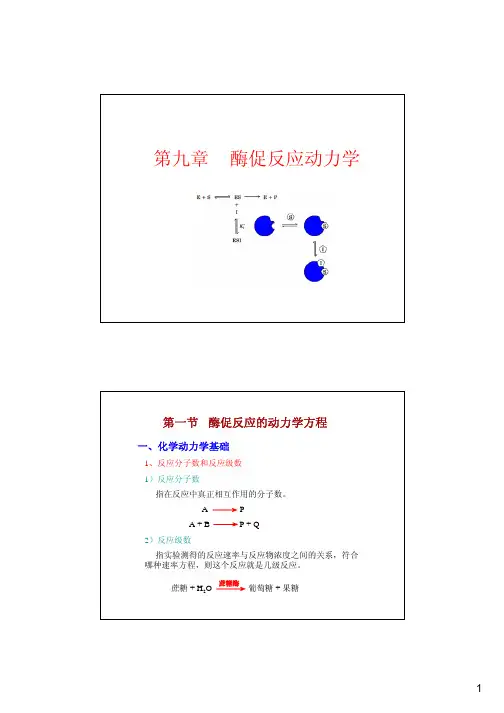
第九章酶促反应动力学（一）底物浓度对酶反应速率的影响用反应初速度v对底物浓度[S]作图得P355 图9-6。

曲线分以下几段：（1）OA段：反应底物浓度较低时v与[S]成正比，表现为一级反应， v = k[S]。

根据酶底物中间络合物学说，酶催化反应时，首先和底物结合生成中间复合物ES，然后再生成产物P，并释放出E。

E + S = ES →P + EOA段上，底物浓度小，酶未被底物饱和，有剩余酶，反应速率取决于ES浓度，与[S]呈线性关系，v正比于[S]。

（2）AB段：反应速度不再按正比升高，表现为混合级反应。

此时酶渐渐为底物饱和，[E S]慢慢增加，v也慢慢增加，为分数级反应。

（3）BC段：反应速度趋于V max，为零级反应，酶促反应表现出饱和现象。

此时底物过量[S]>[E],[E]已全部转为[E S]而恒定，因此反应速率也恒定，为最大反应速率，V max为[E]所决定。

非催化反应无此饱和现象。

酶与底物形成中间复合物已得到实验证实。

（二）酶促反应力学方程式（1）米氏方程推导1913年Michaelis和Menten提出并推导出表示[S]与v之间定量关系的米氏方程V max[S]V =K m + [S]Km：米氏常数，物理意义为反应速率为最大速率V max一半时底物的浓度，单位与底物浓度同。

推导：酶促反应分两步进行。

k1k3E + S ES →P + Ek2v = k3 [ES]一般k3为限速步骤v = k3 [ES] …①1.[ES] 生成速率：d[ES]/dt = k1([E] - [ES]) [S]2.[E S]分解速率：-d[ES] / dt = k2 [ES] + k3 [ES] = (k2 + k3) [ES]3.稳态下[ES]不变，ES生成速率和分解速率相等：k1 ([E]- [ES]) [S] = (k2+k3) [ES]4.引入K m：令K m = k2+k3 / k1代入K m = ([E]- [ES]) [S] / [ES] ,K m [ES] = [E] [S]- [S] [ES], [ES] (K m + S) = [E] [S],[ES] = [E] [S] / K m+[S],5.代入①式：v = k3 [ES] = k3 [E] [S] / K m + [S] …②6.引入V max：为所有酶都被底物饱和时的反应速率，即此时[E]= [ES]V max = k3 [ES] = k3 [E]代入②式：v = V max [S] / K m + [S]米氏方程表示K m及V max已知时，v~[S]的定量关系。

酶促反应动力学目的：酶催化反应的速度及各种因素对反应速度的影响1.米氏方程的推导米氏学说是1913年Michaelis和Menton建立的，认为反应分为两步，先生成酶-底物复合物（中间产物），再分解形成产物，释放出游离酶。

经过Briggs和Haldane的补充与发展，得到了现在的米氏方程。

对于上面的反应，首先有三点假设：第一，底物大过量，即[S]》[E]。

第二，在反应初期，产物浓度极小，忽略逆反应即k-2=0；第三，稳态假设，即随着反应的进行，复合物的形成速度逐渐降低，分解加快，在某一时刻达到平衡，复合物的浓度为常数，这种状态称为“稳态”。

体系达到稳态后，底物的消耗和产物的生成速度都是常数，且相等。

经测定，酶加入体系后，在几毫秒之内即可达到稳态，所以我们测定的初速度通常是稳态速度。

在产物积累较多之前，体系一直保持稳态，所以反应速度v=k2[ES]。

根据稳态假设，有k1[E][S]=(k-1+k2)[ES]，即[ES]=k1[E][S]/(k-1+k2)。

定义(k-1+k2)/k1=Km，因为[E]=[E]0-[ES]，故[ES]= [E]0[S]/(Km+[S])。

代入速度方程，得到v= k2[E]0[S]/(Km+[S])。

因为当[ES]=[E]0时速度最大，所以Vm=k2[E]0。

代入，得到下列米氏方程：2.米氏常数的意义米氏常数的物理意义是反应速度达到最大反应速度一半时的底物浓度。

其酶学意义在于，它是酶的特征常数，只与酶的性质有关，与酶浓度无关。

不同的酶其Km不同，同种酶对不同底物也不同。

在k2极小时1/Km可近似表示酶与底物的亲和力，1/Km越大，亲和力越大。

在酶的多种底物中，Km最小的底物叫做该酶的天然底物。

3.米氏常数的测定从酶的v-[s]图上可以得到Vm，再从1/2Vm处读出[s]，即为Km。

但实际上只能无限接近Vm，却无法达到。

为得到准确的米氏常数，可以把米氏方程加以变形，使它相当于线性方程，通过作图得到准确的米氏常数。

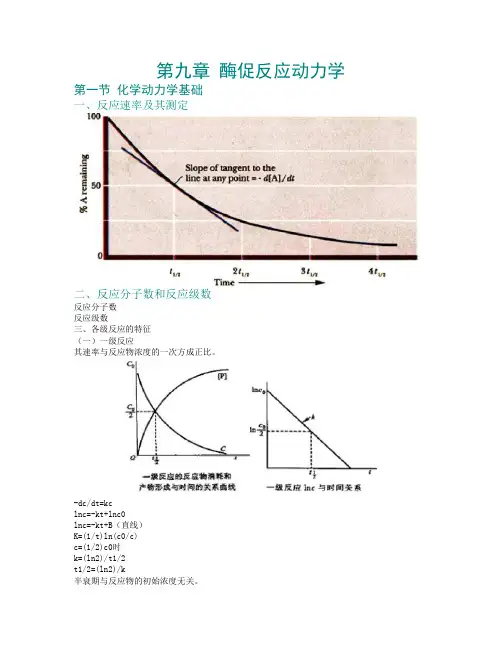
第九章酶促反应动力学第一节化学动力学基础一、反应速率及其测定二、反应分子数和反应级数反应分子数反应级数三、各级反应的特征（一）一级反应其速率与反应物浓度的一次方成正比。

-dc/dt=kclnc=-kt+lnc0lnc=-kt+B（直线）K=(1/t)ln(c0/c)c=(1/2)c0时k=(ln2)/t1/2t1/2=(ln2)/k半衰期与反应物的初始浓度无关。

（二）二级反应反应的速率与反应物浓度的二次方成正比。

1．若A和B为同一物质-dc/dt=kc2，dc/c2=-kdt；c/c0=1/(1+kc0t)；c/c0=1/2时，k=1/c0t1/2。

2．A和B的初始浓度相同k=(1/t){x/[a(a−x)] }3．A和B的初始浓度不同k=[1/t(a−b)]/ln{[b(a−x)]/[a(b−x)]}a：反应物A的初始浓度。

b：反应物B的初始浓度。

(a-x)：反应时间为t时A的浓度。

(b-x)：反应时间为t时B的浓度。

（三）零级反应反应速率与反应物的浓度无关。

-dc/dt=k，或dx/dt=k。

X=kt，或k=x/t。

第二节底物浓度对酶反应速率的影响一、中间产物学说中间产物学说的实验依据：（1）核酸和酶的复合物可直接用电镜观察；（2）下图；（3）复合物的溶解度和稳定性有所变化；（4）有些复合物可直接分离得到。

酶催化的反应中各成份的变化：酶反应的速度在不停地变，实验上只有初速度的测定才有意义。

酶反应的初速度与底物浓度之间的关系：二、酶促反应的动力学方程式（一）米氏方程的推导米氏方程v=Vmax[S]/(Km+[S])符合v-[S]曲线。

若Km>>[S]，v=(Vmax/Km)[S]；若[S]>>Km，v=Vmax；由v=Vmax[S]/(Km+[S])，得Km=[S][(Vmax/v)-1]，为典型的双曲线方程。

（二）动力学参数的意义1．Km的意义a.Km值等于反应速度达最大反应速度一半时的底物浓度，单位是浓度单位，是酶的特征常数，酶对一定的底物只有一个特定的Km：V/2=V[S]/(Km+[S])，则Km=[S]。

酶促反应动力学实验酶动力学综合实验实验（一）——碱性磷酸酶值的测定【目的要求】1.了解底物浓度对酶促反应速度的影响2.了解米氏方程、值的物理意义及双倒数作图求值的方法。

【实验原理】1、碱性磷酸酶：碱性磷酸酶是广泛分布于人体各脏器器官中，其中以肝脏为最多。

其次为肾脏、骨骼、肠和胎盘等组织。

但它不是单一的酶，而是一组同功酶。

本实验用的碱性磷酸酶是从大肠杆菌中提取的。

2、米氏方程：在研究底物浓度与酶促反应速度的定量关系时，导出了酶促反应动力学的基本公式，即：(1)式中：v表示酶促反应速度，表示酶促反应最大速度，[S]表示底物浓度，表示米氏常数。

3、值的测定主要采用图解法，有以下四种：①双曲线作图法（图1-1，a）根据公式（1），以v对[s]作图，此时1/2时的底物浓度[s]值即为值，以克分子浓度（M）表示。

这种方法实际上很少采用，因为在实验条件下的底物浓度很难使酶达到饱和。

实测一个近似值，因而1/2不精确。

此外由于v对[S]的关系呈双曲线，实验数据要求较多，且不易绘制。

②作图法双倒数作图法（图1-1，b）实际工作中，常将米氏方程（式（1））作数学变换，使之成为直线形式，测定要方便、精确得多。

其中之一即取（1）式的倒数，变换为方程式：(2)以对作图，即为形式。

此时斜率为，纵截距为。

把直线外推与横轴相交，其截距相交，其截距即为—。

③作图法（略）把（2）式等号两边乘以，得：(3)以v对作图，这时斜率为，纵截距为，横截距为。

④作图法（略）把（2）式等号两边乘以[S],得：(4)以对[s]作图，这时斜率为，纵截距为。

（a）(b)本实验主要以双倒数法，即作图法来测定碱性磷酸酶值。

具体原理如下：本实验以碱性磷酸酶为例，用磷酸苯二钠为其作用物，碱性磷酸酶能分解磷酸苯二钠产生酚和磷酸，在适宜条件下（10.0，和60℃），准确反应13分钟。

在碱性条件下酚可与酚试剂生成蓝色化合物，以波长620比色。

在一定条件下色泽深浅与光密度成正比。

实验 酶促反应动力学—-—-蔗糖酶米氏常数的测【目的要求】1．了解酶促动力学研究的范围。

2．以蔗糖酶为例，掌握测定米氏常数（Km ）【实验原理】在酶促反应中，当反应体系的温度、pH 和酶浓度恒定时，反应初速度（v ）则随底物 浓度[S ］的增加而加速,最后达到极限,称为最大反应速度（v)。

Michaelis 和Menten 根据反应速度与底物浓度的这种关系，推导出如下方程：][][S k S V v m +=此式称为米氏方程，式中Km 称为米氏常数，按此方程，可用作图法求出Km 。

方法有： 1．以v[S ］作图由米氏方程可知,v=V ／2时,Km ＝［S]即米氏常数值等于反应速度达到最大反应速度一半时所需底物浓度。

因此,可测定一系列不同底物浓度的反应速度v,以v 对[S]作图。

当v ＝V ／2时，其相应底物浓度即为Km 。

2．以1／v 对1／［S ］作图取米氏方程的倒数式：VS V k v m 1][11+•=以1／v 对1／[S]作图可得一直线，其斜率为Km ／V ，截距为1/V .若将直线延长与横轴相交，则该交点在数值上等于—l ／Km.本实验以蔗糖为底物．利用一定量蔗糖酶水解不同浓度蔗糖所形成的产物(葡萄糖和果糖）的量来计算蔗糖酶的Km 值。

葡萄糖和果糖能与3，5—二硝基水杨酸试剂反应,生成桔红色化合物，可于520nm 处比色测定之.【试验材料】 1．试剂(1)标准葡萄糖溶液：准确称取100mg 葡萄糖溶于少量饱和的苯甲酸溶液（0。

3%)，再转移到100ml容量瓶中,用饱和苯甲酸溶液稀释到刻度，混匀，即得浓度为1mg／m1的标准葡萄糖溶液。

冰箱贮藏可长期保存；（2）pH4.5的0。

1mol/L醋酸缓冲液：取lmol/L醋酸钠溶液43m1及lmol／L醋酸溶液57m1，稀释至1000m1即得;(3)pH4.5的10％蔗糖溶液:准确取l0g蔗糖溶于少量pH4.5的0。

1mol／L醋酸缓冲液,转移到100ml容量瓶中,用同样缓冲液稀释到刻度备用；(4)3,5-二硝基水杨酸试剂:溶液I：4.5%NaOH溶液300m1,1％3，5一二硝基水杨酸溶液880m1及酒石酸钾钠（KNaC4O6·4H20）255g三者一起混合均匀。