下载文档原格式
静态时序分析综述报告——孙声震1．静态时序分析静态时序分析（STA）就是套用特定的时序模型（Timing Model），针对特定电路分析其是否违反设计者给定的时序限制（Timing Constraint）。
1．1 背景仿真技术是ASIC设计过程中应用最多的验证手段，然而，现在的单片集成系统设计正在将仿真时间推向无法容忍的极限。
在最后的门级仿真阶段，针对的是几十乃至几百万门的电路，对仿真器第一位的要求是速度和容量，因此，性能（仿真速度）和容量（能够仿真的设计规模）是验证中的关键因素。
传统上采用逻辑仿真器验证功能时序，即在验证功能的同时验证时序，它以逻辑模拟方式运行，需要输入向量作为激励。
随着规模增大，所需要的向量数量以指数增长，验证所需时间占到整个设计周期的50%，而最大的问题是难以保证足够的覆盖率。
鉴于此，这种方法已经越来越少地用于时序验证，取而代之的是静态时序分析技术。
1．2 分类静态时序分析以分析的方式区分，可分为Path-Based及Block-Based两种。
图1如图1所示，为Path-Based这种分析方式。
信号从A点及B点输入，经过中间的逻辑单元，从Y端输出。
套用的Timing Model标示在各逻辑器件上，对于所有输入端到输出端都可以找到相对应的延迟时间。
而使用者给定的TimingConstraint为：1. 信号A到达电路输入端的时间点为2（AT=2，AT为Arrival Time）。
2. 信号B到达电路输入端的时间点为5（AT=5）。
3. 信号必须在时间点10之前到达输出端Y（RT=10，RT为Required Time）。
针对P1及P2 两条路径（Path）来做分析。
P1的起始点为A，信号到达时间点为2。
经过第1个逻辑器件之后，由于有2单位的延迟时间，所以信号到达这个器件输出的时间点为4（2+2）。
依此类推，信号经由P1到达输出Y的时间点为7（2+2+3）。
在和上述第三项Timing Constraint比对之后，我们可以得知对P1这个路径而言，时序（Timing）是满足使用者要求的。
综合与静态时序分析综合与静态时序分析是软件工程中常用的两种分析方法，用于评估系统的性能、可靠性和效率等方面。
本文将详细介绍综合与静态时序分析的基本概念、应用场景以及优缺点，并对两者进行比较，以便读者能够更好地了解和应用这两种方法。
一、综合时序分析综合时序分析是指通过建立模型，对系统进行模拟和分析，得出系统性能和可靠性等相关指标。
综合时序分析主要考虑系统的整体性能，包括处理速度、吞吐量、延迟等方面。
常用的综合时序分析方法有排队网络模型、离散事件模拟等。
综合时序分析的应用场景包括网络通信、分布式系统、并行计算等领域。
在这些领域中，系统的性能和可靠性要求较高，并且通常涉及多个组件之间的协作和交互。
通过综合时序分析，可以预测系统的行为、发现潜在的问题，并提出改进措施。
综合时序分析的优点是可以全面考虑系统的各个方面，分析结果较为准确。
然而，综合时序分析通常需要复杂的模型和大量的计算，对分析人员的要求较高。
此外，由于模型建立和参数设定的不准确性，综合时序分析的结果可能和实际情况存在一定的偏差。
静态时序分析是指在系统的设计和实现阶段，通过对系统的源代码或设计文档进行静态分析，得出系统的时序行为和性能指标。
常用的静态时序分析方法有程序切片、基本块图、语义分析等。
静态时序分析的应用场景包括软件开发、代码审查、性能优化等领域。
在这些领域中，开发人员需要预先了解系统的行为和性能，并进行相应的设计和优化。
通过静态时序分析，可以发现源代码中的潜在问题、提高系统的性能等。
静态时序分析的优点是可以在系统设计和实现的早期阶段就发现问题，并及时进行调整。
此外，静态时序分析可以在不需要运行系统的情况下进行，因此可以节省时间和资源。
然而，静态时序分析通常只考虑系统的源代码和设计文档，可能忽略了系统运行时的复杂环境和其它外部因素的影响。
三、综合时序分析与静态时序分析的比较1.方法论差异：综合时序分析主要基于建模和仿真，而静态时序分析主要基于代码和设计文档的分析。
静态时序分析（STA）基础注：上海交⼤论⽂《数字电路静态时序分析与设计》—学习笔记第⼀章概述1.4 集成电路的设计流程⼀般集成电路设计步骤分为逻辑设计和物理设计如图1-1 所⽰：逻辑设计包括：系统划分：将⼀个⼤规模的系统按功能分成⼏个功能模块设计输⼊：⽤HDL(Hardware Description Language)语⾔或电路原理图的形式对系统进⾏功能级描述的设计输⼊。
功能仿真：对功能级描述进⾏功能和时序仿真验证并在验证功能正确后转变成适⽤于综合器的RTL级(Register Transfer Level)描述的⽹表输⼊。
逻辑综合：把⾼层次设计的描述利⽤某种标准单元库按照⼀定的约束条件转换成优化的门级⽹表。
图1-2给出了基本的计算机辅助逻辑综合的流程图。
设计者只要把精⼒集中在层次的划分、⾼层的设计、描述准确的约束条件和标准单元库的单元优化上，⽽其它⼤量的⼯作由逻辑综合⼯具⾃动完成逻辑综合⼯具经过多次交互处理最终产⽣最优化的门级⽹表。
布局前的模拟：对综合后加⼊单元时延信息的门级⽹表进⾏仿真检查时序上是否满⾜设计系统规范和接⼝规范。
物理设计包括：平⾯规划：其任务是为每个模块和整个芯⽚选择⼀个好的布图⽅案⼀般根据其包含器件数估计模块的⾯积再根据该模块和其它模块的连接关系和上层模块或芯⽚的形状估计该模块的形状和相对位置此过程⼀般⼿⼯完成布局：确定模块中各单元的位置布局问题⽐较复杂⼀般分成初线始布局和改进布局两步。
布线：通常布线分为总体布线(Global Routing)和详细布线(Detailed Routing)两步总体布线把线⽹分配到合适的布线区域不关⼼⾛线的具体位置详细布线最终确定连线的具体位置。
参数提取：确定各个连接处的电阻和电容及互连线的分布参数。
后仿真：加⼊布局布线所增加的各种寄⽣电学参数后再次进⾏时序仿真并进⾏ERC，电学规则检查和DRC，设计规则检查最后进⾏⽹表的验证(LVS Layout Versus Schematic) 来确认版图的正确性。
静态时序分析（statictiminganalysis）静态时序分析（static timing analysis，STA）会检测所有可能的路径来查找设计中是否存在时序违规(timing violation)。
但STA只会去分析合适的时序，⽽不去管逻辑操作的正确性。
其实每⼀个设计的⽬的都相同，使⽤Design Compiler和IC Compile来得到最快的速度，最⼩的⾯积和最少的耗能。
根据设计者提供的约束，这些⼯具会在⾯积，速度和耗能上做出权衡。
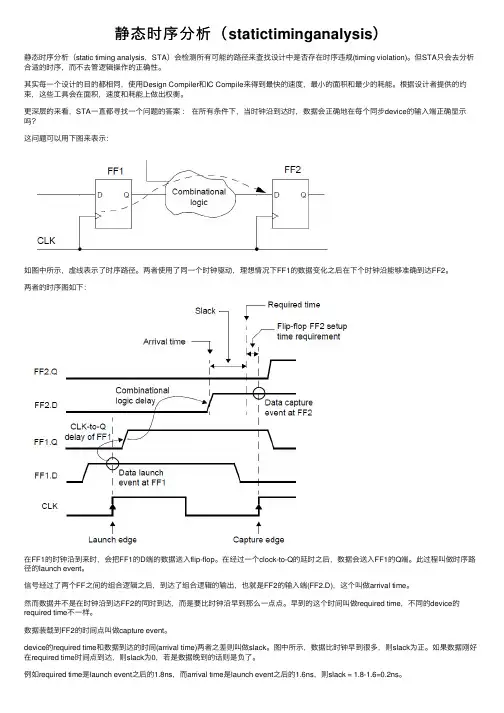
更深层的来看，STA⼀直都寻找⼀个问题的答案：在所有条件下，当时钟沿到达时，数据会正确地在每个同步device的输⼊端正确显⽰吗？这问题可以⽤下图来表⽰：如图中所⽰，虚线表⽰了时序路径。
两者使⽤了同⼀个时钟驱动，理想情况下FF1的数据变化之后在下个时钟沿能够准确到达FF2。
两者的时序图如下：在FF1的时钟沿到来时，会把FF1的D端的数据送⼊flip-flop。
在经过⼀个clock-to-Q的延时之后，数据会送⼊FF1的Q端。
此过程叫做时序路径的launch event。
信号经过了两个FF之间的组合逻辑之后，到达了组合逻辑的输出，也就是FF2的输⼊端(FF2.D)，这个叫做arrival time。
然⽽数据并不是在时钟沿到达FF2的同时到达，⽽是要⽐时钟沿早到那么⼀点点。
早到的这个时间叫做required time，不同的device的required time不⼀样。
数据装载到FF2的时间点叫做capture event。
device的required time和数据到达的时间(arrival time)两者之差则叫做slack。
图中所⽰，数据⽐时钟早到很多，则slack为正。
如果数据刚好在required time时间点到达，则slack为0，若是数据晚到的话则是负了。
例如required time是launch event之后的1.8ns，⽽arrival time是launch event之后的1.6ns，则slack = 1.8-1.6=0.2ns。
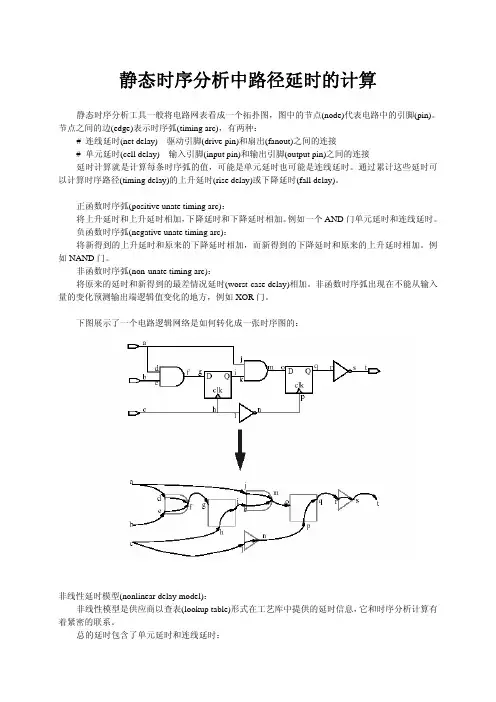
静态时序分析中路径延时的计算静态时序分析工具一般将电路网表看成一个拓扑图，图中的节点(node)代表电路中的引脚(pin)。
节点之间的边(edge)表示时序弧(timing arc)，有两种：# 连线延时(net delay)---驱动引脚(drive pin)和扇出(fanout)之间的连接# 单元延时(cell delay)---输入引脚(input pin)和输出引脚(output pin)之间的连接延时计算就是计算每条时序弧的值，可能是单元延时也可能是连线延时。
通过累计这些延时可以计算时序路径(timing delay)的上升延时(rise delay)或下降延时(fall delay)。
正函数时序弧(positive unate timing arc)：将上升延时和上升延时相加，下降延时和下降延时相加。
例如一个AND门单元延时和连线延时。
负函数时序弧(negative unate timing arc)：将新得到的上升延时和原来的下降延时相加，而新得到的下降延时和原来的上升延时相加。
例如NAND门。
非函数时序弧(non-unate timing arc)：将原来的延时和新得到的最差情况延时(worst-case delay)相加。
非函数时序弧出现在不能从输入量的变化预测输出端逻辑值变化的地方，例如XOR门。
下图展示了一个电路逻辑网络是如何转化成一张时序图的：非线性延时模型(nonlinear delay model)：非线性模型是供应商以查表(lookup table)形式在工艺库中提供的延时信息，它和时序分析计算有着紧密的联系。
总的延时包含了单元延时和连线延时：Dtotal = Dcell + DcDc连线延时。
它有两种计算方法，一是通过operating_conditions中的tree_type属性和wire_load模型；二是在标准延时方程中读入一个SDF文件。
Dcell门自身的延时，典型地是取从输入引脚电压变化到50%到输出引脚电压变化到50%的之间的时间。
第3部分理论知识复习题基本概念数字电路基础一、判断题（将判断结果填入括号中。
正确的填“√”，错误的填“×”）：1.数字信号是由连续变化的模拟信号采样得到的。
（）2.要构成5进制计数器，至少需要3个触发器，其无效状态有3个。
（）3.十进制数（25）D转换为二进制数为（11001）B。
（）4.逻辑变量只有两个值，即0 与1，两者并不表示数量的大小。
（）5.某三个变量逻辑函数F，若以ABC的顺序列真值表，表中F=1的个数为5个。
若以CBA的顺序列真值表，则表中F=1的个数为4个。
（）6.逻辑代数运算与普通代数运算的运算规则相同。
（）7.无关项就是指取值一定为零的最小项。
（）8.组合逻辑电路通常由门电路组合而成。
（）9.组合电路的结构特点是输入信号单向传输的，电路中不含反馈回路。
（）10.奇校验位的值是其余各数据位的异或运算。
（）11.由于门电路平均延迟时间的差异，使信号从输入经不同的通路传输到输出级的时间不同，这样可能导致逻辑电路的错误输出，这种现象称为竞争冒险。
（）12.锁存器对脉冲电平敏感，在时钟脉冲的电平作用下改变状态，而触发器对脉冲边沿敏感，其状态只有在时钟脉冲的上升沿或下降沿的瞬间改变。
（）13.时序逻辑电路中必须含有存储电路，因此必然含有触发器。
（）14.同步时序电路具有统一的时钟CP控制。
（）15.异步时序逻辑电路没有统一的时钟脉冲，电路状态的改变必须考虑外部输入信号及对应存储器的时钟端或控制端有无信号作用。
（）16.异步时序电路没有统一的时钟，状态变化的时刻是不稳定的，通常输入信号只在电路处于稳定状态时才发生变化。
（）17.实现一个8进制计数器最少需要3个D触发器。
（）18.为了获得高精度的D/A转换器，不仅应选择位数较多的高分辨率的D/A转换器，而且还需要选用高稳定度的VREF与低零漂的运算放大器等器件与之配合才能达到要求（）19.模数转换过程，其中采样这一步骤必须遵循采样定律，也就是输入模拟信号的最高频率大于等于采样信号频率的两倍。
静态时序分析电子科技大学詹璨铭什么是静态时序分析⏹静态时序分析STA（static timing analysis）⏹定义⏹与动态时序分析的差异怎样做静态时序分析⏹使用工具primetime （简称pt）与DC ⏹两者的兼容性⏹为什么使用primetime？Primetime与DC的兼容性⏹使用同样的工艺库和设计文件⏹许多指令一样⏹相同的算法，很多结果也一样⏹从一个synthesizable subcircuit 中，pt能捕获一个时序环境，并写成一系列的dc指令，在dc中用其为这个subcircuit定义时间约束和时序优化－－值得关注⏹为dc写的dcsh格式的脚本可以翻译成在pt上用的格式。
在pt中定义为抄本（transcript）格式⏹这两个都支持用SDC（synopsys design constraints）格式指定设计规则，包括时间面积约束。
为什么用pt⏹更快效率更高⏹占用更少的内存⏹具有高级的芯片级的分析能力和高级的建模能力。
STA中的对象⏹Design －完整的设计⏹Cell（instance）－设计中使用的一个元件⏹Net －金属连线⏹Port －design 的I/O口⏹Pin －cell 的I/O口⏹Reference －是元件的参考的源定义⏹Clock －创建的时钟信号时序弧（timing arc）⏹定义：如果把电路看作是一张很大的拓扑图，那么图中的结点就是电路中的引脚（pin）。
结点与结点之间的部分，我们称作是时序弧（timing arc）。
他定义了任意两个结点之间的时序关系。
⏹最直观基本的理解：cell delay与net delay。
这两个也是计算下面时序弧的基础。
每段时序弧的延时就是把这两个值不断相加时序弧分类一：时序的延时⏹组合时序弧（combinational timing arc）⏹边沿时序弧（edge timing arc）⏹重置和清除时序弧（preset and clear timing arc）⏹三态使能/无效时序弧（three state enable/disable timing arc）时序弧分类二：时序约束⏹建立时序弧（setup timing arc）⏹保持时序弧（hold timing arc）⏹恢复时序弧（recovery timing arc）⏹清除时序弧（removal timing arc）⏹宽度时序弧（width timing arc）组合时序弧（combinationaltiming arc）⏹负函数（negative unate）⏹正函数（positive unate）⏹非函数（non-unate）calculation）－－cell delay⏹是从一个逻辑门的输入到输出的延迟量⏹通过工艺库（technology library）来查找的⏹这是个2维表，查找项是输入的过渡时间（input transition），输出的电容负载（output load capacitance）没有对应的值，做一个线性的推导，计算出相应的值。
1引言
在集成电路设计过程中，模拟方法是应用最多的验证时序正确与否的手段，然而，模拟方法在微系统芯片(SoC)时代正面临严竣的挑战。
传统的逻辑模拟方法虽然比较快，但需要输入向量作为激励，给使用带来很多不便；更为严重的是其精度不够高，不能处理SoC时代越来越严重的互连线的耦合电容、电感效应。
电路模拟方法虽然能非常精确地计算SoC时代的各种效应，但其速度太慢，容量也太小。
静态时序分析技术通过提取整个电路的所有时序路径，计算信号沿(上升沿或下降沿)在传播过程的延时，然后检查在最坏情况下电路中是否存在建立时间和保持时间不满足要求的器件，从而确认被验证的电路是否存在时序问题。
它们又分别通过对最大路径延迟和最小路径延迟的分析得到。
静态时序分析不需要输入向量、运行速度快、占用内存少，因而成为SoC时代最主要的时序验证手段。
延时计算和最长/最短路径分析是静态时序分析的关键。
由于互连线结构 [1]对门延时的影响非常大，必须在门延时模型中充分考虑这一因素才能确保静态分析结果的正确性。
广告插播信息
维库最新热卖芯片：
XC9536-15PC44C SN74F244DWR IS62C1024L-70Q SS34HT162288E6050-RJJ AQY210E H KM68V257CJ-15MUR3020PT TL082CDR
本文提出新的Π模型方法，结合了门的等效电容[3]来计算门的延时，我们的方法结合门的互连线负载的拓扑结构和门负载三阶矩求解的方法，采用[4]中提出的等效电容的求解公式，求出门延时计算模型，相比上述两种方法，在静态时序分析中更为合理。
2新的门延时模型
2.1 新的门延时模型
在[4]中，作者提出了利用Π型的RC模型来近似门的互连线输出负载，同时考虑了负载的屏蔽效应。
用该模型等价地计算出门输出驱动点导纳函数前三阶系数。
图1中Y(s)表示准确的RC树的驱动点导纳函数，在s＝0的Taylor展开式表示如下：
将门的输出的RC树的互连线负载等效负载为Π模型，如图2。
通过Π模型得到的门输出驱动点导纳函数和Y (s)的前三项对比得出：
尽管以往模型能够很好地表示等效的输出驱动点导纳函数，但是利用等效电容计算的门延时结果并不理想，所以我们提出了新的模型。
模型中电容的值也采用门输出驱动点导纳函数和 RC树的驱动点导纳函数前三阶近似相等原理[4] 推出来，设该驱动点导纳函数为Yπ的Taylor展开式：
考虑到互连线金属电阻的屏蔽效应以及互连线的分布特性，对于模型中的电阻R1而言，如图3所示，需要求RC树的等效电阻，采用的方法是，将分支中的接地电容去掉，而保留串联的电阻，这时电路中的电阻连接主要以节点之间的串并联的形式出现，则等效电阻 Req，
在[4]中，我们可以看到R1 一般取12/25Req，所以我们新的模型，如图4：
2.2 等效电容模型
这样产生我们新的Π模型，由于传统的门延时模型中门负载是一个电容，[5]提出了利用平均电流相等的
原理，将门负载Π模型，转换为单个电容的等效电容C eff的门负载模型，其等效电容的公式如下：
td、t f分别表示输出门延时和门输出的下降时间，它们是由 k因子表达式来决定的；tt表示输入信号的传输时间，它是已知的。
k因子表达式：
式中CL表示门负载所带电容，各个及表示k因子表达式的参数[3]。
3实验结果
我们选取了与门(and)，在TSMC库0.18mm工艺IP库中的代号(AND2×2)，测试电路我们选取了分别为不具有分支的测试电路1(如图5)和具有分支测试电路2(如图6的主电路及如图7的分支电路)，这样的分支电路有相同的两路，并且这两个分支同时接于主电路图6的1，2，3，4，5，6节点处。
在测试过程中，我们改变门的输入传输时间(tt)和负载电容值(C)，并且采用我们的模型，和Hspice仿真结果，以及
O’Brien/Savarino Π模型(我们在这里称作Y表达式法)，
开端RCΠ模型(我们在这里称作1/6, 5/6法)结果进行比较，不同测试电路的测试结果如表1～表4。
可以看出，我们的模型在门延时的计算方面要比开端RCΠ模型更接近Hspice测试结果，开端RC Π模型平均误差在50％～80％之间，而我们的模型平均误差在5%～15%之间；而与O’Brien/ Savarino Π模型相比，由于O’Brien/Savarino Π模型测试结果有很多情况要比Hspice测试结果小很多，甚至相对误差达到60％，而在静态时序分析中，这种情况是不允许的，它会造成时序分析失败，我们的模型基本相对误差一般在5%～10％左右，较好地克服了这种乐观性，在静态时序的验证方面更可靠，更精确。
除了上述关于与门(and)的测试外，我们还做了反相器(inverter)，或门(or)，加法器(add)的测试，同时我们也使用synopsys库 0.18mm工艺IP库中相同器件进行测试，都有相似的结果和结论。
但是我们也发现，如果上述三种模型测试结果与Hspice的结果相比误差都较小时(大致5％～10％)，我们的模型并不明显比其他模型优越。
这点可以由下面这个例子说明，我们对工业界中一实际电路进行测试，其门负载有100个电阻， 100个电容的有分支电路(简称有分支)和一个门负载14个电阻和14个电容的无分支电路(简称无分支)，其测试结果如表5。
4结论
静态时序分析中的门延时模型对于正确进行静态时序分析有着重要的意义，我们结合了等效电容和门负载的互连线拓扑架构两个概念，提出了新的门延时模型。
通过实验结果说明，它克服了以前门延时模型过于悲观和乐观的计算结果，较好地保证了静态时序分析的精度。
下一步的工作可以集中于门负载是互连线时，存在串扰的情况下的模型，这样可以使模型更加全面。
