沪教版六年级-长方体的再认识讲义

第八章 长方体的再认识 第二课时一、概念1、 长方体的元素：六个面、八个顶点、十二条棱2、 长方体的三元素的特点：（主要是外观特征和数量关系）①长方体的每个面都是长方形；②长方体的十二条棱可以分为三组，每组中的四条棱的长度相等。

③长方体的六个面可以分为三组，每组中的两个面形状大小都相同。

3、 正方体是特殊的长方体。

4、 平面是平的，无边无沿，没有厚度和大小，一般用平行四边形来表示。

记作：平面ABCD 或平面α。

5、 将水平放置的平面画成一边是水平位置，另一边与水平线成45度角的平行四边形。

6、 斜二侧画法画长方体时要注意：宽画成标注尺寸的一半；看不到的线画成虚线；要标字母和尺寸，要写结论。

长方体ABCD-EFGH 、平面ABCD 、棱AB 、顶点A 。

7、 空间中两直线的位置关系有三种：相交、平行、异面① 如果两条直线在同一平面内，有唯一公共点，称这两条直线的位置关系是相交； ② 如果两条直线在同一平面内，没有唯一公共点，称这两条直线的位置关系是平行； ③ 如果两条直线既不平行也不相交，称这两条直线的位置关系是异面。

8、 直线垂直于平面记作：直线PQ ⊥平面ABCD ；直线平行于平面记作：直线PQ ∥平面ABCD 。

9、 计算公式之一：（三条棱长分别是a 、b 、c 的长方体）① 棱长和 = 4()a b c ++ ； ② 体积 = abc ；③ 表面积 = 2()ab bc ac ++ ； ④ 无盖表面积 = S ab -、S bc -、S bc - 10、计算公式之二：（边长是a 正方体）① 棱长和= 12a ；②体积= 3a ；③表面积= 26a ；④无盖表面积 =25a 。

11、长方体不一定是正方体；正方体一定是长方体。

12、长方体中棱与棱的位置关系有3种，分别是平行、相交、异面。

13、长方体中棱与面的位置关系有2种，分别是：平行、垂直。

14、长方体中面与面的位置关系有2种，分别是：平行、垂直。

长方体的再认识复习教学目标1、认识长方体的顶点、棱、面等元素。

2、会画长方体的直观图。

3、熟练掌握长方体中的棱与棱的位置关系,棱与面的位置关系,面与面的位置关系。

4、知道一些简单的检验方法。

5、会求长方体的表面积和体积。

教学重点长方体的概念、画法,长方体中棱、面之间的位置关系。

教学难点对于本章知识点形成一个知识结构，能够从问题中进行归纳总结。

教学过程一、长方体的元素1、长方体有____个面,____个顶点，__________条棱。

2、棱、面的三个特点：(1）长方体的每个面都是__________(2)长方体的十二条棱可以分为_____组，每组中的四条棱长度_______（3）长方体的六个面可以分为___组，每组中的两个面的__________相同。

3、长方体的表面积公式（长为a，宽为b，高为c）：4、长方体的体积公式：［问题］（1）长方体的长、宽、高分别是5cm，4cm,3cm，这个长方体的棱长总和、表面积、体积分别是多少？（2）把长、宽、高分别是5cm、4cm、3cm的两个长方体拼成一个大长方体，表面积减少了多少？二、长方体直观图的画法——斜二侧法练习1:补画下面的图形，使之成为长方体的直观图.三、长方体中棱与棱的位置关系1、平行、相交、异面2、在长方体ABCD-EFGH中，有哪些棱与棱EF相交？平行?异面？3、［归纳]：长方体中任意一条棱有____条棱与它平行，_____条棱与它相交，_____条棱与它异面。

四、长方体中棱与面的位置关系1、垂直、平行2、在长方体ABCD-EFGH中,（1)指出与面ABCD垂直的棱。

（2）指出与面ABCD平行的棱。

(3）指出与棱FG垂直的面。

a bc (4）指出与棱FG 平行的面。

3、 [归纳］：长方体中任意一个面有____条棱与它垂直，_____条棱与它平行。

长方体中任意一条棱有_____个面与它垂直，_____个面与它平行。

4、 检验方法五、 长方体中面与面的位置关系1、垂直、平行2、在长方体ABCD-EFGH 中，(1)指出与面ABCD 垂直的面。

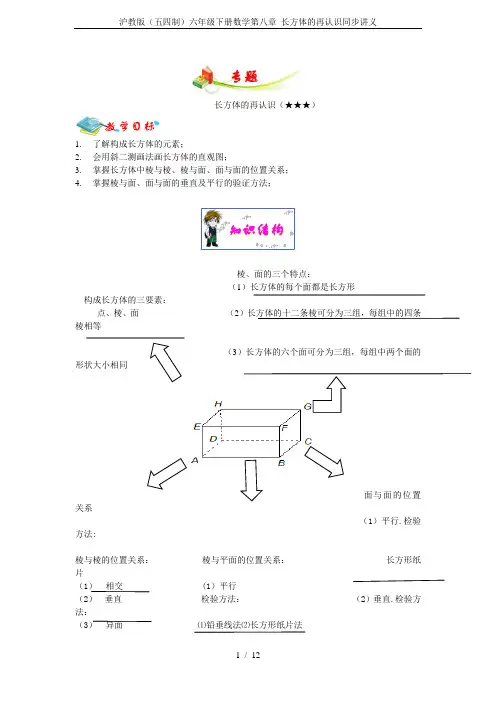
-------------长方体的再认识（★★★）1.了解构成长方体的元素；2.会用斜二测画法画长方体的直观图；3.掌握长方体中棱与棱、棱与面、面与面的位置关系；4.掌握棱与面、面与面的垂直及平行的验证方法；知识结构棱、面的三个特点：（1）长方体的每个面都是长方形构成长方体的三要素：点、棱、面（2）长方体的十二条棱可分为三组，每组中的四条棱相等（3）长方体的六个面可分为三组，每组中两个面的形状大小相同面与面的位置关系（1）平行.检验方法:棱与棱的位置关系：棱与平面的位置关系：长方形纸片（1）相交 (1）平行（2）垂直检验方法：（2）垂直.检验方法：（3）异面⑴铅垂线法⑵长方形纸片法（1）铅垂线（2）三角板法（3）合页型折纸（2）垂直检验方法：⑴铅垂线法⑵三角板法⑶合页型折纸1.本部分建议时长5分钟.2.请学生先试着自行补全上图，发现学生有遗忘时教师帮助学生完成.1.本部分建议时长20分钟.2.进行例题讲解时，教师宜先请学生试着自行解答.若学生能正确解答，则不必做过多的讲解；若学生不能正确解答，教师应对相关概念、公式进行进一步辨析后再讲解例题.3.在每一道例题之后设置了变式训练题，应在例题讲解后鼓励学生独立完成，以判断学生是否真正掌握了相关考点和题型.4.教师应正确处理好例题与变式训练题之间的关系，宜采用讲练结合的方式，切不可将所有例题都讲完后再让学生做变式训练题.例题1一个长方体中，有公共点的三条棱的长度的比为2：3：4，最小的一个面的面积为2162cm ， （1）求这个长方体的所有棱长的总和；“典例精讲”这一部分的教学，可采用下面的策略：“知识结构”这一部分的教学，可采用下面的策略：（2）求这个长方体的表面积； （3）求这个长方体的体积。

（★★）答案：（1）216cm ；（2）18722cm ；（3）51843cm两条较短的棱为长和宽的长方形的面积，是最小的面积，又知三棱长之比，故可求得三棱长，进而可得其他所求。

沪教版数学六年级下册第八章《长方体的再认识》复习教学设计一. 教材分析沪教版数学六年级下册第八章《长方体的再认识》复习教学内容主要包括长方体的特征、表面积和体积的计算方法以及长方体在实际生活中的应用。

本章内容是对长方体知识的系统复习和巩固，旨在帮助学生深化对长方体的认识，提高空间想象能力和解决问题的能力。

二. 学情分析六年级的学生已经学习过长方体的相关知识，对长方体的特征、表面积和体积的计算方法有一定的了解。

但在实际应用中，部分学生可能会遇到困难和问题。

因此，在复习教学中，需要关注学生的学习情况，针对性地进行指导和帮助。

三. 教学目标1.知识与技能：通过对长方体的再认识，使学生掌握长方体的特征、表面积和体积的计算方法，提高空间想象能力和解决问题的能力。

2.过程与方法：通过复习教学，培养学生自主学习、合作学习的能力，提高学生运用数学知识解决实际问题的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的创新精神和团队协作精神，使学生在数学学习中获得成就感。

四. 教学重难点1.教学重点：长方体的特征、表面积和体积的计算方法。

2.教学难点：长方体在实际生活中的应用，空间想象能力的培养。

五. 教学方法1.引导发现法：教师引导学生通过观察、操作、思考，发现长方体的特征和计算方法。

2.案例分析法：教师提供实际生活中的案例，引导学生运用长方体的知识解决问题。

3.小组合作学习法：学生分组讨论，共同完成任务，提高团队协作能力。

六. 教学准备1.教学课件：制作长方体的特征、表面积和体积的计算方法的教学课件。

2.教学案例：收集实际生活中的长方体应用案例。

3.学习任务单：设计学习任务单，引导学生进行自主学习和合作学习。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾长方体的特征、表面积和体积的计算方法，激发学生的学习兴趣。

2.呈现（10分钟）教师利用课件展示长方体的特征和计算方法，让学生直观地感受长方体的结构。

数学学科教师辅导讲义 第一步：画平行四边形ABCD ，使AB 等于长方体的长，AD 等于长方体宽的一半，45BAD ∠=︒（图①）；
、BC、FG.
【答案】④
厘米.
【例6】如图①所示，已知线段a、b、c，画一个长为a，宽为b，高为c的长方体直观图．
【解析】用斜二侧画长方体时要注意三点：(1)长方体直观图中宽是等于已知宽的二分之一；(2)长方体中三个面都是
【例6】如图所示，补画下面的图形，使它们成为长方体的直观图．
【分析】补画长方体时要想清楚补画的面是画长方形还是平行四边形，们先把一个面画完整，再画上其他面．
【解】补画的图形如图所示．
把下列长方体补画完整：
【答案】略. 【随堂练习】
．如图，画一个立方体，使它的棱长为a．
的立方体如图所示：
）平行；（4）异面
AB BC EF EG;（
2）,,,。

沪教版数学六年级下册第八章《长方体的再认识》教学设计一. 教材分析《长方体的再认识》是沪教版数学六年级下册第八章的内容，本节内容是在学生已经掌握了长方体的特征的基础上进行教学的。

教材通过丰富的图片和实际例子，帮助学生进一步理解和掌握长方体的特征，提高学生的空间想象能力和抽象思维能力。

二. 学情分析六年级的学生已经具备了一定的空间想象能力和抽象思维能力，他们对长方体已经有了一定的了解。

但是在具体操作和解决问题时，部分学生可能会存在一些困难。

因此，在教学过程中，教师需要关注学生的个体差异，针对不同学生的学习情况，进行有针对性的教学。

三. 教学目标1.知识与技能：学生能够进一步理解和掌握长方体的特征，提高空间想象能力和抽象思维能力。

2.过程与方法：通过观察、操作、思考、交流等过程，学生能够深化对长方体的认识，培养解决问题的能力。

3.情感态度与价值观：学生能够积极参与数学学习，体验数学学习的乐趣，增强对数学的兴趣。

四. 教学重难点1.教学重点：学生能够进一步理解和掌握长方体的特征。

2.教学难点：学生能够在实际问题中灵活运用长方体的特征，解决问题的能力。

五. 教学方法1.情境教学法：通过丰富的图片和实际例子，激发学生的学习兴趣，提高学生的空间想象能力。

2.引导发现法：教师引导学生观察、操作、思考，发现长方体的特征，培养学生的抽象思维能力。

3.合作交流法：学生通过小组合作、交流，共同解决问题，提高学生的合作能力和沟通能力。

六. 教学准备1.教具准备：长方体模型、图片、实物等。

2.学具准备：学生每人准备一个长方体模型。

七. 教学过程1.导入（5分钟）教师通过展示长方体的图片和生活实例，引导学生回顾长方体的特征，激发学生的学习兴趣。

2.呈现（10分钟）教师通过长方体模型和实物，引导学生观察和操作，让学生直观地感受长方体的特征。

同时，教师引导学生思考：长方体有哪些特征？这些特征是如何体现在实际物体中的？3.操练（10分钟）教师提出一些有关长方体的问题，让学生分组讨论和操作，共同解决问题。

学科教师辅导讲义课题长方体的再认识教学目的1、认识长方体的面、棱、顶点以及长宽高（棱长）的含义。

2、掌握长方体直观图的画法。

3、掌握长方体中棱、面的位置关系，以及空间性质。

教学内容一、作业检查二．长方体知识梳理1.长方体的元素：8个顶点、12条棱，6个面长方体的表面积（6个面的面积之和）、体积（长×宽×高）长方体的每个面都是长方形.长方体的十二条棱可以分成三组:每组中的四条棱的长度相等长方体的六个面可以分成三组,每组中的两个面的形状和大小都相同.2.长方体直观图的画法：斜二侧画法.注意：①12条棱分三组，注意每组4条是互相平行、相等的；其中看不见的三条棱画成虚线，②把水平放置的两个面画成含45°角的平行四边形，③画长方体直观图时，宽要减半画。

3.长方体中棱与棱的位置关系：(1)如图所示的长方体AG中，棱EH与棱EF所在的直线在同一个面内，它们有唯一的公共点，我们称这两条棱相交．(2)棱EF与棱AB所在的直线在同一个面内，但它们没有公共点，我们称这两条棱平行．(3)棱EH与棱AB所在的直线既不平行，也不相交，我们称这两条棱异面．定义：空间两条直线有三种位置关系：相交、平行、异面．(1)一般地，如果直线AB与直线CD在同一平面内，具有唯一公共点，那么称这两条直线的位置关系为相交，读作：直线AB与直线CD相交．(2)如果直线AB与直线CD在同一平面内，但没有公共点，那么称这两条直线的位置关系为平行，记作：AB∥CD，读作：直线AB与直线CD平行．(3)如果直线AB与直线CD既不平行，也不相交，那么称这两条直线的位置关系为异面，读作：直线AB与直线CD异面．4、长方体中棱与面的位置关系：（1）如图所示的长方体AG中，棱(直线)EA垂直于面ABCD。

读作：棱(直线)EA垂直于平面ABCD(2) 如图所示的长方体AG中，棱(直线)EF平行于面ABCD。

读作：棱（直线）EF平行于平面ABCD5、长方体中面与面的位置关系：（1）如图所示的长方体AG中，平面EFBA垂直于面ABCD。

数学六年级〔下〕沪教版〔长方体的再认识Ⅱ〕教师版数学学科教师辅导讲义年级：预初科目：数学课时数：3课题长方体的再认识Ⅱ1.通过熟练掌握长方体的棱与面、面与面之间的位置关系，认识各种图形中的直线与平面、平面与平面之间的垂直与平行关系.教学目的2.结合长方体的总面积、体积和棱长等相关知识进行计算，学会按一定的要求进行补画长方体的局部图形.教学内容【知识梳理】1．通过掌握长方体中棱与面之间的关系有垂直和平行，从而认识各种图形中的直线与平面的垂直〔如图1所示：直线PQ 面ABCD〕与平行〔如图2所示：直线PQ∥面ABCD〕关系：图1 图22．通过掌握长方体中面与面之间的关系有垂直和平行，从而认识各种图形中的平面与平面的垂直〔如图3所示：平面平面〕与平行〔如图4所示：平面∥平面〕关系：图3图4【典型例题讲解】题型一：直线与平面、平面与平面的位置关系【例l】如下图，在长方体ABCD EFGH中，点M,M,P,Q分别是棱AB，CD，GH，EF的中点．(1)哪些棱与面MNPQ平行？1/7数学六年级〔下〕沪教版〔长方体的再认识Ⅱ〕教师版哪些棱与面MNPQ垂直？【分析】(1)可以使用长方形纸片、直角三角尺两次；(2)熟练掌握定义之后，也可以直接进行判读.【解析】(1)AD、DH、HE、AE、BC、CG、GF、BF与面MNPQ平行；AB、CD、GH、EF与面MNPQ垂直．【例2】如下图，一个物体是由三个长方体叠在一起组成的，与面A2B2C2D2平行的面有哪几个？与面A1B1C1D1垂直的面有哪几个?【分析】几个长方体叠合在一起后，判断面与面平行、面与面垂直的方法并没有发生改变，要注意不要重复表示或遗漏某一个平面．【解析】与面A2B2C2D2平行的面有面B1EFA1和面ABCD;与面A1B1C1D1垂直的面有面B2A2AB、面B2E1EC1CB、面E1F1FE、面A2F1FD1DA、面CC2D2D．【方法总结】解这种题时，一定要按平行或垂直的定义或检验平行或垂直的方法来判断，不可盲目判断，注意也不要漏写多写.【借题发挥】如图，在长方体ABCDEFGH中(1)与平面ABCD平行的棱有哪些？(2)与棱BC平行的平面有哪些？(3)与平面ADGF平行的棱有哪些？【答案】〔1〕棱EF、棱HG、棱HE、棱GF；2〕面ADHE、面EFGH、面ADGF；3〕棱HE、棱BC.2.如右图所示，在长方体ABCD EFGH中，分别与ACF的AC、CF、AF中一边平行的面各有哪些？【答案】分别与AC、CF、AF平行的面各有一个，它们分别是平面EFGH、平面AEHD、平面CDHG.题型二：按要求画图题【例3】如下图，补画长方体中与面ABCD平行的棱.2/7数学六年级〔下〕沪教版〔长方体的再认识Ⅱ〕教师版【分析】基于对长方体的认识，可以得出与面ABCD平行的棱有EF、FG、GH、HE，即为与面ABCD平行的面EFGH的4条边，所以在图中只要画出面EFGH即可.【答案】EFHG【借题发挥】平面ABCD线段DH垂直于平面ABCD〔如下列图〕画一个平面HGFE，经过H点，且和ABCD平面平行．【答案】EFG【注意】要把遮挡的局部用虚线表示出来.题型三：综合应用【例4】如果把图中的骰子看作是一个立方体，点数1的对面是6．点数2的对面是5．点数4的对面是点数3．那么与点数2垂直的面的点数和是多少？【分析】与点数2垂直的面分别是点数l、点数3、点数4扣点数6．然后求出点数和.【解析】l 3 4 6=14所以，与点数2垂直的面的和是l4.【例5】(1)如下图，写出互相平行的面，并说明检验的方法．(2)在平面BCGF和平面ADHE之间有两个长方形ABCD和EFGH，所以平面BCGF∥平面ADHE,你认为这句话对吗？为什么？3/7【分析】把面ADHE(长方形)和面ABFE(梯形AB∥EF)看作是长方形纸片交叉地放置两次，而且AB、AD与面ABCD紧贴，EF、EH与面EFGH说明面ABCD∥面EFGH．同样用长方形ABCD和平行四边形BCGF 紧贴，从而可以检验平面ABFE∥平面DCGH．虽然在平面BCGF和平面ADHE之间有两个长方形ABCD和EFGH．但它们不是交叉放置,所以不能检验平面BCGF与平面ADHE平行．【解析】平面ABCD∥平面EFGH．平面ABFE∥平面DCGH；不对，没有交叉放置．【方法总结】要严格按照检验两个面平行的方法去检验，注意方法中的“交叉〞二字．【例6】从一个棱长10厘米的长方体中挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下的外表积是多少？【解析】(1)如果沿一条棱挖，外表积损失了两侧的两个小正方形 2 2 2 8〔平方厘米〕．就是600 8592(平方厘米)(2)如果沿着某一侧上平行于边挖，外表积增加了210 210 248〔平方厘米〕．总外表积为60032632〔平方厘米〕．(3)如果在某一侧面上斜着挖，外表增加了4个面，其面积为22210248(平方厘米)．总面积是60048=648(平方厘米)．(4)挖通两个对面，外表增加了421022272〔平方厘米〕．总面积为60072672〔平方厘米〕．所以综上所述，剩下的面积有四种情况，分别是592平方厘米、632平方厘米、648平方厘米、672平方厘米．【借题发挥】1.如图，在一个正方体的三个面上分别写上1、2、3．在与这三个面分别平行的面上依次写上4、5、6〔1的对面写4，依次类推〕．与写数字2的面垂直的面上的数字和是多少？1.【答案】与写数字2的面垂直的面上的数字和是14.一个长方体的长是20厘米、宽是10厘米、高是8厘米，从这块木头上切下一个最大的正方体后，剩下局部的外表积是多少平方厘米？【答案】752cm2〔最大的正方体的棱长为8厘米〕【随堂练习】看到图时，小明说，因为平面FGEH和平面ABCD之间有两个长方形：ADEH和BCGF，所以平面FGEH与平面ABCD 是平行的，你认为他说的对吗？为什么？4/72．图中点M、N、Q、P分别是长方体的四条高的中点，与平面MNQP平行的平面有哪些？为什么？3．如何检验文件柜的隔板与隔板相互平行？说出你所用的方法．【答案】1.不对，没有交叉放置．2．平面ABCD、平面EFGH.3．可以用“长方形纸片〞检验文件柜的隔板与隔板是否相互平行.把一长方形硬纸片放在两层隔板之间，按交叉的方向放两次，使纸片的一边都紧贴一块隔板，再观察它的对边，如果对边都能与另一块隔板紧贴，那么这两块隔板平行.【课堂总结】【课后作业】1．如图，在长方体ABCD EFGH中，(1)哪些平面与棱CG平行？(2)哪些平面与平面BDHF垂直？(3)哪些棱与平面DBFH平行？5/7(4)哪些棱与平面DBFH垂直？(5)四边形DBFH是什么四边形？2．(1)如图，把一张长方形纸片ABCD对折，EF为折痕，AB与平面CDEF平行吗？用现成的长方形纸片试试，验证一下你的结论．除了“长方形纸片〞，还有什么形状的“纸片〞也能用来检验直线和平面是否平行？为什么？读一读，想一想：这里介绍一种在平面上表达立体图形的又一个常用方法——“三视图〞法，即从三个方向〔前面、上面和左面〕看一个物体，然后描绘三张所看见的图形来表达这个立体的形状的方法．例如，长方体〔图8 20〕无论从前面、上面和左面，看到的都是长方形，所以它的三视图是图8 21．有一个规那么的立体图形，它的三视图如下列图822所示．想一想，这个立体是什么形状呢？【答案】1.〔1〕平面ABFE、平面ADHE、平面DBFH；〔2〕平面ABCD、平面EFGH；〔3〕棱AE、棱CG；〔4〕没有；〔5〕长方形.2.〔1〕平行；现成的长方形纸片是长方形ABFE；〔2〕梯形、平行四边形，因为它们都是至少有一组对边是平行的.3.圆柱.6/7数学六年级〔下〕沪教版〔长方体的再认识Ⅱ〕教师版7/7。