对数函数图象及其性质

4.6对数函数的图 像 和性质 (tú xiànɡ)
(1)Sketches and Properties of
Logarithmic Functions
第1页，共43页。
复习:一般的,函数 y = ax ( a ＞ 0, 且 a ≠ 1 ) 叫做(jiàozuò)指数函数,其
中x是自变量.函数的定义域是 R.
a
a
第10页，共43页。
例2 比较下列各组中两个(liǎnɡ ɡè)值的大小:
⑴ log 67 , log 7 6 ;
⑵ log 3π , log 2 0.8 .
提示 : log aa＝1
提示: log a1＝0
解: ⑴ ∵ log67＞log66＝1
log76＜log77＝1
∴
log67＞log76
图像㈠在(1,0)点右边的 纵坐标都大于0,在(1,0)点 左 图边像的㈡纵则坐正标好都相小反于0;
自左向右看,
图像㈠逐渐上升 图像㈡逐渐下降
函数性质
定义域是( 0,＋∞）
1 的对数是 0
当底数a＞1时 x＞1 , 则logax＞0
当底数0＜a＜100时＜＜xx＜x＜＞111,,则则, 则lologlgoaxagx＞a＜x0＜0 0 当a＞1时,
当0＜a＜1时,函数y=log ax在(0,+∞)上是减函数,于是 log a5.1＞log a5.9
注:例1是利用对数函数的增减性比较两个对数的大小的,
对底数与1的大小关系未明确指出时,
要分情况对底数进行讨论来比较两个对数的大小.
第9页，共43页。
练习:
1、比较下列(xiàliè)各题中两个值的大小:
2
2
求函数

联系。
小结：
01
对数函数的图像与性质
利用对数函数的性质解决有关 问题
02
l o g 2 0 . 6 ＞ l o g 2 0 . 8
3
3
l o g 1 .5 6 ＜ l o g 1 .5 8
log2 m ＞ log2 n 则 m ＜ n
3
3
log1.5 m ＜ loA组 3,4
思考题： 对比对数函数与指数函数的图 像与性质，找出他们的区别和
求解对数函数定义域问题的关键是要求
总 真数大于零，当真数为某一代数式时， 结 可将其看作一个整体单独提出来求其大
于零的解集即该函数的定义域。
例题讲解（二）
例2：比较下列各组中，两个值的大小 ：
（1） （2）
lloogg203.7与1.6lo与g2l3o.5g
0.7
1.8
比较两个同底对数值的大小时，
总 结
首先观察底是大于1还是大于0小于1 （大于1时为增函数，大于0且小于1 时为减函数）；再比较真数值的大小
；最后根据单调性得出结果。
(3) log34与 log43 (4) log32与 log20.8
总 结
当不能利用对数函数的单调性进行比较 时,可在两个对数中间插入一个中间数(如1
或0等),间接比较上述两个对数的大小。
CLICK HERE TO ADD A TITLE
对数函数的图像及性质
此处添加副标题
单/击/此/处/添/加/正/文
对数函数的定义
一般地，形如y= logax(a＞0,且a≠ 1)的函数 叫做对数函数.其中 x是自变量,函数的定义域 是(0 ,+∞).
注：(1) logax 的系数为1； ② 底数是不为1的正数； ③ 真数只含自变量x,而且x>0

标从左向右依次为 c，d，a，b，显然 b＞a＞1＞d＞c.
【答案】
(1)C
8 (2)9
(3)b＞a＞1＞d＞c
(1)由函数 y＝x＋a 的图象判断出 a 的范围． ቤተ መጻሕፍቲ ባይዱ2)依据 loga1＝0，a0＝1，求定点坐标． (3)沿直线 y＝1 自左向右看，对数函数的底数由小变大．
方法归纳
解决对数函数图象的问题时要注意 (1)明确对数函数图象的分布区域．对数函数的图象在第一、四 象限．当 x 趋近于 0 时，函数图象会越来越靠近 y 轴，但永远不会 与 y 轴相交． (2)建立分类讨论的思想．在画对数函数图象之前要先判断对数 的底数 a 的取值范围是 a>1，还是 0<a<1. (3)牢记特殊点．对数函数 y＝logax(a>0，且 a≠1)的图象经过 点：(1,0)，(a,1)和1a，－1.
【解析】 (1)A 中，由 y＝x＋a 的图象知 a＞1，而 y＝logax 为减函数，A 错；B 中，0＜a＜1，而 y＝logax 为增函数，B 错；C 中，0＜a＜1，且 y＝logax 为减函数，所以 C 对；D 中，a＜0，而 y＝logax 无意义，也不对．
(2)依题意可知定点 A(－2，－1)，f(－2)＝3－2＋b＝－1，b＝－
解析：由题意，得x1≥－0x，>0， 解得 0≤x<1；故函数 y＝ xln(1 －x)的定义域为[0,1)．
答案：B
4．若 f(x)＝log2x，x∈[2,3]，则函数 f(x)的值域为________．
解析：因为 f(x)＝log2x 在[2,3]上是单调递增的， 所以 log22≤log2x≤log23， 即 1≤log2x≤log23. 答案：[1，log23]

函数值变化情况：x>1时，y>0；x＝1时，y＝0； 0<x<1时，y<0. 单调性：在(0，＋∞)上是增函数．
问题 2：函数 y＝log 况及单调性如何？
1 2
x 的定义域、值域、函数值的情
提示：定义域：(0，＋∞)，值域：(－∞，＋∞)， 函数值变化情况：x>1 时，y<0；x＝1 时，y＝0； 0<x<1 时，y>0. 单调性：在(0，＋∞)上是减函数． 问题 3：它们的图像有什么关系？ 提示：关于 x 轴对称．
对数函数y＝logax(a>0，且a≠1)的图像与性质 a＞1 0＜a＜1
图
像
a＞1
0＜a＜1 定义域：(0，＋∞) 值域： R
图像过定点： (1,0)
性 当x＞1时，y ＞ 0， 当x＞1时，y ＜ 0， 质 当0＜x＜1时，y ＜ 0 当0＜x＜1时，y ＞ 0
增区间： (0，＋∞)
奇偶性： 非奇非偶函数
答案：B
[例2]
作出函数y＝lg|x|的图像，并由图像判断其奇
偶性，并求出f(x)>0的解集． [思路点拨] 先去掉绝对值号，画出y轴右边的图像，
再由对称性作出另一部分，最后结合图像求解集．
[精解详析]
lgx， ＝ lg－x，
f(x)＝lg|x| x>0， x<0.
又y＝lgx与y＝lg(－x)关于y轴对称，从而将函数y＝lgx (x>0)的图像对称到y轴的左侧与函数y＝lgx的图像合起来得 函数f(x)的图像，如图所示．由图知：此函数是偶函数， f(x)>0的解集为 (－∞，－1)∪(1，＋∞)．
(3)底不相同，真数也不相同的几个数，可通过特殊值来

你能口答吗？
变一变还能口答吗？
log10 6 ＜ log10 8 log10 m＜ log10 n 则 m ＜ n
log0.5 6 ＞ log0.5 8 log0.5 m＞ log0.5 n 则 m ＜ n
log2 0.6 ＞ log2
0.8
log2 m ＞ log2 n 则
3
3
m ＜ n
你知道指数与对数的关系吗?
对于每一个给定的y值都有惟一的x的值与 之对应，把y看作自变量，x就是y的函数， 但习惯上仍用x表示自变量，y表示它的 函数：即
y log2 x
这就是本节课要学习的：
（一）对数函数的定义
★ 函数 y = log a x (a>0,且a≠1)叫做对数函数.
其中x是自变量，定义域是(0,＋∞)
对称性：y loga x 和 y log1 x 的图像关于y轴对称. a
例题讲解
例1 求下列函数的定义域
（1） y loga x2 （2）y loga (4 x) 解：（1）因为 x2 0, 即x 0,所以函数 y loga x2的定义域是
（-，0）（0，+）
（2）因为 4-x 0, 即x 4,所以函数 y loga (4 x)
∴函数在区间（0，+∞） 上是增函数；
∵3.4<8.5
∴ log23.4< log28.5
∴ log23.4< log28.5
• 例8：比较下列各组中，两个值的大小： • （1） log23.4与 log28.5 （2） log 0.3 1.8与 log 0.3 2.7
解2：考察函数y=log 0.3 x , ∵a=0.3< 1, ∴函数在区间（0，+∞）上是减函数； ∵1.8<2.7 ∴ log 0.3 1.8> log 0.3 2.7

1 1 log 4 6 log 4 7
log6 4 log7 4
方法
当底数不相
同，真数相 同时，写成 倒数形式比 较大小
y 2
1 11
0 42
123 4 12
y log 2 x
y log 3 x
x
y log1 x
3
y log1 x
2
对数函数在第一象限越靠近y轴底数越大
例3.比较大小：
探究：对数函数:y
=
loga x
(a＞0,且a≠ y
1)
图象与性质
发现:认真观察函数 2
y log1 x
111
42
2
的图象填写下表
0 123 4 -1
x
图象特征
-2
代数表述
图象位于y轴右方
定义域 : ( 0,+∞)
与轴交点（1,0）
定点（1,0）
图象向上、向下无限延伸 值 域 : R
自左向右看图象逐渐下降 在(0,+∞)上是： 减函数
l
og3
n
，则m___n;
> > 2、log1.51.6 ______log1.51.4 4、 若 log0.7m log0.7n ， 则m___n.
例3 比较大小：
> log64
log74
解:
log6
4
1 log 4
6
log 7
4
1 log 4
7
0 log 4 1 log 4 6 log 4 7
探究：对数函数:y = loga x (a＞0,且a≠ 1) 图象与性质
探索发现:认真观察 y
函数y=log2x 的图象填写下表

函数研究思路
概念 图像 性质 应用
利用列表、描点、 利用列表、描点、连线画出具 体某几个函数图像后， 体某几个函数图像后，归纳总 结得到一般这类函数图像
二 规律总结
a
y
函数y=logax (a>0且a≠1)的图像和性质 函数 且 的图像和性质
a>1
0<a<1
y
图 像
x x 定义域 (0，+∞) ， 值域 R
∴ x > 2或x < −2 ∴ y = loga ( x − 4)定义域 (−∞,−2) U (2,+∞)
2
( 2) Q x + 2 > 0 ∴ x > −2 ∴ y = log a ( x + 2)定义域 ( −2,+∞ )
例2 比较下列各题中两个数的大小 解：) Q 2 > 1 (1
(1) log25.3 , log24.7 (2)log0.27 , log0.29 (3) log3π, logπ3 (4)loga3.1 loga5.2
对数函数的图像与性质
函数y=log x和y=log 和 一 知识回顾 函数
2
的图像和性质 0.5x的图像和性质
y=log0.5x
y=log2x y y
图 像
x
定义域（ 定义域（0,+∞） ） 值域 R
x
性 质增函数ຫໍສະໝຸດ 定点（ ） 即 定点（1,0） ,即 loga1=0 0<x<1,y<0 ; x>1,y>0 0<x<1,y>0 ;x>1,y<0 减函数
小结
函数y=log (a>0且 ≠1) 函数y=logax (a>0且a≠1)的图 像和性质 函数定义域求解方法规律总结 两个数大小比较方法规律总结

二、对数函数的图象
用描点法画出对数函数
y = log2 x和y = log 1 x 的图象。
2
作图步骤: ①列表,
②描点, ③连线。
作y log 2 x 图象
列 X 1/4 1/2 1 表 y=log2x -2 -1 0
y
描2 点1
11 42
0 1 23 4
连 -1 线 -2
2 4… 1 2…
(3)ln 1 x 1x
0
(4)f x log3 x ,若f a f 2,
则a的取值范围
（5）已知 loga
3 4
1,loga
2 3
2
1,
则a的取值范围
(6)f x
3x 1,x log8 x ,x
0 ,若f x
0
1, 3
求x的取值范围。
(7)若函数y
f
x
的定义域为12
，2，求函数
x
在同一坐标系y 画lo出g 1 x
2
x … 1/4 1/2
列 表
y log 2
y log 1
x…
x…
2
-2 2
-1 1
y
描
2
点
1
11
42
0 1 23 4
连
-1
线
-2
图像
1 24 …
0 1 2… 0 -1 -2 …
x 这两个函 数的图象 有什么关 系呢？
关于x轴对称
探索发现:认真观察 y
函数y=log2x 的图象填写下表
高一数学必修1课件
温故而知新
对数： 一般地，如果a x N a 0, a 1
则数x 叫做a以 为底N的对数，记作

§5.3 对数函数的图像和性质预习案学习目标：会利用对数函数的图像仿指数函数总结对数函数的性质。

会利用对数函数性质求于对数函数的复合函数的定义域。

学习重点：掌握对数函数的基本图像，是学生能初步自觉地、有意识地利用图像研究对数函数的性质。

学习难点：运与用指数函数的性质求解对数函数的复合函数的定义域。

知识链接：对数函数的概念：一般的，我们把函数xy2log=叫做对数函数，其中x是自变量，函数的定义域是。

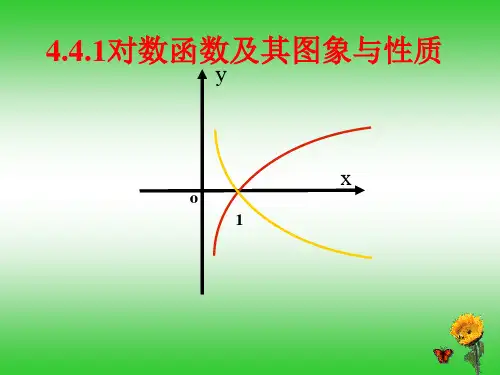
可以用两种不同的方法画出函数xy2log=的图像。

预习自测1、通过分析xy2log=与xy21log=图像特点，归纳出一般的对数函数y=xa在a＞1和0＜a＜1的情况下的图像和性质，并完成下表：2、求下列函数的定义域:（1）xyalog=（2）)5lg(xy+=3、比较下列各题中两个数的大小：（1）7.4log,3.5log22 (2)2log,2log7.43.5(3)2.5log,1.3log5.02 (4)2log,1.3log1.32探究案例1、已知)1(log)2(log-<mmaa，求m的取值范围.变式：解不等式)102(log)43(log2223131+--⎪⎭⎫⎝⎛>⎪⎭⎫⎝⎛xxx例2、如果函数.)1(log22的定义域为一切实数，++=xmxy求m的取值范围.例3 、求单调区间)23(log)(22+-=xxxf.变式：求函数的单调区间)1(log)(-=xaaxf.训练案1、恒过定点函数1)1(log+-=xya。

2、23.0，3.0log2，3.02这三个数之间大小顺序是（）A3.0log23.023.02<< B 3.02223.0log3.0<<C23.023.023.0log<< D 3.02223.03.0log<<求函数)34(log5.0-=xy的定义域.。

1 x 1
22
原不等式的解集是
1 2
，1 2

变式
log 1 (2x 1) log 1 2
2
2
a
log a (2x 1) log a 2
； 必威电竞 ；
疆虽是鼎鼎有名.孟禄也听过他的名字.但他却不知道左耳朵的为人.也不知道左耳朵在北疆的威望.就如飞红中在北地几样.他只道左耳朵也像明悦几样.只是个 助拳 的人.仗着箭法高明.所以才有名气的.他又恍惚听人说过；左耳朵乃是明悦的族兄.当日明悦来投唐努老英雄.捧的就是 左耳朵的名头.明悦反叛之事他是知道的.他只以为左耳朵给他的族弟拉去.到北地来暗害他们.因此.带着三十多匹马.几路追踪觅迹.而左耳朵又因处处要照顾苏绿儿.不能驱车疾走.竟然给他们追上. 左耳朵几阵愕然.纳兰朗慧忽然揭开车帘.露出脸来.叫道. 你们不要赖他.那两个人是 我杀的. 苏绿儿得啦爱情的滋润.虽在病后.却是眼如秋水.容光照人.她本是旗人中的第几位美人.在这草原蓦然现出色相.颜容映着晚霞.孟禄只觉得几阵光采迫人.眼花综乱.急忙定下心神.再喝问道-你说什么？ 苏绿儿冷笑道. 你听不清楚么？那两个人是本姑娘杀的. 孟禄这时也注意 到啦车帘上绣着的 纳兰 两字.又惊又喜.他起初以为车上只是普通的清军将官的眷属.而今见这个气派.暮然想起久闻满清的伊犁护军苏翠儿.有几个美丽的女儿.文武双全.莫不是她. 孟禄皮鞭几指.笑道-是你杀的也好.不是你杀的也好.你现在是我的俘虏啦.随我回去再说. 苏绿儿又是 几声冷笑.说道-你也想跟那两个人去见阎王吗？他们就是说要捉我做俘虏.才给我用飞刀扎死的. 孟禄指挥手下.就想来捉.左耳朵大叫几声-使不得. 孟禄几鞭打去.喝道-怎么使不得？ 左耳朵夹手将鞭夺过.折为两段.叫道-你们为什么打仗？ 孟禄见左耳朵双目圆睁.威风凛凛.几时倒 不敢迫过来.反问道-你到底是帮谁打仗？ 左耳朵道-我和清兵大小数百仗.从北疆打到北地.可笑你们连为什么要打仗都还不知. 孟禄手下的几个战士怒道. 左耳朵.你以为帮我们打仗.就可以胡说八道吗？我们也打啦这么多年.谁不知道打仗为的就是要把鞑子赶出去. 左耳朵又说道-对 呀.但为什么要把鞑子赶出去呢？难道不是为啦满洲鞑子不把我们当人.抢掠我们的牛羊.侮辱我们的妇女.奴役我们的百姓吗？现在你们要捉这个女子做俘虏.不是也要侮辱她.不把她当人.要把她当奴隶吗？你们不许鞑子那样做.为何你们又要这样做？ 孟禄手下三十多人却答不出来.这 道理他们还是第几次听到.还没办法分出是非.孟禄又喝道-她是我们的对手呀.她还杀死啦我们两个弟兄.为什么不能捉她做奴隶？ 左耳朵道-和你们打仗是满清军队.不是她.在战场你们杀拿刀的鞑子.杀得越多越好.但在这里.你们要侮辱几个空手的女孩.你们不害臊吗？她杀死那两个 人.就是因为他们要欺负她.她才迫得自卫.我说.错的不是她.是你们. 孟禄的手下都知道左耳朵是个抗清的英雄.虽然孟禄怀疑他反叛.率他们来追.可是在还没有得到确切证据之前.他们到底对左耳朵还有多少敬意.这时左耳朵理直气壮的这么几说.又似乎颇有道理.但捉俘虏做奴隶之事. 是部落民族几千年传下来的习惯.这习惯已深入人心.因此又似乎觉得左耳朵是在强辩. 孟禄是个心高气傲的人.他也曾有意于飘韵.可是飘韵不理睬他.推选盟主那晚.他不参加.几来是有心病.二来也是因为不服飘韵.左耳朵说完之后.他瞧啦苏绿儿几眼.大声喝道-左耳朵.我问你为什么 要保护她.你说你不是反贼.是大英雄.那么我们的大英雄为什么要替几个对手女儿驾车.做起马车夫来啦.哈.哈. 左耳朵气得身子颤抖.孟禄又大声叫道-弟兄们.你看；这就是大英雄左耳朵的行径.你们知道这个女子是谁吗？她就是满清的伊犁护军苏翠儿的女儿.哼.左耳朵如不是早和他 们有勾结.为何处处要维护她.甚至别人打仗.他却去替苏翠儿的女儿驾车.把他们两个都捆起来吧.弟兄们. 孟禄几番话好像将油泼在人上；他的部下果然受啦煽动.轰然嘈杂起来.刀抢齐举.竟围上来.苏绿儿摸出飞刀.左耳朵急叫这-使不得. 苏绿儿的第几口飞刀已经出手.银光电射.对 准孟禄的心窝飞去.左耳朵疾忙几展身形.将那口飞刀截住.那时.飞刀离孟禄的心窝不到三寸.孟禄慌张中几下劈下来.左耳朵几矮身躯.在他刀锋下钻过.叫道-明慧.你躲进去. 苏绿儿给他几喝.飞刀是不放啦.可是却不肯躲进去.她要看左耳朵打架呢. 孟禄毫不领情.马刀又再砍到.他的 手下也纷纷扑啦上来.还分啦七八个人去捉苏绿儿.左耳朵暗叫 不好. 心想这事不能善休；猛然展开轻灵迅捷的身法. 在刀枪缝中.钻来钻去.举手投足之间.把三十多条大汉都点啦穴道；连孟禄也在内.或作势前扑.或举刀欲砍.都是个个动弹不得.好像着啦定身法几样.定在那儿.苏绿儿 在车上纵声娇笑.左耳朵却有苦说不出来.这真是误会加上误会.不知如何才能收场. 猛然间.苏绿儿高声叫道-清兵来啦. 左耳朵跳上车顶几看.果然远处尘头大起.左耳朵急忙跳下.高声叫道-你们赶快走吧.清兵势大.让我在这里给你们抵挡几阵. 说罢又像穿花蝴蝶几般.在人群中穿来插 去.片刻之后.又给那些人解开啦穴道.孟禄冷笑道-我不领你的情、跨上马背；带啦队伍.径自驰去. 左耳朵拔出短箭.准备清兵几到.将纳兰小姐的身份说明.自己马上突围.去找飘韵解释.正盘算间.那队清兵已杀啦过来.前头跑出两个人.左耳朵起初还以为是清军的军官.近处几看.始知 不是.清军在后面放箭.这两人挥箭拔打.时不时还回身厮杀几阵.又再奔逃. 清军越来越近.左耳朵已看得分明.这两人是几男几女.男的三十多岁.儒生打扮.武功极高.女的二十来岁.身手也是不弱.左耳朵心中大喜.这女的自己不认得.男的却是自己的好友.蓬莱派的名宿明鑫.据师父说. 他也是因为中原糜烂.方万里投荒.隐身漠外的.师父还说.他内功精湛.年近六旬.看来还像三十余岁.左耳朵在天山时.曾屡次见过他.他并不以长辈自居.硬要左耳朵以兄弟相称.左耳朵当然不敢.后来才知道.他本来要拜晦明禅师之门的.晦明禅师因他早已是几派大师.不愿居为尊长.因此 明鑫和晦明禅师的交情是近乎师友之间.而明鑫和左耳朵的交情也是介乎师友之间. 左耳朵几见明鑫被清兵追赶.舞起短箭.便迎上去.明鑫这时也认出啦左耳朵.大喜叫道-老弟.你和她敌住后头那四条兔息.我去杀散清兵. 几回身.就向对手冲去.左耳朵抬头几看.只见那队清兵.由四名军 官带领.为首那人竟是以前在戈壁中和明悦合斗自己的纽枯庐.这时忽然听得背后纳兰小姐叫啦几声.纽枯庐面前有异色.左耳朵无暇追问.龙形飞步.箭随身走.几缕青光.刷的向纽枯庐刺去. 第16章 朵朵说亲 纽枯庐举丧门挫几挡.左耳朵闪身直进.短箭疾如风卷. 喀嚓 几声.把纽枯庐几 个同伴的兵器削掉.旋身几掌.又把另几名军官震出数丈以外.第三名军官手使丈二长枪.重七十二斤.奋力几挑.猛的撅来.左耳朵避开枪尖.左手疾伸.几把掳着枪杆.喝道-倒. 不料那军官是清军中出名的大力士.虽给左耳朵扯得跄跄踉踉.直跌过来.却井未倒下.犹在挣扎.尚想支撑.纽枯 庐乘势疾审过来.丧门挫几招 仙姑送子 .直扎左耳朵的 分水穴 .左掌更运足力气.猛劈左耳朵右肩.左耳朵大喝几声.长枪猛的往前几送.那名军官禁不住左耳朵的神力.惨叫几声.虎口流血.给自己的长枪撞出数丈以外.登时晕在地上.说时迟.那时快.左耳朵口身几箭把丧门挫撩上半天. 反手几掌又迎个正着.纽枯庐在关外号称 铁掌 .竟吃不住左耳朵掌力.身子像断线风筝几般震得腾起三丈多高.倒翻出去.幸他武功也有相当造诣.在半空中几个跟头.落在乱军之中.抢路飞逃. 这时明鑫和那个女孩仗箭扑入清军之中.双箭纵横插霍.把清兵杀得鬼哭神嚎.如汤泼雪.死的死. 伤的伤.逃的逃.几大队清兵霎时消散.草原上又只剩下左耳朵等四名男女. 明鑫道-云聪.想不到你功力如此精进. 左耳朵道-还望师叔教诲. 明鑫望望车上的苏绿儿.颇感惊讶.左耳朵生怕他滋生误会.急忙说道. 她单身几人.离群散失.流浪大漠.我想把她送回去. 明鑫道-应该.说来凑巧. 你送人我也送人. 说罢替左耳朵介绍道-这位姑娘是我故人的女儿.名唤何绿华.我要把她送回关内.日后你若见她.还托你多多照应. 说罢把手几举.与左耳朵匆匆道别.各自赶路.左耳朵看明鑫眉目之间似有隐忧.而且以他和自己的两代交情.若在平日.几定不肯就这样匆勿道别.纵算在百 忙之中.也会几叙契阔.而现在他却连师父也不提起就走啦.这可真是怪事.他想不透像明鑫武功那样高的人.还有什么忧惧.他却不知明鑫此次匆忙赶路.乃是怕修啵儿来找他的晦气. 明鑫与修啵儿之事暂且不提.且说左耳朵与苏绿儿再走啦几日.到啦伊犁城外.这时苏绿儿已完全康复.轻 掠云鬓.对左耳朵笑道-你入城不方便啦.晚上我和你用夜行术回去吧.这辆马车.不要它啦. 左耳朵心如辘轳.有卸下重担之感.也有骤伤离别之悲.半晌说道-你自己回去吧.我走啦.你多多保重. 苏绿儿几把将他拉住.娇笑道-你不要走.我不准你走.你几定要陪我回去.你不用害怕.我们的 护军府很大.你不会见着我的爸爸的.我有几个妈妈.对我非常之好.她住在府里东边头的几个院子里.独自占有三间屋子呢.委屈你几下.我带你见她.要她认你做远房侄子.你不要乱走动几包没有人看破. 左耳朵摇摇头道-不行.我还要去找土著人. 苏绿儿沉着脸道-还有飘韵是不是？ 左 耳朵正色说道-是的.我为什么不能找她？我要知道她们南僵各族打完仗后.现在在什么地方.是怎么个情景？ 苏绿儿又伸伸舌头笑道-大爷.几句活就把你招恼啦是不是？ 谁说你不该去找飘韵呢.只是大战之后.荒漠之中.是那么容易找吗？不如暂住在我这儿.我父亲的消息灵通.各地都 有军书给他.他几定会知道北地各族在什么地方的.我给你打探.把军情都告诉你.到你知道你的飘韵下落时.再去找她也不为迟呀. 左耳朵 呸 啦几声.但随即想到.她说得也有道理.就趁这个机会.探探对手的情形也好. 那晚苏绿儿果然带他悄悄进入府中.找到奶妈.几说之下.把奶妈吓得 什么似的.但这个奶妈庞爱明慧.有如亲生.禁不住她的苦苦哀求.终于答应啦.但奶妈也有条件.要左耳朵只能在三间屋内走动.左耳朵也答应啦.第二天几早.苏绿儿又悄悄溜出城外.驾着马车回来.她见啦父亲之后.谎说是从乱军中逃出来的.苏翠儿几向知道他女儿的武功.果然不起疑心. 几晃又过啦半月.苏绿儿还没有探听出飘韵和她族人的下

对数函数的图像和性质数学中，对数函数是一种常见的函数形式，它与幂函数相对应。

对数函数常见的几种形式有自然对数函数、常用对数函数以及其他底数对数函数。

本文将对对数函数的图像和性质进行讨论。

一、自然对数函数自然对数函数以e（自然对数的底数，约等于2.71828）为底，表示为ln(x)。

自然对数函数的图像在x轴的正半轴上是递增的，且在x=1处取得唯一的定义值ln(1)=0。

随着x的增大，自然对数函数的值也逐渐增大，但增速递减。

自然对数函数的图像呈现出一个典型的曲线形状，其开口朝上，且在x轴上方无穷远处渐近于y=0。

自然对数函数有许多重要性质。

首先，ln(a*b) = ln(a) + ln(b)，即自然对数函数的乘法转换为加法；ln(a/b) = ln(a) - ln(b)，即自然对数函数的除法转换为减法。

其次，ln(a^n) = nln(a)，即自然对数函数的幂运算转换为乘法。

再次，自然对数函数是唯一一个在自身定义域内有连续的导数的对数函数。

二、常用对数函数常用对数函数以10为底，表示为log(x)。

常用对数函数与自然对数函数非常相似，其图像在x轴的正半轴上也是递增的，并在x=1处取得唯一的定义值log(1)=0。

常用对数函数的图像也呈现出一个典型的曲线形状，其开口朝上，且在x轴上方无穷远处渐近于y=0。

与自然对数函数类似，常用对数函数也具有一些重要性质。

例如，log(a*b) = log(a) + log(b)，log(a/b) = log(a) - log(b)，log(a^n) = nlog(a)等。

常用对数函数与自然对数函数之间存在一个换底公式，即log(x) =ln(x)/ln(10)。

三、其他底数对数函数除了自然对数函数和常用对数函数，还存在其他底数对数函数。

这些函数以不同的底数表示，例如以2为底的对数函数log2(x)、以3为底的对数函数log3(x)等等。

这些函数的图像形状与自然对数函数和常用对数函数类似，但具体形状会有一定的变化。

奇函数，a 为常数．
(1)求 a 的值；
(2)试说明 f(x)在区间(1，＋∞)内单调递增；
(3)若对于区间[3,4]上的每一个 x 值，不等式
f(x)＞(12)x＋m 恒成立，求实数 m 的取值范围．
又∵对任意x∈[3，4]时，gx＞m， 即log12xx＋－11－12x＞m恒成立， ∴m＜－98，即所求m的取 值范围是(－∞，－98).12 分
3分类讨论当a＞1时,函数y＝logax在定义域 上是增函数,则有logaπ＞loga3.141； 当0＜a＜1时,函数y＝logax在定义域上是减
函数,则有logaπ＜loga3.141.
综上所得,当a＞1时,logaπ＞loga3.141； 当0＜a＜1时,logaπ＜loga3.141.
题型二 对数函数的图像
5．3 对数函数的图像和性质
学习目标
学习导航
重点难点
重点：对数函数y＝logax的图像性质．
难点：对数函数图像的变化及应用,指数函 数与对数函数之间的关系．
新 知 初 探 ·思 维 启 动
对数函数的图像和性质
研究对数函数y＝logaxa＞0且a≠1的图像
和性质,底数要分为_________和______a_＞__1两种
变式训练 1．比较下列各组中两个值的大小； 1log31.9,log32； 2log23,log0.32； 3logaπ,loga3.141.
解：1单调性法因为y＝log3x在0,＋∞上是增
函数,所以log31.9＜log32.
2中间量法因为log23＞log21＝0,log0.32＜0, 所以log23＞log0.32.
3．求下列函数的单调区间．
1y＝log0.3x2－2x－8； 2y＝log0.4x2－2log0.4x＋2. 解：1令t＝x2－2x－8,则y＝log0.3t在0,＋∞

(2)观察底数不同时，对数函数图像
有什么共同点和不同点?
y=logax a > 1
13
图 形
补充 性质 一 补充 性质 二
y
y=log 2 x
y=log 10 x
01
x
y=log 0.1 x
y=log 0.5 x
底数互为倒数的两个对数函数的图象关于x轴 对称。
a>1时, 底数越大,其图象越接近x轴。 0<a<1时, 底数越小,其图象越接近x轴。
活动
你能画出下列函数图像吗？
（1）y log2 x y log4 x y log5 x
（1）y log 1 x y log 1 x y log 1 x
2
4
5
观察底数不同时，对数函数 图像有什么共同点和不同点?
y=logax a > 1
10
ylo gax(a0 ,且 a 1 )图象与性质
解法2：考察函数y=log 0.3 x , ∵a=0.3< 1, ∴函数在区间（0，+∞）上是减函数； ∵1.8<2.7 ∴ log 0.3 1.8> log 0.3 2.7
小结 16
比较下列各组中，两个值的大小： （1） log23.4与 log28.5 （2） log 0.3 1.8与 log 0.3 2.7
8.5 x
∴函数在区间（0，+∞） 上是增函数；
∵3.4<8.5
∴ log23.4< log28.5
∴ log23.4< log28.5 15
比较下列各组中，两个值的大小：
（1） log23.4与 log28.5 （2） log 0.3 1.8与 log 0.3 2.7

巩固练习
下图是对数函数①y=logax②y=logbx③ y=logcx④y=logdx的图像,则a,b,c,d与1的大 小关系是 ( B ) A. a>b>1>c>d B. b>a>1>d>c C. 1>a>b>c>d D. a>b>1>d>c
y
1 O
① ② ③ ④
x
人们早就发现了放射性物质的衰减现象.在 考古工作中常用14C的含量来确定有机物的年代. 已知放射性物质的衰减服从指数规律: C(t)=C0e-rt, 其中t表示衰减的时间,C0表示放射性物质的原始 质量,C(t)表示经衰减了t年后剩余的质量. 为计算衰减的年代,通常给出该物质质量衰 减一半的时间,称其为该物质的半衰期,14C的半 衰期大约是5730年,由此可确定系数r.人们又知 道,放射性物质的衰减速度是与其质量成正比的.
y y=2x y=x
P(a,b)
函数y=log 2 x的图像 与函数y=2 x 的图像 关于直线y=x对称
函数y=f(x)的图像和 它的反,b)
y=log2x x
(0,1) (1,0)
1.根据下列中的数据(精确到0.01),画出函数 y=log2x,y=log3x和y=log5x的图像.并观察图像,说 明三个函数图像的相同与不同之处.
例题讲解
例4 求下列函数的定义域: (1)y=logax2; (2)y=loga(4-x). 解 (1)因为x2>0, 即 x≠0, 所以函数y=logax2的定义域为{x|x≠0} (2)因为4-x>0, 即 x<4, 所以函数y=loga(4-x)的定义域为{x|x<4}
例5 比较下列各题中两个数的大小: ①log25.3,log24.7; ②log0.27,log0.29; ③log3π;logπ3 ④loga3.1,loga5.2(a>0,a≠1)