下载文档原格式
幂函数•冥函数的定义：一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数。
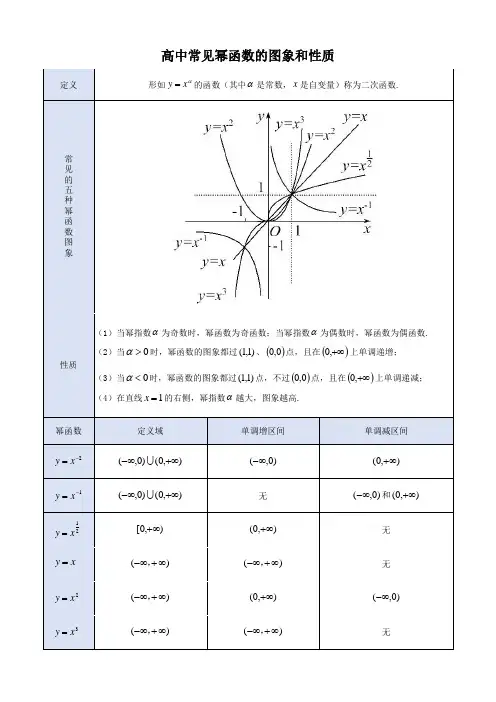
幂函数的解析式：y=xα幂函数的图像：•幂函数图像的性质：所有幂函数在(0，+∞)上都有定义．①α＞0，图像都过定点（0，0）和（1，1）；在区间（0，+∞）上单调递增；②α＜0，图像都过定点（1，1）；在区间（0，+∞）上单调递减;③当O<a<l时，曲线上凸，当a>l时，曲线下凸．④当a=l时，图象为过点(0，0)和(1，1)的直线．⑤当a=0时，表示过点(1，1)且平行于x轴的直线(除去点(0，1)) 。
幂函数图象的其他性质：(1)图象的对称性：把幂函数的幂指数a（只讨论a是有理数的情况）表示成既约分数的形式（整数看作是分母1的分数），则不论a>0还是a<0，幂函数的图象的对称性用口诀记为：“子奇母偶孤单单；母奇子偶分两边；分子分母均为奇，原点对称莫忘记”，(2)图象的形状：①若a>0，则幂函数的图象为抛物线形，当a>l时，图象在[0，+∞）上是向下凸的（称为凸函数）；当O<a<l时，图象在[o，+∞）上是向上凸的（称为凹函数）．②若a<0，则幂函数y=x“的图象是双曲线形，图象与x轴、y轴无限接近，在(0，+∞)上图象都是向下凸的。
幂函数的单调性和奇偶性：对于幂函数（a∈R)．(1)单调性当a>0时，函数在第一象限内是增函数；当a<0时，函数在第一象限内是减函数．(2)奇偶性①当a为整数时，若a为偶数，则是偶函数；若a为奇数，则是奇函数。
②当n为分数，即（p，q互素，p，q∈Z）时，若分母q为奇数，则分子p为奇数时，为奇函数；分子p为偶数时，为偶函数，若分母q为偶数，则为非奇非偶函数．。
1 3.3幂函数
一、幂函数定义及解析式特点
1.定义：一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数。
2.解析式特点：①系数为1；②底为自变量；③指数为常数。
3.幂函数的指数除了可以取整数外，还可以取其他实数。
二、幂函数的图象
1.幂函数主要以11,2,3,,12
α=-为代表，来研究掌握0α<,01α<<,1α>时的大致图象和图象的性质。
2.同一坐标系中画出1232
,,,y x y x y x y x ====和1y x -=的图象，如下图：
三、幂函数图象特点
1.根据幂函数y x α=的图象可得到以下结论： （1）幂函数在()0,+∞都有定义，且都过()1,1点，不一定过()0,0点。
（2）幂函数都过第一象限，不过第四象限；
（3）当0α>时，在第一象限都是增函数；当0α<时在第一象限都是减函数。
2.（1）当0α<时，幂函数在第一象限是减函数，且和1y x
=在第一象限的图象 大致相同；
（2）当0α>时，函数在第一象限是增函数，且在第一象限的大致图象的特点 可细分为两种情况：
①01α<<时,幂函数的图象在第一象限“趴着增”,且在()0,1内，图象在直 线y x =的上方增,在()1,+∞图象在直线y x =的下方增。
②1α>时,幂函数的图象在第一象限“竖着增”,且在()0,1内,图象在直线。
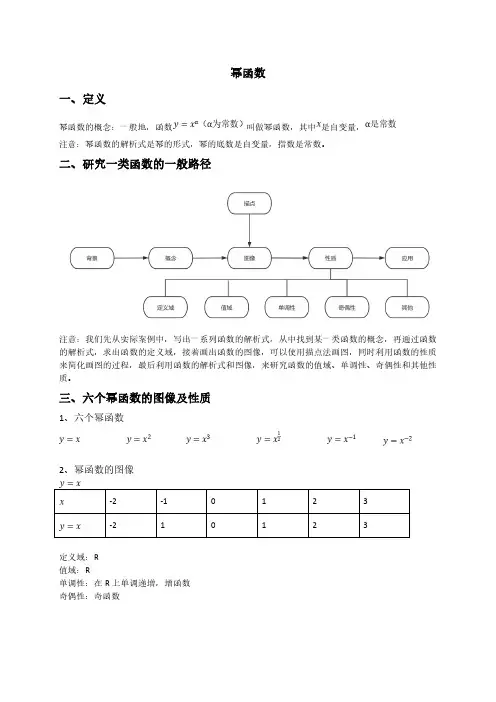
幂函数一、定义幂函数的概念：一般地，函数叫做幂函数，其中是自变量，注意：幂函数的解析式是幂的形式，幂的底数是自变量，指数是常数。
二、研究一类函数的一般路径注意：我们先从实际案例中，写出一系列函数的解析式，从中找到某一类函数的概念，再通过函数的解析式，求出函数的定义域，接着画出函数的图像，可以使用描点法画图，同时利用函数的性质来简化画图的过程，最后利用函数的解析式和图像，来研究函数的值域、单调性、奇偶性和其他性质。
三、六个幂函数的图像及性质1、六个幂函数2、幂函数的图像-2-10123-21123定义域：R 值域：R单调性：在R 上单调递增，增函数奇偶性：奇函数严禁复制-2-1012341149定义域：R 值域：单调性：在上单调递减，减函数，在上单调递增，增函数奇偶性：偶函数-2-10123-8-11827定义域：R 值域：R单调性：在R 上单调递增，增函数奇偶性：奇函数严禁复制124 012定义域：值域：单调性：在上单调递增，增函数奇偶性：非奇非偶函数严禁复制-2122定义域：值域：单调性：在上单调递减，减函数奇偶性：奇函数-2124定义域：值域：单调性：在上单调递减严禁复制奇偶性：偶函数从以上函数分析中，我们得到了6个幂函数的图像总结：6个幂函数具有的共同性质和不同性质1、函数的图像都经过。
2、函数在区间上单调递增，是增函数。
函数和严禁复制在区间上单调递减，是减函数。
在区间上单调递增，是增函数。
和在是单调递减，是减函数。
3、函数、和是奇函数，函数和是偶函数，函数是非奇非偶函数。
4、函数的图像经过原点，函数和的图像不经过原点。
5、已知幂函数，当时，函数在区间上单调递增，当时，函数在区间上单调递减。
四、题型1、幂函数的概念例题1已知幂函数f(x)过点，则f(9)的值为（）（解析）设幂函数，因为过点，所以，解得a=，所以f(9)=。
例题2已知函数f(x)=为幂函数，则f()+f()=（）（解析）因为函数f(x)=为幂函数，所以m-1=1，解得m=2，所以f(x)=，又因为函数f(x)为奇函数，有f()+f()=0。
幂函数的图像与性质一: 核心梳理、茅塞顿开1．根式（1）根式的概念（2）．两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a aa nn ；②a a nn =)(（注意a 必须使n a 有意义）。
2．有理数指数幂 （1）幂的有关概念 ①正数的正分数指数幂:0,,1)mnaa m n N n *=>∈>、且;②正数的负分数指数幂: 10,,1)m nm naa m n N n a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没有意义.注：分数指数幂与根式可以互化，通常利用分数指数幂进行根式的运算。
（2）有理数指数幂的性质①a r a s =a r+s (a>0,r 、s ∈Q);②(a r )s =a rs (a>0,r 、s ∈Q); ③(ab)r =a r b s (a>0,b>0,r ∈Q);.n 为奇数 n 为偶数例2 （1）计算：25.02121325.0320625.0])32.0()02.0()008.0()945()833[(÷⨯÷+---；（2）化简：5332332323323134)2(248aa a a ab aaab b ba a ⋅⋅⨯-÷++--变式：（2007执信A ）化简下列各式（其中各字母均为正数）:（1）;)(65312121132b a ba b a ⋅⋅⋅⋅--（2）.)4()3(6521332121231----⋅÷-⋅⋅b a b a b a(3)100.256371.5()86-⨯-+（三）幂函数 1、幂函数的定义形如y=x α（a ∈R ）的函数称为幂函数，其中x 是自变量，α为常数注：幂函数与指数函数有本质区别在于自变量的位置不同，幂函数的自变量在底数位置，而指数函数的自变量在指数位置。
例题、(1). 下列函数中不是幂函数的是（ ）A．y = B ．3y x = C ．2y x = D ．1y x -=答案：C例2．已知函数()()2531m f x m m x --=--，当 m 为何值时，()f x ：（1）是幂函数；（2）是幂函数，且是()0,+∞上的增函数；（3）是正比例函数；（4）是反比例函数；（5）是二次函数；简解：（1）2m =或1m =-（2）1m =-（3）45m =-（4）25m =-（5）1m =- 变式训练：已知函数()()2223m m f x m m x--=+，当 m 为何值时，()f x 在第一象限内它的图像是上升曲线。
第15讲幂函数及其性质【知识点梳理】（1）幂函数的定义：一般地，()a y x a R =∈(a 为有理数)的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数.（2）幂函数的特征：同时满足一下三个条件才是幂函数①a x 的系数为1；②a x 的底数是自变量；③指数为常数.（3）幂函数的图象和性质常见的幂函数图像及性质：（4对幂函数性质的综合考查，主要体现为单调性、奇偶性，处理时要以常见的具体幂函数的图象和性质1.幂函数的单调性：在区间(0,)+∞上，当0α>时，y x α=是增函数；当0α<时，y x α=是减函数.2.幂函数的奇偶性：令qpα=（其中,p q 互质，*,,1p q N p ∈>）.（1）若p 为奇数，则q py x =的奇偶性取决于q 是奇数还是偶数.当q 是奇数时，q py x =是奇函数；当q 是偶数时，q py x =是偶函数.（2）若p 为偶数，则q 必是奇数，此时qpy x =既不是奇函数，也不是偶函数.1.幂函数的凸性1.上凸函数、下凸函数的定义：设函数(x)f 在[,]a b 上有定义，若对[,]a b 中任意不同两点121212()(),,()22x x f x f x x x f ++≥都成立，则称()f x 在[,]a b 上是上凸的函数，即上凸函数.设函数()f x 在[,]a b 上有定义，若对[,]a b 中任意不同两点121212()(),,()22x x f x f x x x f ++≤都成立，则称()f x 在[,]a b 上是下凸的函数，即下凸函数.这个定义从几何形式上看就是：在函数()f x 的图象上取任意两点，如果函数图象在这两点之间的部分总在连接这两点的线段的上方，那么这个函数就是上凸函数；如果函数图象在这两点之间的部分总在连接这两点的线段的下方，那么这个函数就是下凸函数.根据函数图象判断，一般开口向下的二次函数是上凸函数，开口向上的二次函数是下凸函数.2.幂函数的凸性（1）幂函数,(0,)y x x α=∈+∞，在1α>时，函数是下凸函数；（2）幂函数y x α=，(0,)x ∈+∞，在01α<<时，函数是上凸函数；（3）幂函数,(0,)y x x α=∈+∞，在0α<时，函数是下凸函数.【典型例题】题型一幂函数的概念【例1】在函数21y x=，22y x =，2y x x =+，1y =中，幂函数的个数为（）A ．0B ．1C ．2D ．3【例2】已知()21212223m y m m x n -=+-⋅+-是幂函数，求m 、n 的值．【题型专练】1．现有下列函数：①3y x =；②12xy ⎛⎫= ⎪⎝⎭；③24y x =；④51y x =+；⑤()21y x =-；⑥y x =；⑦(1)x y a a =>，其中幂函数的个数为（）A ．1B ．2C ．3D ．42.已知函数()()()2211 nn f x n n xn Z -+=--∈为幂函数，则()2f =___.3.已知y ＝(m 2＋2m －2)22m x-＋2n －3是幂函数，求m ，n 的值．题型二：幂函数的三要素【例1】幂函数a y x =中a 的取值集合C 是11,0,,1,2,32⎧⎫-⎨⎬⎩⎭的子集，当幂函数的值域与定义域相同时，集合C 为（）A ．11,0,2⎧⎫-⎨⎬⎩⎭B ．1,1,22⎧⎫⎨⎬⎩⎭C ．11,,32⎧⎫-⎨⎬⎩⎭D ．1,1,2,32⎧⎫⎨⎬⎩⎭【例2】已知幂函数()22333mm y m m x--=-+的图象不过原点，则实数m 的取值可以为（）A ．5B ．1C ．2D ．4【题型专练】1.若函数()f x 是幂函数，满足(4)8(2)f f =，则1(1)3f f ⎛⎫+= ⎪⎝⎭_________．2.已知幂函数()f x 的图象经过点22,2⎛⎫⎪ ⎪⎝⎭，则()4f 的值为___．3.设α∈11,132⎧⎫-⎨⎬⎩⎭，，，则使函数y ＝x α的定义域为R 的所有α的值为（）A ．1,3B ．－1,1C ．－1,3D ．－1,1,3题型三：幂函数的性质【例1】幂函数()()2231mm f x m m x+-=--在x ∈（0，+∞）上是减函数，则m ＝（）A ．﹣1B ．2C ．﹣1或2D ．1【例2】幂函数2225()(5)m m f x m m x +-=+-在区间(0,)+∞上单调递增，则(3)f =（）A ．27B ．9C ．19D ．127【例3】已知幂函数()f x 的图象经过点()9,3，则（）A ．函数()f x 为增函数B ．函数()f x 为偶函数C ．当4x ≥时，()2f x ≥D ．当210x x >>时，()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭【例4】已知幂函数()()231mf x m m x =--在其定义域内不单调，则实数m =（）A ．23-B ．1C ．23D ．1-【例5】若幂函数()()223,p p f x qx q R p Z -++=∈∈在()0,∞+上是增函数，且在定义域上是偶函数，则p q +=（）A ．0B ．1C ．2D ．3【题型专练】1．若幂函数()()215m f x m m x -=+-在()0,∞+上单调递减，则m =（）A ．3-或2B ．2C ．3-D ．2-2．已知幂函数()()()224210,m m f x m x ∞-+=-+在上单调递增，则m =（）A ．0B ．13-C ．103-或D ．106-或3．已知幂函数()y f x =的图象过点24⎛ ⎝⎭，则下列关于()f x 说法正确的是（）A ．奇函数B ．偶函数C ．在(0,)+∞单调递减D ．定义域为[0,)+∞4.已知幂函数()223()pp f x x p N --*=∈的图像关于y 轴对称，且在()0+∞，上是减函数，实数a 满足()()233133pp aa -<+，则a 的取值范围是_____．5．写出一个具有性质①②③的函数()f x =______．①()f x 定义域为{}0x x ≠；②()f x 在(),0∞-单调递增；③()()()f ab f a f b =⋅．题型四：幂函数的图象【例1】幂函数a b c d y x y x y x y x ====，，，在第一象限的图像如图所示，则a b c d ，，，的大小关系是（）A ．a b c d >>>B ．d b c a >>>C ．d c b a>>>D ．b c d a>>>【例2】已知幂函数()f x 的图象为曲线C ，有下列四个性质：①()f x 为偶函数；②曲线C 不过原点O ；③曲线C 在第一象限呈上升趋势，④当1≥x 时，()1f x ≥.写出一个同时满足上述四个性质中三个性质的一个函数()f x ___________.【例3】如图所示是函数m ny x =(*N m n ∈、且互质)的图象，则（）A ．m n 、是奇数且1m n<B ．m 是偶数，n 是奇数，且1m n>C ．m 是偶数，n 是奇数，且1m n<D ．m n 、是偶数，且1m n>【题型专练】1．图中1C ，2C ，3C 分别为幂函数1y x =α，2y x =α，3y x α=在第一象限内的图象，则1α，2α，3α依次可以是（）A.12，3，1-B ．1-，3，12C ．12，1-，3D ．1-，12，32.幂函数1y x -=，及直线,1,1y x y x ===将直角坐标系第一象限分成八个“卦限：I, II, III,IV, V, VI, VII, VIII （如图所示），那么，而函数13y x -=的图象在第一象限中经过的“卦限”是（）A ． IV,VIIB ． IV,VIIIC ． III, VIIID ． III, VII3．在同一直角坐标系中，二次函数2y ax bx =+与幂函数(0)ba y x x =>图像的关系可能为（）A ．B ．C ．D ．题型五：幂函数的综合运用【例1】已知幂函数()()2144m f x m m x +=+-在区间()0,+¥上单调递增.（1）求()f x 的解析式；（2）用定义法证明函数()()()43m g x f x x+=+在区间()0,2上单调递减.【例2】已知幂函数()y f x =经过点14,8⎛⎫⎪⎝⎭．(1)求此幂函数的表达式和定义域；(2)若()()232f a f a +<-，求实数a 的取值范围．【题型专练】1．若幂函数221()(22)m f x m m x +=+-在其定义域上是增函数.（1）求()f x 的解析式；（2）若2(2)(4)f a f a -<-，求a 的取值范围.2．已知幂函数()()22122m f x m m x +=+-在()0,∞+上是增函数（1）求()f x 的解析式（2）若(2)(1)f a f a -<-，求a 的取值范围.3．已知幂函数()()225222k k f x m m x -=-+（k ∈Z ）是偶函数，且在()0,∞+上单调递增．（1）求函数()f x 的解析式；（2）若()()212f x f x -<-，求x 的取值范围；（3）若实数a ，b （a ，b +∈R ）满足237a b m +=，求3211a b +++的最小值．。
课件6幕函数图象及性质课件编号：AB I -2-3-1.课件名称：幕函数图象及性质•课件运行环境：几何画板4.0以上版本.课件主要功能：配合教科书“ 2.3幕函数”的教学.利用几何画板绘制函数图象的功能，绘制出幕函数的图象，再利用幕函数的图象研究函数的性质.课件制作过程：（1）新建画板窗口.单击【Graph］（图表）菜单中的【Define Coordinate System!（建立直角坐标系），建立直角坐标系.选中原点，按Ctrl + K，给原点加注标签A,并用【文本］工具把标签改为O.（2）单击【Graph］菜单的【Plot New Function］（绘制函数图象），弹出“NewFunction”函数式编辑器，编辑函数f （x）= x，单击【OK］后画出函数f （x）1, , _ 2 3 —_ 1=x的图象.同法编辑函数g （x）= x，h （x）= x，q（x）=x2和函数r（x）二一的x 图象.选中函数图象，单击【Display］（显示）菜单中的【Line Width］（线型）中的【Thick］（粗线）.把上述图象设置成粗线，单击【Display］（显示）菜单中的【Color］（颜色）的选择各种不同的颜色给每一个函数图象着色，如图1.图1（3）再选中直线f （x） = x，单击【Edit］（编辑）菜单，选择【ActionButtons］（操作类按钮），单击【Hide/Show］（隐藏/显示），此时屏幕上出现【Hide FunctionPlot］（隐藏对象）按钮，选择【文本工具】，双击【Hide Function Plot】按钮，出现对话框，将其中的【Label］（标签）改为“ f （x）= x”，再单击【确定】•此时，单击“f （x）二x”按钮就会隐藏或显示直线f （x）二x •用同样的方法制作1【Hide Function Plot】按钮g （x）= x2，h（x）=x3，q（x）=x2和r（x）二-，如图x2.（4）单击【File】（文件）菜单的【Document Options】（文档选项）对话框，将【Page Namd （页面名称）改为“画图象”，单击【0K】.（5）单击【File】（文件）菜单的【Document Options】（文档选项）对话框，单击【Add Page］（增加页），单击【Blank Pagd （空白页），将页面名称改为“ g 2”（X）= x •（6）单击【Graph】菜单的【Plot New Function】（绘制函数图象），弹出“NewFunction”函数式编辑器，在对话框内依次单击x，A，2，单击【OK】后画出函数g （x）= x2的图象.选中函数g （x）= x2的图象，单击【Con struct】（构造）菜单的【Point On Function Plot】（对象上的点），用【文本工具】给点标签为A，再用【选择工具】选中点A，单击【Measure!（度量）菜单的【CoordinateS I （坐标），屏幕上出现点A的坐标.（7）双击y轴，即将y轴标记为镜面，选中点A，单击【Transform】（变换）菜单的【Reflect］（反射），屏幕上出现点A关于y轴的对称点，发现该点也落在曲线g （x）二x2上•选择【文本工具】，将此点的标签记为“ A”再用【选择工具】选中点A，单击【Measure】（度量）菜单的【Coordinates】（坐标），屏幕上出现点A的坐标.（8）为了进一步验证g （x）二x2的图象关于y轴对称，先同时选中点A、A"，然后按“Ctrl + L”，画出线段AA，单击【Construct】构造）菜单中的【Midpoint】（线段的中点），用【文本工具】将中点的标签记为点M，单击【Measure （度量）菜单的【Coordinates】（坐标），屏幕上出现点M的坐标.（9）用【选择工具】选中点A，单击【Edit】（编辑）菜单的【Action Buttons】（操作类按钮）中的【Animation】（动画），在对话框（图3）中，单击【确定】.屏幕上出现操作类按钮【Animation Point】（运动点），用【文本工具】将按钮名称【Animation Point】改为【运动点A】.单击【运动点A】按钮，点A在函数g （x）= x2的图象上运动或停止运动，发现点M始终在y轴上运动，如图4.（10）单击【File】（文件）菜单的【Document Options】（文档选项）对话框，单击【Add Page］（增加页），单击【Biank Page］（空白页），将页面名称改为“ h（x）=x3” .（11）单击【Graph】菜单的【Plot New Function】（绘制函数图象），弹出“New Function”函数式编辑器，在对话框内依次单击x，A，3，单击【OK】后画出函数h（x） =x3的图象.选中函数h（x^x3的图象，单击【Con struct】（构造）菜单的【Point On Function Plot］（对象上的点），用【文本工具】给点标签为A，再用【选择工具】选中点A,单击【Measure】（度量）菜单的【Coordinates】（坐标）,屏幕上出现点A的坐标.（12）双击原点0,即将原点O标记为对称中心，选中点A,单击【Transform】（变换）菜单的【Rotate]（旋转）,屏幕上出现对话框（图5）,将图5中的“90.0”改为“ 180.0”，再单击【Rotate],此时，屏幕上出现点A关于原点O的对称点，发现该点也落在曲线h（x） =x3上.选择【文本工具】，将此点的标签记为“ A”，再用【选择工具】选中点A，单击【Measurd （度量）菜单的【Coordinates】（坐标）,屏幕上出现点A的坐标.（13）为了进一步验证h（x）=x3的图象关于原点O中心对称，先同时选中点A、A，然后按Ctrl + L,画出线段AA ,单击【Con struct】（构造）菜单中的【Midpoint】（线段的中点），单击【Measurd （度量）菜单的【Coordinates】（坐标），屏幕上出现线段AA中点的坐标O （0, 0）.（14）用【选择工具】选中点A,单击【Edit]（编辑）菜单的【Action Buttons】（操作类按钮）中的【Animation】（动画），在对话框（如图3所示）中，单击【确定】.屏幕上出现操作类按钮【Animation Point】（运动点），用【文本工具】将按钮名称【Animation Point】改为【运动点A].单击【运动点A】按钮，点A 在函数h（x） =x3的图象上运动或停止运动，发现线段AA■中点始终与原点O重合，6.图5（15）单击【File】（文件）菜单的【Document Options】（文档选项）对话框，单击【Add Page］（增加页），单击【Biank Page］（空白页），将页面名称改为“ r（x）=丄”.x（16）单击【Graph］菜单的【Plot New Function］（绘制函数图象），弹出“New Function”函数式编辑器，在对话框内依次单击x，A，—1，单击【0K］后画出函数r（x）二丄的图象.选中函数r（x）二1的图象，单击【Con struct］（构造）x x菜单的【Point On Function Plot］（对象上的点），用【文本工具］给点标签为A，再用【选择工具］选中点A，单击【Measure （度量）菜单的【CoordinateS I （坐标），屏幕上出现点A的坐标.（17）双击原点0,即将原点0标记为对称中心，选中点A,单击【Transform］（变换）菜单的【Rotate］（旋转），屏幕上出现对话框（图5），将图5中的“90.0” 改为“ 180.0”，再单击【Rotate］，此时，屏幕上出现点A关于原点0的对称点，发现该点也落在曲线r（x）二丄上.选择【文本工具］，将此点的标签记为“ A ”，x再用【选择工具］选中点A，单击【Measurd （度量）菜单的【CoordinateQ （坐标），屏幕上出现点A的坐标.1（18）为了进一步验证r（x）=-的图象关于原点0中心对称，先同时选中x点A、A :然后按“ Ctrl + L”，画出线段AA H，单击【Con struct］（构造）菜单中的【Midpoint］（线段的中点），屏幕上出现线段AA中点的为原点0.（19）用【选择工具］选中点A，单击【Edit］（编辑）菜单的【ActionButtons］（操作类按钮）中的【Animation］（动画），在对话框（如图3所示）中，单击【确定］.屏幕上出现操作类按钮【Animation Point ］（运动点），用【文本工具］将按钮名称【Animation Point］改为【运动点A］.单击【运动点A］按钮，点A 1在函数r（x）=-的图象上运动或停止运动，发现线段AA中点始终与原点0重x合，如图7.（20）单击【File］（文件）菜单的【Document 0ptions］（文档选项）对话框，单击【Add Page］（增加页），单击【Blank Page］（空白页），将页面名称P改为“ s（x）=x q”.（21）单击【Graph］菜单的【New Paramete］（新建参数），出现对话框（图8）,将图8中的【Name】（名称）“t［1］”改为“p”，【Value］（值）“ 1.0”改为“7.0”，再单击【OK］.屏幕上出现“p= 1.00”，同法再新建参数“q=1.00”.图7 图8（22）单击【Graph］菜单的【Plot New Function］（绘制函数图象），弹出“New Function”函数式编辑器，在对话框内依次单击x，A，（，p，/，q,），除p、q在屏幕上单击外，其余的都在函数编辑器上，单击【OK］后屏幕上出现函P数s（x）二x q的图象，如图9.17.6&1,00a =P15—=?用甘---------------1r o j课件使用说明:1. 在页面“画图象”中单击“f(x) =x” , “g(x) = X2”, “ h(x) = X3”，“ q(x) = X2”,1和“ r(x)二1”按纽就会隐藏或显示相应函数的图象.x2. 在页面“ g (x)= x2”，“ h(x) = x3”和“ r(x)=」”中，单击按纽【运x动点A】点A就会在相应的函数图象上运动或停止运动，同时点A与点A，的坐标也跟着发生变化，可以让学生观察点A与点A •的坐标的关系，也可以让学生观察线段AA中点的位置特征，通过观察上述函数的图象特征来探究函数的性质(定义域、值域、奇偶性、单调性等).p p3. 在页面“ s(x) =x q”中，选中函数s(x)二x q的图象，单击【Display】(显示)菜单中的【Trace Function Plot】(追踪函数图象).任意选中“ p= 1.00”或“q=1.00”，按“ + ”或“一”号改变p、q的值，同时屏幕上会出现各种幕函数的图象，使学生对幕函数的图象与性质有比较全面的认识.(浙江省台州中学项莉敏吴兰水)。
