第20章 光的偏振
- 格式:doc
- 大小:131.50 KB
- 文档页数:6



第二十章 光的偏振自测题一、选择题1.线偏振光经过λ/2片后,成为( )。
(A )线偏振光 (B )椭圆偏振光 (C )圆偏振光 (D )不是偏振光2.光强为I 0的自然光垂直通过两个偏振片,它们的偏振化方向之间的夹角α =600,设偏振片没有吸收,则出射光强I 与入射光强I 0之比为( )(A )1/4 (B ) 3/4 (C )1/8 (D )3/83.如果两个偏振片堆叠在一起,且偏振化方向之间夹角为600,假设二者对光无吸收,光强为I 0的自然光垂直入在偏振片上,则出射光强为( )(A) I 0/8 (B) 3I 0/8 (C) I 0/4 (D) 3I 0/44.自然光以布儒斯特角入射到两介质界面,则反射光为( )。
(A )自然光 (B )线偏振光 (C )部分偏振光 (D )圆偏振光5.两偏振片堆叠在一起,一束自然光垂直入射其上时没有光线通过。
当其中一偏振片慢慢转动1800时透射光强度发生变化为:( )(A) 光强单调增加。
(B) 光强先增加,后有减小至零(C) 光强先增加,后减小,再增加(D) 光强先增加,然后减小,再增加,再减小至零 6.一束自然光自空气射向一块平板玻璃(如图)射角等于布儒斯特角i 0 ,则在界面2的反射光( )(A) 是自然光(B) 是完全偏振光且光矢量的振动方向垂直入射面 (C) 是完全偏振光且光矢量的振动方向平行入射面(D) 是部分偏振光7.一束自然光入射到一个由四个偏振片所构成的偏振片组上,每个偏振片的透射方向相对于前面一个偏振片沿顺时针方向转过了一个030角,则透过这组偏振片的光强与入射光强之比为(A) 0.41 : 1; (B) 0.32 : 1; (C)0.21 : 1; (D) 0.14 : 18. 在真空中行进的单色自然光以布儒斯特角057=B i 入射到平玻璃板上。
下列哪一种叙述是不正确的?(A) 入射角的正切等于玻璃的折射率;(B) 反射线和折射线的夹角为2/π;(C) 折射光为平面偏振光;(D) 反射光为平面偏振光;9.一束光是自然光和线偏振光的混合光,让它们垂直通过一偏振片,若以此入射光束为轴旋转偏振片,测得透射光强度最大值是最小值的5倍,那么入射光束中自然光和线偏振光的光强比值为( )(A )2/3 ; (B )1/3; (C )1/5; (D ) 1/210.设自然光以入射角057投射于平板玻璃面后,反射光为平面偏振光,试问该平面偏振光的振动面和平板玻璃面的夹角等于多少度?(A) 0; (B) 33; (C) 57; (D) 69;11、两偏振片堆叠在一起,一束自然光垂直入射其上时没有光线通过,当其中一偏振片慢慢转动360°时透射光强度发生的变化为( )(A )光强单调增加;(B )光强先增加,后又减小至零;(C )光强先增加,后减小,再增加;(D )光强先增加,然后减小至零,再增加,再减小至零。


大学物理实验报告
3. 鉴别各种偏振光的方法和步骤
【实验内容】
1. 测定玻璃对激光波长的折射率 2. 产生并检验圆偏振光 3.产生并检验椭圆偏振光
【数据表格与数据记录】
58308250211=-=-=ϕϕp i 57307250212=-=-=ϕϕp i
57307250213=-
=-=ϕϕp i 56306250214=-=-=ϕϕp i 58308250215=-=-=ϕϕp i 57307250216=-=-=ϕϕp i
56306250217=-=-=ϕϕp i
577
7
1=+⋅⋅⋅⋅+=
p p p i i i
5399.157tan tan === n i p
波长为632.8nm 时玻璃对于空气的相对折射率为1.5399。
现象:两次最亮,两次消光。
结论:圆偏振光
如果使检偏器的透振方向与暗方向平行,1/4波片与检偏器透振方向垂直或平行。
现象:两次亮光,两次消光 结论:椭圆偏振光
【小结与讨论】
1. 实验测的了63
2.8nm 时玻璃对空气的折射率为1.5399。
2. 单色自然光经过起偏器和检偏器,旋转检偏器一周,发现光电流相应出现两次消
光现象,是分析其原因。
答:当检偏器的偏振化的方向和检偏器的偏振化的方向为
2π和3
π
时,根据马吕斯定律θ2
0cos I I =可知,出现两次光强为零的情况,即光电流出现了2次消光现象。
3.自己设计实验进行了几种偏振光的检验的工作,搞清了几种偏振光的区别,以及怎样得到他们。
Welcome !!! 欢迎您的下载,资料仅供参考!。

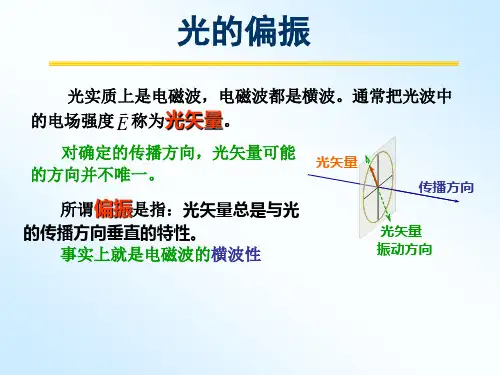
图2 二向色性起偏《大学物理》光的偏振现象的研究实验姓 名学 号 班 级桌 号 教 室实验日期 20 年 月 日 时段 指导教师一. 实验目的1. 观察光的偏振现象,加深对光偏振基本规律的认识;2. 了解产生和检验偏振光的基本方法;3. 验证马吕斯定律;4.1/2波片,1/4波片的研究; 5.利用旋光现象测定蔗糖溶液浓度. 二. 实验仪器导轨和机座, 带布儒斯特窗的氦氖激光器, 激光器架, 偏振片、波片架, 滑动座(4个), 光传感器(光电探头),光功率测试仪,偏振片(2个),1/2波片(波长632.8nm ),1/4波片(波三. 实验原理1. 偏振光的基本概念光波是一种电磁波,它的电矢量 和磁矢量 相互垂直,并垂直于光的传播方向。
通常人们用电矢量 代表光的振动方向,并将电矢量和光的传播方向所构成的平面称为光的振动面。
在传播过程中,电矢量的振动方向始终在某一确定方向的光称为平面偏振光或线偏振光,如图1(a)所示。
振动面的取向和光波电矢量的大小随时间作有规律的变化,光波电矢量末端在垂直于传播方向的平面上的轨迹呈椭圆或圆时,称为椭圆偏振光或圆偏振光,评 分教师签字图1 平面偏振光、自然光和部分偏振光图3 双折射起偏原理图人眼逆光来看,若电矢量末端按照顺时针方向旋转,则称为右旋椭圆或右旋圆偏振光,反之为左旋。
通常光源发出的光波有与光波传播方向相垂直的一切可能的振动方向,没有一个方向的振动比其它方向更占优势。
这种光源发射的光对外不显现偏振的性质,称为自然光,如图1(b)所示;如果光波电矢量的振动在传播过程中只是在某一确定方向上占优势,则此偏振光称为部分偏振光,如图1(c)所示。
将自然光变成偏振光的器件称为起偏器,用来检验偏振光的器件称为检偏器。
实际上,起偏器和检偏器是互为通用的。
下面介绍几种常用的起偏和检偏方法。
2. 二向色性起偏、马呂斯定律、双折射起偏二向色性起偏:物质对不同方向的光振动具有选择吸收的性质,称为二向色性。

光的偏振与干涉:光的波动特性与干涉现象光的波动特性是物理学中一个非常重要的概念,光既可以看作是一种粒子(光子),也可以看作是一种波动。
正是光的波动特性赋予了光学研究以深入和广泛的空间。
一、光的偏振光的偏振指的是光波在传播方向上的振动方向。
普通光是无偏振光,它的振动方向在任何方向上都是随机的。
而偏振光则指的是其振动方向在某一平面上振动的光。
光的偏振可以利用偏振片实现。
偏振片的制备是通过让一束传播方向一致的普通光通过一种特殊的偏振材料而得到。
偏振光的应用十分广泛。
在摄影中,偏振滤镜可用于减少或消除反射,提高画面质量。
在3D电影和电视中,偏振光技术可以实现立体效果。
偏振光还可以用于检测透明材料的应力状态,提高材料的质量。
二、干涉现象干涉是光的波动性质的一种重要表现形式。
当两束或多束相干光波同时作用在同一点上时,它们会相互干涉而产生明暗相间的干涉条纹。
光的干涉现象通过光的波动学来解释。
其中的著名实验是托马斯·杨实验,他通过让光通过一个狭缝后再经过两个狭缝,形成了一组干涉条纹。
该实验证明了光是波动的,并提供了关于光的波动性质的重要线索。
基于这一实验的原理,人们能够更好地理解光的干涉及衍射现象,并将其应用于光学仪器的设计和原理。
另一个经典的干涉实验是迈克尔逊干涉仪。
它是利用光的干涉现象来测量非常小的长度的一种仪器。
通过对光的干涉条纹进行观察和测量,我们可以得出非常精确的长度值,这在科学研究和工程设计中具有重要意义。
三、光的波动特性与干涉现象的意义光的波动特性和干涉现象的研究对我们理解光的性质和应用提供了深入的认识。
首先,通过研究光的偏振现象,我们可以更好地理解光与物质之间的相互作用。
例如,在材料科学中,光的偏振可以用于检测材料的晶格结构和应力状态,为新材料的研发提供了宝贵的信息。
其次,光的干涉现象对我们理解光的传播和衍射提供了新的途径。
通过观察和研究干涉条纹,我们可以探索光的波动性质,并推导出光的传播速度、干涉现象的规律等重要参数。

光的偏振教学设计教案教学目标:1.理解和描述光的偏振现象。
2.能够使用偏振片来实验观察和分析光的偏振现象。
3.掌握如何调节偏振片的方向和角度以控制光的偏振状态。
教学准备:1. ppt演示或黑板。
2.光源和偏振片。
3. 实验器材:偏振片、光源、互相垂直的镜子、10cm长的直线槽、180度回转器、白色光源、滤光片、旋转器。
4.课件或教材。
教学过程:Step 1:导入(10分钟)- 利用ppt或黑板引入光的偏振现象,例:光的传播方式、偏振方向等。
Step 2:理论讲解(20分钟)- 使用ppt或黑板,介绍光的偏振现象的基本原理和偏振片的作用。
-解释光在通过偏振片时发生的现象,并讨论解释为什么光可以被偏振片过滤。
-引导学生理解偏振片和光的偏振方向之间的关系。
Step 3:实验展示(30分钟)-准备实验器材并进行现场演示。
-使用光源、偏振片和直线槽等器材,展示光的偏振现象。
-调整偏振片的角度,让学生观察并描述观察到的变化。
-引导学生猜测并解释变化的原因。
Step 4:小组实验(20分钟)-将学生分成小组,每个小组获得一组实验器材。
-要求小组成员尝试通过调整偏振片的角度和方向来控制光的偏振状态,并观察并记录结果。
-鼓励小组成员互相讨论和交流,分享实验结果和观察到的现象。
Step 5:讨论和总结(20分钟)- 通过ppt或黑板,引导学生回顾整个实验过程,并重点总结实验中观察到的现象。
-引导学生讨论实验结果,解释观察到的现象及其原因。
-引导学生思考光的偏振现象在实际生活中的应用。
Step 6:作业布置(10分钟)-布置作业,要求学生写一份实验报告,包括实验目的、步骤、结果分析和总结,并展示在下一节课。
拓展活动:。

第二十章 光的偏振自测题答案一、 选择题:ACABB BCCDB DBCBD DDABC二、填空题:2I ,I/8,线偏振光,横,光轴,2212cos cos αα,圆,大于,624844.4800'=,600,3I 0/16,3, 91.7 , 8.6,5um三、计算题1、自然光通过两个偏振化方向间成 60°的偏振片,透射光强为 I 1。
今在这两个偏振片之间再插入另一偏振片,它的偏振化方向与前两个偏振片均成 30°角,则透射光强为多少?解:设入射的自然光光强为0I ,则透过第1个偏振片后光强变为2I 0, 3分 透过第2个偏振片后光强变为1020I 60cos 2I =, 3分 由此得 10210I 860cos I 2I == 3分 上述两偏振片间插入另一偏振片,透过的光强变为11020202I 25.2I 4930cos 30cos 2I I === 3分2、 自然光入射到两个互相重叠的偏振片上。
如果透射光强为(1)透射光最大强度的三分之一,(2)入射光强度的三分之一,则这两个偏振片的偏振化方向间的夹角是多少?解:(1)设入射的自然光光强为0I ,两偏振片同向时,透过光强最大,为2I 0。
当透射光强为2I 31I 01⨯=时,有 2分 6I cos 2I I 0201==θ 2分 两个偏振片的偏振化方向间的夹角为445431arccos 01'==θ 2分 (2)由于透射光强 3I cos 2I I 02202==θ 4分 所以有 613632arccos 02'==θ 2分 3、投射到起偏器的自然光强度为0I ,开始时,起偏器和检偏器的透光轴方向平行.然后使检偏器绕入射光的传播方向转过30°,45°,60°,试分别求出在上述三种情况下,透过检偏器后光的强度是0I 的几倍?解:由马吕斯定律有0o 2018330cos 2I I I == 4分 0ο2024145cos 2I I I == 4分 0ο2038160cos 2I I I ==4分 所以透过检偏器后光的强度分别是0I 的83,41,81倍. 4、使自然光通过两个偏振化方向夹角为60°的偏振片时,透射光强为1I ,今在这两个偏振片之间再插入一偏振片,它的偏振化方向与前两个偏振片均成30°,问此时透射光I 与1I 之比为多少?解:由马吕斯定律ο20160cos 2I I =80I = 4分32930cos 30cos 20ο2ο20I I I == 4分 ∴25.2491==I I 4分 5、水的折射率为 1.33,玻璃的折射率为 1.50,当光由水中射向玻璃而反射时,起偏振角为多少?当光由玻璃射向水中而反射时,起偏振角又为多少?这两个起偏振角的数值间是什么关系?解:由布儒斯特定律 120n n i tan =可知,当光由水中射向玻璃而反射时,起偏振角为624833.150.1arctan n n arctan i 0120'===' 5分 光由玻璃中射向水而反射时,起偏振角为434150.133.1arctan n n arctan i 0210'==='' 5分 由此,可见这两个起偏振角的数值间是互余关系,即2i i 00π=''+'。
第20章光的偏振思考题20-1 线偏振光和自然光有什么区别?如何区分线偏振光和自然光?答:线偏振光在与传播方向垂直方向上的振幅不同,自然光在则完全相同.让它们分别穿过偏振片,沿着光传播的方向转动偏振片,如果透射光的光强发生改变,就是线偏振光,否则是自然光.20-2 圆偏振光和线偏振光是否是同一种状态,两束相同的自然光分别经过起偏器后分别变成圆偏振光和线偏振光,哪一束光的光强更大?答:不是.圆偏振光的电矢量的方向在传播过程中不断绕传播方向改变,线偏振光的电矢量始终在同一个平面内.其光强相等.20-3 如图A是起偏器,B是检偏器,以单色光垂直入射,保持A不动,将B绕轴l转动一周,在转动过程中,通过B的光强怎样变化?若保持B不变,将A绕轴l转动一周,通过B的光强怎样变化?答:⑴通过B的光强会发生强度变化,如果AB的起始偏振方向一致,光强从最强变到最弱,再达到最强.⑵如果A绕l转一周,结果完全相同与B旋转相同.20-4 利用双折射现象如何制成波片?答:波片一般是从石英晶体中切割出来的薄片.当一束振幅为A0的平行光垂直入射到波片上时,在入射点分解为e光和o光,并具有相同的相位,光进入晶体后,o光和e光的传播速度不同,二者的波长不同,逐渐形成相位不同的两束光.经过厚度为d的波片后,相位差为dnneo)(2-=∆λπϕAA问题20-3图可见,波片的厚度不同,两束光之间的相位差不同,常见的波片是1/4波片和半波片. 20-5透射的方式能否获得完全的线偏振光?用反射方式呢?它们各有什么特点? 答:能. 也能.略.20-6 马吕斯定律定量描述了一对由起偏器和检偏器组成的偏振器,对透过光线强度的调节作用,如何设计一套可以连续调节光强的实验系统?答:由起偏器和检偏器组成一对同轴调节系统,使起偏器或检偏器绕轴旋转,出射光的光强会连续改变.20-7如图20-26所示,玻璃片堆A 的折射率为n ,二分之一波片C 的光轴与y 轴的夹角为30°,偏振片P 的透振方向沿y 轴方向,自然光沿水平方向入射.⑴ 要使反射光为完全偏振光,玻璃片堆A 的倾角θ应为多少?⑵ 若将部分偏振光看作自然光与线偏振光的叠加,则经过C 后线偏振光的振动面有何变化?说明理由.⑶ 若透射光中自然光的光强为I ,线偏振光的光强为I ′,计算透过后的光强.答:(1)根据马吕斯定律:απθα-==2,arctan n⑵ 椭圆偏振光⑶ 可用相干叠加公式计算.20-8 如图20-27所示,偏振光干涉装置中,C 是劈尖角很小的双折射晶片,折射率c e n n >,P 1、P 2的透振方向相互正交,与光轴方向成45°角,若以波长为λ的单色自然光垂直照射,讨论:⑴ 通过晶片C 不同厚度处出射光的偏振态;⑵ 经过偏振片P 的出射光干涉相长及相消位置与劈尖厚度d 的关系,并求干涉相长的光强与入射光强之比;⑶ 若转动P 2到与P 1平行时,干涉条纹如何变化?为什么?图20-26 思考题20-7用图答:(1)通过晶片C 不同厚度处出射光的偏振态为圆偏振光.(2)这是劈尖干涉,有:ππλπk d n n o e 2)(2=+- (明条纹) ππλπ)12()(2+=+-k d n n o e (暗条纹) 干涉相长时光强I I I I e o 41=+= (3)若转动P 2到与P 1平行时,相位差中的π就没有了,干涉条纹中的明暗条纹互换位置.习题20-1自然光投射到叠在一起的两块偏振片上,则两偏振片的透振方向夹角为多大才能使:⑴ 透射光为入射光强的1/3;⑵ 透射光强为最大透射光强的1/3.解:设夹角为α,则透射光强α20cos I I =通过第一块偏振片后,光强为I 0/2,通过第二块偏振片后,光强为α20cos 21I I =. ⑴ 透射光强为入射光强的1/3,得 3/0I I =,即︒==26.35)32arccos(α ⑵ 当透射光强是最大透射光强的1/3时,即透射光强是入射光强的1/6,得︒=74.54α 图20-27 思考题20-8用图20-2设一部分偏振光由一自然光和一线偏振光混合构成,现通过偏振片观察到这部分偏振光在偏振片由对应最大透射光强位置转过60°时,透射光强减为一半,试求部分偏振光中自然光和线偏振光的比例. 解:由10max 21I I I +=, ︒+=60cos 21210max I I I ,解得3:1:10=I I 20-3在透振方向正交的两偏振片P 1、P 2之间,插入一晶片,其光轴平行于表面且与起偏器的透振方向成35°角,求:⑴ 由晶片分成的o 光和e 光的强度之比;⑵ 经检偏器后两光的强度之比.解:(1)由晶片分成的o 光的振幅:θsin A A o =, e 光 的振幅θcos A A e =强度之比是振幅之比的平方: θθ22cos sin =e o I I =0.49 (2)经起偏器后两光中o 光的振幅:θθcos sin A A o =,e 光的振幅:θθsin cos A A e = 即强度之比是1:120-4把一个楔角为0.33°的石英劈尖(光轴平行于棱)放在透振方向正交的两偏振片之间.用λ = 654.3nm 的红光垂直照射,并将透射光的干涉条纹显示在屏上,已知石英的折射率o 1.5419,n =e 1.5509,n =计算相邻干涉条纹的间距.解:选择劈尖的暗条纹,则条纹位置为:ππλπ)12()(2+=+-k d n n o e ,λk d n n o e =-)(,那么这样的劈尖的相邻条纹的间距:mm n n d o e 6.12)(=-=θλ20-5两个偏振片P 1、P 2叠在一起,其透振方向之间的夹角为30°,由强度相同的自然光和线偏振光混合而成的光束垂直入射在偏振片上,已知穿过后的透射光强为入射光强的比为2/3,求:⑴ 入射光线中线偏振光的光矢量振动方向与P 1的透振方向的夹角θ为多少?⑵ 连续穿过 P 1 、P 2 后的透射光强与入射光强之比.解:设I 0为自然光强.由题意知入射光强为I 0.(1)4I 0 = 0.5I 0 + I 0cos2θ ,θ =24.1°(2)I 1=2(2 I 0)/3, I 2 = I 1 cos 230° , I 1/I 0 = 1/220-6用水晶材料制造对汞灯绿光(波长λ = 546.1×10-9m )适用的四分之一波片,已知对此绿光水晶的主折射率分别为n o =1.5462、n e =1.5554.求此四分之一波片的最小厚度d .解: d = λ/[4(n e - n o )] = 14.84μm20-7线偏振光垂直入射于石英晶片上(光轴平行于入射面),石英主折射率n o = 1.544,n e =1.553.⑴ 若入射光振动方向与晶片的光轴成60°角,不记反射与吸收损失,估算透过的o 光与e 光的强度之比⑵ 若晶片的厚度为0.50mm ,透过的o 光与e 光的光程差多少?解:(1)o 光振幅 A o = A sinθe 光振幅 A e = A cosθθ = 60°,晶片厚度d = 0.50mm两光强之比 I o /I e = (A o / A e )2 = 3(2)两光光程差 δ = ( n e - n o ) d = 4.5μm20-8一束单色自然光自空气(n = 1)入射到一块方解石晶体上,晶体光轴方向如图20-28所示,其主折射率n o = 1.658、n e =1.486,已知晶体厚度d = 2.00 cm ,入射角i = 60°.⑴ 求a 、b 两透射光间的垂直距离;⑵ 两束透射光中,哪一束在晶体中是寻常光?哪一束在晶体中是非寻常光?解:(1)在此特殊情况下,o 光与e 光在晶体内的传播均服从通常的折射定律,对o 光, n o sin r 0 = sin i , 得 r 0 = 31.49°对e 光, n e sin r e = sin i , 得 r e =35.65°由图知a 、b 之间的垂直距离为0.105cm , b 为寻常光,其光矢量振动方向垂直于纸面. 2-9在两个相互正交的偏振片之间放一块水晶的旋光晶片(光轴垂直水晶的表面),如图20-29所示,入射光为纳黄光(λ = 589.3×10-9 m ),对此波长水晶的旋光率α = 21.750/mm ,若使出射光最强,求晶片的最小厚度. 图20-28 习题20-8用图解:设旋光晶片厚度为L ,为使出射光强最大,应使钠黄光在通过水晶旋光晶体后,其振动面旋转90°,此时应满足 △φ = αL = 90° 则 L = 4.14mm .2-10一束单色自然光(波长λ = 589.3×10-9 m )垂直入射在方解石晶片上,光轴平行于晶片的表面,如图20-30所示.已知晶片厚度d = 0.05 mm ,对该光方解石的主折射率n o =1.658、n e =1.486.求⑴ o 、e 两光束穿出晶片后的光程差;⑵ o 、e 两光束穿出晶片后相位差.解:(1)△L = (n o - n e ) d = 8.6μm(2)△φ = (2π/λ) △L = 91.7rad .图20-30 习题20-10用图 2-11一束单色线偏振光(λ = 589.3×10-9 m)沿光轴方向通过水晶块,如图20-31所示.已知对右、左旋圆偏振光的水晶折射率分别为n R = 1.55812、n L = 1.54870,若通过晶体和右旋和左旋圆偏振光所发生的位相差为π,则晶体厚度L 为多大?解:根据题设 π = (2πL /λ)(Nr - nL ) ,则 L = 3.128×10-5m .2-12两个偏振片叠在一起,在它们的透振方向成α1 = 30° 时观测一束单色自然光,又在α2 = 45°观测另一束单色自然光,若两次所得的透射光强度相等,求两次入射自然光的强度之比.解:令I 1和I 2分别为两入射光束的光强.透过起偏器后,光的强度分别为I 1/2、I 2/2. 根据马吕斯定律,透过检偏器的光强分别为I 1′ = I 1cos2α1/2, I 2′ = I 2cos2α2/2按题意,I 1′= I 2′,于是 I 1cos2α1/2 = I 2cos2α2/2,得I 1/I 2 = 2/3.图20-29 习题20-9用图图20-31 习题20-11用图。