第五章 光的偏振
- 格式:doc
- 大小:390.00 KB
- 文档页数:15

《光的偏振》讲义一、光的偏振现象在日常生活中,我们可能不太会注意到光的偏振现象,但它其实无处不在。
当我们通过偏振片观察某些光源时,会发现光的强度发生了变化,这就是光的偏振现象在起作用。
想象一下,光是一种电磁波,就像在平静水面上传播的水波一样。
但光的振动方向与传播方向垂直,而且这个振动方向并不是固定不变的。
在普通的自然光中,光的振动方向在各个方向上是均匀分布的。
然而,当光经过某些特殊的处理或在特定的环境中传播时,它的振动方向会变得具有一定的规律,这就是偏振光。
例如,我们在观看 3D 电影时,佩戴的眼镜就是利用了光的偏振原理。
通过让左眼和右眼分别看到不同偏振方向的光,从而产生立体的视觉效果。
二、偏振光的产生那么,偏振光到底是如何产生的呢?主要有以下几种方式:1、反射和折射当光在两种介质的界面上发生反射和折射时,反射光和折射光往往会成为部分偏振光。
而且,在特定的角度下,反射光可以成为完全偏振光。
2、双折射某些晶体具有双折射的特性,当一束光入射到这样的晶体中时,会分裂成两束偏振方向不同的光。
3、偏振片这是一种常见的产生偏振光的器件。
偏振片上有一些特殊的方向,只允许光沿着这些方向的振动通过,从而将自然光转化为偏振光。
三、偏振光的类型偏振光主要有三种类型:线偏振光、圆偏振光和椭圆偏振光。
线偏振光的振动方向始终保持在一个固定的方向上。
如果光的电场矢量端点的轨迹是一个圆,那就是圆偏振光。
而当轨迹是一个椭圆时,就是椭圆偏振光。
四、偏振光的检测要检测光是否是偏振光以及其偏振状态,我们可以使用偏振片来进行检测。
将待检测的光通过一个偏振片,并旋转偏振片。
如果光的强度不发生变化,那么这束光可能是非偏振光;如果光的强度发生变化,且在某个角度光完全消失,那么这束光就是线偏振光。
对于圆偏振光和椭圆偏振光的检测,则需要更复杂的光学系统和分析方法。
五、光的偏振在实际中的应用光的偏振在许多领域都有着广泛的应用。
在通信领域,偏振复用技术可以大大提高光通信的容量和效率。


《光的偏振》讲义一、光的偏振现象在日常生活中,我们可能不太会留意到光的偏振现象,但它其实无处不在。
当阳光透过云层的缝隙洒下来,或者汽车前挡风玻璃反射的光线,都可能包含着偏振的信息。
光的偏振,简单来说,就是光振动方向的规律性。
普通的自然光,比如太阳光,它的振动方向是随机的,向各个方向都有。
而偏振光则具有特定的振动方向。
为了更直观地理解偏振现象,我们可以做一个简单的实验。
拿两块偏振片,让自然光先通过第一块偏振片,这时我们会发现光的强度减弱了一半。
这是因为只有与偏振片透光轴方向一致的光振动能够通过。
然后,再让通过第一块偏振片的光通过第二块偏振片,如果两块偏振片的透光轴方向平行,光能够顺利通过;如果两者的透光轴方向垂直,就几乎没有光能够通过。
二、偏振光的产生偏振光不是自然存在的,通常需要通过一些特殊的方法来产生。
一种常见的方法是反射和折射。
当自然光以一定的角度从一种介质入射到另一种介质时,反射光和折射光都会成为部分偏振光。
而且,当入射角满足特定条件时,反射光会成为完全偏振光,其振动方向垂直于入射面。
另一种产生偏振光的方法是利用偏振片。
偏振片是一种具有特殊光学性质的材料,它只允许特定方向振动的光通过。
还有双折射现象也能产生偏振光。
比如方解石等晶体,当一束光入射到晶体中时,会分解成两束折射光,这两束光就是偏振方向相互垂直的偏振光。
三、偏振光的类型偏振光主要有三种类型:线偏振光、圆偏振光和椭圆偏振光。
线偏振光的振动方向始终保持在一个固定的方向上。
我们通过前面提到的偏振片得到的通常就是线偏振光。
圆偏振光的电场矢量端点在垂直于光传播方向的平面内描绘出一个圆。
当两个相互垂直、振幅相等、相位差为±π/2 的线偏振光叠加时,就会形成圆偏振光。
椭圆偏振光则是电场矢量端点描绘出一个椭圆。
它是两个相互垂直、振幅不相等、相位差不为±π/2 的线偏振光叠加的结果。
四、光的偏振在生活中的应用光的偏振在我们的生活中有许多重要的应用。






第五章光的偏振自我检测题一、选择题 (每题3分计18分) 1.光的偏振现象证实了[ ]A .光具有波、粒二象性 B.光是电磁波 C .光是横波 D.光是纵波2.两个偏振片叠放在一起,其偏振化方向之间的夹角为600,以光强为0I 的自然光照射,设无吸收损失,则出射的光强为[ ]。
A .8I 0 B.83I 0 C.4I 0 D.43I 03.一束平面偏振光以布儒斯特角入射到两个介质的界面,其振动面与入射面平行,此时反射光为[ ]A .振动方向垂直于入射面的平面偏振光。
B .振动方向平行于入射面的平面偏振光。
C .无反射光。
4.在空气中进行的单色自然光以布儒斯特角i =57°入射到平玻璃板上。
下列叙述中,不正确的说法是[ ]A .入射角的正切等于玻璃板的折射率;B .反射线和折射线的夹角为90°;C .折射光为部分偏振光;D .反射光为平面偏振光;E .反射光的电矢量的振动面平行于入射面。
5.右旋圆偏振光垂直通过1/2波片后,其出射光的偏振态为[ ]A 平面偏振光B 左旋圆偏振光C 右旋圆偏振光D 右旋椭圆偏振光 6.以入射光线为轴转动偏振片时,若入射光是自然光,则将看到什么?若入射光是线偏振光,则将看到什么?若入射光是部分偏振光,则将看到什么?将以下三个解释按照问题提出的先后顺序依次排列正确的是[ ](1) 当偏振片转到某一方向时光的强度最大,再转过90°时光的强度最小(但不为零)(2) 光的强度不变(3) 当偏振片转到某一方向时光的强度最大,再转过90°时光的强度等于零 A.(1)(2)(3) B.(3)(1)(2) C.(2)(1)(3) D.(2)(3)(1) 7、一束单色线偏振光,其振动方向与1/4波片的光轴夹角为4πα=,此偏振光经过1/4波片后[ ]A.仍为线偏振光B.振动面旋转了2πC.振动面旋转了4πα=D.变为圆偏振光二、填空题(每空3分计27分)1.两偏振片的透振方向成30º角时,透过的光强为I ,若入射光光强保持不变,而偏振片透振方向的夹角为45º时,透射光光强为 2.如图所示,一束自然光入射到折射率分别 为1n 和2n 的两种介质的交界面上,发生反射和折射。

第五章光的偏振(Polarization of light)●学习目的通过本章的学习使得学生了解光通过各向异性介质时所产生的偏振现象,初步掌握自然光、线偏振光、椭圆偏振光的检测方法。
●内容提要1、阐明惠更斯作图法,说明光在晶体中的传播规律;2、介绍布儒斯特定律和马吕斯定律;3、阐明自然光、线偏振光、椭圆偏振光的概念和检测方法;4、介绍1/4波片的功用;5、讨论光在各向异性介质中的传播情况。
●重点1、偏振光的检测方法;2、光在晶体中的传播行为。
●难点1、偏振光的检测方法;2、各向异性介质光的传播行为。
●计划学时计划授课时间10学时●教学方式及教学手段课堂集中式授课,采用多媒体教学。
●参考书目1、《光学》第二版章志鸣等编著,高等教育出版社,第七章2、《光学。
近代物理》陈熙谋编著,北京大学出版社,第四章第一节 自然光与偏振光一、光的偏振性1、纵波:波的振动方向和波的传播方向相同的波称为纵波。
2、横波:波的振动方向和波的传播方向相互垂直的波称为纵波。
3、偏振:波的振动方向相对于传播方向的不对称性称为偏振。
只有横波才有偏振现象。
4、振动面:电矢量和光的传播方向所构成的平面称为偏振光的振动面。
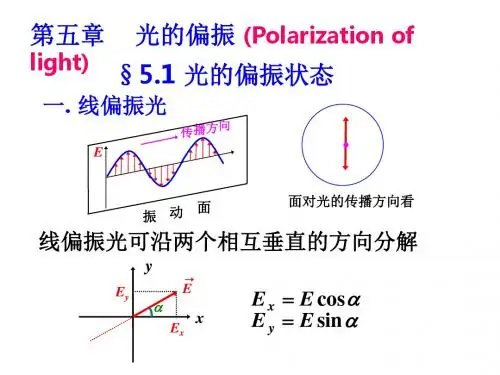
二、自然光和偏振光(natural light )1、偏振光的种类● 平面偏振光:光在传播过程中电矢量的振动只限于某一平面内,则这种光称为平面偏振光。
● 线偏振光:(linearly polarized light )光在传播过程中电矢量在传播方向垂直的平面上的投影为一条直线,则这种光称为线偏振光。
线偏振光的表示法:● 部分偏振光(partially polarized light )彼此无固定相位关系、振动方向任意、不同方向上振幅不同的大量光振动的组合称部分偏振光。
部分偏振光可分解为两束振动方向相互垂直、不等幅、不相干的线偏振光。
▲部分偏振光的表示:迎着光的传播方向看· · · ·· 光振动垂直板面光振动平行板面圆偏振光和椭圆偏振光光矢量按一定频率在垂直传播方向的平面内旋转(左旋或右旋),其矢端轨迹是圆的称圆偏振光(circularly polarized light );其矢端轨迹是椭圆的称椭圆偏振光(ellipticly polarized light )。
第五章 光的偏振1 试确定下面两列光波的偏振态。
)]2/cos()cos([01πωω--+-=kz t e kz t e A E y x)]2/sin()sin([02πωω--+-=kz t e kz t e A E y x解:(1)两分振动的振幅:A x =A y =A 0 ,相位差:φy -φx = -π/2所以该光为左旋圆偏振光。
(2)振动方程可写为:)]2/2/cos()2/cos([01ππωπω+--++-=kz t e kz t e A E y x 两分振动的振幅:A x =A y =A 0 ,相位差:φy -φx = -π/2该光仍然为左旋圆偏振光。
2 为了比较两个被自然光照射的表面的亮度,对其中一个表面直接进行观察,另一个表面通过两块偏振片来观察。
两偏振片的透振方向的夹角为600,若观察到两表面的亮度相同,则两表面的实际亮度比是多少?已知光通过每一块偏振片后损失入射光能量的10%。
解:设直接进行观察的表面的强度为I 0,用偏振片进行观察的表面的强度为I ;已知两偏振片透振方向的夹角θ=600。
表面反射的光经过第一个偏振片后的光强度:I I I 209%)101(21=-=' 经过第二个偏振片后的光强度:I I I 80081%)101(cos 2=-'=''θ 因观察到两表面的亮度相等,则有:0I I =''解得两表面的实际亮度之比:10:1800:81:0≈=I I3 两个尼科耳N 1和N 2的夹角为600,在它们之间放置另一个尼科耳N 3,让平行的自然光通过这个系统。
假设各尼科耳对非常光均无吸收,试问N 3和N 1的透振方向的夹角为何值时,通过系统的光强最大?设入射光强度为I 0,求此时所能通过的最大光强。
解:设第三个尼科尔N 3与第一个N 1的夹角为θ,则与第二个N 2的夹角有两种情况:(1)β= 600 -θ (2)β= 600 +θ在β= 600 -θ的情况下:设平行自然光的强度为I 0,通过N 1的光强度为:0121I I = 通过N 3的光强度为: θθ20213cos 21cos I I I == 图(1) 图(2) 最后通过N 2的光强度为: )60(cos cos 21)60(cos 02200232θθθ-=-=I I I 应用三角变换公式:)]cos()[cos(21cos cos y x y x y x ++-= 化简得到:2002]21)602[cos(81+-=βI I 使I 2取极大值的条件:1)602cos(0=-β即:030=β,或:030=θ, N 3与N 1的夹角:030=θ 最后通过系统的光强度:02329I I = 用同样的方法可解出图(2)中,N 3与N 1的夹角:030=θ4 在两个正交的理想偏振片之间,有一个偏振片以匀角速度ω绕光的传播方向旋转(见图),若入射的自然光强度为I 0,试证明透射光强度为: )4cos 1(160t I I ω-= 解:设在计时起点,N 1与N 2的夹角为0,则在t 时刻,N 1与N 2的夹角为:θ=ωt ,与N 3的夹角为β=900-ωt 。
通过N 1的光强度为: 0121I I =通过N 2的光强度为:t I t I I ωω20212cos 21cos == 最后通过N 3的光强度为: )90(cos cos 21)90(cos 02200223t t I I I ωωθ-=-=因:t t t t t ωωωωω2sin 21sin cos )90cos(cos 0==- 24cos 12sin t t ωω-±= 最后证得:)4cos 1(160t I I ω-=5 线偏振光入射到折射率为1.732的玻璃片上,入射角是600,入射光的电矢量与入射面成300角。
求由分界面上反射的光强占入射光强的百分比。
解:根据折射定律:2211sin sin i n i n =已知入射角: 0160=i计算得到折射角:0230=i把入射线偏光矢量A 沿与入射面垂直和平行两个方向分解,分别为:A A A s 2130sin 0== A A A p 2330cos 0== 根据菲涅耳公式:)sin()sin(2121i i i i A A s s +-=' )()(2121i i tg i i tg A A p p +-=' 计算得到,反射光沿与入射面垂直和平行方向的分振幅:A A A s s 4121==' 0='p A 则合振幅:A A 41=' 反射光强与入射光强之比: %25.6)41(2=='AA I I6 一线偏光垂直入射到一方解石晶体上,它的振动面和主截面成300角,两束折射光通过在方解石后面的一个尼科耳棱镜,其主截面与入射光的振动方向成500角,计算两束透射光的相对强度。
解:设入射线偏光的光振幅为A ,经方解石透射出来的两束线偏光的光振幅分别为: 030sin A A o = 030cos A A e =尼科耳主截面NN '与入射光的振动方AA '向成500角,与方解石主图1 图2截面OO '的夹角有两种情况,见图(1)和图(2)。
在图(1)中,经尼科耳棱镜出射的两束线偏光的光振幅:000110sin 30cos 10sin A A A e ==000210cos 30sin 10cos A A A o == 两束透射光的相对强度:0933.0)(22121==A A I I 在图(2)中,经尼科耳棱镜出射的两束线偏光的光振幅:000120sin 30sin 10sin A A A e == 000220cos 30cos 10cos A A A o == 两束透射光的相对强度:044.0)(22121==A A I I7 线偏振光垂直入射到一块光轴平行于表面的方解石波片上,光的振动面和波片的主截面成300角,求:(1)透射出来的寻常光和非常光的相对强度是多少?(2)用钠光入射时如要产生900的相位差,波片的厚度应为多少?(λ=589nm )解:(1)经波片透射,形成的o 、e 两束线偏光的振幅:030sin A A o = 030cos A A e =相对光强度:3:1:=e o I I(2)已知方解石:n e =1.486、n o =1.658,波长:λ=589nm由: )(2e o n n d -=∆λπϕ 且知: 2πϕ=∆ 得到波片的厚度:cm n n d e o 5102.8)(4-⨯=-=λ8 有一块平行石英片是沿平行于光轴方向切出的,要把它切成一块黄光的1/4波片,问这块石英片应切成多厚?石英:n e =1.552、n o =1.543、λ=589.3nm解:由: 4)12()(λ+=-k n n d e o 得到波片的厚度:cm k d 31064.1)12(-⨯⨯+=9 (1)线偏振光垂直入射到一个表面和光轴平行的波片,透射出来后,原来在波片中的寻常光和非常光产生了π的相位差,问波片的厚度为多少?已知::n e =1.553、n o =1.544、λ=500nm 。
(2)问这块波片应怎样放置才能使透射出来的光是线偏光,而且它的振动面和入射光的振动面成900角?解:(1)根据题意,这是一个1/2波片,由: 2)12()(λ+=-k n n d e o 得到波片的厚度:cm k d 31075.2)12(-⨯⨯+=(2)线偏光经过1/2波片后仍然是线偏光,但透射光矢量的振动方向将从原来的方向转过2θ,已知:2θ= 900 ,则应使波片的光轴与入射光矢量的方向成450角。
10 线偏振光垂直入射到一块表面平行于光轴的双折射波片,光的振动面和波片光轴成250角,问波片中的寻常光和非常光透射出来后的相对强度如何?解:经波片透射,形成的o 、e 两束线偏光的振幅:025sin A A o = 025cos A A e =相对光强度:2174.0:=e o I I11 在两个正交尼科耳棱镜N 1和N 2之间垂直插入一块波片,发现N 2后面有光出射,但当N 2绕入射光向顺时针转过200后,N 2的视场全暗。
此时,把波片也绕入射光顺时针转过200,N 2视场又亮了。
问:(1)这是什么性质的波片;(2)N 2要转过多大的角度才能使N 2的视场又变为全暗?解:(1)当N 2绕入射光向顺时针转过200后,视场变为全暗的,只有线偏光才会产生这种全暗的现象,并且光经N 1后为线偏光,线偏光经过半波片后仍然是线偏光,所以该波片是1/2波片。
(2)根据题意,线偏光光矢量的方向经过半波片后,转过的角度是400,若要使N 2的视场又变为全暗,必须也要转过400角。
12 一束圆偏振光,(1)垂直入射到1/4波片上,求透射光的偏振状态;(2)垂直入射到1/8波片上,求透射光的偏振状态。
解:因入射光为圆偏振光,则两线谝光的相位差为:2/0πϕ±=∆(1)当透过1/4波片时,产生的附加相位差:2/πϕ±='∆ 则两线偏光的合相位差:πϕϕϕ±='∆+∆=∆0 或00='∆+∆=∆ϕϕϕ 即圆偏光通过1/4波片后,透射光为线偏光。
(2)当通过1/8波片后,产生的附加相位差:4/πϕ±='∆则两线偏光的合相位差:4/30πϕϕϕ±='∆+∆=∆ 或 4/0πϕϕϕ±='∆+∆=∆即圆偏光通过1/8波片后,透射光为椭圆偏光。
13 试证明一束左旋圆偏光和一束右旋圆偏光,当它们的振幅相等时,合成的光是线偏振光。
解:根据题意,可写出两光的波方程。
左旋圆偏光:])sin()[cos(1j kz t i kz t A E ---=ωω 右旋圆偏光:])sin()[cos(2j kz t i kz t A E -+-=ωω 两个方程变形为:j kz t i kz t A E )sin()cos(/1---=ωωj kz t i kz t A E )sin()cos(/2-+-=ωω将两个方程两边平方相加: 2222221=+AE A E 即: 222212A E E =+ 说明合成的光波是线偏光。
14 设一方解石波片沿平行光轴方向切开,其厚度为0.0343mm ,放在两个正交的尼科耳棱镜间。
平行光束经过第一尼科耳棱镜后,垂直地射到波片上,对于钠光(λ=589.3nm)而言,晶体的折射率:n e =1.486、n o =1.658,问:通过第二个尼科耳棱镜后,光束发生的干涉是加强还是减弱?如果两个尼科耳棱镜的主截面是相互平行的,结果又如何?解:根据题义,把方解石切割为波晶片,系统最后透射出来的光产生偏光干涉现象。