随机过程 第二章
- 格式:ppt
- 大小:1.42 MB
- 文档页数:4




第二章 随机过程的一般概念2.1 随机过程的基本概念和例子定义2.1.1:设(P ,,F )Ω为概率空间,T 是某参数集,若对每一个,是该概率空间上的随机变量,则称为随机过程(Stochastic Process)。
T t ∈),(w t X ),w t (X 随机过程就是定义在同一概率空间上的一族随机变量。
随机过程可以看成定义在),(w t X Ω×T 上的二元函数,固定Ω∈0w ,即对于一个特定的随机试验,称为样本路径(Sample Path),或实现(realization),这是通常所观测到的过程;另一方面,固定,是一个随机变量,按某个概率分布随机取值。
),(0w t X T t ∈0),(0w t X抽象一点:令,即∏∈=Tt T R R T R 中的元素为),(T t x X t t ∈=,为其Borel域(插乘)(T R B σ域),随机过程实质上是()F ,Ω到())(,T T R R B 上的一个可测映射,在())(,T TR RB 上诱导出一个概率测度:T P ()B X P B P R B T T T ∈=∈∀)(),(B 。
一般代表的是时间。
根据参数集T 的性质,随机过程可以分为两大类: t 1)为可数集,如T {}L ,2,1,0=T 或{}L L ,1,0,1,−=T ,称为离散参数随机过程,也称为随机序列;2)为不可数集,如T {}0≥=t t T 或{}∞<<∞−=t t T ,称为连续参数随机过程。
随机过程的取值称为过程所处的状态(State),所有状态的全体称为状态空间(State Space)。
通常以表示随机过程的状态空间。
根据状态空间的特征,一般把随机过程分为两大类:T t t X ∈),(S 1) 离散状态,即取一些离散的值; )(t X 2)连续状态,即的取值范围是连续的。
)(t X离散参数离散状态随机过程: Markov 链 连续参数离散状态随机过程: Poisson 过程 离散参数连续状态随机过程: *Markov 序列连续参数连续状态随机过程: Gauss 过程,Brown 运动例2.1.1:一醉汉在路上行走,以的概率向前迈一步,以q 的概率向后迈一步,以p r 的概率在原地不动,1=++r q p ,选定某个初始时刻,若以记它在时刻的位置,则就是直线上的随机游动(Random Walk)。






第⼆章随机过程第 2 章随机过程2.1 引⾔确定性信号是时间的确定函数,随机信号是时间的不确定函数。
?通信中⼲扰是随机信号,通信中的有⽤信号也是随机信号。
描述随机信号的数学⼯具是随机过程,基本的思想是把概率论中的随机变量的概念推⼴到时间函数。
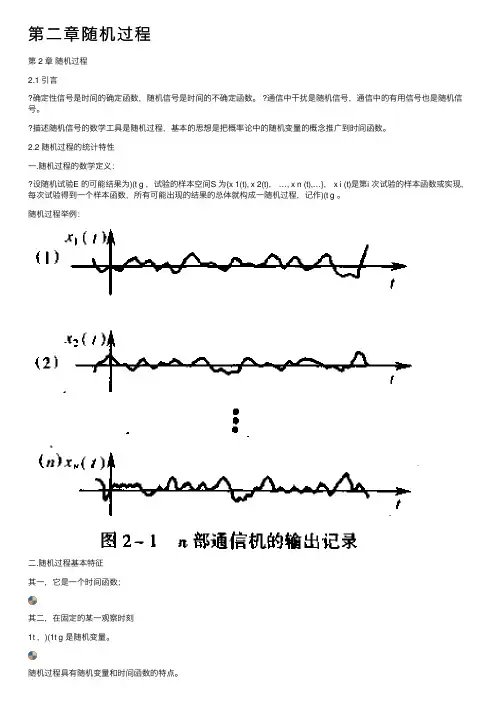
2.2 随机过程的统计特性⼀.随机过程的数学定义:设随机试验E 的可能结果为)(t g ,试验的样本空间S 为{x 1(t), x 2(t), …, x n (t),…}, x i (t)是第i 次试验的样本函数或实现,每次试验得到⼀个样本函数,所有可能出现的结果的总体就构成⼀随机过程,记作)(t g 。
随机过程举例:⼆.随机过程基本特征其⼀,它是⼀个时间函数;其⼆,在固定的某⼀观察时刻1t ,)(1t g 是随机变量。
随机过程具有随机变量和时间函数的特点。
●随机过程)(t g 在任⼀时刻都是随机变量;●随机过程)(t g 是⼤量样本函数的集合。
三.随机过程的统计描述设)(t g 表⽰随机过程,在任意给定的时刻T t ∈1, )(1t g 是⼀个⼀维随机变量。
1.⼀维分布函数:随机变量)(t g ⼩于或等于某⼀数值x 的概率,即})({);(1x t g P t x P ≤= 2.2.12.⼀维概率密度函数:⼀维概率分布函数对x 的导数.xt x P t x p ??=);(),(11 2.2.2 3.对于任意两个时间1t 和2t ,随机过程的对应的抽样值)(1t g )(2t g 为两个随机变量.他们的联合分布定义为)(t g 的⼆维分布})(;)({),;,(221121212x t g x t g P t t x x P ≤≤= 2.2.34.⼆维分布密度定义为212121221212),;,(),;,(x x t t x x P t t x x p = 2.2.4 四.随机过程的⼀维数字特征设随机过程)(t g 的⼀维概率密度函数为),(1t x p .1.数学期望(Expectation)dx t x xp t g E t g );()]([)(1?∞∞-==µ 2.2.5 2.⽅差(Variance)dx t x p t x t t g E t g Var t g g g ),()]([]))()([()]([)(1222µµσ-=-==?∞∞- 2.2.6五.随机过程的⼆维数字特征1.⾃协⽅差函数(Covariance)21212122211221121),;,())())((())]()())(()([(),(dx dx t t x x p t x t x t t g t t g E t t C g g g g g µµµµ--=--=??∞∞-∞∞- 2.2.72. ⾃相关函数(Autocorrelation)2121212212121),;,()]()([),(dx dx t t x x p x x t g t g E t t R g ∞∞-∞∞-== 2.2.83.⾃相关函数和⾃协⽅差函数的关系)]([)]([),(),(212121t g E t g E t t R t t C g g ?-= 2.2.94.设两个随机过程分别为)(),(t h t g ,在时刻1t 和2t ,对)(),(t h t g 抽样,两个随机过程的互相关函数(Cross-correlation)定义为)]()([),(2121t h t g E t t R gh = 2.2.105.两个随机过程的互协⽅差函数(Cross-covariance)定义为)]()())(()([(),(221121t t h t t g E t t C h g gh µµ--= 2.2.112.3 平稳随机过程⼀.狭义平稳的随机过程(严平稳的随机过程)对于任意的正整数n 和实数τ,若随机过程)(t g 的n 维概率密度函数满⾜ ),,;,,(),,;,,,(21212121n n n n n n t t t x x x p t t t x x x p=+???++???τττ 2.3.1 则称)(t g 为狭义平稳的随机过程.统计特性不随时间的推移⽽变化的随机过程称为平稳随机过程。