7.6用锐角三角函数解决问题

§7.6 锐角三角函数的简单应用(3) (教案) 备课时间: 主备人:班级__________ 姓名__________ 学号_________【知识要点】1．斜坡坡度i =斜坡的垂直高度斜坡的水平距离2．通常我们将坡度i 写成1:m 的形式，坡度i 与坡角α之间的关系为tan i α=。

【典型例题】1．小明沿着坡角为20°的斜坡向上前进80m, 则他上升的高度是( ).2．如图是一个拦水大坝的横断面图,AD ∥BC, .斜坡AB=10m,大坝高为8m, (1)则斜坡AB 的坡度 (2)如果坡度,则坡角 (3)如果坡度 ,则大坝高度为___.3．如图,水坝的横截面是梯形ABCD,迎水坡BC 的坡角 为30°,背水坡AD 的坡度 为1:1.2, 坝顶宽DC=2.5米,坝高4.5米. 求:(1)背水坡AD 的坡角 (精确到0.1°); (2)坝底宽AB 的长(精确到0.1米).3．思考:在上题中,为了提高堤坝的 防洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD 加80.cos 20A m ︒80.sin 20B m ︒.80sin 20C m︒.80cos 20D m︒____.AB i =ABi =____.B ∠=1:2,8AB i AB m ==αi β宽0.5米,背水坡AD的坡度改为1:1.4,已知堤坝的总长度为5㎞,求完成该项工程所需的土方(精确到0.1米3)若把此堤坝加高0.5米，需要多少土方？4．安装在屋顶的太阳能热水器的横截面示意图如图所示.已知集热管AE与支架BF所在直线相交与水箱横截面⊙O的圆心O,⊙O的半径为0.2m,AO与屋面AB的夹角为32°，与铅垂线OD的夹角为40°，BF⊥AB于B，OD⊥AD于D，AB＝2m,求屋面AB的坡度和支架BF的长.课后练习：【基础演练】1.某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为52米，则这个坡面的坡度为__________2.如图，一束光线照在坡度为,被斜坡上的平面镜反射成与地面平行的光线，则这束光线与坡面的夹角α是_________度.3．如图，小明从点A处出发，沿着坡度为10°的斜坡向上走了120m到达点B，然后又沿着坡度为15°的斜坡向上走了160m到达点C。

响水县双语学校九（8）班数学导学案（058）课题：7.6锐角三角函数的简单应用第2课学生姓名教学目标：进一步掌握解直角三角形的方法，比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题，培养学生把实际问题转化为数学问题的能力。

教学过程：一、自主探究1.给出仰角、俯角的定义如右图，从下往上看，视线与水平线的夹角叫仰角，从上往下看，视线与水平线的夹角叫做俯角。

右图中的∠1就是仰角，∠2就是俯角。

二、自主合作1.为了测量停留在空中的气球的高度，小明先站在地面上某点观测气球，测得仰角为27°，然后他向气球方向前进了50m，此时观测气球，测得仰角为40°。

若小明的眼睛离地面1.6m ，小明如何计算气球的高度呢?三、自主展示3.大海中某小岛的周围10km 范围内有暗礁。

一艘海轮在该岛的南偏西55°方向的某处，由西向东行驶了20km 后到达该岛的南偏西25°方向的另一处。

如果该海轮继续向东行驶，会有触礁的危险吗？四、自主拓展1. 如图所示,小明在家里楼顶上的点A 处，测量建在与小明家楼房同一水平线上相邻的电梯楼的高，在点A 处看电梯楼顶部点B 处的仰角为60°，在点A 处看这栋电梯楼底部点C 处的俯角为45°，两栋楼之间的距离为30m ，则电梯楼的高BC 为 米（精确到0.1）.（参考数据：414.12≈ 732.13≈）2．如图，A 、B 是两幢地平高度相等、隔岸相望的建筑物，B 楼不能到达，由于建筑物密集，在A 楼的周围没有开阔地带，为测量B 楼的高度，只能充分利A 楼的空间，A 楼的各层都可到达且能看见B 楼，现仅有测量工具为皮尺和测角器(皮尺可用于测量长度，测角器可以测量仰角、俯角或两视线的夹角)。

(1)你设计一个测量B 楼高度的方法，要求写出测量步骤和必需的测量数据 (用字母表示)，并画出测量图形。

(2)用你测量的数据(用字母表示)写出计算B 楼高度的表达式。

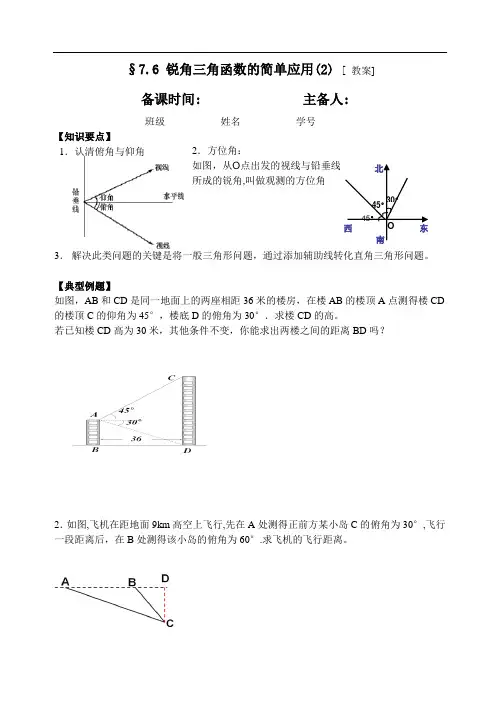
§7.6 锐角三角函数的简单应用(2) [ 教案]备课时间: 主备人:班级__________ 姓名__________ 学号_________【知识要点】1．认清俯角与仰角3． 解决此类问题的关键是将一般三角形问题，通过添加辅助线转化直角三角形问题。

【典型例题】如图，AB 和CD 是同一地面上的两座相距36米的楼房，在楼AB 的楼顶A 点测得楼CD 的楼顶C 的仰角为45°，楼底D 的俯角为30°．求楼CD 的高。

若已知楼CD 高为30米，其他条件不变，你能求出两楼之间的距离BD 吗？2．如图,飞机在距地面9km 高空上飞行,先在A 处测得正前方某小岛C 的俯角为30°,飞行一段距离后，在B 处测得该小岛的俯角为60°.求飞机的飞行距离。

2．方位角： 如图，从O 点出发的视线与铅垂线 所成的锐角,叫做观测的方位角3．如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.4．气象局发出预报:如图, 沙尘暴在A市的正东方向400km的B处以40km/h的速度向北偏西600的方向转移,距沙尘暴中心300km的范围内将受到影响,A市是否受到这次沙尘暴的影响?如果受到影响,将持续多长时间?5．如图, 海上有一灯塔P, 在它周围3海里处有暗礁. 一艘客轮以9海里/时的速度由西向东航行, 行至A点处测得P在它的北偏东60度的方向, 继续行驶20分钟后, 到达B处又测得灯塔P在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?课后练习：【基础演练】1．如图，一座塔的高度TC=120m ，甲、乙两人分别站在塔的西、东两侧的点A 、B 处，测得塔顶的仰角分别为28º、15º。

求A 、B 两点间的距离_________（精确到0.1米） (参考数据：tan 280.53,tan150.27︒≈︒≈)2．如图所示，小华同学在距离某建筑物6米的点A 处测得广告牌B 点、C 点的仰角分别为60°和45°，则广告牌的高度BC 为_____________米(结果保留根号)．3．如图，小明同学在东西方向的环海路A 处，测得海中灯塔P 在北偏东60°方向上，在A 处向东500米的B 处，测得海中灯塔P 在北偏东30°方向上，则灯塔P 到环海路的距离PC＝米（结果保留根号）题1图题2图 题3图 4．如图，在某广场上空飘着一只汽球P ，A 、B 是地面上相距90米的两点，它们分别在汽球的正西和正东，测得仰角∠PAB=45o ，仰角∠PBA=30o ，求汽球P 的高度。

7.6用锐角三角函数解决问题同步习题一．选择题1．如图，大楼高30m，远处有一塔BC，某人爬到楼顶D测得塔顶的仰角为30°，且测得D、B相距30m，则塔高BC为（）m．A．40B．45C．30+D．302．如图，已知点C从点B出发，沿射线BD方向运动，运动到点D后停止，则在这个过程中，从A观测点C的俯角将（）A．增大B．减小C．先增大后减小D．先减小后增大3．如图是某河坝横断面示意图，AC为迎水坡，AB为背水坡，过点A作水平面的垂线AD，BD ＝2CD，设斜坡AC的坡度为i AC，坡角为∠ACD，斜坡AB的坡度为i AB，坡角为∠ABD，则下列结论正确的是（）A．i AC＝2i AB B．∠ACD＝2∠ABD C．2i AC＝i AB D．2∠ACD＝∠ABD 4．如图，小王在山坡上E处，用高1.5米的测角仪EF测得对面铁塔顶端A的仰角为25°，DE 平行于地面BC，若DE＝2米，BC＝10米，山坡CD的坡度i＝1：0.75，坡长CD＝5米，则铁塔AB的高度约是（）（参考数据：sin25°≈0.42，cos25°≈0.91，tan25°≈0.47 ）A．11.1米B．11.8米C．12.0米D．12.6米5．如图，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60°，然后在坡顶D测得树顶B的仰角为30°，已知斜坡CD的长度为10m，DE的长为5m，则树AB的高度是（）m．A．10B．15C．15D．15﹣56．如图是某市一座人行天桥的示意图，天桥离地面的高BC是10米，坡面AC的倾斜角∠CAB ＝45°，在距A点10米处有一建筑物HQ．为了方便行人推车过天桥，市政府部门决定降低坡度，使新坡面DC的倾斜角∠BDC＝30°，若新坡面下D处与建筑物之间需留下HD长的人行道，问人行道HD的长度是（）米．（计算最后结果保留一位小数）．（参考数据：≈1.414，≈1.732）A．2.7B．3.4C．2.5D．3.17．如图，一个直角梯形的堤坝坡长AB为6米，斜坡AB的坡角为60°，为了改善堤坝的稳固性，准备将其坡角改为45°，则调整后的斜坡AE的长度为（）A．3米B．3米C．（3﹣2）米D．（3﹣3）米8．为加快5G网络建设，某移动通信公司在一个坡度为2：1的山腰上建了一座5G信号通信塔AB，在距山脚C处水平距离39米的点D测得通信塔底B处的仰角是35°，测得通信塔顶A 处的仰角是49°（如图），则通信塔AB的高度约为（）参考数据：sin35°＝0.57，tan35°＝0.70，sin49°＝0.75，tan49°＝1.15）A．27米B．31米C．48米D．52米9．如图，某货船以24海里/时的速度从A处向正东方向的D处航行，在点A处测得某岛C在北偏东60°的方向．该货船航行30分钟后到达B处，此时测得该岛在北偏东30°的方向上．则货船在航行中离小岛C的最短距离是（）A．12海里B．6海里C．12海里D．24海里10．“五一”期间，小明和妈妈到某景区游玩，小明想利用所学的数学知识，估测景区里的观景塔DE的高度．他从点D处的观景塔出来走到点A处．沿着斜坡AB从A点走了8米到达B 点，此时回望观景塔，更显气势宏伟．在B点观察到观景塔顶端的仰角为45°且AB⊥BE，再往前走到C处，观察到观景塔顶端的仰角30°，测得BC之间的水平距离BC＝10米，则观景塔的高度DE约为（）米．（＝1.41，＝1.73）A．14B．15C．19D．20二．填空题11．如图，在坡角为30°的斜坡上有两棵树，它们间的水平距离AC为3m，则这两棵树间的坡面距离AB的长为m．12．如图，在一次测绘活动中，在港口A的位置观测停放于B、C两处的小船，测得船B在港口A北偏东75°方向12海里处，船C在港口A南偏东15°方向9海里处，则船B与船C之间的距离为海里．13．如图，为了测量矗立在高速公路上水平地面上的交通警示牌的高度CD，在与M相距4米的A处，测得警示牌下端D的仰角为45°，再笔直往前走8米到达B处，在B处测得警示牌上端C的仰角为30°，则警示牌CD的高度为米（结果保留根号）．14．水务人员为考察水情，乘快艇以每秒10米的速度沿平行于岸边的航线AB由西向东行驶．如图所示，在A处测得岸边一建筑物P在北偏东30°方向上，继续行驶40秒到达点B处，测得建筑物P在北偏西60°方向上，则建筑物P到航线AB的距离为米．15．2019年，徐州马拉松成为世界马拉松大满贯联盟的候选赛事，这大幅度提升了徐州市的国际影响力，如图，在一场马拉松比赛中，某人在大楼A处，测得起点拱门CD的顶部C的俯角为35°，底部D的俯角为45°，如果A处离地面的高度AB＝20米，求起点拱门CD的高度m．（结果精确到1米；参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）．三．解答题16．如图，某办公大楼正前方有一根高度是15米的旗杆ED，从办公大楼顶端A测得旗杄顶端E 的俯角α是45°，旗杄底端D到大楼前梯坎底边的距离DC是10米，梯坎坡长BC是10米，梯坎坡度i BC＝1：，求大楼AB的高．17．如图，在瞭望塔AB前有一段坡比为1：的斜坡BC，经测量BC＝8米，在海岸上取点D，使CD＝45米，在点D测得瞭望塔顶端A的仰角为40°，求瞭望塔AB的高度约为多少米．（结果精确到0.1米，参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，≈1.41）18．某数学兴趣小组要测量实验大楼部分楼体的高度（如图1所示，CD部分），在起点A处测得大楼部分楼体CD的顶端C点的仰角为45°，底端D点的仰角为30°，在同一剖面沿水平地面向前走16米到达B处，测得顶端C的仰角为63.4°（如图2所示），求大楼部分楼体CD的高度约为多少米？（精确到1米）（参考数据：sin63.4°≈0.89，cos63.4°≈0.45，tan63.4°≈2.00，≈1.41，≈1.73）参考答案一．选择题1．解：过点D作DE⊥BC于点E，∵∠BDE＝30°，BD＝30m，∴BE＝BD＝15m，∵AD＝30m，∴CE＝30m，∴BC＝CE+BE＝30+15＝45m．故选：B．2．解：点C从点B出发，沿射线BD方向运动，运动到点D后停止，则在这个过程中，从A观测点C的俯角将增大，故选：A．3．解：斜坡AC的坡度i AC＝，斜坡AB的坡度i AB＝，∵BD＝2CD，∴i AC＝2i AB，A正确，C错误；∠ACD≠2∠ABD，B错误；2∠ACD≠∠ABD，D错误；故选：A．4．解：如图，过点E、F分别作AB的垂线，垂足分别为G、H，得矩形EFHG，∴GH＝EF＝1.5，HF＝GE＝GD+DE＝GD+2，过点D作BC延长线的垂线，垂足为M，得矩形DMBG，∵CD的坡度i＝1：0.75＝4：3，CD＝5，∴DM＝4，CM＝3，∴DG＝BM＝BC+CM＝10+3＝13，BG＝DM＝4，∴HF＝DG+2＝15，在Rt△AFH中，∠AFH＝25°，∴AH＝FH•tan25°≈15×0.47≈7.05，∴AB＝AH+HG+GB≈7.05+1.5+4≈12.6（米）．答：铁塔AB的高度约是12.6米．故选：D．5．解：在Rt△CDE中，∵CD＝10m，DE＝5m，∴sin∠DCE＝，∴∠DCE＝30°．∵∠ACB＝60°，DF∥AE，∴∠BGF＝60°∴∠ABC＝30°，∠DCB＝90°．∵∠BDF＝30°，∴∠DBF＝60°，∴∠DBC＝30°，∴BC＝＝＝10（m），∴AB＝BC•sin60°＝10×＝15（m）．故选：B．6．解：根据题意可知：∠CBA＝90°，∠CAB＝45°，∴∠ACB＝45°，∴AB＝CB＝10，AH＝10，设DH＝x米，则AD＝AH﹣DH＝（10﹣x）米，∴BD＝AD+AB＝（20﹣x）米，在Rt△DCB中，∠CDB＝30°，∴tan30°＝，即＝，解得x≈2.7．所以人行道HD的长度是2.7米．故选：A．7．解：作AH⊥BC于H，在Rt△ABH中，sin∠ABH＝，cos∠ABH＝，则AH＝AB•sin∠ABH＝6×＝3，∵∠E＝45°，∴AE＝AH＝×3＝3，故选：A．8．解：设CE＝x米，∵斜坡BC的坡度为2：1，∴BE＝2x米，在Rt△BDE中，tan∠BDE＝，则＝0.7，解得，x＝21，∴DE＝39+x＝60，在Rt△ADE中，tan∠ADE＝，则AE＝DE•tan∠ADE＝69，∴AB＝AE﹣BE＝69﹣42＝27（米），故选：A．9．解：作CE⊥AB交AB的延长线于E，由题意得，AB＝24×＝12，∠CBE＝60°，∠CAE＝30°，∴∠ACB＝30°，∴∠CAE＝∠ACB，∴BC＝AB＝12，在Rt△CBE中，sin∠CBE＝，∴CE＝BC×sin∠CBE＝12×＝6（海里），故选：B．10．解：作BF⊥DE于F，AH⊥BF于H，∵∠EBF＝45°，∴∠ABH＝45°，∴AH＝BH＝8×＝4，在Rt△ECF中，tan∠ECF＝，则CF＝EF，在Rt△EBF中，∠EBF＝45°，∴BF＝EF，由题意得，EF﹣EF＝10，解得，EF＝5+5，则DE＝EF+DF＝5+5+4≈19，故选：C．二．填空题11．解：由题意知，在Rt△ABC中，AC＝3m，∠A＝30°，∵cos∠A＝，∴AB＝＝＝6（m），故答案为：6．12．解：根据题意得：∠BAC＝90°，AB＝12海里，AC＝9海里，在Rt△ABC中，BC＝＝15海里，故答案为：15．13．解：在Rt△ADM中，∵AM＝4，∠MAD＝45°，∴DM＝AM＝4，∵AB＝8，∴MB＝AM+AB＝12，在Rt△BCM中，∵∠MBC＝30°，∴MC＝MB tan30°＝4，∴DC＝MC﹣DM＝（4﹣4）（米）答：警示牌的高度CD为（4﹣4）米，故答案为：（4﹣4）．14．解：过P点作PC⊥AB于C，由题意可知：∠P AC＝60°，∠PBC＝30°，在Rt△P AC中，＝tan∠P AC＝tan60°，∴AC＝PC，在Rt△PBC中，＝tan∠PBC＝tan30°，∴BC＝PC，∵AB＝AC+BC＝PC＝10×40＝400，∴PC＝100（米），故答案为：100．15．解：作CE⊥AB于E，则四边形CDBE为矩形，∴CE＝DB，CD＝BE，在Rt△ADB中，∠ADB＝45°，∴AB＝DB＝20，∴CE＝20，在Rt△ACE中，tan∠ACE＝，∴AE＝CE•tan∠ACE≈20×0.70＝14，∴CD＝BE＝AB﹣AE＝6m，故答案为：6．三．解答题16．解：如图，过点E作EF⊥AB于点F，作BG⊥CD于点G，∵ED⊥CD，∴四边形DEFG是矩形，∴EF＝DG，ED＝FG，根据题意可知：∠AEF＝α＝45°，∴AF＝EF，∵坡度，∴BG：CG＝3：4，设BG＝3x，CG＝4x，则BC＝5x，∴5x＝10，解得x＝2，∴CG＝8，BG＝6，∴EF＝DG＝CG+CD＝8+10＝18，∴AF＝EF＝18，∵FG＝ED＝15，∴FB＝FG﹣BG＝15﹣6＝9，∴AB＝AF+FB＝18+9＝27（米）．答：大楼AB的高为27米．17．解：如图，延长AB，交直线DC于点F．∵在Rt△BCF中，，∴设BF＝k，则，．又∵，∴k＝8，∴BF＝8，．∵DF＝DC+CF，∴．∵在Rt△ADF中，，∴（米）．∵AB＝AF﹣BF，∴AB＝47.28﹣8≈39.3（米）．答：瞭望塔AB的高度约为39.3米．18．解：设楼高CE为x米，∵在Rt△AEC中，∠CAE＝45°，∴AE＝CE＝x，∵AB＝16，∴BE＝x﹣16，在Rt△CEB中，CE＝BE•tan63.4°≈2（x﹣16），∴2（x﹣16）＝x，解得：x＝32（米），在Rt△DAE中，DE＝AE tan30°＝32×＝，∴CD＝CE﹣DE＝32﹣≈14（米），答：大楼部分楼体CD的高度约为14米．。

[7.6 第1课时 与坡度、坡角有关的问题]一、选择题1．图K －32－1是一水库大坝横断面的一部分，坝高h ＝6 m ，迎水斜坡AB ＝10 m ，斜坡AB 的坡角为α，则tan α的值为( )图K －32－1A.35B.45C.43D.342．2017·温州如图K －32－2，一辆小车沿倾斜角为α的斜坡向上行驶13米，已知cos α＝1213，则小车上升的高度是链接听课例1归纳总结( )图K －32－2A ．5米B ．6米C ．6.5米D ．12米3．如图K －32－3，先锋村准备在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两棵树在坡面上的距离AB 为( )图K －32－3A ．5cos α米 B.5cos α米C ．5sin α米 D.55sin α米4．某水库大坝的横断面为梯形ABCD ，坝顶宽AD ＝6 m ，坝高为24 m ，斜坡AB 的坡角是45°，斜坡CD 的坡比i ＝1∶2，则坝底BC 的长是( )A ．(30＋8 3)mB ．(30＋24 3)mC ．42 mD ．78 m 二、填空题5．如图K －32－4，小明爬一土坡，他从A 处爬到B 处所走的直线距离AB ＝4米，此时，他距离地面高度h ＝2米，则这个土坡的坡角∠A ＝________°图K－32－46．某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为2 5米，则这个坡面的坡度为________．7．2017·天门为加强防汛工作，某市对一拦水坝进行加固．如图K－32－5，加固前拦水坝的横断面是梯形ABCD，已知迎水坡面AB＝12米，背水坡面CD＝12 3米，∠B＝60°，加固后拦水坝的横断面为梯形ABED，tan E＝3 313，则CE的长为________米.链接听课例2归纳总结图K－32－5三、解答题8．2018·徐州如图K－32－6，一座堤坝的横截面是梯形，根据图中给出的数据，求坝高和坝底宽(精确到0.1 m．9．某学校校园内有一小山坡，如图K－32－7所示，经测量，坡角∠ABC＝30°，斜坡AB的长为12米．为方便学生行走，决定开挖小山坡，使斜坡BD的坡比是1∶3(即CD与BC 的长度之比)，A，D两点处于同一铅垂线上，求开挖后小山坡下降的高度AD.图K－32－710．如图K－32－8，拦水坝的横断面为梯形ABCD，坝顶宽BC＝6米，坝高3.2米，迎水坡CD的坡度为i＝1∶2.为了提高水坝的拦水能力，需将水坝加高2米，并且保持坝顶宽度不变，迎水坡CD的坡度不变，但是背水坡的坡度由原来的i＝1∶2变成i′＝1∶2.5(有关数据在图上已注明)，求加高后的坝底HD的长．图K－32－811．如图K－32－9，某校教学楼AB后方有一斜坡，已知斜坡CD的长为12米，坡角α为60°，根据有关部门的规定，∠α≤39°时，才能避免滑坡危险，学校为了消除安全隐患，决定对斜坡CD进行改造，在保持坡脚C不动的情况下，学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全？(结果取整数，参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81，2≈1.41，3≈1.73，5≈2.24)链接听课例1归纳总结图K－32－912．某地的一座天桥如图K－32－10所示，天桥的高为6米，坡面BC的坡度为1∶1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1∶ 3.(1)求新坡面的坡角α；(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除？请说明理由．图K－32－10建模思想2018·泰州日照间距系数反映了房屋日照情况．如图K－32－11①，当前后房屋都朝向正南时，日照间距系数＝L∶(H－H1)，其中L为楼间水平距离，H为南侧楼房高度，H1为北侧楼房底层窗台至地面高度．如图②，山坡EF朝北，EF长为15 m，坡度为i＝1∶0.75(即EH∶FH＝1∶0.75)，山坡顶部平地EM上有一高为22.5 m的楼房AB，底部A到点E的距离为4 m.(1)求山坡EF的水平宽度FH；(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD，已知该楼底层窗台P处至地面C处的高度为0.9 m，要使该楼的日照间距系数不低于1.25，底部C距F处至少多远？图K－32－11详解详析[课堂达标]1．[解析] D 过点A 作AC ⊥BC 于点C ，可求得BC ＝8 m ，所以tan α＝34，故选D .2．[解析] A 如图，设AC ＝13，过点C 作CB ⊥AB 于点B.∵cos α＝1213＝ABAC，∴AB ＝12，∴BC ＝AC 2－AB 2＝132－122＝5， ∴小车上升的高度是5米． 故选A .3．[解析] B 合理选择三角函数是解决问题的关键．4．[解析] D 画出草图，作AF ⊥BC 于点F ，DE ⊥BC 于点E ，由条件分别求出BF ，CE 的长即可．5．[答案] 30[解析] sin A ＝h AB ＝24＝12，所以∠A ＝30°.6．1∶2 7．[答案] 8[解析] 过点A 作AF ⊥BC 于点F ，过点D 作DG ⊥BC 于点G ，AF ＝AB·sin B ＝6 3，∴DG ＝6 3.在Rt △DCG 中，利用勾股定理，得CG ＝18.在Rt △DEG 中，tan E ＝DG GE ＝6 3GE ＝3 313，∴GE ＝26，∴CE ＝GE －CG ＝26－18＝8(米)．8．解：如图，分别过点A ，D 作AF ⊥BC ，DE ⊥BC ，垂足分别为F ，E ，则四边形AFED 是矩形．在Rt △CDE 中，∵sin C ＝DE CD ，cos C ＝CECD，∴DE ＝sin 30°·CD ＝12×14＝7(m )，CE ＝cos 30°·CD ＝32×14＝7 3≈12.124≈12.12(m )． ∵四边形AFED 是矩形，∴EF ＝AD ＝6 m ，AF ＝DE ＝7 m . 在Rt △ABF 中， ∵∠B ＝45°，∴BF ＝AF ＝7 m ，∴BC ＝BF ＋EF ＋CE ≈7＋6＋12.12＝25.12≈25.1(m )． 答：该坝的坝高为7 m ，坝底宽约为25.1 m .9．[解析] 因为AD ＝AC －CD ，故欲求AD ，只需先求AC ，CD.为此可先解Rt △ABC ，求出BC ，再根据坡比即可求出CD.解：在Rt △ABC 中，∠ABC ＝30°，∴AC ＝12AB ＝6米，BC ＝AB·cos ∠ABC ＝12×32＝6 3(米)．∵斜坡BD 的坡比是1∶3， ∴CD ＝13BC ＝2 3 米，∴AD ＝AC －CD ＝(6－2 3)米．答：开挖后小山坡下降的高度AD 为(6－2 3)米．10．[解析] 应把所求的HD 进行合理分割，过点E 作EF ⊥HD 于点F ，过点M 作MN ⊥HD 于点N ，HD ＝HN ＋NF ＋FD ，可利用Rt △HMN 和Rt △DEF 来求解．解：过点M 作MN ⊥HD ，过点B 作BG ⊥HD ，过点E 作EF ⊥HD ，垂足分别为N ，G ，F. ∵BG ＝3.2米，∴加高后MN ＝EF ＝5.2米， ME ＝NF ＝BC ＝6米．在Rt △HMN 和Rt △DEF 中，MN HN ＝12.5，EF FD ＝12， ∴HN ＝52MN ＝13米，FD ＝2EF ＝10.4米，∴HD ＝HN ＋NF ＋FD ＝13＋6＋10.4＝29.4(米)．答：加高后的坝底HD 的长为29.4米．11．[解析] 假设点D 移到D′的位置时，恰好∠α＝39°，过点D 作DE ⊥AC ，交AC 的延长线于点E ，过点D′作D′E′⊥AC 于点E′，根据锐角三角函数的定义求出DE ，CE ，CE ′的长，进而可得出结论．解：假设点D 移到D′的位置时，∠α＝39°.如图，过点D 作DE ⊥AC ，交AC 的延长线于点E ，过点D′作D′E′⊥AC ，交AC 的延长线于点E′.∵CD ＝12米，∠DCE ＝60°，∴DE ＝CD·sin 60°＝12×32＝6 3(米)，CE ＝CD ·cos 60°＝12×12＝6(米)． ∵DE ⊥AC ，D ′E ′⊥AC ，DD ′∥CE ′， ∴四边形DEE′D′是矩形， ∴D ′E ′＝DE ＝6 3米． ∵∠D ′CE ′＝39°，∴CE ′＝D′E′tan 39°≈6 30.81≈12.8，∴EE ′＝CE′－CE ≈12.8－6＝6.8≈7(米)．答：学校至少要把坡顶D 向后水平移动7米才能保证教学楼的安全． 12．解：(1)∵新坡面的坡度为1∶3， ∴tan α＝tan ∠CAB ＝13＝33，∴α＝30°. 答：新坡面的坡角α为30°.(2)文化墙PM 不需要拆除．理由如下： 如图，过点C 作CD ⊥AB 于点D ，则CD ＝6.∵坡面BC 的坡度为1∶1，新坡面的坡度为1∶3， ∴BD ＝CD ＝6，AD ＝6 3， ∴AB ＝AD －BD ＝6 3－6＜8， ∴文化墙PM 不需要拆除．[素养提升]解：(1)∵i EF ＝1∶0.75＝43＝EH FH ，∴可设EH ＝4x m ，FH ＝3x m ，则EF ＝（3x ）2＋（4x ）2＝5x ＝15 m ，∴x ＝3，∴FH ＝9 m ，即山坡EF 的水平宽度FH 为9 m . (2)如图，延长BA ，FH 交于点G ，则AG ＝EH ＝12 m ，GH ＝AE ＝4 m ，∴BG ＝AB ＋AG ＝22.5＋12＝34.5(cm )．设CF ＝y m ，则CG ＝CF ＋FH ＋GH ＝y ＋9＋4＝(y ＋13)m . 由题意知CG ∶(BG －CP)≥1.25，∴y ＋1334.5－0.9≥1.25，解得y ≥29，∴底部C 距F 处至少29 m 远．。

2022-2023学年苏科版九年级数学下册《7.6用锐角三角函数解决问题》解答专项练习题（附答案）1．胜利黄河大桥犹如一架巨大的竖琴，凌驾于滔滔黄河之上，使黄河南北“天堑变通途”．已知主塔AB垂直于桥面BC于点B，其中两条斜拉索AD、AC与桥面BC的夹角分别为60°和45°，两固定点D、C之间的距离约为33m，求主塔AB的高度（结果保留整数，参考数据：≈1.41，≈1.73）2．某型号飞机的机翼形状如图所示，根据图中数据计算AB的长度（结果保留小数点后一位，≈1.7）．3．如图是某水库大坝的横截面，坝高CD＝20m，背水坡BC的坡度为i1＝1：1．为了对水库大坝进行升级加固，降低背水坡的倾斜程度，设计人员准备把背水坡的坡度改为i2＝1：，求背水坡新起点A与原起点B之间的距离．（参考数据：≈1.41，≈1.73．结果精确到0.1m）4．动感单车是一种新型的运动器械．图①是一辆动感单车的实物图，图②是其侧面示意图．△BCD为主车架，AB为调节管，点A，B，C在同一直线上．已知BC长为70cm，∠BCD 的度数为58°．当AB长度调至34cm时，求点A到CD的距离AE的长度（结果精确到1cm）．（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）5．在一次综合实践活动中，某小组对一建筑物进行测量．如图，在山坡坡脚C处测得该建筑物顶端B的仰角为60°，沿山坡向上走20m到达D处，测得建筑物顶端B的仰角为30°．已知山坡坡度i＝3：4，即tanθ＝，请你帮助该小组计算建筑物的高度AB．（结果精确到0.1m，参考数据：≈1.732）6．如图，希望中学的教学楼AB和综合楼CD之间生长着一棵高度为12.88米的白杨树EF，且其底端B，D，F在同一直线上，BF＝FD＝40米．在综合实践活动课上，小明打算借助这棵树的高度测算出综合楼的高度，他在教学楼顶A处测得点C的仰角为9°，点E 的俯角为16°．问小明能否运用以上数据，得到综合楼的高度？若能，请求出其高度（结果精确到0.01米）；若不能，说明理由．解答过程中可直接选用表格中的数据哟！科学计算器按键顺序计算结果（已取近似值）0.1560.1580.2760.2877．如图，小文在数学综合实践活动中，利用所学的数学知识测量居民楼的高度AB，在居民楼前方有一斜坡，坡长CD＝15m，斜坡的倾斜角为α，cosα＝．小文在C点处测得楼顶端A的仰角为60°，在D点处测得楼顶端A的仰角为30°（点A，B，C，D在同一平面内）．（1）求C，D两点的高度差；（2）求居民楼的高度AB．（结果精确到1m，参考数据：≈1.7）8．位于岘山的革命烈士纪念塔是襄阳市的标志性建筑，是为纪念“襄樊战役”中牺牲的革命烈士及第一、第二次国内革命战争时期为襄阳的解放事业献身的革命烈士而兴建的，某校数学兴趣小组利用无人机测量烈士塔的高度．无人机在点A处测得烈士塔顶部点B 的仰角为45°，烈士塔底部点C的俯角为61°，无人机与烈士塔的水平距离AD为10m，求烈士塔的高度．（结果保留整数．参考数据：sin61°≈0.87，cos61°≈0.48，tan61°≈1.80）9．北京时间2022年4月16日9时56分，神舟十三号载人飞船返回舱成功着陆．为弘扬航天精神，某校在教学楼上悬挂了一幅长为8m的励志条幅（即GF＝8m）．小亮同学想知道条幅的底端F到地面的距离，他的测量过程如下：如图，首先他站在楼前点B处，在点B正上方点A处测得条幅顶端G的仰角为37°，然后向教学楼条幅方向前行12m到达点D处（楼底部点E与点B，D在一条直线上），在点D正上方点C处测得条幅底端F的仰角为45°，若AB，CD均为1.65m（即四边形ABDC为矩形），请你帮助小亮计算（结果精确到0.1m．参考数据：sin37°≈0.60，cos37°条幅底端F到地面的距离FE的长度．≈0.80，tan37°≈0.75）10．随着我国科学技术的不断发展，5G移动通信技术日趋完善，某市政府为了实现5G网络全覆盖，2021～2025年拟建设5G基站3000个，如图，在斜坡CB上有一建成的5G 基站塔AB，小明在坡脚C处测得塔顶A的仰角为45°，然后他沿坡面CB行走了50米到达D处，D处离地平面的距离为30米且在D处测得塔顶A的仰角53°．（点A、B、C、D、E均在同一平面内，CE为地平线）（参考数据：sin53°≈，cos53°≈，tan53°≈）（1）求坡面CB的坡度；（2）求基站塔AB的高．11．如图，一艘货轮在海面上航行，准备要停靠到码头C，货轮航行到A处时，测得码头C 在北偏东60°方向上．为了躲避A，C之间的暗礁，这艘货轮调整航向，沿着北偏东30°方向继续航行，当它航行到B处后，又沿着南偏东70°方向航行20海里到达码头C．求货轮从A到B航行的距离（结果精确到0.1海里．参考数据：sin50°≈0.766，cos50°≈0.643，tan50°≈1.192）．12．如图，我国某海域有A，B，C三个港口，B港口在C港口正西方向33.2nmile（nmile 是单位“海里”的符号）处，A港口在B港口北偏西50°方向且距离B港口40nmile处，在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船，求货船与A港口之间的距离．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，sin53°≈0.80，cos53°≈0.60，tan53°≈1.33．）13．2022年6月5日，“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射．如图是处于工作状态的某型号手臂机器人示意图，OA是垂直于工作台的移动基座，AB、BC为机械臂，OA＝1m，AB＝5m，BC＝2m，∠ABC＝143°．机械臂端点C到工作台的距离CD＝6m．（1）求A、C两点之间的距离；（2）求OD长．（结果精确到0.1m，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，≈2.24）14．某镇为创建特色小镇，助力乡村振兴，决定在辖区的一条河上修建一座步行观光桥．如图，河旁有一座小山，山高BC＝80m，点C、A与河岸E、F在同一水平线上，从山顶B 处测得河岸E和对岸F的俯角分别为∠DBE＝45°，∠DBF＝31°．若在此处建桥，求河宽EF的长．（结果精确到1m）[参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60]15．如图是一矩形广告牌ACGE，AE＝2米，为测量其高度，某同学在B处测得A点仰角为45°，该同学沿GB方向后退6米到F处，此时测得广告牌上部灯杆顶端P点仰角为37°．若该同学眼睛离地面的垂直距离为1.7米，灯杆PE的高为2.25米，求广告牌的高度（AC或EG的长）．（精确到1米，参考数据：sin37°≈0.6，tan37°≈0.75）16．如图，小谢想测某楼的高度，她站在B点从A处望向三楼的老田（D），测得仰角∠DAG 为30°，接着她向高楼方向前进1m，从E处仰望楼顶F，测得仰角∠FEG为45°，已知小谢身高（AB）1.7m，DF＝6m．（参考数据：≈1.7，≈1.4）（1）求GE的距离（结果保留根号）；（2）求高楼CF的高度（结果保留一位小数）．17．如图，AB为东西走向的滨海大道，小宇沿滨海大道参加“低碳生活•绿色出行”健步走公益活动，小宇在点A处时，某艘海上观光船位于小宇北偏东68°的点C处，观光船到滨海大道的距离CB为200米．当小宇沿滨海大道向东步行200米到达点E时，观光船沿北偏西40°的方向航行至点D处，此时，观光船恰好在小宇的正北方向，求观光船从C处航行到D处的距离．（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin68°≈0.93，cos68°≈0.37，tan68°≈2.48）18．我市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔，塔旁有一棵唐代古槐，称为“宋塔唐槐”（如图①）．数学兴趣小组利用无人机测量古槐的高度，如图②所示，当无人机从位于塔基B点与古槐底D点之间的地面H点，竖直起飞到正上方45米E点处时，测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°（点B，H，D三点在同一直线上）．已知塔高为39米，塔基B与树底D的水平距离为20米，求古槐的高度（结果精确到1米）．（参考数据：sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50，sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）19．数学活动小组欲测量山坡上一棵大树CD的高度，如图，DC⊥AM于点E，在A处测得大树底端C的仰角为15°，沿水平地面前进30米到达B处，测得大树顶端D的仰角为53°，测得山坡坡角∠CBM＝30°（图中各点均在同一平面内）．（1）求斜坡BC的长；（2）求这棵大树CD的高度（结果取整数），（参考数据：sin53°≈，cos53°≈，tan53°≈，≈1.73）20．如图，是放在水平桌面上的台灯的几何图，已知台灯底座高度为2cm，固定支点O到水平桌面的距离为7.5cm，当支架OA、AB拉直时所形成的线段与点M共线且与底座垂直，此时测得B到底座的距离为31.64cm（线段AB，AO，OM的和），经调试发现，当∠OAB＝115°，∠AOM＝160°时，台灯所投射的光线最适合写作业，测量得A到B的水平距离为10cm，求此时点B到桌面的距离．（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，）参考答案1．解：在Rt△ADB中，∠ADB＝60°，tan∠ADB＝，∴BD＝＝，在Rt△ABC中，∠C＝45°，tan∠C＝，∴BC＝＝AB，∵BC﹣BD＝CD＝33m，∴AB﹣＝33，∴AB＝≈78（m）．答：主塔AB的高约为78m．2．解：如图，过点C、D分别作BE的平行线交BA的延长线于点M、N，在Rt△BDE中，∠BDE＝90°﹣45°＝45°，∴DE＝BE＝14m，在Rt△ACM中，∠ACM＝60°，CM＝BE＝14m，∴AM＝CM＝14（m），∴AB＝BM﹣AM＝CE﹣AM＝20+14﹣14≈10.2（m），答：AB的长约为10.2m．3．解：在Rt△BCD中，∵BC的坡度为i1＝1：1，∴＝1，∴CD＝BD＝20米，在Rt△ACD中，∵AC的坡度为i2＝1：，∴＝，∴AD＝CD＝20（米），∴AB＝AD﹣BD＝20﹣20≈14.6（米），∴背水坡新起点A与原起点B之间的距离约为14.6米．4．解：∵AB＝34cm，BC＝70cm，∴AC＝AB+BC＝104cm，在Rt△ACE中，sin∠BCD＝，∴AE＝AC•sin∠BCD≈104×0.85≈88cm．答：点A到CD的距离AE的长度约88cm．5．解：过点D作DE⊥AC，垂足为E，过点D作DF⊥AB，垂足为F，则DE＝AF，DF＝AE，在Rt△DEC中，tanθ＝＝，设DE＝3x米，则CE＝4x米，∵DE2+CE2＝DC2，∴（3x）2+（4x）2＝400，∴x＝4或x＝﹣4（舍去），∴DE＝AF＝12米，CE＝16米，设BF＝y米，∴AB＝BF+AF＝（12+y）米，在Rt△DBF中，∠BDF＝30°，∴DF＝＝＝y（米），∴AE＝DF＝y米，∴AC＝AE﹣CE＝（y﹣16）米，在Rt△ABC中，∠ACB＝60°，∴tan60°＝＝＝，解得：y＝6+8，经检验：y＝6+8是原方程的根，∴AB＝BF+AF＝18+8≈31.9（米），∴建筑物的高度AB约为31.9米．6．解：小明能运用以上数据，得到综合楼的高度，理由如下：作EG⊥AB，垂足为G，作AH⊥CD，垂足为H，如图：由题意知，EG＝BF＝40米，EF＝BG＝12.88米，∠HAE＝16°＝∠AEG＝16°，∠CAH ＝9°，在Rt△AEG中，tan∠AEG＝，∴tan16°＝，即0.287≈，∴AG＝40×0.287＝11.48（米），∴AB＝AG+BG＝11.48+12.88＝24.36（米），∴HD＝AB＝24.36米，在Rt△ACH中，AH＝BD＝BF+FD＝80米，tan∠CAH＝，∴tan9°＝，即0.158≈，∴CH＝80×0.158＝12.64（米），∴CD＝CH+HD＝12.64+24.36＝37.00（米），答：综合楼的高度约是37.00米．7．解：（1）过点D作DE⊥BC，交BC的延长线于点E，∵在Rt△DCE中，cosα＝，CD＝15m，∴（m）．∴（m）．答：C，D两点的高度差为9m．（2）过点D作DF⊥AB于F，由题意可得BF＝DE，DF＝BE，设AF＝xm，在Rt△ADF中，tan∠ADF＝tan30°＝，解得DF＝x，在Rt△ABC中，AB＝AF+FB＝AF+DE＝（x+9）m，BC＝BE﹣CE＝DF﹣CE＝（x﹣12）m，tan60°＝＝，解得，经检验，是原方程的解且符合题意，∴AB＝++9≈24（m）．答：居民楼的高度AB约为24m．8．解：由题意得，∠BAD＝45°，∠DAC＝61°，在Rt△ABD中，∠BAD＝45°，AD＝10m，∴BD＝AD＝10m，在Rt△ACD中，∠DAC＝61°，tan61°＝≈1.80，解得CD≈18，∴BC＝BD+CD＝10+18＝28（m）．∴烈士塔的高度约为28m．9．解：设AC与GE相交于点H，由题意得：AB＝CD＝HE＝1.65米，AC＝BD＝12米，∠AHG＝90°，设CH＝x米，∴AH＝AC+CH＝（12+x）米，在Rt△CHF中，∠FCH＝45°，∴FH＝CH•tan45°＝x（米），∵GF＝8米，∴GH＝GF+FH＝（8+x）米，在Rt△AHG中，∠GAH＝37°，∴tan37°＝＝≈0.75，解得：x＝4，经检验：x＝4是原方程的根，∴FE＝FH+HE＝5.65≈5.7（米），∴条幅底端F到地面的距离FE的长度约为5.7米．10．解：（1）如图，过点D作AB的垂线，交AB的延长线于点F，过点D作DM⊥CE，垂足为M．由题意可知：CD＝50米，DM＝30米．在Rt△CDM中，由勾股定理得：CM2＝CD2﹣DM2，∴CM＝40米，∴斜坡CB的坡度＝DM：CM＝3：4；（2）设DF＝4a米，则MN＝4a米，BF＝3a米，∵∠ACN＝45°，∴∠CAN＝∠ACN＝45°，∴AN＝CN＝（40+4a）米，∴AF＝AN﹣NF＝AN﹣DM＝40+4a﹣30＝（10+4a）米．在Rt△ADF中，∵DF＝4a米，AF＝（10+4a）米，∠ADF＝53°，∴tan∠ADF＝，∴＝，∴解得a＝，∴AF＝10+4a＝10+30＝40（米），∵BF＝3a＝米，∴AB＝AF﹣BF＝40﹣＝（米）．答：基站塔AB的高为米．11．解：过B作BD⊥AC于D，由题意可知∠ABE＝30°，∠BAC＝30°，则∠C＝180°﹣30°﹣30°﹣70°＝50°，在Rt△BCD中，∠C＝50°，BC＝20（海里），∴BD＝BC sin50°≈20×0.766＝15.32（海里），在Rt△ABD中，∠BAD＝30°，BD＝15.32（海里），∴AB＝2BD＝30.64≈30.6（海里），答：货轮从A到B航行的距离约为30.6海里．12．解：过点A作AE⊥CD，垂足为E，过点B作BF⊥AE，垂足为F，由题意得：EF＝BC＝33.2海里，AG∥DC，∴∠GAD＝∠ADC＝53°，在Rt△ABF中，∠ABF＝50°，AB＝40海里，∴AF＝AB•sin50°≈40×0.77＝30.8（海里），∴AE＝AF+EF＝64（海里），在Rt△ADE中，AD＝≈＝80（海里），∴货船与A港口之间的距离约为80海里．13．解：（1）如图，过点A作AE⊥CB，垂足为E，在Rt△ABE中，AB＝5m，∠ABE＝37°，∵sin∠ABE＝，cos∠ABE＝，∴＝0.60，＝0.80，∴AE＝3m，BE＝4m，∴CE＝6m，在Rt△ACE中，由勾股定理AC＝＝3≈6.7m．（2）过点A作AF⊥CD，垂足为F，∴FD＝AO＝1m，∴CF＝5m，在Rt△ACF中，由勾股定理AF＝＝2m．∴OD＝2≈4.5m．14．解：在Rt△BCE中，BC＝80m，∠BEC＝∠DBE＝45°，∴∠CBE＝45°，∴∠BEC＝∠CBE＝45°，∴CE＝BC＝80m．在Rt△BCF中，BC＝80m，∠BFC＝∠DBF＝31°，tan∠BFC＝，∴．∴CF≈133.3．∴EF＝CF﹣CE＝133.3﹣80＝53.3≈53（m）．答：河宽EF的长约为53m．15．解：由题意：DH＝BF＝6米，DB＝HF＝1.7米，PE＝2.25米，如图，设直线DH交EG于M，交AC于N，则EM＝AN．设AN＝x，则PM＝x+2.25，在Rt△AND中，∵∠ADN＝45°，∴AN＝ND＝x，∵AE＝MN＝2，则MH＝6+x+2＝8+x，在Rt△PHM中，∵tan37°＝，∴，解得x≈15，∴AC＝AN+NC＝15+1.7≈17（米），故广告牌的高度为17米．16．解：（1）设GE＝xm，∵∠EGF＝90°，∠FEG＝45°，∴△EFG是等腰直角三角形，∴FG＝EG＝xm，在Rt△ADG中，∠DAG＝30°，AG＝EG+AE＝（x+1）m，∵tan∠DAG＝＝tan30°＝，∴DG＝AG＝（x+1）m，∵FG﹣DG＝DF，∴x﹣（x+1）＝6，解得：x＝，答：GE的距离为m；（2）由（1）得：FG＝GE＝m，∵GC＝AB＝1.7m，∴CF＝FG+GC＝+1.7≈17.2（m），答：高楼CF的高度约为17.2m．17．解：过点C作CF⊥DE于F，由题意得，∠D＝40°，∠ACB＝68°，在Rt△ABC中，∠CBA＝90°，∵tan∠ACB＝，∴AB＝CB×tan68°≈200×2.48＝496（m），∴BE＝AB﹣AE＝496﹣200＝296（m），∵∠CFE＝∠FEB＝∠CBE＝90°，∴四边形FEBC为矩形，∴CF＝BE＝296m，在Rt△CDF中，∠DFC＝90°，∵sin∠D＝，∴CD≈＝462.5（m），答：观光船从C处航行到D处的距离约为462.5m．18．解：过点A作AM⊥EH于M，过点C作CN⊥EH于N，由题意知，AM＝BH，CN＝DH，AB＝MH，在Rt△AME中，∠EAM＝26.6°，∴tan∠EAM＝，∴AM＝＝≈＝12米，∴BH＝AM＝12米，∵BD＝20，∴DH＝BD﹣BH＝8米，∴CN＝8米，在Rt△ENC中，∠ECN＝76°，∴tan∠ECN＝，∴EN＝CN•tan∠ECN≈8×4.01＝32.08米，∴CD＝NH＝EH﹣EN＝12.92≈13（米），即古槐的高度约为13米．19．解：（1）由题意得：∠CAE＝15°，AB＝30米，∵∠CBE是△ABC的一个外角，∴∠ACB＝∠CBE﹣∠CAE＝15°，∴∠ACB＝∠CAE＝15°，∴AB＝BC＝30米，∴斜坡BC的长为30米；（2）在Rt△CBE中，∠CBE＝30°，BC＝30米，∴CE＝BC＝15（米），BE＝CE＝15（米），在Rt△DEB中，∠DBE＝53°，∴DE＝BE•tan53°≈15×＝20（米），∴DC＝DE﹣CE＝20﹣15≈20（米），∴这棵大树CD的高度约为20米．20．解：过点A作AC平行于水平桌面，过点B作BC⊥AC于点C，再延长MO交AC于点D，由题意可知：OD⊥AC，AC＝10cm，OM＝7.5﹣2＝5.5cm，∵∠AOM＝160°，∴∠AOD＝180°﹣∠AOM＝20°，∵OD⊥AC，∴∠ADO＝90°，∴∠OAD＝90°﹣∠AOD＝70°，∵∠OAB＝115°，∴∠BAC＝∠OAB﹣∠OAD＝115°﹣70°＝45°，∴∠ABC＝∠BAC＝45°，∴AC＝BC＝10cm，在Rt△ABC中，cos∠BAC＝，∴AB＝，∵AB+AO+OM＝31.64cm，∴AO＝12cm，在Rt△AOD中，cos∠AOD＝，∴OD＝AO•cos∠AOD＝12×cos20°≈11.28cm，∴BC+OD+7.5＝11.28+10+7.5＝28.78cm，∴点B到桌面得距离为28.78cm．。

2021-2022学年苏科版九年级数学下册《7.6用锐角三角函数解决问题》同步达标训练（附答案）1．已知海面上一艘货轮A在灯塔B的北偏东30°方向，海监船C在灯塔B的正东方向5海里处，此时海监船C发现货轮A在它的正北方向，那么海监船C与货轮A的距离是（）A．10海里B．5海里C．5海里D．海里2．如图，一艘船从A处向北偏东30°的方向行驶10千米到B处，再从B处向正西方向行驶20千米到C处，这时这艘船与A的距离（）A．15千米B．10千米C．10千米D．5千米3．如果小丽在楼上点A处看到楼下点B处小明的俯角是35°，那么点B处小明看点A处小丽的仰角是（）A．35°B．45°C．55°D．65°4．如图，传送带和地面所成斜坡的坡度i＝1：2.4，如果它把某物体从地面送到离地面10米高的地方，那么该物体所经过的路程是（）A．10米B．24米C．25米D．26米5．如图，电线杆CD的高度为h，两根拉线AC与BC互相垂直（A、D、B在同一条直线上），设∠CAB＝α，那么拉线BC的长度为（）A．B．C．D．6．直升飞机在离地面2000米的上空测得上海东方明珠底部的俯角为30°，此时直升飞机与上海东方明珠底部之间的距离是（）A．2000米B．米C．4000米D．米7．如图，下列角中为俯角的是（）A．∠1B．∠2C．∠3D．∠48．如果从货船A测得小岛b在货船A的北偏东30°方向500米处，那么从小岛B看货船A 的位置，此时货船A在小岛B的（）A．南偏西30°方向500米处B．南偏西60°方向500米处C．南偏西30°方向250米处D．南偏西60°方向250米处9．如图，传送带和地面所成斜坡AB的坡度为1：2，物体从地面沿着该斜坡前进了10米，那么物体离地面的高度为（）A．5 米B．5米C．2米D．4米10．我们约定：如果一个四边形存在一条对角线，使得这条对角线是四边形某两边的比例中项，那么就称这个四边形为“闪亮四边形”，这条对角线为“闪亮对角线，”相关两边为“闪亮边”．例如：图1中的四边形ABCD中，AB＝AC＝AD，则AC2＝AB•AD，所以四边形ABCD是闪亮四边形，AC是闪亮对角线，AB、AD是对应的闪亮边．如图2，已知闪亮四边形ABCD中，AC是闪亮对角线，AD、CD是对应的闪亮边，且∠ABC＝90°，∠D＝60°，AB＝4，BC＝2，那么线段AD的长为．11．一段公路路面的坡度为i＝1：2.4，如果某人沿着这段公路向上行走了130米，那么此人升高了米．12．如图，一艘轮船由西向东航行，在A处测得灯塔P在北偏东60°的方向，继续向东航行40海里后到B处，测得灯塔P在北偏东30°的方向，此时轮船与灯塔之间的距离是海里．13．如图，某水库大坝的横断面是梯形ABCD，坝顶宽AD是6米，坝高4米，背水坡AB 和迎水坡CD的坡度都是1：0.5，那么坝底宽BC是米．14．如图，飞机于空中A处观测其正前方地面控制点C的俯角为30°，若飞机航向不变，继续向前飞行1000米至B处时，观测到其正前方地面控制点C的俯角为45°，那么该飞机与地面的高度是米（保留根号）．15．为了测量某建筑物BE的高度（如图），小明在离建筑物15米（即DE＝15米）的A处，用测角仪测得建筑物顶部B的仰角为45°，已知测角仪高AD＝1.8米，则BE＝米．16．如图，一辆小汽车在公路l上由东向西行驶，已知测速探头M到公路l的距离MN为9米，测得此车从点A行驶到点B所用的时间为0.6秒，并测得点A的俯角为30o，点B 的俯角为60o．那么此车从A到B的平均速度为米/秒．（结果保留三个有效数字，参考数据：≈1.732，≈1.414）17．图1是某地摩天轮的图片，图2是示意图．已知线段BC经过圆心D且垂直于地面，垂足为点C，当座舱在点A时，测得摩天轮顶端点B的仰角为15°，同时测得点C的俯角为76°，又知摩天轮的半径为10米，求摩天轮顶端B与地面的距离．（精确到1米）参考数据：sin15°≈0.26，cos15°≈0.96，tan15°≈0.27，sin76°≈0.97，cos76°≈0.24，tan76°≈4.01．18．如图1，一扇窗户打开后可以用窗钩AB将其固定，窗钩的一个端点A固定在窗户底边OE上，且与转轴底端O之间的距离为20cm，窗钩的另一个端点B可在窗框边上的滑槽OF上移动，滑槽OF的长度为17cm，AB、BO、AO构成一个三角形．当窗钩端点B与点O之间的距离是7cm的位置时（如图2），窗户打开的角∠AOB的度数为37°．（1）求钩AB的长度（精确到1cm）；（2）现需要将窗户打开的角∠AOB的度数调整到45°时，求此时窗钩端点B与点O之间的距离（精确到1cm）．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，≈1.4）19．一块显示屏斜挂在展示厅的墙面上，如图是显示屏挂在墙面MD的正侧面示意图，其中AB表示显示屏的宽，AB与墙面MD的夹角α的正切值为，在地面C处测得显示屏顶部A的仰角为45°，屏幕底部B与地面CD的距离为2米，如果C处与墙面之间的水平距离CD为3.4米，求显示屏的宽AB的长．（结果保留根号）20．水城门位于淀浦河和漕港河三叉口，是环城水系公园淀浦河梦蝶岛区域重要的标志性景观．在课外实践活动中，某校九年级数学兴趣小组决定测量该水城门的高．他们的操作方法如下：如图，先在D处测得点A的仰角为20°，再往水城门的方向前进13米至C处，测得点A的仰角为31°（点D、C、B在一直线上），求该水城门AB的高．（精确到0.1米）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）21．如图是某地下停车库入口的设计示意图，已知坡道AB的坡比i＝1：2.4，AC的长为7.2米，CD的长为0.4米．按规定，车库坡道口上方需张贴限高标志，根据图中所给数据，确定该车库入口的限高数值（即点D到AB的距离）．22．如图，某小区A栋楼在B栋楼的南侧，两楼高度均为90m，楼间距为MN．春分日正午，太阳光线与水平面所成的角为55.7°，A栋楼在B栋楼墙面上的影高为DM；冬至日正午，太阳光线与水平面所成的角为30°，A栋楼在B栋楼墙面上的影高为CM．已知CD ＝44.5m．（1）求楼间距MN；（2）若B号楼共30层，每层高均为3m，则点C位于第几层？（参考数据：tan30°≈0.58，sin55.7°≈0.83，cos55.7°≈0.56，tan55.7°≈1.47）23．如图，一座古塔AH的高为33米，AH⊥直线l，某校九年级数学兴趣小组为了测得该古塔塔刹AB的高，在直线l上选取了点D，在D处测得点A的仰角为26.6°，测得点B 的仰角为22.8°，求该古塔塔刹AB的高．（精确到0.1米）【参考数据：sin26.6°＝0.45，cos26.6°＝0.89，tan26.6°＝0.5，sin22.8°＝0.39，cos22.8°＝0.92，tan22.8°＝0.42】24．如图1，一辆吊车工作时的吊臂AB最长为20米，吊臂与水平线的夹角∠ABC最大为70°，旋转中心点B离地面的距离BD为2米．（1）如图2，求这辆吊车工作时点A离地面的最大距离AH（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）；（2）一天，王师傅接到紧急通知，要求将这辆吊车立即开到40千米远的某工地，因此王师傅以每小时比平时快20千米的速度匀速行驶，结果提前20分钟到达，求这次王师傅所开的吊车速度．25．在一次数学综合实践活动中，小明计划测量城门大楼的高度，在点B处测得楼顶A的仰角为22°，他正对着城楼前进21米到达C处，再登上3米高的楼台D处，并测得此时楼顶A的仰角为45°．（1）求城门大楼的高度；（2）每逢重大节日，城门大楼管理处都要在A，B之间拉上绳子，并在绳子上挂一些彩旗，请你求出A，B之间所挂彩旗的长度（结果保留整数）．（参考数据：sin22°≈，cos22°≈，tan22°≈）参考答案1．解：如图，在Rt△ABC中，∠ABC＝90°﹣30°＝60°，BC＝5海里，∴AC＝BC•tan60°＝5（海里），即海监船C与货轮A的距离是5海里，故选：B．2．解：如图，∵BC⊥AE，∴∠AEB＝90°，∵∠EAB＝30°，AB＝10千米，∴BE＝5米，AE＝5千米，∴CE＝BC﹣BE＝20﹣5＝15（千米），∴AC＝（千米），故选：C．3．解：因为从点A看点B的仰角与从点B看点A的俯角互为内错角，大小相等．所以小丽在楼上点A处看到楼下点B处小明的俯角是35°，点B处小明看点A处小丽的仰角是35°．故选：A．4．解：作AB⊥CB于B，由题意得，AB＝10米，∵斜坡的坡度i＝1：2.4，∴＝，即＝，解得，BC＝24，由勾股定理得，AC＝＝＝26（米），故选：D．5．解：∵AC⊥BC，CD⊥AB，∴∠CAD+∠ACD＝90°，∠ACD+∠BCD＝90°，∴∠CAD＝∠BCD，在Rt△BCD中，∵cos∠BCD＝，∴BC＝＝，故选：B．6．解：根据题意：直升飞机与上海东方明珠底部之间距离是＝＝4000米．故选：C．7．解：根据俯角的定义，首先确定水平线，水平线以下与视线的夹角，即是俯角．故选：C．8．解：如图所示：∵小岛B在货船A的北偏东30°方向500米处，∴货船A在小岛B的南偏西30°方向500米处，故选：A．9．解：作BC⊥地面于点C，设BC＝x米，∵传送带和地面所成斜坡AB的坡度为1：2，∴AC＝2x米，由勾股定理得，AC2+BC2＝AB2，即（2x）2+x2＝102，解得，x＝2，即BC＝2米，故选：C．10．解，如图，作CH⊥AD于H．∵AC2＝DA•DC时∵DH＝CD•cos∠D，CH＝CD•sin∠D，AH＝AD﹣CD•cos∠D，∴AC2＝AH2+CH2＝（AD﹣CD•cos∠D）2+（CD•sin∠D）2＝AD2+CD2﹣2AD•CD•cos∠D＝AD2+CD2﹣AD•CD，∵AC2＝AD•CD，∴AD2﹣2AD•CD+CD2＝0，∴（AD﹣CD）2＝0，∴AD＝CD，∵∠D＝60°，∴△ACD是等边三角形，∴AD＝AC＝＝＝2．故答案为：2．11．解：设此人升高了x米，∵坡比为1：2.4，∴他行走的水平宽度为2.4x米，由勾股定理得，x2+（2.4x）2＝1302，解得，x＝50，即他沿着垂直方向升高了50米，故答案为：50．12．解：如图所示：由题意可得，∠P AB＝30°，∠DBP＝30°，故∠PBE＝60°，则∠P＝∠P AB＝30°，可得：AB＝BP＝40海里．故答案为：40．13．解：过点A作AE⊥BC，DF⊥BC，由题意可得：AD＝EF＝6m，AE＝DF＝4m，∵背水坡AB和迎水坡CD的坡度都是1：0.5，∴BE＝FC＝2m，∴BC＝BE+FC+EF＝6+2+2＝10（m）．故答案为：10．14．解：作CD⊥AB于点D．∴∠BDC＝90°，∵∠DBC＝45°，∴BD＝CD，∵∠DAC＝30°，∴tan30°＝＝＝＝，解得CD＝BD＝500+500（米）．答：该飞机与地面的高度是（500+500）米．故答案为：（500+500）．15．解：过A作AC⊥BE于C，则AC＝DE＝15，根据题意：在Rt△ABC中，有BC＝AC×tan45°＝15，则BE＝BC+CE＝16.8（米），故答案为：16.8．16．解：在Rt△AMN中，AN＝MN×tan∠AMN＝MN×tan60°＝9×＝9．在Rt△BMN中，BN＝MN×tan∠BMN＝MN×tan30°＝9×＝3．∴AB＝AN﹣BN＝9﹣3＝6．则A到B的平均速度为：＝＝10≈17.3（米/秒）．故答案为：17.3．17．解：连接AB、AD、AC，过点A作AE⊥BC于E，则∠AEB＝∠AEC＝90°，由题意得：点A、B在圆D上，∴DB＝DA，在Rt△ABE中，∠BAE＝15°，∴∠DBA＝∠DAB＝75°，∠DAE＝60°，∵DA＝10米，∴AE＝5（米），∴BE＝AE×tan15°≈5×0.27＝1.35（米），∵∠EAC＝76°，∴CE＝AE×tan76°≈5×4.01＝20.05（米），∴BC＝BE+CE＝1.35+20.05≈21（米），答：摩天轮顶端B与地面的距离约为21米．18．解：（1）如图2，过点A作AH⊥OF于H，∵sin O＝＝0.6，∴AH＝20×0.6＝12（cm），∴OH＝＝＝16（cm），∴BH＝16﹣7＝9（cm），∴AB＝＝＝15（cm）；（2）∵∠AOB＝45°，AH⊥OF，∴AH＝OH＝10（cm），∴BH＝＝＝5（cm），∴OB＝OH﹣BH＝14﹣5＝9（cm），答：时窗钩端点B与点O之间的距离为9cm．19．解：过A作AP⊥DM于P，AH⊥CD于H，过B作BN⊥AH于N，∵tan∠ABM＝，∴设AP＝BN＝2x，AN＝PB＝5x，∵BD＝2，CD＝3.4，∴HN＝2，CH＝3.4﹣2x，∴AH＝5x+2，∵∠ACD＝45°，∴AH＝CH，∴3.4﹣2x＝5x+2，解得：x＝0.2，∴PB＝1，AP＝0.4，∴AB＝＝＝（米），答：显示屏的宽AB的长为米．20．解：由题意得，∠ABD＝90°，∠D＝20°，∠ACB＝31°，CD＝13，在Rt△ABD中，∵tan∠D＝，∴BD＝＝，在Rt△ABC中，∵tan∠ACB＝，∴BC＝＝，∵CD＝BD﹣BC，∴13＝，解得AB≈11.7米．答：水城门AB的高为11.7米．21．解：如图，延长CD交AB于E，∵i＝1：2.4，∴，∴，∵AC＝7.2，∴CE＝3，∵CD＝0.4，∴DE＝2.6，过点D作DH⊥AB于H，∴∠EDH＝∠CAB，∵，∴，，答：该车库入口的限高数值为2.4米．22．解：（1）过点P作PE∥MN，交B栋楼与点E，则四边形PEMN为矩形．∴EP＝MN由题意知：∠EPD＝55.7°∠EPC＝30°．在Rt△ECP中，EC＝tan∠EPC×EP＝tan30°×EP＝EP≈0.58EP，在Rt△EDP中，ED＝tan∠EPD×EP＝tan55.7°×EP≈1.47EP，∵CD＝ED﹣EC，∴1.47EP﹣0.58EP＝44.5∴EP＝MN＝50（m）答：楼间距MN为50m．（2）∵EC＝0.58EP＝0.58×50＝29（m）∴CM＝90﹣29＝61（m）∵61÷3≈20.3≈21（层）答：点C位于第21层．23．解：∵AH⊥直线l，∴∠AHD＝90°，在Rt△ADH中，tan∠ADH＝，∴DH＝＝，在Rt△BDH中，tan∠BDH＝，∴DH＝＝，∴＝，解得：AB≈5.3m，答：该古塔塔刹AB的高为5.3m．24．解：（1）根据题意，得AB＝20，∠ABC＝70°，CH＝BD＝2，在Rt△ACB中，∵∠ACB＝90°，∴AC＝AB•sin70°＝20×0.94＝18.8，∴AH＝20.8．答：这辆吊车工作时点A离地面的最大距离AH为20.8米；（2）设这次王师傅所开的吊车的速度为每小时x千米，由题意，得，解得，x1＝60，x2＝﹣40，经检验：x1＝60，x2＝﹣40都是原方程的解，但x2＝﹣40符合题意，舍去，答：这次王师傅所开的吊车的速度为每小时60千米．25．解：（1）作AF⊥BC交BC于点F，交DE于点E，如右图所示，由题意可得，CD＝EF＝3米，∠B＝22°，∠ADE＝45°，BC＝21米，DE＝CF，∵∠AED＝∠AFB＝90°，∴∠DAE＝45°，∴∠DAE＝∠ADE，∴AE＝DE，设AF＝a米，则AE＝（a﹣3）米，∵tan∠B＝，∴tan22°＝，即，解得，a＝12，答：城门大楼的高度是12米；（2）∵∠B＝22°，AF＝12米，sin∠B＝，∴sin22°＝，∴AB＝32，即A，B之间所挂彩旗的长度是32米．。

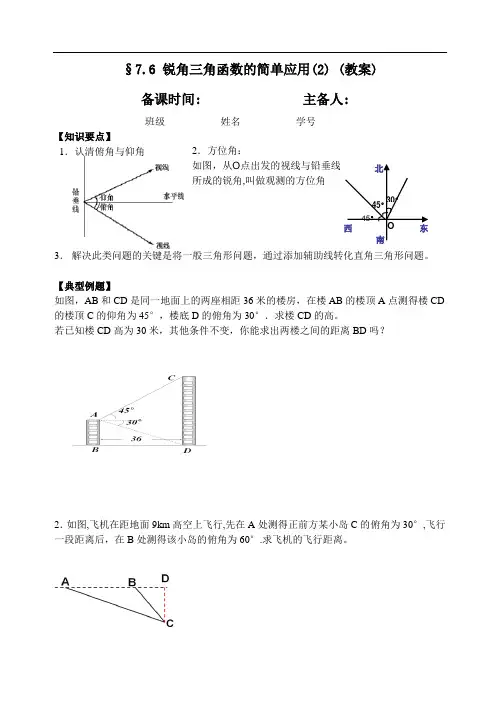
§7.6 锐角三角函数的简单应用(2) (教案)备课时间: 主备人:班级__________ 姓名__________ 学号_________【知识要点】1．认清俯角与仰角3． 解决此类问题的关键是将一般三角形问题，通过添加辅助线转化直角三角形问题。

【典型例题】如图，AB 和CD 是同一地面上的两座相距36米的楼房，在楼AB 的楼顶A 点测得楼CD 的楼顶C 的仰角为45°，楼底D 的俯角为30°．求楼CD 的高。

若已知楼CD 高为30米，其他条件不变，你能求出两楼之间的距离BD 吗？2．如图,飞机在距地面9km 高空上飞行,先在A 处测得正前方某小岛C 的俯角为30°,飞行一段距离后，在B 处测得该小岛的俯角为60°.求飞机的飞行距离。

2．方位角： 如图，从O 点出发的视线与铅垂线 所成的锐角,叫做观测的方位角3．如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.4．气象局发出预报:如图, 沙尘暴在A市的正东方向400km的B处以40km/h的速度向北偏西600的方向转移,距沙尘暴中心300km的范围内将受到影响,A市是否受到这次沙尘暴的影响?如果受到影响,将持续多长时间?5．如图, 海上有一灯塔P, 在它周围3海里处有暗礁. 一艘客轮以9海里/时的速度由西向东航行, 行至A点处测得P在它的北偏东60度的方向, 继续行驶20分钟后, 到达B处又测得灯塔P在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?课后练习：【基础演练】1．如图，一座塔的高度TC=120m ，甲、乙两人分别站在塔的西、东两侧的点A 、B 处，测得塔顶的仰角分别为28º、15º。

求A 、B 两点间的距离_________（精确到0.1米） (参考数据：tan 280.53,tan150.27︒≈︒≈)2．如图所示，小华同学在距离某建筑物6米的点A 处测得广告牌B 点、C 点的仰角分别为60°和45°，则广告牌的高度BC 为_____________米(结果保留根号)．3．如图，小明同学在东西方向的环海路A 处，测得海中灯塔P 在北偏东60°方向上，在A 处向东500米的B 处，测得海中灯塔P 在北偏东30°方向上，则灯塔P 到环海路的距离PC＝米（结果保留根号）题1图题2图 题3图 4．如图，在某广场上空飘着一只汽球P ，A 、B 是地面上相距90米的两点，它们分别在汽球的正西和正东，测得仰角∠PAB=45o ，仰角∠PBA=30o ，求汽球P 的高度。