下载文档原格式
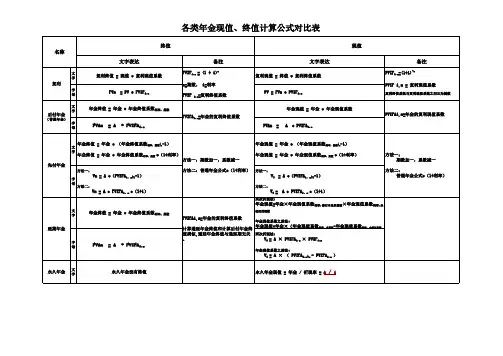
普通年金现值系数表普通年金现值系数表年金现值系数，就是按利率每期收付一元钱折成的价值。
也是知道了现值系数就可求得一定金额的年金现值之和。
别称等额支付系列现值系数，年金因子表达式PVA/A=1/i -1/i(1+i)^n应用学科经济学;金融学;建筑工程经济适用领域范围建筑工程概念首先说什么是年金，年金是每隔相等时间间隔收到或支付相同金额的款项，如每年年末收到养老金10000元，即为年金。
年金现值是指按照利率把发生期收到的年金利息折成价值之和。
计算公式年金现值系数公式:PVA/A =1/i-1/[i (1+i)^n]其中i表示报酬率，n表示期数,PVA表示现值,A表示年金。
比如你在银行里面每年年末存入1200元，连续5年，年利率是10%的话，你这5年所存入资金的现值=1200/(1+10%)+1200/(1+10%)^2+1200/(1+10%)^3+1200/(1+10%)^4+1200/(1+10%)^5= 1200*[1-(1+10%)]/10%=1200*3.7908=4548.96 这是终值的算法1200元就是年金，4548.96就是年金现值，1/10%-1/10%*1.1=3.7908就是年金现值系数。
不同的报酬率、不同的期数下，年金现值系数是不相同的。
终值1、普通年金终值指一定时期内，每期期末等额收入或支出的本利和，也就是将每一期的金额，按复利换算到最后一期期末的终值，然后加总，就是该年金终值.例如:每年存款1元，年利率为10%，经过5年，逐年的终值和年金终值，可计算如下:1元1年的终值=(1+10%)=1.100(元)1元2年的终值=(1+10%)=1.210(元)1元3年的终值=(1+10%)=1.331(元)1元4年的终值=(1+10%)=1.464(元)1元5年的终值=(1+10%)5=1.611元1元年金5年的终值=6.715(元)如果年金的期数很多，用上述方法计算终值显然相当繁琐。
终值和现值的计算公式是什么？
公式如下：
1、年金终值计算公式为：F=A*(F/A，i，n)=A*(1+i)n-1/i
其中(F/A，i，n)称作“年金终值系数”。
2、年金现值计算公式为：P=A*(P/A，i，n)=A*[1-(1+i)-n]/i
其中(P/A，i，n)称作“年金现值系数”。
扩展资料：
如果年金的期数n很多，用上述方法计算现值显然相当繁琐。
由于每年支付额相等，折算现值的系数又是有规律的，所以，可找出简便的计算方法。
先付年金现值：是其最后一期期末时的本利和，相当于各期期初等额收付款项的复利现值之和。
n期先付年金与n期普通年金的收付款次数相同，但由于付款时间不同，n期先付年金现值比n期普通年金的现值多计算一期利息。
因此在n期普通年金现值的基础上乘以（1+i）而将分母加1就得出n期先付年金的现值了。
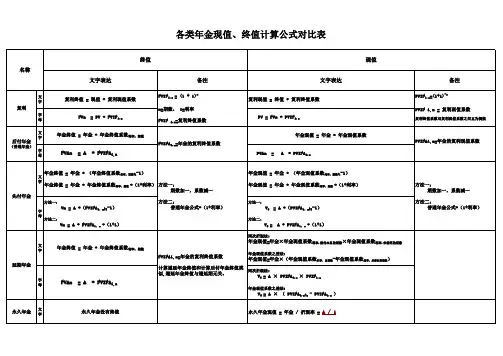
PV=P*[1-(1+r)^(-n)]/r
其中
PV是普通年金的现值
P是每年的付款金额
r是每年的折现率（利率）
n是年金的期限（年数）。
这个公式是基于贴现的原理，即将未来的现金流折现到现在的价值。
公式的步骤如下：
1.将每年付款金额P乘以n，得到总金额。
2.计算折现率r+1，并将其与年金的期限n相乘，得到一个值。
3.将这个值除以折现率r，并得到一个小数。
4.从1中减去3中得到的小数，得到一个新的值。
5.将1中得到的总金额与4中得到的新值相乘，得到普通年金的现值PV。
需要注意的是，如果折现率r小于0，或者年金的期限n为无穷大，
那么公式中的计算结果将趋向于无穷大。
这是因为未来的现金流在无穷时
间内折现的价值会趋近于无穷大。
在实际应用中，这种情况很少发生。
此外，如果每年付款金额P是不变的，并且每年付款的时间间隔是相
等的，那么该年金被称为等额年金。
在这种情况下，计算公式可以简化为：PV=P*[(1-(1+r)^(-n))/r]
这是因为等额年金的付款金额是不变的，所以每一期的现值计算可以通过简化公式得到。
年金现值计算方法详解年金是一种常见的投资方式，计算年金的现值是帮助投资者了解未来现金流的价值。
合理的现值计算方法可以帮助投资者做出明智的决策，下面我们来详细讨论年金现值的计算方法。
一、普通年金现值计算方法普通年金是指每期支付的金额相同的年金，其现值计算方法可以通过如下公式进行：\[PV = PMT \times \left(\dfrac{1 - (1 + r)^{-n}}{r}\right)\]其中，PV代表年金的现值，PMT代表每期支付的金额，r代表利率，n代表年数。
二、年金现值的不同情况计算方法1. 当年金是年末支付时，现值公式为：\[PV = PMT \times \left(\dfrac{1 - (1 + r)^{-n}}{r}\right)\]2. 当年金是年初支付时，现值公式为：\[PV = PMT \times \left(\dfrac{1 - (1 + r)^{-n}}{r}\right) \times (1 + r)\]3. 当年金是不定期支付时，现值公式为：\[PV = FV \times \left(\dfrac{1}{(1 + r)^n}\right)\]其中，FV代表年金的终值。
三、利用现金流表计算年金现值除了使用上述的公式计算年金的现值，我们也可以通过制作现金流表的方式来计算年金的现值。
现金流表可以清晰地展示出每期的现金流量，帮助投资者更直观地了解年金的价值。
四、利率对年金现值的影响利率是影响年金现值的重要因素之一。
当利率上升时，年金的现值会下降，因为未来现金流的折现率变高；反之，当利率下降时，年金的现值会上升。
五、风险对年金现值的影响除了利率变动，风险也会对年金的现值产生影响。
高风险的年金会被折现得更低，因为投资者认为高风险带来的未来现金流不稳定。
六、结语通过上述的详细讨论，我们了解了年金现值的计算方法及影响因素。
在进行投资决策时，投资者应该充分考虑年金的现值，以便做出科学的投资规划。
年金是指按照一定的时间间隔、一定的利率和一定的期限，定期支付的一笔固定金额的现金流。
年金的计算可以使用不同的公式，下面将总结一些常用的年金公式。
1.普通年金公式：普通年金是指在一定的时间间隔内，每期支付相同数额的现金流。
普通年金公式包括PV（现值）、FV（未来值）、PMT（每期支付金额）、n （总期数）、i（利率）五个变量。
普通年金公式如下：PV=PMT×[(1-(1+i)^(-n))/i]FV=PMT×[((1+i)^n-1)/i]其中PV是现值，指将未来的现金流折算到现在所对应的金额；FV是未来值，指在一定期限内所有现金流的总和；PMT是每期支付金额；n是总期数；i是利率。
2.分期付款公式：分期付款是一种特殊的年金，在分期付款中，每期支付的金额是不同的。
分期付款公式包括PV（现值）、FV（未来值）、n（总期数）三个变量，公式如下：PV=C1/(1+i)^1+C2/(1+i)^2+…+Cn/(1+i)^nFV=C1×(1+i)^1+C2×(1+i)^2+…+Cn×(1+i)^n其中PV是现值，指将未来的现金流折算到现在所对应的金额；FV是未来值，指在一定期限内所有现金流的总和；C1、C2、…、Cn是每期支付的金额；n是总期数；i是利率。
3.延期年金公式：延期年金是指在一定的时间间隔内，推迟一段时间后开始支付的现金流。
延期年金公式包括PV（现值）、FV（未来值）、PMT（每期支付金额）、d（延迟期数）、n（总期数）、i（利率）六个变量，公式如下：PV=PMT×[(1-(1+i)^(-n))/i]×(1+i)^-dFV=PMT×[((1+i)^n-1)/i]×(1+i)^-d其中PV是现值，指将未来的现金流折算到现在所对应的金额；FV是未来值，指在一定期限内所有现金流的总和；PMT是每期支付金额；d是延迟期数；n是总期数；i是利率。
现值年金6个公式【原创实用版】目录1.现值年金的概念2.现值年金的 6 个公式3.公式的运用和实例正文一、现值年金的概念现值年金是指在一定的利率下，一定期限内每期等额收付款项的现值之和。
简单来说，就是将未来一系列定期支付的现金流量折算到现在的价值总和。
现值年金在金融、投资等领域具有广泛的应用，例如计算保险费、投资回报等。
二、现值年金的 6 个公式1.普通年金现值公式普通年金现值公式为：P = R × (1 - (1 + i)^(-n)) / i其中，P 表示现值年金，R 表示每期支付的金额，i 表示利率，n 表示期数。
2.先付年金现值公式先付年金现值公式为：P = R × (1 - (1 + i)^(-n)) / i × (1 + i) 其中，P 表示现值年金，R 表示每期支付的金额，i 表示利率，n 表示期数。
3.等额本金现值公式等额本金现值公式为：P = Σ(R × (1 - (1 + i)^(-n+k))) / i其中，P 表示现值年金，R 表示每期支付的金额，i 表示利率，n 表示期数，k 表示每期支付的次数。
4.等额本息现值公式等额本息现值公式为：P = Σ(R × (1 + i)^(-n+k)) / i其中，P 表示现值年金，R 表示每期支付的金额，i 表示利率，n 表示期数，k 表示每期支付的次数。
5.递增年金现值公式递增年金现值公式为：P = Σ(R × (1 - (1 + i)^(-n+k))) / i ×(1 + i)^k其中，P 表示现值年金，R 表示每期支付的金额，i 表示利率，n 表示期数，k 表示每期支付的次数。
6.递减年金现值公式递减年金现值公式为：P = Σ(R × (1 + i)^(-n+k))) / i × (1 + i)^(-k)其中，P 表示现值年金，R 表示每期支付的金额，i 表示利率，n 表示期数，k 表示每期支付的次数。
