扩散双电层理论和Zeta 电势
- 格式:pdf
- 大小:322.80 KB
- 文档页数:8

Zeta电位概念及检测原理浅析一、Zeta电位的概念Zeta电位是一个表征分散体系稳定性的重要指标。
粒子表面存在的净电荷,影响粒子周围区域的离子分布,导致接近表面抗衡离子(与粒子电荷相反的离子)浓度增加。
于是,每个粒子周围均存在双电层。
根据Stern双电层理论可将双电层分为两部分,即内层区和外层分散区(又称Stern层和扩散层)。
在内层区离子与粒子紧紧地结合在一起;在外层分散区,离子不那么紧密的与粒子相吸附。
在分散区内,有一个抽象边界,在边界内的离子和粒子形成稳定实体。
当粒子运动时(如由于重力),在此边界内的离子随着粒子运动,但此边界外的离子不会随着粒子运动。
这个边界称为流体力学剪切层或滑动面(slipping plane)。
在这个边界上存在的电位即称为Zeta电位。
上述描述用通俗的语言表述就是:带电颗粒吸附分散系中的反相电荷的粒子,颗粒表面的离子被强力束缚,距离较远的离子则形成一个相对松散的电子云,电子云的内外电位差就叫Zeta电位。
Zeta电位也称电动电位(只有当胶体颗粒在介质中运动时才会表现出来),实际上就是扩散层的电位差。
二、影响Zeta电位的因素分散体系的Zeta电位可因下列因素而变化:1. pH 的变化2. 溶液(分散剂)电导率的变化3. 特殊添加剂及其浓度Zeta电位与pH值影响zeta电位重要的因素是pH值,当谈论zeta电位时不指明pH值没有意义。
假设悬浮液中有一个带负电的颗粒,往这一悬浮液中加入碱性物质,颗粒更难以得到正电。
如果往悬浮液中加入酸性物质,在一定程度时,颗粒的电荷将会被中和。
进一步加入酸,颗粒将会带更多的正电。
用Zeta电位与pH值作相关曲线图,在低pH值点将是正的,在高pH值点将是负的,曲线有一点会通过零zeta电位,这一点称为等电点,是相当重要的一点,通常在这一点胶体是不稳定的。
电位滴定法可用于测定样品的等电点。
电位滴定图可以显示Zeta电位与pH值之间的关系变化。

64扩散双电层理论和Zeta 电势胶体粒子的表面常因解离、吸附、极化、摩擦等原因而带电,分散介质则带反电荷,因此,在相界面上便形成了双电层。
胶体的这种结构决定了它的电学性质,并对其稳定性起着十分重要的作用。
本专题便来讨论胶体的双电层结构,并从中引出一个决定胶体电学性质和稳定性的重要指标——ς(Zeta)电势。
1.双电层模型(1) Helmholtz 模型1879年,Helmholtz 在研究胶体在电场作用下运动时,最早提出了一个双电层模型。
这个模型如同一个平板电容器,认为固体表面带有某种电荷,介质带有另一种电荷,两者平行,且相距很近,就像图64-1所示。
图64-1 Helmholtz 双电层模型按照这个模型,若固体表面的电势为0ψ,正、负电荷的间距为δ,则双电层中的电势随间距直线下降,且表面电荷密度σ与电势0ψ的关系如下式表示δεψσ0= (64-1) 式中ε为介质的介电常数。
显然,这是一个初级双电层模型,它只考虑到带电固体表面对介质中反离子的静电作用,而忽视了反离子的热运动。
虽然,它对胶体的早期研究起过一定的作用,但无法准确地描述胶体在电场作用下的运动。
(2) Gouy(古依)—Chapman (恰普曼)模型由于Helmholtz 模型的不足,1910和1913年,Gouy 和Chapman 先后作出改进,提出了一个扩散双电层模型。
这个模型认为,介质中的反离子不仅受固体表面离子的静电吸引力,从而使其整齐地排列在表面附近,而且还要受热运动的影响,使其离开表面,无规则地分散在介质中。
这便形成如图64-2所示的扩散双电层结构。
图64-2 Gouy —Chapman 扩散双电层模型他们还对模型作了定量的处理,提出了如下四点假设:① 假设表面是一个无限大的平面,表面上电荷是均匀分布的。
② 扩散层中,正、负离子都可视为按Boltzmanm 分布的点电荷。
③ 介质是通过介电常数影响双电层的,且它的介电常数各处相同。


zeta-电位Zeta电位是指电双层中离子层的电位差,也叫做表面电位,是表征固体颗粒表面电荷性质的一个重要参数。
Zeta电位可以用来定量描述固体颗粒的表面电荷分布情况,如电荷的分布、电荷的大小和电荷的偏置程度等。
对于胶体体系,Zeta电位可以用来判断胶体颗粒的稳定性,评估溶液中的胶体性质。
在固液界面处,由于固体颗粒表面和溶液中的电解质之间的相互作用,会形成一个称为电双层的结构。
电双层由两层电荷组成,靠近固体表面的一层是吸附在固体表面的离子,称为固定电荷层;远离固体表面的一层是游离离子的电层,又称为扩散电荷层。
固液界面处的电势差就是Zeta电位。
Zeta电位是通过测量物质在交变电场中的电泳迁移速度来确定的。
在所施加的电场中,固体颗粒会自发地向电场的一侧迁移,迁移速度与离子在扩散电荷层中的浓度和固体表面电荷密度有关。
通过测量颗粒的迁移速度,可以计算出Zeta 电位。
具体的计算公式为:V = μE/ε其中,V是Zeta电位,μ是颗粒的电泳迁移速度,E是电场强度,ε是介质的介电常数。
Zeta电位的数值通常以毫伏为单位。
Zeta电位的数值可以用来判断固体颗粒的表面电荷特性。
当Zeta电位为正时,表示固体表面呈现阳电荷,这意味着颗粒表面上吸附了负电荷离子,例如氧化物颗粒表面吸附了羟基离子。
相反,当Zeta电位为负时,表示固体表面呈现阴电荷,这意味着颗粒表面上吸附了正电荷离子,例如金属离子或氨基离子等。
Zeta 电位的绝对值越大,表示颗粒表面的电荷越多,颗粒的稳定性越高。
Zeta电位对于胶体体系的稳定性也有重要的影响。
当胶体颗粒中的Zeta电位绝对值小于30mV时,胶体颗粒之间的排斥力不够强,容易出现颗粒的聚集和沉降现象,胶体体系不稳定。
而当Zeta电位的绝对值大于30mV时,胶体颗粒之间的排斥力可以有效地抑制颗粒的聚集和沉降,胶体体系则比较稳定。
总之,Zeta电位是描述固体颗粒表面电荷和介质中离子浓度分布的一个重要参数,可以用来评估固体颗粒表面电荷特性和胶体体系的稳定性。



双电层理论表面物理化学所涉及的内容非常宽广,固体在溶液中的荷电性质,实际上影响着固体表面性质和界面区的电荷转移反应及其进行的速度。
由于多种极其重要的表面电化学效应的发现,表面电化学引起了许多种科学家的重视和研究。
第一节 双 电 层2.1.1 双电层的产生在自然界中,固体与液体接触时,固体表面的荷电现象实际上是普遍存在的。
它导致了固—液界面的液体一侧带着相反电荷,这种界面电荷影响界面周围介质中的离子分布,与界面电荷符号相反的介质中的离子被吸向界面(这种离子称为反离子Counter -ions ),而相同符号的离子(称为同离子Co -ions )则被排离界面。
与此同时,离子的热运动又促使它们均匀混合在一起。
因此,在带电界面上形成一个扩散双电层(diffuse double layer )。
所谓扩散,就是界面周围介质中的反离子的过量是以扩散形式分布的,而不是非常整齐地集中排列在带电界面的周围。
例如,人体内与血液接触的动静脉壁和血液中胶粒等界面区都存在双电层结构,致使血液在血管中畅通无阻地流动以输送全身新陈代谢的营养而不产生血栓。
双电层理论研究反离子的扩散分布和带电界面的性质。
固体在溶液中荷电而构成双电层的原因,除了外加电场之外,大致上可归纳为以下几种情况: ① 电离作用固体表面在溶液中产生电离或溶液中的电离成分依靠某种结合力与固体表面结合而使其荷电。
例如,玻璃与水接触时,玻璃中的硅酸盐可电离出钾离子、钠离子或氢离子等,于是使玻璃带负电性而溶液带正电性;蛋白质分子具有的羧基(—COOH)和胺基(—NH 2)官能团,当pH 值降低时(酸性),溶液中电离的H +与胺基以氢键结合,从而使蛋白质带正电,-NH 2+H 2O -NH 3++OH -,而溶液一侧带负电,即在羧酸介质中—COOH 的电离被高氢浓度离子所抑制:—COOH+H 2O -COO -+H 3O+ 当pH 值升高时(碱性),蛋白质的羧基电离而使其带负电。

二、双电层与ζ电势(1)胶团结构因为胶粒的大小介于1~100nm 之间,故每一胶粒必然是由许多分子或原子聚集而成的。
我们往往将组成胶粒核心部分的固态微粒称为胶核。
例如用稀AbNO3溶液和KI 溶液制备AgI 溶胶时,由反应生成的AgI 微粒首先形成胶核。
胶核常具有晶体结构,它很容易从溶液中选择性地吸附某种组成与之相似的离子而使胶核带电,因此,胶核实际上应包括固体微粒表层的带电离子。
胶核表层荷电后,留在溶液中的反离子(即与被胶核吸附的离子带相反电荷的离子)由于离子静电作用必围绕于胶核周围,但离子本身的热运动又使一部分反离子扩散到较热的介质中去。
可见,一些紧紧地吸引于胶核近旁的反离子与被吸附于胶核表层的离子组成"紧密层",而其余的反离子则组成"扩散层"。
胶核与紧密层组成胶粒(Colloidal particle),而胶粒与扩散层中的反离子组成胶团(micelle)。
胶团分散于液体介质中便是通常所说的溶胶。
用AgNO3稀溶液和KI 溶液制备AgI 溶胶时,其胶团结构式可以表示为:有关双电层的模型请参考电化学中"扩散双电层"部分内容。
以下仅介绍滑动面和ζ电势。
滑动面是当固液两相发生相对移动时呈现在固液交界处的一个高低不平的曲面,它位于紧密层之外,扩散层之中且距固体表面的距离约为分子直径大小处(见图13-17(动画观看))。
滑动面与溶液本体之间的电势差称为ζ电势。
有时也称为电动电势,这是因为只有当固液两相发生相对移动时才有ζ电势,可见,ζ电势是滑动面存在的结果,而滑动面是ζ 电势产生的基础。
当电解质的浓度增加时,介质中反离子的浓度加大,将压缩扩散层使其变薄,把更多的反离子挤进滑动面以内,使ζ电势在数值上变小,如图13-18所示。
当电解质的浓度足够大时,可使ζ电势为零。
此时相应的状态,称为等电态。
处于等电态的粒子是不带电的,电泳,电渗的速度也必然为零。

Zeta电位及其测定方法Zeta电位(Zeta potential),又叫电动电位或电动电势(ζ电位或ζ电势),是指滑动面(Shear Plane)的电位。
它是表征胶体分散系稳定性的重要指标。
目前测量Zeta电位的方法主要有电泳法、电渗1、Zeta电位及Stern模型1.1胶体双电层理论、胶团结构:胶体粒子间的静电排斥力减少相互碰撞的频率,使聚结的机会大大降低,从而增加了相对的稳定性。
当固体与液体接触时,可以是固体从溶液中选择性吸附某种离子,也可以是固体分子本身发生电离作用而使离子进入溶液,以致使固液两相分别带有不同符号的电荷,在界面上形成了双电层的结构。
对于双电层的具体结构,最早于1879年Helmholz(亥姆霍兹)提出平板型模型;1910年Gouy和1913年Chapmar修正了平板型模型,提出了扩散双电层模型;后来Stern又提出了Stern模型。
1.1.1亥姆霍兹平板型模型亥姆霍兹认为固体的表面电荷与溶液中带相反电荷的(即反离子)构成平行的两层,如同一个平板电容器。
整个双电层厚度为汉固体表面与液体内部的总的电位差即等于热力学电势仰,在双电层内,热力学电势呈直线下降。
在电场作用下,带电质点和溶液中的反离子分别向相反方向运动。
该模型过于简单,由于离子热运动,不可能形成平板电容器也不能解释带电质点的表面电势仰与质点运动时固液两相发生相对移动时所产生的电势差—Zeta电势(电动电势)的区别,也不能解释电解质对Zeta电势的影响等。
1.1.2扩散双电层模型Gouy(古依)和Chapman(查普曼)认为,由于正、负离子静电吸引和热运动两种效应的结果,溶液中的反离子只有一部分紧密地排在固体表面附近,相距约一、二个离子厚度称为紧密层;另一部分离子按一定的浓度梯度扩散到本体溶液中,离子的分布可用玻兹曼公式表示,称为扩散层。
双电层由紧密层和扩散层构成。
移动的切动面为AB面。
Gouy一ChaPman理论虽然考虑到了静电吸引力和热运动力的平衡,但是它没有考虑到固体表面上的吸附作用,尤其是特殊的吸附作用。

zeta电位检测原理
Zeta电位检测原理是基于电二重层理论的。
电二重层是电解质溶液与电极表面的分界处形成的电荷层,包括紧贴电极表面的一个物理吸附层和一个均匀分布的电解质离子层。
在Zeta电位检测中,通常使用电动势法或光散射法来测量Zeta电位。
在电动势法中,通过施加一个电场,在电解质溶液中部分离子会向电极移动。
这些移动的离子会产生一个电流,称为Zeta电流。
根据法拉第定律,Zeta电流与电极表面电势差之间存在一个线性关系。
测量这个电势差,即可得到Zeta 电位。
光散射法是另一种常用的Zeta电位检测方法。
根据斯托克斯散射公式,当悬浊液中的颗粒受到光的照射时,颗粒会发生散射现象。
通过测量散射角度和散射强度的变化,可以得到颗粒的表面电势差,即Zeta电位。
总体来说,Zeta电位的测量原理是通过施加电场或观察光散射的变化来获得电解质溶液中颗粒的表面电势差,从而得到Zeta电位的数值。
溶液中zeta电位的原理与应用溶液的zeta电位是指溶质颗粒在溶液中形成的电荷层与溶剂的界面处的电位差。
它是表征溶质颗粒在溶液中稳定性和相互作用的重要参数。
本文将介绍zeta电位的概念、测量方法、影响因素和应用领域。
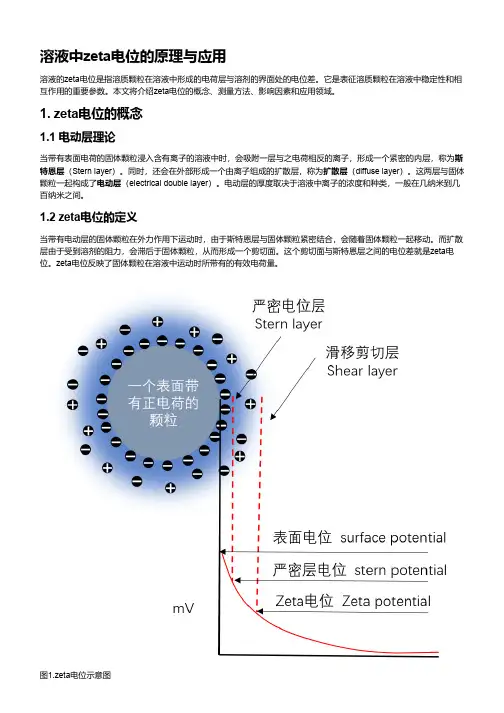
1. zeta电位的概念1.1 电动层理论当带有表面电荷的固体颗粒浸入含有离子的溶液中时,会吸附一层与之电荷相反的离子,形成一个紧密的内层,称为斯特恩层(Stern layer)。
同时,还会在外部形成一个由离子组成的扩散层,称为扩散层(diffuse layer)。
这两层与固体颗粒一起构成了电动层(electrical double layer)。
电动层的厚度取决于溶液中离子的浓度和种类,一般在几纳米到几百纳米之间。
1.2 zeta电位的定义当带有电动层的固体颗粒在外力作用下运动时,由于斯特恩层与固体颗粒紧密结合,会随着固体颗粒一起移动。
而扩散层由于受到溶剂的阻力,会滞后于固体颗粒,从而形成一个剪切面。
这个剪切面与斯特恩层之间的电位差就是zeta电位。
zeta电位反映了固体颗粒在溶液中运动时所带有的有效电荷量。
图1.zeta电位示意图2. zeta电位的测量方法zeta电位的测量方法主要有两种:电泳法(electrophoresis)和流变法(rheology)。
2.1 电泳法电泳法是利用带有电动层的固体颗粒在外加电场作用下产生运动速度的现象,通过测量其运动速度来计算zeta电位。
根据亥姆霍兹-斯莫卢霍夫斯基方程(Helmholtz-Smoluchowski equation),zeta电位与运动速度成正比,即:ζ=εε0μE η其中,ζ是zeta电位,ε是介电常数,ε0是真空介电常数,μ是迁移率,E是外加电场强度,η是溶液粘度。
电泳法测量zeta电位的仪器称为Zetasizer。
它主要由激光光源、样品池、检测器和计算机组成。
其工作原理是将激光束照射到样品池中,观察样品中固体颗粒在外加交变电场作用下的散射光信号,利用多普勒效应(Doppler effect)分析其运动速度,从而计算出zeta电位。
第十二章胶体化学扩散双电层理论溶胶粒子为什么带电?固体表面可选择性地吸附某种离子而带电AgI溶胶:溶液中I—过量时,可吸附I—而带负电,溶液中Ag+过量时,可吸附Ag+ 而带正电。
电离:固体表面上的分子在溶液中发生电离而带电蛋白质中的氨基酸分子:在pH低时氨基形成—NH3+而带正电;在pH 高时羧基形成—COO—而带负电。
带电的固体表面在静电力作用下,必然要吸引等电量的、与固体表面上带有相反电荷的离子(即反离子或异电离子)环绕在固体粒子的周围,这样便在固液两相之间形成了双电层。
几个有代表性的关于双电层的理论:亥姆霍兹模型、古依—查普曼模型、斯特恩模型。
常用名词:双电层:质点表面电荷与周围介质中的反离子构成的电层。
表面电势 0:带电质点表面与液体的电势差。
电势:固、液两相发生相对运动的边界处与液体内部的电势差。
亥姆霍兹(Helmholtz)模型1879年,亥姆霍兹首先提出在固液两相之间的界面上形成类似于平行板电容器那样的双电层:正负离子整齐地排列于界面层的两侧;两层间距与离子半径相当;外电场作用下,带电质点和反离子分别向相反方向运动。
缺点:1)不能解释表面电势 0与ζ电势的区别;2)不能解释电解质对ζ电势的影响。
古依和查普曼(Gouy—Chapman)模型1910年,古依和查普曼提出了扩散双电层理论静电力:使反离子趋向表面热运动:使反离子均匀分布总结果:反离子呈扩散状态分布古依和查普曼给出−−距表面x处的电势 与表面电势为 0的关系:式中κ的倒数κ-1具有双电层厚度的意义。
古依-查普曼模型正确反映了反离子在扩散层中分布的情况及相应电势的变化,这些观点在今天看来仍是正确的。
缺点:把离子视为点电荷,没有考虑离子的溶剂化; 没有考虑固体表面上的固定吸附层。
斯特恩(Stern )模型1924年斯特恩提出扩散双电层:离子有一定的大小;部分反离子被牢固吸附,形成固定吸附层或斯特恩层。
Stern 模型:固定层+扩散层三个面、三个电势固体表面 Stern 面: Stern 层中反离子 电性中心所形成的假想面 滑动面:固液两相发生相对移动时界面三 个 面 热力学电势 0:固体面—溶 液本体Stern 电势ϕδ: Stern 面—溶液本体ζ 电势: 滑动面—溶液本体 三个电势电解质的影响: 溶液中电解质浓度增加时,介质中反离子的浓度加大,将压缩扩散层使其变薄,把更多的反离子挤进滑动面以内,使ζ电势在数值上变小直至为0ζ 电势的大小,反映了胶粒带电的程度 ζ = 0 时,为等电态,胶粒间无静电斥力, 溶胶极易聚沉。
zeta电位和双电层的关系
Zeta电位和双电层之间存在密切关系。
双电层是粒子表面存在的净电荷影响粒子界面周围区域的离子分布,导致接近表面抗衡离子(与粒子电荷相反的离子)浓度增加的现象。
这些带电粒子在液体中形成了一个双电层结构,其中内层区离子与粒子紧密结合,外层分散区离子则相对较松散。
在双电层结构中,存在一个抽象边界,被称为流体力学剪切层或滑动面(slipping plane),在这个边界上的电位即称为Zeta电位。
Zeta电位是一个重要的物理量,可以表征分散体系的稳定性。
当粒子运动时(如由于重力),滑动面内的离子会随着粒子运动,但滑动面外的离子不会随着粒子运动。
因此,Zeta电位和双电层是相互关联的,它们共同作用维持着分散体系的稳定性。
通过对Zeta电位的研究,可以更好地理解粒子在液体中的行为和性质。
斯特恩模型的三个电势zeta斯特恩(Stern)是在古依(Gouty)—查普曼(Chapman)分散双层模型基础上发展起来的,同时又吸取了亥姆霍茨紧密双层模型的合理部分。
1924年,斯特恩提出一种改进后的Zeta电位双层模型。
根据这一模型,双电层可以同时具有紧密性和分散性。
这种模型认为:当电极表面电荷密度较大,同时电解质溶液的总浓度较大(约几摩尔/升以上)时,液相中离子倾向于紧密地分布在界面上,这时可能形成所谓“紧密双电层”,与一个荷电的平板电容器相似。
如果溶液中离子浓度不够大,或是电极表面电荷密度比较小,则是由于离子热运动,致使溶液中的剩余电荷不可能全部集中排列在界面上,而使电荷分布具有一定的“分散性”。
这种情况下,双电层包括“紧密层”与“分散层”两部分。
设d为水化离子的半径,在与电极距离x=0至x=d的薄层中不可能存在电荷,也就是说,在紧密双电层中(x≤d)不存在离子电荷,故电场强度为恒指,电位梯度也保值不变,在此间隔中电位与x成线性变化,且此直线很陡。
在x>d的区间内,当x增大,电场强度及电位梯度的数值也随之变小,直至趋近于零。
因此在分散层中,电位ψ随距离x呈曲线变化,曲线的形状先陡后缓。
这时电极与溶液之间的zeta电位双电层斯特恩模型差ψ实际包含两个组成部分:①紧密双电层中的电位差,ψ减ψ1;②分散层中的电位差,ψ1.这里的ψ和ψ1都是相对溶液内部的电位(规定为零)而言的。
根据上面的讨论容易看出:如果电极表面所带电荷多,静电作用占优势,离子热运动的影响减小,双电层结构较紧密,在整个电位中,紧密层电位占地比例较大,即ψ1电位的值变小。
溶液浓度增大时,离子热运动变困难,故分散层厚度减小,ψ1的值也减小。
所以,电极表面带的电荷很多,并且溶液中离子的浓度很大时,分散层厚度几乎等于零,可以认为ψ1约等于0;反之,当金属表面所带电荷极少,且溶液很稀,则分散层厚度可以变得相当大,以至于近似认为双层中紧密层不复存在。
64扩散双电层理论和Zeta 电势胶体粒子的表面常因解离、吸附、极化、摩擦等原因而带电,分散介质则带反电荷,因此,在相界面上便形成了双电层。
胶体的这种结构决定了它的电学性质,并对其稳定性起着十分重要的作用。
本专题便来讨论胶体的双电层结构,并从中引出一个决定胶体电学性质和稳定性的重要指标——ς(Zeta)电势。
1.双电层模型(1) Helmholtz 模型1879年,Helmholtz 在研究胶体在电场作用下运动时,最早提出了一个双电层模型。
这个模型如同一个平板电容器,认为固体表面带有某种电荷,介质带有另一种电荷,两者平行,且相距很近,就像图64-1所示。
图64-1 Helmholtz 双电层模型按照这个模型,若固体表面的电势为0ψ,正、负电荷的间距为δ,则双电层中的电势随间距直线下降,且表面电荷密度σ与电势0ψ的关系如下式表示δεψσ0= (64-1) 式中ε为介质的介电常数。
显然,这是一个初级双电层模型,它只考虑到带电固体表面对介质中反离子的静电作用,而忽视了反离子的热运动。
虽然,它对胶体的早期研究起过一定的作用,但无法准确地描述胶体在电场作用下的运动。
(2) Gouy(古依)—Chapman (恰普曼)模型由于Helmholtz 模型的不足,1910和1913年,Gouy 和Chapman 先后作出改进,提出了一个扩散双电层模型。
这个模型认为,介质中的反离子不仅受固体表面离子的静电吸引力,从而使其整齐地排列在表面附近,而且还要受热运动的影响,使其离开表面,无规则地分散在介质中。
这便形成如图64-2所示的扩散双电层结构。
图64-2 Gouy —Chapman 扩散双电层模型他们还对模型作了定量的处理,提出了如下四点假设:① 假设表面是一个无限大的平面,表面上电荷是均匀分布的。
② 扩散层中,正、负离子都可视为按Boltzmanm 分布的点电荷。
③ 介质是通过介电常数影响双电层的,且它的介电常数各处相同。
④ 假设分散系统中只有一种对称的电解质,即正、负离子的电荷数均为z 。
于是,若表面电势为0ψ,相距x 处的电势为ψ,便可按Boltzmanm 分布定律,写出相距x 处的正、负离子的数密度为⎟⎠⎞⎜⎝⎛−=+kT ze n n ψexp 0 (64-2) ⎟⎠⎞⎜⎝⎛=−kT ze n n ψexp 0 (64-3) 式中0n 为0=ψ即距表面无限远处正或负离子的数密度。
距表面x 处的电荷密度当为()⎟⎠⎞⎜⎝⎛⋅−=⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛−=−=−+kT ze zen kT ze kT ze zen n n ze ψψψρsinh 2 exp exp 00 (64-4) 式中函数()y y y −−=e e 21sinh ,称为双曲正弦函数。
根据静电学中的Poisson 方程,电荷密度与电势间应服从如下关系ερψ−=∇2 (64-5) 式中2222222///z y x ∂∂+∂∂+∂∂=∇为Laplace 算符,ε为分散介质的介电常数。
对于表面为平面的情况,222/x ∂∂=∇ 因此⎟⎠⎞⎜⎝⎛⋅=−=∂∂kT ze zen x ψεερψsinh 2022 (64-6)这是一个二阶微分方程,满足如下边界条件:当0=x 时,0ψψ=;当∞=x 时,0=ψ,且0/=∂∂x ψ。
略去推导的过程,式(64-6)解得结果为x κγγ−=e 0 (64-7)其中 ()()12/exp 12/exp +−=kT ze kT ze ψψγ,()()12/exp 12/exp 000+−=kT ze kT ze ψψγ 21222102222⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛=kT Lc e z kT n e z εεκ (64-8) 式中c 为电解质浓度,L 为Avogadro 常数。
κ的倒数具有长度的量纲,它是一个重要的物理量,相当于专题57的离子氛厚度。
式(64-7)在某些情况下可以简化。
例如,在0ψ很小时,由于()kT ze 2/exp 0ψkT ze 2/10ψ+≈,T /4ze 00k Ψ≈γ。
同理,因ψψ>0,kT ze 4/ψγ≈。
故式(64-7)可简化为()x κψψ−=exp 0 (64-9) 由此可见,κ的大小决定了电势ψ随距离x 的衰减快慢。
此外,由电中性条件,可得固体表面的电荷密度σ与扩散层中电荷密度ρ间的关系为 ∫∞−= 0 d x ρσ (64-10)将式(64-5)代入式(64-10),可得0d 0 22=∞=∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂=∫∞x x x x x ψεψεσ 00εκψψε=⎟⎠⎞⎜⎝⎛∂∂−==x x (64-11) 这是因为边界条件∞=x 时,0=∂∂x ψ。
又,式(64-9)对x 求导,可得()00κψψ−=∂=x x 。
现若将式(64-11)与式(64-1)比较,便可知道1−κ相当于将扩散双电层等效于平板电容器时的板间距δ,故称其为扩散双电层的厚度。
由式(64-8)可见,κ随电解质的浓度c 和电荷数z 的增大而增大,这就是说,扩散双电层的厚度1−κ随c 和z 的增大而变薄。
图64-3(a)和(b)分别为按式(64-9)画出的不同电解质浓度和电荷数时的x ~0ψψ曲线。
它们表明了电解质的浓度和电荷数对双电层本性有很敏感的影响。
图64-3 离子浓度(a)和电荷数(b)对x ~0ψψ曲线的影响Gouy —Chapman 模型的最主要贡献便是使双电层模型能够定量地描述,它所得到的上述规律对研究胶体的稳定性具有重要的意义。
(3)Stern(斯特恩)模型 但是,Gouy —Chapman 模型至少有两点是不符合实际情况的:一是离子并非点电荷,它们有一定的大小;二是邻近表面的离子由于受固体表面的静电作用和van der Waals 引力,其分布不同于溶液的体相,而是被紧密地吸附在固体表面上。
据此,1924年,Stern 进一步改进了Gouy —Chapman 扩散双电层模型,使它能够满意地用来描述胶体的电学性质和稳定性。
Stern 认为Gouy —Chapman 模型中的扩散层应分成两个部分:第一部分包括吸附在表面的一层离子,形成一个内部紧密的双电层,称为Stern 层;第二部分才是Gouy —Chapman 扩散层。
就像图64-4所示。
两层中的离子是相互平衡的。
在Stern 层中,反离子的中心构图64-4 Stern 双电层模型成了一个面,称为Stern 面,就如图64-4中虚线所示,在这个层内,电势的变化如同Helmholtz 模型,由表面电势0ψ直线下降至δψ,δψ称为Stern 电势。
在扩散层内,电势则是由δψ下降至零,其变化规律服从Gouy —Chapman 公式。
因此,Stern 双电层模型可视为由Helmholtz 模型和Gouy —Chapman 模型组合而成。
c =按照Stern模型,胶体离子在运动时,应该与Stern层不可分离,似乎切动面就是Stern 面。
但由于固体表面吸附的离子仍保持着溶剂化(至少在扩散层的一侧),故粒子运动除了与吸附离子一起外,还会带着一薄层溶剂化的液体,因此实际运动的切动面在Stern面更右侧一点,就如图64-4中的波纹线所示。
这个切动面上的电势称为ς(Zeta)电势或动电势。
它与ψ非常接近,甚至数值上可以近似地视为等同。
Stern电势δς电势是胶体稳定性的一个重要指标,因为胶体的稳定是与粒子间的静电排斥力密切相关的。
ς电势的降低会使静电排斥力减小,致使粒子间的van der Waals吸引力占优,从而引起胶体的聚沉和破坏。
故研究ς电势的变化规律是十分重要的。
上面已述,Stern层与扩散层内的离子处在平衡之中,若分散介质中电解质的浓度和电ψ荷数增大时,不仅扩散层的厚度会变薄,而且会有更多的反离子进入Stern层,从而使δ和ς电势降低。
如果外加电解质中含有高价或表面活性的反离子,那末,它们进入Stern层ψ和ς电势变成负号,就如图64-5(a)所示。
同理,若进入Stern层的是后,甚至有可能使δψ和ς电势不仅与表面电势0ψ同号,而且同号表面活性离子,那末,就如图64-5(b)所示,δψ。
这些现象是前面两个双电层模型所无法解释的。
大于(a) (b)ψ和ς电势图64-5 Stern层有异号(a)或同号(b)表面活性离子进入后的δ(4) Grahame (格拉哈姆)模型1947年,D C Grahame进一步改进了Stern模型,他将Stern层细分成两层。
对于带负电荷的固体表面,他认为首先化学吸附不水化的负离子○-和在固体表面定向排列的水分子○→,形成一个以内Helmholtz平面(IHP)表示的内层,紧接着吸附水化的正离子,形成以外Helmholtz平面(OHP)表示的外层。
在外层的外面才是Gouy-Chapman扩散层,就像图图64-6 Grahame 模型示意64-6示意。
在这个双电层模型中,所有活性吸附离子都在IHP 上。
在IHP 内和IHP 与OHP 之间电势随x 的变化都是线形的。
图中画出了电势随表面距离的变化曲线,其中δΨ即Stern 电势。
目前,普遍认同Stern 模型和Grahame 模型是较正确的双电层模型。
2.电动现象与ς电势的测定鉴于ς电势是切动面上的电势,故设法使胶体离子与分散介质作相对运动,便能测定这个电势值。
所谓电动现象就是指这种相对运动与电学性质间的关系。
电动现象主要有下列四种:(1) 电泳在外电场的作用下,胶体粒子向着与自己的电荷相反的电极方向迁移,而与分散介质作相对运动,这种现象称为电泳。
(2) 电渗在外电场的作用下,分散介质向着与自己的电荷相反的电极方向迁移,而分散相,诸如,沉积的固体颗粒、毛细管等固定不动,这种现象称为电渗。
(3) 流动电势在外力的作用下,使分散介质沿着分散相颗粒表面流动所产生的电势称为流动电势。
这种现象正好与电渗相反。
(4) 沉降电势在重力或离心力的作用下,使带电的颗粒相对于分散介质沉降所产生的电势称为沉降电势。
这种现象是电泳的逆过程。
上述四种电动现象都可用来测定ς电势,但实用上,电泳用得最多,它已广泛地用于医学、环保、化工、生化等领域。
下面,仅对电泳测定ς电势作概要的介绍:倘若胶体粒子带有的电量为q ,在电场强度为E 的外电场中迁移,则其所受的静电作用力为qE 。
当粒子在分散介质中运动时,它还要受摩擦力的作用。
摩擦力的大小正比于粒子的运动速度υ,摩擦力的方向与运动方向相反,即摩擦力为υf −,其中f 为阻力系数。
对于球形粒子,按照Stokes 定律r f ηπ6=式中r 为粒子半径,η为介质粘度。
故摩擦力为υηr π6−。
当粒子在介质中匀速迁移时,应IHP OHP满足下式υηr qE π6= (64-12)又,根据静电学,对于球形粒子,可以近似认为切动面上的电量q 与扩散层中的电量q −构成一个同心圆球电容器,ς就是这个电容器的电势,因此,()()r r q r q r q κεκεες+=+−=−1π4π4π41 (64-13) 式中ε为介质的介电常数。