当前位置：文档之家 › 周期三角波的傅里叶级数-推荐下载

周期三角波的傅里叶级数-推荐下载

  • 格式：pdf
  • 大小：207.58 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

周期信号的傅里叶级数表

周期信号的傅里叶级数表
17
分量e j0t 可表示为
1
0
cos 0t
1 2
(e
j0t
e
j0tபைடு நூலகம்
)
表示为
1
1
2
2
0 0 0
因此，当把周期信号 x(t)表示为傅里叶级数
x(t) ake jk0t时，就可以将 x(t) 表示为 k
a1a0 a1
a3a2
a2 a3
0 0
这样绘出的图
称为频谱图
18
频谱图其实就是将 a随k 频率的分布表示出来，
14
有 x(t) ake jk0t , k 0, 1, 2
k
显然 x(也t)是以
为2周 期的。该级数就是傅里叶级
0
数， 称为a傅k 立叶级数的系数。
这表明用傅里叶级数可以表示连续时间周期信号，
即: 连续时间周期信号可以分解成无数多个复指数谐 波分量。
例1：
x(t)
cos 0t
1 e j0t 2
6
3.1历史的回顾 （A Historical Perspective）
任何科学理论, 科学方法的建立都是经过许多人 不懈的努力而得来的, 其中有争论, 还有人为之献 出了生命。历史的经验告诉我们, 要想在科学的 领域有所建树，必须倾心尽力为之奋斗。今天我 们将要学习的傅立叶分析法，也经历了曲折漫长 的发展过程，刚刚发布这一理论时，有人反对， 也有人认为不可思议。但在今天，这一分析方法 在许多领域已发挥了巨大的作用。
即： x(t) akeskt
k
同理： x(n)
ak
Z
n k
k
y(t) ak H (sk )eskt
k

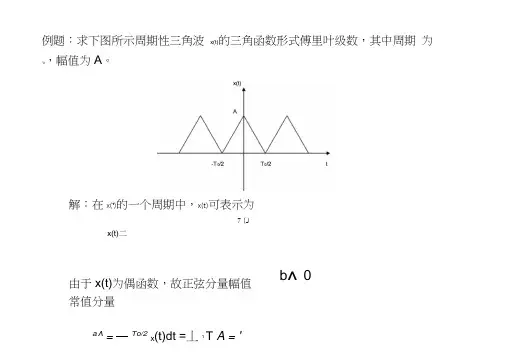
第一章周期三角波的傅里叶级数

第一章周期三角波的傅里叶级数

例题：求下图所示周期性三角波 x(t)的三角函数形式傅里叶级数，其中周期 为T，幅值为A 。

解：在x(t)的一个周期中，x(t)可表示为7 (Jx(t)二由于x(t)为偶函数，故正弦分量幅值 b^ 0常值分量a^ = —To/2x (t)dt =丄1TA = '1 571而余弦分量幅值为2 T o /22 T o /22Ax(t)cos n o tdt2(A t)cos n o tdtT o"八T o o、 T o' 4A ^2A2(cosn -1)=n 二4A sin2n2 2 31n =1,3,5丄展开式为x(t)=-2n 二 2,4,6,L警(cos ot32COS3O'12cos5 0t L )24A(a)幅值频谱图例题：求下图所示周期性三角波x(t)的复指数函数形式 傅里叶级数，其中周 期为T o，幅值为A 。

4A3V 4A4A7V …―1 ---------- ►7&>0…(b)相位频谱图x(t)解：方法一：在x(t)的一个周期中，x(t)可表示为r A TA t ( 0< t < 0)T o 2 2x(t)=A - A t (0 w t w —°)% 2 i 2)QOx(tp C n e jn o t n = 0厂1厂2」lln 二一：：方法二：在x(t)的一个周期中，x(t)可表示为A t (〜互 < t w 0) T o 2 V 2 x(t)二I ATA t (0 < t w 』) T o 2 2□01T °/2 T o-T o /2x(t)ejn 0tdt1x(tp、C n e jn o t n 二0厂1厂2」11n --：：C n = 2®「jb n)盯???b廿？？？。

周期信号傅里叶级数

周期信号傅里叶级数
07
分析公式 （正变换）
连续时间傅里叶级数对：
称为傅里叶系数或频谱系数
综合公式 （反变换）
3.三角形式傅立叶级数
若 f (t)为实函数，则有 利用这个性质可以将指数Fourier级数表示写为 令 由于C0是实的，所以b0=0，故 由此可以推出：
三角形式傅立叶级数
傅里叶系数 连续时间周期信号三角形式傅立叶级数为：
建议同学多看国外电子与通信教材系列 ，先看翻译版，再看英文硬印版
集成电路版图基础（英文影印版） (4小时出库)
Layout Basics:A Practical Guide
作者: CHRISTOPHER SAINT,JUDY SAINT
市场价: ￥45.00
模拟CMOS集成电路设计（英文影印版） (4小时出库) sign of Analog CMOS Integrated Circuits 作者: （美）BEHZAD RAZAVI 市场价: ￥68.00
四、周期信号的功率谱
周期信号属于功率信号，周期信号f(t)在1欧姆电阻上消耗的平均功率为：
单击此处添加小标题
由下面关系可以推导出，帕什瓦尔(Parseval)功率守恒定理：
单击此处添加小标题
01
02
四、周期信号的功率谱
物理意义：任意周期信号的平均功率等于信号所包含的直流、基波以及各次谐波的平均功率之和。
[解] 周期矩形脉冲的傅立叶系数为
将A=1，T=1/4，=1/20，w0=2p/T=8p 代入上式 功率谱
信号的平均功率为 包含在有效带宽(0~2p/t)内的各谐波平均功率为 周期矩形脉冲信号包含在有效带宽内的各谐波平均功率之和占整个信号平均功率的90%。
求f (t)的功率。

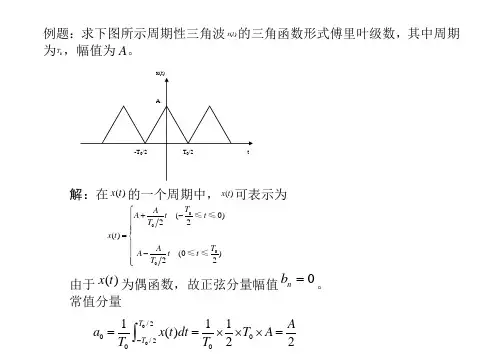
周期三角波的傅里叶级数

周期三角波的傅里叶级数

例题：求下图所示周期性三角波()x t 的三角函数形式傅里叶级数，其中周期为0T ，幅值为A 。

解：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤由于()x t 为偶函数，故正弦分量幅值0=n b 。

常值分量00/200/200111()22T T A a x t dt T A T T -==⨯⨯⨯=⎰而余弦分量幅值为000/2/200/202222222222()cos d 2()cos d 41,3,5,24(cos 1)sin 202,4,6,T T n T Aa x t n t t A t n t tT T T A n n A A n n n n n ωωπ-==-⎧=⎪ππ⎪=--==⎨ππ⎪⎪=⎩⎰⎰展开式为000222411()(cos cos3cos5)235A A x t t t t ωωω=++++π(a) 幅值频谱图(b) 相位频谱图例题：求下图所示周期性三角波()x t的复指数函数形式傅里叶级数，其中周期为0T，幅值为A。

解：方法一：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤0()0,1,2,jn tnn x t C en ω∞=-∞==±±∑方法二：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤()000/2/21()0,1,2,.......T jn tn T C x t edtn T ω--==±±=⎰0()0,1,2,jn tnn x t C en ω∞=-∞==±±∑下面考虑n 取不等于0的整数：000/2/200/20002222222222()cos d 2()cos d 41,3,5,24(cos 1)sin 202,4,6,T T n T Aa x t n t t A t n t tT T T A n n A A n n n n n ωωπ-==-⎧=⎪ππ⎪=--==⎨ππ⎪⎪=⎩⎰⎰由于()x t 为偶函数，故正弦分量幅值0=n b 。

周期信号的傅里叶级数(1)

周期信号的傅里叶级数(1)

sin 3t
1
3
sin
3
xˆ3
a3e j30t
a e j30t 3
2
3
cos3t
k k
5 : a5e j50t
1
5
5 : a5e j50t
cos5t j 1 5
1 cos5t j 5
sin
1
5
5t
sin 5t
xˆ5
a5e j50t
a5e j50t
2
5
cos5t
k k
2 : a2e j20t 0 2 : a2e j20t
为：
3
x(t) ak e jk 2t
k 3
其中， a0 1, a1 a1 1 4, a2 a2 1 2, a3 a3 1 3 求其三角函数傅里叶级数
注：大多数情况下，复指数和三角函数傅里叶 级数间的互换可以通过欧拉公式来完成
cos x e jx e jx , sin x e jx e jx
6
3、系统的特征函数(Eigenfunction)
若系统对一个输入信号的输出响应仅是一个幅度因子 常数（可能是复数）乘以该输入信号，则称该信号为 系统的特征函数，而该幅度因子常数称为系统的特征 值(eigenvalue )。
est 是连续LTI系统的特征函数
zn 是离散LTI系统的特征函数
对一个特定 sk 或 zk , H (sk )或 H就(zk是) 对应的特征值。
T
本证明供学有余力同学参考
x(t)
ak e jk0t x(t)e jn0t
a e e jk0t jn0t k
k
k
两边都从0 ~ T对t求积分：
T x(t)e jn0tdt T

周期信号的傅里叶级数分解

周期信号的傅里叶级数分解

4
n
Fn
1 T
T1 f (t ) e jn1t d t
0
5
• 周期信号可分解为 , 区间上的指数信号ejn1t
的线性组合。
• 如给出Fn，则f t 惟一确定， (4)、(5)式是一对
变换对。
8
X
第
两种系数之间的关系
9 页
Fn
1 T1
T1 0
f (t )e jn1t
d t 利用欧拉公式
1
f (t) E
T1 T1 2
0 T1 T1 2
t
f (t)
E 2
4E 2 [cos(1t)
1 9 cos(31t)
1 25
cos(51t
)
]
14
X
第
2．奇函数
15 页
波形相对于纵坐标是反对称的：f (t ) f (t )
1
a0 T1
T1
2 T1
f (t)d t = 0
2
f (t)
1
f (t)
E 2
E
[sin(21t )
1 2 sin(41t )
1 3
s
i
n
(61t
)
]
20
X
0 (m n)
t0 t0
T1
cos(m1t ) cos(n1t )dt
T1 2
(m n 0)
T1 (m n 0)
0
t0 T1 t0
si n (m1t ) si n (n1t )dt
T1 2
(m n) (m n 0)
t0 T1 cos(m1t )sin(n1t )dt 0,
2 t0 T1

周期信号的傅里叶级数表示

周期信号的傅里叶级数表示

弦波叠加起来，合成复杂的周期信号。
信号分析
02
对于给定的周期信号，可以利用傅里叶级数进行频谱分析，得
到信号中各个频率分量的幅度和相位信息。
频谱特性
03
通过傅里叶级数展开，可以清晰地展示信号在频域上的特性，
如主频、谐波分量等。
信号调制与解调
01 02
调制
在通信系统中，常常需要将低频信号调制到高频载波上进行传输。利用 傅里叶级数，可以将低频信号表示为一系列正弦波的叠加，进而实现调 制过程。
WENKU DESIGN
WENKU DESIGN
2023-2026
END
THANKS
感谢观看
KEEP VIEW
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
https://
PART 01
傅里叶级数基本概念
周期信号与非周期信号
周期信号
具有固定时间周期的信号，即信 号在某个时间周期内重复出现。
非周期信号
不具有固定时间周期的信号，即 信号不会重复出现。
傅里叶级数定义及公式
傅里叶级数定义
将周期信号表示为一系列正弦波和余弦波的叠加，这些正弦波和余弦波具有不 同的频率和幅度。
数值计算与仿真实验
数值计算方法简介
01
离散傅里叶变换 （DFT）
将连续时间信号在时域上进行离 散化，并通过傅里叶变换得到频 域上的离散表示。
02
快速傅里叶变换 （FFT）
利用DFT中冗余计算的特点，采 用分治策略减少计算量，提高计 算效率。
03
迭代法
通过逐步逼近的方式求解傅里叶 系数，如雅可比迭代和高斯-赛 德尔迭代等。

周期函数的傅里叶级数

周期函数的傅里叶级数

设有
f (x)
a0 2


(ak
k 1
cos kx bk
sinkx)
(1) 求 a0 . 两边积分

f ( x)dx

a0 dx 2


k 1
(ak
cos kx bk sinkx)dx 三角函数系的正交性


a0 2
dx
u 和u(函t)的数图图象象
Em
O

t
Em
傅里叶(Fourier)级数
例
函数 f ( x)以 2 为周期, 且 将 f (x) 展开为傅里叶级数.
f
(
x)

x, 0,
解 f (x) 的图象
y
x 0, 0 x,
3 2
2 3
计算傅里叶系数
f
(x)
~
a0 2


(an
n1
cos nx

bn
sin nx)
1
bn

u(t)sin ntdt 偶
2Em

sin ntdt
0

2Em cos nt
n
0
2Em (1 cos n ) n

2Em
n
[1 (1)n ]
4Em
n
若 x 为 f (x)的连续点，
s( x)

f (x) 2
f (x) ,
若
x为
f ( x) 的第一类间断点,
其中s(x) 为 f (x)的傅里叶级数的和函数.
傅里叶(Fourier)级数

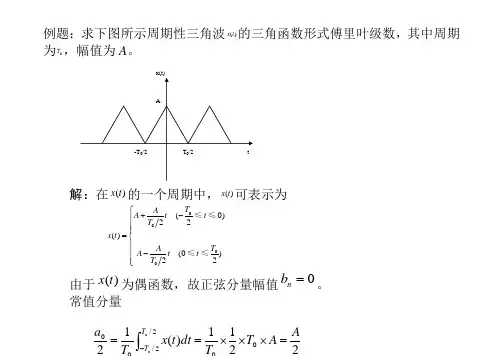
第一章 周期三角波的傅里叶级数

第一章 周期三角波的傅里叶级数

例题：求下图所示周期性三角波()x t 的三角函数形式傅里叶级数，其中周期为0T ，幅值为A 。

解：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤由于()x t 为偶函数，故正弦分量幅值0=n b 。

常值分量11)(102/2/000A A T dt t x a T T =⨯⨯⨯==⎰-而余弦分量幅值为000/2/200/202222222222()cos d 2()cos d 41,3,5,24(cos 1)sin 202,4,6,T T n T Aa x t n t t A t n t tT T T A n n A A n n n n n ωωπ-==-⎧=⎪ππ⎪=--==⎨ππ⎪⎪=⎩⎰⎰展开式为000222411()(cos cos3cos5)235A A x t t t t ωωω=++++π(a) 幅值频谱图(b) 相位频谱图例题：求下图所示周期性三角波()x t的复指数函数形式傅里叶级数，其中周期为0T，幅值为A。

解：方法一：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤0()0,1,2,jn t nn x t C e n ω∞=-∞==±±∑方法二：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤()000/2/21()0,1,2,.......T jn tn T C x t edtn T ω--==±±=⎰0()0,1,2,jn tnn x t C en ω∞=-∞==±±∑1()2n n n C a jb =-n n a b ==总黄酮生物总黄酮是指黄酮类化合物，是一大类天然产物，广泛存在于植物界，是许多中草药的有效成分。

周期信号的频谱分析—傅里叶级数

周期信号的频谱分析—傅里叶级数

4
bnT1
T1 2
0
f(t)sinn1tdt
X
2266
第第
六．周期信号的功率 页页
P1 T
T 0
f2(t)dt
a 0 2 1 2 n 1a n 2 b n 2 a 0 2 1 2 n 1 c n 2 n F n 2
这是帕塞瓦尔定理在傅里叶级数情况下的具体体现; 它表明：
相频特性 n arctanabnn
an bn
F(n1)
n1
关于 的偶函数（n实取际正值） 关于 的奇函数（n实取际正值） 关于 的偶函数 关于的奇函数
X
频谱图
幅度频谱 cn ~
或 Fn ~ 曲线
cn c1
c0
c3
O 1 3 1
n
相位频谱
n ~曲线
O 1 3 1
第第 页页
离散谱，谱线
X
1122
n
0 . 25 π
1
O
2 1
0 . 15 π
n
0.15 π
0.25 π
2 1 1 O
1 2 1
0.25 π
0.15 π
X
1177
第第
四．总结
页页
（11））周周期期信信号号ff((tt)的)的傅傅里里叶叶级级数数有有两两种种形形式式
（22））两两种种频频谱谱图图的的关关系系
（33））周周期期信信号号的的频频谱谱是是离离散散谱谱，，三三个个性性质质
X
44
第第
2．级数形式
页页
周 期f信 t,周 号期 T1,基 为波
在满足狄氏条件时，可展成
角1频 2 T 1率
为
f(t)a 0 a nco n s 1 tb nsin n 1 t 1 n 1

第三章周期信号的傅里叶级数表

第三章周期信号的傅里叶级数表

2T1 T0
Sa k
2
T0
T1
谱线为离散的（谐波性），在
k0
k
2
T0
时取值，
脉冲周期越大，谱线间隔 0 越小，越密；
各点频谱大小与脉宽 T1 成正比，与周期 T0 成反比；
频谱包络线形状：抽样函数，过零点为最大值为 2T1
T0
主要能量在第一过零点内，第一个零点坐标为:
k 1, kω0T1
k
k
ak
1 T
x(t)e jk0tdt 1
T
T
x(t)e jk(2 T )tdt
T
28
29
解：方法一：直接利用公式进行求解
ak
1 T
x(t)e jk0t dt 1
T
T
x(t)e jk(2 T )t dt
T
方法二：
x(t)
a k e jk0t
a e jk(2 T )t k
k
46
47
48
这两组条件并不完全等价。它们都是傅里叶级 数收敛的充分条件。相当广泛的信号都能满足这 两组条件中的一组，因而用傅里叶级数表示周期 信号具有相当的普遍适用性。
49
50
三 、吉伯斯（Gibbs）现象 满足Dirichlet条件的信号，其傅里叶级数
是如何收敛于 的x。t 特别当 具有xt间
7
补充例题：
例:对单位冲激响应 h(t) 的 (LtT) I系统，其特征函数，
相应的特征值是什么?
解：Q h(t) (t) 的 LTI 系统是恒等系统，所以任何函 数都是它的特征函数，其特征值为 1。
例:如果一个LTI系统的单位冲激响应为， h(t) (t T)

【最新精选】周期三角波的傅里叶级数

【最新精选】周期三角波的傅里叶级数

例题：求下图所示周期性三角波()x t 的三角函数形式傅里叶级数，其中周期为0T ，幅值为A 。

解：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤由于()x t 为偶函数，故正弦分量幅值0=n b 。

常值分量00/200/200111()22T T A a x t dt T A T T -==⨯⨯⨯=⎰而余弦分量幅值为000/2/200/202222222222()cos d 2()cos d 41,3,5,24(cos 1)sin 202,4,6,T T n T Aa x t n t t A t n t tT T T A n n A A n n n n n ωωπ-==-⎧=⎪ππ⎪=--==⎨ππ⎪⎪=⎩⎰⎰L L展开式为000222411()(cos cos3cos5)235A A x t t t t ωωω=++++πL(a) 幅值频谱图(b) 相位频谱图例题：求下图所示周期性三角波()x t的复指数函数形式傅里叶级数，其中周期为0T，幅值为A。

解：方法一：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤0()0,1,2,jn t nn x t C e n ω∞=-∞==±±∑方法二：在()x t 的一个周期中，()x t 可表示为0000(0)22()(0)22T A A t t T x t T A A t t T ⎧+-⎪⎪⎪=⎨⎪⎪-⎪⎩≤≤≤≤()000/2/21()0,1,2,.......T jn tn T C x t edtn T ω--==±±=⎰0()0,1,2,jn tnn x t C en ω∞=-∞==±±∑下面考虑n 取不等于0的整数：000/2/200/20002222222222()cos d 2()cos d 41,3,5,24(cos 1)sin 202,4,6,T T n T Aa x t n t t A t n t tT T T A n n A A n n n n n ωωπ-==-⎧=⎪ππ⎪=--==⎨ππ⎪⎪=⎩⎰⎰L L由于()x t 为偶函数，故正弦分量幅值0=n b 。

三角傅里叶级数定义

三角傅里叶级数定义

三角傅里叶级数定义三角傅里叶级数定义三角傅里叶级数是一种用于表示周期函数的展开式。

它由一系列正弦和余弦函数组成，这些函数的频率是原始函数频率的整数倍。

三角傅里叶级数在信号处理、图像处理、音频编码和其他领域中得到广泛应用。

一、基本概念1.1 周期函数周期函数是指满足f(x+T) = f(x)的函数，其中T是一个正常数。

周期函数在一个周期内具有相同的形状，因此可以通过对一个周期内的函数进行分析来了解整个周期性函数的行为。

1.2 周期延拓如果一个周期性函数f(x)在一个周期内已知，那么可以将其延拓到整个实轴上。

具体而言，可以将f(x)在每个周期上复制，并将这些副本放置在相邻的区间上。

这样就得到了一个无限延续的周期性函数。

1.3 正交性两个不同频率的正弦或余弦波之间是正交的，即它们在任何区间上积分为0。

这意味着，在三角傅里叶级数中使用不同频率的正弦和余弦波时，它们之间不会相互干扰。

二、三角傅里叶级数的定义2.1 基本形式设f(x)是一个周期为2π的连续函数，其三角傅里叶级数表示为：f(x) = a0 + Σ(an*co s(nx) + bn*sin(nx))其中n是正整数，an和bn是系数。

a0是f(x)在一个周期内的平均值。

2.2 系数计算三角傅里叶系数可通过以下公式计算：an = (1/π) * ∫[0, 2π] f(x)*cos(nx)dxbn = (1/π) * ∫[0, 2π] f(x)*sin(nx)dx即将f(x)与cos(nx)和sin(nx)乘积在一个周期上积分，并除以π。

2.3 收敛性对于任何连续的周期函数，其三角傅里叶级数都会收敛到原始函数。

这意味着，通过使用有限数量的正弦和余弦波来逼近原始函数，可以得到足够准确的结果。

三、应用举例三角傅里叶级数在信号处理中得到广泛应用。

例如，在音频编码中，可以使用三角傅里叶级数将音频信号转换为频域表示，并压缩数据以减小文件大小。

在图像处理中，可以使用离散三角傅里叶变换将图像转换为频域表示，并应用滤波器以改善图像质量。

测试技术周期性三角波的傅立叶级数

测试技术周期性三角波的傅立叶级数
2 2 2 1 4 n n 2
二阶系统的特点：
2 n arctan 2 1 n
H 1；当 n时 ， H 0 。 1）当 n时， 2）二阶系统的伯德图可用折线来近似。在 2 n 段，A(ω) 可用0dB水平线近似。在 0.5 n 段，可用斜率为-40dB/10 倍频的直线来近似。
将展开式中的同频项合并，
4A An a b 2 2 n
2 n 2 n
n arctan
bn 0 an
可改写成
A 4A x(t ) 2 2 cosn0 t 2 n1 n (n 1,3,5,...)
2.2周期信号与离散频谱 • 1.三角函数的复数形式
根据欧拉公式：
2.3 非周期信号与连续频谱书17 傅立叶变换的主要性质
2.4 典型信号的频谱分析 正、余弦函数及其频谱
3.3 测试系统的动态响应特性
五、一阶、二阶系统的特性
（一）一阶系统
如图，装置分属于力学、电学范畴，但均属于一阶系统，均可 用一阶微分方程来描述。 R 一般形式的一阶微分方程为
x(t)
a
改写为 式中
令 则 或
令n＝0，±1，±2，…得
x ( t ) a0 (a n cos n 0 t bn si nn 0 t )
n
T0 2 T 0 2
x ( t )e jn 0 t dt
1 a0 T 2 an T 2 bn T

T 2 T 2 T 2 T 2
1

点称转折频率。
一阶系统主要的动态特性参数是时间常数。

周期函数的傅里叶级数

周期函数的傅里叶级数
41
1 2
An
2

2 (1 ) T
2 3
0
11
21
1
31

8 t 1 2 ( cos n1t sin n1t ) 2 T n1 (n1 ) 0 2 (1) n 1 n
n 1
T 2

f (t )
( 1)
n 1
2

1 2n sin t n T
§ 周期信号的傅立叶级数
4 T 2 2 bn f (t ) sin n1tdt (1 ) 0 T T T 4 T 4 4 4 2 [ t sin n1tdt T (2 t ) sin n1tdt] T 0 T T 4 T 4 16 t 1 2 [( cos n1t sin n1t ) 2 T n1 (n1 ) 0
下形式在一个周期内可写为如出其频谱图求其傅立叶展开式并画如图所示有一偶函数其波形为偶数为奇数下形式在一个周期内可写为如出其频谱图求其傅立叶展开式并画如图所示有一奇函数其波形下形式在一个周期内可写为如出其频谱图求其傅立叶展开式并画形如图所示有一奇谐函数其波coscos出其频谱图求其傅立叶展开式并画形如图所示有一偶谐函数其波sinsin为偶数为奇数周期信号的傅立叶级数周期信号的频谱为了能既方便又明白地表示一个信号中包含有哪些频率分量各分量所占的比重怎样就采用了称为频谱图的表示方法
n
bn
an
bn an
n tg 1
§ 周期信号的傅立叶级数
根据傅里叶级数理论，任何满足满足狄里克雷 (Dirichlet)条件的周期连续信号 f t 都可表示为 无限多个、频率为基频倍数的复正弦信号的加权 和，若 f t f t kT 其中， 为任何整数，k 为周 期， T 为基频， f 1 1 为相应的角频率，则

周期三角波的傅里叶级数

周期三角波的傅里叶级数
解：在 x（t）的一个周期中，可表示为
A T / 2 t 0 t T0 / 2 0 x(t ) A t T / 2 t 0 0 T / 2 0
由于 x (t ) 为偶函数，故正弦分量幅值 常值分量 而余弦分量幅值为
1 a0 T0
bn 0 。
x(t )
n
jn0t C e n

n 0, 1, 2,
1 T0 / 2 1 1 C0 a0 x(t )dt T0 A / T0 A T / 2 T0 0 2 2 下面考虑 n 取不等于 0 的整数：
1 Cn (an jbn ) 2 2 T /2 2 an x(t ) cos n 0 tdt T0 T / 2 T0
x(t )
n
jn0t C e n

n 0, 1, 2,
1 Cn T0

T0 / 2
T0 / 2
x(t ቤተ መጻሕፍቲ ባይዱe jn0t dt
n 0, 1, 2,
.......
方法二： 在 x(t ) 的一个周期中， x(t ) 可表示为
T0 A A t ( ≤ t ≤ 0) T0 2 2 x(t ) T A A t (0 ≤ t ≤ 0 ) T0 2 2
1 1 A T0 / 2 x(t )dt T0 2 T0 A 2
T0 / 2
an 4 T0
2 T0

T0 / 2
T0 / 2
x(t ) cos n0tdt
4 T0

T0 / 2
0
x(t ) cos n0tdt
T0 / 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例题：求下图所示周期性三角波()x t 的三角函数形式傅里叶级数，其中周期为0
T ，幅值为A。

解：在()x t 的一个周期中，()x t 可表示为
0000(0)22()(0)
22T A A t t T x t T A A t t T ⎧
+-⎪⎪⎪=⎨
⎪⎪-⎪⎩
≤≤≤≤ 由于()x t 为偶函数，故正弦分量幅值0=n b 。

常值分量
00/2
00/20
0111()22
T T A a x t dt T A T T -=
=⨯⨯⨯=⎰
而余弦分量幅值为
000/2
/2
00/20
222222222
2()cos d 2()cos d 41,3,5,24(cos 1)sin 20
2,4,6,T T n T A
a x t n t t A t n t t
T T T A n n A A n n n n n ωωπ-=
=-⎧=⎪ππ⎪=--==⎨
ππ⎪
⎪=⎩⎰
⎰
L L
展开式为
000222411
()(cos cos3cos5)
235A A x t t t t ωωω=++++πL
(a) 幅值频谱图
(b) 相位频谱图
例题：求下图所示周期性三角波()x t的复指数函数形式傅里叶级数，其中
周期为0T，幅值为A。

解：方法一：
在()x t 的一个周期中，()x t 可表示为
0000(0)22()(0)
22T A A t t T x t T A A t t T ⎧
+-⎪⎪⎪
=⎨
⎪⎪-⎪⎩
≤≤
≤≤ 0()0,1,2,jn t
n
n x t C e
n ω∞
=-∞
=
=±±∑
方法二：
在()x t 的一个周期中，()x t 可表示为
0000(0)22()(0)
22T A A t t T x t T A A t t T ⎧
+-⎪⎪⎪
=⎨
⎪⎪-⎪⎩
≤≤
≤≤ ()
000/2
/2
1()0,1,2,.......
T jn t
n T C x t e
dt
n T ω--=
=±±=⎰
0()0,1,2,jn t n
n x t C e n ω∞
=-∞
=
=±±∑
下面考虑n 取不等于0的整数：
00
/2/2
00/2000
2222222222()cos d 2()cos d 41,3,5,24(cos 1)sin 20
2,4,6,T T n T A a x t n t t A t n t t
T T T A n n A A n n n n n ωωπ-==
-⎧=⎪ππ⎪=--==⎨
ππ⎪
⎪=⎩⎰⎰
L
L
由于()x t 为偶函数，故正弦分量幅值0=n b 。

从而，
1
()
2n n n C a jb =-2222
1421,3,5,....
1
1
A
A n ⎧==±±±⎪00/20000/20111()/22
T T C a x t dt T A T A
T -====⎰
从而其复指数形式是
从而幅频谱图是：
n C ω-22
21,3,5,....02,4,6,....
/2000,1,3,5,....
n n A
n n C n A n n πϕ⎧=±±±⎪⎪==±±±⎨⎪=⎪⎩
==±±±0222();1,3,5,2jn t
A A x t e n n ωπ
=+=±±±⋅⋅⋅
∑
相频谱图是：
n ϕω-
注：
其中积分计算：
000000
0000
1
cos sin 1[sin sin ]11[sin cos ]t n tdt td n t
n t n t n tdt n t n t n t C n n ωωωωωωωωωω==-=++⎰⎰⎰P22 例1-1 图1-6 把x(t)轴平移到T 0/2处后，求
其傅里叶级数的三角函数展开式，并画出其幅频谱及相频谱图。

解：在x （t ）的一个周期中，可表示为
00
00/2/2()/20
/2
A
t t T T x t A t T t T ⎧<<⎪⎪=⎨
⎪--<<⎪⎩由于()x t 为偶函数，故正弦分量幅值0=n b 。

常值分量
而余弦分量幅值为
00/2
00/20
0111()22
T T A
a x t dt T A T T -=
=⨯⨯⨯=⎰
00000/2/200/2000/2
/200020
000000222224()cos ()cos cos 4281cos sin 41,3,5,....2(cos 1)02,4,6,....T T n T T T a x t n tdt x t n tdt T T n t A A t n tdt t n t T T T n n A n A n n n n ωωωωωωωπππ-==⎡⎤==+⎢⎥⎣⎦-⎧=⎪=-=⎨⎪=⎩⎰⎰⎰展开式为000222411()(cos cos3cos5....)235A A x t t t t ωωωπ=-+++ 幅频谱 0224()1,3,5,....A A n n n ωπ==相频谱 0()01,3,5,....n n ϕω==
从而，其幅频谱图是
相频谱图是
--------------------展开式也可以为：000222411()[sin()sin(3)sin(5....]223252A A x t t t t πππωωωπ=+-+-+-+幅频谱 0224()1,3,5,....A A n n n ωπ==相频谱 0()1,3,5,....2n n π
ϕω=-=。