数学建模论文-投资规划

公司最优投资方案的数学模型摘要本文解决的是某公司在未来5年内最优的投资方案问题,通过对该公司财务分析人员提供的数据〔附录一到四〕的统计分析,我们建立了三个最优化模型.对于问题一,在考虑该公司现有资本与收益的情况下,以第五年末所得利润的最大值作为目标函数,以每年的投资上限和各项目投资方式限制作为约束条件,建立了单目标最优化模型.然后利用Lingo编程求得该公司在第五年末可以获利大,我们采用将灰色预测和时间序列模型的二次指数平滑法组合的预测方式进行预测,预测了今后五年各项目独立投资与项目之间相互影响下的投资的到期利润率,以样本数据的方差值作为各项目的风险损失率,运用Matlab编程求出到期利润率,并利用Excel求出风险损失率,其具体结果见表十、十一和十二.对于问题三,结合问题二的预测结果,考虑该公司争取到的资金捐赠,建立了与问题一相同的目标函数,即第五年末所得利润的最大值,改变了约束条件.然后利用Lingo编程求得该公司在第五年末可以获利润38.1238亿元,最佳的投资方案见表十三.对于问题四,建立了与问题三相同的模型,即目标函数相同.问题四是在问题三的基础上考虑了风险投资率,即增加了约束条件.依照该模型求得该公司在第五年末可以获利润13.2814亿元,最佳的投资方案见表十四.对于问题五,根据题目要求,采用同样的思想建立模型五,以第五年末还贷款后回收的总金额〔包括投资本利和,存款本金与利息〕作为目标函数,建立新的约束条件〔考虑投资风险率〕.利用Lingo求得该公司在第五年末可以获利润33.9814亿元,最佳的投资方案见表十五.关键词：单目标最优化灰色预测模型二次指数平滑法组合预测1.问题重述1.1 问题背景某公司现有数额为20亿的一笔资金可作为未来5年内的投资资金,市场上有8个投资项目〔如股票、债券、房地产、…〕可供公司作投资选择.其中项目1、项目2每年初投资,当年年末回收本利〔本金和利润〕；项目3、项目4每年初投资,要到第二年末才可回收本利；项目5、项目6每年初投资,要到第三年末才可回收本利；项目7只能在第二年年初投资,到第五年末回收本利；项目8只能在第三年年初投资,到第五年末回收本利.在本文中,我们考虑提出该公司最优的投资方案.该公司的财务分析人员收集了8个项目近20年的投资额与到期利润数据时发现,在具体对这些项目投资时,实际还会出现项目之间相互影响等情况.而在未来5年的投资计划中,还包含了对投资项目1,公司管理层争取到一笔资金捐赠,若在项目1中投资超过20000万,则同时可获得该笔投资金额的1%的捐赠,用于当年对各项目的投资；项目5的投资额固定为500万,可重复投资以与各投资项目都有投资上限〔见附录四〕的情况.1.2 需要解决的问题问题一：根据附录一给出的数据,确定五年内如何安排该公司的投资计划,并使得第五年末所得利润最大.问题二：根据附录二和三提供的数据,预测今后五年各项目独立投资与项目之间相互影响下的投资的到期利润率、风险损失率.问题三：考虑到未来5年的投资计划中的其他情况,根据问题二预测结果,确定5年内如何安排20亿的投资并使得第五年末所得利润最大.问题四：将投资风险考虑到问题三中的投资问题,又该如何决策.问题五：为了降低投资风险,公司可拿一部分资金存银行,为了获得更高的收益,公司可在银行贷款进行投资,在此情况下,公司又应该如何对5年的投资进行决策？2.模型的假设与符号说明2.1 模型的假设假设一：在投资期内,我们只考虑不可预测因素引起的平均风险损失；假设二：投资项目以与银行的利润率在预测期内是稳定不变的；假设三：附录一中给定的数据真实可靠,具有较好的代表性.假设四：只考虑项目3、4、5、6和5、6、8同时投资时之间存在相互影响,其他情况不做考虑.假设五：当用20亿资金投资若干种项目时,总体风险可用所投资的项目中最大的一个风险来度量假设六：银行未来五年内的存款年利润率和贷款年利润率不变3.问题分析此题研究的是某公司未来5年内的投资资金的使用问题,属于经济模型中的决策模型.虽然我们针对问题一、三和四建立的三个单目标最优化模型的目标函数相同,但由于各个项目都有投资要求和回收本利的时间限制,所以对于不同的情况,就具有不同的约束条件.针对问题一,考虑到项目1、2每年初投资,当年年末回收本利；项目3、4每年初投资,要到第二年末才可回收本利；项目5、6每年初投资,第三年末才可回收本利；项目7只能在第二年年初投资,到第五年末回收本利；项目8只能在第三年年初投资,到第五年末回收本利作为约束条件,以与初始资金共20亿.以第五年末所得利润最大为目标函数,建立了一个单目标最优化模型.针对问题二,要对各项目独立投资与项目之间相互影响下的投资的到期利润率进行预测,首先,要求出历年来的各项目独立投资与项目之间相互影响下的投资的到期利润率,然后考虑采用插值拟合对附录二、三的缺省值进行预测,在选择适合本问题精度较高的预测模型,进行对比后,我们采用了综合灰色预测模型和二次指数平滑法的预测方式.对于风险投资率,以样本数据的方差值作为各项目的风险损失率.针对问题三,在问题一的模型上改变了约束条件,即各项目的投资上限,项目5的投资额固定为500万且可重复投资和资金捐赠问题.结合问题二的预测结果,和问题一相同的目标函数的单目标最优化问题.针对问题四,是在问题三的投资问题上增加了风险投资率.也就是将问题三中的到期利润率换成实际利润率即可求解.即目标函数不变,增加了约束条件的单目标最优化问题.针对问题五,考虑到降低风险投资,该公司决定拿出一部分资金存入银行.为了获得更高的收益,当投资风险率高时,公司应选择在银行存大部分资金,而用小部分资金投资；当投资风险率低时,应选择在银行贷款进行投资.所以,我们以第五年末还贷款后回收的总金额〔包括投资本利和,存款本金与利息〕最大作为目标函数的单目标最优化模型.4.数据分析4.1 数据处理题目附录四中给出了各种投资项目的方案以与投资上限,我们利用Excel软件和Matlab编程对这些数据进行了相关统计分析和处理.首先,我们根据附录二、三求出项目独立投资与项目之间相互影响下的投资的到期利润率.其中,整理求得后的数据见附录五、六〔相关程序见附录〕.4.2 数据预测为方便分析以与组合预测法预测,我们对附录二、三的到期利润率的缺省值进行预测,采用多项式插值拟合的方式.4.2.1 多项式插值拟合的建立所谓插值,就是由有限个已知数据点,构造一个解析表达式,由此计算数据点之间的函数值.曲线拟合就是计算出两组数据之间的一种函数关系,由此可描绘其变化曲线与估计非采集数据对应的变量信息.我们选择项目一历年的到期利润率利用Excel软件对其分析,见下图.可见历年来,项目一的利润率变化波动比较大,同样的操作,发现所有项目的到期利润率波动都比较大.而且经过我们统计分析,这8个项目不管是独立投资还是同时投资时,历年来到期利润率的波动性都比较大.所以,我们采用三次多项式的插值拟合对数据进行预测.通过对每组数据,使用matlab构造解析表达式,再进行预测<相关程序见附录>.在本题中,我们将年份即从1986年开始到20##之间的时间作为自变量,设为t；到期利润率作为因变量,设为y.其中时间t,从1986年开始,即设为单位1,以此类推.4.2.2 预测结果通过插值拟合对各投资项目独立投资和一些项目同时投资时历年的到期利润率的缺省值进行预测的结果记录于下表〔具体数据见附录五、六〕：表一：各投资项目独立投资时03—05年的到期利润率与预测值〔加粗斜体为预测值〕5.问题一的解答问题一要求确定5年内的投资方案使得第五年末所得利润最大,且属于无风险投资.这是线性规划中的最优解问题.针对问题一,我们建立了模型一. 5.1 模型一的建立 5.1.1 确定目标函数该模型是为了解决公司在五年内如何安排投资和在第五年末所获得的最大利润.为解决此问题,我们将公司在第五年末所得利润的最大值作为目标函数. 该公司第一年年初只能对前六个项目〔项目1,项目2项目6〕进行投资,且6个投资项目预计到期利润率都大于0〔见附录一〕,所以第一年20亿全用于投资.当第一年年末将本金和利息都回收后再在第二年利用该资金对一部分项目进行再次投资即可,所以建立了如下的目标函数〔第五年末所得利润值〕： 5.1.2 确定约束条件〔1〕对于这8个项目,每年年初该公司的投资金额应不大于其各自的投资上限〔见附录一〕,即：〔2〕每年年初总投资金额应不大于所有可投资的金额〔前一年回收的本金利润和〕,即：其中,第一年的总投资金额不应大于20亿,则j Z 为： 注：1Z =20亿元表示第一年年初可用于投资的总金额〔3〕对于项目1,2,每年初投资,当年年末回收本利；对于项目7只能在第二年年初投资,到第五年末回收本利；对于项目8只能在第三年年初投资,到第五年末回收本利；则： 特别地,〔4〕对于项目3,4,每年年初投资,第二年末回收本利,则：,1(1)i j i j i y x p -=+,3,4i =,2,3,4,5j = 〔5〕对于项目5,6每年年初投资,第三年末回收本利,则：,2(1)i j i j i y x p -=+,5,6i =,3,4,5j =综合〔1〕、〔2〕、〔3〕、〔4〕和〔5〕可得到,问题一的约束条件.5.1.3 综上所述,得到问题一的单目标最优化模型 5.2 模型一的求解根据上述的目标函数,我们利用Lingo 编程〔相关程序见附录八〕,求出了该公司5年内最佳的投资方案〔投资金额〔单位：亿元〕〕,具体数据见下表：数据的灵敏度分析同样适用Lingo 求解,具体结果见附录八.6.问题二的解答对于问题二,要预测今后五年各项目独立投资与项目之间相互影响下的投资的到期利润率、风险损失率,首先要对提供的数据进行处理.我们已经通过插值拟合对附录表二、三的数据的缺省值进行了预测,见附录五、六. 6.1 模型二的准备首先对今后五年各项目独立投资与项目之间相互影响下的投资的到期利润率进行灰色预测,得到的结果误差较大〔最高的百分绝对误差为5.3704%〕, 又利用时间序列预测模型中的一、二、三次指数平滑预测法进行预测,结果也都不理想.通过用一、二、三次的指数平滑法来预测1986—20##的到期利润率,与真实值比较后发现,二次指数平滑法的预测效果要好于其他两种〔具体对比数据见附录七〕.所以我们采用组合预测方法,组合预测方法就是先利用两种或两种以上不同的单项预测法对同一预测对象进行预测,然后对各个单独的预测结果做适当的加权平均,最后取其加权平均值作为最终的预测结果的一种预测方法. 6.2 模型二的建立在本题中,我们采用灰色GM<1,1〕法和二次指数平滑法的组合预测模型来预测今后五年各项目独立投资与项目之间相互影响下的投资的到期利润率.这里采用均方误差确定加权系数.首先,我们把1986-20##分为两个时间段,即：前十年为一段,后十年为一段.然后,我们分别用灰色GM<1,1〕法和二次指数平滑法根据1986-1995年到期利润率预测1996-20##的到期利润率. 6.2.1 灰色预测模型的建立⑴原始数据,原始数据1986-1995年的到期利润率数据〔即〕表示为⑵ 计算生成序列(1)X ,用GM<1,1>建模时,首先我们对原始数据(0)X作一次累加得到(1)X序列(1)(0)1()()(1,2...)i m x i x m i n == =∑可以得到相应的K的递增系列()()()()(1)(1)(1)(1)1,2,,X x x xn = ⑶得到模型的白化方程,首先对(1)X 计算紧邻均值生成(1)jZ：接着我们根据GM<1,1>建模,写出灰色函数：()()()()01x k a z k b +=根据最小二乘参数估计法估计参数矩阵再利用离散数据系列建立近似的微分方程模型,得到GM<1,1>的白化方程即：()()()()11d x t a x t b d t+=⑷ 白化方程的求解,得到预测值(0)^X表达式,其白色方程的解为时间响应函数()()()()()1011a t b b x k x e a a--⎛⎫=-+ ⎪⎝⎭通过改变k 的值我们可以得出原始数据序列(0)X 的预测值为：6.2.2 灰色模型的预测在已知各投资项目独立投资和一些同时投资的项目从1986年到20##到期利润率的前提下,应用灰色预测对06—10年的到期利润率进行预测.预测结果见表四、五.[1]原始数据,原始数据1986-1995年设为时间序列为T t y y y y ,,,,21,[2]取移动平均的项数T N <,则移动平均数的递推公式有 以)1(t M 作为N t y -的最佳估计,则有)1(1)1(1)1(1)1()11(----+=-+=t t t t t tM NN y N M y MM；[3]计算一次指数平滑公式,令N1=α,α为加权系数,对于该模型我们采用.20=α〔通过比较8.0,6.0,2.0分别取α后的预测结果,我们采用误差较小的0.2作为加权系数〕,以t S 代替)1(t M ,即得:∑∞=----=-+=0)1(1)1()1()1(j j t jt t ty S y Sαααα,其中,1)1(1)1(0=--=-∑∞=ααααj j得到一次指数平滑公式为：[4]建立二次平滑指数公式,根据一次指数平滑公式,再做二次指数平滑,利用滞后偏差的规律建立直线趋势模型,计算公式为当时间序列{}t y ,从某时期开始具有直线趋势时,可用直线趋势模型进行预测.由于时间序列的数据较多,为20个,初始值对以后的预测值影响较小,所以,我们选用第一个数据为初始值. 6.2.4 二次指数平滑法的预测应用二次指数平滑法对2006—20##的到期利润率进行预测.预测结果见表六、七.应用两种预测法对1996-20##的到期利润率进行预测.这10年的实际值与预测值见附录五.由1996-20##预测值与实际值的均方误差〔MSE 〕确定加权系数. 〔1〕设n x y t t ,,〔nt ,2,1=〕分别表示预测值,实际值和预测数据个数,那么由公式 ∑=-⋅=n t tt x y n 12)(1MSE 可分别求出灰色GM<1,1〕法和二次指数平滑法的均方误差1MSE ,2MSE .故 ：灰色GM<1,1〕法的权系数： 211MSE MSE MSE 1+-=α二次指数平滑法的权系数： 212MSE MSE MSE 1+-=β〔2〕设21,y y 分别表示灰色GM<1,1〕法和二次指数平滑法的预测值,则组合预测值为21y y y βα+=. 6.2.6组合预测模型的预测应用Excel 求出灰色GM<1,1〕法和二次指数平滑法的均方误差1MSE ,2MSE 与权系数α,β见下表八,表九：为了检验预测效果,我们引入均方根误差〔Root Mean Squared Error,简称RMSE 〕对预测性能进行评价,它是一种常用的误差度量标准,其计算公式为： 其中,i x 是实测值,'i x 为预测值,n 为预测检验个数.显然,该指标的值越小说明预测精度越高.我们采用均方根误差对组合预测法进行精度检验,使用的数据中,预测值为对1996—20##五年的组合预测法计算出的数据,实测值是这五年的真实数据.采用EXCEL 软件对数据统计分析,将计算得到结果记录于下表中：从上表可以看出得到的均方差的值都较小,将其与灰色预测模型和二次指数平滑法相比较,发现其效果稍好.说明检验效果很好. 6.3 模型二的求解 〔1〕对该公司从2006—20##的各项目独立投资与项目之间相互影响下的投资的到期利润率的组合预测值为：由于投资越分散.总的风险越小,预测风险损失率可以通过方差分析来实现.由此建立了如下的方差模型：根据该方差模型可分别计算出今后五年各项目独立投资与项目之间相互影响下的投资的风险损失率. 6.4 问题二的结果最终今后五年各项目独立投资与项目之间相互影响下的投资的到期利润率的预测结果见表十、十一；风险损失率的预测结果见表十二.7.问题三的解答问题三是在问题二的预测结果基础上,利用公司争取到的资金捐赠,确定合理的投资方案,使得第五年年末公司所得利润最大,且属于无风险有捐赠投资.模型三同模型一,建立以公司在第五年末所得利润的最大为目标的单目标最优化模型.7.1 模型三的建立 7.1.1 确定目标函数由于问题三与问题一的目标函数相同,即使第五年末所得利润值最大,我们建立了如模型一的目标函数： 7.1.2 确定约束条件由问题三可知,模型三与模型一在各项目的投资回收要求上具有相同的约束条件,再结合问题二的预测结果,得到关于各项目投资回收的新约束条件为： 〔1〕对于项目1,2,7,8：(1)i j i j i j y x p =+,1,2,7,8i =,1,2,3,4,5j = 特别地,70,1,3,4,5j x j ==；80,1,2,4,5j x j ==〔2〕对于项目3,4：,1(1)i j i j i j y x p -=+,3,4i =,2,3,4,5j = 〔3〕对于项目5,6：,2(1)i j i j i j y x p -=+,5,6i =,3,4,5j =而对于问题三,该公司未来5年的投资计划中,还包含以下情况：〔4〕项目5的投资额固定,为500万,可重复投资,即：〔5〕对投资项目1,公司管理层争取到一笔资金捐赠,若在项目1中投资超过20000万,则同时可获得该笔投资金额的1%的捐赠,用于当年对各项目的投资.为方便建模,我们定义了一个判别函数：即当在项目1中投资超过20000万时,1)(=t f ；反之,0)(=t f .则对各项目投资的总金额和到期回收的本利总金额,有：第一年,对于投资项目1,2,3,4,5,6,有 第二年,对于投资项目1,2,3,4,5,6,8 ,有 第三年,对于投资项目1,2,3,4,5,6,8 , 第四年,对于投资项目1,2,3,4,有 第五年,对于投资项目1,2,有综合〔1〕、〔2〕、〔3〕、〔4〕和〔5〕可得到,问题三的约束条件. 7.1.3 综上所述,得到问题三的单目标最优化模型 7.2 模型三的求解根据上述的目标函数,我们利用Lingo 编程〔相关程序见附录八〕,求出了该公司5年内最佳的投资方案〔投资金额〔单位：亿元〕〕,具体数据见下表十三：8.问题四的解答问题四是在问题三的基础上,考虑投资风险,即问题四是有风险有捐赠的投资.目标函数相同,针对问题四,我们建立了模型四. 8.1 模型四的建立 8.1.1 确定目标函数为使第五年末所得利润值最大,我们建立了目标函数： 8.1.2 确定约束条件对于问题四,当考虑投资风险时,那么投资时就要考虑投资风险率,即实际利润率=到期利润率—风险损失率；表示为：所以,对于问题四,是在问题三的基础上考虑了风险投资率；所以问题四只需在问题三的模型中,将到期利润率换成实际利润率即可求解.得到关于各项目投资回收的新约束条件为：〔1〕对于项目1,2,7,8：(1)i j i j i j y x R =+,1,2,7,8i =,1,2,3,4,5j = 特别地,70,1,3,4,5j x j ==；80,1,2,4,5j x j ==〔2〕对于项目3,4：,1(1)i j i j i j y x R -=+,3,4i =,2,3,4,5j = 〔3〕对于项目5,6：,2(1)i j i j i j y x R -=+,5,6i =,3,4,5j =特别地,50.05,1,2,3,4,5j x j == （4）对于问题四,考虑投资项目1的捐赠问题,同问题三,使用判别函数)(t f ,即：对于第一年,投资项目1,2,3,4,5,6,有对于第二年,投资项目1,2,3,4,5,6,7 ,有 对于第三年,投资项目1,2,3,4,5,6,8 ,有 对于第四年,投资项目1,2,3,4,有 对于第五年,投资项目1,2,有 综合〔1〕、〔2〕、〔3〕和〔4〕可得到,问题四的约束条件. 8.1.3综上所述,得到问题四的单目标最优化模型 8.2 模型四的求解根据上述的目标函数,我们利用Lingo 编程〔相关程序见附录八〕,求出了该公司5年内最佳的投资方案〔投资金额〔单位：亿元〕〕,具体数据见下表十四：9.问题五的解答在问题五中,为了降低投资风险,该公司选择拿出一部分资金存银行.针对该问题,我们建立了模型五. 9.1 模型五的准备为了获得更高的收益,当投资风险率高时,公司应选择在银行存大部分资金,而用小部分资金投资；当投资风险率低时,公司应选择在银行贷款进行投资.我们在网上查得银行的存款利润率为3.50%〔取中国人民银行一年定期存款年利率〕,设为k ,银行的贷款利润率为6.40%〔取中国人民银行中长期贷款年利率〕,设为l . 9.2 模型五的建立 9.2.1 确定目标函数模型五的目标函数是在模型一的基础上考虑了存款本息以与利息,即第五年末还贷款后回收的总金额〔包括投资本利和,存款本金与利息〕,所以建立了如下的目标函数：9.2.2 确定约束条件 〔1〕对于项目1,2,7,8：(1)i j i j i j y x R =+,1,2,7,8i =,1,2,3,4,5j =特别地,70,1,3,4,5j x j ==；80,1,2,4,5j x j ==〔2〕对于项目3,4：,1(1)i j i j i j y x R -=+,3,4i =,2,3,4,5j = 〔3〕对于项目5,6：,2(1)i j i j i j y x R -=+,5,6i =,3,4,5j =特别地,〔4〕考虑到投资项目的风险损失率与银行存款和贷款,为方便建模,定义了如下的判别函数：11,0.5()0,0.5i i q g t q >⎧=⎨≤⎩,21,0.5()0,0.5i i q g t q ≤⎧=⎨>⎩它们分别表示当投资风险率高时,公司应选择在银行存大部分资金,而用小部分资金投资；当投资风险率低时,公司应选择在银行贷款进行投资.则对各项目投资金额和存款金额的总和以与还贷款后回收的总金额,有： 第一年,对于投资项目1,2,3,4,5,6,有 第二年,对于投资项目1,2,3,4,5,6,8 ,有 第三年,对于投资项目1,2,3,4,5,6,8 ,有 第四年,对于投资项目1,2,3,4,有 第五年,对于投资项目1,2,有 综合〔1〕、〔2〕、〔3〕和〔4〕可得到,问题五的约束条件. 9.2.3 综上所述,得到问题五的单目标最优化模型 9.3 模型五的求解根据上述的目标函数,我们利用Lingo 编程〔相关程序见附录八〕,求出了该公司5年内最佳的投资方案〔投资金额〔单位：亿元〕〕,具体数据见下表十五：10.模型的评价、改进与推广10.1模型的评价优点：〔1〕我们考虑各个项目都有投资要求和回收本利的时间限制这些要求以与该公司现有的资本,综合以上,建立的模型在一定程度上可使该公司在第五年末获得利润.〔2〕在预测分析中,现有的很多方法预测结果往往不够准确,问题二中我们采用了由预测精度都较高的灰色模型和时间序列模型中的二次指数平滑法组成的预测法,使预测结果较为理想.缺点：〔1〕没有对所有模型进行模拟仿真.〔2〕由于所给数据太少且1986—20##之间的到期利润率的波动较大,在统计数据时不是很准确,也给提高预测的精确度带来了困难.〔3〕问题五中,由于没有提供银行每年的贷款利润率与存款利润率,所以我们假定该值在这五年内没有变化.然而,事实上银行的利润率根据情况每年是有所改变的.所以,导致我们的投资计划具有不合理性.10.2 模型的改进〔1〕查询更多的数据,可以将年到期率提高为月到期率,以使得统计数据和预测值更准确.〔2〕所见模型是针对当前数据给出的,而银行贷款以与利润都是不断变化的,所以,如果建立了动态模型,能得出更加合理化的投资方案.10.3模型的推广本文针对公司投资这一随机变化的动态系统,提出的组合预测法可以应用与工程项目投资和股票预测的中长期预测,且预测率精度较高.参考文献[1] 宋来忠,王志明,数学建模与实验,：科学,2005.[2] 张志宇, 亢政刚,马尔可夫灰色模拟模型与其程序实现,##商学院学报,第21卷,第3期,20##5月.[3]平平,刘大有,杨博等,组合预测模型在猪肉价格预测中的应用研究,计算机工程与科学, 第32卷,第5期,20##3月.附录附录七：一、二、三次的指数平滑法来预测1986—20##的到期利润率和真实值的图表附录八：程序<1>Matlab 程序〔求到期利润率〕各项目独立投资以与一些项目同时投资时的到期利润率的计算程序：a1=[4791261338910-79555586225918987353749204115487044-2291-396914570403787000000];72326886507079297480546330414830 53086272633367494034739264424092 7403503368596707537747835202635530825083000000];c1=a1./b120502778344447330021549108203005244831810874750-17914000201526095168-29303170-2351446015101724-1248984-4299330710170320424887598-4722-96814900-2294325826468671-655111460-4521-80393047368200000];5070792974805463748054634830633367494034739240347392409254746473507363455073634530446859670753774783537747836355487738447434422274344222596062556925659860436598604379886471776000000];c2=a2./b2<2>三次多项式插值拟合的求解代码:x=1:1:20;y=[%到期利润率];n=3;p=polyfit<x,y,n>xi=linspace<0,1,100>;z=polyval<p,xi>; %多项式求值plot<x,y,’o’,xi,z,’k:’,x,y,’b’>legend<‘原始数据’,’3阶曲线’><3>问题一用lingo求解的代码:model:sets:lr/1..8/:p;。

期末考试论文论文名称个人理财指导老师许小芳老师班级08级信息与计算科学一班姓名王云肖鸶鸶代梦佳学号********** （03 17 35）时间2010.12.20—2010.12.272010—2011年第一学期目录1.摘要 (2)2.问题的提出 (2)3.问题的分析 (2)4.建模过程 (3)1）模型的假设 (3)2）符号的说明 (3)3）模型建立 (3)4）模型求解 (3)5.模型分析 (5)6.参考文献 (5)7.附录 (5)一、摘要“个人理财”是一个时髦的词儿，然而一般人对理财的认识存在着两个误区：一是认为理财就是生财，就是今年投下10万，明年收获12万，也就是投资赚钱。

二是认为理财是有钱人的事儿，老百姓没有几个钱，无所谓理不理财。

实际上，这两种理财观念都是狭隘的。

理财其实是一种个人或家庭的人生规划，根本上是指我们要善用钱财，尽量使得个人及家庭的财务状况处于最佳状态，从而提高生活质量。

如何有效地利用每一分钱，如何及时地把握每一个投资机会，是理财的关键所在。

本文导论了投资所得利润的问题针对投资问题进行全面分析，在不考虑项目之间相互影响和风险的情况下，应用线性规划的数学模型，建立一个利润优化模型，不仅求出了最大本利，还指出了投资的最优方案。

关键词：个人理财、投资、数学模型、线性规划、最优方案、二、问题的提出如何有效地利用每一分钱，如何及时地把握每一个投资机会，是理财的关键所在。

同时，理财与我们每个人的生活息息相关，理财不是富人的专利。

目前，比较流行的理财手段有储蓄、保险、国债、股票、基金、期货、外汇、房地产、珠宝、邮票、古玩字画、钱币及拍卖品等。

无论哪种理财手段，都有其自身的特点及不可替代性。

这其中无所谓孰好孰坏，风险与收益并存。

到底选择哪种投资组合，一定要根据自身实际情况，自己的风险承受能力来决定。

不同的人应当制定不同的理财计划。

某人正考虑在今后5年内在以下4个方向投资：A珠宝：从第一年到第四年年初投资，并于次年回收本利115％；B房地产：从第三年年初开始投资，到第五年年末能回收本利125％，但规定最大投资额不超过400万；C股票：从第二年年初投资，到第五年年末能回收本利140%，但规定最大投资额不超过300万；D国债：五年内每年年初可以购买国债，于当年末归还并加利息6%；该人现有资金1000万，应该如何确定这些方向的投资，使得五年后拥有的资金总额最大？三、问题的分析题目中四个投资项目之间存在相互影响，要求如何投资以获得最大利润的问题，属于线性规划问题的数学模型。

2013-2014学年 第二学期 《数学建模与实验》 科目考查论文基金使用计划摘要本文研究了对学校基金的使用计划，本文的整体方案在于满足实际要求使得奖金数额最大。

第一问，只能进行银行存款，年底发放奖金。

我们在不影响奖金发放的情况下，为了实现基金最优使用计划，可得出只有在每年年初可以进行存入一年期、二年期、三年期、五年期存款。

通过列出所有可能发生的情况，然后建立一个线性方程组，求出最大奖学金额度，方程组如下（符号说明见下文）： ,1,2,3,5i i i i i S x x x x =+++1,1(1)(1)i i W r x Ai =+⨯-= 1,121,2(1)(12)(2)i i i W r x r x Ai -=+⨯++⨯-= 1,121,232,3(1)(12)(13)(3,4)i i i i W r x r x r x i --=+⨯++⨯++⨯= 1,121,232,354,5(1)(12)(13)(15)(5,6,7,8,9,10)i i i i i W r x r x r x r x Ai ---=+⨯++⨯++⨯++⨯-=使用lingo 软件编程求解，计算出奖金的最大金额为106.3403万元，具体存款情况参见表二。

第二问，在第一问的基础上进行了修改，校方允许购买国库券。

经过分析发现，由于国库券的发行不稳定，会产生三种不同的情况。

所以我们对这三种情况分别进行分析，运用第一题的思路，根据题目要求同样建立了一个线性方程组（具体方程组见下文），求得最大金额为113.9584万元，具体存款情况参见表五。

、第三问，可以分为两种情况。

我们对第一问和第二问中的方程组加以改进（改进方案见下文），将方程组中第6年支出的奖金额数上调20%，就能够得到满意的答案。

最后，还是通过使用Lingo 软件解出线性方程组，这种情况下的奖金数额是104.2806万元。

第二种在既可以选择国库券又可以存款，在这种情况下采用问题二中的模型分别列出线性方程组，求解出奖金数额111.7739万元。

1998年A题《资产投资收益与风险》题目、论文、点评投资组合与模糊规划模型王正方,赵文明,倪德娟本文讨论了投资的风险与收益的问题,首先我们给出了一个比较完整的模型,然后,考虑投资数额相当大时的一个近似处理模型,并分别用偏好系数加权法和模糊线性规划法进行了求解,接下来,我们又考虑了如何处理投资额相对较小的情况下的最优投资组合情况,引入了绝对收益率进行了较为有效的解决。

投资组合与模糊规划模型.pdf (275.8 KB)投资组合模型伍仕刚,孟宪丽,胡子昂本文建立了考虑交易费用情况下的市场资产组合投资模型,并采用偏好系数加权法对资产的预期收益和总风险进行评价,给出在不同偏好系数下的模型最优解,然后模型讨论了一般情况下的最优投资求解方法,给出定理,在总金额大于某一量值时,可化为线性规划求解。

投资组合模型.pdf (134.92 KB)风险投资分析程文鑫,苑青,骆文润本文主要研究多种资产的组合投资问题,根据题目所给信息,建立了在一定简化条件下的多目标规划模型和单目标风险约束模型,并对问题一与问题二分别使用上述两模型进行求解得到多种投资组合方案,同时对一般情况进行了讨论,最后模型进行了相应的灵敏度分析,讨论了简化条件的适用情况,结果表明模型是较为符合实际的风险投资分析.pdf (241.54 KB)资产投资收益与风险模型陈定涛,蒋浩,肖红英本文应用多目标决策方法建立模型,并通过简化,成为一个单目标线性规划问题。

计算后得到了一个合乎公司要求的、净收益尽可能大,而总体风险尽可能小的最优方案,如下所示: 问题1的最佳投资方案对表二中的数据进行同样的计算和分析,也获得了一个理想的投资方案;从而证明了我们的模型具有一般性。

资产投资收益与风险模型.pdf (298.22 KB)资本市场的最佳投资组合闫珺,王璐,韩嘉睿市场上有多种可提供投资者选择的资产。

本文试图对各种收益和风险进行分析,在一定的标准下给出全部资产组合的效益前沿,即有效资产组合,为投资者提供参考。

1998年A题风险投资组合的线性规划模型1摘要对市场上的多种风险资产和一种无风险资产（存银行）进行组合投资策略的设计需要考虑两个目标：总体收益尽可能大和总体风险尽可能小，而这两个目标在一定意义上是对立的。

本文给出组合投资方案设计的一个线性规划模型。

主要思路是通过线性加权综合两个设计目标；假设在投资规模相当大的基础上，将交易费函数近似线性化；通过决策变量的选取化解风险函数的非线性。

模型的最大优点是：计算过程稳定性好，速度快。

我们对各种加权因子，求得了最优化决策方案，从而得到问题的有效投资曲线。

根据有效投资曲线，投资者可以由自己的主观偏好，直观地选择自己的投资方向。

最后通过非线性规划，说明线性规划的结果对于交易费收取的阈值有一定的容忍度。

一. 问题的提出在风险市场的投资问题中，风险与收益始终是一对矛盾。

一般来说想要追求高收益，风险也大; 若想风险小，收益也会相应减少。

研究表明，大部分的投资者具有以下的行为偏好：对于收益来说，总是越多越好；从风险的角度来说，大部分人都属于风险回避者。

我们可以通过选取适当的组合投资方案，在取得良好收益的同时使总体风险减少。

设某公司有一笔数额相当大的资金，投资购买若干种风险资产或存银行生息。

风险资产收益高但风险大，存银行生息无风险但收益低。

公司财务人员对多种资产进行了评估，估算出在这一时期内各种资产的平均收益率和风险损失率，并考虑购买时需付一定的交易费（不买当然无须付费，购买额不超过阈值时，交易费按阈值计算）。

现在需要设计一种投资组合方案，以利用好这笔资金使得净收益尽可能大，而总风险尽可能小。

二. 模型的基本假设及符号说明(一)基本假设H1: 只考虑给定时间内的收益和风险，且银行存款利率在给定时间内保持不变;H2: 公司用于投资的资金数额相当大，且无贷款或透支;H3: 各种资产投资风险相互独立。

H4: 总体风险可用所投资的资产中最大的一个风险来度量。

(二)符号说明S i: 第i种资产(i=1，2，...，n，n+1)，其中S n+1表示存入银行;r i : S i的平均收益率;q i : S i的风险损失率;p i : S i的交易费率;1本文发表于《数学的实践与认识》1999. No1. p39-42.u i : S i 购买额阈值;M: 资金总额;X i: 投资S i 占总额的比重(不含交易费) ， 以下简称投资; Y i: 投资S i 的交易费占总额的比重， 以下简称交易费; f 1: 净收益; f 2: 总体风险; λ: 权因子;三. 模型的建立(一) 基本模型我们的目标是对各种资产投资以后，不仅收益尽可能大，同时总体风险还要尽可能小。

动态投资摘要本文解决的是地区在制定投资计划时合理、有效地利用金融资源，确定最好的投资方案的问题，以获得最大的投资总利润。

对于该问题不同的投资方案，我们建立目标线性规划模型，利用matlab软件进行求解，得到在最大利润化模型。

若每年都采纳第一种投资方案，则该地区在三年内可获最大利润有2.184万元。

但经规划后，该地区在今后三年内可获最大利润为：2.75 万元，比之增加了5660元。

关键字：线性规划，资金闲置，投资决策，MATHLAB模型求解1.问题重述某地区在今后三年内有四种投资机会:(1) 在三年内每年年初投资,年底可获利20%,并可将本金收回;(2) 在第一年年初投资,第二年年底可获利50%,并可将本金收回,但该项投资不得超过2万元;(3) 在第二年年初投资,第三年年底收回本金,并可获利60%,但该项投资不得超过1.5万元;(4) 在第三年年初投资,于该年年底收回本金,且可获利40%,但该项投资不得超过1万元.现在该地区准备拿出3万元资金,问如何制订投资计划,可使到第三年年底本利和最大?2.基本假设1.假设该投资为连续投资，即三年内中途不会中断投资，且三年内资金周转正常2.假设每年的投资收益外界因素稳定不变3.假设投资过程中不需要任何交易费/税收或者交易费/税收远远少于投资金额哈所获得的收益，可以忽略不计；4.假设各投资方法相互独立，且各自风险损失率为零5.假设该投资没有风险3.符号说明x——第i年初投资第j种机会的金额（万元）ijx——第一年初投资第一种机会的金额（万元）11x——第一年初投资第二种机会的金额（万元）12x——第二年初投资第一种机会的金额（万元）21x——第二年初投资第三种机会的金额（万元）23x——第三年初投资第一种机会的金额（万元）31x——第三年初投资第四种机会的金额（万元）34Z ——投资后获得的总收益（万元）4.问题分析与模型建立对于该投资问题，为解决该投资方案问题，采取连续投资模型，根据所给的客观条件来确定各种投资方案，并利用线性规划模型对方案进行选择方案，以获得最大收益。

数学建模投资与风险论文Document number：BGCG-0857-BTDO-0089-2022投资收益和风险[问题提出]随着经济的发展，人们的生活水平越来越高，于是就有了剩余的资金，为了让剩余的资金获得更多的利润，所以人们就把剩余的资金进行投资，市场上有n种资产si进行投资，某公司有一大笔资金M进行投资，于是公司财务人员对市场上这n种资产进行评估，估算出在这一时期内购买Si 的平均收益率为，并预测出购买Si的风险损失率为。

考虑到投资越分散，总的风险越小，公司规定，当用这笔资金购买若干种资产时，总体风险可用所投资的Si 中最大的一个风险来度量。

购买Si要付交易费，费率为，并且当购买额不超过给定值时，交易费按购买计算（不买当然无须付费）。

另外，假定同期银行存款利率是, 且既无交易费又无风险（=5%）。

于是公司要求设计一种投资组合方案，即用给定的资金，有选择地购买若干种资产或存银行生息，使净收益尽可能大，而总体风险尽可能小。

[问题分析]由题目可得，该公司财务人员对这n种资产进行评估投资，使得净收益最大，总体风险最小，于是就得到投资模型[变量定义] M=总投资金额Si=第i种资产（i=1,2,3……n）ri =购买Si的平均收益率qi =购买Si的风险率p i =购买Si的交易费率r=银行存款利率M i =购买Si的金额Di=所需交易费y=净收益U i =Si的交易定额=衡量资产优劣的指标[模型假设]1.投资数额M足够大，设为1，假设购买额Si都大于ui，；2.各种资产不相互影响，相互独立的，且不受外界因素影响；3.投资方不会中途撤离或追加资金；4.投资越分散，总的风险越小。

5.总体风险可用投资Si的中最大的一个风险来度量。

6.净收益和总体风险不受意外因素的影响。

[模型建立]1.总体风险可用投资Si的中最大的一个风险来度量，即Max{Mi qi/i=1,2,……n}2.各项投资净收益可表示为：1ni iiM r=∑-1ni iiM p=∑（M i>u I）y= 0 (Mi=0)1ni iiM r=∑-1ni iiM u=∑（M i<=u i）3.为使净收益最大，投资风险最小，可得出一个目标函数：MAX{1ni iiM r=∑-1ni iiM p=∑}MIN{ Max(Miqi/i=1,2,……n)}约束条件：1(1)niii p MM=+=∑M i ≥0;i=0,1,2……,n4.从3中可以看出，要同时满足净收益最大，投资风险最小，得到的是一个多目标规划。

题 目 基金使用计划摘要本文研究了关于基金使用计划的问题，主要目的在于设计资金的合理安排方法，实现在一定条件下，使用有限的资金合理投资，达到最大的利润。

并且我们建立了相应的数学模型对该问题进行分析求解。

对于第一问，我们在不影响奖学金发放的情况下，对利率较小的银行存款进行排除，对每年的资金来源进行分析，列出所有可能发生的情况，然后建立一个线性方程组，求出最大奖学金额度，方程组如下： ,1,2,3,5i i i i i S x x x x =+++1,1(1)(1)i i W r x Ai =+⨯-= 1,121,2(1)(12)(2)i i i W r x r x Ai -=+⨯++⨯-= 1,121,232,3(1)(12)(13)(3,4)i i i i W r x r x r x i --=+⨯++⨯++⨯= 1,121,232,354,5(1)(12)(13)(15)(5,6,7,8,9,10)i i i i i W r x r x r x r x Ai ---=+⨯++⨯++⨯++⨯-=使用L i n g o 软件对其进行编程求解，最后的得出最大奖学金额数为109.8169()Z =万元。

然而对于第二问，情况与第一问相似，但是又存在不同点，校方允许了购买国库券这种投资方式。

经过分析发现，由于国库券的发行不稳定，会产生三种不同的情况。

所以我们对这三种情况分别进行分析，运用第一题的思路，根据题目要求同样建立了一个线性方程组（具体方程组见下文）。

同样也是使用Lingo 软件对其进行编程求解。

最后得出在第一种情况下，校方每年能够发放的最大奖学金额数为 146.8578()Z =万元；而第二种方案的最大奖学金额数为127.5222()Z =万元；最后第三种方案的最大奖学金额数为131.7896()Z =万元第三问比较简单，校方要求第三年的奖金能够多出20%，但是因为没有规定是只存款不购国库券还是可存款也可购国库券，所以又要分成两个情况去讨论。

房地产投资分析摘要房地产业发展涉及到国计民生的众多行业，其受各种因素的多元化影响，对于房产业发展相关问题的有效研究可以对国民经济的健康可持续发展产生积极的影响。

虽然国家多次进行宏观调控，多次调整利率、存款准备金率等，试图对房地产市场进行调控，但自1998年实行房改以来，我国大部分城市的房价出现了普遍持续上涨情况。

一方面，房价的上涨使得新进入城市或需要购房者的生存成本大幅增加，导致许多中低收入人群买房难，其它消费也无法提升；另一方面，部分投资或投机者通过各种融资渠道买入房屋进行出租或空置，期望因房价上涨而获得超高回报，导致房价居高不下。

因此，如何分析影响房地产市场的因素，从而进行有效的抑制房地产价格的过快上涨，同时能够抑制房地产市场的投机行为，是一个需要进行全面而深入研究的问题，也是普罗大众非常关心的社会问题。

国家为此出台了多种政策或宏观调控措施。

关键字：SPSS GM（1，1）投资风险出租贷款组合投资问题重述在缺乏可靠投资渠道的情况下，有的家庭选择利用余钱或贷款购置房屋进行投资。

请根据市场房屋价格的变化情况，综合考虑家庭收入、租金收入、储蓄及贷款利率、房屋折旧率、房屋空置率等因素，建立数学模型，为家庭进行住房投资做出决策。

问题分析在当前的房地产红火以及政府宏观调控的大形势下，房屋价格很难有相当明显的下跌。

研究房价未来的发展趋势，是住房投资的前提。

购房后对于房屋的租赁问题，有必须研究出一套利润最大化方案，确定房租价格。

考虑到市场的潜在风险，需要研究出一套基于租—售的最佳时机的模型，也就是在一定时期内可以“以租养贷”，在另一时期内即有特殊情况出现时，可以将其售出，以达到尽可能规避风险和实现利润最优化。

对于低收入家庭而言，如何负担第一套住房都存在一定困难，基本上可以不考虑其投资第二套住房的情况。

而对于高收入家庭而言，其拥有的资产数额庞大，投资领域多样，对于风险的承受力很大，研究价值不是很明显。

因此，焦点应集中于占相当比例的中等收入家庭，其资金有限，抗风险能力差，使得建立一套模型来寻求利润的最大化以及风险的最小化就显得尤为必要。

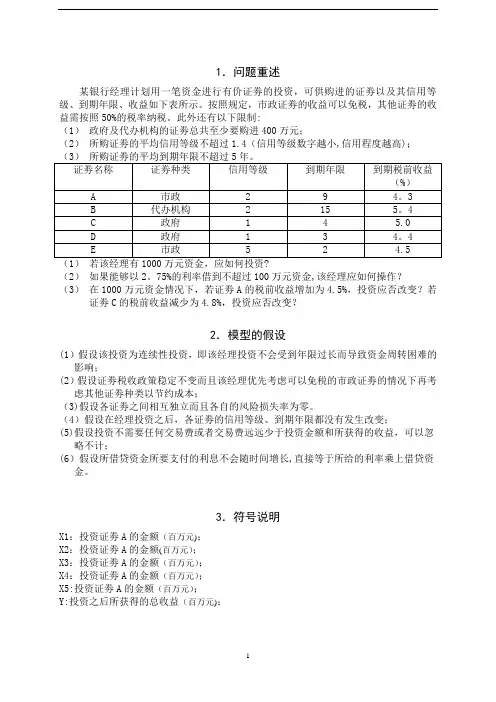
某银行经理计划用一笔资金进行有价证劵的投资，可供购进的证劵以及其信用等级、到期年限、收益如下表所示。

按照规定，市政证劵的收益可以免税，其他证劵的收益需按照50%的税率纳税。

此外还有以下限制:（1）政府及代办机构的证劵总共至少要购进400万元；（2）所购证劵的平均信用等级不超过1.4（信用等级数字越小,信用程度越高)；（2）如果能够以2。

75%的利率借到不超过100万元资金,该经理应如何操作？（3）在1000万元资金情况下，若证劵A的税前收益增加为4.5%，投资应否改变？若证劵C的税前收益减少为4.8%，投资应否改变？2．模型的假设(1）假设该投资为连续性投资，即该经理投资不会受到年限过长而导致资金周转困难的影响；(2）假设证劵税收政策稳定不变而且该经理优先考虑可以免税的市政证劵的情况下再考虑其他证劵种类以节约成本；（3)假设各证劵之间相互独立而且各自的风险损失率为零。

（4）假设在经理投资之后，各证劵的信用等级、到期年限都没有发生改变；(5)假设投资不需要任何交易费或者交易费远远少于投资金额和所获得的收益，可以忽略不计；(6）假设所借贷资金所要支付的利息不会随时间增长,直接等于所给的利率乘上借贷资金。

3．符号说明X1：投资证劵A的金额（百万元)；X2：投资证劵A的金额(百万元）；X3：投资证劵A的金额（百万元）；X4：投资证劵A的金额（百万元）；X5:投资证劵A的金额（百万元）；Y:投资之后所获得的总收益（百万元)；对于该经理根据现有投资趋势,为解决投资方案问题,运用连续性投资模型，根据所给的客观的条件，来确定各种投资方案，并利用线性规划模型进行选择方案，以获得最大的收益。

问题一，该经理优先考虑可以免税的市政证劵的情况下再考虑其他证劵种类以节约成本，我们可以在所提出的假设都成立的前提下(尤其是假设所借贷资金所要支付的利息不会随时间增长,直接等于所给的利率乘上借贷资金）以及综合考虑约束资金和限制条件，将1000万元的资金按照一定的比例分别投资个各种证劵。

投资策略解：一•问题分析该问题要求通过调整买入和卖出汽车的时间来使总的花费最少，属于规本题中，优化的目标是5年内的总花费，可行域是汽车的数量以及其他的限制条件，然后ffl lingo软件求解。

二.建立模型已知aij表示在年i的开始买进汽车并在年j的开始卖出汽车的净成本,0469122000571116令 A = (aij) =000681300008110000010为净成本矩阵。

再设B = (b叽6, bi j表示第i年买进的汽车在第j年卖出的数量(设数量为1)。

于是，净成本可表示为5 6minZ =工工认(1)!=1 7=1公司为了保证车队的正常运行，要保证车的总数不变，于是每年在卖出一定的数量的汽车的同时，还要买入同等数量的汽车，定义C = (C；.),6, q6表示第i年初买入的汽车数量，才C( 1)=1, C(6)二0,且C(i)二=/=1(1=2, ...... , 5)同时，在第i年买进的汽车要在后面的几年时间里全部卖出，于是5c(i) =工切(i二1,・・・，5)/=i另有，第i年买进的汽车在第j年卖出的数量一定小于第i年买进的汽车在第j年初剩下的数量，所以有关系：町 <=心一£工瓦/=1 心 1目标函数min Z的最优解可出lingo软件编程求得，将上面的目标函数以及约束条件转换为ling。

程序:model:sets :setl/1••5/：c；set2/l••6/；link(setl,set2):b,a；endsetsdata :A=0 4 6 9 12 200 0 5 7 11 160 0 0 6 8 130 0 0 0 8 110 0 0 0 0 10;enddatamin=@sum(setl(i):®sum(set2(j):b(i,j)*a(i,j)))；c(l)=l；@for(setl (i) :b( i,l)=0)；@for(setl(i) |i#GT#l:c(i)=@sum(setl(j) ：b(j z i)))；@for(setl(i):c(i)=@sum(set2(j):b(i,j)))；@for(setl(i)：@for(set2(j):b(i,j)<=c(i)-@sum(set2(k)|k#LT#j:b(i,k) )));end求解的结果Global optimal solution found•Objective value:Infeasibilities:Total solver iterations:CostC( 1) 1.000000 0.000000 C( 2) 0.000000 0.000000 19.00000 0.000000Variable Value ReducedC( 3) 1.000000 0.000000 C( 4) 0.000000 0.000000C( 5) 0.000000 0.000000B( lz 1) 0.000000 0.000000 B( lz 2) 0.000000 0.000000 B( 1, 3) 1.000000 0.000000 B( 1/ 4) 0.000000 0.000000 B( lz 5) 0.000000 0.000000 B( lz 6) 0.000000 0.000000 B( 2, 1) 0.000000 0.000000 B( 2, 2) 0.000000 0.000000 B( 2, 3) 0.000000 3.000000 B( 2, 4) 0.000000 2.000000 B( 2, 5) 0.000000 3.000000 B( 2Z 6) 0.000000 0.000000 B( 3, 1) 0.000000 0.000000 B( 3Z 2) 0.000000 2.000000 B( 3, 3) 0.000000 0.000000 B( 3, 4) 0.000000 3.000000 B( 3, 5) 0.000000 2.000000 B( 3, 6) 1.000000 0.000000 B( 4, 1) 0.000000 0.000000 B( 4, 2) 0.000000 5.000000 B( 4, 3) 0.000000 3.000000 B( 4, 4) 0.000000 0.000000 B( 4, 5) 0.000000 5.000000 B( 4, 6) 0.000000 0.000000 B( 5, 1) 0.000000 0.000000 B( 5, 2) 0.000000 8.000000 B( 5, 3) 0.000000 6.000000 B( 5, 4) 0.000000 3.000000 B( 5, 5) 0.000000 0.000000 B( 5, 6) 0.000000 0.000000 A( lz 1) 0.000000 0.000000 A( lz 2) 4.000000 0.000000 A( lz 3) 6.000000 0.000000 A( lz 4) 9.000000 0.000000 A( 1/ 5) 12.00000 0.000000 A( 1, 6) 20.00000 0.000000 A( 2, 1) 0.000000 0.000000 A( 2Z 2) 0.000000 0.000000 A( 2, 3) 5.000000 0.000000 A( 2Z 4) 7.000000 0.000000 A( 2, 5) 11.00000 0.000000 A( 2, 6) 16.00000 0.000000 A( 3, 1) 0.000000 0.000000A( 3, 2) 0.000000 0.000000 A( 3, 3) 0.000000 0.000000 A( 3, 4) 6.000000 0.000000 A( 3, 5) 8.000000 0.000000 A( 3, 6) 13.00000 0.000000 A( 4, 1) 0.000000 0.000000 A( 4, 2) 0.000000 0.000000 A( 4, 3) 0.000000 0.000000 A( 4, 4) 0.000000 0.000000 A( 4, 5) 8.000000 0.000000 A( 4, 6) 11.00000 0.000000 A( 5, 1) 0.000000 0.000000 A( 5, 2) 0.000000 0.000000 A( 5, 3) 0.000000 0.000000 A( 5, 4) 0.000000 0.000000 A( 5, 5) 0.000000 0.000000 A( 5, 6) 10.00000 0.000000■1.000000-19.00000 19.00000 15.00000 13.00000 10.000007.000000-15.00000 ・13.00000-10.00000 ・7.000000 20.00000 Row1Slack or Surplus Dual Price19.000002 0.0000003 0.0000004 0.0000005 0.0000006 0.0000007 0.0000008 0.0000009 0.00000010 0.00000011 0.00000012 0.00000013 0.000000000000*0 9E000000 * 0 000000*0000000 * 0 000000-Toooooo-0 000000-T 乙£oooooo•0 000000 • T000000-0 000000-T 0£000000*0 000000*T 6乙OOOOOO•0 000000 • 083OOOOOO•T 000000*0 LZ000000*0 000000*0 9乙OOOOOO•0 000000*0 S3OOOOOO-0 000000*0OOOOOO•0 000000•0£乙OOOOOO-0 000000*0 乙乙OOOOOO•T 000000*0 TSOOOOOO•0 000000*0 0乙OOOOOO-0 000000*0 6TOOOOO O•0 000000 • T8TOOOOOO-0 000000*1 LI00000*01 000000*0 9T00000•TT 000000*0 SI00000•£1 000000*000000*910.00000036 0.0000000 ・ 00000037 0.0000000.00000038 0.0000000.00000039 0.000000 1.00000040 0.000000 0.00000041 0.0000000 ・ 00000042 0.0000000.00000043 0.0000000 ・ 00000044 0.000000 0.00000045 0.000000 3.00000046 0.0000000 ・ 000000分析运行结果可知，才C (1)二C (3)二b(l,3)二b(3,6)二1, 其余全部为0,即最优方案为：第一年年初买入所需的汽车，第3年初卖出全部的汽车再买入所需的汽车，最后第6年初卖出全部的汽车。

解决组合投资收益最优问题一、 摘要本论文主要讨论并解决了在组合投资问题中的投资收益与风险的有关问题。

分别在不考虑投资项目之间的影响和考虑投资项目之间的影响以及不考虑风险和考虑风险的情况下，建立相应的数学模型，来使得投获得的总利润达到最大。

模型一应用多目标决策方法建立模型，以投资效益没目标，对投资问题建立个一个优化模型，不同的投资方式具有不同的风险和效益，该模型根据优化模型的原理，提出了两个准则，并从众多的投资方案中选出若干个，使在投资额一定的条件下，经济效益尽可能大，风险尽可能小。

模型二给出了组合投资方案设计的一个线性规划模型，主要思想是通过线性加权综合两个设计目标：假设在投资规模相当大的基础上，将交易费函数近似线性化，通过决策变量化解风险函数的非线性。

二、 关键字：经济效益 线性规划模型 有效投资方案 线性加权三、 问题重述市场上有n 种资产（如储蓄、保险、国债、股票、基金、期货、外汇、房地产、珠宝、邮票、古玩字画、钱币及拍卖品等）S i ( i=1,…n) 供投资者选择，将数额1000万的一笔相当大的资金可用作一个时期的投资。

现对这n 种资产进行了评估，估算出在这一时期内购买Si 的平均收益率为i r 并预测出购买Si 的风险损失率为i q 。

考虑到投资越分散，总的风险越小，当用这笔资金购买若干种资产时，总体风险用所投资的S i 中最大的一个风险来度量。

购买S i 要付交易费，费率为i p ，并且当购买额不超过给定值i u 时，交易按购买i u 计算（不买当然无须付费）。

另外，假定同期银行存款利率是0r , 且既无交易费又无风险。

（0r =5%） (%) (或存银行生 息，使净收益尽可能大，而总体风险尽可能小。

资产(%)的盈亏数据，以及一般情况的讨论。

这是一个优化问题，要决策的是每种资产的投资额，要达到目标包括两方面的要求:净收益最大和总风险最低，即本题是一个双优化的问题，一般情况下，这两个目标是矛盾的，因为净收益越大则风险也会随着增加，反之也是一样的，所以，我们很难或者不可能提出同时满足这两个目标的决策方案，我们只能做到的是：在收益一定的情况下，使得风险最小的决策，或者在风险一定的情况下，使得净收益最大，或者在收益和风险按确定好的偏好比例的情况下设计出最好的决策方案，这样的话，我们得到的不再是一个方案，而是一个方案的组合，简称组合方案。

项目投资的最优问题摘要本文主要讨论项目投资的最优化问题。

首先对该问题进行分析，建立相应的数学模型，以使得投资获得的总利润达到最大值。

这是一个典型的线性规划问题，我们首先建立单目标的优化模型，以第五年末所拥有的本利息总额为目标函数，以资金流转分析加上各种投资金额的限制为约束条件。

再用lingo软件对问题进行求解，得到比较理想的结果：现有10万元的可用资金经最优投资到第五年末拥有总资金为143750元，即盈利43.75%。

在本文最后我们对项目投资最优的建模方法做了评价，对其算法（如：自行设计算法，利用软件进一步求解，多种方法相结合等）进行综合考虑并做了简要分析。

关键词：线性规划优化模型 lingo一问题的提出1.背景随着全球经济的高速发展，改革开放的不断推进，社会主义市场经济在中国不断完善，投资项目的最优化设计日渐突显其重要意义。

在这样的市场经济条件下，企业追求的目标是利润最大化。

由于企业的资金是有限的，对资金进行合理有效的配置，可以降低企业的成本，提高资金的使用效益，使企业获得最优效益。

投资项目的最优化设计日渐突显其重要意义。

2.问题的提出某部门在今后5年内考虑给以下4个项目投资：项目A：从第一年到第四年年初需要投资，并于次年末回收本利115%；项目B：从第三年年初需要投资，到第五年年末能回收本利125%，但规定最大投资额不超过4万元。

项目C：从第二年年初需要投资，到第五年年末能收回本利140%,但规定最大投资额不超过3万。

项目D：五年内，每年年初可以够买公债，于当年末归还并加利息6%；该部门现有资金10万元，问应该如何确定给这些项目的投资额，使第五年末拥有资金的本利总额最大？二问题的分析显然这是一个最优化问题，解决这类问题最常用方法就是线性规划方法。

线性规划可以合理地分配、使用有限的资源，使其能够获得“最优效益”。

目标函数是第五年末拥有资金的本利息总额。

为使资金得到有效利用，应在每年年初将手头全部资金投出去，每年年末回收各项投资的本利息即为第二年初手头拥有的投资总额，又全部投入到第二年年初所有可能的投资机会中去，以此类推，每年年初投资额等于头年末返回本利总额，这些资金流转分析加上各种投资金额的限制成为约束条件。