高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

怎样计算水准高程？
（一）有附合水准路线高差闭合量计算公式fn=∑h-(H终-H始）fn—高差闭合差∑h—各测站测得的高差总和H终—终点水准点高程H始—始点水准点高程闭合水准路线高差闭合差的计算公式fn=∑h支线水准路线高差闭合差计算公式fn=|∑h终|-|∑h始|∑h终|和∑h
始分别为往返测高差的绝对值。

（二）容许闭合差计算，并比较fn容=±8 mm n—测得数进行比较，若fn＜fn容，说明观测成果符合要求，可以进行高差闭合差调整。

（三）高程计算每一个测得的闭合差调整值=-fn/n=-16/16=-1（ mm）在计算每一测站的闭合量调整值时，必须改变原高差闭合差的符号。

坡度计算公式-坡度-
高程-公式
-CAL-FENGHAI.-(YICAI)-Company One1
坡度计算公式
表示方法:坡度是地表单元陡缓的程度,通常把坡面的垂直高度h和水平宽度l的比叫做坡度(或叫做坡比)用字母i表示，即坡角的正切值。

i=h/l
坡度的表示方法有: 百分比法、度数法、密位法和分数法四种，其中以百分比法和度数法较为常用。

(1) 百分比法
表示坡度最为常用的方法，即两点的高程差与其水平距离的百分比，其计算公式如下：坡度＝ (高程差/水平距离)x100% 使用百分比表示时，即：i=h/l×100％例如：坡度3% 是指水平距离每100米,垂直方向上升(下降)3米；1%是指水平距离每100米,垂直方向上升(下降)1米。

以次类推！
(2) 度数法
用度数来表示坡度，利用反三角函数计算而得，其公式如下：tanα(坡度)＝高程差/水平距离
所以α(坡度)＝ tan-1 (高程差/水平距离)
不同角度的正切及正弦坡度角度正切正弦
0° 0% 0% 5° 9% 9% 10° 18% 17% 30° 58% 50%
45° 100% 71% 60° 173% 87%问：已知高程差为12M，坡度
为%，求水平距离是多少
坡度=高程差/水平距离*100%
即：水平距离=12/%=
2。

道路曲线高程计算公式 Final revision by standardization team on December 10, 2020.高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

平整场地计算公式平整场地是指通过移除地表的凸起或凹陷部分，使其表面变得平坦。

这个过程可以通过人工或机械手段来完成，以满足场地使用的需要。

在进行平整场地之前，需要先制定一些计算公式来确定平整的标准和方法。

下面是一些常见的平整场地计算公式。

1.场地高程计算公式：场地高程是指场地上其中一点与基准点之间的垂直距离。

在进行场地平整之前，需要确定场地高程的变化范围。

通常情况下，平整后的场地高程应该与基准点相等。

场地高程计算公式可以表示为：E=B-Z其中，E表示场地高程，B表示基准点高程，Z表示场地其中一点的高程。

2.场地面积计算公式：场地面积是指场地在水平方向上的覆盖面积。

在进行场地平整之前，需要确定需要平整的范围的面积。

场地面积计算公式可以表示为：A=L×W其中，A表示场地的面积，L表示场地的长度，W表示场地的宽度。

3.场地体积计算公式：场地体积是指场地上需要移除或添加的土方的体积。

在进行场地平整之前，需要确定需要移除或添加的土方的体积。

场地体积计算公式可以表示为：V=A×D其中，V表示场地的体积，A表示场地的面积，D表示场地的平整厚度。

4.场地平整时间计算公式：场地平整时间是指完成场地平整工作所需要的时间。

在进行场地平整工作之前，需要确定工作的进度和计划。

场地平整时间计算公式可以表示为：T=(A×t)/p其中，T表示场地平整时间，A表示场地的面积，t表示每单位面积所需时间，p表示工作人员的数量。

5.场地平整成本计算公式：场地平整成本是指完成场地平整工作所需要的费用。

在进行场地平整工作之前，需要确定工作的预算和成本。

场地平整成本计算公式可以表示为：C=(A×c)+(T×s)其中，C表示场地平整成本，A表示场地的面积，c表示每单位面积的成本，T表示场地平整时间，s表示每单位时间的成本。

以上是一些常见的平整场地计算公式，可以根据具体的场地平整需求进行调整和应用。

高程计算公式
高程计算公式是用于计算地球表面高程的数学公式。

在地理信息系统（GIS）和土地测量学中，高程计算是非常重要的，因为它可以帮助我们确定地面的高度和形状，以及进行地形分析和地图制作。

以下是高程计算公式的详细说明：
1. 大地水准面高程计算公式
大地水准面是一个理论上的平面，它是一个通过地球上所有点的平均海平面。

大地水准面高程计算公式是：
H = h + N
其中，H是大地水准面高程，h是椭球面高程，N是大地水准面高程和椭球面高程之间的差异，也称为大地高。

2. 椭球面高程计算公式
椭球面高程是指地球表面相对于参考椭球体的高度。

椭球面高程计算公式是：h = N + H
其中，h是椭球面高程，N是大地高，H是大地水准面高程。

3. 垂直高程计算公式
垂直高程是指地面相对于某个基准面的高度。

垂直高程计算公式是：
E = H - h
其中，E是垂直高程，H是大地水准面高程，h是椭球面高程。

4. 坡度计算公式
坡度是指地面的倾斜程度。

坡度计算公式是：
S = tan(a)
其中，S是坡度，a是地面的倾斜角度。

5. 坡向计算公式
坡向是指地面的朝向。

坡向计算公式是：
α = atan2(d y, dx)
其中，α是坡向，dy是地面在y轴方向上的变化量，dx是地面在x轴方向上的变化量。

以上是高程计算公式的详细说明。

在实际应用中，我们需要根据具体的情况选择合适的公式进行计算。

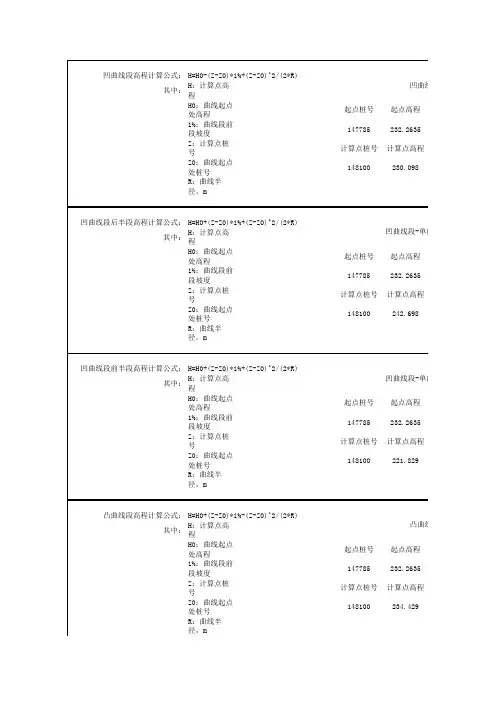
其中：H：计算点高程H0：曲线起点处高程起点桩号起点高程i%：曲线段前段坡度147785232.2635Z：计算点桩号计算点桩号计算点高程Z0：曲线起点处桩号148100230.098R：曲线半径，m其中：H：计算点高程H0：曲线起点处高程起点桩号起点高程i%：曲线段前段坡度147785232.2635Z：计算点桩号计算点桩号计算点高程Z0：曲线起点处桩号148100242.698R：曲线半径，m其中：H：计算点高程H0：曲线起点处高程起点桩号起点高程i%：曲线段前段坡度147785232.2635Z：计算点桩号计算点桩号计算点高程Z0：曲线起点处桩号148100221.829R：曲线半径，m其中：H：计算点高程H0：曲线起点处高程起点桩号起点高程i%：曲线段前段坡度147785232.2635Z：计算点桩号计算点桩号计算点高程Z0：曲线起点处桩号148100234.429R：曲线半径，m凹曲线段后半段高程计算公式：H=H0+(Z-Z0)*i%+(Z-Z0)^2/(2*R)凸曲线段凸曲线段高程计算公式：H=H0+(Z-Z0)*i%-(Z-Z0)^2/(2*R)凹曲线段凹曲线段-单向坡凹曲线段前半段高程计算公式：H=H0+(Z-Z0)*i%+(Z-Z0)^2/(2*R)凹曲线段-单向坡凹曲线段高程计算公式：H=H0-(Z-Z0)*i%+(Z-Z0)^2/(2*R)曲线段纵坡半径/m2%12000单向坡上坡段纵坡半径/m2%12000单向坡下坡段纵坡半径/m2%12000曲线段纵坡半径/m2%12000。

水准测量高程计算公式
在水准测量中，求解高程的计算公式是基于大地水准面理论和海平面高程的基准点。

1. 高程差计算公式：
高程差 = 前视高程 - 后视高程
2. 高程改正数计算公式：
高程改正数 = 观测高差 - 改正数
其中，观测高差为实测得到的高程差，改正数为校正仪器误差、大气压力、气温等因素引起的修正值。

3. 世界大地水准面的高程计算公式：
高程 = 海平面高程 + 高程差 + 高程改正数
4. 对流层改正公式：
对流层改正数= γ * L
其中，γ为对流层梯度系数（通常取7×10^-6/℃），L为观
测点与海洋基准点之间的大地纬度差。

需要注意的是，水准测量中的高程计算公式可能因为具体测量方法、精度要求等因素而有所差异，以上是一般情况下的计算公式。

在实际应用中，还需要考虑一些其他因素对高程的影响，并进行相应的修正和校正。

道路曲线高程计算公式集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

高程测量计算公式在我们的日常生活和工作中，高程测量可是个相当重要的事儿。

你想想，建造高楼大厦、铺设道路桥梁、规划水利工程等等，哪一样能离得开准确的高程测量呢？而要实现准确的高程测量，就得依靠那些神奇的计算公式啦。

先来说说高差法。

这就好比我们爬楼梯，每一层之间的高度差就是我们要关注的重点。

假设我们在 A 点测得了一个高程值 HA，然后又在 B 点测量得到了一个读数 HB，那么 A、B 两点之间的高差 hAB 就可以通过公式 hAB = HB - HA 计算出来。

我记得有一次，我们学校要修建一个新的花坛。

当时施工队的师傅们就用到了高差法来确定花坛各个位置的高度。

他们拿着水准仪，在不同的点上认真测量读数，然后在小本子上迅速计算高差。

我在旁边好奇地看着，只见他们一会儿抬头看看水准仪，一会儿低头写写算算，那专注的神情仿佛在完成一项极其重要的使命。

再讲讲视线高法。

这个方法就像是给我们的视线设定了一个基准高度。

假设我们知道了一个水准点的高程 Hi，然后在测量点上读取的中丝读数为 a，那么该测量点的高程 HB 就可以用公式 HB = Hi + a - b 来计算，其中 b 是水准尺的读数。

这让我想起之前去爬山的时候，我突发奇想，想要测一测从山脚下到山顶的高程变化。

我虽然没有专业的测量工具，但我用手机上的简单测量 APP 模拟了一下这个过程。

我把山脚下当作已知高程的点，然后随着自己不断往上爬，想象着读取不同位置的“虚拟读数”，用视线高法在心里默默计算着高程的变化。

那种感觉，就好像自己也变成了一个小小的测量工程师。

还有一种常用的方法是三角高程测量法。

这就有点像我们从不同的角度观察一个物体，通过角度和距离来推算它的高度。

公式 h = D ×tanα + i - v 中，D 是两点之间的水平距离，α 是观测的竖直角，i 是仪器高，v 是目标高。

记得有一回，我在公园里看到一群测绘专业的学生在进行实地测量作业。

他们有的拿着全站仪，有的拿着记录板，分工明确，配合默契。

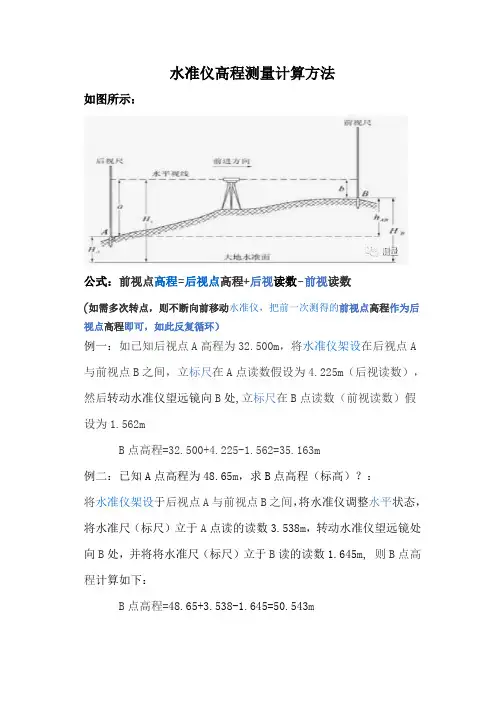
水准仪高程测量计算方法
如图所示：
公式：前视点高程=后视点高程+后视读数-前视读数
(如需多次转点，则不断向前移动水准仪，把前一次测得的前视点高程作为后视点高程即可，如此反复循环）
例一：如已知后视点A高程为32.500m，将水准仪架设在后视点A 与前视点B之间，立标尺在A点读数假设为4.225m（后视读数），然后转动水准仪望远镜向B处,立标尺在B点读数（前视读数）假设为1.562m
B点高程=32.500+4.225-1.562=35.163m
例二：已知A点高程为48.65m，求B点高程（标高）？：
将水准仪架设于后视点A与前视点B之间，将水准仪调整水平状态，将水准尺（标尺）立于A点读的读数3.538m，转动水准仪望远镜处向B处，并将将水准尺（标尺）立于B读的读数1.645m, 则B点高程计算如下：
B点高程=48.65+3.538-1.645=50.543m。

三角高程计算公式及其含义在地理测量和地理信息系统中，三角高程计算是一种常用的方法，用于确定地表上各点的高程。

三角高程计算公式是一种基于三角测量原理的数学公式，通过测量三角形的边长和角度，来计算出三角形的高程。

这种方法可以用来确定地表上任意点的高程，对于地形测量和地图制图非常有用。

三角高程计算公式的一般形式如下：h = (a sin(B)) / sin(A)。

其中，h表示目标点的高程，a表示已知边长，B表示已知角度，A表示未知角度。

这个公式基于正弦定理，通过已知的边长和角度来计算出目标点的高程。

这种方法可以用来测量地表上任意点的高程，无论是平原还是山地，都可以通过三角高程计算公式来确定其高程。

三角高程计算公式的含义非常重要，它可以帮助测量员确定地表上各点的高程，从而绘制出精确的地形图。

地形图是地理信息系统中非常重要的一部分，它可以用来确定地表的起伏和坡度，对于农业、建筑和城市规划等领域都非常有用。

通过三角高程计算公式，可以确定地表上各点的高程，从而绘制出准确的地形图，为各种应用提供重要的参考数据。

三角高程计算公式的应用非常广泛，不仅可以用于地形测量和地图制图，还可以用于工程测量和建筑规划。

在工程测量中，三角高程计算可以帮助工程师确定工程场地的高程，从而进行设计和施工。

在建筑规划中，三角高程计算可以帮助规划师确定建筑场地的高程，从而进行布局和设计。

通过三角高程计算公式，可以为各种工程和建筑提供准确的高程数据，为实际施工和规划提供重要的参考。

总之，三角高程计算公式是地理测量和地理信息系统中非常重要的一种方法，它可以帮助确定地表上各点的高程，为地形测量、地图制图、工程测量和建筑规划提供重要的参考数据。

通过三角高程计算公式，可以为各种应用提供准确的高程数据，为实际工作提供重要的支持。

因此，掌握和应用三角高程计算公式是地理测量和地理信息系统工作者的基本技能，也是各种应用领域的重要工具。

测绘导线的计算公式测绘导线是指在地面上用标志物、测量仪器、测绘工具等设备进行测量和标示的一条直线，用以确定地面上的地理位置和地理方向。

在测绘导线的工作中，计算是至关重要的一部分，因为准确的计算可以保证测绘结果的准确性和可靠性。

本文将介绍测绘导线的计算公式，以帮助读者更好地理解测绘导线的工作原理。

1. 导线长度的计算公式。

在测绘导线的工作中，最基本的计算就是导线的长度。

导线长度的计算公式如下：L = √(ΔX^2 + ΔY^2 + ΔZ^2)。

其中，L表示导线的长度，ΔX、ΔY、ΔZ分别表示导线两端点的坐标差值。

这个公式是根据勾股定理推导出来的，通过计算两个点之间的水平、垂直和高程差值，就可以得到导线的长度。

2. 导线方位角的计算公式。

导线的方位角是指导线与正北方向之间的夹角，通常以度数表示。

导线方位角的计算公式如下：α = arctan(ΔY/ΔX)。

其中，α表示导线的方位角，ΔX、ΔY分别表示导线两端点的坐标差值。

这个公式是根据三角函数的性质推导出来的，通过计算两个点之间的水平差值和垂直差值的比值的反正切值，就可以得到导线的方位角。

3. 导线坐标的计算公式。

在测绘导线的工作中，通常需要计算导线上各个点的坐标，以便后续的测量和标示工作。

导线坐标的计算公式如下：X = X0 + L cos(α)。

Y = Y0 + L sin(α)。

Z = Z0 + ΔZ。

其中，X、Y、Z分别表示导线上某一点的坐标，X0、Y0、Z0分别表示导线起点的坐标，L表示导线的长度，α表示导线的方位角，ΔZ表示导线上某一点的高程差值。

这个公式是根据三角函数的性质和直角坐标系的性质推导出来的，通过已知导线起点的坐标、导线长度和方位角，就可以计算出导线上任意点的坐标。

4. 导线高程的计算公式。

导线高程是指导线上各个点的高程，通常以米为单位表示。

导线高程的计算公式如下：H = H0 + ΔZ。

其中，H表示导线上某一点的高程，H0表示导线起点的高程，ΔZ表示导线上某一点的高程差值。

基底普挖高程计算公式在土木工程中，基底普挖高程计算是一个非常重要的问题。

基底普挖高程是指在土地开发和建筑施工中，为了确保建筑物的稳定性和安全性，需要对基础的挖掘深度进行计算。

这个计算涉及到土壤力学和结构力学等多个学科知识，是土木工程中的一个重要环节。

基底普挖高程计算的公式是根据土壤的力学性质和建筑物的结构特点来确定的。

一般来说，基底普挖高程计算公式可以分为两种情况，一种是在均匀土层中的计算，另一种是在非均匀土层中的计算。

下面我们将分别介绍这两种情况下的计算公式。

在均匀土层中的基底普挖高程计算公式如下：H = (q γ H) / γ。

其中，H表示基底普挖高程，q表示建筑物的设计荷载，γ表示土壤的容重，H表示土层的深度。

这个公式是根据土壤的承载力和建筑物的荷载来确定的，通过这个公式可以计算出在均匀土层中的基底普挖高程。

在非均匀土层中的基底普挖高程计算公式稍微复杂一些，一般可以采用有限元法或者其他数值计算方法来进行计算。

在非均匀土层中，土壤的力学性质会发生变化，这就需要考虑土壤的非均匀性对基底普挖高程的影响。

一般来说，在非均匀土层中的基底普挖高程计算公式可以表示为：H = (q ∑(γi Hi)) / ∑(γi)。

其中，H表示基底普挖高程，q表示建筑物的设计荷载，γi表示第i层土层的容重，Hi表示第i层土层的深度。

这个公式是根据土壤的非均匀性和建筑物的荷载来确定的，通过这个公式可以计算出在非均匀土层中的基底普挖高程。

在实际的工程中，基底普挖高程计算是一个非常复杂的问题，需要考虑多个因素的影响。

除了土壤的力学性质和建筑物的荷载外，还需要考虑土地的地质情况、地下水位、周围建筑物的影响等因素。

因此，在进行基底普挖高程计算时，需要进行详细的勘察和分析，以确保计算结果的准确性和可靠性。

除了基底普挖高程计算公式外，还需要考虑基底普挖的施工方法和施工工艺。

在实际的工程中，基底普挖通常采用挖掘机等机械设备进行挖掘，需要考虑挖掘机的工作范围和挖掘深度等因素。