工作常用坐标高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

计算细那么1、坐标计算：X 1=X+Dcosα,Y1=Y+Dsin α。

式中Y 、 X 为坐标， D 为两点之间的距离，Α 为方位角。

2、方位角计算：1〕、方位角 =tan=两坐标增量的比值，然后用计算器按出他们的反三角函数〔±号判断象限〕。

2〕、方位角： arctan〔 y2- y1)/(x2-x 1)。

加减 180〔大于 180 就减去 180〔还大于 360 就在减去 360〕、小于 180 就加 180 如果 x 轴坐标增量为负数，那么结果加 180°。

如果为正数，那么看 y 轴的坐标增量，如果 Y 轴上的结果为正，那么算出来的结果就是两点间的方位角，如果为负值，加360°。

S=√（y2- y1)+(x2-x 1),1)、当 y2- y1>0，x2-x 1>0 时；α =arctan〔 y2- y1)/(x2-x 1)。

2)、当 y2- y1<0，x2-x 1>0 时；α =360° +arctan〔y2- y1)/(x2-x 1)。

3)、当 x2-x 1<0 时；α =180° +arctan〔y2- y1)/(x2-x 1)。

再用两点之间的距离公式可算距离(根号下两个坐标距离差的平方相加〕。

拨角： arctan〔y2- y1)/(x2-x 1)1、例如：两条巷道要互相平行掘进的话，求它们的拨角：方法〔前视边方位角减后视边方位〕在此后视边方位要加减 180°，假设拨角结果为负值为左偏“逆时针〞〔 +360°就可化为右偏，正值为右偏“顺时针〞。

2、在图上标识方位的方法：就是导线边与Y 轴的夹角。

3、高程计算：目标高程 =测点高程 +?h〔高差〕 +仪器高—占标高。

4、直角坐标与极坐标的换算：〔直角坐标用坐标增量表示；极坐标用方位角和边长表示〕1〕、坐标正算〔极坐标化为直角坐标〕一个点的坐标及该点至未知点的距离和方位角，计算未知点坐标方位角，知A(Xa,Ya) 、Sab、αab，求 B(Xa,Ya)解： ?Xab=Sab×COSαab 那么有 Xb=Xa+?Xab ?Yab=Sab × SIN αab Yb=Ya+?Yab2)、坐标反算，两点的坐标，求两点的距离〔称反算边长〕和方位角(称反算方位角〕的方法A(Xa,Ya) 、 B(Xb,Yb), 求α ab、 Sab。

4211521095摘要：施工测量中的坐标、高程的几种计算方法，利用CAD、EXCEL、软件以及程序计算器互相校核,为外业提供准确的数据，从而保证工程施工的顺利进行。

关键词：施工放样坐标、高程计算。

1概况“兵马未动、粮草先行”测量工作向来被称为工程施工的“粮草"。

其重要性不言而喻。

近年来随着全站仪等光电仪器的使用,使我们的测量外业工作变的日益轻松.但是不管仪器怎么先进，我们的内业工作确一直是测量的重头戏。

测量内业计算的正确与否，直接影响着我们的施工.2施工测量内业计算测量内业的计算，主要是施工放样的坐标计算和高程计算.CAD、EXCEL、测量软件以及程序计算器的使用给我们的计算带来了极大的便利。

而且几种方法的互相检算也保证了我们内业资料的正确性。

现结合本人的经验,就上述几种方法作一介绍. 2。

1 利用CAD制图计算（1）施工放样的资料计算在施工放样的资料计算,首先我们利用CAD结合施工所使用的坐标系绘制所建工程的平面图,把所有的结构物按照实际坐标跃然于纸上.在这个步骤中最主要关键的问题是坐标系的转换。

大地坐标系中上方为正北方向，代表的是X轴，而在CAD中X州代表的为正东方向，所以在绘图中我们要利用CAD的UCS工具条中的坐标轴旋转UCS功能，利用Z轴旋转把UCS旋转90度，然后利用X轴旋转把UCS旋转90度,如图所示：然后按照图纸所给的控制点坐标和所给的结构物与控制点坐标的相对关系，把结构物一一绘制到CAD中。

特别注意的一点是必须一步步找到结构物的每个关键点与控制点的相对关系.不能按照图纸所给的结构物坐标绘制。

做完这一步我们可以对设计的资料进行复核了。

按照设计所给的点在CAD上选取就可以了。

外业放样的资料读取。

1、按照坐标放样，我们之需要在图纸上选取我们需要的点为即可。

2、极坐标的放样的放样有两个方案,一个是把坐标选取后用计算器算;一个是在图纸上绘制致镜点坐标和后视点坐标。

然后量取放样点所需的角度和距离。

坐标计算公式LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】坐标计算公式1．坐标正算用坐标正算计算测点X、Y坐标值（注意，全站仪测得的边长分水平距与斜距，坐标正算公式用的是水平距）测点高程=测站高程+高差坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

编辑本段计算实例实例1，设直线AB的边长DAB和一个端点A的坐标XA、YA为已知，则直线另一个端点B的坐标为：XB=XA+ΔXABYB=YA+ΔYAB式中，ΔXAB、ΔYAB称为坐标增量，也就是直线两端点A、B的坐标值之差。

根据三角函数，可写出坐标增量的计算公式为：ΔXAB=DAB·cosαABΔYAB=DAB·sinαAB式中ΔX、ΔY的符号取决于方位角α所在的象限。

实例2. 已知直线B1的边长为，坐标方位角为211°07′53〃，其中一个端点B的坐标为（，），求直线另一个端点1的坐标X1，Y1。

解: 先代入公式（）、（），求出直线B1的坐标增量：ΔXB1=DB1·CosαB1=×cos211°07′53〃=－ΔYB1=DB1·sinαB1=×sin211°07′53〃〃=－然后代入公式（）、（），求出直线另一端点1的坐标：X1=XB+ΔXB1=－=Y1=YB+ΔYB1=－=坐标增量计算也常使用小型计算器计算，而且非常简单。

如使用fx140等类型的计算器，可使用功能转换键INV和极坐标与直角坐标换算键P→R以及x←→y键。

按键顺序为：D INV P→R α ＝显示ΔX X←→y 显示ΔY。

如上例，按INV P→R 211°07′53〃＝显示－107．31（ΔXB1）；按x←→y 显示－（ΔYB1）追问能不能再来一个简单的实例全数字的，不用公式代替，参考资料：根据直线起点的坐标、直线长度及其坐标方位角计算直线终点的坐标，称为坐标正算。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

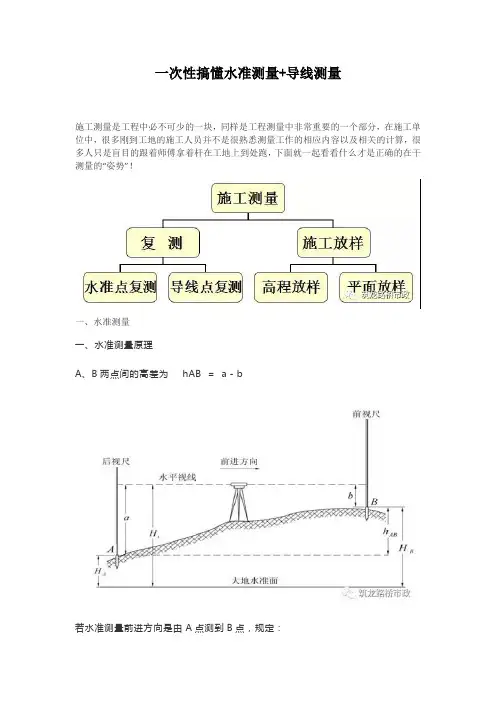
一次性搞懂水准测量+导线测量施工测量是工程中必不可少的一块，同样是工程测量中非常重要的一个部分，在施工单位中，很多刚到工地的施工人员并不是很熟悉测量工作的相应内容以及相关的计算，很多人只是盲目的跟着师傅拿着杆在工地上到处跑，下面就一起看看什么才是正确的在干测量的“姿势”！一、水准测量一、水准测量原理A、B两点间的高差为hAB ＝a－b若水准测量前进方向是由A点测到B点，规定：A点为后视点，A点尺上的读数a 为后视读数B点为前视点，B点尺上的读数b 为前视读数高差＝后视读数－前视读数当a 大于b 时，hAB 值为正，B点高于A点；当a 小于b 时，hAB 值为负，B点低于A点。

hAB表示由A点至B点的高差；hBA表示由B点至A点的高差，hAB ＝－hBA直接利用高差hAB计算B点高程的方法称为高差法。

若已知A 点的高程HA，求未知点B 的高程HBHB＝HA＋hAB利用仪器视线高程Hi 计算B点高程的方法称为视线高法。

Hi ＝HA＋aHB＝HA＋（a－b）＝Hi－b若A、B两点之间相距较远或高差较大时连续设站水准测量转点起传递高程的作用二、DS3微倾式水准仪一）水准仪的分类1．按精度划分分为DS05、DS1、DS3、DS10等四个等级，“D”和“S”分别为“大地测量”和“水准仪”的汉语拼音第一个字母，下标05、1、3、10表示仪器的精度等级，即“每千米往返测高差中数的中误差（单位：mm）。

”DS05、DS1称为精密水准仪，DS3、DS10称为普通水准仪。

2．按结构划分光学水准仪；微倾式水准仪；自动安平水准仪；电子水准仪望远镜、水准器和基座主要由物镜、目镜、十字丝分划板、调焦透镜、调焦螺旋和镜筒组成。

十字丝中心交点与物镜光心的连线称为望远镜的视准轴。

2．水准器（1）圆水准器球面中心刻有一个小圆圈，小圆圈的中心称为圆水准器的零点。

通过零点的球面法线，称为圆水准器轴。

当圆水准气泡中心与零点重合时，即气泡居中，说明圆水准器轴处于铅垂位置。

地质工作中常用的坐标系坐标是表达地面位置的重要参数，从事地质勘查工作的人时时刻刻都在与坐标打交道，一切地质工作都建立在坐标定位之上，是地质工作的基础。

地球是一个球体，球面上的位置，是以经纬度来表示，我们把它称为“球面坐标系统”或“地理坐标系统”。

在球面上计算角度距离十分麻烦，而且地图是印刷在平面纸张上，要将球面上的物体画到纸上，就必须展平，这种将球面转化为平面的过程，称为“投影”。

经由投影的过程，把球面坐标换算为平面直角坐标。

§ 1.1 地理坐标系统地质工作常用的地理坐标系统有北京54坐标系、西安80坐标系、美国WGS84坐标，目前在全国第二次土地调查中使用的2000国家大地坐标系，在地勘行业中不常用。

一个完整的坐标系统是由坐标系和基准2个方面要素所构成的。

下面主要介绍 WGS-84大地坐标系、1954年北京坐标系和1980年国家大地坐标系、2000国家大地坐标系 4 种坐标系统及其参考椭球的基本常数 (基准) 及手持 GPS 接收机WGS-84、1954年北京坐标系和1980年国家大地坐标系转换参数计算。

一、 WGS-84 大地坐标系WGS － 84 （ World Geodetic System ， 1984 年）是美国国防部研制确定的大地坐标系，其坐标系的几何定义是：原点在地球质心， z 轴指向 BIHl984.0 定义的协议地球极 (CTP) 方向， x 轴指向 BIHl984.0 的零子午面和 CTP 赤道的交点， Y 轴与 x 轴和 z 轴构成右手坐标系。

该椭球的参数为：长半轴： a=6378137m ；第一偏心率： e2=0.00669437999013 ；第二偏心率： e ” =0.006739496742227 ；扁率： F=1/298.25223563 。

二、 1954 年北京坐标系 (BJ 一 54)建国前，我国没有统一的大地坐标系统，建国初期，在苏联专家的建议下，我国根据当时的具体情况，建立起了全国统一的 1954 年北京坐标系。

坡度的表示方法有百分比法、度数法、密位法和分数法四种，其中以百分比法和度数法较为常用。

(1) 百分比法表示坡度最为常用的方法，即两点的高程差与其水平距离的百分比，其计算公式如下：坡度＝(高程差/水平距离)x100% 使用百分比表示时，即：i=h/l×100％例如：坡度3% 是指水平距离每100米,垂直方向上升(下降)3米；1%是指水平距离每100米,垂直方向上升(下降)1米。

以次类推！
(2)度数法用度数来表示坡度，利用反三角函数计算而得，其公式如下：tanα(坡度)＝高程差/水平距离所以α(坡度)＝tan-1 (高程差/水平距离) 不同角度的正切及正弦坡度角度正切正弦0° 0% 0% 5° 9% 9% 10° 18% 17% 30° 58% 50% 45° 100% 71% 60° 173% 87%
角度计算
余弦定理，设三个角为A，B，C，对边分别为a，b，c
则c2＝a2＋b2－2*a*b*COSC c2，a2，b2表示平方
COSC=(a2＋b2－c2)/(2*a*b)
COSB,COSA的值类推。