吉林省初三数学总复习经典压轴题总结
- 格式:pdf
- 大小:618.55 KB
- 文档页数:15

九年级培优班期末复习——以二次函数为背景的压轴题解题方法一、常见的类型及解题策略1、【“平行于y 轴的动线段长度的最大值”的问题】由于平行于y 轴的线段上各个点的横坐标相等(设为t ),借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式下上y y -,把动线段的长度就表示成为一个自变量为t ,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标。
2、【“在定直线(常为抛物线的对称轴,或x 轴或y 轴或其它的定直线)上是否存在一点,使之到两定点的距离之和最小”的问题】 先求出两个定点中的任一个定点关于定直线的对称点的坐标,再把该对称点和另一个定点连结得到一条线段,该线段的长度〈应用两点间的距离公式计算(勾股定理)〉即为符合题中要求的最小距离,而该线段与定直线的交点就是符合距离之和最小的点,其坐标很易求出(利用求交点坐标的方法)。
3、【三角形周长的“最值(最大值或最小值)”问题】在定直线上是否存在一点,使之和两个定点构成的三角形周长最小”的问题(简称“一边固定两边动的问题):方法:由于有两个定点,所以该三角形有一定边(其长度可利用两点间距离公式(勾股定理)计算),只需另两边的和最小即可(做对称)。
四边形周长问题同理4、【三角形面积的最大值问题】“抛物线上是否存在一点,使之与一条定线段构成的三角形面积最大”的问题(简称“一边固定两边动的问题”): 过动点向y值。
5、【一抛物线上是否存在一点,使之和另外三个定点构成的四边形面积最大的问题”】由于该四边形有三个定点,从而可把动四边形分割成一个动三角形与一个定三角形(连结两个定点,即可得到一个定三角形)的面积之和,所以只需动三角形的面积最大,就会使动四边形的面积最大,而动三角形面积最大值的求法及抛物线上动点坐标求法与上面相同。
6、“定四边形面积的求解”问题:有两种常见解决的方案:方案(一):连接一条对角线,分成两个三角形面积之和;方案(二):过不在x 轴或y 轴上的四边形的一个顶点,向x 轴(或y 轴)作垂线,或者把该点与原点连结起来,分割成一个梯形(常为直角梯形)和一些三角形的面积之和(或差),或几个基本模型的三角形面积的和(差)7、【“某函数图象上是否存在一点,使之与另两个定点构成等腰三角形”的问题】方法:两圆一线8、【“某图象上是否存在一点,使之与另外三个点构成平行四边形”问题】进一步有:① 若是否存在这样的动点构成矩形呢?先让动点构成平行四边形,再验证两条对角线相等否?若相等,则所求动点能构成矩形,否则这样的动点不存在。

一、中考数学压轴题1.已知:菱形 ABCD ,点 E 在线段 BC 上,连接 DE ,点 F 在线段 AB 上,连接 CF 、DF , CF 与 DE 交于点 G ,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.(1)求证:CD=CF ;(2)设∠CED = x ,∠DCF = y ,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围) (3)在(2)的条件下,当 x =45°时,以 CD 为底边作等腰△CDK ,顶角顶点 K 在菱形 ABCD 的内部,连接 GK ,若 GK ∥CD ,CD =4 时,求线段 KG 的长.2.如图1,在平面直角坐标系中,抛物线2393344y x x =--x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C .(1)过点C 的直线5334y x =-x 轴于点H ,若点P 是第四象限内抛物线上的一个动点,且在对称轴的右侧,过点P 作//PQ y 轴交直线CH 于点Q ,作//PN x 轴交对称轴于点N ,以PQ PN 、为邻边作矩形PQMN ,当矩形PQMN 的周长最大时,在y 轴上有一动点K ,x 轴上有一动点T ,一动点G 从线段CP 的中点R 出发以每秒1个单位的速度沿R K T →→的路径运动到点T ,再沿线段TB 以每秒2个单位的速度运动到B 点处停止运动,求动点G 运动时间的最小值:(2)如图2, 将ABC ∆绕点B 顺时针旋转至A BC ''∆的位置, 点A C 、的对应点分别为A C ''、,且点C '恰好落在抛物线的对称轴上,连接AC '.点E 是y 轴上的一个动点,连接AE C E '、, 将AC E ∆'沿直线C E '翻折为A C E ∆'', 是否存在点E , 使得BAA ∆'为等腰三角形?若存在,请求出点E 的坐标;若不存在,请说明理由.3.已知抛物线217222y x mx m 的顶点为点C . (1)求证:不论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)若抛物线的对称轴为直线3x =,求m 的值和C 点坐标;(3)如图,直线1y x =-与(2)中的抛物线并于A B 、两点,并与它的对称轴交于点D ,直线x k =交直线AB 于点M ,交抛物线于点N .求当k 为何值时,以C D M N 、、、为顶点的四边形为平行四边形.4.“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x ,十位上和个位上的数字之和为y ,如果x y =,那么称这个四位数为“和平数”. 例如:1423,14x =+,23y =+,因为x y =,所以1423是“和平数”.(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________; (2)求同时满足下列条件的所有“和平数”:①个位上的数字是千位上的数字的两倍;②百位上的数字与十位上的数字之和是12的倍数;(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.例如:1423于4132为“相关和平数”求证:任意的两个“相关和平数”之和是1111的倍数.5.已知.在Rt △OAB 中,∠OAB=90°,∠BOA=30°,OA=23,若以O 为坐标原点,OA 所在直线为x 轴,建立如图所示的平面直角坐标系,点B 在第一象限内,将Rt △OAB 沿OB 折叠后,点A 落在第一象限内的点C 处.(1)求经过点O ,C ,A 三点的抛物线的解析式.(2)若点M 是抛物线上一点,且位于线段OC 的上方,连接MO 、MC ,问:点M 位于何处时三角形MOC 的面积最大?并求出三角形MOC 的最大面积.(3)抛物线上是否存在一点P ,使∠OAP=∠BOC ?若存在,请求出此时点P 的坐标;若不存在,请说明理由.6.如图1,已知,⊙O 是△ABC 的外接圆,AB=AC=10,BC=12,连接AO 并延长交BC 于点H .(1)求外接圆⊙O 的半径;(2)如图2,点D 是AH 上(不与点A ,H 重合)的动点,以CD ,CB 为边,作平行四边形CDEB ,DE 分别交⊙O 于点N ,交AB 边于点M .①连接BN ,当BN ⊥DE 时,求AM 的值;②如图3,延长ED 交AC 于点F ,求证:NM ·NF=AM ·MB ;③设AM=x ,要使2ND -22DM <0成立,求x 的取值范围.7.如图,在平面直角坐标中,点O 为坐标原点,ABC ∆的三个顶点坐标分别为()A O m ,,(),B m O -,(),C n O ,5AC =且OBA OAB ∠=∠,其中m ,n 满足725m n m n +=⎧⎨-=⎩.(1)求点A ,C 的坐标;(2)点P 从点A 出发,以每秒1个单位长度的速度沿y 轴负方向运动,设点P 的运动时间为t 秒.连接BP 、CP ,用含有t 的式子表示BPC ∆的面积为S (直接写出t 的取值范围);(3)在(2)的条件下,是否存在t 的值,使得ΔΔ32PAB POC S S =,若存在,请求出t 的值,并直接写出BP 中点Q 的坐标;若不存,请说明理由. 8.如图,在ABC ∆中,14AB =,45B ∠=︒,4tan 3A =,点D 为AB 中点.动点P 从点D 出发,沿DA 方向以每秒1个单位长度的速度向终点A 运动,点P 关于点D 对称点为点Q ,以PQ 为边向上作正方形PQMN .设点P 的运动时间为t 秒.(1)当t =_______秒时,点N 落在AC 边上.(2)设正方形PQMN 与ABC ∆重叠部分面积为S ,当点N 在ABC ∆内部时,求S 关于t 的函数关系式.(3)当正方形PQMN 的对角线所在直线将ABC ∆的分为面积相等的两部分时,直接写出t 的值.9.对于平面直角坐标系xOy 中的图形W 1和图形W 2.给出如下定义:在图形W 1上存在两点A ,B (点A ,B 可以重合),在图形W 2上存在两点M ,N ,(点M 于点N 可以重合)使得AM=2BN ,则称图形W 1和图形W 2满足限距关系(1)如图1,点C(1,0),D(-1,0),E(0,3),点P 在线段DE 上运动(点P 可以与点D ,E 重合),连接OP ,CP .①线段OP 的最小值为_______,最大值为_______;线段CP 的取值范直范围是_____; ②在点O ,点C 中,点____________与线段DE 满足限距关系;(2)如图2,⊙O 的半径为1,直线3y x b =+(b>0)与x 轴、y 轴分别交于点F ,G .若线段FG 与⊙O 满足限距关系,求b 的取值范围;(3)⊙O 的半径为r(r>0),点H ,K 是⊙O 上的两个点,分别以H ,K 为圆心,1为半径作圆得到⊙H 和 K ,若对于任意点H ,K ,⊙H 和⊙K 都满足限距关系,直接写出r 的取值范围.10.综合与探究:如图1,在平面直角坐标系xOy 中,四边形OABC 是边长为4的菱形,60C ︒∠=(1)把菱形OABC 先向右平移4个单位后,再向下平移()03m m <<个单位,得到菱形''''O A B C ,在向下平移的过程中,易知菱形''''O A B C 与菱形OABC 重叠部分的四边形'AEC F 为平行四边形,如图2.试探究:当m 为何值时,平行四边形'AEC F 为菱形:(2)如图,在()1的条件下,连接''',AC B O G 、为CE 的中点J 为EB 的中点,H 为AC 上一动点,I 为''B O 上一动点,连接,,,GH HI IJ 求GH HI IJ ++的最小值,并直接写出此时,H I 点的坐标.11.问题背景:如图,四边形ABCD 中,AD BC ∥,8BC =,17AD =+,32AB =,45ABC ∠=︒,P 为边AD 上一动点,连接BP 、CP .问题探究(1)如图1,若30PBC ∠=︒,则AP 的长为__________.(2)如图2,请求出BPC △周长的最小值;(3)如图3,过点P 作PE BC ⊥于点E ,过点E 分别作EM PB ⊥于M ,EN PC ⊥于点N ,连接MN①是否存在点P ,使得PMN 的面积最大?若存在,求出PMN 面积的最大值,若不存在,请说明理由;②请直接写出PMN 面积的最小值.12.注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.如图,将一个矩形纸片ABCD ,放置在平面直角坐标系中,()0,0A ,()4,0B ,()0,3D ,M 是边CD 上一点,将ADM 沿直线AM 折叠,得到ANM .(Ⅰ)当AN 平分MAB ∠时,求DAM ∠的度数和点M 的坐标;(Ⅱ)连接BN ,当1DM =时,求ABN 的面积;(Ⅲ)当射线BN 交线段CD 于点F 时,求DF 的最大值.(直接写出答案) 在研究第(Ⅱ)问时,师生有如下对话:师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题. 小明:我是这样想的,延长MN 与x 轴交于P 点,于是出现了Rt NAP △.小雨:我和你想的不一样,我过点N 作y 轴的平行线,出现了两个Rt NAP △.13.在平面直角坐标系中,点O 为坐标原点,抛物线(2)()y a x x m =++与x 轴交于点A C 、(点A 在点C 的左侧),与y 轴正半轴交于点B ,24OC OB ==.(1)如图1,求a m 、的值;(2)如图2,抛物线的顶点坐标是M ,点D 是第一象限抛物线上的一点,连接AD 交抛物线的对称轴于点N ,设点D 的横坐标是t ,线段MN 的长为d ,求d 与t 的函数关系式;(3)如图3,在(2)的条件下,当154d =时,过点D 作DE x 轴交抛物线于点E ,点P 是x 轴下方抛物线上的一个动点,连接PE 交x 轴于点F ,直线211y x b =+经过点D 交EF 于点G ,连接CG ,过点E 作EH CG 交DG 于点H ,若3CFG EGH S S =△△,求点P 的坐标.14.新定义,若关于x ,y 的二元一次方程组①111222a x b y c a x b y c +=⎧⎨+=⎩的解是00x x y y =⎧⎨=⎩,关于x ,y 的二元一次方程组②111222e x f y d e x f y d +=⎧⎨+=⎩的解是11x x y y =⎧⎨=⎩,且满足100.1x x x -≤,1000.1y y y -≤,则称方程组②的解是方程组①的模糊解.关于x ,y 的二元一次方程组222104x y m x y m +=+⎧⎨-=+⎩的解是方程组10310x y x y +=⎧⎨+=-⎩的模糊解,则m 的取值范围是________. 15.如图,在矩形ABCD 中,6AB cm =,8AD cm =,连接BD ,将ABD △绕B 点作顺时针方向旋转得到A B D '''△(B ′与B 重合),且点D '刚好落在BC 的延长上,A D ''与CD 相交于点E .(1)求矩形ABCD 与A B D '''△重叠部分(如图1中阴影部分A B CE '')的面积; (2)将A B D '''△以每秒2cm 的速度沿直线BC 向右平移,如图2,当B ′移动到C 点时停止移动.设矩形ABCD 与A B D '''△重叠部分的面积为y ,移动的时间为x ,请你直接写出y 关于x 的函数关系式,并指出自变量x 的取值范围;(3)在(2)的平移过程中,是否存在这样的时间x ,使得AA B ''△成为等腰三角形?若存在,请你直接写出对应的x 的值,若不存在,请你说明理由.16.将一个直角三角形纸片ABO ,放置在平面直角坐标系中,点0(3)A ,,点()0, 3B ,点(0,0)O(I)过边OB 上的动点D (点D 不与点B ,O 重合)作DE OB ⊥交AB 于点E ,沿着DE 折叠该纸片,点B 落在射线BO 上的点F 处.①如图,当D 为OB 中点时,求E 点的坐标;②连接AF ,当AEF ∆为直角三角形时,求E 点坐标:(Ⅱ) P 是AB 边上的动点(点 P 不与点B 重合),将AOP ∆沿OP 所在的直线折叠,得到'A OP ∆,连接'BA ,当'BA 取得最小值时,求P 点坐标(直接写出结果即可).17.如图,抛物线25y ax bx =+-交x 轴于点A 、B (A 在B 的左侧),交y 轴于点C ,且OB OC =,()2,0A -.(1)求抛物线的解析式;(2)点P 为第四象限抛物线上一点,过点P 作y 轴的平行线交BC 于点D ,设P 点横坐标为t ,线段PD 的长度为d ,求d 与t 的函数关系式.(不要求写出t 的取值范围) (3)在(2)的条件下,F 为BP 延长线上一点,且45PFC ∠=︒,连接OF 、CP 、PB ,FOB ∆的面积为3600169,求PBC ∆的面积. 18.如图①,△ABC 是等腰直角三角形,在两腰AB 、AC 外侧作两个等边三角形ABD 和ACE ,AM 和AN 分别是等边三角形ABD 和ACE 的角平分线,连接CM 、BN ,CM 与AB 交于点P .(1)求证:CM =BN ;(2)如图②,点F 为角平分线AN 上一点,且∠CPF =30°,求证:△APF ∽△AMC ; (3)在(2)的条件下,求PF BN 的值. 19.已知抛物线2y ax bx c =++过点(6,0)A -,(2,0)B ,(0,3)C -.(1)求此抛物线的解析式;(2)若点H 是该抛物线第三象限的任意一点,求四边形OCHA 的最大面积;(3)若点Q 在y 轴上,点G 为该抛物线的顶点,且45GQA ∠=︒,求点Q 的坐标.20.如图,在▱ABCD 中,对角线AC ⊥BC ,∠BAC =30°,BC =3AB 边的下方作射线AG ,使得∠BAG =30°,E 为线段DC 上一个动点,在射线AG 上取一点P ,连接BP ,使得∠EBP =60°,连接EP 交AC 于点F ,在点E 的运动过程中,当∠BPE =60°时,则AF =_____.21.如图,在平面直角坐标系xOy 中,已知Rt ABC 的直角顶点()0,12C ,斜边AB 在x 轴上,且点A 的坐标为()9,0-,点D 是AC 的中点,点E 是BC 边上的一个动点,抛物线212y ax bx =++过D ,C ,E 三点.(1)当//DE AB 时,①求抛物线的解析式;②平行于对称轴的直线x m =与x 轴,DE ,BC 分别交于点F ,H ,G ,若以点D ,H ,F 为顶点的三角形与GHE △相似,求点m 的值.(2)以E 为等腰三角形顶角顶点,ED 为腰构造等腰EDG △,且G 点落在x 轴上.若在x 轴上满足条件的G 点有且只有一个时,请直接写出....点E 的坐标. 22.如图1,以AB 为直径作⊙O ,点C 是直径AB 上方半圆上的一点,连结AC ,BC ,过点C 作∠ACB 的平分线交⊙O 于点D ,过点D 作AB 的平行线交CB 的延长线于点E .(1)如图1,连结AD ,求证:∠ADC =∠DEC .(2)若⊙O 的半径为5,求CA •CE 的最大值.(3)如图2,连结AE ,设tan ∠ABC =x ,tan ∠AEC =y ,①求y 关于x 的函数解析式; ②若CB BE =45,求y 的值. 23.在菱形ABCD 中,点P 是对角线BD 上一点,点M 在CB 的延长线上,且PC PM =, 连接PA .()1如图①,求证:PA PM =;()2如图②,连接,AM PM 与AB 交于点,120O ADC ︒∠=求证 =PC AM ;()3连接AM ,当 90ADC ︒∠=时,PC 与AM 的数量关系是24.(1)探究发现数学活动课上,小明说“若直线21y x =-向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”经过一番讨论,小组成员展示了他们的解答过程:在直线21y x =-上任取点()01A -,, 向左平移3个单位得到点()31,'--A 设向左平移3个单位后所得直线所对应的函数表达式为2y x n =+.因为2y x n =+过点()31,'--A , 所以61n -+=-,所以5n =,填空:所以平移后所得直线所对应函数表达式为(2)类比运用已知直线21y x =-,求它关于x 轴对称的直线所对应的函数表达式;(3)拓展运用将直线21y x =-绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .25.如图,在平面直角坐标系中,点(1,2)A ,(5,0)B ,抛物线22(0)y ax ax a =->交x 轴正半轴于点C ,连结AO ,AB .(1)求点C 的坐标;(2)求直线AB 的表达式;(3)设抛物线22(0)y ax ax a =->分别交边BA ,BA 延长线于点D ,E .①若2AE AO =,求抛物线表达式;②若CDB △与BOA △相似,则a 的值为 .(直接写出答案)【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.D解析:(1)见解析;(2)y=1603x +;(2)232 【解析】【分析】(1)根据翻折的性质得△DFG ≌△DFA ,从而推导得出∠FDC=∠DFG ,进而得到CF=DC ; (2)在等腰△DGC 和等腰△CFD 中,可用y 表示出∠GDC 、∠FDC 的值,从而求出∠ADF ,根据∠ADE=∠DEC ,得出y 与x 的关系式;(3)先证△KCD 是等腰直角三角形,根据CD 的长得到KC 的值,然后再△KGC 中求得KG 的值.【详解】(1)∵将菱形ABCD 沿DF 翻折,点A 恰好落在点G 上∴△DFG ≌△DFA ,∠AFD=∠FDC∴∠AFD=∠DFG∴∠FDC=∠DFG∴CF=DC ;(2)∵AD=DG=DC=FC ,∠DCF=y∴在△DGC 中,∠DGC=y ,∠GDC=180-2y在△CFD 中,∠CFD=∠CDF=902y - ∴∠FDG=∠FDC -∠GDC=3902y - ∴∠ADF=∠FDG=3902y -,∴∠ADE=3y -180 ∵AD ∥BC∴∠ADE=∠DEC ,即3y -180=x化简得:y=1603x +; (3)如下图,过点K 作CD 的垂线,交CD 于点I ,延长KG 交BC 于点L ,过点C 作GL 的垂线,交GL 于点Q ,过点C 作GD 的垂线,交GD 于点N ,∵x=45°,∴y=75°,∠ADE=x=45°∴∠DGC=∠DCG=75°,∴∠NDC=30°,∴∠ADC=45°+30°=75°,∵四边形ABCD 是菱形,∴∠B=75°,∵KG ∥DC ,∴KG ∥AB ,∠KGD=∠NDC=30°,∴∠GLC=∠B=75°,∠KGC=30°+75°=105°,∴∠LGC=75°,∴∠CGL=∠CGN,∴GC是∠LGN的角平分线,∴CQ=CN,∵CD=4,∠CDE=30°,∴在Rt△CND中,CN=2,∴CQ=2,∵KG∥CD,∴∠QKI=∠KIC=90°∵CQ⊥KL∴四边形CQKI是矩形,∵CK=KD,KI⊥CD,∴CI=ID=2,∴CI=CQ=2,∴矩形CQKI是正方形∴IK=CQ=2,∴在Rt△KIC中,CK=22,如下图,过点G作CK的垂线,交CK于点M,∴△KGM是等腰直角三角形,△GMC是直角三角形,且∠C=30°,设GM=x,则在Rt△GKM中,KM=GM=x,在Rt△GMC中,CG=2x,3x,∴322解得:62x.∴2=232【点睛】本题考查菱形的性质和翻折的性质,需要注意,翻折后的图形和翻折前的图形时完全相等的,这个条件不可忽略.2.A解析:(1)min 119342t R H '==+;(2)(0,3-3)或(0,6)或(0,3+3)或(0,12).【解析】【分析】(1)根据题意设239(,33)4P m m m --,5(,33)4Q m m -,以及作R 关于y 轴对称3(3,33)2R '--,并过R '点作直线3:43x l y =-的垂线交于H 点R H '即为所求,从而进行分析求解即可; (2)根据题意分四种情形即①当AA''=A''B 时;②当AA''=AB 时;③当AA''=A''B 时;④当A''B=AB 时分别画出图形并进行分析求解.【详解】解:(1)设239(,33)4P m m m --,5(,33)4Q m m -, 23932()2(3)422PQMN C QP NP m m ∴=+=-+-矩形, 30-<,开口向下, ∴当33m =时,(33,33)P -,最少时间12t RK RK TB =++, 3(3,33)2R -,作R 关于y 轴对称3(3,33)2R '--,过R '点作直线3:4x l y =的垂线交于H 点R H '即为所求, 令y=0,解得5312x =, 12()530H ∴,,t R K K T TH =+''+'',∴过R ''作R H l ''⊥, 22min 3119(33)(330)3242125t R H ∴==++'--=+. (2)①当AA''=A''B 时,如图2中,此时,A''在对称轴上对称性可知∠AC′E=∠A''C′E又∠HEC′=∠A''C′E∴∠AC′E=∠HEC′∴HE=HC'=5 3−2 3=3 3,∴OE=HE-HO=3 3−3,∴E(0,3−3 3),②当AA''=AB 时,如图3中,设A″C′交y 轴于J .此时AA''=AB=BC'=A''C',∴四边形A''ABC'为菱形,由对称性可知,∠AC'E=∠A''C'E=30°,∴3=32, ∴OE=OJ-JE=6∴E (0,6)③当AA''=A''B 时,如图4中,设AC′交y 轴于M .此时,A''在对称轴上∠MC'E=75°又∠AMO=∠EMC'=30°∴∠MEC'=75°∴ME=MC' ∴MC'=3 3,∴OE=3+3 3,∴E (0,3+3).④当A''B=AB 时,如图5中,此时AC'=A''C'=A''B=AB∴四边形AC'A''B 为菱形由对称性可知,C'',E ,B 共线 由抛物线2393344y x x =--x 轴交于A B 、两点(点A 在点B 的左侧)可知, 令x=0,解得y=−3x=0,解得:x 1=3,x 23 ∴A (−30),30),3∴3=12,∴E (0,12).综上满足条件的点E 坐标为(0,3)或(0,6)或(0,3)或(0,12). 【点睛】本题考查二次函数综合题,解题的关键是学会构建二次函数解决最值问题,学会利用垂线段最短解决最短问题,学会用分类讨论的思想思考问题,属于中考压轴题. 3.(1)详见解析;(2)3m =,点C 坐标为(3,2)-;(3)5k =或417k或417k 时,可使得C D M N 、、、为顶点的四边形是平行四边形. 【解析】【分析】(1)从2172022x mx m 的判别式出发,判别式总大于等于3,而证得; (2)根据抛物线的对称轴32bx a 来求m 的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点C 的坐标;(3)根据平行四边形的性质得到:215|1(3)|422MN k k k CD . 需要分类讨论:①当四边形CDMN 是平行四边形,2151(3)422MNk k k ,通过解该方程可以求得k 的值;②当四边形CDNM 是平行四边形,2153(1)422NMk k k ,通过解该方程可以求得k 的值.【详解】解:(1)2217()4(2)(2)322m m m , ∵不论m 为何实数,总有2(2)0m -≥,2(2)30m ,∴无论m 为何实数,关于x 的一元二次方程2172022x mx m 总有两个不相等的实数根,∴无论m 为何实数,抛物线217222yx mx m 与x 轴总有两个不同的交点. (2)抛物线的对称轴为直线3x =,3122m,即3m =,此时,抛物线的解析式为221513(3)2222yx x x , ∴顶点C 坐标为(3,2)-;(3)//,CD MN C D M N 、、、为顶点的四边形是平行四边形,∴四边形CDMN 是平行四边形(直线在抛物线的上方)或四边形CDMN (直线在抛物线的下方),如图所示,由已知215(3,2),(,1),(3)22D M k k N k k k ,, (3,2)C , 4CD ∴=,2151(3)422MN k k k CD ,①当四边形CDMN 是平行四边形,2151(3)422MN k k k ,整理得,28150k k -+=,解得13k =(不合题意,舍去),25k =; ②当四边形CDNM 是平行四边形,2153(1)422NM k k k , 整理得2810k k , 解得,12417417k k ,, 综上,5k =或417k 或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形.【点睛】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,抛物线的顶点公式和平行四边形的判定与性质.在求有关动点问题时要注意分析题意分情况讨论结果.4.(1)1001;9999;(2)2754和4848;(3)见解析【解析】【分析】(1)根据“和平数”的定义可直接得出最小的“和平数”是1001,最大的“和平数”是9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又由029a ≤≤得到a 的可能取值为1,2,3,4;根据百位上的数字与十位上的数字之和是12的倍数,可知m +n =12,得到122a m +=,由a 的可能取值可得m 的取值,即可求得符合条件的“和平数”;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c ,计算它们的和,根据“和平数”的定义可知a+b=c+d ,因式分解可得原式= 1111(a+b ),即可证明.【详解】解:(1)根据“和平数”的定义可得:最小的“和平数”1001,最大的“和平数”9999,故答案为1001;9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又∵029a ≤≤,∴a 的可能取值为1,2,3,4;∵百位上的数字与十位上的数字之和是12的倍数,∴m+n =0或m+n =12,∵“和平数”中a+m =n+2a ,当m+n =0时,即m=n =0,则此时a =0,不符合题意,∴m+n =12,∴a+m =12−m +2a ,解得:122a m +=, ∵a 的可能取值为1,2,3,4;且m 为正整数,∴m 的可能取值为7,8;当a =2时,m =7,这个“和平数”是2754;当a =4时,m =8,这个“和平数”是4848;综上所述,满足条件的“和平数”是2754和4848;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c , ∴(100010010)(100010010)a b c d b a d c +++++++110011001111a b c d =+++1100()11()a b c d =+++由“和平数”的定义可知:a+b =c+d ,∴原式1100()11()a b a b =+++1111()a b =+,∵a ,b 为正整数,则1111()a b +能被1111整除,即(100010010)(100010010)a b c d b a d c +++++++能被1111整除,∴任意的两个“相关和平数”之和是1111的倍数.【点睛】本题考查新定义运算、因式分解的应用;能够读懂题意,根据数的特点,确定数的取值范围,进行正确的因式分解是解题关键.5.C解析:(1)y=﹣x 2;(2)⎝⎭3)存在,53)或(﹣73)【解析】【分析】(1)根据折叠的性质可得OC=OA ,∠BOC=∠BAO=30°,过点C 作CD ⊥OA 于D ,求出OD 、CD ,然后写出点C 的坐标,再利用待定系数法求二次函数解析式解答;(2)求出直线OC 的解析式,根据点M 到OC 的最大距离时,面积最大;平行于OC 的直线与抛物线只有一个交点,利用根的判别式求出m 的值,利用锐角三角函数的定义求解即可;(3)分两种情况求出直线AP 与y 轴的交点坐标,然后求出直线AP 的解析式,与抛物线解析式联立求解即可得到点P 的坐标.【详解】解:(1)∵Rt △OAB 沿OB 折叠后,点A 落在第一象限内的点C 处,∴OC=OA=23,∠BOC=∠BAO=30°,∴∠AOC=30°+30°=60°,过点C 作CD ⊥OA 于D ,则OD=1233 33, 所以,顶点C 33),设过点O ,C ,A 抛物线的解析式为为y=ax 2+bx ,则223)33(23)230a b a b ⎧=⎪⎨+=⎪⎩, 解得:123a b =-⎧⎪⎨=⎪⎩∴抛物线的解析式为y=﹣x 23;(2)∵C 33),∴直线OC 的解析式为:3y x =,设点M 到OC 的最大距离时,平行于OC 的直线解析式为3y x m =+,联立2y x ⎨=-+⎪⎩, 消掉未知数y并整理得,20x m +=,△=(2-4m=0,解得:m=34.∴2304x +=,∴x =; ∴点M 到OC 的最大距离=34×sin30°=313428⨯=;∵OC ==∴1328MOC S ∆=⨯⨯= 此时,M ⎝⎭(3)∵∠OAP=∠BOC=∠BOA =30°,∴2=, ∴直线AP 与y 轴的交点坐标为(0,2)或(0,﹣2), 当直线AP经过点(0)、(0,2)时,解析式为2y x =+,联立22y x y x ⎧=-+⎪⎨=+⎪⎩,解得110x y ⎧=⎪⎨=⎪⎩2253x y ⎧=⎪⎪⎨⎪=⎪⎩. 所以点P53), 当直线AP经过点(0)、(0,﹣2)时,解析式为23y x =-,联立32y x ⎪⎨=-⎪⎩解得11230x y ⎧=⎪⎨=⎪⎩,22373x y ⎧=-⎪⎪⎨⎪=-⎪⎩; 所以点P 的坐标为(33-,73-). 综上所述,存在一点P (3,53)或(﹣3,﹣73),使∠OAP=∠BOA . 【点睛】本题是二次函数综合题型,主要利用了折叠的性质,待定系数法求二次函数解析式,联立两函数解析式求交点的方法,(2)判断出点M 到OC 的距离最大是,平行于OC 的直线与抛物线只有一个交点是解题的关键,(3)确定出直线AP 的解析式是解题的关键.6.A解析:(1)O 半径为254;(2)①458AM =;②详见解析;③当1251017x <<时,有2220ND DM -<成立.【解析】【分析】(1)如下图,在Rt △ABH 中,先求得AH 的值,设OA=r ,在Rt △OBH 中,利用勾股定理可求得r 的长;(2)①如下图,在Rt BCN ,可求得BN 的长,然后在矩形NBHD 中,求得AD 的值,最后利用cos ∠MAD 求得AM ;②如下图,同过证AMN NFC △∽△可得结论;③如下图,通过转换,先得出222ND DM -=22AM MB DM ⋅这个等式,然后利用3sin 5DM MAD AM ∠==,设AM=x ,可得到关于x 的方程,进而求出x 的取值范围. 【详解】 解:(1)如图1,连接OB ,∵AH 过圆心O ,∴AH BC ⊥,∵AB AC =,∴162BH CH BC ===, 在Rt ABH △中,221068AH =-=,设半径OA OB r ==,则8OH r =-,在Rt OBH 中,222(8)6r r -+=, 解得254r =,即O 半径为254. (2)①如图2,连接CN在平行四边形CDEB 中,DE BC ∥,∴ENB NBC ∠=∠.∵BN DE ⊥,即90ENB ∠=︒,∴90NBC ∠=︒.∴CN 是O 的直径.2522CN r ==. ∴在Rt BCN 中,2272BN CN BC =-=. ∵四边形CDEB 是平行四边形,NB ⊥BH ,DH ⊥BH∴四边形NBHD 是矩形,∴72DH BN ==,6ND BH ==,∴79822AD AH DH =-=-=. ∴在Rt ADM △中,4cos 5AD AH MAD AM AB ∠===,∴458AM =, ②如图3,连接AN ,CN ,∵DE BC ∥,∴DNC NCB ∠=∠.∵NAB NCB ∠=∠,∴NAB DNC ∠=∠.由DE BC ∥,AB AC =可得AMD ABC ACB AFD ∠=∠=∠=∠,∴AMN NFC ∠=∠,AM AF =.∴AMN NFC △∽△,MB CF =.∴NM NM AM CF MB NF ==,即NM NF AM MB ⋅=⋅. ③∵AH BC ⊥,DE BC ∥,∴AD MF ⊥,∵AM AF =,∴MD DF =,∴222222ND DM ND DM DM -=-- 2()()ND DM ND DM DM =-+-2NM NF DM =⋅-22AM MB DM =⋅.∵AM x =,∴10BM x =-,由3sin 5DM MAD AM ∠==,得35DM x =, ∴22223342(10)10525ND DM x x x x x ⎛⎫-=--=-+ ⎪⎝⎭.(010)x << 该函数图象的示意图如图4易求得点P 坐标为125,017⎛⎫⎪⎝⎭ ∴当1251017x <<时,有2220ND DM -<成立. 【点睛】本题考查几何图形的综合,解题过程中用到了勾股定理、相似、三角函数和平行四边形、圆的性质,解题关键是将这些知识点综合起来分析题干.7.A解析:(1)A (0,4),C (3,0);(2)S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩;(3)存在,满足条件的t 的值为3617或36,点Q 的坐标为162,17⎛⎫- ⎪⎝⎭或()2,16--. 【解析】【分析】(1)解方程组求出m ,n 即可解决问题.(2)分两种情形:如图1中,当0<t <4时,如图2中,当t >4时,根据S=12•BC•OP求解即可.(3)分两种情形分别构建方程求解即可.【详解】解:(1)由725m n m n +=⎧⎨-=⎩, 解得:43m n =⎧⎨=⎩, ∴A (0,4),C (3,0);(2)如图1中,当0<t <4时,S=12•BC•OP=12×5×(4-t )=-52t+10. 如图2中,当t >4时,S=12•BC•OP=12×5×(t-4)=52t-10. 综上所述,S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩, (3)当04t <<时,由题意,1314(4)3222t t ⨯⨯=⨯⨯-⨯, 解得3617t =, 此时,363241717OP =-=,32(0,)17P ∴, (4,0)B -,BQ ∴的中点Q 的坐标为162,17⎛⎫- ⎪⎝⎭, 当4t >时,由题意,1314(4)3222t t ⨯⨯=⨯⨯-⨯, 解得36t =,此时36432OP =-=,(0,32)P ∴-,(4,0)B -,BP ∴的中点Q 的坐标为(2,16)--.综上所述,满足条件的t 的值为3617或36.点Q 的坐标为16(2,)17-或(2,16)--. 【点睛】本题属于三角形综合题,考查了解方程组,三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型. 8.A解析:(1)145;(2)2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩;(3)t的值为7或7.【解析】【分析】(1)如下图,根据4tan 3A =,可得出PN 与AP 的关系,从而求出t 的值; (2)如下图,存在2种情况,一种是点M 在△ABC 内,另一种是点M 在△ABC 外部,分别根据正方形和三角形求面积的公式可求解;(3)如下图,存在2种情况,一种是PM 所在的直线将△ABC 的面积平分,另一种是QN 所在的直线将△ABC 的面积平分.【详解】(1)如图1,点N 在AC 上图1由题意可知:PD=DQ=t ,AP=7-t∴PN=PQ=2t ∵4tan 3A = ∴43NP AP =,即2473t t =- 解得:t=145 (2)①如图2,图2四边形PQMN 是正方形,90BQM ∴∠=︒,45B ∠=︒,BQ MQ ∴=,即72t t -=解得73t =, 故当0t <≤73时,22(2)4S t t ==; ②如图3, 图390BQF ∠=︒,45B ∠=︒,7BQ FQ t ∴==-,45BFQ MFE ∠=∠=︒,则37MF MQ QF t =-=-,90M ∠=︒,37ME MF t ∴==-, 则2221149(2)(37)21222S t t t t =--=-+-71435t ⎛⎫<< ⎪⎝⎭; 综上,2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩. (3)如下图,过点C 作AB 的垂线,交AB 于点G图4∵4tan 3A = ∴设CG=4x ,则AG=3x∵∠B=45°∴△CBG 是等腰直角三角形∴GB=GC=4x∵AB=14∴3x+4x=14,解得:x=2∴1148562ABC S== ∴1282ABCS = 情况一:PM 所在的直线平分△ABC 的面积,如下图,PM 与BC 交于点E图5则28PBES=∵四边形PQMN是正方形,∴∠EPB=45°∵∠B=45°∴△PBE是等腰直角三角形∵1282PBES PE PB==∴PE=PB=214∴PB=47∵PB=AB-PA=14-(7-t)=7+t∴7+t=47t=477-情况二:如下图,QN所在线段平分△ABC的面积,QF交AC于点F,过点F作AB的垂线,交AB于点H图6同理,28AFQS=∵四边形PQMN是正方形,∴∠EQH=45°∴△FHQ是等腰直角三角形∵4 tan3A=∴设FH=4y,则AH=3y,HQ=FH=4y,∴AQ=7y∴174282AFQS y y==,解得:2∵AQ=AB-QB=14-(7-t)=7+t∴2解得:27∴综上得:t的值为477或727.【点睛】本题考查动点问题,解题关键是根据动点的变化情况,适当划分为几种不同的形式分别分析求解.9.C解析:(1)①32,3,32CP ≤≤,②O;(2)13b ≥;(3)0<r≤3. 【解析】【分析】 (1)①根据垂线段最短以及已知条件,确定OP ,CP 的最大值,最小值即可解决问题.②根据限距关系的定义判断即可.(2)直线3y x b =+与x 轴、y 轴分别交于点F ,G (0,b ),分三种情形:①线段FG 在⊙O 内部,②线段FG 与⊙O 有交点,③线段FG 与⊙O 没有交点,分别构建不等式求解即可.(3)如图3中,不妨设⊙K ,⊙H 的圆心在x 轴上位于y 轴的两侧,根据⊙H 和⊙K 都满足限距关系,构建不等式求解即可.【详解】(1)①如图1中,∵D (-1,0),E(03,∴OD=1,3OE =∴3OE tan EDO OD∠== ∴∠EDO=60°,当OP ⊥DE 时,3•60OP OD sin =︒=,此时OP 的值最小, 当点P 与E 重合时,OP 3当CP ⊥DE 时,CP 的值最小,最小值•603CD cos =︒=当点P 与D 或E 重合时,PC 的值最大,最大值为2,3332CP ≤. ②根据限距关系的定义可知,线段DE 上存在两点M ,N ,满足OM=2ON ,故点O 与线段DE 满足限距关系.故答案为O .(2)直线3y x b =+与x 轴、y 轴分别交于点F ,G (0,b ),当0<b <1时,线段FG 在⊙O 内部,与⊙O 无公共点,此时⊙O上的点到线段FG的最小距离为1-b,最大距离为1+b,∵线段FG与⊙O满足限距关系,∴1+b≥2(1-b),解得13 b≥,∴b的取值范围为131b≤<.当1≤b≤2时,线段FG与⊙O有公共点,线段FG与⊙O满足限距关系,当b>2时,线段FG在⊙O的外部,与⊙O没有公共点,此时⊙O上的点到线段FG的最小距离为121b-,最大距离为b+1,∵线段FG与⊙O满足限距关系,∴11212b b⎛⎫+≥-⎪⎝⎭,而11212b b⎛⎫+≥-⎪⎝⎭总成立,∴b>2时,线段FG 与⊙O满足限距关系,综上所述,b的取值范围为13 b≥.(3)如图3中,不妨设⊙K,⊙H的圆心在x轴上位于y轴的两侧,两圆的距离的最小值为2r-2,最大值为2r+2,∵⊙H和⊙K都满足限距关系,∴2r+2≥2(2r-2),解得r≤3,故r的取值范围为0<r≤3.【点睛】本题属于圆综合题,考查了解直角三角形,垂线段最短,直线与圆的位置关系,限距关系的定义等知识,解题的关键是理解题意,学会利用参数构建不等式解决问题,属于中考创新题型.10.H解析:(1)3;(2)最短距离为:21,H(914,13314),I(275,235) 【解析】【分析】 (1)根据菱形性质,得到A 、B 、C 、O 四点坐标,然后根据平移得到对应点坐标,故可求得C E '和C F '的长,令它们相等可得m 的值;(2)点G 作以C A '为对称轴的点G ',交C F '于点G ',点J 作以O B ''为对称轴的点J ',交A B ''于点J ',G J ''与C A '、A B ''的交点便是点H 、I ;先利用对称的性质,求解得出点G '、J '的坐标,然后利用代入系数法求得线段对应函数解析式,最后联立方程得到点H 、I 的坐标. 【详解】(1)如下图,CB 与y 轴交于点M ,过点C 作x 轴的垂线,交x 轴于点N∵在菱形ABCO 中,∠C=60°,菱形边长为4∴在Rt △COM 中,CM=2,3∴O(0,0),A(4,0),B(2,3,C(-2,3∵将菱形OABC 先向右平移4个单位后,再向下平移() 03m m <<个单位,得到菱形''''O A B C∴O '(4,-m),A '(8,-m),B '(6,3m -),C '(2,3m -)∴直线AB 的解析式为:y=343x +∵点E 的纵坐标为:3m -,代入解析式得:x=32+∴E(32+,3m -) 同理,F(343m -,0) ∵四边形AE C F '是菱形∴E F C C '='E 3C '=。

吉林省,2020~2021年中考数学压轴题精选解析吉林省中考数学压轴题精选~~第1题~~(2020吉林.中考真卷) 如图,在平面直角坐标系中,抛物线与x轴正半轴交于点A,且点A的坐标为,过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作于点Q;M是直线l上的一点,其纵坐标为,以,为边作矩形.(1)求b的值.(2)当点Q与点M重合时,求m的值.(3)当矩形是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)当抛物线在矩形内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.~~第2题~~(2019吉林.中考真卷) 如图,抛物线与x轴相交于两点(点在点的左侧),与轴相交于点.为抛物线上一点,横坐标为,且.(1)求此抛物线的解析式;(2)当点位于轴下方时,求面积的最大值;(3)设此抛物线在点与点之间部分(含点和点)最高点与最低点的纵坐标之差为.①求关于的函数解析式,并写出自变量的取值范围;②当时,直接写出的面积.~~第3题~~(2019吉林.中考模拟) 定义:若抛物线的顶点和抛物线与x轴的两个交点所组成的三角形为等边三角形时,则称此抛物线为正抛物线.概念理解:(1) 如图,在△ABC 中,∠BAC=90°,点D 是BC 的中点。
试证明:以点A 为顶点,且与x 轴交于D 、C 两点的抛物线是正抛物线;(2) 已知一条抛物线经过x 轴上的两点E 、F(点E 在点F 左边),E(1,0),且EF=2,若此条抛物线为正抛物线,求这条抛物线的解析式;(3) 将抛物线y =-x +2 x+9向下平移9个单位长度后得新的抛物线y .抛物线y 的顶点为P ,与x 轴的两个交点分别为M 、N (点M 在点N 左侧),把△PMN 沿x 轴正半轴无滑动翻滚,当边PN 与x 轴重合时记为第1次翻滚,当边PM 与x 轴重合时记为第2次翻滚,依此类推,请求出第2019次翻滚后抛物线y 的顶点P 的对应点坐标。

初三数学总复习之压轴题解法分析压轴题是指考试前夕给学生的一份重要的综合试题,目的是检测学生对所学知识的掌握程度和解题能力。
在初中数学考试中,压轴题往往是整个试卷的难点,也是考察学生能力的重要环节。
在本文中,我将从解题方法的角度,分析几种常见的压轴题解法策略,帮助初三学生更好地应对数学考试。
一、代数题解法代数题是初中数学中最常见的题型之一,也是压轴题的常客。
在解代数题时,我们可以采用以下几种解法:1. 消元法:将方程组中的一个未知数表示为另一个未知数的函数,并代入到另一个方程中,从而得到一个只有一个未知数的方程。
然后通过求解这个方程,就可以得到所有未知数的值。
3. 凑整法:通过适当的变换,将方程转化为更简单的形式。
将含有平方项的方程凑成完全平方的形式,再进行求解。
以上三种解法是解代数题的常见方法,需要根据具体情况选择使用。
1. 图形分析法:通过观察图形性质和推理,找出问题中的关键信息,并推导出结论。
这种方法需要学生对几何知识的掌握程度较高。
2. 图像法:通过画图来辅助解题。
画图可以直观地表示问题中的信息,帮助学生更好地理解问题,从而找到解题的思路。
3. 字母代换法:将几何问题中的一些条件用字母代替,构建方程或者不等式,利用代数方法求解。
这种方法需要学生对代数知识的掌握程度较高。
1. 函数性质法:通过分析函数的性质和变化规律,找到函数值的范围、最值点等关键信息,从而得到解题的思路。
2. 代数方法:通过解方程或者不等式来求解函数问题。
求解函数的零点、最值等问题。
压轴题是考察学生综合能力的重要环节,解题方法的选择对于解题的效果至关重要。
在解压轴题时,学生需要根据具体题目的要求,选择合适的解题方法,并进行深入分析和思考,找到解题的关键点。
通过不断的练习和总结,学生可以逐渐提高解题的能力,更好地应对数学考试。
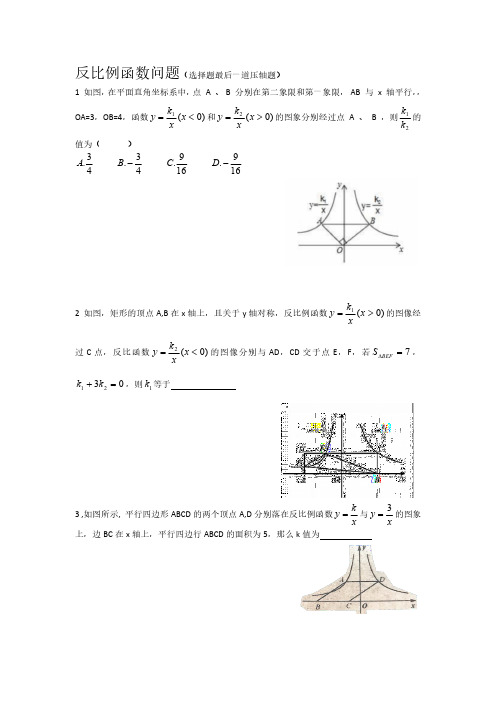
反比例函数问题(选择题最后一道压轴题)1如图,在平面直角坐标系中,点A 、B 分别在第二象限和第一象限,AB 与x 轴平行,,OA=3,OB=4,函数)0(1<=x x k y 和)0(2>=x x k y 的图象分别经过点A 、B ,则21k k 的值为()43.A 43.-B 169.C 169.-D 2如图,矩形的顶点A,B 在x 轴上,且关于y 轴对称,反比例函数)0(1>=x x k y 的图像经过C 点,反比函数)0(2<=x xk y 的图像分别与AD ,CD 交于点E ,F ,若7=∆BEF S ,0321=+k k ,则1k 等于3,如图所示,平行四边形ABCD 的两个顶点A,D 分别落在反比例函数x k y =与xy 3=的图象上,边BC 在x 轴上,平行四边行ABCD 的面积为5,那么k 值为4如图,四边形OABF 中,o 90=∠=∠B OAB ,点A 在x 轴上,双曲线x k y =点过点F ,交AB 点E ,连接EF 。
若32=OA BF ,4=∆BEF S ,则k 的值为()A.6B.8C.12D.16二次函数抛物线问题1、如图,在平面直角坐标系中,点A .B 的坐标分别为A (1,0)、B (3,0).抛物线4222-+-=m mx x y 的顶点为P ,与y 轴的交点为Q.(1)填空:点P 的坐标为___;点Q 的坐标为___(均用含m 的代数式表示)(2)当抛物线经过点A 时,求点Q 的坐标。
(3)连接QA 、QB ,设△QAB 的面积为S ,当抛物线与线段AB 有公共点时,求S 与m 之间的函数关系式。
(4)点P 、Q 不重合时,以PQ 为边作正方形PQMN (P 、Q 、M 、N 分别按顺时针方向排列)。
当正方形PQMN 的四个顶点中,位于x 轴两侧或y 轴两侧的顶点个数相同时,直接写出此时m 的取值范围。
2、如图.抛物线c bx ax y ++=2经过点A (-3,0),C (0,3),并且对称轴为x =-1.点P 为x 轴上方的抛物线上一点,且在对称轴的左侧,过点P 作PQ ∥AB 交抛物线于点Q ,分别过点P ,Q 作x 轴的垂线PM 和QN ,垂足为M 、N ,得到了矩形PQNM ,设点P 的横坐标为m.(1)求抛物线的函数关系式;(2)求矩形PQNM 的周长C (用含m 的代数式表示),并求出当周长取最大值时m 的值;(3)过点A 、C 作直线,交PM 于点E ,与PQ 或QN 交于点F ,若直线AC 将矩形PQNM 的周长分成1:2的两部分,求m 的值.(4)在(2)的条件下,当矩形PQNM 的周长最大时,将矩形中直线AC 上方的图形绕点C 逆时针旋转)(o 180α0α≤<,直线PE 与直线AC 交于点G ,与y 轴交于点H ,当△CGH 为等腰三角形时,请直接写出α的度数。

初三数学压轴题解题技巧1. 哎呀,初三数学压轴题可难倒不少人呢!但咱别怕,先来说说认真审题这一招。
就像你走路得看清路一样,不看清题目怎么能找到解题的方向呢?比如有这么一道题:已知一个圆的半径,让你求它的周长,那你就得先看准半径是多少呀!这认真审题是不是很重要呀?2. 嘿,要善于转化条件呀!很多时候,题目里的条件看似复杂,其实就像隐藏的宝藏,等你去挖掘转化呢!比如说有个题给了你一堆边的长度,那你想想能不能把它们转化成三角形或者四边形的条件来求解呢,就像给你一堆零件,你得组装起来呀!你说是不是这个理?3. 哇塞,一定要多角度思考问题呀!别在一棵树上吊死嘛。
就好比你找东西,不能只在一个地方找呀。
比如有道题你用常规方法解不出来,那咱是不是可以从图形的对称性或者特殊点入手呢?就像找路一样,多找几条路试试呀!4. 嘿,别忘了归纳总结呀!做完一道题,你得想想,这题有啥特点,解题方法能不能用到其他题上呢。
好比你找到了一把万能钥匙,以后碰到类似的门都能开呀!像那种求最值的题,是不是有一些通用的思路可以总结呢?5. 哎呀呀,要敢于尝试大胆假设呢!反正又不扣分,怕啥呀。
比如有个题不知道从哪里开始,那咱就假设一个条件,顺着往下推呀,说不定就找到答案啦!这就像摸着石头过河,大胆往前走呀!6. 注意细节呀,同学们!一个小细节可能就是你解题的关键呢。
就像拼图少了一块就不完整一样。
比如计算的时候,小数点可别点错啦!那不是前功尽弃啦?你说能不重视细节吗?7. 嘿,建立模型也很重要哦!把一些复杂的问题简化成模型,就好解决多啦。
就跟搭积木一样,有了模型就能搭出漂亮的建筑。
比如遇到行程问题,我们可以建立速度、时间、路程的模型呀,是不是很形象?8. 还有哦,要保持冷静呀!遇到难题别慌张,一慌就容易出错啦。
就像考试紧张就发挥不好一样。
你要冷静思考,相信自己能解决它呀!你能做到的,对吧?9. 最后呀,多练习才是硬道理!熟能生巧嘛。
做的题多了,自然就熟练了。
目录考点01:基本方法和结论 (3)考点02:直角三角形 (8)考点03:点到直线的距离 (12)考点04:等腰三角形 (15)考点05:多边形的面积 (22)考点06:相似三角形 (30)考点07:梯形 (35)考点08:平行四边形 (44)考点09:交点坐标 (52)考点10:旋转 (55)考点11:翻折 (61)考点12:平移 (67)考点13:对称 (70)考点14:角平分线性质 (79)考点01:基本方法和结论1、若要在平面直角坐标系中求某一点的坐标:⑴求一般的点的坐标:过该点作x 轴或y 轴的垂线。
⑵求函数及坐标轴的交点坐标:①求函数及x 轴的交点坐标:令0=y ;②求函数及y 轴的交点坐标:令0=x ;⑶求两个函数的交点坐标:将函数解析式联立成方程组,方程组的一组解就是一个交点坐标;⑷求函数图象上的点的坐标:设其坐标为(x ,该函数的解析式);2、抛物线c bx ax y ++=2的性质:⑴配方为:c bx ax y ++=2a ac b a b x a 44222--⎪⎭⎫ ⎝⎛+= ⑵开口方向及最值:①当0>a 时,函数图象开口向上,函数有最低点(a b 2-,),当时,函数有最小值为;②当0<a 时,函数图象开口向下,函数有最高点(a b 2-,),当时,函数有最大值为;⑶对称轴是:直线;⑷顶点坐标为:(ab 2-,); ⑸抛物线c bx ax y ++=2及抛物线2ax y =的形状相同,是由抛物线2ax y =的图象向左平移ab 2个单位,向下平移个单位得到的; ⑹抛物线c bx ax y ++=2及x 轴的交点情况: ①当△>0时,抛物线及x 轴有两个不同的交点,交点坐标分别为:(,0)、(,0);②当△=0时,抛物线及x 轴只有一个交点,交点坐标为(ab 2-,0);③当△<0时,抛物线及x 轴没有交点;3、求二次函数解析式的方法:⑴当已知二次函数图象上的一般三点时,设其解析式为一般式:c bx ax y ++=2;⑵当已知二次函数及x 轴的交点坐标为(1x ,0)、(2x ,0)时,设其解析式为交点式:()()21x x x x a y --=;⑶当已知二次函数的对称轴或最值或顶点坐标为(k ,h )时,设其解析式为顶点式:()h k x a y +-=2;4、由抛物线c bx ax y ++=2的大致图象确定a 、b 、c 符号的方法: ⑴a 看方向:开口向上,a>0,开口向下,a<0。
初中数学:30个经典压轴题(附详解),细...
对于初三的同学们来说,现在已经正式进入了然中考倒计时阶段,各科新知识的学习掌握都已经告一段落,都开始准备中考复习了,但是在数学学科的复习过程中,很多同学都会对最后的一个压轴题产生畏惧心理,因为压轴题都十分复杂,很多同学根本不知道该从哪里入手去解决。
但我们都知道,数学高手之间的竞争往往都出现在压轴题上,能够在考场中从容应对各种类型的压轴题,是数学取得高分的关键所在,因此数学成绩要想优异,就必须要把最后的压轴题进行一个全面的突破提升。
很多同学都表示,数学压轴自己不会做,但是一道中考数学压轴题解不出来,不等于“一点不懂、一点不会”,要将整道题目解题思路转化为得分点。
中考数学压轴题一般在大题下都有两至三个小题,难易程度是第1小题较易,大部学生都能拿到分数;第2小题中等,起到承上启下的作用;第3题偏难,不过往往建立在1、2两小题的基础之上。
而压轴题要想实突破,就必须要多做多练,把一些典型的题例做一做练一练,去提升突破。
眼看距离中考的脚步越来越近,老师这次就把初中数学常考的30个经典压轴题分享给大家(附详解),都是中考中最常考的题型,同学们可以打印出来认真做一做,2020中考冲刺必练!。
初三数学难题压轴题通常包括代数和几何两个方面的内容。
以下是一些常见的初三数学难题压轴题:
代数问题:例如,找出一个数列的通项公式,或者通过给定的数列前n项和求出某一项的值。
有时候也会涉及到函数的最值问题或者函数的零点问题。
几何问题:通常会涉及三角形、四边形或者圆等形状,求解这些形状的面积、周长等。
有时候也会涉及到图形的旋转、平移、对称等几何变换问题。
以下是一道初三数学难题压轴题的示例:
已知AB是圆O的直径,直线CD与圆O相交于点E,F,且点E是CD的中点,连接AC,AD,BF和CB。
求证:CD平分∠BAC 和∠CBF。
这道题目涉及到圆、三角形和四边形的性质和判定,需要运用多种数学知识点,难度较大。
以上信息仅供参考,如果您还有疑问,建议咨询初三数学老师或查阅相关资料。
初三数学压轴题解题技巧和方法
1. 压轴题解题技巧
认真审题,弄清题意。
压轴题通常会给出含多个未知数的一元二次方程或
二元一次方程组,并伴随一些其他条件或限制。
首先,要明确题目要求解什么,以及给出的条件和限制是什么。
尝试化简方程或方程组。
如果方程或方程组较为复杂,尝试将其化简,以
便更容易找到解题思路。
寻找等量关系。
压轴题中通常会有一些等量关系,如面积、体积、角度等。
找到这些等量关系,可以帮助我们找到解题的突破口。
尝试使用代数方法。
对于一些压轴题,代数方法可能比较适用。
例如,通
过对方程进行变形、替换或解方程等,可以找到未知数的值。
画图分析。
对于一些几何压轴题,可以通过画图来帮助分析。
在画图的过
程中,可以更好地理解题目的条件和要求,从而找到解题思路。
2. 压轴题方法总结
代数法:通过对方程进行变形、替换或解方程等,找到未知数的值。
几何法:通过画图来帮助分析,更好地理解题目的条件和要求,从而找到
解题思路。
等量关系法:通过寻找等量关系,如面积、体积、角度等,找到解题的突
破口。
化简法:将复杂的方程或方程组化简,以便更容易找到解题思路。