脉冲压缩雷达与匹配滤波【定稿材料】

雷达系统中的信号处理技术摘要本文介绍了雷达系统及雷达系统信号处理的主要内容，着重介绍与分析了雷达系统信号处理的正交采样、脉冲压缩、MTD和恒虚警检测几种现代雷达技术，雷达系统通过脉冲压缩解决解决雷达作用距离和距离分辨力之间的矛盾，通过MTD来探测动目标，通过恒虚警〔CFAR〕来实现整个系统对目标的检测。

关键词雷达系统正交采样脉冲压缩MTD 恒虚警检测1雷达系统概述雷达是Radar〔Radio Detection And Ranging〕的音译词，意为“无线电检测和测距”，即利用无线电波来检测目标并测定目标的位置，这也是雷达设备在最初阶段的功能。

雷达的任务就是测量目标的距离、方位和仰角，还包括目标的速度，以及从目标回波中获取更多有关目标的信息。

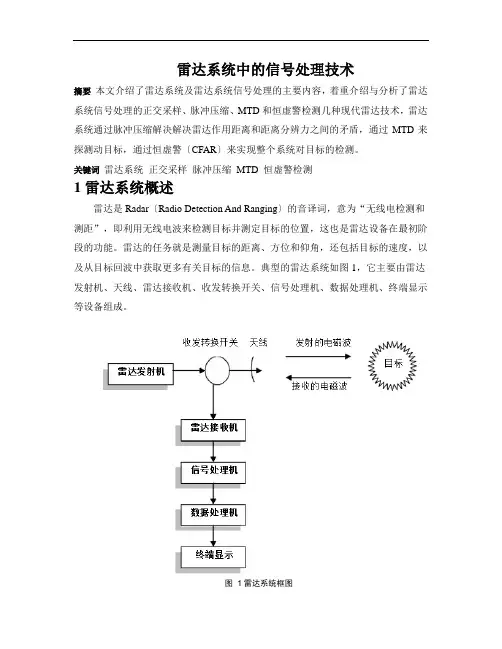
典型的雷达系统如图1，它主要由雷达发射机、天线、雷达接收机、收发转换开关、信号处理机、数据处理机、终端显示等设备组成。

图1雷达系统框图随着现代电子技术的不断发展，特别是数字信号处理技术、超大规模集成数字电路技术、电脑技术和通信技术的告诉发展，现代雷达信号处理技术正在向着算法更先进、更快速、处理容量更大和算法硬件化方向飞速发展，可以对目标回波与各种干扰、噪声的混叠信号进行有效的加工处理，最大程度低剔除无用信号，而且在一定的条件下，保证以最大发现概率发现目标和提取目标的有用信息。

雷达发射机产生符合要求的雷达波形，然后经馈线和收发开关由发射天线辐射出去，遇到目标后，电磁波一部分反射，经接收天线和收发开关由雷达接收机接收，然后对雷达回波信号依次进行信号处理、数据处理，就可以获知目标的相关信息。

雷达信号处理的流程如下：图 2 雷达信号处理流程2雷达信号处理的主要内容雷达信号处理是雷达系统的主要组成部分。

信号处理消除不需要的杂波，通过所需要的目标信号，并提取目标信息。

内容包括雷达信号处理的几个主要部分：正交采样、脉冲压缩、MTD和恒虚警检测。

正交采样是信号处理的第一步，担负着为后续处理提供高质量数据的任务。

雷达脉冲压缩算法研究雷达脉冲压缩算法是一种通过对短脉冲信号进行加窗和相关运算，从而实现高分辨率雷达成像的算法。

这种算法在目标探测、识别以及跟踪等领域中有着广泛的应用。

在本文中，我们将深入地探讨雷达脉冲压缩算法的基本原理、发展历史以及未来的研究方向。

一、基本原理脉冲雷达技术中，发射的信号被目标反射后接收到信号会被传回雷达接收机。

然而，目标信号在传输过程中会遭受多径效应的干扰，这导致接收到的信号在时间域上发生扩展，时间分辨率会降低。

为了解决这个问题，雷达脉冲压缩技术应运而生。

雷达脉冲压缩算法主要基于短脉冲信号的性质，即其具有宽带性和瞬时功率很大。

算法的基本步骤为：先对短脉冲信号进行加窗，使其具有良好的频谱特性；然后进行相关运算，使反射信号会在一段极短的时间内被压缩，从而提高时间分辨率。

加窗操作的目的是消除反射信号的频率偏移，使其具有宽带性。

常用的窗函数有海明窗、布莱克曼窗、汉宁窗等。

这些窗函数在保留谱线的同时，在频域上也可以压缩主瓣宽度。

相关运算的基本原理是将原始信号与一个匹配滤波器进行卷积，从而使信号被在一小段时间内压缩。

匹配滤波器通常是原始信号的逆时域复共轭，其功率频谱密度与信号的功率频谱密度接近，但是带宽更宽。

二、历史发展雷达脉冲压缩算法的诞生最早可以追溯到20世纪50年代初。

当时，人们意识到脉冲雷达系统的时间分辨率受到多径效应的限制，无法满足目标识别和跟踪的需求。

为解决这个问题，一些科学家开始研究如何对反射信号进行压缩，并尝试应用于实际应用中。

在此后的数十年中，雷达脉冲压缩算法经历了一个逐步发展的过程。

20世纪70年代末，复合式高分辨雷达（SAR）系统的出现使得脉冲压缩技术得到了广泛的应用。

90年代初，人们开始对逆问题进行研究，从而进一步提高了脉冲压缩算法的效率和精度。

三、未来研究方向在当今的信息技术快速发展的时代，雷达脉冲压缩算法如何更好地适应未来的发展成为了一个重要的问题。

未来研究方向主要包括以下三个方面：1. 面向多异步输入的实时压缩算法。

从匹配滤波的角度说明脉冲压缩的基本原理
脉冲压缩是雷达信号处理中的一种重要技术，其基本原理是将宽脉冲信号通过匹配滤波器进行压缩，以提高雷达的分辨率和探测能力。

下面从匹配滤波的角度解释脉冲压缩的基本原理。

匹配滤波器是一种特殊的线性滤波器，其输出信号的频谱与输入信号的频谱成共轭对称。

在雷达信号处理中，匹配滤波器被用于接收和处理回波信号，以获得最大的信噪比。

在脉冲压缩雷达中，发射信号通常是一个宽脉冲，其频谱具有较大的带宽。

当这个宽脉冲信号照射到目标后，目标的散射回波信号被接收。

由于目标的距离不同，回波信号的延迟时间也不同。

为了实现高分辨率，需要对回波信号进行匹配滤波处理。

匹配滤波器对输入信号的频谱具有选择性，只有与滤波器频谱相匹配的信号才能通过滤波器。

在脉冲压缩雷达中，匹配滤波器的频谱与发射信号的频谱相匹配，因此，当回波信号通过匹配滤波器时，其频谱会被压缩。

由于匹配滤波器输出的信号与输入信号的频谱成共轭对称，因此输出信号的带宽与输入信号相同。

通过匹配滤波器的压缩处理，回波信号的脉冲宽度被显著压缩，从而提高了雷达的分辨率。

同时，由于匹配滤波器能够使回波信号的信噪比最大化，因此提高了雷达的探测能力。

总之，脉冲压缩的基本原理是通过匹配滤波器的压缩处理，将宽脉冲信号转换为窄脉冲信号，同时保持其带宽不变，从而实现高分辨率和探测能力的提升。

匹配滤波技术在雷达信号处理中的应用一 、匹配滤波原理在输入为确知加白噪声的情况下，所得输出信噪比最大的线性滤波器就是匹配滤波器，设一线性滤波器的输入信号为 ：)(t x)()()(t n t s t x +=其中)(t s 为确知信号，)(t n 为均值为零的平稳白噪声，功率谱密度为2/No 。

设线性滤波器系统的冲击响应为)(t h ，其频率响应为)(ωH ，其输出响应：)()()(t n t s t y o o +=输入信号能量：∞<=⎰∞∞-dt t s s E )()(2输入、输出信号频谱函数：dte t s S t j ⎰∞∞--=ωω)()()()()(ωωωS H S o =ωωωπωωd eS H t s tj o ⎰∞-=)()(21)(输出噪声的平均功率：ωωωπωωπd P H d P t n E n n o o⎰⎰∞∞-∞∞-==)()(21)(21)]([22)()()(21)()(2122ωωωπωωπωωd P H d eS H SNR n t j o o⎰⎰∞∞-∞∞-=利用Schwarz 不等式得：ωωωπd P S SNR n o ⎰∞∞-≤)()(212式取等号时，滤波器输出功率信噪比o SNR 最大取等号条件：otj n e P S H ωωωαω-=)()()(*当滤波器输入功率谱密度是2/)(o n N P =ω的白噪声时，MF 的系统函数为：,)()(*o t j e kS H ωωω-=oN k α2=k 为常数1，)(*ωS 为输入函数频谱的复共轭，)()(*ωω-=S S ，也是滤波器的传输函数)(ωH 。

oso N E SNR 2=Es 为输入信号)(t s 的能量，白噪声)(t n 的功率谱为2/o No SNR 只输入信号)(t s 的能量Es 和白噪声功率谱密度有关。

白噪声条件下，匹配滤波器的脉冲响应：)()(*t t ks t h o -=如果输入信号为实函数，则与)(t s 匹配的匹配滤波器的脉冲响应为：)()(t t ks t h o -=k 为滤波器的相对放大量，一般1=k 。

标准文档脉冲压缩雷达的仿真脉冲压缩雷达与匹配滤波的MATLAB仿真姓名：--------学号：----------2014-10-28西安电子科技大学一、 雷达工作原理雷达，是英文Radar 的音译，源于radio detection and ranging 的缩写，原意为"无线电探测和测距"，即用无线电的方法发现目标并测定它们的空间位置。

因此，雷达也被称为“无线电定位”。

利用电磁波探测目标的电子设备。

发射电磁波对目标进行照射并接收其回波，由此获得目标至电磁波发射点的距离、距离变化率（径向速度）、方位、高度等信息。

雷达发射机的任务是产生符合要求的雷达波形（Radar Waveform ），然后经馈线和收发开关由发射天线辐射出去，遇到目标后，电磁波一部分反射，经接收天线和收发开关由接收机接收，对雷达回波信号做适当的处理就可以获知目标的相关信息。

但是因为普通脉冲在雷达作用距离与距离分辨率上存在自我矛盾，为了解决这个矛盾，我们采用脉冲压缩技术，即使用线性调频信号。

二、 线性调频（LFM ）信号脉冲压缩雷达能同时提高雷达的作用距离和距离分辨率。

这种体制采用宽脉冲发射以提高发射的平均功率，保证足够大的作用距离；而接受时采用相应的脉冲压缩算法获得窄脉冲，以提高距离分辨率，较好的解决雷达作用距离与距离分辨率之间的矛盾。

脉冲压缩雷达最常见的调制信号是线性调频（Linear Frequency Modulation ）信号,接收时采用匹配滤波器（Matched Filter ）压缩脉冲。

LFM 信号的数学表达式：（2.1）其中c f 为载波频率，()t rect T为矩形信号：（2.2）其中BKT=是调频斜率，信号的瞬时频率为()22cT Tf Kt t+ -≤≤，如图（图2.1.典型的LFM信号（a）up-LFM(K>0)（b）down-LFM(K<0)）将式1改写为：（2.3）其中（2.4）是信号s(t)的复包络。

目录一．匹配滤波器————————————————P2 一．脉冲压缩雷达———————————————P2 三．线性调频脉冲压缩—————————————P3 二．线性调频脉冲信号匹配滤波—————————P5 五．附录———————————————————P8一．匹配滤波器匹配滤波器是在白噪声背景中检测信号的最佳线性滤波器，其输出信噪比在某个时刻达到最大。

如果一直输入信号u(t),其频谱为U(ω)，则可以证明匹配滤波器在频率域的特性为)ex p()()(0*jwt kU H -=ωω式中，U*(ω)为频谱U(ω)的共轭值；k 为滤波器的增益常数；t 0是使滤波器实际上能够实现所必需的延迟时间，在t 0时刻将有信号的最大输出。

同样可以证明，匹配滤波器在时间域的函数，即其脉冲响应为)()(h 0*t t ku t -=式中，u*(t 0-t)为输入信号的镜像，它与输入信号u(t)的波形相同，但从时间t 0开始反转过来。

在对匹配滤波器作理论研究时，延时t 0和增益常数k 可以不予考虑，因此匹配滤波器的上述方程式特性可以简化为)()()()(**t u t h U H -==ωω从上式可以看出：匹配滤波器的传输函数是输入信号频谱的复共轭值，匹配滤波器的脉冲响应是输入信号的镜像函数。

还可以进一步证明，匹配滤波器在输出端给出的最大瞬时信噪比为max 2)(N E N S =式中，N 0是输入噪声的谱密度，它是匹配滤波器输入端单位频带内的噪声功率；E 是输入信号能量：⎰⎰+∞∞-+∞∞-==dt |u(t)|df |U(f)|E 22二．脉冲压缩雷达我们知道，雷达的距离分辨力取决于信号带宽。

在普通脉冲雷达中，雷达信号的时宽带宽积为一敞亮（约为1），因此不能兼顾距离分辨力和速度分辨力两项指标。

近年来，从改进雷达体制方面来矿大作用距离和提高距离分辨力方面已有很大进展。

这种体制就是脉冲压缩（PC ）雷达体制，它采用宽脉冲发射以提高发射的平均功率，保证足够的最大作用距离，而在接收时则采用相应的脉冲压缩法获得窄脉冲，以提高距离分辨力，因而能较好地解决作用距离和分辨能力之间的矛盾。

目录一．匹配滤波器————————————————P2 一．脉冲压缩雷达———————————————P2 三．线性调频脉冲压缩—————————————P3 二．线性调频脉冲信号匹配滤波—————————P5 五．附录———————————————————P8一．匹配滤波器匹配滤波器是在白噪声背景中检测信号的最佳线性滤波器，其输出信噪比在某个时刻达到最大。

如果一直输入信号u(t),其频谱为U(ω)，则可以证明匹配滤波器在频率域的特性为)ex p()()(0*jwt kU H -=ωω式中，U*(ω)为频谱U(ω)的共轭值；k 为滤波器的增益常数；t 0是使滤波器实际上能够实现所必需的延迟时间，在t 0时刻将有信号的最大输出。

同样可以证明，匹配滤波器在时间域的函数，即其脉冲响应为)()(h 0*t t ku t -=式中，u*(t 0-t)为输入信号的镜像，它与输入信号u(t)的波形相同，但从时间t 0开始反转过来。

在对匹配滤波器作理论研究时，延时t 0和增益常数k 可以不予考虑，因此匹配滤波器的上述方程式特性可以简化为)()()()(**t u t h U H -==ωω从上式可以看出：匹配滤波器的传输函数是输入信号频谱的复共轭值，匹配滤波器的脉冲响应是输入信号的镜像函数。

还可以进一步证明，匹配滤波器在输出端给出的最大瞬时信噪比为max 2)(N E N S =式中，N 0是输入噪声的谱密度，它是匹配滤波器输入端单位频带内的噪声功率；E 是输入信号能量：⎰⎰+∞∞-+∞∞-==dt |u(t)|df |U(f)|E 22二．脉冲压缩雷达我们知道，雷达的距离分辨力取决于信号带宽。

在普通脉冲雷达中，雷达信号的时宽带宽积为一敞亮（约为1），因此不能兼顾距离分辨力和速度分辨力两项指标。

近年来，从改进雷达体制方面来矿大作用距离和提高距离分辨力方面已有很大进展。

这种体制就是脉冲压缩（PC ）雷达体制，它采用宽脉冲发射以提高发射的平均功率，保证足够的最大作用距离，而在接收时则采用相应的脉冲压缩法获得窄脉冲，以提高距离分辨力，因而能较好地解决作用距离和分辨能力之间的矛盾。

脉冲压缩雷达的仿真脉冲压缩雷达与匹配滤波的MATLAB 仿真一、 "，即用无速度）二、 （LFM 信号的数学表达式：（2.1）其中c f 为载波频率，()t rect T为矩形信号：2014-10-28乐享科技 信息对抗技术（2.2）其中BKT=是调频斜率，信号的瞬时频率为()22cT Tf Kt t+ -≤≤，如图（图2.1.典型的LFM信号（a）up-LFM(K>0)（b）down-LFM(K<0)）将式1改写为：（因此，Matlab%%xlabel('频率/MHz');title('LFM的频域特性');gridon;axistight;（图2.2：LFM信号的时域波形和频域特性）三、压缩脉冲的匹配滤波信号()s t的匹配滤波器的时域脉冲响应为：(3.1)0t 是使滤波器物理可实现所附加的时延。

理论分析时，可令0t ＝0，重写3.1式，(3.2)将2.1式代入3.2式得:(3.3)图3.1：LFM 信号的匹配滤波如图3.1,()s t 经过系统()h t 得输出信号()o s t ，(3.4)当0t ≤(3.5)当T t -≤合并3.5和3.6两式：(3.7)3.7式即为LFM 脉冲信号经匹配滤波器得输出,它是一固定载频c f 的信号。

当t T ≤时，包络近似为辛克（sinc ）函数。

(3.8)图3.2：匹配滤波的输出信号如图3.2，当πB t=±π时，t=±1/B为其第一零点坐标；当πB t=±π/2时，t=±1/2B，习惯上，将此时的脉冲宽度定义为压缩脉冲宽度。

(3.9)LFM信号的压缩前脉冲宽度T和压缩后的脉冲宽度 之比通常称为压缩比D，(3.10)式3.10表明，压缩比也就是LFM信号的时宽频宽积。

由以下title('线性调频信号经过匹配滤波器');subplot(212)%放大N0=3*Fs/B;t2=-N0*Ts:Ts:N0*Ts;t2=B*t2;plot(t2,Z(N-N0:N+N0),t2,Z1(N-N0:N+N0),'r.');axis([-inf,inf,-50,inf]);gridon;set(gca,'Ytick',[-13.4,-4,0],'Xtick',[-3,-2,-1,-0.5,0,0.5,1,2,3]);xlabel('时间sec\times\itB');ylabel('振幅,dB');title('线性调频信号经过匹配滤波器（放大）');结果：图3.3：线性调频信号的匹配滤波上图中，时间轴进行了归一化，（t/(1/B)=txB）。

基本雷达信号处理流程一、脉冲压缩窄带(或某些中等带宽)的匹配滤波:相关处理，用FFT数字化执行，即快速卷积处理，可以在基带实现（脉冲压缩）快速卷积,频域的匹配滤波脉宽越小,带宽越宽，距离分辨率越高;脉宽越大，带宽越窄，雷达能量越小，探测距离越近；D=BT(时宽带宽积）;脉压流程：频域：回波谱和参考函数共轭相乘时域：相关即输入信号的FFT乘上参考信号FFT的共轭再逆FFT；Sc=ifft(fft（Sb）.＊conj(fft（S)）);Task1f0=10e9;%载频tp=10e—6；%脉冲宽度B=10e6；%信号带宽fs=100e6；％采样率R0=3000;%目标初始距离N=4096;c=3e8;tau=2*R0/c;beita=B/tp；t=(0：N-1）/fs;Sb=rectpuls(t—tp/2-tau,tp).＊exp（j＊pi＊beita＊（t—tp/2—tau)。

^2）.*exp(—2j*pi*f0＊tau）；％回波信号x 107S=rectpuls(t —tp/2,tp).*exp （i ＊pi*beita*（t-tp/2)。

^2);%发射信号（参考信号）x 10-5x 10-5x 107So=ifft(fft(Sb ）.*conj(fft （S ）)）；%脉压 figure （7）；plot （t ＊c/2,db （abs （So ）/max(So ）))%归一化dB grid on-400-350-300-250-200-150-100-500二、去斜处理（宽带的匹配滤波)去斜处理“有源相关"，通常用来处理极大带宽的LFM波形（如果直接采样的话因为频带很宽所以在高频的时候需要的采样率就很大，采样点数就很多，所以要经过去斜处理）Stretch方法是针对线性调频信号而提出的,其方法是将输入信号与参考信号（经适当延迟的本振信号，延迟量通常由窄带信号测距结果估计出）混频，则每一个散射点就对应一个混频后的单频分量,对混频输出的信号进行DFT处理，即可获得目标的距离像，对参考信号的要求是应具有与输入信号相同的调频斜率。

雷达脉冲压缩技术应用分析摘要：脉冲压缩技术能在雷达发射功率受限的情况下，有效提高雷达探测距离能力，同时还能保证较高的分辨力，是雷达反隐身、多目标精确检测和抗外部干扰的重要手段。

本文介绍了脉冲压缩技术原理、波形分类和实现方法，并对主要波形信号的性能特点进行了分析。

关键词：脉冲压缩线性调频相位编码1 引言现代社会对空天的利用愈发重视，新型技术层出不穷，相应人们对雷达在作用距离、分辨能力和测量精度等方面也产生了更高的需求。

根据雷达系统理论可知，随着发射机功率的提升，雷达探测距离相应提高，但分辨能力却会降低，长距离与高精度貌似不可兼得，但脉冲压缩技术在雷达系统中的应用有效解决了这一矛盾。

在现代战争日益复杂的电磁环境下，脉冲压缩雷达通过发射大时宽信号以提升发射功率，有效增加了雷达信干比和测量距离，通过压缩得到的窄脉冲又提高了探测精度，还能有效对抗箔条干扰和抑制杂波，已广泛应用于跟踪监视和空中交通管制等领域，AN/TPS-59、AN/FPS-117和ASR-12等先进雷达系统都采用了脉冲压缩技术。

2 脉冲压缩原理雷达发展初期，根据距离分辨率公式=cτ/2n (c为光速，τ为脉冲时间宽度），通常认为距离分辨率由雷达发射的脉冲时间宽度决定，由于发射机峰值功率的限制，想要提高测量距离只能延长发射脉冲时间，而这势必降低距离分辨率，这使得同时提高距离与距离分辨率变的不可行。

随着科学技术的发展，根据信号与系统原理，距离分辨率公式演变为 =c/2B(B为雷达信号带宽），距离分辨率变为由雷达信号带宽决定，而带宽只决定于信号幅度和频率的变化，那么，对信号进行调幅或调频就可以增大信号的等效带宽，这就使得同时提高距离与距离分辨率变的可行。

雷达脉冲压缩技术的原理就是调制一个带宽为B，持续时间为T的宽脉冲，以提高发射平均功率，获得较远的探测距离，接收时利用匹配滤波器处理目标回波，把接收的宽脉冲压缩为一个持续时间τ=1/B的窄脉冲，从而得到较高的分辨率精度。

雷达信号处理中的脉冲压缩算法研究雷达是一种广泛应用于军事、航空航天、气象、交通等领域的探测和测距技术。

而在雷达信号的处理过程中，脉冲压缩算法是一项重要的技术手段。

脉冲压缩算法旨在提高雷达系统的距离分辨率和目标检测性能。

本文将对脉冲压缩算法进行深入研究，探讨其原理、应用以及当前的研究进展。

脉冲压缩算法的原理是利用波形发射与接收信号的相关性对接收信号进行处理，从而提高雷达的分辨能力。

传统的脉冲压缩算法包括匹配滤波器法、快速脉冲压缩法等。

匹配滤波器法通过与已知脉冲形状进行相关，实现信号压缩，从而提高雷达系统的距离分辨率。

而快速脉冲压缩法则通过FFT算法将时域信号变换到频域，进而实现信号的压缩。

这些传统的脉冲压缩算法在实际应用中已经取得了很好的效果，然而随着科技的进步和需求的变化，研究者们对脉冲压缩算法进行了进一步改进和创新。

近年来，基于稀疏表示及压缩感知理论的脉冲压缩算法备受关注。

这种算法利用了雷达信号的稀疏性，通过基于迭代算法的方法实现高精度的信号重构和压缩。

这种方法具有较好的抗噪声能力和更高的计算效率，适用于各种复杂环境下的雷达信号处理。

另外，人工智能技术的应用也为脉冲压缩算法的研究带来了新的思路。

例如，深度学习方法可以通过学习大量数据样本来提取雷达信号中的特征，从而提高信号的压缩效果和目标检测能力。

这些新兴的脉冲压缩算法在实际应用中取得了一定的突破，对于提高雷达系统的性能具有重要意义。

在实际应用中，脉冲压缩算法在雷达目标检测、距离分辨和抗干扰能力方面发挥着重要作用。

首先，脉冲压缩算法可以提高雷达的目标检测能力。

通过对接收信号的压缩处理，可以有效增强目标回波信号的强度，从而提高雷达对目标的识别和跟踪能力。

其次，脉冲压缩算法可以提高雷达的距离分辨能力。

由于信号经过压缩处理后的带宽增加，因此可以提高雷达的距离分辨率，实现对目标的更精确探测。

此外，脉冲压缩算法还可以提高雷达的抗干扰能力。

通过压缩处理，可以减少背景杂波和噪声对雷达系统的影响，提高雷达对目标回波信号的识别和提取能力。

脉冲压缩技术在雷达系统中的应用作者：游建来源：《数字技术与应用》2014年第03期摘要：早期雷达系统中存在着非常典型的难题，即检测能力与分辨率的矛盾，脉冲压缩为解决这一问题提供了有效的技术途径。

本文对目前在雷达信号处理系统中应用较为广泛的脉冲压缩技术进行了介绍。

首先对介绍了脉冲压缩技术和线形调频脉冲信号，然后介绍了线形调频信号的压缩过程及其压缩方法。

关键词：脉冲压缩线形调频匹配滤波中图分类号：TN959 文献标识码：A 文章编号：1007-9416（2014）03-0069-02在早期时，脉冲雷达多采用简单的矩形脉冲信号，脉冲信号能量E=Pt，Pt是脉冲功率，为脉冲宽度。

如果想要增加雷达探测目标的作用距离，根据公式，可以加大信号能力E。

一种方法是增加发射机的功率，但是，受到峰值功率以及传输线功率容量等因素限制，所以，并不能单纯的通过增加发射机功率来达到增加雷达的作用距离。

另一种方法，在发射机平均功率不变的条件下，可以用增加脉冲宽度，使得信号能量E增大。

但是，矩形脉冲条件下，距离分辨力取决于脉冲宽度。

增加脉冲宽度，会直接影响距离分辨力。

在简单脉冲信号中，很难解决满足雷达的探测能力所需的功率以及保证必需的距离分辨力这两个条件，因此需要采用其他复杂的信号形式。

脉冲压缩作为现代雷达的一项重要技术，有效地解决了雷达分辨率和平均功率间的矛盾，并在现代雷达中广泛应用。

1 脉冲压缩概述采用窄脉冲实现远作用距离的一个严重局限性是大脉冲能量要有高峰值功率。

特别在高频时，雷达的传输线会因为高峰值功率而被电压击穿。

如果峰值功率受到击穿的限制，则脉冲就不会有足够的能量。

例如，一部雷达，它的脉冲宽度为1ms，峰值功率为1MW，那么这个脉冲中的能量为1J。

一个1ms的脉冲它的距离分辨力为150米，如果想要得到15厘米的分辨力，脉冲宽度必须减小到1ns，而且它的峰值功率要增加到109W，这样才能维持1J的脉冲能量。

由于这是一个非常大的峰值功率，在微波雷达频段的传输线上使用肯定会被击穿。