数字信号处理-原理实现及应用(高西全-第3版)第5章 信号的相关函数及应用

数字信号处理的原理及应用1. 简介数字信号处理（Digital Signal Processing，简称DSP）是指对数字信号进行处理、分析和控制的技术和方法。

它涉及将连续的模拟信号转换为离散的数字信号，并对其进行数字化、运算和处理，以提取出有用的信息或实现特定的功能。

数字信号处理在现代通信、音频处理、图像处理、雷达、生物医学工程等领域有着广泛的应用。

2. 数字信号处理的原理数字信号处理的原理可以概括为以下几个方面：2.1 采样与量化采样是指将连续的模拟信号在时间上离散化，即在一定的时间间隔内取样取值。

量化是指对采样得到的离散信号进行幅度上的离散化处理，将连续的信号幅度量化为一系列离散的取值。

2.2 快速傅里叶变换（FFT）快速傅里叶变换是一种高效的算法，用于将时域信号转换到频域，可以对信号的频谱进行分析和处理。

它能够将离散的时域信号转换为连续的频域信号，从而提取出信号的频域特征。

2.3 滤波器设计滤波器通常用于去除信号中的噪声和无用的频率成分，或者增强感兴趣的频率成分。

数字信号处理中常用的滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。

2.4 时频分析时频分析是将信号在时间和频率上同时进行分析的方法，常用的时频分析方法包括短时傅里叶变换（STFT）、小波变换和时频分布等。

3. 数字信号处理的应用数字信号处理在各个领域有着广泛的应用，以下列举了其中几个主要领域的应用示例：3.1 通信领域在通信领域，数字信号处理用于调制解调、信道编解码、无线通信信号处理、频谱分析、自适应滤波等方面的应用。

它可以提高通信系统的抗干扰性能、提高信号的传输速率和可靠性。

3.2 音频处理在音频处理中，数字信号处理可以用于音频压缩、音频增强、音频特效、音频识别等方面的应用。

例如，通过数字信号处理技术可以实现音频的降噪、均衡、消除回声等功能。

3.3 图像处理数字信号处理在图像处理中有着广泛的应用，可以实现图像的去噪、增强、分割、压缩等处理。

数字信号处理第三版高西全实验数字信号处理第三版高西全实验》是一本旨在介绍数字信号处理的实际应用的教材。

本文档旨在概述该教材的目的和内容。

该教材的目的是通过实验教学的方式，帮助学生更好地理解数字信号处理的原理和技术，并将其应用到实际问题中。

它旨在培养学生的实践能力和解决问题的能力，使他们能够熟练地进行数字信号处理的实际操作。

该教材内容包括许多实验，涵盖了数字信号处理的各个方面。

每个实验都介绍了一个特定的概念或技术，并通过实际的操作和实验数据展示了其应用方式和效果。

学生通过完成实验，可以深入了解数字信号处理的各种算法和方法，研究如何使用相关工具和软件进行信号处理，以及如何分析和评估处理结果。

通过研究《数字信号处理第三版高西全实验》，学生将能够掌握数字信号处理的基本概念和技术，并能够独立地应用这些知识解决实际问题。

这将有助于他们在工程、通信、音视频处理等领域中的职业发展，也为进一步深入研究数字信号处理奠定了坚实的基础。

希望该教材能够对学生们的研究和实践有所帮助，使他们能够更好地理解和运用数字信号处理的方法和技术。

实验目标：本实验旨在介绍数字信号的采样和重构过程，并加深对这两个概念的理解。

实验目标：本实验旨在介绍数字信号的采样和重构过程，并加深对这两个概念的理解。

实验步骤：实验步骤：准备实验所需的信号发生器和示波器设备。

设置信号发生器，产生模拟信号，例如正弦波。

调整示波器参数，将模拟信号接入示波器进行显示。

使用采样器采样模拟信号，并记录采样得到的数字信号。

对采样得到的数字信号进行重构，恢复为原始模拟信号。

使用示波器将重构后的信号进行显示，并比较与原始信号的差异。

实验要点：了解采样和重构的基本概念和原理。

熟悉信号发生器和示波器的操作。

掌握采样器的使用方法。

理解数字信号与模拟信号的差异及其影响。

请参考实验指导书中的详细步骤和注意事项进行实验操作，并记录实验数据和结果。

本文档旨在解释《数字信号处理第三版高西全实验》中的实验二内容。

%实验1：系统响应及系统稳定性close all;clear all%======内容1：调用filter解差分方程，由系统对u(n)的响应判断稳定性====== A=[1,-0.9];B=[0.05,0.05]; %系统差分方程系数向量B和Ax1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号x1(n)=R8(n)x2n=ones(1,128); %产生信号x2(n)=u(n)hn=impz(B,A,58); %求系统单位脉冲响应h(n)subplot(2,2,1);y='h(n)';tstem(hn,y); %调用函数tstem绘图title('(a) 系统单位脉冲响应h(n)');box ony1n=filter(B,A,x1n); %求系统对x1(n)的响应y1(n)subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b) 系统对R8(n)的响应y1(n)');box ony2n=filter(B,A,x2n); %求系统对x2(n)的响应y2(n)subplot(2,2,4);y='y2(n)';tstem(y2n,y);title('(c) 系统对u(n)的响应y2(n)');box on%===内容2：调用conv函数计算卷积============================x1n=[1 1 1 1 1 1 1 1 ]; %产生信号x1(n)=R8(n)h1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)];y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);y='h1(n)';tstem(h1n,y); %调用函数tstem绘图title('(d) 系统单位脉冲响应h1(n)');box onsubplot(2,2,2);y='y21(n)';tstem(y21n,y);title('(e) h1(n)与R8(n)的卷积y21(n)');box onsubplot(2,2,3);y='h2(n)';tstem(h2n,y); %调用函数tstem绘图title('(f) 系统单位脉冲响应h2(n)');box onsubplot(2,2,4);y='y22(n)';tstem(y22n,y);title('(g) h2(n)与R8(n)的卷积y22(n)');box on%=========内容3：谐振器分析========================un=ones(1,256); %产生信号u(n)n=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49]; %系统差分方程系数向量B和Ay31n=filter(B,A,un); %谐振器对u(n)的响应y31(n)y32n=filter(B,A,xsin); %谐振器对u(n)的响应y31(n)figure(3)subplot(2,1,1);y='y31(n)';tstem(y31n,y);title('(h) 谐振器对u(n)的响应y31(n)');box onsubplot(2,1,2);y='y32(n)';tstem(y32n,y);title('(i) 谐振器对正弦信号的响应y32(n)');box on10.2.2 实验程序清单1 时域采样理论的验证程序清单% 时域采样理论验证程序exp2a.mTp=64/1000; %观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000;T=1/Fs;Fs=1000;T=1/Fs;M=Tp*Fs;n=0:M-1;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M); %M点FFT[xnt)]yn='xa(nT)';subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on;title('(a) Fs=1000Hz');k=0:M-1;fk=k/Tp;subplot(3,2,2);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz');xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%=================================================% Fs=300Hz和Fs=200Hz的程序与上面Fs=1000Hz完全相同。

数字信号处理及其应用数字信号处理（Digital Signal Processing，DSP）是一种将连续时间下的信号转换为离散时间下的信号，并对这些离散时间信号进行处理的技术。

它已经成为现代通信、控制系统、音频和图像处理等领域中不可或缺的一部分。

本文将介绍数字信号处理的基本概念和原理，并探讨它在各个领域中的应用。

数字信号处理是通过对信号进行采样、量化和编码来实现的。

首先，连续时间信号在一定时间间隔内进行采样，将其离散化为序列信号；接着，通过量化将每个采样值用有限数量的离散级别表示；最后，使用编码将每个离散级别表示为二进制数。

将信号数字化后，就可以用计算机进行处理了。

在数字信号处理中，最常见的操作是滤波，它用于去除信号中的噪声、增强感兴趣信号或提取特定频率下的信息。

滤波可以分为两种类型：时域滤波和频域滤波。

时域滤波是通过对信号序列进行一系列的加权平均操作来实现的，常见的时域滤波器有移动平均滤波器和中值滤波器。

频域滤波是通过将信号序列转换到频域，对频域信号进行滤波，然后再转换回时域实现的，常见的频域滤波器有高通滤波器和低通滤波器。

数字信号处理在各个领域中都有广泛的应用。

在通信领域，数字信号处理用于调制、解调、信道均衡和误码控制等方面。

例如，在无线通信中，数字信号处理技术被用于将语音或视频信号转换为数字信号，以便通过无线信道传输。

在医学领域，数字信号处理被广泛应用于医学图像处理和生物信号处理。

例如，医学图像处理可以用于对X射线、CT扫描、MRI扫描等影像进行增强和分析，以提供更准确的医学诊断。

生物信号处理可以用于心电图（ECG）信号的滤波、特征提取等方面，帮助医生做出准确的诊断。

在音频和音乐领域，数字信号处理广泛应用于音频信号的合成、编码和增强等方面。

例如，数字音频播放器可以对音频信号进行数学处理，以提供高品质的音乐听觉体验。

此外，数字信号处理还在雷达、图像处理、语音识别、音频和视频编码、控制系统等众多领域中发挥着重要作用。

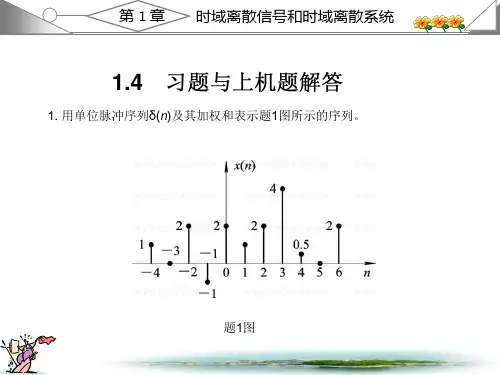
数字信号处理课后答案 高西全、丁美玉版1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列； （3）令1()2(2)x n x n =-，试画出1()x n 波形； （4）令2()2(2)x n x n =+，试画出2()x n 波形； （5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14； （2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。