数字信号处理(第四版)(高西全)章 (2)

2－1 试求如下序列的傅里叶变换： （1）)()(01n n n x -=δ （2）)1(21)()1(21)(2--++=n n n n x δδδ （3）),2()(3+=n u a n x n10<<a（4）)4()3()(4--+=n u n u n x（5）∑∞=-⎪⎭⎫⎝⎛=05)3(41)(k nk n n x δ（6）()6cos ,14()0,n n x n π⎧-≤≤=⎨⎩其他解： （1） 010()()j n j j nn X e n n ee ωωωδ∞--=-∞=-=∑（2） 2211()()122j j nj j n X e x n e e e ωωωω∞--=-∞==+-∑ωsin 1j +=（3） 2232()(2)1j j nj nn j nj n n a e X e a u n ea eaeωωωωω-∞∞---=-∞=-=+==-∑∑， 10<<a（4） []4()(3)(4)j j nn X e u n u n eωω∞-=-∞=+--∑∑-=-=33n nj e ω∑∑==-+=313n n j n nj e eωω（等比数列求解）ωωωωωj j j j j e e e e e --+--=--111134=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=----ωωωωω21sin 27sin 1137j j j e ee ((1-e^a)提出e^(0.5a))（5） 3350011()(3)44nkj jn j k n k k X e n k e e ωωωδ∞∞+∞--=-∞==⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∞+=--⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛=033411141k j kj e e ωω（6） 44336441()cos 32j j j jn jn n n X e nee e e ππωωωπ---=-=-⎛⎫==+ ⎪⎝⎭∑∑994()()4()()3333001122j j n j j n n n e e e e ππππωωωω--++===+∑∑ ()9()9334()4()33()()3311112211j j j j j j e e e e e e ππωωππωωππωω-+-+-+⎡⎤⎡⎤--⎢⎥⎢⎥=+⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⎣⎦2－2 设信号}1,2,3,2,1{)(---=n x ，它的傅里叶变换为)(ωj e X ，试计算(1)0()j X e （２）()j X ed πωπω-⎰（３）2()j X e d πωπω-⎰。

目　录第1章　离散时间信号与系统1.1　复习笔记1.2　课后习题详解1.3　名校考研真题详解第2章　Z变换与离散时间傅里叶变换（DTFT）2.1　复习笔记2.2　课后习题详解2.3　名校考研真题详解第3章　离散傅里叶变换（DFT）3.1　复习笔记3.2　课后习题详解3.3　名校考研真题详解第4章　快速傅里叶变换（FFT）4.1　复习笔记4.2　课后习题详解4.3　名校考研真题详解第5章　数字滤波器的基本结构5.1　复习笔记5.2　课后习题详解5.3　名校考研真题详解第6章　几种特殊滤波器及简单一、二阶数字滤波器设计6.1　复习笔记6.2　课后习题详解6.3　名校考研真题详解第7章　无限长单位冲激响应（IIR）7.1　复习笔记7.2　课后习题详解7.3　名校考研真题详解第8章　有限长单位冲激响应（FIR）数字滤波器设计方法8.1复习笔记8.2　课后习题详解8.3　名校考研真题详解第9章　序列的抽取与插值——多抽样率数字信号处理基础9.1　复习笔记9.2　课后习题详解9.3　名校考研真题详解第10章　数字信号处理中的有限字长效应10.1　复习笔记10.2　课后习题详解10.3　名校考研真题详解第1章　离散时间信号与系统1.1　复习笔记一、离散时间信号——序列1．序列序列可以有三种表示法。

（1）函数表示法。

例如x（n）＝a n u（n）。

（2）数列的表示法。

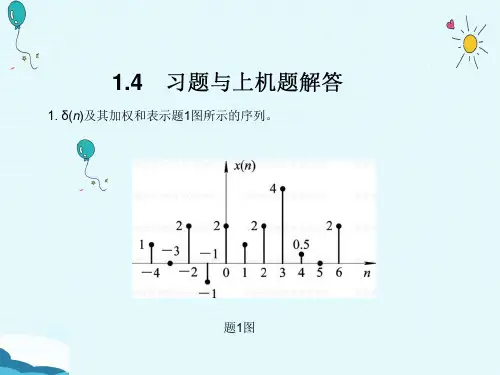
例如x（n）＝{...，－5，－3，－l，0，2，7，9，…）本书中，凡用数列表示序列时，都将n=0时x（o）的值用下划线（_）标注，这个例子中有z（－1）＝－3，x（0）＝－l，x（1）＝0，…（3）用图形表示，如图l-1所示。

图1-1 离散时间信号的图形表示2．序列的运算（1）基于对序列幅度x（n）的运算序列的简单运算有①加法；②乘法；③累加；④序列绝对和；⑤序列的能量；⑥平均功率。

（2）基于对n的运算①移位，某序列为x（n）则x（n－m）就是x（n）的移位序列，当m＝正数时，表示序列x（n）逐项依次右移（延时）m位；当m＝负数时，表示序列 x（n）逐项依次左移（超前）m位；②翻褶，若序列为x（n），则x（－n）是以n＝0为对称轴将x（n）序列加以翻褶；③时间尺度变换。

《数字信号处理》上机全部源代码调试通过，完整版（高西全，第四版）实验一%实验1：系统响应及系统稳定性close all;clear all%调用fliter解差分方程，由系统对un的响应判断稳定性%内容1：调用filter解差分方程，由系统对u(n)的响应判断稳定性A=[1,-0.9];B=[0.05,0.05];x1n=[1 1 1 1 1 1 1 1 zeros(1,50)];x2n=ones(1,128);hn=impz(B,A,58);subplot(2,2,1);y='h(n)';tstem(hn,y);title('(a) 系统单位脉冲响应h(n)')y1n=filter(B,A,x1n);subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b) 系统对R8(n)的响应y1(n)')y2n=filter(B,A,x2n);subplot(2,2,4);y='y2(n)';tstem(y2n, y);title('(c) 系统对u(n)的响应y2(n)')y1n=filter(B,A,x1n);subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b) 系统对R8(n)的响应y1(n)')y2n=filter(B,A,x2n);subplot(2,2,4);y='y2(n)';tstem(y2n, y);title('(c) 系统对u(n)的响应y2(n)')%内容2：调用conv函数计算卷积x1n=[1 1 1 1 1 1 1 1]; %产生信号x1n=R8nh1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)]y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);y='h1(n)';tstem(h1n,y);%调用函数tstem绘图title('(d) 系统单位脉冲响应h1(n)')subplot(2,2,2);y='y21(n)';tstem(y21n,y);title('(e) h1(n)与R8(n)的卷积y21(n)')subplot(2, 2,3); y='h2(n)';tstem(h2n,y); %调用函数tstem绘图title('(f) 系统单位脉冲响应h2(n)')subplot(2, 2, 4); y='y22(n)';tstem(y22n, y);title('(g) h2(n)与R8(n)的卷积y22(n)')%=====================================%内容3：谐振器分析un=ones(1, 256); %产生信号unn=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49];%系统差分方程系数向量B和Ay31n=filter(B,A,un); %谐振器对un的响应y31n y32n=filter(B,A,xsin);%谐振器对正弦信号的响应y32nfigure(3)subplot(2,1,1);y='y31(n)';tstem(y31n,y)title('(h) 谐振器对u(n)的响应y31(n)')subplot(2,1,2);y='y32(n)';tstem(y32n,y);title('(i) 谐振器对正弦信号的响应y32(n)')function tstem(xn,yn)n = 0:length(xn)-1;stem(n,xn,'.');xlabel('n');ylabel('yn');%xlabel('n' );ylabel(yn);axis([0,n(end),min(xn),1.2*max(xn)]);实验二%时域采样理论验证程序exp2a.mTp=64/1000;%观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000; T=1/Fs;Fs=1000; T=1/Fs;M=Tp*Fs; n=0:M-1;A=444.128; alph=pi*50*2^0.5; omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M);%M点FFT[xnt)]yn='xa(nT)';subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on; title('(a) Fs=1000Hz');k=0:M-1; fk=k/Tp;subplot(3,2,2); plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz');xlabel('f(Hz)'); ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%=================================% Fs=300Hz和Fs=200Hz的程序与上面Fs=1000Hz的程序完全相同。