下载文档原格式
天津市高等教育自学考试课程考试大纲课程名称: 数字信号处理课程代码:0817、4701、4659第一部分课程性质与设置目标一、课程性质与特点数字信号处理是高等教育自学考试电子信息工程专业所开设的专业基础课之一,它是一门理论性较强的课程。
本课程系统地讨论了数字信号处理的基本理论、基本分析方法和基本实现方法。
深入浅出，条理清楚，具有实例分析。
二、课程设置的目的和要求设置本课程，为了使学生牢固掌握数字信号处理的基本理论、基本分析方法和基本实现方法。
通过本课程的学习，要求学生掌握数字信号处理的基本理论，训练用基本分析方法和基本实现方法分析和解决实际问题，从而提高学生分析问题和解决问题的能力。
三、与本专业其它课程的关系数字信号处理是电子信息工程专业学生的专业基础课,它与本专业的其他课程有着密切的关系。
电路理论、信号与系统、积分变换是本课程的基础。
第二部分课程内容与考核目标第一章离散时间信号与系统一、学习的目的和要求通过本章的学习，掌握连续信号的抽样、离散时间信号的概念和线性移不变系统的概念以及描述该系统的数学模型—常系数线性差分方程。
二、考核知识点与考核目标（一）离散时间信号-序列（重点）理解：离散时间信号-序列的概念、图形；应用：序列的运算，包括：移位、翻褶、和、积、累加、差分、卷积；常用序列、序列的周期性、用单位抽样序列来表示任意序列。
（二）线性移不变系统（重点）应用：线性移不变系统的概念、性质、因果系统、系统稳定性的概念；（三）常系数线性差分方程(一般)应用：序列域求解法；（四）连续时间信号抽样（重点）应用：理想抽样、奈奎斯特抽样定理、实际抽样。
第二章 Z变换一、学习的目的和要求通过本章的学习，复习Z变换的定义与收敛域，基本性质和定理，Z反变换，为在变换域分析序列和系统做准备。
理解序列的Z变换与连续信号的拉普拉斯变换、傅里叶变换的关系，序列的傅里叶变换和一些对称性质，离散系统的系统函数、系统的频率响应。
数字信号处理上机实验代码文件名：tstem.m（实验一、二需要）程序：f unction tstem(xn,yn)%时域序列绘图函数%xn:被绘图的信号数据序列，yn:绘图信号的纵坐标名称（字符串）n=0:length(xn)-1;stem(n,xn,'.');xlabel('n');ylabel('yn');axis([0,n(end),min(xn),1.2*max(xn)]);文件名：tplot.m（实验一、四需要）程序：function tplot(xn,T,yn)%时域序列连续曲线绘图函数%xn:信号数据序列,yn:绘图信号的纵坐标名称（字符串）%T为采样间隔n=0;length(xn)-1;t=n*T;plot(t,xn);xlabel('t/s');ylabel(yn);axis([0,t(end),min(xn),1.2*max(xn)]);文件名：myplot.m（实验一、四需要）%(1)myplot;计算时域离散系统损耗函数并绘制曲线图。
function myplot(B,A)%B为系统函数分子多项式系数向量%A为系统函数分母多项式系数向量[H,W]=freqz(B,A,1000)m=abs(H);plot(W/pi,20*log10(m/max(m)));grid on;xlabel('\omega/\pi');ylabel('幅度(dB)')axis([0,1,-80,5]);title('损耗函数曲线');文件名：mstem.m（实验一、三需要）程序：function mstem(Xk)%mstem(Xk)绘制频域采样序列向量Xk的幅频特性图M=length(Xk);k=0:M-1;wk=2*k/M;%产生M点DFT对应的采样点频率（关于pi归一化值）stem(wk,abs(Xk),'.');box on;%绘制M点DFT的幅频特性图xlabel('w/\pi');ylabel('幅度');axis([0,2,0,1.2*max(abs(Xk))]);文件名：mpplot.m（实验一需要）%(2)mpplot;计算时域离散系统损耗函数和相频特性函数，并绘制曲线图。
《数字信号处理》上机全部源代码调试通过，完整版（高西全，第四版）实验一%实验1：系统响应及系统稳定性close all;clear all%调用fliter解差分方程，由系统对un的响应判断稳定性%内容1：调用filter解差分方程，由系统对u(n)的响应判断稳定性A=[1,-0.9];B=[0.05,0.05];x1n=[1 1 1 1 1 1 1 1 zeros(1,50)];x2n=ones(1,128);hn=impz(B,A,58);subplot(2,2,1);y='h(n)';tstem(hn,y);title('(a) 系统单位脉冲响应h(n)')y1n=filter(B,A,x1n);subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b) 系统对R8(n)的响应y1(n)')y2n=filter(B,A,x2n);subplot(2,2,4);y='y2(n)';tstem(y2n, y);title('(c) 系统对u(n)的响应y2(n)')y1n=filter(B,A,x1n);subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b) 系统对R8(n)的响应y1(n)')y2n=filter(B,A,x2n);subplot(2,2,4);y='y2(n)';tstem(y2n, y);title('(c) 系统对u(n)的响应y2(n)')%内容2：调用conv函数计算卷积x1n=[1 1 1 1 1 1 1 1]; %产生信号x1n=R8nh1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)]y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);y='h1(n)';tstem(h1n,y);%调用函数tstem绘图title('(d) 系统单位脉冲响应h1(n)')subplot(2,2,2);y='y21(n)';tstem(y21n,y);title('(e) h1(n)与R8(n)的卷积y21(n)')subplot(2, 2,3); y='h2(n)';tstem(h2n,y); %调用函数tstem绘图title('(f) 系统单位脉冲响应h2(n)')subplot(2, 2, 4); y='y22(n)';tstem(y22n, y);title('(g) h2(n)与R8(n)的卷积y22(n)')%=====================================%内容3：谐振器分析un=ones(1, 256); %产生信号unn=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49];%系统差分方程系数向量B和Ay31n=filter(B,A,un); %谐振器对un的响应y31n y32n=filter(B,A,xsin);%谐振器对正弦信号的响应y32nfigure(3)subplot(2,1,1);y='y31(n)';tstem(y31n,y)title('(h) 谐振器对u(n)的响应y31(n)')subplot(2,1,2);y='y32(n)';tstem(y32n,y);title('(i) 谐振器对正弦信号的响应y32(n)')function tstem(xn,yn)n = 0:length(xn)-1;stem(n,xn,'.');xlabel('n');ylabel('yn');%xlabel('n' );ylabel(yn);axis([0,n(end),min(xn),1.2*max(xn)]);实验二%时域采样理论验证程序exp2a.mTp=64/1000;%观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000; T=1/Fs;Fs=1000; T=1/Fs;M=Tp*Fs; n=0:M-1;A=444.128; alph=pi*50*2^0.5; omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M);%M点FFT[xnt)]yn='xa(nT)';subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on; title('(a) Fs=1000Hz');k=0:M-1; fk=k/Tp;subplot(3,2,2); plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz');xlabel('f(Hz)'); ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%=================================% Fs=300Hz和Fs=200Hz的程序与上面Fs=1000Hz的程序完全相同。
实验一熟悉MATLAB环境一、实验目的(1)熟悉MATLAB的主要操作命令。
(2)学会简单的矩阵输入和数据读写。
(3)掌握简单的绘图命令。
(4)用MATLAB编程并学会创建函数。
(5)观察离散系统的频率响应。
二、实验内容认真阅读本章附录，在MATLAB环境下重新做一遍附录中的例子，体会各条命令的含义。
在熟悉了MATLAB基本命令的基础上，完成以下实验。
上机实验内容：(1)数组的加、减、乘、除和乘方运算。
输入A=[1 2 3 4]，B=[3 4 5 6]，求C=A+B，D=A-B，E=A.*B，F=A./B，G=A.^B并用stem语句画出A、B、C、D、E、F、G。
实验程序：A=[1 2 3 4];B=[3 4 5 6];n=1:4;C=A+B;D=A-B;E=A.*B;F=A./B;G=A.^B;subplot(4,2,1);stem(n,A,'fill');xlabel ('时间序列n');ylabel('A');subplot(4,2,2);stem(n,B,'fill');xlabel ('时间序列n ');ylabel('B');subplot(4,2,3);stem(n,C,'fill');xlabel ('时间序列n ');ylabel('A+B');subplot(4,2,4);stem(n,D,'fill');xlabel ('时间序列n ');ylabel('A-B');subplot(4,2,5);stem(n,E,'fill');xlabel ('时间序列n ');ylabel('A.*B');subplot(4,2,6);stem(n,F,'fill');xlabel ('时间序列n ');ylabel('A./B');subplot(4,2,7);stem(n,G,'fill');xlabel ('时间序列n ');ylabel('A.^B');运行结果：(2)用MATLAB实现以下序列。
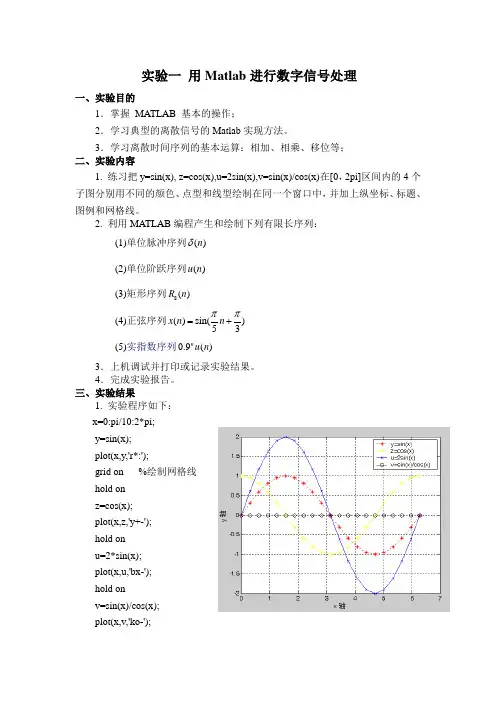
实验一 用Matlab 进行数字信号处理一、实验目的1．掌握 MATLAB 基本的操作；2．学习典型的离散信号的Matlab 实现方法。
3．学习离散时间序列的基本运算：相加、相乘、移位等； 二、实验内容1. 练习把y=sin(x), z=cos(x),u=2sin(x),v=sin(x)/cos(x)在[0，2pi]区间内的4个子图分别用不同的颜色、点型和线型绘制在同一个窗口中，并加上纵坐标、标题、图例和网格线。
2. 利用MATLAB 编程产生和绘制下列有限长序列： (1)单位脉冲序列()n δ (2)单位阶跃序列()u n (3)矩形序列8()R n(4)正弦序列()sin()53x n n ππ=+(5)实指数序列0.9()n u n3．上机调试并打印或记录实验结果。
4．完成实验报告。
三、实验结果1. 实验程序如下：x=0:pi/10:2*pi;y=sin(x); plot(x,y,'r*:');grid on %绘制网格线 hold on z=cos(x); plot(x,z,'y+-'); hold on u=2*sin(x); plot(x,u,'bx-'); hold on v=sin(x)/cos(x); plot(x,v,'ko-');hold onxlabel('x 轴'); %x轴注释ylabel('y 轴'); %y轴注释legend({'y=sin(x)','z=cos(x)', 'u=2sin(x) ', 'v=sin(x)/cos(x) '}); %图形注解2. 程序如下：n=-20:20;n0=0;n1=8;w0=pi/5; w1=pi/3;x1=[(n-n0)==0];x2=[(n-n0)>=0];x3=[(n-n0)>=0& (n-n1)<=0];x4=sin(w0*n+w1);x5=0.9.^n.*x2;subplot(511);stem(n,x1);axis([ -20 20 0 2]);ylabel('\sigma(n)'); subplot(512);stem(n,x2);axis([ -20 20 0 2]);ylabel('u(n)');subplot(513);stem(n,x3);axis([ -20 20 0 2]);ylabel('R8(n)'); subplot(514);stem(n,x4);axis([ -20 20 -2 2]);ylabel(' sin(w0n+w1) '); subplot(515);stem(n,x5);axis([ -20 20 0 2]);ylabel('0.9nu(n)'); xlabel('n');实验二离散信号与系统一、实验目的1．掌握卷积定理、熟悉离散信号和系统的时域特性；2．学习Matlab进行卷积计算方法；3．学习Matlab求解差分方程二、实验内容1．离散信号的基本运算：对序列x(n)={2,3,4,1,2,5} ,n=0,1,2,3,4,5,的移位、乘法、加法、翻转及尺度变换。
数字信号处理上机实验及参考程序数字信号处理实验实验⼀离散时间信号与系统及MA TLAB实现1.单位冲激信号：n = -5:5;x = (n==0);subplot(122);stem(n, x);2.单位阶跃信号：x=zeros(1,11);n0=0;n1=-5;n2=5;n = n1:n2;x(:,n+6) = ((n-n0)>=0);stem(n,x);3.正弦序列：n = 0:1/3200:1/100;x=3*sin(200*pi*n+1.2);stem(n,x);4.指数序列n = 0:1/2:10;x1= 3*(0.7.^n);x2=3*exp((0.7+j*314)*n);subplot(221);stem(n,x1);subplot(222);stem(n,x2);5.信号延迟n=0:20;Y1=sin(100*n);Y2=sin(100*(n-3));subplot(221);stem(n,Y1);subplot(222);stem(n,Y2);6.信号相加X1=[2 0.5 0.9 1 0 0 0 0];X2=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7];X=X1+X2;stem(X);7.信号翻转X1=[2 0.5 0.9 1];n=1:4;X2=X1(5-n);subplot(221);stem(n,X1);subplot(222);stem(n,X2);8.⽤MATLAB计算序列{-2 0 1 –1 3}和序列{1 2 0 -1}的离散卷积。
a=[-2 0 1 -1 3]; b=[1 2 0 -1];c=conv(a,b);M=length(c)-1;n=0:1:M;stem(n,c);xlabel('n');ylabel('幅度');9．⽤MA TLAB计算差分⽅程当输⼊序列为时的输出结果。
N=41;a=[0.8 -0.44 0.36 0.22];b=[1 0.7 -0.45 -0.6];x=[1 zeros(1,N-1)];k=0:1:N-1;y=filter(a,b,x);stem(k,y)xlabel('n');ylabel('幅度')10.冲激响应impzN=64;a=[0.8 -0.44 0.36 0.22];b=[1 0.7 -0.45 -0.6];x=[1 zeros(1,N-1)];k=0:1:N-1;y=impz(a,b,N);stem(k,y)xlabel('n');ylabel('幅度')11.传递函数频率响应a=[0.8 -0.44 0.36 0.22];%分⼦的系数数组b=[1 0.7 -0.45 -0.6];%分母的系数数组n=(0:500)*pi/500%在pi范围内取501个采样点[h,f]=freqz(a,b,n);%求系统的频率响应subplot(2,1,1),plot(n/pi,abs(h));grid%作系统的幅度频响图axis([0,1,1.1*min(abs(h)),1.1*max(abs(h))]);ylabel('幅度');subplot(2,1,2),plot(n/pi,angle(h));grid %作系统的相位频响图axis([0,1,1.1*min(angle(h)),1.1*max(angle(h))]);ylabel('相位');xlabel('以pi为单位的频率');12.系统零极点图a=[0.8 -0.44 0.36 0.22];b=[1 0.7 -0.45 -0.6];h=zplane(a,b);实验⼆离散信号变换1.解⽅程y(n)-2y(n-1)+3y(n-2)=4x(n)-5x(n-1)+6x(n-2)-7x(n-3)a=[4,-5,6,-7];b=[1,-2,3];n=[0:7]; x=ones(length(n));Y=[-1,1];X=[1,-1];xic=filtic(b,a,Y,X);y1=filter(b,a,x,xic)stem(n,y1);xlabel('n');ylabel('y(n)');2．对连续的单⼀频率周期信号按采样频率采样，截取长度N分别选N =20和N =16，观察其DFT结果的幅度谱。
数字信号处理实验1--5含代码实验一离散时间信号的时域分析 1. 在MATLAB中利用逻辑关系式n,,0来实现序列，显示范围。
(产生如下，，,n,nn,n,n012图所示的单位脉冲信号的函数为impseq(n0,n1,n2)，程序如示例所示),3,n,10并利用impseq函数实现序列:; ，，，，，，yn,2,n,3，,n,6，，xn1nnnn120源代码:impseq.mfunction y=impseq(n0,n1,n2)n=[n1:n2]y=[(n-n0)==0]exp01-1.mfunction impseq(n0,n1,n2)n=-3:1:10y=2*impseq(3,-3,10)+impseq(6,-3,10);stem(n,y)n,,0，，2. 在MATLAB中利用逻辑关系式来实现序列，显示范围。
(自己编写un,nn,n,n012产生单位阶跃信号的函数，函数命名为stepseq(n0,n1,n2)) 并利用编写的stepseq函数实现序列: ，，，，，，yn,un，2，un,2,5,n,10源代码:stepseq.mfunction y=stepseq(n0,n1,n2)n=n1:1:n2y=[(n-n0)>=0]exp01-2.mfunction stepseq(n0,n1,n2)n=-5:1:20y=stepseq(-2,-5,20)+stepseq(2,-5,20)stem(n,y)3. 在MATLAB中利用数组运算符“.^”来实现一个实指数序列。
如: n ，，，，xn,0.30,n,15源代码:n=0:1:15;x=0.3.^nstem(n,x)4. 在MATLAB中调用函数sin或cos产生正余弦序列，如:π,, ，，，，xn,3sin0.4πn，，5cos0.3πn0,n,20,,5,,源代码:n=0:1:20x=11*sin(0.3*pi*n+pi/5)+5*cos(0.3*pi*n)stem(n,x)思考题:1.在MATLAB环境下产生单位脉冲序列和单位阶跃序列各有几种方法,如何使用,2.在MATLAB环境下进行序列的相乘运算时应注意什么问题,实验二离散时间系统的时域分析1. 在MATLAB中利用内部函数conv来计算两个有限长序列的卷积。
研究生《数字信号处理》（dsp）上机MATLAB实验实验1熟悉MATLAB环境，会用FFT求信号频谱，相关方法去除噪声。
%生成一个带有噪声的正弦信号clear;t=linspace(-2*pi,2*pi,1000);y=sin(t)+rand(1,1000);plot(y);波形图：%把带有噪声的正弦信号进行FFT分解z=fft(y);plot(t,z);波形图：%用相关方法除噪声f=xcorr(y,y); plot(f);波形图：实验2利用相关算法求信号的幅值和相位%用相关性求信号的幅值与相位clear;t=linspace(-2*pi,2*pi,1000);s=5*sin(t+pi/6)+rand(1,1000);y=3*sin(t)+rand(1,1000);ss=s.*s;sy=s.*y;yy=y.*y;x1=length(ss);x2=length(yy);x3=length(sy);rx0=sum(ss)/x1;ry0=sum(yy)/x2;rxy0=sum(sy)/x3;A=sqrt(2*rx0);B=sqrt(2*ry0);C=acos(2*rxy0/(A*B));sprintf('A=%d,B=%d,C=%d',A,B,C)命令窗口输出结果：A=5.086632e+00,B=3.109529e+00,C=5.355640e-01 %用改进的相关算法求幅值和相位clear;t=linspace(-2*pi,2*pi,1000);s=5*sin(t+pi/6)+rand(1,1000);z=3*sin(t);z1=3*cos(t);zz=z.*z;sz=s.*z;sz1=s.*z1;x1=length(sz);x2=length(zz);x3=length(sz1);rz=sum(zz)/x2;rsz=sum(sz)/x1;rsz1=sum(sz1)/x3;B=sqrt(2*rz);C=atan(rsz1/rsz);A=2*rsz/(B*cos(C));sprintf('A=%d,B=%d,C=%d',A,B,C)命令窗口输出结果：A=4.986266e+00,B=2.998500e+00,C=5.264407e-01 实验三设计一个巴尔低通滤波器%设计一个巴尔沃特低通滤波器，fp=1khz,fs=2khz,ap=1db,as=40db;fp=1000;fs=2000;wp=2*pi*fp;ws=2*pi*fs;ap=1;as=40;[n,wc]=buttord(wp,ws,ap,as,'s');fprintf('阶数为%d\n',n);[num,den]=butter(n,wc,'s');%[z,p,k]=buttap(n);disp('分子多项式系数分别为');fprintf('%.4e\n',num);disp('分母多项式系数分别为');fprintf('%.4e\n',den);w=[wp ws];h1=freqs(num,den,w);fprintf('Ap=%.4e\n',-20*log10(abs(h1(1)))); fprintf('As=%.4e\n',-20*log10(abs(h1(2)))); w1=[0:200:12000*pi];h=freqs(num,den,w1);gain=20*log10(abs(h)); plot(w1/(2*pi),gain); xlabel('Hz');ylabel('dB');title('幅频特性');输出结果：阶数为8分子多项式系数分别为0.0000e+000.0000e+000.0000e+000.0000e+000.0000e+000.0000e+000.0000e+000.0000e+006.2187e+30分母多项式系数分别为1.0000e+003.6222e+046.5603e+087.7093e+126.4060e+163.8498e+201.6360e+244.5108e+276.2187e+30Ap=6.1668e-01As=4.0000e+01图形为实验四设计一个高通滤波器%设计一个高通滤波器fp=5khz,fs=1khz,ap<=1db,as>=40db; fp=5000;fs=1000;ap=1;as=40;wp=1/(2*pi*fp);ws=1/(2*pi*fs);[n,wc]=buttord(wp,ws,ap,as,'s');disp('阶数为');disp(n);[num,den]=butter(n,wc,'s');[numt,dent]=lp2hp(num,den,1);disp('高通滤波器分子多项式系数');fprintf('%.4e\n',numt)disp('高通滤波器分母多项式系数');fprintf('%.4e\n',dent)w=[1/wp 1/ws];h1=freqs(numt,dent,w);fprintf('Ap=%.4e\n',-20*log10(abs(h1(1))))fprintf('Bp=%.4e\n',-20*log10(abs(h1(2))))w1=[0:200:12000*pi];h=freqs(numt,dent,w1);gain=20*log10((abs(h)));plot(w1/(2*pi),gain);xlabel('频率');ylabel('幅值');输出结果：阶数为4高通滤波器分子多项式系数1.0000e+000.0000e+000.0000e+000.0000e+000.0000e+00高通滤波器分母多项式系数1.0000e+005.1920e+041.3478e+092.0497e+131.5585e+17Ap=1.0977e-01Bp=4.0000e+01图形实验5 用FFT设计低通滤波器%用fft变换设计低通滤波器clear;N=100;n=0:(N-1);fs=100;%采样频率f1=1;f2=10;y=sin(2*pi*f1/fs*n)+sin(2*pi*f2/fs*n);%原始信号subplot(211);plot(2*pi*f2/fs*n,y,'k');%显示波形xlabel('时间');ylabel('幅值');title('原始信号');ffty=fft(y);%进行快速傅里叶变换ffty1=ffty;ffty1(f2/(fs/N)+1)=0;%f2频率对应的幅值为零ffty1((N-f2)/(fs/N)+1)=0;%f2/2频率对应f2的对称频率值对应幅值为零yy=ifft(ffty1);%逆fft变换subplot(212);plot(2*pi*f2/fs*n,yy);xlabel('时间');title('滤波以后的低频信号');输出图形为实验六用FFT高通滤波器设计%用fft变换设计低通滤波器clear;N=100;n=0:(N-1);fs=100;%采样频率f1=1;f2=10;y=sin(2*pi*f1/fs*n)+sin(2*pi*f2/fs*n);%原始信号subplot(211);plot(2*pi*f2/fs*n,y,'k');%显示波形xlabel('时间');ylabel('幅值');title('原始信号');ffty=fft(y);%进行快速傅里叶变换ffty1=ffty;ffty1(f1/(fs/N)+1)=0;%f2频率对应的幅值为零ffty1((N-f1)/(fs/N)+1)=0;%f2/2频率对应f2的对称频率值对应幅值为零yy=ifft(ffty1);%逆fft变换subplot(212);plot(2*pi*f2/fs*n,yy);xlabel('时间');title('滤波以后的高频信号');输出图形为实验7 用双线性设计数字滤波器%用双线性设计数字滤波器,wp=0.2pi,ws=0.6Pi,ap=2db,as=15db; wp=0.2*pi;ws=0.6*pi;fs=1/2;ap=2;as=15;Wp=2*fs*tan(wp/2);Ws=2*fs*tan(ws/2);[n,wc]=buttord(Wp,Ws,ap,as,'s');[num,den]=butter(n,wc,'s');[numz,denz]=bilinear(num,den,fs);disp('分子多项式的系数');fprintf('%.4e\n',numz);disp('分母多项式的系数');fprintf('%.4e\n',denz);w=[wp ws];h=freqz(numz,denz,w);fprintf('ap=%.4f\n',-20*log10(abs(h(1))));fprintf('as=%.4f\n',-20*log10(abs(h(2)))); w=linspace(0,2*pi,1024);h=freqz(numz,denz,w);gain=20*log10(abs(h));plot(w/pi,gain);xlabel('Normalized frequency');ylabel('Gain,dB');axis([0 1 -50 0]);grid;输出结果分子多项式的系数1.5777e-013.1555e-011.5777e-01分母多项式的系数1.0000e+00-6.0620e-012.3730e-01ap=0.3945as=15.0000图形为实验8切比雪夫1型设计低通和高通滤波器%用切比雪夫1型设计低通滤波器%wp=2*pi*1000,ws=2*pi*2000,ap=1,as=40;clear;wp=2*pi*1000,ws=2*pi*2000,ap=1,as=40;[n,wc]=cheb1ord(wp,ws,ap,as,'s');[num,den]=cheby1(n,ap,wc,'s');disp('分子多项式的系数');fprintf('%.4f\n',num)disp('分母多项式的系数');fprintf('%.4f\n',den)w=[wp ws];h=freqs(num,den,w);fprintf('ap=%.4f\n',-20*log10(abs(h(1))));fprintf('as=%.4f\n',-20*log10(abs(h(2))));w=0:200:12000*pi;h=freqs(num,den,w);gain=20*log10(abs(h));plot(w/(2*pi),gain);输出结果分子多项式的系数0.00000.00000.00000.00000.00001202796127888840400.0000分母多项式的系数1.00005886.214566671782.4829241699153902.8650904788863911639.00001202796127888840400.0000ap=1.0000as=45.3060图形%用切比雪夫1型设计高通滤波器wp=2*pi*5000,ws=2*pi*1000,ap=1,as=40;wp=1/wp;ws=1/ws;[n,wc]=cheb1ord(wp,ws,ap,as,'s');[num,den]=cheby1(n,ap,wc,'s');[numz,denz]=lp2hp(num,den,1);w=[1/wp 1/ws];h=freqs(numz,denz,w);fprintf('ap=%.4e\n',-20*log10(abs(h(1)))); fprintf('as=%.4e\n',-20*log10(abs(h(2)))); w=0:200:12000*pi;h=freqs(numz,denz,w);gain=20*log10(abs(h));plot(w/(2*pi),gain);输出结果ap=1.0000e+00as=4.7847e+01输出图形实验9 用切比雪夫2型设计低通和高通滤波器%用切比雪夫2型设计低通滤波器%wp=2*pi*1000,ws=2*pi*2000,ap=1,as=40;clear;wp=2*pi*1000,ws=2*pi*2000,ap=1,as=40;[n,wc]=cheb2ord(wp,ws,ap,as,'s');[num,den]=cheby2(n,as,wc,'s');disp('分子多项式的系数');fprintf('%.4f\n',num)disp('分母多项式的系数');fprintf('%.4f\n',den)w=[wp ws];h=freqs(num,den,w);fprintf('ap=%.4f\n',-20*log10(abs(h(1))));fprintf('as=%.4f\n',-20*log10(abs(h(2))));w=0:200:12000*pi;h=freqs(num,den,w);gain=20*log10(abs(h)); plot(w/(2*pi),gain);输出结果分子多项式的系数0.0000566.39190.0000290688415499.92920.0000 29837909134910329000.0000分母多项式的系数1.000024344.5782296168842.7942 2252800523365.8032 10820843108280358.0000 29837909134910292000.0000 ap=1.0000as=44.1570图形%用切比雪夫1型设计高通滤波器wp=2*pi*5000;ws=2*pi*1000;ap=1;as=40;wp=1/wp;ws=1/ws;[n,wc]=cheb2ord(wp,ws,ap,as,'s');[num,den]=cheby2(n,as,wc,'s');[numz,denz]=lp2hp(num,den,1);w=[1/wp 1/ws];h=freqs(numz,denz,w);fprintf('ap=%.4e\n',-20*log10(abs(h(1))));fprintf('as=%.4e\n',-20*log10(abs(h(2))));w=0:200:12000*pi;h=freqs(numz,denz,w);gain=20*log10(abs(h));plot(w/(2*pi),gain);xlabel('频率');ylabel('幅值');title('幅频特性曲线');输出结果ap=1.0000e+00as=4.4779e+01输出图形实验10画一个信号的频谱图clear;fs=1000;f1=50;f2=100;f3=200;N=100t=0:N-1;data=25+22*sin(2*pi*f1/fs*t)+30*sin(2*pi*f2/fs*t)+50*sin(2*pi*f3/fs*t );%原始信号y = fft(data);yabs =abs(y);n = 0:N/2;yabs(1)=yabs(1)/2;stem(n*fs/N,2*yabs(1:N/2+1)/N);频谱图实验11 数字高通滤波器的设计%数字高通滤波器的设计，ws=0.2pi,wp=0.6pi,as=15,ap=2;用巴特沃斯滤波器设计。
《数字信号处理》上机全部源代码调试通过，完整版（高西全，第四版）实验一%实验1：系统响应及系统稳定性close all;clear all%调用fliter解差分方程，由系统对un的响应判断稳定性%内容1：调用filter解差分方程，由系统对u(n)的响应判断稳定性A=[1,-0.9];B=[0.05,0.05];x1n=[1 1 1 1 1 1 1 1 zeros(1,50)];x2n=ones(1,128);hn=impz(B,A,58);subplot(2,2,1);y='h(n)';tstem(hn,y);title('(a) 系统单位脉冲响应h(n)')y1n=filter(B,A,x1n);subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b) 系统对R8(n)的响应y1(n)')y2n=filter(B,A,x2n);subplot(2,2,4);y='y2(n)';tstem(y2n, y);title('(c) 系统对u(n)的响应y2(n)')y1n=filter(B,A,x1n);subplot(2,2,2);y='y1(n)';tstem(y1n,y);title('(b) 系统对R8(n)的响应y1(n)')y2n=filter(B,A,x2n);subplot(2,2,4);y='y2(n)';tstem(y2n, y);title('(c) 系统对u(n)的响应y2(n)')%内容2：调用conv函数计算卷积x1n=[1 1 1 1 1 1 1 1]; %产生信号x1n=R8nh1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)]y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);y='h1(n)';tstem(h1n,y);%调用函数tstem绘图title('(d) 系统单位脉冲响应h1(n)')subplot(2,2,2);y='y21(n)';tstem(y21n,y);title('(e) h1(n)与R8(n)的卷积y21(n)')subplot(2, 2,3); y='h2(n)';tstem(h2n,y); %调用函数tstem绘图title('(f) 系统单位脉冲响应h2(n)')subplot(2, 2, 4); y='y22(n)';tstem(y22n, y);title('(g) h2(n)与R8(n)的卷积y22(n)')%=====================================%内容3：谐振器分析un=ones(1, 256); %产生信号unn=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号A=[1,-1.8237,0.9801];B=[1/100.49,0,-1/100.49];%系统差分方程系数向量B和Ay31n=filter(B,A,un); %谐振器对un的响应y31n y32n=filter(B,A,xsin);%谐振器对正弦信号的响应y32nfigure(3)subplot(2,1,1);y='y31(n)';tstem(y31n,y)title('(h) 谐振器对u(n)的响应y31(n)')subplot(2,1,2);y='y32(n)';tstem(y32n,y);title('(i) 谐振器对正弦信号的响应y32(n)')function tstem(xn,yn)n = 0:length(xn)-1;stem(n,xn,'.');xlabel('n');ylabel('yn');%xlabel('n' );ylabel(yn);axis([0,n(end),min(xn),1.2*max(xn)]);实验二%时域采样理论验证程序exp2a.mTp=64/1000;%观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000; T=1/Fs;Fs=1000; T=1/Fs;M=Tp*Fs; n=0:M-1;A=444.128; alph=pi*50*2^0.5; omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M);%M点FFT[xnt)]yn='xa(nT)';subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on; title('(a) Fs=1000Hz');k=0:M-1; fk=k/Tp;subplot(3,2,2); plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz');xlabel('f(Hz)'); ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%=================================% Fs=300Hz和Fs=200Hz的程序与上面Fs=1000Hz的程序完全相同。
%%%%%%%%%%%% fs=300HzTp=64/1000;%观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000; T=1/Fs;Fs=300; T=1/Fs;M=Tp*Fs; n=0:M-1;A=444.128; alph=pi*50*2^0.5; omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M);%M点FFT[xnt)]yn='xa(nT)';figure(2);subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on; title('(b) Fs=300Hz');k=0:M-1; fk=k/Tp;subplot(3,2,2); plot(fk,abs(Xk));title('(b) T*FT[xa(nT)],Fs=1000Hz');xlabel('f(Hz)'); ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%%%%%%%%%%%%%%%%%%% fs=200HzTp=64/1000;%观察时间Tp=64微秒%产生M长采样序列x(n)% Fs=1000; T=1/Fs;Fs=200; T=1/Fs;M=Tp*Fs; n=0:M-1;A=444.128; alph=pi*50*2^0.5; omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M);%M点FFT[xnt)]yn='xa(nT)';figure(3);subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on; title('(c) Fs=200Hz');k=0:M-1; fk=k/Tp;subplot(3,2,2); plot(fk,abs(Xk));title('(c) T*FT[xa(nT)],Fs=1000Hz');xlabel('f(Hz)'); ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%频域采样理论验证程序exp2b.mM=27;N=32;n=0:M;%产生M长三角波序列x(n)xa=0:floor(M/2); xb= ceil(M/2)-1:-1:0; xn=[xa,xb];Xk=fft(xn,1024);%1024点FFT[x(n)], 用于近似序列x(n)的TFX32k=fft(xn,32);%32点FFT[x(n)]x32n=ifft(X32k);%32点IFFT[X32(k)]得到x32(n)X16k=X32k(1:2:N);%隔点抽取X32k得到X16(K)x16n=ifft(X16k,N/2);%16点IFFT[X16(k)]得到x16(n)subplot(3,2,2);stem(n,xn,'.');box ontitle('(b) 三角波序列x(n)');xlabel('n');ylabel('x(n)');axis([0,32,0,20])k=0:1023;wk=2*k/1024;%subplot(3,2,1);plot(wk,abs(Xk));title('(a)FT[x(n)]');xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');axis([0,1,0,200])k=0:N/2-1;subplot(3,2,3);stem(k,abs(X16k),'.');box ontitle('(c) 16点频域采样');xlabel('k');ylabel('|X_1_6(k)|');axis([0,8,0,200])n1=0:N/2-1;subplot(3,2,4);stem(n1,x16n,'.');box ontitle('(d) 16点IDFT[X_1_6(k)]');xlabel('n');ylabel('x_1_6(n)');axis([0,32,0,20]) k=0:N-1;subplot(3,2,5);stem(k,abs(X32k),'.');box ontitle('(e) 32点频域采样');xlabel('k');ylabel('|X_3_2(k)|');axis([0,16,0,200]) n1=0:N-1;subplot(3,2,6);stem(n1,x32n,'.');box ontitle('(f) 32点IDFT[X_3_2(k)]');xlabel('n');ylabel('x_3_2(n)');axis([0,32,0,20])function tstem(xn,yn)n = 0:length(xn)-1;stem(n,xn,'.');xlabel('n');ylabel('yn');%xlabel('n' );ylabel(yn);axis([0,n(end),min(xn),1.2*max(xn)]);实验三%实验三程序exp3.m%用FFT对信号作频谱分析%clear all;close all%实验内容(1)================================ x1n=[ones(1,4)];%产生序列向量x1(n)=R4(n)M=8;xa=1:(M/2); xb=(M/2):-1:1;x2n=[xa,xb]; %产生长度为8的三角波序列x2(n) x3n=[xb,xa];X1k8=fft(x1n,8); %计算x1n的8点DFTX1k16=fft(x1n,16); %计算x1n的16点DFTX2k8=fft(x2n,8); %计算x1n的8点DFTX2k16=fft(x2n,16); %计算x1n的16点DFTX3k8=fft(x3n,8); %计算x1n的8点DFTX3k16=fft(x3n,16); %计算x1n的16点DFT%以下绘制幅频特性曲线subplot(2,2,1);mstem(X1k8);%绘制8点DFT的幅频特性图title('(1a) 8点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X1k8))])subplot(2,2,3);mstem(X1k16);%绘制16点DFT的幅频特性图title('(1b)16点DFT[x_1(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X1k16))])figure(2)subplot(2,2,1);mstem(X2k8);%绘制8点DFT的幅频特性图title('(2a) 8点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X2k8))])subplot(2,2,2);mstem(X2k16);%绘制16点DFT的幅频特性图title('(2b)16点DFT[x_2(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X2k16))])subplot(2,2,3);mstem(X3k8);%绘制8点DFT的幅频特性图title('(3a) 8点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X3k8))])subplot(2,2,4);mstem(X3k16);%绘制16点DFT的幅频特性图title('(3b)16点DFT[x_3(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X3k16))])%实验内容(2) 周期序列谱分析=================== N=8;n=0:N-1; %FFT的变换区间N=8x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k8=fft(x4n); %计算x4n的8点DFTX5k8=fft(x5n); %计算x5n的8点DFTN=16;n=0:N-1; %FFT的变换区间N=16x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k16=fft(x4n); %计算x4n的16点DFTX5k16=fft(x5n); %计算x5n的16点DFTfigure(3)subplot(2,2,1);mstem(X4k8);%绘制8点DFT的幅频特性图title('(4a) 8点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X4k8))])subplot(2,2,3);mstem(X4k16);%绘制16点DFT的幅频特性图title('(4b)16点DFT[x_4(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X4k16))])subplot(2,2,2);mstem(X5k8);%绘制8点DFT的幅频特性图title('(5a) 8点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X5k8))])subplot(2,2,4);mstem(X5k16);%绘制16点DFT的幅频特性图title('(5b)16点DFT[x_5(n)]');xlabel('ω/π');ylabel('幅度');axis([0,2,0,1.2*max(abs(X5k16))])%实验内容(3) 模拟周期信号谱分析================= figure(4)Fs=64;T=1/Fs;N=16;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);%对x6(t)16点采样X6k16=fft(x6nT); %计算x6nT的16点DFTX6k16=fftshift(X6k16); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F;%产生16点DFT对应的采样点频率（以零频率为中心）subplot(3,1,1);stem(fk,abs(X6k16),'.');box on %绘制8点DFT的幅频特性图title('(6a) 16点|DFT[x_6(nT)]|');xlabel('f(Hz)'); %%%%%%%%%%%%%%%%%%ylabel('幅度');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k16))])N=32;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);%对x6(t)32点采样X6k32=fft(x6nT); %计算x6nT的32点DFTX6k32=fftshift(X6k32); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F;%产生16点DFT对应的采样点频率（以零频率为中心）subplot(3, 1, 2);stem(fk, abs(X6k32), '.');box on %绘制8点DFT的幅频特性图title('(6b) 32点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');axis([-N*F/2-1, N*F/2-1,0, 1.2*max(abs(X6k32))])N=64;n=0:N-1; %FFT的变换区间N=16x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);%对x6(t)64点采样X6k64=fft(x6nT); %计算x6nT的64点DFTX6k64=fftshift(X6k64); %将零频率移到频谱中心Tp=N*T;F=1/Tp; %频率分辨率Fk=-N/2:N/2-1;fk=k*F;%产生16点DFT对应的采样点频率（以零频率为中心）subplot(3,1,3);stem(fk,abs(X6k64),'.');box on%绘制8点DFT的幅频特性图title('(6a) 64点|DFT[x_6(nT)]|');xlabel('f(Hz)');ylabel('幅度');axis([-N*F/2-1,N*F/2-1,0, 1.2*max(abs(X6k64))])function mstem(Xk)%mstem(Xk)绘制频域采样序列向量Xk的幅频特性图M=length(Xk);k=0:M-1;wk=2*k/M;%产生M点DFT对应的采样点频率（关于pi归一化值) stem(wk,abs(Xk),'.');box on;%绘制M点DFT的幅频特性图?xlabel('w/\pi');ylabel('幅度');axis([0,2,0,1.2*max(abs(Xk))]);实验四%实验四程序exp4.m% IIR数字滤波器设计及软件实现%clear all; close allFs=10000; T=1/Fs; %采样频率%调用信号产生函数mstg产生由三路抑制载波调幅信号相加构成的复合信号st st=mstg;%低通滤波器设计与实现=========================fp=280; fs=450;wp=2*fp/Fs; ws=2*fs/Fs; rp=0.1; rs=60;%DF指标（低通滤波器的通、阻带边界频率）[N,wp]=ellipord(wp,ws,rp,rs);%调用ellipord计算椭圆DF阶数N和通带截止频率wp[B,A]=ellip(N,rp,rs,wp);%调用ellip计算椭圆带通DF系统函数系数向量B和Ay1t=filter(B,A,st); %滤波器软件实现% 低通滤波器设计与实现绘图部分figure(2); subplot(3,1,1);myplot(B,A);%调用绘图函数myplot绘制损耗函数曲线yt='y_1(t)';subplot(3,1,2); tplot(y1t,T,yt);%调用绘图函数tplot绘制滤波器输出波形%===========================================%带通滤波器设计与实现=========================fpl=440; fpu=560; fsl=275; fsu=900;wp=[2*fpl/Fs,2*fpu/Fs];ws=[2*fsl/Fs,2*fsu/Fs]; rp=0.1; rs=60;[N,wp]=ellipord(wp,ws,rp,rs);%调用ellipord计算椭圆DF阶数N和通带截止频率wp[B,A]=ellip(N,rp,rs,wp);%调用ellip计算椭圆带通DF系统函数系数向量B和Ay2t=filter(B,A,st); %滤波器软件实现% 带通滤波器设计与实现绘图部分（省略）%补充1figure(2); subplot(3,1,3);myplot(B,A);%--figure(3);yt='y_2(t)';subplot(3,1,1); tplot(y2t,T,yt);%===========================================%高通滤波器设计与实现===========================fp=890; fs=600;wp=2*fp/Fs; ws=2*fs/Fs; rp=0.1; rs=60;%DF指标（低通滤波器的通、阻带边界频率）[N,wp]=ellipord(wp,ws,rp,rs);%调用ellipord计算椭圆DF阶数N和通带%截止频率wp [B,A]=ellip(N,rp,rs,wp,'high');%调用ellip计算椭圆带通DF系统函数系数向量B和Ay3t=filter(B,A,st); %滤波器软件实现% 高低通滤波器设计与实现绘图部分（省略）%补充2figure(3); subplot(3,1,2);myplot(B,A);%--figure(3);yt='y_3(t)';subplot(3,1,3); tplot(y3t,T,yt);%===========================================function st=mstg%产生信号序列向量st,并显示st的时域波形和频谱%st=mstg 返回三路调幅信号相加形成的混合信号,长度N=1600 N=1600 %N为信号st的长度Fs=10000;T=1/Fs;Tp=N*T;%采样频率Fs=10 kHz, Tp为采样时间t=0:T:(N-1)*T;k=0:N-1;f=k/Tp;fc1=Fs/10;%第1路调幅信号的载波频率fc1=1000 Hzfm1=fc1/10;%第1路调幅信号的调制信号频率fm1=100 Hzfc2=Fs/20;%第2路调幅信号的载波频率fc2=500 Hzfm2=fc2/10;%第2路调幅信号的调制信号频率fm2=50 Hzfc3=Fs/40;%第3路调幅信号的载波频率fc3=250 Hzfm3=fc3/10;%第3路调幅信号的调制信号频率fm3=25 Hzxt1=cos(2*pi*fm1*t).*cos(2*pi*fc1*t);%产生第1路调幅信号xt2=cos(2*pi*fm2*t).*cos(2*pi*fc2*t);%产生第2路调幅信号xt3=cos(2*pi*fm3*t).*cos(2*pi*fc3*t);%产生第3路调幅信号st=xt1+xt2+xt3; %三路调幅信号相加fxt=fft(st,N); %计算信号st的频谱%以下为绘图部分，绘制st的时域波形和幅频特性曲线subplot(3,1,1)plot(t,st);grid;xlabel('t/s');ylabel('s(t)');axis([0,Tp/8,min(st),max(st)]);title('(a) s(t)的波形')subplot(3,1,2)stem(f,abs(fxt)/max(abs(fxt)),'.');grid;title('(b) s(t)的频谱')axis([0,Fs/5,0,1.2]);xlabel('f/Hz');ylabel('幅度')function myplot(B,A)%时域离散系统损耗函数绘图%B为系统函数分子多项式系数向量%A为系统函数分母多项式系数向量[H,W]=freqz(B,A,1000);m = abs(H);plot(W/pi,20*log10(m/max(m))); grid on;xlabel('\omega/\pi'); ylabel('幅度(dB)');axis([0,1,-80,5]); title('损耗函数曲线');function tplot(xn,T,yn)%时域序列连续曲线绘图函数%xn：信号数据序列，yn：绘图信号的纵坐标名字(字符串) %T为采样间隔n = 0:length(xn)-1; t=n*T;plot(t,xn);xlabel('t/s'); ylabel(yn);axis([0,t(end),min(xn),1.2*max(xn)])实验五%实验五程序exp5.m%FIR数字滤波器设计及软件实现clear all; close all;%==调用xtg产生信号xt, xt长度N=1000,并显示xt及其频谱,=======N=1000;xt=xtg(N);fp=120; fs=150; Rp=0.2; As=60; Fs=1000;%输入给定指标%(1) 用窗函数法设计滤波器wc=(fp+fs)/Fs; %理想低通滤波器截止频率(关于pi归一化）B=2*pi*(fs-fp)/Fs; %过渡带宽度指标Nb=ceil(11*pi/B); %blackman窗的长度Nhn=fir1(Nb-1,wc,blackman(Nb));Hw=abs(fft(hn,1024));%求设计的滤波器频率特性ywt=fftfilt(hn,xt,N); %调用函数fftfilt对xt滤波%以下为用窗函数法设计法的绘图部分（滤波器损耗函数, 滤波器输出信号波形）（省略）f=[0:1023]*Fs/1024;figure(2)subplot(2,1,1)plot(f,20*log10(Hw/max(Hw)));grid;title('(3)低通滤波器幅频特性')axis([0,Fs/2,-120,20]);xlabel('f/Hz');ylabel('幅度')t=[0:2*N-1]/Fs;Tp=N/Fs; %%%%%%%%%%subplot(2,1,2);plot(t,ywt);grid;axis([0,Tp/2,-1,1]);xlabel('t/s');ylabel('y_w(t)');title('(4)滤波噪声后的信号波形');%(2) 用等波纹最佳逼近法设计滤波器fb=[fp,fs]; m=[1,0];%确定remezord函数所需参数f,m,devdev=[(10^(Rp/20)-1)/(10^(Rp/20)+1),10^(-As/20)];[Ne,fo,mo,W]=remezord(fb,m,dev,Fs);%确定remez函数所需参数hn=remez(Ne,fo,mo,W);%调用remez函数进行设计Hw=abs(fft(hn,1024));%求设计的滤波器频率特性yet=fftfilt(hn,xt,N); %调用函数fftfilt对xt滤波%以下为用等波纹设计法的绘图部分（滤波器损耗函数, 滤波器输出信号yw(t)波形）%(省略)f=[0:1023]*Fs/1024;figure(3)subplot(2,1,1)plot(f,20*log10(Hw/max(Hw)));grid;title('(5)低通滤波器幅频特性')axis([0,Fs/2,-80,10]);xlabel('f/Hz');ylabel('幅度')%t=[0:N-1]/Fs;Tp=N/Fs;subplot(2,1,2)plot(t,yet);grid;axis([0,Tp/2,-1,1]);xlabel('t/s');ylabel('y_e(t)');title('(6)滤波噪声后的信号波形');function xt=xtg(N)%实验五信号x(t)产生函数,并显示信号的幅频特性曲线%xt=xtg 产生一个长度为N,有加性高频噪声的单频调幅信号xt,采样频率Fs=1000 Hz %载波频率fc=Fs/10=100Hz，调制正弦波频率f0=fc/10=10 HzN=2000; Fs=1000; T=1/Fs; Tp=N*T;t=0:T:(N-1)*T;fc=Fs/10; f0=fc/10; %载波频率fc=Fs/10, 单频调制信号频率为f0=Fc/10mt=cos(2*pi*f0*t);%产生单频正弦波调制信号mt, 频率为f0ct=cos(2*pi*fc*t); %产生载波正弦波信号ct, 频率为fcxt=mt.*ct; %相乘产生单频调制信号xtnt=2*rand(1,N)-1; %产生随机噪声nt%====设计高通滤波器hn,用于滤除噪声nt中的低频成分,生成高通噪声====fp=150; fs=200; Rp=0.1; As=70;% 滤波器指标fb=[fp,fs]; m=[0,1];% 计算remezord函数所需参数f,m,devdev=[10^(-As/20),(10^(Rp/20)-1)/(10^(Rp/20)+1)];[n,fo,mo,W]=remezord(fb,m,dev,Fs);% 确定remez函数所需参数hn=remez(n,fo,mo,W);% 调用remez函数进行设计，用于滤除噪声nt中的低频成yt=filter(hn,1,10*nt);%滤除随机噪声中低频成分, 生成高通噪声yt%=======================================xt=xt+yt; %噪声加信号fst=fft(xt,N); k=0:N-1; f=k/Tp;subplot(3,1,1); plot(t,xt); grid;xlabel('t/s'); ylabel('x(t)');axis([0,Tp/5,min(xt),max(xt)]);title('(a) 信号加噪声波形')subplot(3,1,2); plot(f,abs(fst)/max(abs(fst)));grid; title('(b) 信号加噪声的频谱')axis([0,Fs/2,0,1.2]);xlabel('f/Hz');ylabel('幅度');实验6%实验六程序exp6.m% DTMF双频拨号信号的生成和检测程序%clear all;clc;tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; % DTMF信号代表的16个数N=205;K=[18, 20, 22, 24, 31, 34, 38, 42];f1=[697,770,852,941]; % 行频率向量f2=[1209,1336,1477,1633]; % 列频率向量TN=input('键入6位电话号码= '); % 输入6位数字TNr=0; % 接收端电话号码初值为零for l=1:6;d=fix(TN/10^(6-l));TN=TN-d*10^(6-l);for p=1:4;for q=1:4;if tm(p,q)==abs(d); break,end% 检测码相符的列号qendif tm(p,q)==abs(d); break,end% 检测码相符的行号pendn=0:1023; % 为了发声, 加长序列x = sin(2*pi*n*f1(p)/8000) + sin(2*pi*n*f2(q)/8000);% 构成双频信号sound(x,8000); % 发出声音pause(0.1)% 接收检测端的程序X=goertzel(x(1:205),K+1);% 用Goertzel算法计算八点DFT样本val = abs(X); % 列出八点DFT向量subplot(3,2,l);stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|') % 画出DFT(k)幅度axis([10 50 0 120])limit = 80;for s=5:8;if val(s) > limit, break, end % 查找列号endfor r=1:4;if val(r) > limit, break, end % 查找行号endTNr=TNr+tm(r,s-4)*10^(6-l);enddisp('接收端检测到的号码为:')% 显示接收到的字符disp(TNr)%实验六程序exp6.m%改成识别8位电话号码% DTMF双频拨号信号的生成和检测程序%clear all;clc;tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; % DTMF信号代表的16个数N=205;K=[18, 20, 22, 24, 31, 34, 38, 42];f1=[697,770,852,941]; % 行频率向量f2=[1209,1336,1477,1633]; % 列频率向量TN=input('键入8位电话号码= '); % 输入8位数字TNr=0; % 接收端电话号码初值为零for l=1:8;d=fix(TN/10^(8-l));TN=TN-d*10^(8-l);for p=1:4;for q=1:4;if tm(p,q)==abs(d); break,end% 检测码相符的列号qendif tm(p,q)==abs(d); break,end% 检测码相符的行号pendn=0:1023; % 为了发声, 加长序列x = sin(2*pi*n*f1(p)/8000) + sin(2*pi*n*f2(q)/8000);% 构成双频信号sound(x,8000); % 发出声音pause(0.1)% 接收检测端的程序X=goertzel(x(1:205),K+1);% 用Goertzel算法计算八点DFT样本val = abs(X); % 列出八点DFT向量subplot(4,2,l);stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|') % 画出DFT(k)幅度axis([10 50 0 120])limit = 80;for s=5:8;if val(s) > limit, break, end % 查找列号endfor r=1:4;if val(r) > limit, break, end % 查找行号endTNr=TNr+tm(r,s-4)*10^(8-l);enddisp('接收端检测到的号码为:')% 显示接收到的字符disp(TNr)。
