2422切线长定理1

切线长定理一知识讲解(基础)责编：康红梅【学习目标】1. 了解切线长定义；理解三角形的内切圆及内心的定义；2. 掌握切线长定理；利用切线长定理解决相关的计算和证明【要点梳理】要点一、切线长定理1.切线长：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长要点诠释：切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称•切线是直线，而非线段•2 .切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角要点诠释：切线长定理包含两个结论：线段相等和角相等3 •圆外切四边形的性质：圆外切四边形的两组对边之和相等•要点二、三角形的内切圆1.三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆•这个三角形叫作圆的外切三角形•2 •三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心•三角形的内心是这个三角形的三条角平分线的交点•要点诠释：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即；:- 1 I'：(S 为三角形的面积，P为三角形的周长，r为内切圆的半径).2内心(三角形三角形三条角平分线X(1)到三角形三边距离相等;内切圆的圆的交点(2)OA、OB OC分别平分心)M BAG M ABG M ACB⑶内心在三角形内部.【典型例题】类型一、切线长定理1. (2015秋?湛江校级月考)已知PA PB分别切OO于A B, E为劣弧AB上一点，过E点的切线交PA于C、交PB于D.(1 )若PA=6,求厶PCD的周长.(2)若/ P=50°求/ DOC解：(1)连接OE••• PA PB与圆O相切，••• PA=PB=6同理可得：AC=CE BD=DE△ PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+P；=12(2)T PA PB与圆O相切，•••/ OAP M OBP=90 / P=50°,•••/ AOB=360 - 90°- 90°- 50° =130°,在Rt △ AOC和Rt △ EOC 中，r OA=OEOC=OC，L• Rt△AO Q Rt△EOC( HL),•••/ AOC H COE同理：/ DOE M BOD•••/ COD= M AOB=65 .2【总结升华】本题考查的是切线长定理和全等三角形的判定和性质，掌握切线长定理是解题的关键.2 . (2016秋?江阴市校级期中)如图，AB、AC、BD是O O的切线，P、C、D为切点，如果AB=5 ,AC=3，贝U BD的长为 _________【解析】解: •/ AC 、AP 为O O 的切线, 举一反三： 【变式】已知：如图，OO过点A 作AD _ BF 于点D .求证：DA 为OOAC 、BD 是O O 的切线，贝U AC=AP , BP=BD ，求出BP 的长即可求出 BD 的长.••• AC=AP ,•/ BP 、BD 为O O 的切线,• BP=BD , • BD=PB=AB - AP=5 - 3=2.故答案为：2.【总结升华】本题考查了切线长定理，两次运用切线长定理并利用等式的性质是解题的关键. 为.：ABC 的外接圆，BC 为OO 的直径，作射线 BF ，使得BA 平分三CBF , 的切线.AO = BO2 = . 3 .BA 平分.CBF ,• • 1 =. 2. • Z 3 Z 1 .DB // AO .AD _DB , • £BDA =90 . /.Z DAO =90 .AO 是O O半径，• DA 为O O 的切线. 3.如图，正方形 ABCD 边长为4cm ，以正方形的一边 BC 为直径在正方形 ABCD 内作半圆，过 A 作半圆的切线，与半圆相切于F 点，与DC 相交于E 点，则△ ADE 的面积（ ）【答案】2.【答案】 连接AO .A.12B.24C.8D.6【答案】D;【解析】••• AE与圆0切于点F,显然根据切线长定理有AF=AB=4cm , EF=EC ,设EF=EC=xcm ,则DE= (4 - x) cm, AE= (4+x) cm ,在三角形ADE中由勾股定理得：2 2 2(4 - x) +4 = (4+x),x=1cm,/• CE=1cm ,.DE=4 -仁3cm ,2--S^\DE=AD ?DE -=2=3 ^4^2=6cm -【总结升华】此题主要考查圆的切线长定理，正方形的性质和勾股定理等知识，解答本题关键是运用切线长定理得出AB=AF , EF=EC .类型二、三角形的内切圆4. (2015?青江市校级二模)如图，在△ABC中，I是内心，O是AB边上一点，00经过B点且与AI相切于I点.(1)求证：AB=AC(2)若BC=16 00的半径是5，求AI的长.【解题思路】(1)延长AI交BC于D,连结OI,如图，根据内心的性质得/ OBI=Z DBI,则可证明OI// BD 再根据切线的性质得OI 丄AI，贝U BDLAD加上AI平分/ BAC所以△ ABC为等腰三角形，得到AB=AC (2)由OI// BC得到△ AOI sA ABD 得到比例式，再根据勾股定理求得A D JA B2— BD2=贸，于是就可得. 【答案与解析】解：(1)延长AI交BC于D,连结OI，如图,• AI= ?AD= 'XBD 8二11 ~=~••T是厶ABC的内心，••• BI 平分/ ABC 即/ OBI=Z DBI, •/ OB=O|•••/ OBI=Z OIB,•••/ DBI=Z OIB,•01 // BD•/AI为OO的切线，•01 丄AI,•BDLAD•/ AI 平分/ BAC•△ ABC为等腰三角形，•AB=AC(2)T OI // BC•△AOI sA ABD•-y•l i. H i ii，•订:•/.=:,AB』• Ai2"32,【总结升华】本题考查了三角形的内切圆与内心，等腰三角形的判定和性质，相似三角形的判定和性质等，正确的作出辅助线是解题的关键.举一反三：【变式】已知如图，△ ABC中，/ C=90°, BC=4, AC=3求厶ABC的内切圆O O的半径r.【答案】连结OA OB OC•/△ ABC中，/ C=90°, BC=4, AC=3 • AB=5.1111贝U S\AO+S A CO+S^AO(=S^ABC即卩5r+ 4r+ 3r= 3 4 r=12 2 2 2，。

初中数学什么是切线长定理
初中数学中，切线长定理是与圆相关的一个重要概念。

下面我将详细介绍切线长定理的定义、性质和相关概念。

1. 切线长定理的定义：
-切线长定理：在一个圆上，一个角的顶点在切点上，另外两个顶点在圆上，这个角的两条边分别与切线相交，那么这两条切线的长度相等。

2. 切线长定理的性质：
-定理性质1：切线长度相等。

如果一个圆上的两条切线与同一个角相交，且角的顶点在切点上，那么这两条切线的长度相等。

3. 切线长定理的相关概念：
-切点：切线与圆相交的点称为切点。

-切线长度：切线的长度即为从切点到圆心的距离。

切线长定理是初中数学中的一个重要概念，它可以帮助我们理解和应用几何知识，解决与切线和圆相关的问题。

在应用切线长定理时，需要注意定理的定义和性质，并运用几何知识进行推理和分析。

例如，如果我们需要判断两条切线的长度是否相等，我们可以先找到这两条切线与同一个角相交，并且角的顶点在切点上。

然后根据切线长定理的性质，我们可以得出这两条切线的长度相等。

希望以上内容能够满足你对切线长定理的了解。

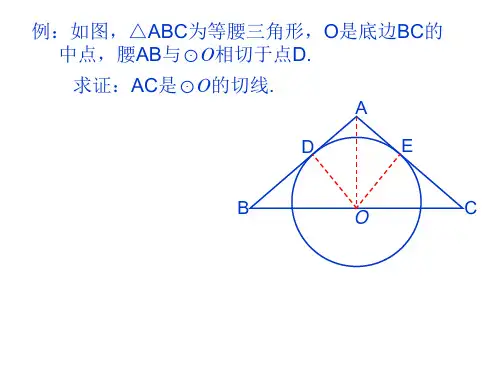
切线长定理—知识讲解责编：常春芳【学习目标】1.了解切线长定义,掌握切线长定理；2.了解圆外切四边形定义及性质；3. 利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线长定理1．切线长： 经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长.要点诠释： 切线长是指圆外一点和切点之间的线段的长，不是“切线的长”的简称.切线是直线，而非线段. 2．切线长定理： 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.要点诠释： 切线长定理包含两个结论：线段相等和角相等.要点二、圆外切四边形的性质1.圆外切四边形四边形的四条边都与同一个圆相切,那这个四边形叫做圆的外切四边形.2.圆外切四边形性质圆外切四边形的两组对边之和相等.【典型例题】类型一、切线长定理1．（2015秋•湛江校级月考）已知PA、PB分别切⊙O于A、B，E为劣弧AB上一点，过E点的切线交PA于C、交PB于D．（1）若PA=6，求△PCD的周长．（2）若∠P=50°求∠DOC．【答案与解析】解：（1）连接OE，∵PA、PB与圆O相切，∴PA=PB=6，同理可得：AC=CE，BD=DE，△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12；（2）∵PA PB与圆O相切，∴∠OAP=∠OBP=90°∠P=50°，∴∠AOB=360°﹣90°﹣90°﹣50°=130°，在Rt△AOC和Rt△EOC 中，，∴Rt△AOC≌Rt△EOC（HL），∴∠AOC=∠COE，同理：∠DOE=∠BOD，∴∠COD=∠AOB=65°．【总结升华】本题考查的是切线长定理和全等三角形的判定和性质，掌握切线长定理是解题的关键．2．如图，△ABC中，∠ACB=90°，以AC为直径的⊙O交AB于D，E为BC中点.求证：DE是⊙O切线.【答案与解析】连结OD、CD，AC是直径，∴OA=OC=OD，∴∠OCD=∠ODC，∠ADC=90°，∴△CDB是直角三角形.∵E是BC的中点，∴DE=EB=EC，∴∠ECD=∠EDC，∠ECD+∠OCD=90°，∴∠EDC+∠ODC=90°，即OD⊥ED，∴DE是⊙O切线.【总结升华】自然连接OD，可证OD⊥DE.举一反三：【变式】已知：如图，⊙O为ABC∆的外接圆，BC为⊙O的直径，作射线BF，使得BA平分CBF∠，过点A作AD BF⊥于点D.求证：DA为⊙O的切线.FCFC【答案】连接AO.∵AO BO=，∴23∠=∠.∵ BA CBF ∠平分，∴ 12∠=∠. ∴ 31∠=∠ .∴ DB ∥AO .∵ AD DB ⊥,∴ 90BDA ∠=︒.∴ 90DAO ∠=︒.∵ AO 是⊙O 半径，∴ DA 为⊙O 的切线. 3．如图，正方形ABCD 边长为4cm ，以正方形的一边BC 为直径在正方形ABCD 内作半圆，过A 作半圆的切线，与半圆相切于F 点，与DC 相交于E 点，则△ADE 的面积（ ）A.12B.24C.8D.6【答案】D ；【解析】∵AE 与圆O 切于点F ，显然根据切线长定理有AF=AB=4cm ，EF=EC ，设EF=EC=xcm ，则DE=（4﹣x）cm ，AE=（4+x ）cm ，在三角形ADE 中由勾股定理得：（4﹣x）2+42=（4+x ）2，∴x=1cm，∴CE=1cm，∴DE=4﹣1=3cm，∴S △ADE =AD•DE÷2=3×4÷2=6cm 2．【总结升华】此题主要考查圆的切线长定理，正方形的性质和勾股定理等知识，解答本题关键是运用切线长定理得出AB=AF ，EF=EC ．类型二、圆外切四边形　4.（2015•西青区二模）已知四边形ABCD 中，AB∥CD，⊙O 为内切圆，E 为切点．（Ⅰ）如图1，求∠AOD 的度数；（Ⅱ）如图1，若AO=8cm ，DO=6cm ，求AD 、OE 的长；（Ⅲ）如图2，若F 是AD 的中点，在（Ⅱ）中条件下，求FO 的长．【答案与解析】解：（Ⅰ）∵⊙O为四边形ABCD的内切圆，∴AD、AB、CD为⊙O的切线，∴OD平分∠ADC，OA平分∠BAD，即∠ODA=∠ADC，∠OAD=∠BAC，∵AB∥CD，∴∠ADC+∠BAC=180°，∴∠ODA+∠OAD=90°，∴∠AOD=90°；（Ⅱ）在Rt△AOD中，∵AO=8cm，DO=6cm，∴AD==10（cm），∵AD切⊙O于E，∴OE⊥AD，∴OE•AD=OD•OA，∴OE==（cm）；（Ⅲ）∵F是AD的中点，∴FO=AD=×10=5（cm）．【总结升华】本题考查了三角形的内切圆与内心，也考查了切线长定理．举一反三：【变式】在圆外切四边形ABCD中，AB:BC:CD:AD只可能是（）.A.2:3:4:5B.3:4:6:5C.5:4:1:3D.3:4:2:5【答案】B.。

切线长定理几何语言
切线长定理是一个数学定理，它定义了某个特定几何图形的特定部分。

它可以定义圆的外切矩形或者椭圆的外切矩形等。

1. 定义：
切线长定理是指，在几何图形中，曲线上任意一点到图形对称轴（如
椭圆的长轴和短轴）所形成的距离，乘以它到两个焦点之间的距离，
始终等于一定值。

2. 应用：
（1）圆的外切矩形：任意一点到圆心的距离乘以它到两个圆心之间的
距离，始终都等于圆的半径的平方，这就是切线长定理。

（2）椭圆的外切矩形：任意点到椭圆的长轴的距离乘以它到椭圆的两
个焦点之间的距离，始终都等于椭圆的短轴的平方，这也是切线长定理。

3. 证明：
切线长定理可以用几何证明来得到，比如用三角函数证明，则可以把
椭圆看作一个具有参数的曲线，利用曲线两点间的切线的中点的距离
的一定等式，来证明切线长定理。

4. 结论：
根据以上证明，可以得出：在一定特定的几何形状中，曲线上任意一点到图形的对称轴的距离，乘以它到两个焦点之间的距离，始终等于一定值，这就是切线长定理。

No.39 课题： 24.2.2 切线长（1）课型：新授主编：李芹审核：杨艳芳验收负责人：赵翠英授课时间：学习目标：1．理解切线长定义；
2．掌握切线长定理并能运用切线长定理解决问题.
重点：切线长定理
难点：切线长定理与其它定理的综合运用
学习过程：
一、预习导学
如图，点A是⊙O外一点，AC切⊙O 于点C，OA交⊙O于点B，
且∠A=30°，BC=1.求⊙O的半径.
二、学习研讨
1．如图，经过平面内一点，画出⊙O的切线．
切线长定义：
. 2．如图，点P 为⊙O 外一点，PA、PB为⊙O的切线，A、B为切点. 连接OP，则线段PA与PB，∠APO与∠BPO分别有什么关系？为什么？
由此我们得到切线长定理：
.
推理形式：简记
o
A
B P
O _B
_O _C
_A
例题 如图，PA 、PB 、DE 分别切⊙O 于点A 、B 、C ，DE 交PA 、PB 于点D 、E ， 简 记
已知点P 到⊙O 的切线长是8cm ．求△PDE 的周长.
三、巩固提高
如图，已知AB 、BC 、CD 分别与⊙O 切于点E 、F 、G ，且AB //CD ，
BO=6cm ，CO=8cm . 求BC 的长.
四、学后反思
C
D。