(3)写出图中所有的全等三角形?
△ AOP≌ △ BOP, △ AOC≌ △ BOC,△ ACP≌ △ BCP
(4)写出图中所有的等腰三角形?
△ ABP,△ AOB
练习
1.如图, P 为⊙O 外一点,PA,PB 为⊙O的切线,A和B为切点. (1)若PA=3,则PB= _3__ (2)若PA=2x-1,PB=x+5,则x=_6__
中考链接
如图,PA,PB切⊙O于A,B,MN切
⊙O于C,交PA于M,交PB于N,
PA=7.5cm,则△PMN的周长是( C)
A.7.5cm
B.10cm
C.15cm
D.12.5cm
巩固练习
△ABC中,∠ ABC=50°, ∠ACB=70 °, 点O是⊙O的内心,求∠ BOC的度数.
解:∵点O是⊙O的内心 ∴BO平分∠ABC,CO平分∠ACB ∴∠1=1/2∠ABC=25° ∠3=1/2∠ACB=35° ∴∠BOC=180°-25°-35° =120°
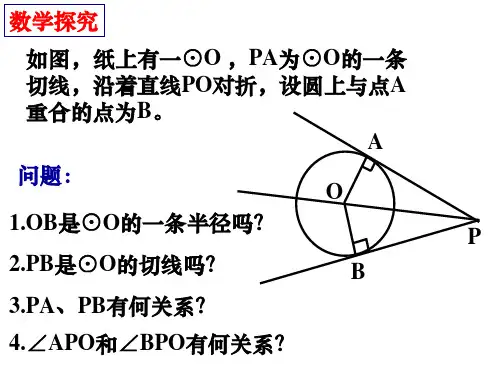
解:连接AO,BO. ∵PA,PB是⊙O的两条切线, ∴OA⊥AP ,OB⊥BP.
又 OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP (HL)
∴ PA=PB, ∠OPA=∠OPB.
切线长定理:
从圆外一点可以引圆的两 条切线,它们的切线长相等, 这一点和圆心的连线平分两 条切线的夹角.
符号语言
24.2.2 直线和圆的位置关系
第3课时 切线长定理
1.理解切线长的概念.理解并掌握切线长 定理.
2.知道三角形内切圆、内心的概念.
3.运用切线长定理和三角形内切圆知识 解题.
复习旧知
1、直线和圆有什么位置关系?
相交、相切、相离