人教版九年级数学与圆有关的位置关系讲义(含解析)(2020年最新)

初三数学圆和圆的位置关系知识精讲圆和圆的位置关系1. 基本概念（1）两圆外离、外切、相交、内切、内含的定义；（2）两圆的公切线、外公切线、内公切线、公切线长的定义； （3）两圆的连心线、圆心距、公共弦。

两圆的位置 圆心距d 与两圆的半径R 、r 的关系 外公切线条数内公切线条数公切线条数外离 d R r >+ 2 2 4 外切 d R r =+2 13 相交 R r d R r R r -<<+≥()2 0 2 内切 d R r R r =->()1 0 1 内含d R r R r <->()说明：（1）两圆的位置关系和半径，圆心距的数量关系是互相对应的，即知道位置关系就可以确定数量关系，知道数量关系也可以确定位置关系；（2）如果遇到“相离”或“相切”问题时，都要分两种情况来解决。

3. 相交两圆的性质相交两圆的连心线垂直平分两圆的公共弦。

4. 相切两圆的性质如果两圆相切，那么切点一定在连心线上。

5. 两圆中常引用的辅助线（1）相切：过切点引公切线，引连心线。

（2）相交：引连心线、公共弦（将两圆半径、圆心距、公共弦的一半集中在一个三角形中） （3）遇两条内公切线或外公切线：引过切点的半径，构造直角三角形（将半径、圆心距、例：（1997某某）如图，已知：两圆内切于点A，P是两圆公切线上的一点过P作小圆的割线PBC，连结AB、AC，并延长分别交大圆于D、E，求证：PCPBAEAD=22。

证明：连结DEPA是两圆的公切线，∴∠=∠=∠PAD PCA E∴∴=BC DEAEADACAB//PA是⊙O1的切线，PBC是⊙O1的割线∴=⋅PA PB PC2又 ∠=∠∠=∠PCA PAB CPA APB，∴∴=∆∆PAB PCAACABPCPA~∴=∴==⋅=AEADPCPAAEADPCPAPCPB PCPCPB22222即PCPBAEAD=22说明：相切两圆中公切线是联系两圆中角的最有利条件，利用两圆的公切线，构造两圆的弦切角来进行角的转化。

九年级数学圆与圆的位置关系、圆的全章复习人教版【本讲教育信息】一. 教学内容：圆与圆的位置关系、圆的全章复习［学习目标］1. 掌握圆与圆的五种位置关系，类比于点与圆，直线与圆的位置关系，能通过两圆半径r 1，r 2及圆心距d 三者的数量关系，判断两圆位置关系，或通过位置关系，判断数量关系。

2. 在数轴上表示当d 在不同位置时，两圆的位置关系。

3. 在证明两圆的或多圆的图形时，常加的辅助线：公共弦、公切线；圆心距，连心线。

4. 当两圆相交时，连心线垂直平分公共弦。

当两圆内切时，连心线垂直于公切线。

当两圆外切时，连心线垂直于内公切线。

5. 公切线是指两个圆公共的切线，如果两圆在公切线同旁则称外公切线，如果两圆在公切线两旁则称内切线。

公切线上两切点间线段的长叫公切线长。

6. 如图内公切线长=-+d R r 22()（外离时）外公切线长=--d R r 22()（外离、外切、相交时）d 圆心距R 大圆半径r 小圆半径R ≥r内公切线夹角一半的正弦值==+sin αR r d 外公切线夹角一半的正弦值==-sin βR rd7. 公切线条数①内含0≤<-d R r 0条 ②内切d R r =- 1条 ③相交R r d R r -<<+ 2条 ④外切d R r =+ 3条 ⑤外离d R r >+ 4条 8. 圆的全章复习 （1）圆的基础知识 ①圆的有关概念：弦，弧，半圆，弓形，弓形高，等弧（隐含同圆等圆），弦心距，直径等。

②圆的确定圆心决定位置，半径决定大小，不共线的三点确定一个圆。

注意：作图（两边中垂线找交点），外心的位置，外心到三角形各顶点距离等③圆的对称性：轴对称，中心对称，旋转不变性（2）圆与其它图形<1>点与圆三种<2>直线与圆①一条直线与圆三种②两条直线与圆有关的角：圆周角，弦切角，圆外角等比例线段：圆幂定理等⎧⎨⎩③三条直线与圆三角形内切圆与圆外切三角形三角形内心（角平分线交点）位置永远在三角形内部到三角形各边距离相等④四条直线与圆圆外切四边形两组对边的和相等AB DC AD BC+=+<3>两圆与直线两圆外切时连心线过内公切线切点与该切线垂直。

中考经典几何题讲义系列：直线、圆和圆的位置关系目录一、考点知识梳理二、中考典例精析三、基础巩固训练四、考点训练一、考点知识梳理考点一点和圆的位置关系1．点和圆的位置关系：如果圆的半径是r，点到圆心的距离为d，那么：(1)点在圆上⇔d＝r；(2)点在圆内⇔d<r；(3)点在圆外⇔d>r.2．过三点的圆(1)经过三点的圆：①经过在同一直线上的三点不能作圆；②经过不在同一直线上的三点，有且只有一个圆．(2)三角形的外心：经过三角形各顶点的圆叫做三角形的外接圆；外接圆的圆心叫做三角形的外心；这个三角形叫做这个圆的内接三角形．(3)三角形外接圆的作法：①确定外心：作任意两边的中垂线，交点即为外心；②确定半径：两边中垂线的交点到三角形任一个顶点的距离为半径．温馨提示锐角三角形的外心在三角形内部；直角三角形的外心在斜边中点处；钝角三角形的外心在三角形的外部.考点二直线与圆的位置关系1．直线与圆的位置关系的有关概念(1)直线和圆有两个公共点时，叫做直线和圆相交，这时的直线叫做圆的割线；(2)直线和圆有唯一公共点时，叫做直线和圆相切，唯一的公共点叫做切点，这时的直线叫做圆的切线；(3)直线和圆没有公共点时，叫做直线和圆相离．2．直线和圆的位置关系的性质与判定如果⊙O的半径为r，圆心O到直线l的距离为d，那么：(1)直线l和⊙O相交⇔d<r；(2)直线l和⊙O相切⇔d＝r；(3)直线l和⊙O相离⇔d>r.考点三切线的判定与性质1．切线的判定方法(1)和圆只有一个公共点的直线是圆的切线；(2)到圆心的距离等于半径的直线是圆的切线；(3)过半径外端点并且和这条半径垂直的直线是圆的切线．2．切线的性质(1)切线的性质定理：圆的切线垂直于经过切点的半径；(2)推论1：经过切点且垂直于切线的直线必经过圆心；(3)推论2：经过圆心且垂直于切线的直线必经过切点．温馨提示1.要证的直线与圆有公共点，且存在连结公共点的半径，此时可直接根据“经过半径的外端并且垂直于这条半径的直线是圆的切线”来证明.口诀是“见半径，证垂直”.2.给出了直线与圆的公共点，但未给出过这点的半径，则连结公共点和圆心，然后根据“经过半径的外端且垂直于这条半径的直线是圆的切线”来证明.口诀是“连半径，证垂直”.3.当直线与圆的公共点不明确时，则过圆心作该直线的垂线，然后根据“圆心到直线的距离等于圆的半径，则该直线是圆的切线”来证明.口诀是“作垂线，证相等”.考点四圆与圆的位置关系设R，r为两圆的半径，d为圆心距．则(1)两圆外离⇔d>R＋r；(2)两圆外切⇔d＝R＋r；(3)两圆相交⇔R－r<d<R＋r(R≥r)；(4)两圆内切⇔d＝R－r(R>r)；(5)两圆内含⇔d<R－r(R>r)．温馨提示当两圆内含时，如果d为0，则两圆为同心圆.考点五三角形的内切圆1．与三角形内切圆有关的一些概念和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．2．三角形的内心的性质三角形的内心是三角形三条角平分线的交点，它到三边的距离相等，且在三角形内部．温馨提示确定三角形的内心，只需画出两内角平分线的交点即可；内心与三角形各顶点的连线平分三角形各内角.二、中考典例精析考点一直线与圆的位置关系如图，射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM＝MB＝2 cm，QM＝4 cm.动点P从点Q出发，沿射线QN以每秒1 cm的速度向右移动，经过t秒，以点P为圆心， 3 cm为半径的圆与△ABC的边相切(切点在边上)，请写出t可取的一切值t＝2或3≤t≤7或t＝8(单位：秒)．【思路点拨】分三种情况讨论：当⊙P与AB边相切时；当⊙P与AC边相切时；当⊙P 与BC边相切时；即当圆心P到AB，AC，BC的距离为3时对应的t值即为所求．解析：因为⊙P的半径为3，所以圆心P从Q点开始运动时，圆会与△ABC的边3次相切，而AM＝MB，AC∥QN，所以MN为正三角形ABC的中位线，MN＝2.(1)当圆与正三角形AB边相切时，如图①，则PD＝3，易得DM＝1，PM＝2，则QP ＝2，则t＝2；(2)当圆与正三角形AC边相切时，如图②，事实上圆的半径刚好等于AC与射线QN之间的距离3，所以AP1＝3，则P1M＝1，QP1＝3.同理NP2＝1，QP2＝7，而在此之间圆始终与AC边相切，所以3≤t≤7；(3)当圆与正三角形BC边相切时，如图③，则PD＝3，易得DN＝1，PN＝2，则QP ＝8，则t＝8.图③综上所述，t＝2或3≤t≤7或t＝8.方法总结根据直线上的点到圆心的距离判断直线与圆的位置关系，一定要分清这个点到圆心的距离是不是直线到圆心的垂直距离.Rt△ABC中，∠C＝90°，AC＝3 cm，BC＝4 cm，以C为圆心，r为半径作圆，若⊙C与直线AB相切，则r的值为(B)A．2 cm B．2.4 cm C．3 cm D．4 cm解析：作CD⊥AB于点D，在Rt△ABC中，∠C＝90°，AC＝3 cm，BC＝4 cm，由勾股定理，可得AB＝5(cm)．再由面积法，求得CD＝2.4(cm)，即r的值为2.4 cm.故选B.如图，△ABC中，AB＝6，AC＝8，BC＝10，D，E分别是AC，AB的中点，则以DE为直径的圆与BC的位置关系是()A．相交B．相切C．相离D．无法确定解析：∵AB＝6，AC＝8，BC＝10，AB2＋AC2＝62＋82＝100＝102＝BC2，∴△ABC是直角三角形，∠A＝90°.∵D，E分别是AC，AB的中点，∴DE＝12BC＝5，DE∥BC.过点A作AF⊥BC，垂足是F，交DE于点G，由面积公式可得AF＝6×810＝4.8，∴AG＝FG＝2.4.以DE为直径作圆，则半径为2.5,2.5＞2.4，∴以DE为直径的圆与BC相交．故选A.答案：A考点二切线的性质与判定如图，△ABC内接于⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连结AF.(1)判断AF与⊙O的位置关系，并说明理由；(2)若⊙O的半径为4，AF＝3，求AC的长．【思路点拨】(1)连结OC，由PC为切线可得OC⊥PC.由OB＝OC及OF∥BC可得∠AOF ＝∠COF，进而可证△AOF≌△COF，∠OAF＝∠OCF＝90°；(2)由AF垂直于OA，在Rt△AOF中，由OA与AF的长，利用勾股定理求出OF的长．而OA＝OC，OF为角平分线，利用三线合一得到E为AC的中点，OE垂直于AC，利用面积法求出AE的长，即可确定AC的长．解：(1)AF为⊙O的切线．理由如下：如图，连结OC，∵PC 为⊙O 的切线，∴CP ⊥OC ，∴∠OCP ＝90°.∵OF ∥BC ，∴∠AOF ＝∠B ，∠COF ＝∠OCB .∵OC ＝OB ，∴∠OCB ＝∠B ，∴∠AOF ＝∠COF .在△AOF 和△COF 中，⎩⎪⎨⎪⎧ OA ＝OC ，∠AOF ＝∠COF ，OF ＝OF ，∴△AOF ≌△COF (SAS )，∴∠OAF ＝∠OCF ＝90°.又∵点A 在⊙O 上，∴AF 为⊙O 的切线．(2)由(1)，知∠AOF ＝∠COF ，∵OA ＝OC ，∴E 为AC 的中点，即AE ＝CE ＝12AC ，OE ⊥AC . ∵OA ⊥AF ，∴在Rt △AOF 中，OA ＝4，AF ＝3，OF ＝OA 2＋AF 2＝5.∵S △AOF ＝12·OA ·AF ＝12·OF ·AE ， ∴AE ＝125，∴AC ＝2AE ＝245. 方法总结切线的证明分三种情况：一是直线与圆有公共点，且有连结公共点的半径，可证明半径与直线互相垂直，记为“有半径，证垂直”；二是直线与圆有公共点，但没有连结公共点的半径，可连结半径，证明半径与直线互相垂直，记为“连半径，证垂直”；三是没有指明直线和圆的公共点，可以过圆心作直线的垂线段，证明等于半径，记为“作垂直，证半径”.如图，已知线段OA 交⊙O 于点B ，且OB ＝AB ，点P 是⊙O 上的一个动点，那么∠OAP 的最大值是( D )A ．90°B ．60°C ．45°D ．30°如图①，△ABC 中，CA ＝CB ，点O 在高CH 上，OD ⊥CA 于点D ，OE ⊥CB于点E ，以O 为圆心，OD 为半径作⊙O .(1)求证：⊙O 与CB 相切于点E ；(2)如图②，若⊙O 过点H ，且AC ＝5，AB ＝6，连结EH ，求△BHE 的面积和tan ∠BHE 的值．解：(1)证明：∵CA ＝CB ，点O 在高CH 上，∴∠ACH ＝∠BCH .∵OD ⊥CA ，OE ⊥CB ，∴OE ＝OD ，∴⊙O 与CB 相切于点E .(2)∵CA ＝CB ，CH 是高，∴AH ＝BH ＝12AB ＝3， ∴CH ＝CA 2－AH 2＝4.∵点O 在高CH 上，⊙O 过点H ，∴⊙O 与AB 相切于H 点．由(1)得⊙O 与CB 相切于点E ，∴BE ＝BH ＝3.如图，过点E 作EF ⊥AB ，则EF ∥CH ，∴△BEF ∽△BCH ，∴BE BC ＝EF CH ，即35＝EF 4，解得EF ＝125. ∴S △BHE ＝12BH ·EF ＝12×3×125＝185. 在Rt △BEF 中，BF ＝BE 2－EF 2＝95， ∴HF ＝BH －BF ＝3－95＝65， 则tan ∠BHE ＝EF HF ＝2.考点三 圆和圆的位置关系如图，⊙O 的半径为4 cm ，直线l 与⊙O 相交于A ，B 两点，AB ＝4 3 cm ，P 为直线l 上一动点，以1 cm 为半径的⊙P 与⊙O 没有公共点，设PO ＝d cm ，则d 的范围是d ＞5cm 或2cm ≤d ＜3cm .【思路点拨】根据两圆内切和外切，求出两圆圆心距，进而得出d 的取值范围． 解析：如图，连结OP ，⊙O 的半径为4 cm ，⊙P 的半径为1 cm ，则当d ＝5时，两圆外切；当d ＝3时，两圆内切．过点O 作OD ⊥AB 于点D ，OD ＝42－(23)2＝2(cm)，当点P运动到点D时，OP最小为2 cm，此时两圆没有公共点．∴以1 cm为半径的⊙P 与⊙O没有公共点时，d＞5 cm或2 cm≤d＜3 cm.方法总结判断两圆的位置关系关键是求出两圆圆心的距离以及两圆半径的和与差，然后作出比较，得出相应的结论.(2013·平凉)已知⊙O1与⊙O2的半径分别是方程x2－4x＋3＝0的两根，且圆心距O1O2＝t＋2，若这两个圆相切，则t＝2或0 .如图，⊙O1，⊙O2的圆心O1，O2在直线l上，⊙O1的半径为2 cm，⊙O2的半径为3 cm，O1O2＝8 cm.⊙O1以1 cm/s的速度沿直线l向右运动，7 s后停止运动，在此过程中，⊙O1与⊙O2没有出现的位置关系是()A．外切B．相交C．内切D．内含解析：当停止运动时，d＝8－7＝1＝3－2，此时两圆内切，且在左侧内切，∴在运动的过程中，两圆的位置关系有外切、相交、内切，但没有内含．故选D.答案：D三、基础巩固训练1．⊙O的半径为8，圆心O到直线l的距离为4，则直线l与⊙O的位置关系是(B)A．相切B．相交C．相离D．不能确定2. 如图，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO＝40°，则∠OCB 的度数为(C)A．40°B．50°C．65°D．75°3．已知⊙O1与⊙O2相交，它们的半径分别是4,7，则圆心距O1O2可能是(C) A．2 B．3 C．6 D．124．如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是(C)A．AG＝BG B．AB∥EFC．AD∥BC D．∠ABC＝∠ADC5．如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10 cm，小圆半径为6 cm，则弦AB的长为16 cm.6．如图，小圆的圆心在原点，半径为3，大圆的圆心坐标为(a,0)，半径为5.如果两圆内含，那么a的取值范围是－2<a<2.7．如图，已知P是⊙O外一点，PO交⊙O于点C，OC＝CP＝2，弦AB⊥OC，劣弧AB的度数为120°，连结PB.(1)求BC的长；(2)求证：PB是⊙O的切线．解：(1)连结OB，∵弦AB⊥OC，劣弧AB的度数为120°，∴∠COB＝60°.又∵OC＝OB，∴△OBC是正三角形，∴BC＝OC＝2.(2)证明：∵BC＝CP，∴∠CBP＝∠P.∵△OBC是正三角形，∴∠OBC＝∠OCB＝60°，∴∠CBP＝30°，∴∠OBP＝∠CBP＋∠OBC＝90°，∴OB⊥BP.∵点B在⊙O上，∴PB是⊙O的切线．8．如图，在△ABC中，以AB为直径的⊙O交BC于点P，PD⊥AC于点D，且PD 与⊙O相切．(1)求证：AB＝AC；(2)若BC＝6，AB＝4，求CD的值．解：(1)证明：连结OP，则OP＝OB，则∠B＝∠OPB.又∵PD与⊙O相切，∴OP⊥PD.又∵PD⊥AC，∴OP∥AC .∴∠C＝∠OPB，∴∠C＝∠B，∴AB＝AC.(2)已知AB＝4，∴AC＝4.连结AP.∵AB为直径，∴∠APB＝90°，即AP⊥BC.∵AB＝AC，∴P为BC的中点．∵BC＝6，∴PC＝3.∵∠DCP＝∠PCA，∠PDC＝∠APC，∴△CDP∽△CPA，∴CDPC＝PCAC，即CD3＝34，∴CD＝94.9．直线l与半径为r的⊙O相交，且点O到直线l的距离为6，则r的取值范围是(C) A．r＜6 B．r＝6 C．r＞6 D．r≥610．已知⊙O1和⊙O2的半径分别是方程x2－4x＋3＝0的两根，且两圆的圆心距等于4，则⊙O1与⊙O2的位置关系是(B)A．外离B．外切C．相交D．内切11．直线AB与⊙O相切于B点，C是⊙O与OA的交点，点D是⊙O上的动点(D与B，C不重合)，若∠A＝40°，则∠BDC的度数是()A．25°或155°B．50°或155°C．25°或130°D．50°或130°解析：如图，连结OB，当点D在优弧BC上时，∵直线AB与⊙O相切于B点，∴OB⊥BA，∴∠OBA＝90°.∵∠A＝40°，∴∠AOB＝50°，∴∠BDC＝12∠AOB＝25°；当点D在劣弧BC上时，即在D′点处，如图，∵∠BDC＋∠BD′C＝180°，∴∠BD′C＝180°－25°＝155°，∴∠BDC的度数为25°或155°.故选A.答案：A12．如图，已知⊙O1的半径为1 cm，⊙O2的半径为2 cm，将⊙O1，⊙O2放置在直线l上，如果⊙O1在直线l上任意滚动，那么圆心距O1O2的长不可能是(D)A．6 cm B．3 cm C．2 cm D．0.5 cm解析：由题意知当两圆内切时，圆心距最小，此时圆心距为1 cm，所以圆心距不可能是0.5 cm.故选D.13．如图，⊙O1，⊙O2相交于A，B两点，两圆半径分别为6 cm和8 cm，两圆的连心线O1O2的长为10 cm，则弦AB的长为()A．4.8 cm B．9.6 cm C．5.6 cm D．9.4 cm解析：如图，连结O1A，O2A，设O1O2与AB相交于点C，由题意，知O1A＝6 cm，O2A＝8 cm，O1O2＝10 cm.由勾股定理的逆定理，可得△O1O2A是直角三角形．再由圆的对称性可知，AB⊥O1O2，且AC＝BC.在Rt△O1O2A中，由面积法，可得AC＝6×810＝4.8(cm)，∴AB＝2AC＝9.6(cm)．故选B.答案：B14．如图，半圆O与等腰直角三角形两腰CA，CB分别切于D，E两点，直径FG在AB上，若BG＝2－1，则△ABC的周长为()A．4＋2 2 B．6C．2＋2 2 D．4解析：如图，连结OD，OE，∵半圆O与等腰直角三角形两腰CA，CB分别切于D，E两点，∴∠C＝∠OEB＝∠OEC＝∠ODC＝90°，∴四边形ODCE是矩形．又∵OD＝OE，∴四边形ODCE 是正方形，∴CD＝CE＝OE.∵∠A＝∠B＝45°，∴△OEB是等腰直角三角形．设OE＝r，则BE＝OG＝r，∴OB＝OG＋BG＝r＋2－1，∵OB＝2OE＝2r，∴r＋2－1＝2r，∴r＝1.∴AC＝BC＝2r＝2，AB＝2OB＝2×(1＋2－1)＝2 2.∴△ABC的周长为AC＋BC＋AB＝4＋2 2.故选A.答案：A15．如图，已知⊙O是以数轴的原点O为圆心，半径为1的圆，∠AOB＝45°，点P 在数轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设OP＝x，则x的取值范围是(C)A．－1≤x≤1B．－2≤x≤ 2C．0≤x≤ 2D．x＞2解析：当过点P的直线与⊙O相切时，有一个公共点，此时x＝2，∵OP为线段的长，∴x≥0，∴0≤x≤ 2.16．如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，O1O2＝8，若将⊙O1绕点P按顺时针方向旋转360°，在旋转过程中，⊙O1与正方形ABCD的边只有一个公共点的情况一共出现()A．3次B．5次C．6次D．7次解析：如图所示，PO1＝8－3＝5，以P为圆心，5为半径画圆P，圆P上有2个点D1与D2到边AD的距离为1，有一个点D3(直线PO2与圆P的交点)到边CD的距离为1，有2个点D 4与D 5到边BC 的距离为1，所以以这5个点为圆心，1为半径作圆，这五个圆都与正方形ABCD 的边相切且只有一个公共点，因此在旋转的过程中，⊙O 1与正方形ABCD 的边只有一个公共点的情况一共出现5次．答案：B17．如图，已知⊙O 是△ABC 的内切圆，且∠A ＝50°，则∠BOC 为115度． 解析：∵内心O 是△ABC 三条角平分线的交点，∴OB ，OC 分别平分∠ABC ，∠ACB ，∴∠BOC ＝180°－(∠OBC ＋∠OCB )＝180°－12(180°－∠A )＝180°－ 12(180°－50°)＝115°. 18． 如图，在Rt △AOB 中，OA ＝OB ＝32，⊙O 的半径为1，点P 是AB 边上的动点，过点P 作⊙O 的一条切线PQ (点Q 为切点)，则切线PQ 的最小值为22 .解析：如图，连结OP ，OQ ，∵PQ 是⊙O 的切线，∴OQ ⊥PQ .由勾股定理可知PQ 2＝OP 2－OQ 2，∴当OP ⊥AB 时，OP 最短，即PQ 最短．∵在Rt △AOB 中，OA ＝OB ＝32，∴AB ＝2OA ＝6，∴OP ＝OA ·OB AB ＝3，∴PQ ＝OP 2－OQ 2＝32－12＝2 2.19．如图，已知⊙P 的半径为2，圆心P 在抛物线y ＝12x 2－1上运动，当⊙P 与x 轴相切时，圆心P 的坐标为 (6，2)或(－6，2) ．解析：当⊙P 与x 轴相切时，有y ＝2，代入抛物线解析式得x ＝±6，所以P 的坐标为(6，2)或(－6，2)．20． 如图，在边长为3的正方形ABCD 中，⊙O 1与⊙O 2外切，且⊙O 1分别与DA ，DC 边相切，⊙O 2分别与BA ，BC 边相切，则圆心距O 1O 2为 6－3 2.解析：如图所示，分别作出经过两圆圆心和切点的两条直线，设它们交于点O，设⊙O1与⊙O2的半径分别为R，r，根据相切两圆的性质得O1O2＝R＋r，OO1＝OO2＝3－R－r，所以R＋r＝2(3－R－r)．解得R＋r＝6－3 2.21．如图，AB是⊙O的直径，D为⊙O的上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C.(1)求证：CT为⊙O的切线；(2)若⊙O的半径为2，CT＝3，求AD的长．解：(1)证明：连结OT，∵OA＝OT，∴∠OAT＝∠OTA.又∵AT平分∠BAD，∴∠DAT＝∠OAT，∴∠DAT＝∠OTA，∴OT∥AC.又∵CT⊥AC，∴CT⊥OT.又∵点T在⊙O上，∴CT为⊙O的切线．(2)过点O作OE⊥AD于点E，则点E为AD的中点，又∵CT⊥AC，∴OE∥CT，∴四边形OTCE为矩形．∵CT＝3，∴OE＝ 3.又∵OA ＝2，∴在Rt△OAE中，AE＝OA2－OE2＝22－(3)2＝1，∴AD＝2AE＝2.22．如图，在Rt△ABC中，∠ACB＝90°，AC＝6 cm，BC＝8 cm.P为BC的中点，动点Q从点P出发，沿射线PC方向以2 cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s.(1)当t＝1.2时，判断直线AB与⊙P的位置关系，并说明理由．(2)已知⊙O为△ABC的外接圆，若⊙P与⊙O相切，求t的值．解：(1)直线AB与⊙P相切．如图所示，过P作PD⊥AB，垂足为D.在Rt△ABC中，∠ACB＝90°，∵AC＝6 cm，BC＝8 cm，∴AB＝AC2＋BC2＝10(cm)．∵P为BC的中点，∴PB＝4 cm.∵∠PDB＝∠ACB＝90°，∠PBD＝∠ABC，∴△PBD∽△ABC.∴PDAC＝PBAB，即PD6＝410.∴PD＝2.4 (cm)．当t＝1.2时，PQ＝2t＝2.4(cm)，∴PD＝PQ，即圆心P到直线AB的距离等于⊙P的半径．∴直线AB与⊙P相切．(2)∵∠ACB＝90°，∴AB为△ABC的外接圆的直径．∴OB＝12AB＝5(cm)．连结OP.∵P为BC的中点，∴OP＝12AC＝3(cm)．∵点P在⊙O内部，∴⊙P与⊙O只能内切．∴5－2t＝3或2t－5＝3.∴t＝1或t＝4.∴⊙P与⊙O相切时，t的值为1或4.四、考点训练1． 两个圆的半径分别为2和3，当圆心距d ＝5时，这两个圆的位置关系是( D )A ．内含B ．内切C ．相交D ．外切2． 如图，AB 是⊙O 的弦，BC 与⊙O 相切于点B ，连结OA ，OB .若∠ABC ＝70°，则∠A 等于( B )A ．15°B ．20°C ．30°D ．70°3． 在一个圆中，给出下列命题，其中正确的是( C )A ．若圆心到两条直线的距离都等于圆的半径，则这两条直线不可能垂直B ．若圆心到两条直线的距离都小于圆的半径，则这两条直线与圆一定有4个公共点C ．若两条弦所在直线不平行，则这两条弦可能在圆内有公共点D ．若两条弦平行，则这两条弦之间的距离一定小于圆的半径4． 如图，⊙O 的半径为2，点O 到直线l 的距离为3，点P 是直线l 上的一个动点，PB 切⊙O 于点B ，则PB 的最小值是( B )A. 13B. 5 C ．3 D ．25． 如图，用邻边长分别为a ，b (a <b )的矩形硬纸板裁出以a 为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆．把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽(拼接处材料忽略不计)，则a 与b 满足的关系式是( )A ．b ＝3aB ．b ＝5＋12a C ．b ＝52a D ．b ＝2a 解析：如图，设小圆的半径为x ，则MF ＝AN ＝x ，NE ＝a 2－x ，NF ＝b 2，EF ＝a 2＋x ，由勾股定理可得(b 2)2＋(a 2－x )2＝(a 2＋x )2①，再根据小圆周长等于半圆弧长可得2πx ＝π·a 2②，联立①②，消去x ，可得b ＝2a .故选D. 答案：D6． 在同一平面内，已知线段AO ＝2，⊙A 的半径为1，将⊙A 绕点O 按逆时针方向旋转60°得到的像为⊙B ，则⊙A 与⊙B 的位置关系为外切．7． 如图，在⊙O 中，过直径AB 延长线上的点C 作⊙O 的一条切线，切点为D .若AC＝7，AB ＝4，则sin C 的值为 25.8． 如图，已知AB 是⊙O 的直径，BC ⊥AB ，连结OC ，弦AD ∥OC ，直线CD 交BA 的延长线于点E .(1)求证：直线CD 是⊙O 的切线；(2)若DE ＝2BC ，求AD ∶OC 的值．解：(1)证明：如图，连结DO ，∵AD ∥OC ，∴∠DAO ＝∠COB ，∠ADO ＝∠COD .又∵OA ＝OD ，∴∠DAO ＝∠ADO ，∴∠COD ＝∠COB .又∵CO ＝CO ，OD ＝OB ，∴△COD ≌△COB ，∴∠CDO ＝∠CBO ＝90°.又∵点D 在⊙O 上，∴CD 是⊙O 的切线．(2)∵△COD ≌△COB ，∴CD ＝CB .∵DE ＝2BC ，∴DE ＝2CD .∵AD ∥OC ，∴△EDA ∽△ECO ，∴AD OC ＝DE CE ＝23. 9． 如图，AB 为⊙O 的直径，EF 切⊙O 于点D ，过点B 作BH ⊥EF 于点H ，交⊙O于点C，连结BD.(1)求证：BD平分∠ABH；(2)如果AB＝12，BC＝8，求圆心O到BC的距离．解：(1)证明：如图，连结OD，∵EF是⊙O的切线，∴OD⊥EF.又∵BH⊥EF，∴OD∥BH，∴∠ODB＝∠DBH，而OD＝OB，∴∠ODB＝∠OBD，∴∠OBD＝∠DBH，∴BD平分∠ABH.(2)如图，过点O作OG⊥BC于点G，则BG＝CG＝4，在Rt△OBG中，OG＝OB2－BG2＝62－42＝2 5.10．已知直线PD垂直平分⊙O的半径OA于点B，PD交⊙O于点C，D，PE是⊙O 的切线，E为切点，连结AE，交CD于点F.(1)若⊙O的半径为8，求CD的长；(2)证明：PE＝PF；(3)若PF＝13，sin A＝513，求EF的长．解：(1)如图，连结OD，∵PD平分OA，OA＝8，∴OB＝4.根据勾股定理，得BD＝OD2－OB2＝4 3.∵PD⊥OA，∴CD＝2BD＝8 3.(2)证明：∵PE是⊙O的切线，∴∠PEO＝90°，∴∠PEF＝90°－∠AEO，∠PFE＝∠AFB＝90°－∠A.∵OE＝OA，∴∠A＝∠AEO，∴∠PEF＝∠PFE，∴PE＝PF.(3)如图，作PG⊥EF于点G，∵∠PFG＝∠AFB，∴∠FPG＝∠A，∴FG＝PF·sin A＝13×513＝5.∵PE＝PF，∴EF＝2FG＝10.。

九年级数学圆与圆的位置关系在我们学习数学的过程中，有些知识总是能让人拍案叫绝，比如说圆与圆之间的位置关系。

你想啊，两个圆就像两个好朋友，有时候紧紧相拥，有时候则是形同陌路。

今天咱们就来聊聊这些圆的“社交”动态，保准让你听了哈哈大笑，边学边乐。

首先呢，咱们得知道圆和圆之间的基本关系。

两个圆如果能够相交，形成两个交点，那就叫做“相交”。

这就好比是两位朋友在某个聚会上聊得火热，结果发现两个人的兴趣爱好还真是有那么一点点相似，嘿嘿，意外的发现吧。

如果这两个圆的距离刚刚好，让它们只轻轻碰了一下，那就叫做“相切”。

就像两个朋友在街上偶遇，点头致意一下，心照不宣，继续各自的旅程，既亲密又有些距离。

哦，对了，记得咱们的圆心距离和半径的关系。

圆心距小于半径之和，那就能相交；等于半径之和，那就相切；大于半径之和，嘿，那就各自飞了。

咱们得聊聊“相离”这种情况。

两圆如果完全不相交，远得像两个恋人各自生活在两个城市，联系得少之又少，那就是“相离”。

你想啊，两个圆心的距离大于半径之和，真是远得像是天涯海角，不同的生活方式，不同的爱好，没啥交集，生活就这么各自精彩。

想象一下，两个圆在画纸上悄悄地待着，互不干扰，彼此就是那种“风马牛不相及”的感觉。

再来看看特殊的情况。

比如，当两个圆的圆心重合，但半径不同，那就有点意思了。

想象一下，有个圆在外面转来转去，另一个圆在它的“肚子”里悄悄待着。

这个时候，内圆完全被外圆包裹住了，像极了朋友间的包容。

总有那么一个人，给你无条件的支持，虽然不总是被看到，但心里永远有那么一个位置。

可惜，这种情况可不是每个人都能理解的。

说到这里，咱们再来琢磨一下这些圆之间的关系的意义。

生活中，朋友之间的关系也好，爱人之间的互动也罢，都是那么复杂又简单。

有人总是希望彼此相交，有人则想要独立。

相交的朋友就像是在一起打游戏，总是能碰撞出各种火花，而相切的朋友则是在适当的时候给予彼此空间，既能相互支持，又能保留个人的独特性。

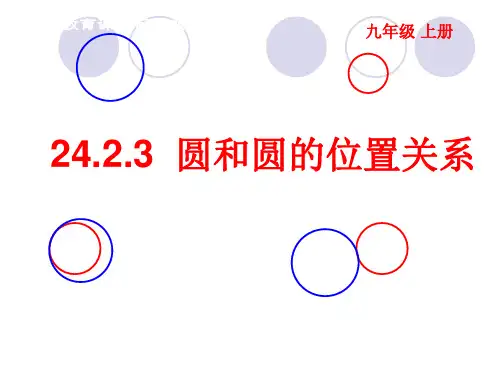
_l_( a )_( b )_( c )_..._B _A _C_D第17讲 与圆有关的位置关系（一）知识要点梳理：一、点与圆的位置关系及判定：设⊙O 的半径为r ，点P 到圆心的距离为d ，则有：①点P 在圆外⇔d>r ②点P 在圆上⇔d=r ③点P 在圆内⇔d<r 二、不在同一直线上的三个点确定一个圆也就是，经过三角形的三个顶点可以做一个圆，这个圆叫做三角形的外接圆． 外接圆的圆心是三角形三条边垂直平分线的交点，叫做这个三角形的外心． 三、直线与圆的位置关系及判定：设⊙O 的半径为r ，圆心到直线L 的距离为d ， ①直线L 和⊙O 相交⇔d<r ，如图（a ）所示； ②线L 和⊙O 相切⇔d=r ，如图（b ）所示； ③直线L 和⊙O 相离⇔d>r ，如图（c ）所示．四、切线的判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线 五、切线的性质定理: 圆的切线垂直于过切点的半径六、切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．经典例题：例1．如图，PA ，PB 分别为⊙O 的切线，AC 为直径，切点分别为A 、B ，∠P =70°，则∠C=例2．如图，已知Rt △ABC 的斜边AB=8cm ，AC=4cm ．（1）以点C 为圆心作圆，当半径为多长时，直线AB 与⊙C 相切？为什么？ （2）以点C 为圆心，分别以2cm 和4cm 为半径作两个圆，这两个圆与直线AB 分别有怎样的位置关系？ACB 例3．如图，AB 为⊙O 的直径，C 是⊙O 上一点，D 在AB 的延长线上，且∠DCB=∠A ． （1）CD 与⊙O 相切吗？如果相切，请你加以证明，如果不相切，请说明理由．（2）若CD 与⊙O 相切，且∠D=30°，BD=10，求⊙O 的半径．例4.如图：AB 是⊙O 的直径，AD 是弦，22.5DAB ∠= ，延长AB 到点C ， 使得2ACD DAB ∠=∠．(1)求证：CD 是⊙O 的切线； (2)若AB =，求BC 的长．例5.如图，在ABC ∆中，90ABC ∠=︒，O 是AB 上一点，以O 为圆心，OB 为半径的圆与AB 交于点E ，与AC 切于点D ，AD =2，AE =1，求BCD S ∆。

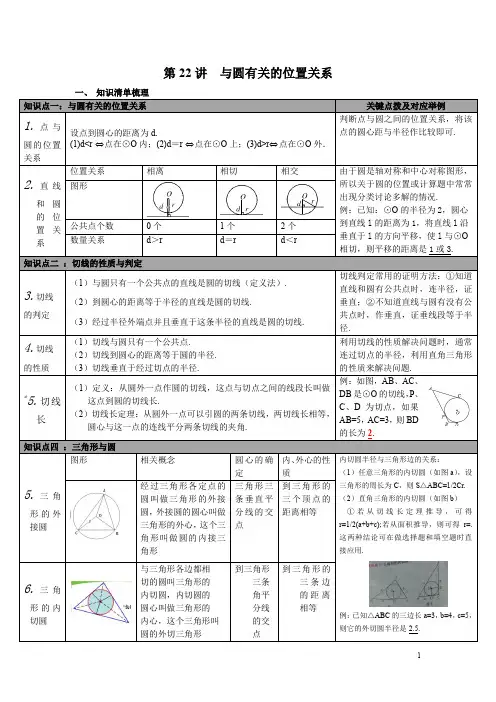
@ 第11讲与圆有关的位置关系修剧知识定位讲解用时：3分钟A、适用范围：人教版初三,根底偏上B、知识点概述：本讲义主要用于人教版初三新课,本节课我们首先学习与圆有关的三类位置关系：点与圆的位置关系、直线与圆的位置关系以及圆与圆的位置关系,重点掌握各种与圆位置关系的判断方法, 其次学习切线的有关性质与判定以及切线长定理及应用,能够结合题意证实相关切线, 最后掌握圆的外接三角形与三角形内切圆概念.本节课的重点是三类位置关系的判断方法以及切线的性质与判定定理,属于中考重点内容,也是难点之一,希望同学们能够好好学习, 扎实根底.品I识梳理讲解用时：25分钟：与圆有关的位置关系? ■(1)点与圆的位置关系点与圆的位置关系有3种,设..的半径为r,点P到圆心的距离OP=d, 那么有：.点P在圆外Od> r.点P在圆上O d=r.点P在圆内Od< r 注意：点的位置可以确定该点到圆心距离与半径的关系,反过来点到圆心距离与半径的关系可以确定该点与圆的位置关系.(2)直线与圆的位置关系直线和圆的3种位置关系：.相离：一条直线和圆没有公共点；.相切：一条直线和圆只有一个公共点,这条直线叫圆的切线,唯一的公共点叫切点；.相交：一条直线和圆有两个公共点,这条直线叫圆的割线；判断直线和圆的位置关系：.直线l和.0相交.d< r.直线l和.0相切.d=r.直线l和.0相离.d> r(3)圆与圆的位置关系.外离：两个圆没有公共点,并且每个圆上的点都在另一个圆的外部；.外切：两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部；.相交：两个圆有两个公共点；.内切：两个圆有唯一公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部；.内含：两个圆没有公共点,并且一个圆上的点都在另一个圆的内部.判断圆和圆的位置关系：.两圆外离Od>R+r；.两圆外切Od=R+r；.两圆相交.R - r<d<R+r (R>»;.两圆内切Od=R- r (R>r);.两圆内含.d<R-r (R>r).切线的性质与判定>(1)切线的性质.圆的切线垂直于经过切点的半径；.经过圆心且垂直于切线的直线必经过切点；.经过切点且垂直于切线的直线必经过圆心.如果一条直线符合以下三个条件中的任意两个, 那么它一定满足第三个条件,这三个条件是：.直线过圆心；.直线过切点；.直线与圆的切线垂直.(2)切线的判定切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线. 注意：.切线必须满足两个条件：a、经过半径的外端；b、垂直于这条半径,否那么就不是圆的切线；.切线的判定定理实际上是从“圆心到直线的距离等于半径时,直线和圆相切这个结论直接得出来的；.在判定一条直线为圆的切线时,当条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证实该线段的长等于半径,可简单的说成无交点,作垂线段,证半径〞；当条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证实该半径垂直于这条直线,可简单地说成有交点,作半径,证垂直〞.切线长定理/(1)圆的切线长定义经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长；(2)切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.三角形外接圆与内切圆(1)三角形的外接圆与外心外接圆：经过三角形的三个顶点的圆,叫做三角形的外接圆；外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点.概念说明：O接〞是说明三角形的顶点在圆上,或者经过三角形的三个顶点；.锐角三角形的外心在三角形的内部,直角三角形的外心为直角三角形斜边的中点,钝角三角形的外心在三角形的外部；.找一个三角形的外心,就是找一个三角形的两条边的垂直平■分线的交点,三角形的外接圆只有一个,而一个圆的内接三角形却有无数个.(2)三角形的内切圆与内心内切圆：与三角形各边都相切的圆叫三角形的内切圆；内心：三角形的内切圆的圆心是三角形三个内角角平分线的交点.概念说明：.任何一个三角形有且仅有一个内切圆,而任一个圆都有无数个外切三角形；.三角形内心的性质：三角形的内心到三角形三边的距离相等,三角形的内心与三角形顶点的连线平分这个内角【例题11到圆心的距离不大于半径的点的集合是〔〕.A.圆的外部B.圆的内部C.圆D.圆的内部和圆【答案】D【解析】此题考查圆的熟悉以及点与圆的位置关系,根据点和圆的位置关系,知圆的内部是到圆心的距离小于的所有点的集合；圆是到圆心的距离等于半径的所有点的集合.所以与圆心的距离不大于半径的点所组成的图形是圆的内部〔包括边界〕.应选：D.讲解用时：3分钟解题思路：根据圆是到定点距离等于定长的点的集合, 以及点和圆的位置关系即可解决. 教学建议：理解圆上的点、圆内的点和圆外的点所满足的条件.难度：3 适应场景：当堂例题例题来源：吁哈县校级月考年份：2021秋【练习11RtOABC 中,OC=90, AC=3, BC=币,CDD AB,垂足为点D,以点D为圆心作OD ,使得点A在.D外,且点B在.D内,设.D的半径为r,那么r 的取值范围是.4 4【解析】此题考查的是点与圆的位置关系,ORtOABC^, OACB=90, AC=3, BC= 41 ,OAB= 32〔 7〕24,OCDDAB, OCD=4OAD?BD=CD2,9设AD=x , BD=4 — x.解得x 一 ,4.点A在圆外,点B在圆内,一 .一一7 9r的范围是-r -4 4■讲解用时：5分钟解题思路：先根据勾股定理求出AB的长,进而得出CD的长,由点与圆的位置关系即可得出结论.教学建议：熟知点与圆的三种位置关系.难度：3 适应场景：当堂练习例题来源：普陀区一模年份：2021【例题2】I1//I2,已12之间的距离是3cm,圆心O到直线l i的距离是1cm,如果圆O 与直线l i、I2有三个公共点,那么圆O的半径为—cm【答案】2或4【解析】此题考查直线和圆的位置关系,如以下图所示,设圆的半径为r如图一所示,r - 1=3,得r=4,如下图,r+1=3,得r=2,故答案为：2或4.讲解用时：4分钟解题思路：根据题意可以画出相应的图形,从而可以解答此题.教学建议：利用数形结合的思想解答.难度：3 适应场景：当堂例题例题来源：浦东新区二模年份：2021【练习2】在△ ABC中,/C=90° , AC = 5, BC = 12,假设以C为圆心,R为半径,所作的圆与斜边AB 没有公共点,那么R 的取值范围是【答案】0 R 60或R>1213【解析】此题考查直线和圆的位置关系以及勾股定理,圆心C 到斜边AB 的距离d 60 ,13【例题3】如果两圆的半径之比为3: 2,当这两圆内切时圆心距为3,那么当这两圆相交时, 圆心距d 的取值范围是.【答案】3V d<15【解析】此题考查了圆和圆的位置与两圆的圆心距、半径的数量之间的关系,设两圆半径分别为3x, 2x,由题意,得3x -2x=3,解得x=3,那么两圆半径分别为9, 6,所以当这两圆相交时,圆心距 d 的取值范围是9-6<d<9+6,即 3Vd<15.讲解用时：3分钟解题思路：先根据比例式设两圆半径分别为 3x 、2x,根据内切时圆心距列出等 式求出半径,然后利用相交时圆心距与半径的关系求解.教学建议：熟知圆与圆的五种位置关系..当圆C 与AB 相离时,0 R当边AB 所有点都在圆内部时, 60 13, R>12, 讲解用时:解题思路: R 60或 R>12. 13 4分钟 先求出圆心C 到斜边AB 的距离d 60 ,那么当圆C 与AB 相离时, 13,当边AB 所有点都在圆内部时,R>12.教学建议：注意分类讨论. 难度：3 适应场景：当堂练习 例题来源：无 年份：2021难度：3 适应场景：当堂例题 例题来源：金山区二模 【练习3】如图,在.ABC 中,00=90 , AC=3, BC=4, OB 的半径为 BC 相交,且与OB 没有公共点,那么OA 的半径可以是〔A. 4B. 5C. 6D. 7【答案】D【解析】此题考查了圆与圆的位置关系以及勾股定理,ORtOABCJ^, OC=90°, AC=3, BC=4,.由勾股定理得 AB=5 ,OOA> OB 没有公共点,OOA 与.B 外离或内含,OOB 的半径为1,.假设外离,那么OA 半径r 的取值范围为：0<r<5-1=4,假设内含,那么OA 半径r 的取值范围为r> 1+5=6,OOA 半径r 的取值范围为：0<r<4或r>6,应选：D.讲解用时：5分钟解题思路：由RtOABC 中,OC=90, AC=3, BC=4,利用勾股定理即可求得 AB 的长,又由OA 、OB 没有公共点,可得OA 与.B 外离或内含,然后利用两圆位 置关系与圆心距d,两圆半径R, r 的数量关系间的联系求得答案.教学建议：熟练掌握两圆的位置关系.难度：4 适应场景：当堂练习 例题来源：松江区二模 年份：2021【例题4】如图,PA 、PB 切.0 于点 A 、B, PA=4, OAPB=60 ,点 E 在AB 上,且CD 切.0 于点E,交PA 、PB 于C 、D 两点,那么CD 的最小值是.【答案】83【解析】此题主要考查了切线长定理及等边三角形的性质与判断, 当CD//AB 时,切线CD 的长最小, 由切线长定理,得PA=PB=4, AC=CE,ED=DB,年份：20211,OA 与直线OL OCDP=PC+PD+CD=PC+CE+PD+DE=PC+CA+PD+DB=PA+PB=8,O O APB=60, PA=PB, O O PA更等边三角形,O O PAB=60,由于CD//AB , OOPCD0PAB=6O ,8O O PC此等边二角形,O CD=83讲解用时：7分钟解题思路：首先判断在什么情况下CD最短.利用切线长定理,说明OPCD 是等边三角形,求OPCD的周长并得结论教学建议：熟练利用切线长定理解答.难度：4 适应场景：当堂例题例题来源：资中县一模年份：2021【练习4】如图.BAC=60,半径长1的.0与.BAC的两边相切,P为.0上一动点, 以P为圆心,PA长为半径的OP交射线AB、AC于D、E两点,连接DE, 那么线段DE长度的最大值为【答案】3.3【解析】此题考查了切线的性质、等边三角形的判定与性质、勾股定理,连接AO并延长,与ED交于F点,与圆O交于P点,此时线段ED最大,连接OM, PD,可得F为ED的中点,OOBAC=60, AE=AD , OOAED为等边三角形,OAF为角平分线,即OFAD=30,在RtOAOM 中,OM=1 , 00AM=30 , O OA=2,O PD=PA=AO+OP=33在Rt.PDF中,OFDP=30, PD=3, OPF=-,2根据勾股定理得: FD=3-^ ,2贝U DE=2FD=3 J3 .讲解用时：8分钟解题思路：连接AO并延长,与圆O交于P点,当AF垂直于ED时,线段DE 长最大,设圆O与AB相切于点M,连接OM, PD,由对称性得到AF为角平分线,得到OFAD为30度,根据切线的性质得到OM垂直于AD,在直角三角形AOM中,利用30度角所对的直角边等于斜边的一半求出AO的长,由AO+OP 求出AP的长,即为圆P的半径,由三角形AED为等边三角形,得到DP为角平分线,在直角三角形PFD中,利用30度所对的直角边等于斜边的一半求出PF的长,再利用勾股定理求出FD的长,由DE=2FD求出DE的长,即为DE的最大值.教学建议：熟练掌握切线的性质是解此题的关键.难度：4适应场景：当堂练习例题来源：鄂州一模年份：2021【例题5】如图,00的半径为6, OABC是.0的内接三角形,连接假设.BAC£ BOC=180 ,那么弦BC的长为.【答案】6 3【解析】此题考查了三角形的外接圆与外心, 作OHDBC于H,如图,贝U BH=CH , 一一一一 . 一—一1一一一OOBACEBOC=180,而.BAC=1.BOC,OB、OC,2-1 -BOC£BOC=180 ,解得.BOC=120, 2OOB=OC, OO OBC=3O,OOH=1OB=3, O BH=<3 OH=3 v13 ,2OBC=2BH=6V3 .讲解用时：8分钟解题思路：作OHDBC于H,如图,利用垂径定理得到BH=CH,再根据圆周角定理可计算出OBOC=120,那么.B=30°,然后利用含30度的直角三角形三边的关系求解.教学建议：熟记三角形外接圆的圆心是三角形三条边垂直平分线的交点难度：4适应场景：当堂例题例题来源：花都区一模年份：2021【练习5】如图,RtOABC中,00=90,假设AC=4, BC=3,那么.ABC的内切圆半径r=o【答案】1【解析】此题主要考查了勾股定理以及直角三角形内切圆半径求法等知识, 如图,设.ABC 的内切圆与各边相切于D、E、F,连接OD, OE, OF,那么OED BC, OF? AB , ODD AC, 设半径为r, CD=r,OOC=90； AC=4, BC=3, OAB=5, OBE=BF=3- r, AF=AD=4 - r, 04- r+3 -r=5, CDr=1.ABC的内切圆白半径为1.讲解用时：8分钟解题思路：首先求出AB的长,再连圆心和各切点,利用切线长定理用半径表示AF和BF,而它们的和等于AB,得到关于r的方程,即可求出.教学建议：熟练掌握切线长定理和勾股定理是解题的关键.难度：4适应场景：当堂练习例题来源：大庆模拟年份：2021【例题61如图,在平面直角坐标系中,A (0, 273),动点B、C从原点O 同时出发,分别以每秒1个单位和每秒2个单位长度的速度沿x 轴正方向运动,以点A为圆心,OB的长为半径画圆；以BC为一边,在x轴上方作等边OBCD,设运动的时间为t秒,当.A与.BCD 的边BD所在直线相切时,求t的值【答案】4 ... 3 +6【解析】此题考查了切线的性质以及等边三角形的性质,作AHDBD于H,延长DB交y轴于E,如图,OOA与.BCD的边BD所在直线相切,OAH=OB=t,O O BCM等边三角形,O O DBC=60,OO OBE=60, OO OEB=30,在RtOOBE中,OE=T3OB=T3t,在Rt.AHE 中,AE=2AH=2t ,OA (0, 2<3), OOA=2j3,O2V3 +V3t=2t, Ot=4V3 +6.讲解用时：10分钟解题思路：作AHDBD于H,延长DB交y轴于E,如图,利用切线的性质得AH=OB=t ,再利用等边三角形的性质得O DBC=60 ,贝UO OBE=60 ,所以OE= V3 OB= J3t, AE=2AH=2t,从而得到2“q+ 73t=2t,然后解关于t的方程即可.教学建议：假设出现圆的切线,必连过切点的半径,得出垂直关系.难度：4 适应场景：当堂例题例题来源：滨湖区一模年份：2021【练习6】如图,直线y=x-4与x轴、y轴分别交于M、N两点,©0的半径为2,将.0以每秒1个单位的速度向右作平移运动,当移动时问秒时,直线MN恰好与圆相切【答案】4-2行或4+2行【解析】此题考查了直线与圆的位置关系、一次函数图象上点的坐标特征以及平移的性质,作EF平行于MN,且与.0切,交x轴于点E,交y轴于点F,如下图.设直线EF的解析式为y=x+b ,即x- y+b=0,OEF与.0相切,且00的半径为2,O1b2=1 X2¥5|b|,解彳#: b=2 &或b= -2立,2 2.直线EF的解析式为y=x+2,2或y=x - 272 ,.点E的坐标为(2桓,0)或(-2J2 , 0).令y=x —4 中y=0,贝U x=4,.点M (4, 0)..根据运动的相对性,且00以每秒1个单位的速度向右作平移运动,.移动的时间为4- 2 72秒或4+2 J2秒.讲解用时：10分钟解题思路：作EF平行于MN,且与.0切,交x轴于点E,交y轴于点F,设直线EF的解析式为y=x+b,由.0与直线EF相切结合三角形的面积即可得出关于b的含绝对值符号的一元一次方程,解方程即可求b值,从而得出点E的坐标,根据运动的相对性,即可得出结论.教学建议：解题的关键是求出点E、M的坐标利用运动的相对性变移圆为移直线.难度：5 适应场景：当堂练习例题来源：绥化模拟年份：2021【例题7】.0中,AC为直径,MA、MB分别切..于点A、B.(1)如图.,假设.BAC=23,求.AMB的大小；【解析】此题考查了等边三角形性质和判定、切线性质、线段垂直平分线性质、垂径定理以及平行四边形的性质和判定的应用,(1)连接OB,CDMA、MB 分别切..于A、B, OO OBM=OAM=90 ,.弧BC对的圆周角是OBAC,圆心角是OBOC,.BAC=23 ,OO BOC=2〕BAC=46 ,OO BOA=180-46o =134°OOAMB=360 -90 -90 - 134° =46°〔2〕连接AD, AB,OBD//AM, DB=AM ,.四边形BMAD是平行四边形,O BM=AD ,CDMA切..于A, OACXDAM,OBD//AM, OBD3AC,OA^O, OBE=DE, OAB=AD=BM , /[ \CDMA、MB 分别切..于A、B, / \\OMA=MB, O BM=MA=AB , “~,国①O O BMA是等边三角形,O O AMB=60 .讲解用时：15分钟解题思路：〔1〕根据切线性质求出OOBM =OAM=90 ,根据圆周角定理求出OCOB,求出.BOA,即可求出答案；〔2〕连接AB、AD,得出平行四边形,推出MB=AD ,求出等边三角形AMB , 即可得出答案.教学建议：〔2〕关键证出三角形AMB是等边三角形.难度：4 适应场景：当堂例题例题来源：安徽模拟年份：2021【练习7】在直角坐标系中,CDA与.B只有一个公共点,CDA与.B的半径分别为2和6, 点A的坐标为〔2, 1〕,点B为x轴上一点,求点B的坐标.【答案】 2 布,0、2 715,0、2 3月,0、2 36,0【解析】此题考查了圆与圆的位置关系,设B(x,0),那么圆心距d AB v(x 2)2 1 ,OOA与.B只有一个公共点OOA与.B相切当OA 与CDB 内切时,r B-r A=d,即4 J(x 2)2 1 ,解得：x1 2 vl5 , x2 2 而；当.A 与.B 外切时,r B+r A=d,即8 J(x 2)2 1 ,解得：xi 2 3万,x2 2 3".综上,点B的坐标为 2 /5,0、2 屈,0、23/,0、23/7,0.讲解用时：10分钟解题思路：当两圆内切时r B-r A=d,当两圆外切时r B+r A=d,然后再代入相关长度计算即可. 教学建议：注意分类讨论.难度：4 适应场景：当堂练习例题来源：广东模拟年份：2021课后作业【作业11圆A的半径长为4,圆B的半径长为7,它们的圆心距为d,要使这两圆没有公共点,那么d的值可以取〔〕.A. 11B. 6C. 3D. 2【答案】D【解析】此题考查了圆与圆的位置关系,假设两圆没有公共点,那么可能外离或内含,外离时的数量关系应满足d > 11;内含时的数量关系应满足0&k 3.观察选项,只有D符合题意.讲解用时：3分钟难度：3 适应场景：练习题例题来源：长宁区二模年份：2021【作业2】如图,00过正方形ABCD的顶点A、B,且与CD相切,假设正方形ABCD的边长为2,那么.0的半径为【答案】54【解析】此题主要考查了正方形、圆及直角三角形的性质,连接OE、OB,延长EO交AB于F;OE 是切点,OOEDCD,OOFOAB, OE=OB;设OB=R, WJ OF=2- R,在RtOOBF中,BF=1AB= 1 X 2=1 OB=R, OF=2- R, 2 25OR2= (2- R) 2+12,解得R=5 .4讲解用时：5分钟难度：4 适应场景：练习题例题来源：寿光市模拟年份：2021【作业3】如图,点P是.0外任意一点,PM、PN分别是.0的切线,M、N是切点.设OP与.0交于点K,那么点K是.PMN的(A.三条高线的交点B,三条中线的交点C.三个角的角平分线的交点D,三条边的垂直平分线的交点【答案】C【解析】此题考查了切线的性质、全等三角形的性质与判定、圆周角定理的应用等,连接OM、ON、MK、NK,0 PM PN分别是.0的切线,OPM=PN,OO PMN0PNM,O OM=ON 易证O POIM) O PON,OOP是.MPN的平分线,由圆周角定理可得OPMK=1 OMOK, OPNK=1 ONOK, ONMK=- O NOK, 2 2 2 OMNK=1OMOK, 2OO PMKONMKQPNK电MNK.点K是.PMN的三个角的角平分线的交点,应选：C.讲解用时：8分钟难度：4 适应场景：练习题例题来源：鼓楼区一模年份：2021【作业4】在RtOABC中,OACB=90 , BE平分.ABC, D是边AB上一点,以BD为直径的00经过点E,且交BC于点F.(1)求证：AC是.0的切线；(2)假设BF=6, 00的半径为5,求CE的长.【答案】(1)证实：连接OE.OOE=OB, OOOBE电OEB,.BE平分.ABC, OO OBEOEBC, OOEBCWOEBOOEDBC, OO OEAOC ,OO ACB=90, OO OEA=90,OAC是.0的切线；(2) CE=4【解析】此题考查了切线的判定定理、垂径定理以及勾股定理的运用,(1)证实：连接OE.OOE=OB, OO OBEOOEB,OBE平分.ABC, OO OBEOEBC, OOEBCWOEBOOEDBC, OO OEAOC ,OO ACB=90, OO OEA=90,OAC是.0的切线；(2)解：连接OE、OF,过点O作OHDBF交BF于H, 由题意可知四边形OECH为矩形,OOH=CE,OBF=6, OBH=3,在RtOBHO中,OB=5,.由勾股定理得OH=4, OCE=4讲解用时：10分钟难度：4 适应场景：练习题例题来源：聊城二模年份：2021。

O C与圆有关的位置关系（讲义）知识点睛1. 点与圆的位置关系d 表示的距离，r 表示．①点在圆外 ； A②点在圆上 ； ③点在圆内．三点定圆定理：．B注：三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆，外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．2. 直线与圆的位置关系d 表示的距离，r 表示 ．①直线与圆相交； ②直线与圆相切 ； ③直线与圆相离 ．切线的判定定理：； 切线的性质定理： ． *切线长定理：．注：与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心． *3. 圆与圆的位置关系d 表示 的距离，R 表示 ，r 表示 ．①圆与圆外离 ； ②圆与圆外切 ； ③圆与圆内切 ； ④圆与圆内含 ； ⑤圆与圆相交 ．4. 圆内接正多边形叫做圆内接正多边形，这个圆叫做该正多边形的 .正多边形的中心：；O OOO 1 O 2O 1O 2O 1 O 2O 1O 2O 2O 1与圆有关的位置关系，关键是找 d ．和 ．r ． 只要把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形．5 正多边形的半径： ； 正多边形的中心角： ； 正多边形的边心距： ．精讲精练1. 矩形ABC D 中，AB =8，BC3，点P 在AB 边上，且BP =3AP ，如果圆 P 是以点 P 为圆心，PD 为半径的圆，那么下列判断正确的是（ ） A ．点 B ，C 均在圆 P 外B ．点 B 在圆 P 外、点C 在圆 P 内C ．点 B 在圆 P 内、点 C 在圆 P 外D ．点 B ，C 均在圆 P 内2. 如图，在 5×5 的正方形网格中，一条圆弧经过 A ，B ，C 三点， 那么这条圆弧所在圆的圆心是点 ．第 2 题图第 3 题图3. 小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示， 为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（）A ．第①块B ．第②块C ．第③块D ．第④块A4. 如图，在 Rt △ABC 中，∠C =90°，∠A =60°，BC =4 cm ，以点 C 为圆心，以 3 cm 长为半径作圆，则⊙C 与 AB 的位置关系是 ． CB5. 在 Rt △ABC 中，∠C =90°，AC =3，BC =4．以 C 为圆心，R 为半径所作的圆与斜边 AB 有且只有一个公共点，则 R 的取值范围是 ． 6. 在△ABC 中，∠C =90°，AC =3 cm ，BC =4 cm ．若⊙A ，⊙B 的半径分别为 1 cm ，4 c m ，则⊙A ，⊙B 的位置关系是．A B C P Q R M②① ③④O7. 若有两圆相交于两点，且圆心距为 13 cm ，则下列哪一选项中的长度可能为此两圆的半径（ ） A ．25 cm ，40 cm B ．20 cm ，30 cm C ．1 cm ，10 cmD ．5 cm ，7 cm8. 如图，AB 是⊙O 的直径，C ，D 是⊙O 上的两点，∠CDB =20°， 过点 C 作⊙O 的切线，交 AB 的延长线于点 E ，则∠E = ．AP第 8 题图第 9 题图9. 如图，PA ，PB 是⊙O 的切线，A ，B 是切点，点 C 是劣弧 AB 上的一个动点，若∠P =40°，则∠ACB = ． 10. 如图，EB ，EC 是⊙O 的两条切线，B ，C 是切点，A ，D 是 ⊙O 上两点，如果∠E =46°，∠DCF =32°，那么∠A =．AE DFBC第 10 题图第 11 题图1. 如图，O 是正方形 ABCD 的对角线 BD 上一点，⊙O 与边 AB ，BC 都相切，点 E ，F 分别在边 AD ，DC 上．现将△DEF 沿着 EF 对折，折痕EF 与⊙O 相切，此时点D 恰好落在圆心O 处．若DE =2，则正方形 ABCD 的边长是 ．12. 如图，在⊙O 中，FC 为直径，长为 8．分别以 F ，C 为圆心， 以⊙O 的半径 R 为半径作弧，与⊙O 相交于点 E ，A 和 D ，B ， 则 A ，B ，C ，D ，E ，F 是⊙O 的六等分点，顺次连接 AB ，BC ，CD ，DE ，EF ，FA ． 过点 O 作 OG ⊥BC ，垂足为 G ，则 OG 长为．3 3 A F O M CD， ， ， 13. 如图，正六边形 ABCDEF 内接于⊙O ，半径为 4，则这个正︵六边形的边心距 OM 和BC 的长分别为（ ）A ． 23 B ． 2 3 ， C ．23D ． 2 4 B E314. 如图，⊙O 的直径为 AB ，点 C 在圆周上（异于 A ，B ）， A D ⊥CD ． （1）若 BC =3，AB =5，求 AC 的长；（2）若 AC 是∠DAB 的平分线，求证：直线 CD 是⊙O 的切线．DCAOB15. 如图，在△ABC 中，∠C =90°，点 O 在 AC 上，以 OA 为半径的⊙O 交 AB于点 D ，BD 的垂直平分线交 BC 于点 E ，交 BD 于点 F ，连接 DE ． （1）判断直线 DE 与⊙O 的位置关系，并说明理由； （2）若 AC =6，BC =8，OA =2，求线段 DE 的长．EO ADFB【参考答案】知识点睛1.点到圆心；圆的半径；d r ；d r ；d r ．不在同一条直线上的三个点确定一个圆．2.圆心O 到直线l；圆的半径；d r ；d r ；d r ．经过半径的外端且垂直于该半径的直线是圆的切线；圆的切线垂直于过切点的半径．从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．3.圆心之间；大圆半径；小圆半径．d R r ；d R r ；d R r ；0≤d R r ；R r d R r ．4.顶点都在同一圆上的正多边形；外接圆．一个正多边形的外接圆的圆心叫做这个正多边形的中心；外接圆的半径叫做正多边形的半径；正多边形每一边所对的圆心角叫做正多边形的中心角；中心到正多边形的一边的距离叫做正多边形的边心距．精讲精练1. C2.Q3. B4.相交125. 3 R ≤4 或R56.外切7. B8. 50°9. 110°10. 99°11. 2212. 2 313. D14. （1）AC=4；（2）证明略1915. （1）直线DE与⊙O相切，理由略；（2）DE4。