厦门大学大学物理第二学期期末习题集(振动与波习题)
- 格式:ppt
- 大小:2.27 MB
- 文档页数:24


大学物理振动与波练习题与答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第二章 振动与波习题答案12、一放置在水平桌面上的弹簧振子,振幅2100.2-⨯=A 米,周期50.0=T 秒,当0=t 时 (1) 物体在正方向的端点;(2) 物体在负方向的端点;(3) 物体在平衡位置,向负方向运动; (4) 物体在平衡位置,向正方向运动。
求以上各种情况的谐振动方程。
【解】:π=π=ω45.02 )m ()t 4cos(02.0x ϕ+π=, )s /m ()2t 4cos(08.0v π+ϕ+ππ=(1) 01)cos(=ϕ=ϕ,, )m ()t 4cos(02.0x π=(2) π=ϕ-=ϕ,1)cos(, )m ()t 4cos(02.0x π+π=(3) 21)2cos(π=ϕ-=π+ϕ, , )m ()2t 4cos(02.0x π+π= (4) 21)2cos(π-=ϕ=π+ϕ, , )m ()2t 4cos(02.0x π-π=13、已知一个谐振动的振幅02.0=A 米,园频率πω4=弧度/秒,初相2/π=ϕ。
(1) 写出谐振动方程;(2) 以位移为纵坐标,时间为横坐标,画出谐振动曲线。
【解】:)m ()2t 4cos(02.0x π+π= , )(212T 秒=ωπ=15、图中两条曲线表示两个谐振动(1) 它们哪些物理量相同,哪些物理量不同? (2) 写出它们的振动方程。
【解】:振幅相同,频率和初相不同。
虚线: )2t 21cos(03.0x 1π-π= 米实线: t cos 03.0x 2π= 米16、一个质点同时参与两个同方向、同频率的谐振动,它们的振动方程为t 3cos 4x 1= 厘米)32t 3cos(2x 2π+= 厘米试用旋转矢量法求出合振动方程。
【解】:)cm ()6t 3cos(32x π+=17、设某一时刻的横波波形曲线如图所示,波动以1米/秒的速度沿水平箭头方向传播。
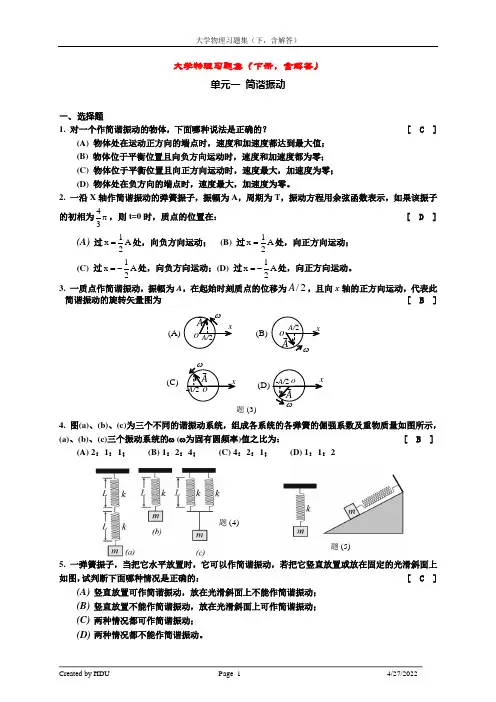
大学物理习题集(下册,含解答)单元一 简谐振动一、 选择题1. 对一个作简谐振动的物体,下面哪种说法是正确的? [ C ](A) 物体处在运动正方向的端点时,速度和加速度都达到最大值; (B) 物体位于平衡位置且向负方向运动时,速度和加速度都为零; (C) 物体位于平衡位置且向正方向运动时,速度最大,加速度为零;(D) 物体处在负方向的端点时,速度最大,加速度为零。
2. 一沿X 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,振动方程用余弦函数表示,如果该振子的初相为43π,则t=0时,质点的位置在: [ D ](A) 过1x A 2=处,向负方向运动; (B) 过1x A 2=处,向正方向运动;(C) 过1x A 2=-处,向负方向运动;(D) 过1x A 2=-处,向正方向运动。
3. 一质点作简谐振动,振幅为A ,在起始时刻质点的位移为/2A ,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为 [ B ]x o A x ω(A) A/2 ω (B) (C)(D)o ooxxxA x ω ωAxAxA/2 -A/2 -A/2 (3)题4. 图(a)、(b)、(c)为三个不同的谐振动系统,组成各系统的各弹簧的倔强系数及重物质量如图所示,(a)、(b)、(c)三个振动系统的ω (ω为固有圆频率)值之比为: [ B ](A) 2:1:1; (B) 1:2:4; (C) 4:2:1; (D) 1:1:25. 一弹簧振子,当把它水平放置时,它可以作简谐振动,若把它竖直放置或放在固定的光滑斜面上如图,试判断下面哪种情况是正确的: [ C ](A) 竖直放置可作简谐振动,放在光滑斜面上不能作简谐振动;(B) 竖直放置不能作简谐振动,放在光滑斜面上可作简谐振动; (C) 两种情况都可作简谐振动; (D) 两种情况都不能作简谐振动。
(4)题(5)题6. 一谐振子作振幅为A 的谐振动,它的动能与势能相等时,它的相位和坐标分别为: [ C ]2153(A),or ;A;(B),;A;3326623223(C),or ;A;(D),;A442332ππ±±π±±±π±ππ±±π±±±π±7. 一质点沿x 轴作简谐振动,振动方程为 10.04cos(2)3x t ππ=+(SI ),从t = 0时刻起,到质点位置在x = -0.02 m 处,且向x 轴正方向运动的最短时间间隔为 [ D ](A)s 81; (B) s 61; (C) s 41; (D) s 218. 图中所画的是两个简谐振动的振动曲线,这两个简谐振动叠加后合成的余弦振动的初相为[ C ]xtOx 1x 2(8)题(A) π23; (B) π; (C) π21 ; (D) 0二、 填空题9. 一简谐振动用余弦函数表示,振动曲线如图所示,则此简谐振动的三个特征量为: A=10cm , /6rad /s =ωπ,/3=φπ10. 用40N 的力拉一轻弹簧,可使其伸长20 cm 。
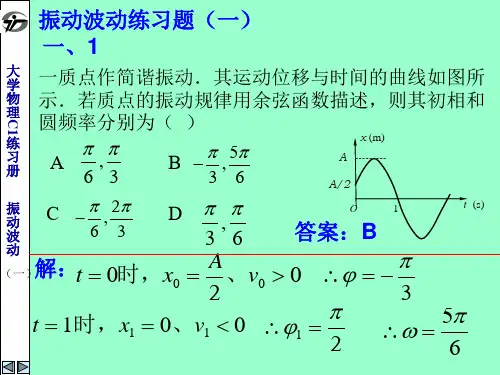

振动与波练习题2005一、填空题1.一物体作简谐振动,振动方程为x = A cos (ωt +π/ 4 )。
在t =T / 4 (T 为周期)时刻,物体的加速度为 .2.一质点沿x 轴作简谐振动,振动方程为x = 4×10-2 cos (2πt + π31) (SI) 。
从t = 0 时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为 0t =时,03πφ=;t 时刻,20x cm υ=->且43πφ所以=。
433t ππωπ∆=-=由可得0.5()2t s ππωπ∆===3.已知两个简谐振动曲线如图1所示。
x 1的位相比x 2的位相为 B 。
(A) 落后π/2 (B )超前π/2 (C) 落后π (D) 超前π4.一质点作简谐振动,周期为T 。
质点由平衡位置向X 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为2222sin(/4)sin(/4)2cos(/4)cos(/4)/4112,222dx A t A t dt T d a A t A t dt T t T A a A πυωωπωπυπωωπωπυωω=-+=-+=-+=-+====代入得=-解:由旋转矢量图可知6πϕ=∆,所以1226TTt==∆=∆ππωϕ5.一平面简谐波,沿x轴负方向传播。
圆频率为ω,波速为u 。
设t=T/4时刻的波形如图2所示,则该波的表达式为。
由t = 0的旋转矢量图可知:y0=-A,φπ=O点振动方程cos()y A tωπ=+波动方程:cos()xy A tuωπ⎡⎤=++⎢⎥⎣⎦6.当机械波在媒质中传播时,一媒质质元的最大变形量发生在位置处。
平衡位置处7.如图3所示两相干波源S1和S2相距λ/4,(λ为波长)S1的位相比S2的位相超前π/2,在S1,S2的连线上,S1外侧各点(例如P点)两波引起的两谐振动的位相差是.解:P点情况()21211222()2242r r S P S Pπππϕϕλλλπππλ---+=+=+=8.一质点作简谐振动。

1. 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ⨯10-2 m 。
假如使物体上下振动,且规定向下为正方向。
〔1〕t =0时,物体在平衡位置上方8.0 ⨯10-2 m处,由静止开始向下运动,求运动方程。
〔2〕t = 0时,物体在平衡位置并以0.60m/s 的速度向上运动,求运动方程。
题1分析:求运动方程,也就是要确定振动的三个特征物理量A 、ω,和ϕ。
其中振动的角频率是由弹簧振子系统的固有性质〔振子质量m 与弹簧劲度系数k 〕决定的,即m k /=ω,k 可根据物体受力平衡时弹簧的伸长来计算;振幅A 和初相ϕ需要根据初始条件确定。
解:物体受力平衡时,弹性力F 与重力P 的大小相等,即F = mg 。
而此时弹簧的伸长量m l 2108.9-⨯=∆。
如此弹簧的劲度系数l mg l F k ∆=∆=//。
系统作简谐运动的角频率为1s 10//-=∆==l g m k ω〔1〕设系统平衡时,物体所在处为坐标原点,向下为x 轴正向。
由初始条件t = 0时,m x 210100.8-⨯=,010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ;应用旋转矢量法可确定初相πϕ=1。
如此运动方程为])s 10cos[()m 100.8(121π+⨯=--t x〔2〕t = 0时,020=x ,120s m 6.0-⋅=v ,同理可得m 100.6)/(22202022-⨯=+=ωv x A ,2/2πϕ=;如此运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2.某振动质点的x -t 曲线如下列图,试求:〔1〕运动方程;〔2〕点P 对应的相位;〔3〕到达点P 相应位置所需要的时间。
题2分析:由运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。
此题就是要通过x -t 图线确定振动的三个特征量量A 、ω,和0ϕ,从而写出运动方程。
曲线最大幅值即为振幅A ;而ω、0ϕ通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比拟方便。
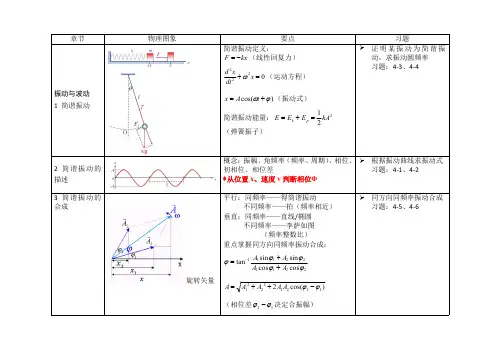

振动和波一、选择题1.(3分,答D )已知一平面简谐波的表达式为cos()y A at bx =-(,a b 为正值常量),则 (A )波的频率为a (B )波的传播速度为/b a (C )波长为/b π (D )波的周期为2/a π2.(本题3分,答B )一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[]3. (3分,答B )一质点在x 轴上作简谐振动,振幅A =4cm ,周期T =2s ,其平衡位置取作坐标原点,若t =0时刻质点第一次通过x =-2cm 处,且向x 轴负方向运动,则质点第二次通过x =-2cm 处的时刻为(A) 1s (B) (2/3)s (C)(4/3)s (D) 2s4. (3分,答D )一劲度系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为T 1.若将此弹簧截去一半的长度,下端挂一质量为m 21的物体,则系统振动周期T 2等于 (A) 2 T 1 (B) T 1(C)T 12/ (D) T 1 /2 (E) T 1 /45.(本题3分,答A )轴一简谐波沿Ox 轴正方向传播,t = 0 时刻的波形曲线如图所示,已知周期为 2 s ,则 P 点处质点的振动速度v 与时间t 的关系曲线为:6.(3分,答B )一平面简谐波在弹性媒质时,某一时刻媒质中某质元在负最大位移处,则它的能量是(A ) 动能为零 势能最大 (B )动能为零 势能为零 (C ) 动能最大 势能最大 (D )动能最大 势能为零v (m/s)O 1 t (s)ωA(C)· v (m/s)O1 t (s)ω A(A)·1 v (m/s)t (s)(D)O-ω A1 v (m/s) t (s)-ωA(B) O ··x o A x A 21 ω(A)A 21ω(B) A 21-(C) (D)o oo A 21-xxxAxAxAxω ω2O 1 y (m)x (m)t =0 A u图17.(3分,答D )沿相反方向传播的两列相干波,其波动方程为y 1=A cos2π (νt -x /λ)y 2=A cos2π (νt + x /λ) 叠加后形成的驻波中,波节的位置坐标为(A)x =±k λ.(B)x =±k λ/2 .(C)x =±(2k +1)λ/2 .(D)x =±(2k +1)λ/4 . 其中k = 0 , 1 , 2 , 3…….8.(3分,答D )如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为y =A cos(ω t+φ0),则B 点的振动方程为 (A )y =A cos[ω t-(x/u )+φ0] (B )y =A cos ω[ t+(x/u )] (C )y =A cos{ω [t-(x/u ) ]+φ0} (D )y =A cos{ω[ t+(x/u ) ]+φ0}9.(3分,答D )一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中:(A )它的动能转换成势能. (B )它的势能转换成动能. (C )它从相邻的一段质元获得能量,其能量逐渐增大. (D )它把自己的能量传给相邻的一段质元,其能量逐渐减小. 10.(3分,答B )在波长为λ的驻波中,两个相邻波腹之间的距离为 (A )λ/4 (B )λ/2 (C )3λ/4 (D )λ11.(3分,答C )某时刻驻波波形曲线如图所示,则a 、b 两点振动的相位差是 (A )0 (B )/2π (C )π (D )5/4π12.(本题3分,答B)在驻波中,两个相邻波节间各质点的振动(A )振幅相同,相位相同 (B )振幅不同,相位相同 (C )振幅相同,相位不同 (D )振幅不同,相位不同 二、填空题1. (3分)已知一个简谐振动的振幅A=2cm, 角频率14s ωπ-=,以余弦函数表达式运动规律时的A -Ayxλ λ/2O ··a b · · · · · · · · ··x 2A A/2x 1初相12φπ=,试画出位移和时间的关系曲线(振动图线) 2.(4分)两个简谐振动方程分别为x 1=Acos(ω t ) ;x 2=Acos(ω t +π/3) 在同一坐标上画出两者的x-t 曲线.3. (3分)有两相同的弹簧,其劲度系数均为k .(1)把它们串联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为;(2)把它们并联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为.[答案:(1)22m k π,(2)22mkπ] 4.(4分)一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的劲度系数,振子的振动频率.[答案:2210N/m,1.6Hz ⨯]5.(3分)一平面机械波沿x =-1m 轴负方向传播,已知处质点的振动方程cos()y A t ωϕ=+,若波速为u ,求此波的波函数.[答案:cos{[(1)/]}y A t x u ωϕ=+++]6.(3分)一作简谐振动的振动系统,振子质量为2kg ,系统振动频率为1000Hz ,振幅为0.5cm ,则其振动能量为.(答案:29.9010J ⨯ )7.(3分)两个同方向同频率的简谐振动211310cos(),3x t ωπ-=⨯+221410cos()(SI)6x t ωπ-=⨯-,它们的合振幅是. (答案:2510m -⨯ )8.(3分)一平面简谐波沿Ox 轴正方向传播,波动表达式为cos[(/)/4]y A t x u ωπ=-+,则1x L =处质点的振动方程是;2x L =-处质点的振动和1x L =处质点的振动相位差为21φφ-=. (答案:1cos[(/)/4]y A t L u ωπ=-+,12()/L L u ω+)9.(5分)一余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在该时刻的运动方向.A 向下 ,B 向上 ,C 向上.10. (本题4分)一平面简谐波的表达式cos (/)cos(/)y A t x u A t x u ωωω=-=-其中/x u 表示,/x u ω表示,y 表示.[答案:波从坐标原点传至x 处所需时间(2分),x 处质点此原点处质点滞后的相位(1分),t 时刻x 处质点的振动位移(1分)]11. (本题3分)如图所示,两相干波源S 1和S 2相距为3λ/4,λ为波长,设两波在S 1 S 2连O Cyxu · · · A B线上传播,它们的振幅都是A ,并且不随距离变化,已知在该直线上S 1左侧各点的合成波强度为其中一个波强度的4倍,则两波源应满足的相位条件是__π/2_ 12. (3分)一驻波的表达式为y =2A cos(2πx/λ) cos(2πνt ),两个相邻波 腹之间的距离是.(答案:λ/2) 三、计算题1. (5分)一质点作简谐运动,其振动方程为110.24cos()()23x t SI ππ=+,试用旋转矢量法求出质点由初始状态运动到x =-0.12 m ,v <0的状态所经过的最短时间. 解:旋转矢量如图所示.图3分 由振动方程可得π21=ω,π=∆31φ1分667.0/=∆=∆ωφt s 1分2(本题10分)一质量m =0.25kg 的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点,弹簧的劲度系数k =25N/m.(1)求振动的周期T 和频率ω. (2)如果振幅A =15cm ,t =0时物体位于x =7.5cm 处,且物体沿x 轴反方向运动,求初速度v 0及初相φ.(3)写出振动的数值表达式. 解:(1)12/10k m s ωπ-== (2分)2/0.63T s πω== (1分)(2) A=15cm , 在t =0时,07.5cm x =,00v < 由2200(/)A x v ω=+得2200 1.3m/s v A x ω=--=- (2分)100(/)/3/3tg v x φωππ-=-=或400,/3x φπ>∴=(3分)(3)21510cos(10/3)(SI)x t π-=⨯+(2分)3.(10分)在一轻弹簧下端悬挂0100g m =砝码时,弹簧伸长8cm. 现在这根弹簧下端悬挂0250g m =物体,构成弹簧振子,将物体从平衡位置向下拉动4cm ,并给以向上的21cm/s 的初速度(令这时t=0).选x 轴向下,求振动方程的数值式.解:k = m 0g / ∆l 25.12N/m 08.08.91.0=⨯=N/mx (m) ωωπ/3π/3t = 0t0.12 0.24 -0.12 -0.24 OAAO xS 1S 211s 7s 25.025.12/--===m k ω(2分) 5cm )721(4/2222020=+=+=ωv x A cm (2分) 4/3)74/()21()/(tg 00=⨯--=-=ωφx v ,φ = 0.64 rad (3分))64.07cos(05.0+=t x (SI) (1分)4.(8分)在一竖直轻弹簧的下端悬挂一小球,弹簧被拉长0 1.2cm l =而平衡.再经拉动后,该小球在竖直方向作振幅为2cm A =的振动,试证此振动为简谐振动;选小球在正最大位移处开始计时,写出此振动的数值表达式.解:设小球的质量为m ,则弹簧的劲度系数(图参考上题)0/k mg l = 选平衡位置为原点,向下为正方向. 小球在x 处时,根据牛顿第二定律得202()d x mg k l x m dt -+=将k 代入整理后得 220d x g x dt l =-所以振动为简谐振动,其角频率为0/28.589.1(rad/s)g l ωπ===(5分)设振动表达式为 c o s ()x A t ωφ=+ 由题意:t=0时,200210m0x A v -==⨯=解得:0φ=2210cos(9.1)x t π-∴=⨯m (3分)5.(10分)在一轻弹簧下端悬挂m 0=100g 的砝码时,弹簧伸长8cm,现在这根弹簧下端悬挂m =250g 的物体, 构成弹簧振子. 将物体从平衡位置向下拉动4cm,并给以向上的21cm/s 的初速度(这时t =0) ,选x 轴向下,求振动方程的数值式. 解:物体受向下的重力和向上的弹性力.k=m 0g/∆l , x 0=4×10-2m, v 0=-21×10-2m/sω=()m l g m m k Δ0==7s -1A=22020ω/v x +=5×10-2m因A cos ϕ=4×10-2m, A sin ϕ=-v 0/ω=3×10-2m,有 ϕ=0.64rad 所以x=5×10-2cos(7t +0.64) (SI)6.(本题5分)一质量为0.2kg 的质点作简谐振动,其振动方程为10.6cos(5)(SI)2x t π=-求:(1)质点的初速度;(2)质点在正向最大位移一半处所受的力.解:(1)003.0sin(5)()0, 3.0m/s 2dx v t SI t v dt π==--==(2分) (2)2F ma m x ==-ω12x A =时, 1.5N F =-(无负号扣1分) (3分) 7.(5分)一平面简谐波沿x 轴正方向传播,波速为1m/s ,在x 轴上某质点的振动频率为1Hz ,振幅为0.01m. t = 0时该质点恰好在正最大位移处,若以该质点的平衡位置为x 轴的原点. 求此一维简谐波的表达式.解. 0.01cos[2()](m)y t x =-π8.(本题10分)某质点作简谐振动,周期为2s ,振幅为0.06m ,t =0时刻,质点恰好处在负最大位移处,求(1)该质点的振动方程.(2)此振动以波速u =2m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3)该波的波长. 解:(1)振动方程 00.06cos(2/2)0.06cos()(SI)y t t ππππ=+=+3分 (2)0.06cos[((/))0.06cos[(/2))(SI)y t x u t x ππππ=-+=-+ 4分(3)波长4m uT λ==9.(10分)一列平面简谐波在以波速5m/s u =,沿x 轴正向传播,原点O 处质点的振动曲线如图所示.1)求解并画出25cm x =处质元的振动曲线 2)求解并画出3s t =时的波形曲线 解:1)原点O 处质元的振动方程为211210cos(),(SI)22y t ππ-=⨯-(2分)波的表达式 (2分)211210cos((/5)),(SI)22y t x ππ-=⨯--x =25m 处质元的振动方程21210cos(3),(SI)2y t ππ-=⨯-振动曲线如右y-t 图 (2分)2)t=3s 时的波形曲线方程2210cos(/10),(SI)y x ππ-=⨯-(2分)波形曲线见右y-x 图 (2分)10.(10分)某质点作简谐振动,周期为2s ,振幅为0.6m ,t =0时刻,质点恰好处在负最大4O2 y(cm)t (s)2位移处,求(1)该质点的振动方程;(2)此振动以波速u =2m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3)该波的波长.解:(1) 振动方程)22cos(06.00π+π=ty )cos(06.0π+π=t (SI) (3分) (2) 波动表达式])/(cos[06.0π+-π=u x t y (4分)])21(cos[06.0π+-π=x t (SI)(3) 波长4==uT λm (3分)11.(5分)如图所示,一简谐波向x 轴正向传播,波速0500/,1,u m s x m P ==点的振动方程为10.03cos(500)(SI)2y t ππ=-. (1) 按图所示坐标系,写出相应的波的表达式; (2) 在图上画出t=0时刻的波形曲线.解:(1) 2m )250/500(/===νλu m 波的表达式 ]/2)1(21500cos[03.0),(λπ--π-π=x t t x y110.03cos[500(1)2/2]0.03cos(500)(SI)22t x t x =π-π--π=π+π-π(3分)(2) t = 0时刻的波形曲线x x x y π=π-π=sin 03.0)21cos(03.0)0,( (SI) (2分)12.(10分)图示一平面余弦波在t = 0 时刻与t = 2 s 时刻的波形图(波向左传播).已知波速为u ,波的周期大于2 s ,求(1) 坐标原点处介质质点的振动方程;(2) 该波的波动表达式. 解:(1) 比较t = 0 时刻波形图与t = 2 s 时刻波形图,可知此波向左传播.在t = 0时刻,O 处质点φcos 0A =,φωsin 00A -=<v ,故2πφ-= 又t = 2 s ,O 处质点位移为)24cos(2/ππ-=νA A 所以244πππ-=-ν,ν = 1/16 Hz 振动方程为)28/cos(0ππ-=t A y (SI)(2) 波速u = 20 /2 m/s = 10 m/s,波长λ = u /ν = 160 m 波动表达式]21)16016(2cos[π-+π=x t A y (SI) x (m)uP y (m)O-2-112-0.030.03x (m)O160A y (m)8020t =0t =2 s2A。
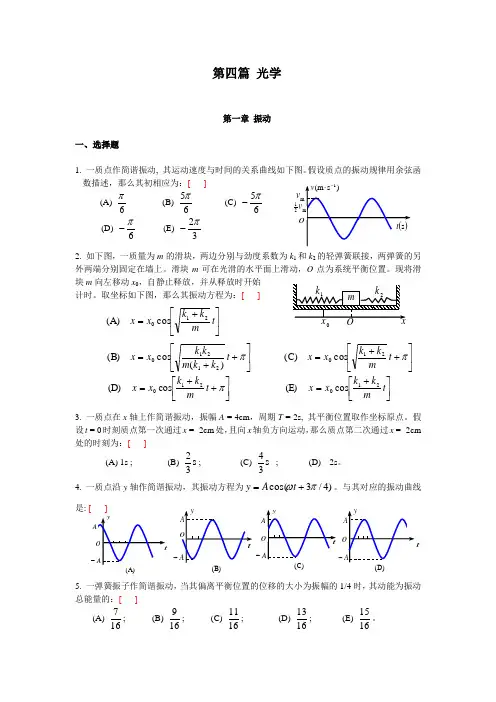
第四篇 光学第一章 振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。
假设质点的振动规律用余弦函数描述,那么其初相应为:[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图,一质量为m 的滑块,两边分别与劲度系数为k 1和k 2的轻弹簧联接,两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动,O 点为系统平衡位置。
现将滑块m 向左移动x0,自静止释放,并从释放时开始计时。
取坐标如下图,那么其振动方程为:[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动,振幅A = 4cm ,周期T = 2s, 其平衡位置取作坐标原点。
假设t = 0时刻质点第一次通过x = -2cm 处,且向x 轴负方向运动,那么质点第二次通过x = -2cm 处的时刻为:[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。
4. 一质点沿y 轴作简谐振动,其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的:[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。
(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线,假设 这两个简谐振动可叠加,那么合成的余弦振动 的初相为: [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ,0=t 时的初位移为0.04m, s -1,那么振幅A = ,初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动,经过0.5s 后,第二个振子才从正方向的端点开始运动,那么这两振动的相位差为 。

一、选择题:1.3001:把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ [ ]2.3002:两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处。
则第二个质点的振动方程为:(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x [ ]3.3007:一质量为m 的物体挂在劲度系数为k 的轻弹簧下面,振动角频率为ω。
若把此弹簧分割成二等份,将物体m 挂在分割后的一根弹簧上,则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 [ ]4.3396:一质点作简谐振动。
其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦函数描述,则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 [ ]5.3552:一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去,相应的周期分别为1T '和2T '。
则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' [ ] 6.5178:一质点沿x 轴作简谐振动,振动方程为)312cos(1042π+π⨯=-t x (SI)。

大学物理-习题-简谐振动和波-学生版一.选择题《机械振动和机械波》模块习题 1. 对一个作简谐振动的物体,下面哪种说法是正确的?---------------------------------- 【C 】 (A) 物体处在运动正方向的端点时,速度和加速度都达到最大值; (B) 物体位于平衡位置且向负方向运动时,速度和加速度都为零; (C) 物体位于平衡位置且向正方向运动时,速度最大,加速度为零; (D) 物体处在负方向的端点时,速度最大,加速度为零。
2. 一个质点作简谐运动,振幅为 A,在起始时刻质点的位移为- A ,且向 x 轴正方向运动, 2 代表此简谐运动的旋转矢量为---------------------------------------------------------------------【B 】3. 一质点沿 x 轴作简谐振动,振动方程为x = 0.04 cos(2p t +1 p ) (SI),从 t = 0 时刻起, 3 到质点位置在 x = -0.02 m 处,且向 x 轴正方向运动的最短时间间隔为--------- 【D 】 1 1 1 1 (A) s ; (B) s ; (C) s ; (D) s 8 64 2 4 一弹簧振子,振动方程为x=0.1cos(πt-π/3)·m,若振子从 t=0 时刻的位置到达 x=-0.05m处,且向 X 轴负向运动,则所需的最短时间为------------------------【D 】(A)s/3;(B) 5s/3;(C) s/2;(D) 1s。
1 5. 频率为 100 Hz,传播速度为 300 m/s 的平面简谐波,波线上距离小于波长的两点振动的相位差为 p ,则此两点相距 --------------------------------------------------------------【C 】 3 (A) 2.86 m (B) 2.19 m (C) 0.5m (D) 0.25 m T 6. 一平面简谐波,沿 x 轴负方向传播,角频率为ω,波速为 u.设t = 时刻的波形如图(a) 4 所示,则该波的表达式为---------------------------------------------------------------------【】é æ x ö ùé æ x ö p ù (A)y = A cos êw ç t - u ÷ + p ú (B) y= A cos êw ç t - u ÷ + 2 ú ë è ø û ë è ø û é æx ö p ù é æ x ö ù (C)y = A cos êw ç t + u ÷ - 2ú (D)y = A cos êw ç t + u ÷ + p ú ë è ø û ë èø û 7. 在简谐波传播过程中,沿传播方向相距为l/2 ,(l为波长)的两点的振动速度必定:【A 】 (A) 大小相同,而方向相反; (B) 大小和方向均相同; (C) 大小不同,方向相同; (D) 大小不同,而方向相反。
《大学物理学》机械振动与机械波部分练习题(解答)一、选择题1.一弹簧振子,当把它水平放置时,它作简谐振动。
若把它竖直放置或放在光滑斜面上,试判断下列情况正确的是 ( C )(A )竖直放置作简谐振动,在光滑斜面上不作简谐振动; (B )竖直放置不作简谐振动,在光滑斜面上作简谐振动; (C )两种情况都作简谐振动; (D )两种情况都不作简谐振动。
2.两个简谐振动的振动曲线如图所示,则有 ( A )(A )A 超前/2π; (B )A 落后/2π; (C )B 超前/2π; (D )B 落后/2π。
3.一个质点作简谐振动,周期为T ,当质点由平衡位置向x 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的最短时间为: ( D )(A )/4T ; (B )/6T ; (C )/8T ; (D )/12T 。
4.分振动方程分别为13cos(50)4x t ππ=+和234cos(50)4x t ππ=+(SI 制)则它们的合振动表达式为: ( C )(A )5cos(50)4x t ππ=+; (B )5cos(50)x t π=;(C )115cos(50)27x t tg ππ-=++; (D )145cos(50)23x t tg ππ-=++。
5.两个质量相同的物体分别挂在两个不同的弹簧下端,弹簧的伸长分别为1l ∆和2l ∆,且1l ∆=22l ∆,两弹簧振子的周期之比T 1:T 2为 ( B )(A )2; (B )2; (C )1/2; (D )2/1。
6.一个平面简谐波沿x 轴负方向传播,波速u=10m/s 。
x =0处,质点振动曲线如图所示,则该波的表式为(A ))2202cos(2πππ++=x t y m ;-(B ))2202cos(2πππ-+=x t y m ; (C ))2202sin(2πππ++=x t y m ;(D ))2202sin(2πππ-+=x t y m 。
振动与波动题库一、选择题(每题3分)1、当质点以频率ν 作简谐振动时,它的动能的变化频率为( )(A ) 2v(B )v (C )v 2 (D )v 42、一质点沿x 轴作简谐振动,振幅为cm 12,周期为s 2。
当0=t 时, 位移为cm 6,且向x 轴正方向运动。
则振动表达式为( ) (A))(3cos 12.0ππ-=t x (B ))(3cos 12.0ππ+=t x (C ))(32cos 12.0ππ-=t x (D ))(32cos 12.0ππ+=t x3、 有一弹簧振子,总能量为E ,如果简谐振动的振幅增加为原来的两倍,重物的质量增加为原来的四倍,则它的总能量变为 ( )(A )2E (B )4E (C )E /2 (D )E /4 4、机械波的表达式为()()m π06.0π6cos 05.0x t y +=,则 ( ) (A) 波长为100 m (B) 波速为10 m·s-1(C) 周期为1/3 s (D) 波沿x 轴正方向传播 5、两分振动方程分别为x 1=3cos (50πt+π/4) ㎝ 和x 2=4cos (50πt+3π/4)㎝,则它们的合振动的振幅为( )(A) 1㎝ (B )3㎝ (C )5 ㎝ (D )7 ㎝6、一平面简谐波,波速为μ=5 cm/s ,设t= 3 s 时刻的波形如图所示,则x=0处的质点的振动方程为 ( )(A) y=2×10-2cos (πt/2-π/2) (m)(B) y=2×10-2cos (πt + π) (m)(C) y=2×10-2cos(πt/2+π/2) (m)(D) y=2×10-2cos (πt -3π/2) (m)7、一平面简谐波,沿X 轴负方向 传播。
x=0处的质点的振动曲线如图所示,若波函数用余弦函数表示,则该波的初位相为( ) (A )0 (B )π (C) π /2 (D) - π /28、有一单摆,摆长m 0.1=l ,小球质量g 100=m 。
第二章 振动与波习题答案12、一放置在水平桌面上的弹簧振子,振幅2100.2-⨯=A 米,周期50.0=T 秒,当0=t 时 (1) 物体在正方向的端点;(2) 物体在负方向的端点;(3) 物体在平衡位置,向负方向运动;(4) 物体在平衡位置,向正方向运动。
求以上各种情况的谐振动方程。
【解】:π=π=ω45.02)m ()t 4cos(02.0x ϕ+π=, )s /m ()2t 4cos(08.0v π+ϕ+ππ=(1) 01)cos(=ϕ=ϕ,, )m ()t 4cos(02.0x π=(2) π=ϕ-=ϕ,1)cos(, )m ()t 4cos(02.0x π+π= (3) 21)2cos(π=ϕ-=π+ϕ, , )m ()2t 4cos(02.0x π+π= (4) 21)2cos(π-=ϕ=π+ϕ, , )m ()2t 4cos(02.0x π-π=13、已知一个谐振动的振幅02.0=A 米,园频率πω4=弧度/秒,初相2/π=ϕ。
(1) 写出谐振动方程;(2) 以位移为纵坐标,时间为横坐标,画出谐振动曲线。
【解】:)m ()2t 4cos(02.0x π+π= , )(212T 秒=ωπ=15、图中两条曲线表示两个谐振动(1) 它们哪些物理量相同,哪些物理量不同?(2) 写出它们的振动方程。
【解】:振幅相同,频率和初相不同。
虚线: )2t 21cos(03.0x 1π-π= 米 实线: t cos 03.0x 2π= 米16、一个质点同时参与两个同方向、同频率的谐振动,它们的振动方程为t 3cos 4x 1= 厘米)32t 3cos(2x 2π+= 厘米 试用旋转矢量法求出合振动方程。
【解】:)cm ()6t 3cos(32x π+=17、设某一时刻的横波波形曲线如图所示,波动以1米/秒的速度沿水平箭头方向传播。
(1) 试分别用箭头表明图中A 、B 、C 、D 、E 、F 、H 各质点在该时刻的运动方向;(2) 画出经过1秒后的波形曲线。
第4章 振动与波动填空题(1)一质点在X 轴上作简谐振动,振幅A =4cm ,周期T =2s ,其平衡位置取作坐标原点。
若t =0时质点第一次通过x =-2cm 处且向x 轴负方向运动,则质点第二次通过x =-2cm 处的时刻为__ __s 。
[答案:23s ](2)一水平弹簧简谐振子的振动曲线如题4.2(2)图所示。
振子在位移为零,速度为-ωA 、加速度为零和弹性力为零的状态,对应于曲线上的____________点。
振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力为-KA 的状态,则对应曲线上的____________点。
习题4.2(2) 图[答案:b 、f ; a 、e](3)一质点沿x 轴作简谐振动,振动范围的中心点为x 轴的原点,已知周期为T ,振幅为A 。
(a )若t=0时质点过x=0处且朝x 轴正方向运动,则振动方程为x=___________________。
(b )若t=0时质点过x=A/2处且朝x 轴负方向运动,则振动方程为x=_________________。
[答案:cos(2//2)x A t T ππ=−; cos(2//3)x A t T ππ=+](4)一横波的波动方程是))(4.0100(2sin 02.0SI x t y −=π,则振幅是____,波长是____,频率是____,波的传播速度是____。
[答案:0.02;2.5;100;250/m m Hz m s ](5)产生机械波的条件是 和 。
[答案:波源;有连续的介质](6)两列波叠加产生干涉现象必须满足的条件是 , 和 。
[答案:频率相同,振动方向相同,在相遇点的位相差恒定。
]计算题 振动4.3 质量为kg 10103−⨯的小球与轻弹簧组成的系统,按20.1cos(8)(SI)3x t ππ=+的规律作谐振动,求:(1)振动的周期、振幅和初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差;解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,相比较则有:3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m −⋅ 51.2=1s m −⋅2.632==A a m ω2s m −⋅(2) 0.63N m m F ma ==J 1016.32122−⨯==m mv E J 1058.1212−⨯===E E E k p当p k E E =时,有p E E 2=, 即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=−=−=∆t t4.4 一质量为kg 10103−⨯的物体作谐振动,振幅为cm 24,周期为s 0.4,当0=t 时位移为cm 24+.求:(1)s 5.0=t 时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到cm 12=x 处所需的最短时间; (3)在cm 12=x 处物体的总能量. 解:由题已知 s 0.4,m 10242=⨯=−T A∴ 1s rad 5.02−⋅==ππωT又,0=t 时,0,00=∴+=φA x 故振动方程为m )5.0cos(10242t x π−⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=−t x πN102.417.0)2(10103232−−⨯−=⨯⨯⨯−=−=−=πωxm ma F方向指向坐标原点,即沿x 轴负向. (2)由题知,0=t 时,00=φ,t t =时 3,0,20πφ=<+=t v A x 故且 ∴ s 322/3==∆=ππωφt (3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222−−⨯=⨯⨯⨯===πωA m kA E4.6 题4.6图为两个谐振动的t x −曲线,试分别写出其谐振动方程.习题4.6图解:由题4.6图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2−⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题4.6图(b)∵0=t 时,35,0,2000πφ=∴>=v A x01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯= ∴ πω65=故 m t x b )3565cos(1.0ππ+=波动4.11 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10x t ππ4−),式中x ,y 以米计,t 以秒计.求:(1)绳子上各质点振动时的最大速度和最大加速度;(2)求x =0.2m 处质点在t =1s 时的位相,它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25s 时刻到达哪一点? 解: (1)将题给方程与标准式2cos()y A t x πωλ=−相比,得振幅05.0=A m ,圆频率10ωπ=,波长5.0=λm ,波速2.52u ωλυλπ===1s m −⋅.绳上各点的最大振速,最大加速度分别为ππω5.005.010max =⨯==A v 1s m −⋅222max 505.0)10(ππω=⨯==A a 2s m −⋅(2)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s 故2.0=x m ,1=t s 时的位相就是原点(0=x ),在92.008.010=−=t s 时的位相,即 2.9=φπ. 设这一位相所代表的运动状态在25.1=t s 时刻到达x 点,则825.0)0.125.1(5.22.0)(11=−+=−+=t t u x x m4.12 一列平面余弦波沿x 轴正向传播,波速为5m ·s -1,波长为2m ,原点处质点的振动曲线如题4.12图所示.(1)写出波动方程;(2)作出t =0时的波形图及距离波源0.5m 处质点的振动曲线. 解: (1)由题4.14(a)图知,1.0=A m ,且0=t 时,0,000>=v y ,∴230πφ=, 又5.225===λυuHz ,则ππυω52==习题4.12图(a)取 ])(cos[0φω+−=ux t A y , 则波动方程为30.1cos[5()]52x y t ππ=−+m(2) 0=t 时的波形如题4.12(b)图习题4.12图(b) 习题4.12图(c)将5.0=x m 代入波动方程,得该点处的振动方程为50.530.1cos[5]0.1cos(5)52y t t πππππ⨯=−+=+m 如题4.12(c)图所示.第7章静电场7.2 填空题(1)在静电场中,电势不变的区域,场强必定为 。