(完整word版)第五章第2节《探索轴对称的性质》复习题

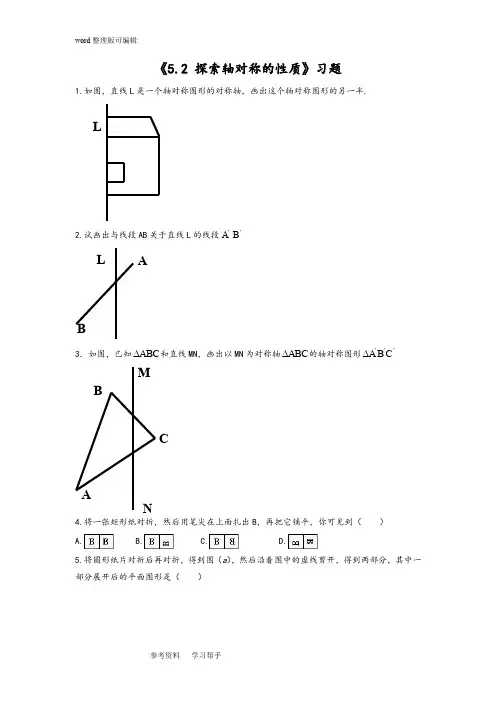
《5.2 探索轴对称的性质》习题
1.如图，直线L 是一个轴对称图形的对称轴，画出这个轴对称图形的另一半.
2.试画出与线段AB 关于直线L 的线段'A 'B
3．如图，已知ABC ∆和直线MN ，画出以MN 为对称轴ABC ∆的轴对称图形'''C B A ∆
4.将一张矩形纸对折，然后用笔尖在上面扎出B ，再把它铺平，你可见到（ ）
A. B. C. D.
5.将圆形纸片对折后再对折，得到图（a ），然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是（ ）
A
B B
N A
C
M
L
L
6.把一张正方形的白纸沿对角线对折后，得到一个等腰直角三角形，再沿斜边上的高线折叠后又得到一个更小的等腰三角形，在重叠的这张纸上剪出一个花纹，打开后得到一个图案.那么这个图案的对称轴最少有（ ）
A.1条
B.2条
C.3条
D.4条
7.如图是一个在19×16的点阵图上画出的中国结，点阵的每行及每列之间的距离都是1.请你画出中国结的对称轴，并直接写出图中阴影部分的面积.
8、猜时间，给出镜子中看到的时钟的像，问实际上的时间
.
9．你能运用学过的知识把下面这个数学中不可能的式子变为可能吗？
A B C D 图3
图a。

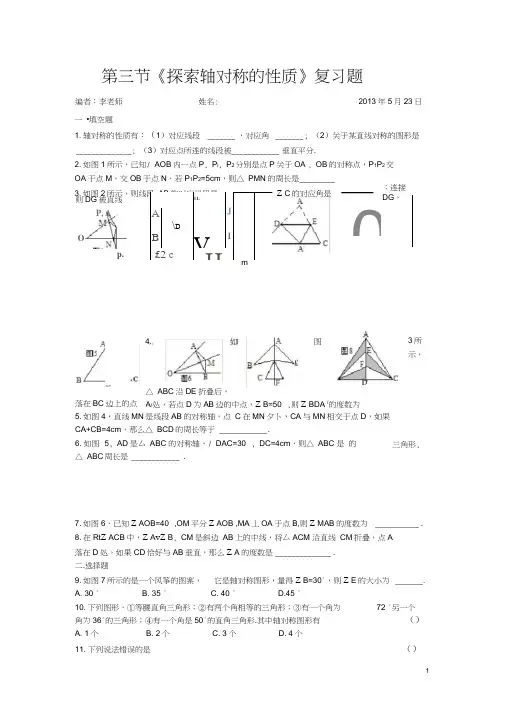
第三节《探索轴对称的性质》复习题编者：李老师 姓名: 2013年5月23日 一 •填空题 1. 轴对称的性质有：（1）对应线段 _______ ，对应角 _______ ; （2）关于某直线对称的图形是 ______________ ; （3）对应点所连的线段被____________ 垂直平分. 2. 如图1所示，已知/ AOB 内一点P , P i , P 2分别是点P 关于OA , OB 的对称点，P 1P 2交 OA 于点M ，交OB 于点N ，若P 1P 2=5cm ，则△ PMN 的周长是_________ 3. 如图2所示，则线段 AB 的对应线段是 ___________ ; Z C 的对应角是 OP, A p.EL JA\DB VI£2 c H则DG 被直线 m；连接DG ，如 4. £△ ABC 沿DE 折叠后，A /处，若点D 为AB 边的中点，Z B=50° ,则Z BDA /的度数为 图D3所 示，落在BC 边上的点 5. 如图4，直线MN 是线段AB 的对称轴，点 C 在MN 夕卜，CA 与MN 相交于点D ，如果 CA+CB=4cm ，那么△ BCD 的周长等于 ____________ . 6. 如图 △ ABC 5, AD 是厶 ABC 的对称轴，/ DAC=30° , DC=4cm ，则△ ABC 是 的周长是 ____________ . 三角形,7. 如图6，已知Z AOB=40° ,OM 平分Z AOB ,MA 丄OA 于点B,则Z MAB 的度数为 ___________ . 8. 在Rt Z ACB 中，Z A vZ B , CM 是斜边 AB 上的中线，将厶ACM 沿直线 CM 折叠，点A 落在D 处，如果CD 恰好与AB 垂直，那么Z A 的度数是 ______________ . 二.选择题 9. 如图7所示的是一个风筝的图案， 它是轴对称图形，量得Z B=30°，则Z E 的大小为 _______ . A. 30 ° B. 35 ° C. 40 ° D.45 ° 10. 下列图形，①等腰直角三角形；②有两个角相等的三角形；③有一个角为 72 °另一个 角为36°的三角形；④有一个角是50°的直角三角形.其中轴对称图形有 （） A. 1个 B. 2个 C. 3个 D. 4个 11. 下列说法错误的是（）14. 如图 8,在厶 ABC 中，AB=AC ，AD=4， 阴影部分的面积是 A. 6 B.12C. 24二•选择题15. 如图9所示，AD ABC 的角平分线, 丄AC 于点F ,试说明E , F 关于AD 对称.BC=6，点E , F 是中线AD 上的两点，则图中16. 如图10所示，在厶ABC 中，0是线段AB 的对称轴与线段 对称轴的交点，试说明/ B0C=2 / BAC .17. 如图11,已知△ ABC 中，AB=AC , D 是CB 延长线上的一点，/ ADB=60° , E 是AD 上一点，且有DE=DB .求证：AE=BE+BC .18. 如图 12,已知 AB=AC , BD 丄AC 于 D.求证：/ DBC=1/2 / BAC .A.等边三角形是轴对称图形 C.成轴对称的两条线段在对称轴同侧B.轴对称图形的对应边相等、对应角相等D.成轴对称的匠对应点的连线被对称轴垂直平分 12.两个图形关于某直线成轴对称，对应点一定在 A.这条直线的两旁 B.在这条直线上 C.在这条直线同旁 13. 下 列 说 法 正 确 的 是 () A.圆是轴对称图形，对称轴有无数条，是过圆心的直线 B.圆不是 轴对称图形 C.圆的对称轴是过圆心的直线， 有两条 D.圆的对称轴有无 D.直线两旁或直线上 数条，都是它的半径D. 30DE 丄 AB 于点 E , DFAC 的U1119. 如图13,A ABC中，AB=AC , D是底边BC上的一点，DM丄AB , DN丄AC，垂足分别为M , N.求证：DM+DN=定值（一腰上的高）.。

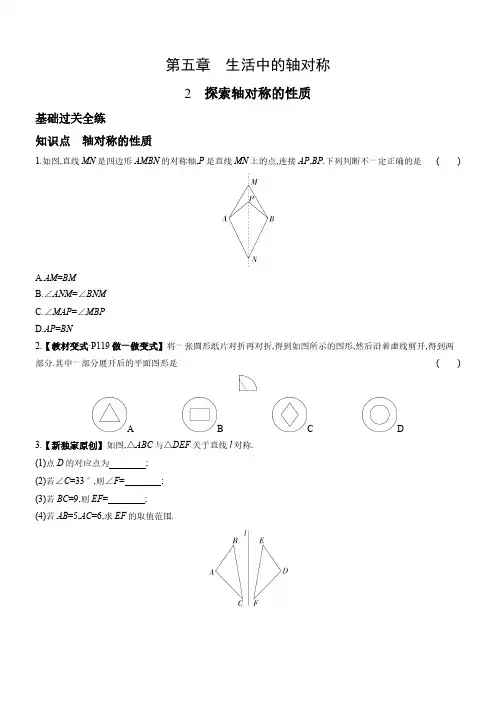
第五章　生活中的轴对称2　探索轴对称的性质基础过关全练知识点　轴对称的性质1.如图,直线MN是四边形AMBN的对称轴,P是直线MN上的点,连接AP,BP.下列判断不一定正确的是( )A.AM=BMB.∠ANM=∠BNMC.∠MAP=∠MBPD.AP=BN2.【教材变式·P119做一做变式】将一张圆形纸片对折再对折,得到如图所示的图形,然后沿着虚线剪开,得到两部分.其中一部分展开后的平面图形是( )A B C D3.【新独家原创】如图,△ABC与△DEF关于直线l对称.(1)点D的对应点为 ;(2)若∠C=33°,则∠F= ;(3)若BC=9,则EF= ;(4)若AB=5,AC=6,求EF的取值范围.能力提升全练4.【新考法】(2022河北中考改编,2,)如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )A.中线B.既是中线,又是角平分线C.高线D.角平分线5.(2022河北保定十七中期末,16,)如图,直线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )A.0B.5C.6D.76.【分类讨论思想】(2022河北张家口一模,15,)如图,平行线m,n间的距离为5,直线l与m,n分别交于点A,B,α=45°,在m上取点P(不与点A重合),作点P关于l的对称点Q.若PA=3,则点Q到n的距离为( )A.2B.3C.2或8D.3或87.【跨学科·物理】(2022山东济南高新期末,10,)如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到长方形的边时反弹,反弹时入射角等于反射角(即∠1=∠2,∠3=∠4).小球从P点出发第1次碰到长方形边上的点记为A点,第2次碰到长方形边上的点记为B点,……,第2 022次碰到长方形边上的点为图中的( )A.P点B.B点C.C点D.D点8.(2022浙江杭州余杭期中,10,)将一张细长的长方形纸条按如图所示的方式折叠,始终使得边AB∥CD,则下列关于∠1与∠2的判断正确的是( )A.∠1=∠2B.∠1=2∠2C.无论怎么折叠,∠1与∠2不可能相等D.若∠1=50°,则∠2=40°素养探究全练9.【抽象能力】如图,要在公路MN旁修建一个货物中转站,分别向A,B两个开发区运货,若要货物中转站到A,B 两个开发区的距离和最小,那么货物中转站应修建在何处?说明理由.10.【抽象能力】如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.(1)试说明:△FGC≌△EBC;(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.答案全解全析基础过关全练1.D　∵直线MN是四边形AMBN的对称轴,∴AM=BM,∠MAP=∠MBP,∠ANM=∠BNM.由于AP和BN不是对应线段,故AP不一定等于BN.故选D.2.C　根据题意知,剪去的纸片一定是一个四边形,且对角线互相垂直平分.故选C.3.解析　(1)点A.(2)∠C的对应角为∠F,∴∠F=∠C=33°.(3)9.(4)∵AB=5,AC=6,∴1<BC<11,∵EF=BC,∴1<EF<11.能力提升全练4.D　如图,由折叠的性质可知∠CAD=∠BAD,∴AD是△ABC的角平分线,故选D.5.B　如图,连接OP1,OP2,P1P2,∵点P关于直线l,m的对称点分别是点P1,P2,∴OP1=OP=2.8,OP2=OP=2.8,∵OP1+OP2>P1P2,∴0<P1P2<5.6,故选B.6.C　如图①,当点P在点A左侧时,作点P关于l的对称点Q,连接AQ.由轴对称,得QA=PA=3,∠PAQ=2α=90°,故点Q到n的距离为5-3=2;图①图②如图②,当点P在点A右侧时,同理,点Q到n的距离为5+3=8.综上所述,点Q到n的距离为2或8.故选C.7.A　如图所示,小球第6次碰到长方形边时,回到出发点P,∵2 022÷6=337,∴第2 022次碰到长方形的边时的点为图中的点P,故选A.8.D　如图,由折叠知∠1=∠BAE,∠2=∠DCF,∴∠BAB'=2∠1,∠DCD'=2∠2,∵AB∥CD,∴∠BAC=∠DCD',∴180°-2∠1=2∠2,∴2∠1+2∠2=180°,∴∠1+∠2=90°,当∠1=∠2=45°时,∠1=∠2,故选项C错误,选项A错误;当∠1=60°,∠2=30°时,才有∠1=2∠2,故选项B错误;∵∠1+∠2=90°,∠1=50°,∴∠2=90°-∠1=40°,故选项D 正确.故选D.素养探究全练9.解析　①作点A关于直线MN的对称点A';②连接BA'交MN 于点P ,则点P 就是货物中转站的位置.理由:在直线MN 上取一点P'(不与点P 重合),连接AP ,A'P',AP',BP'.因为点A ,A'关于直线MN 对称,点P ,P'在直线MN 上,所以PA =PA',P'A =P'A'.所以PA +PB =PA'+PB =A'B.在△A'P'B 中,因为A'B <P'A'+P'B =P'A +P'B ,所以PA +PB <P'A +P'B ,故点P 就是货物中转站的位置.10.解析　(1)由题意知∠B =∠G =∠BCF =∠ECG =90°,GC =BC ,所以∠GCF +∠FCE =90°,∠FCE +∠BCE =90°,所以∠GCF =∠BCE.所以△FGC ≌△EBC.(2)由题意及(1)知四边形ECGF 的面积=四边形AEFD 的面积=四边形EBCF 的面积=12四边形ABCD 的面积=12×8×4=16.。

密区教师填写 内容 考试类型 考查【 】 命题人 张媛 绝密★启用前探索轴对称的性质测试时间:15分钟一、选择题1.下列说法正确的是( )A.如果图形甲和图形乙关于直线MN 对称,则图形甲是轴对称图形B.任何一个图形都有对称轴,有的图形不止一条对称轴C.平面上两个大小、形状完全一样的图形一定关于某直线对称D.如果△ABC 和△EFG 成轴对称,那么它们的面积一定相等2.(2017内蒙古呼和浩特中考)下图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC 这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )A.(1)B.(2)C.(3)D.(4)3.篆刻是中国独特的传统艺术,篆刻出来的艺术品叫印章.印章的文字刻成凸状的称为“阳文”,刻成凹状的称为“阴文”.如图所示的“希望”即为阳文印章在纸上盖出的效果,此印章是下列选项中的(阴影表示印章中的实体部分,白色表示印章中的镂空部分)( )4.国际数学家大会的会标如图1所示,把这个图案沿图中线段剪开后,能拼成如图2所示的四个图形,则其中是轴对称图形的有( )A.1个B.2个C.3个D.4个二、填空题5.如图所示,△ABC 与△A'B'C'关于直线l 对称,则∠B 的度数为 .三、解答题6.(2015安徽中考)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).请画出△ABC 关于直线l 对称的△A 1B 1C 1.7.如图,方格纸中每个小正方形的边长均为1,四边形ABCD 的四个顶点都在小正方形的顶点上,点E 在BC 边上,且点E 在小正方形的顶点上,连接AE.(1)在图中画出△AEF,使△AEF 与△AEB 关于直线AE 对称,点F 与点B 是对称点;(2)请直接写出△AEF 与四边形ABCD 重叠部分的面积.参考横线以内不许答题参考答案一、选择题1.答案D A.如果图形甲和图形乙关于直线MN 对称,则图形甲与图形乙成轴对称,但图形甲不一定是轴对称图形,错误;B.有些图形没有对称轴,错误;C.平面上两个大小、形状完全一样的图形是全等图形,但其不一定成轴对称,错误;D.如果△ABC 和△EFG 成轴对称,那么它们全等,故它们的面积一定相等,正确.故选D.2.答案 A 根据轴对称的性质可知,序号(1)对应的三角形与△ABC 的对应点所连的线段被一条直线(对称轴)垂直平分,故选A.3.答案 D 易得“望”字应在左边,字以外的部分为镂空部分,故选D.4.答案 C 题图2所示的四个图形中是轴对称图形的有①③④,共3个.二、填空题5.答案 100°解析 ∵△ABC 与△A'B'C'关于直线l 对称,∴∠C=∠C'=30°, ∴∠B=180°-∠A -∠C=180°-50°-30°=100°.故填100°.三、解答题6.解析 △A 1B 1C 1如图所示.7.解析 (1)如图.(2)6.。

《探索轴对称的性质》同步练习一、训练平台（第1～4小题各5分，第5小题10分，共30分）1．如图1所示，△ABC中，AB=AC，AD⊥BC，•若∠BAD=•25•°，•则∠C•的大小为______．(1) (2) (3) (4)2．如图2所示，菱形ABCD中，对角线AC和BD都是其对称轴，则∠AOB=______；若∠ABO=40°，则∠ODC的大小为_______．3．如图3所示，等腰梯形ABCD中，AD=BC，DC∥AB，EF是其对称轴，若∠A=50°，则∠C的大小为_______．4．如图4所示，OP是∠AOB的平分线，OE=OF，∠OEP=110°，∠AOB=40•°，•则∠OPF的大小为_______．5．如图所示，观察下列各图形，说出哪些图形可以放在一起形成轴对称．（可以将图形上下放置或左右放置）二、提高训练（每小题10分，共50分）1．如图所示的图形有对称轴吗？若有的话，请画出来．2．画出已知图形关于直线L的对称图形．3．指出如图所示的5个图形中，哪些是轴对称图形？哪些不是？把不是轴对称图形的补画成轴对称图形．4．如图，求作一点P，使PC=PD，并且使P到∠AOB的两边距离相等．5．两个全等的三角板，可以拼出各种不同的图形，如图所示已画出其中一个三角形，请你分别补画另一个与其全等的三角形，使每个图形分别成不同的轴对称图形．三、探索发现（共9分）数的运算中会有一些有趣的对称形式，仿照等式（1）的形式填空，•并检验等式是否成立：（1）12×231=132×21；（2）12×462=______×_______；（3）18×891=______×_______；（4）24×231=______×_______．四、拓展创新（共11分）如图所示，在△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，•图中有轴对称图形吗？请找出来，哪些线段相等？哪些角相等？试求△ABC的周长．参考答案一、1．65° 2．90° 40° 3．130° 4．50° 5．（1）和（6），（2）和（4），（5）和（10），（7）和（8），（9）和（10）．二、1．甲有2条，乙有1条，画图略 2．略 3．略4．解：如图所示，连接CD，作CD的垂直平分线，交∠AOB的平分线于点P，P即为所求．5．如图所示．三、（2）264×（3）198×81 （4）132×42四、解：图中有轴对称图形，是△ADC；相等线段有：AD=CD，AE=CE；相等的角有：∠ADE=∠CDE，∠DAE=∠DCE，∠AED=∠CED；三角形ABC的周长=AB+BD+CD+AC=AB+BD+•AD+2AE=13+2×3=19（cm）．。

七年级下册第五单元5.2探索轴对称的性质课时练习一、选择题(共15题)1.下列说法正确的是( )A.两个全等的三角形一定关于某条直线对称B.关于某条直线的对称的两个三角形一定全等C.直角三角形是轴对称图形D.锐角三角形都是轴对称图形答案：B解析：解答：根据轴对称的性质，A全等三角形不一定关于某直线对称，故错；C直角三角形中，等腰直角三角形是轴对称图形，其他一般的直角三角形不是，故错；D锐角三角形不一定是轴对称图形，如三个角分别是50°、60°、70°的三角形就不是轴对称图形.故选B.分析：本题考察轴对称的性质，关键是把握住对称一定全等，但反过来不成立.2.下列说法中正确的有( )①角的两边关于角平分线对称; ②两点关于连结它的线段的中垂线对称③成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称④到直线l距离相等的点关于l对称A.1个B.2个C.3个D.4个答案：B解析：解答：根据轴对称的性质，①应该为角的两边关于“角平分线所在直线”对称; ②“两点关于连结它的线段的中垂线对称”正确；③“成轴对称的两个三角形的对应点,或对应线段,或对应角也分别成轴对称”正确；④“到直线l距离相等的点关于l对称”不正确；故选B.分析：本题容易出错的是最后一个，可以通过下图来说明：AB3.下列说法错误的是( )A.等边三角形是轴对称图形;B.轴对称图形的对应边相等,对应角相等C.成轴对称的两条线段必在对称轴一侧D.成轴对称的两个图形对应点的连线被对称轴垂直平分答案：C解析：解答：根据轴对称的性质可知，A 、B 、D 都成立，故选C.分析：本题思路的关键是考虑线段与对称轴的相对位置，可以通过下图来说明：4.观察下列平面图形：其中属于轴对称图形的有()A.1个B.2个C.3个D.4个 答案：C 解析：解答：根据轴对称的性质可知，前三个图形分别有5条、5条、3条对称轴，最后一个图形三角形内的图案没有对称轴，故选C.分析：本题思路的关键是利用轴对称的性质，不但要看图形的外部图案，还要考虑到图形的内部图案，必须沿某条直线折叠后都能够重合，才能判断是轴对称图形.5.如图所示，在桌面上坚直放置两块镜面相对的平面镜，在两镜之间放一个小凳，那么在两镜中共可得到小凳的像( )A.2个B.4个C.16个D.无数个答案：D解析：解答：∵两块镜面相对∴在每一块镜面中，都能有对方镜面的图像∴小凳在每一个镜面中都有图像∵第一镜面中的小凳都在对面镜子中有图像∴循环往复，图像无数故选D分析：本题思路的关键是利用轴对称的性质，得到镜面在对方镜子中的图像无数，相应得到小凳的图像无数，还可以通过实际操作来解决思维上的困惑. l6.如果一个三角形是轴对称图形，且有一个内角是60°,那么这个三角形是( )A.等边三角形B.等腰直角三角形C.等腰三角形D.含30°角的直角三角形答案：A解析：解答：∵这个三角形是轴对称图形∴一定有两个角相等∴这是一个等腰三角形∵有一个内角是60°∴根据有一个角是60°的等腰三角形是等边三角形得这是一个等边三角形分析：本题思路的关键是利用轴对称的性质，得到两个锐角相等，从而得到等腰三角形，再根据等边三角形的判定方法得到结论.7.以下结论正确的是( )．A．两个全等的图形一定成轴对称B．两个全等的图形一定是轴对称图形C．两个成轴对称的图形一定全等D．两个成轴对称的图形一定不全等答案：C解析：解答：根据轴对称的性质，可以判断A中说法错误，应该是轴对称的两个图形一定全等，反过来不对；B中前后矛盾，两个全等的图形，是指两个图形，而后面的轴对称图形是指一个图形；D中根据轴对称的性质可以知道，成轴对称的两个图形，一定全等，所以D错；故选C.分析：此题解决的关键是正确理解成轴对称的两个图形的关系，以及轴对称图形的意义. 8.两个图形关于某直线对称，对称点一定( )A．这直线的两旁B．这直线的同旁C．这直线上D．这直线两旁或这直线上答案：D解析：解答：这是考察对成轴对称的两个图形的位置的理解，成轴对称的两个图形的对称点，或者在对称轴上，或者在对称轴两旁.故选D.分析：此题解决的关键是正确理解成轴对称的两个图形的位置关系，思维含量低.9.轴对称图形沿对称轴对折后，对称轴两旁的部分( )A．完全重合B．不完全重合C．两者都有 D.不确定答案：A解析：解答：这是直接考察轴对称图形的意义，故选A.分析：此题解决的关键是正确理解轴对称图形的意义，思维含量低.10.下面说法中正确的是( )A.设Ａ、Ｂ关于直线MN对称，则AB垂直平分MN.B.如果△ABC≌△DNF,则一定存在一条直线MN，使△ABC与△DNF关于MN对称.C.如果一个三角形是轴对称图形，且对称轴不止一条，则它是等边三角形.D.两个图形关于MN对称，则这两个图形分别在MN的两侧.答案：C解析：解答：A中应该是直线MN垂直平分线段AB；B中错在全等，不一定对称；D中错在这两个图形不一定要在直线两侧，可以直线两侧都有.故选C.分析：此题中最不好理解的是对于D的判断，可以用下图去理解.11.已知互不平行的两条线段AB，CD关于直线l对称，AB，CD所在直线交于点P，下列结论中：①AB=CD；②点P在直线l上；③若A、C是对称点，则l垂直平分线段AC；④若B、D是对称点，则PB=PD.其中正确的结论有( )A. 1个B. 2个C. 3个D. 4个答案：D解析：解答：此题根据轴对称的性质容易得到结果，特别是对于②③④，可以通过画图来确定一下.分析：此题需要注意一下题干中的“互不平行”这个词语.否则对于②的判断就会出错. 12.下列推理中，错误的是( )A．∵∠A＝∠B＝∠C，∴△ABC是等边三角形B．∵AB＝AC，且∠B＝∠C，∴△ABC是等边三角形C．∵∠A＝60°，∠B＝60°，∴△ABC是等边三角形D．∵AB＝AC，∠B＝60°，∴△ABC是等边三角形答案：B解析：解答：A正确；B重复且条件不足；C可以得到三个角都是60°，正确；D根据有一个角是60°的等腰三角形是等边三角形可以得到.故选B.分析：本题容易出错的是看到B选项中，既有边相等，又有角相等，就判断正确.此题不难，但是容易出错.A．0 B．1 C．2 D．3答案：B解析：解答： 根据轴对称的性质知①正确；②对称轴是直线，但顶角的平分线不是直线，故错；经过该线段中点的直线还需要垂直于这条线段才正确；④全等三角形不一定关于某直线对称，故错.综上，只有①是正确的，故选B分析：本题容易出错的是对②③的判断.需要明确的是，对称轴是直线；经过线段中点的直线可以有无数条，因此必须是垂直于这条线段的才是对称轴.14．△ABC 中，AB ＝AC ，点D 与顶点A 在直线BC 同侧，且BD ＝AD ．则BD 与CD 的大小关系为( )A ．BD ＞CDB ．BD ＝CDC ．BD ＜CD D ．BD 与CD 大小关系无法确定 答案：D解析：解答： 根据图示，很明显可以看到有三种情况：(1) BD ＞CD (2) BD ＝CD (3) BD ＜CD故选D 分析：本题关键是考虑到，把点D 放在线段AD 的垂直平分线上，通过运动来研究BD 与CD 的大小关系，这样就不会出错了.15．在等腰△ABC 中，AB ＝AC ，O 为不同于A 的一点，且OB ＝OC ，则直线AO 与底边BC 的关系为( )A ．平行B ．垂直且平分C ．斜交D ．垂直不平分答案：B解析：解答：∵等腰△ABC 中，AB ＝AC∴将等腰△ABC 中折叠，使B 与C 重合，则点A 在折痕上AAA∴点A在线段BC的对称轴上∵OB＝OC∴点O在折痕上∴点O在线段BC的对称轴上∴直线AO就是线段BC的对称轴∴直线AO与底边BC垂直且平分故选B分析：本题关键是利用折叠来引入，从而利用轴对称的性质解决问题.二、填空题（共5题)16.设A、B两点关于直线MN轴对称,则_______垂直平分________.答案：直线MN｜线段AB解析：解答：∵A、B两点关于直线MN轴对称∴由轴对称的性质可得直线MN垂直平分线段AB分析：本题易错处是漏掉直线与线段这些表达线的类型的词语.17.若直角三角形是轴对称图形,则其三个内角的度数分别为________.答案：90°|45°|45°解析：解答：∵直角三角形是轴对称图形∴一定有两个角相等又直角三角形一定有一个角为90°∴相等的是两个锐角∵直角三角形的两个锐角互余∴每一个锐角为45°分析：本题思路的关键是利用轴对称的性质，得到两个锐角相等，再根据直角三角形的两个锐角互余，进而求出各角度数.18.已知在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称轴是B',如图所示,则与线段BC相等的线段是____，与线段AB相等的线段是_______和_______, 与∠B相等的角是________和_______,因此可得到∠B=________.答案：B ’C |AB ′|B B ’|∠B ’|∠BAB ’|60°解析：解答：∵以直线AC 为对称轴,点B 的对称轴是B '∴B ’C =BC ∠B ’CA =∠BCA =90° AB ’=AB =2BC∴AB ’=AB =BB ’∴∠B ’ =∠B =∠B ’AB =60°分析：本题思路的关键是利用轴对称的性质，得到对应线段相等，再根据AB =2BC ，得到一个等边三角形，进而求出各角度数.19.如图，已知点A 、B 直线MN 同侧两点， 点A ’、A 关于直线MN 对称.连接A ’B 交直线MN 于点P ,连接AP .若A ’B ＝5cm ，则AP +BP 的长为答案：5cm解析：解答：∵点A ’、A 关于直线MN 对称点P 在对称轴MN 上，∴A ’P 、AP 关于直线MN 对称∴A ’P =AP∴AP +BP = A ’P +PB =A ’B ＝5cm分析：本题思路的关键是利用轴对称的性质，得到对应线段相等，进而求出AP +BP 的长.20.如图,∠AOB 内一点P ,分别画出P 关于OA 、OB 的对称点P 1、P 2连P 1P 2交OA 于M ,交OB 于N ,若P 1P 2=5cm ,则△PMN 的周长为 . B 'C B A答案：5cm解析：解答：∵P、P1,P、P2关于OA、OB对称∴PM=P1M,PN=P2N∴△PMN的周长=P1P2∴△PMN的周长是5 cm分析：本题思路的关键是利用轴对称的性质，得到对应线段相等，进而求出△PMN的周长.三、解答题( 共5题)21.找出图中是轴对称图形的图形,并找出两对对应点、两对对应线段、两对对应角.(1)(2) (3)答案：第一个图形是轴对称图形，如图,若以NF为对称轴,则点A与点B、点M与点N、点C与点D等是对称点.线段AG与BH、CM与DN、PG与PH等是对应线段,∠A与∠B、∠C与∠D、∠AMC与∠BND等是对应角.解析：解答：如上图所示，第一个图形是轴对称图形，若以NF 为对称轴,则点A 与点B 、点M 与点N 、点C 与点D 等是对称点.线段AG 与BH 、CM 与DN 、PG 与PH 等是对应线段,∠A 与∠B 、∠C 与∠D 、∠AMC 与∠BND 等是对应角.本题解答只是回答了其中一种情况，而原来的图形，还可以以直线MN 为对称轴来进行回答.分析：本题易错点是被忽视了阴影部分.如果没有阴影，那么可以有六种不同情况；因为有了阴影部分，所以原题的解答只能有两种情况，这是需要注意的.22. 如图,△ABC 关于直线L 的轴对称图形是△DNF , 如果△ABC 的面积为6CM 2,且DN =3CM ， 求△ABC 中AB 边上的高h .答案：h=4cm解析：解答：∵△ABC 关于直线L 的轴对称图形是△DNF∴△DNF 的面积等于△ABC 的面积= 6cm 2AB =DN =3cmDN 上的高等于AB 上的高∴h=6×2÷3=4cm分析：本题思路的关键是利用轴对称图形的性质，得到面积相等，对应边相等以及对应线段相等.23.小红想在卧室放一穿衣镜，能看到自己的全身像，那么她至少应买多高(宽度适当)的穿衣镜？ A B C DA B ''答案：镜高至少为身高的一半解析：解答：如下图所示，设小红用线段AB 表示，则A 头部，通过镜子下沿D 处可以看到自己的脚的映像，而根据轴对称的性质，可以通过镜子顶端C 处看到自己的头部映像，因此，镜子调试至少需要自己身体的一半高度.分析：本题思路的关键是既要考虑到关于点的对称，又要考虑到关于线的对称.L24.下列各图都是一个汉字的一半,你能想像出它的另一半并能确定它是什么字吗?(有几个字的笔划在对称轴上)(1)答案：中(2)答案：林(3)答案：南(4)答案：京(5)答案：米解析：解答：根据汉字的对称结构来确定是哪个汉字，对于第(1)个图，思考可能是口或中，但是口没有那么扁平；故为中；第二个图左边应该也是一个木，这样原来的汉字应该是林；第三个图形，根据轴对称可以容易得到是一个南字；第四个从对称上来研究，应该左边下方也有一个点，再考虑对称轴上可能有笔画，容易得到是京字；第五个图，从对称可以得到右边有点、横、捺，可是不是我们所学过的汉字，再考虑对称轴上的笔画，可以有个竖，因此得到最后一个字是米。

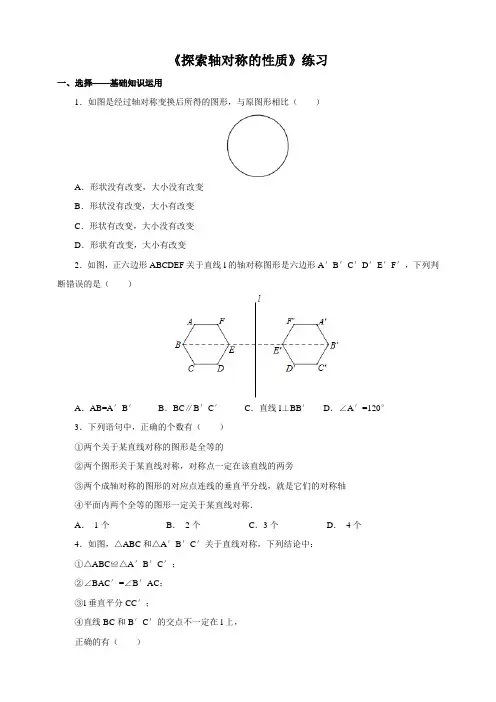
《探索轴对称的性质》练习一、选择——基础知识运用1．如图是经过轴对称变换后所得的图形，与原图形相比（）A．形状没有改变，大小没有改变B．形状没有改变，大小有改变C．形状有改变，大小没有改变D．形状有改变，大小有改变2．如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′，下列判断错误的是（）A．AB=A′B′B．BC∥B′C′C．直线l⊥BB′D．∠A′=120°3．下列语句中，正确的个数有（）①两个关于某直线对称的图形是全等的②两个图形关于某直线对称，对称点一定在该直线的两旁③两个成轴对称的图形的对应点连线的垂直平分线，就是它们的对称轴④平面内两个全等的图形一定关于某直线对称．A．1个B．2个C．3个D．4个4．如图，△ABC和△A′B′C′关于直线对称，下列结论中：①△ABC≌△A′B′C′；②∠BAC′=∠B′AC；③l垂直平分CC′；④直线BC和B′C′的交点不一定在l上，正确的有（）A．4个B．3个C．2个D．1个5．已知△ABC关于直线MN对称，则下列说法错误的是（）A．△ABC中必有一个顶点在直线MN上B．△ABC中必有两个角相等C．△ABC中，必有两条边相等D．△ABC中必有有一个角等于60°二、解答——知识提高运用6．如图，△ABC和△A′B′C′关于直线l对称，求证：△ABC≌△A′B′C′．若△ABC≌△A′B′C′，那么△ABC和△A′B′C′一定关于某条直线l对称吗？若一定请给出证明，若不一定请画出反例图。

7．如图，△ABC和△A′B′C′关于直线m对称。

（1）结合图形指出对称点．（2）连接A、A′，直线m与线段AA′有什么关系？（3）延长线段AC与A′C′，它们的交点与直线m有怎样的关系？其它对应线段（或其延长线）的交点呢？你发现了什么规律，请叙述出来与同伴交流。

8．如图所示，已知O是∠APB内的一点，点M、N分别是O点关于PA、PB的对称点，MN与PA、PB分别相交于点E、F，已知MN=5cm，求△OEF的周长。

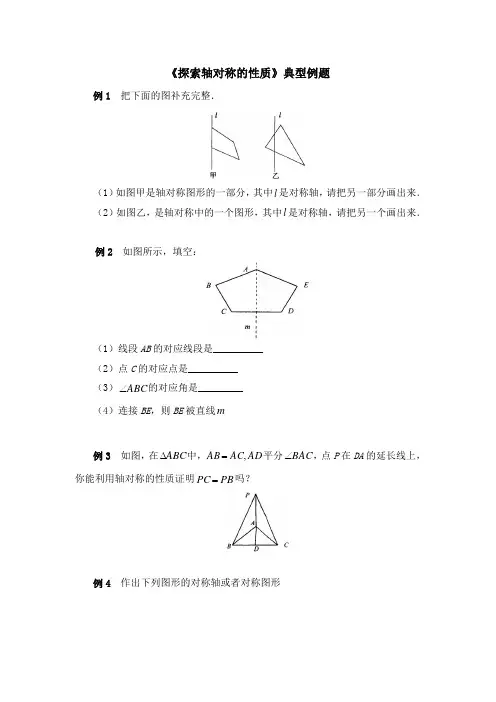
《探索轴对称的性质》典型例题例1 把下面的图补充完整．（1）如图甲是轴对称图形的一部分，其中l 是对称轴，请把另一部分画出来．（2）如图乙，是轴对称中的一个图形，其中l 是对称轴，请把另一个画出来．例2 如图所示，填空：（1）线段AB 的对应线段是__________（2）点C 的对应点是__________（3）ABC ∠的对应角是_________（4）连接BE ，则BE 被直线_____m例3 如图，在ABC ∆中，AD AC AB ,=平分BAC ∠，点P 在DA 的延长线上，你能利用轴对称的性质证明PB PC =吗？例4 作出下列图形的对称轴或者对称图形图1 图2例5分析下列图形中，哪些是轴对称图形？如果是轴对称图形，作出对称轴．（1）线段；（2）角；（3）任意三角形；（4）等腰三角形参考答案例1 作法：（1）①过A 、B 两点分别作直线l 的垂线，交l 于E 、F 两点；②截取FB B F EA A E ='=',；③连结D B A C ''、、，就是所求作图形．（2）类似于（1）可以作出（2）来．说明：我们作图的依据就是轴对称（或轴对称图形）的对称轴，垂直平分它们对应点连成的线段．例2 分析：依据轴对称或轴对称图形的性质可以得到解：分别是（1）AE （2）D （3）AED ∠ （4）垂直平分例3 分析：轴对称性质可以证明线段相等解：因为AC AB =DAC BAD ∠=∠AD AD =所以BAD ∆≌CAD ∆所以AD 垂直平分BC点P 在DA 的延长线上所以PA 、PB 关于PD 对称所以PB PC =本题的其他解法略例4 分析：在图1中给出对称轴，可以根据对称轴的性质，对应点连线被对称轴垂直平分画出另一部分，在图2中，根据轴对称的性质，很容易画出对称轴．解：如图1′，2′图1′图2′ 就是要求做的对称图形OEF直线m就是所求做的对称轴．例5分析：线段、角、等腰直角三角形是轴对称图形．解：线段的对称轴是线段AB所在的直线和它的垂直平分线．（如图1）角的对称轴是角的平分线所在的直线；（如图2）等腰直角三角形的对称轴是底边的垂直平分线．（如图3）图1 图2 图3学生每日提醒～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～励志名言：1、泰山不是垒的，学问不是吹的。

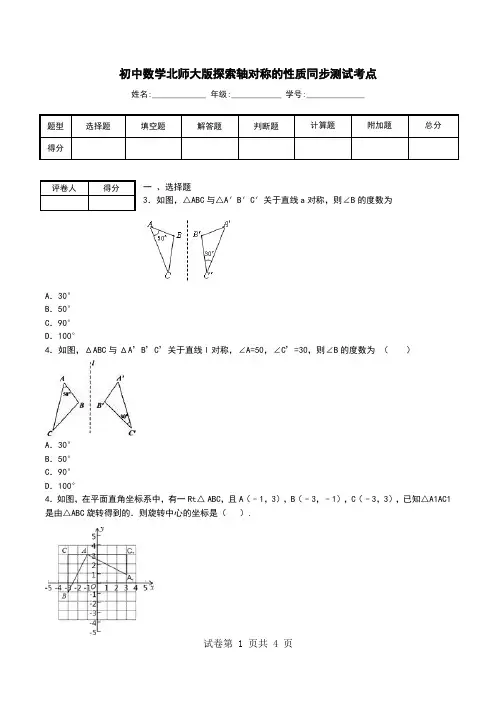
初中数学北师大版探索轴对称的性质同步测试考点姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分一、选择题3．如图，△ABC与△A′B′C′关于直线a对称，则∠B的度数为A．30°B．50°C．90°D．100°4．如图，ΔABC与ΔA’B’C’关于直线l对称，∠A=50，∠C’=30，则∠B的度数为（）A．30°B．50°C．90°D．100°4．如图，在平面直角坐标系中，有一Rt△ ABC，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．则旋转中心的坐标是（）.评卷人得分A．（0，0）B．（﹣1，0）C．（1，0）D．（0，﹣1）11．如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A/B/C/D/E/F/．下列判断错误的是（）．A．AB=A/B/B．BC//B/C/C．直线l⊥BB/D．∠A/=120°6．（2015秋•广元校级期中）如图，∠AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA 于点M，交OB于点N．若△PMN的周长是5cm，则P1P2的长为（）A．3cm B．4cm C．5cm D．6cm8．（2015秋•东莞校级期中）下列图形：①三角形，②线段，③正方形，④直角、⑤圆，其中是轴对称图形的个数是（）A．4个B．3个C．2个D．1个3．点M（﹣3，2）关于y轴对称的点的坐标为（）A．（﹣3，﹣2）B．（3，﹣2）C．（3，2）D．（﹣3，2）14．点P（3，－5）关于轴对称的点的坐标是______________．18．如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=3cm，PN=4cm，MN=4．5cm，则线段QR的长为__________。

初中数学北师大版探索轴对称的性质模拟考试卷考点姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分一、选择题2．下列说法中，正确的是（）A．两个全等三角形一定关于某直线对称B．等边三角形的高、中线、角平分线都是它的对称轴C．两个图形关于某直线对称，则这两个图形一定分别位于这条直线的两侧D．关于某直线对称的两个图形是全等形4．下列轴对称图形中，可以用没有刻度的直尺画出对称轴的有（）A．1个 B.2个 C.3个 D，4个4．如图，ΔABC与ΔA’B’C’关于直线l对称，∠A=50，∠C’=30，则∠B的度数为（）A．30°B．50°C．90°D．100°4．如图，在平面直角坐标系中，有一Rt△ ABC，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．则旋转中心的坐标是（）.评卷人得分A．（0，0）B．（﹣1，0）C．（1，0）D．（0，﹣1）5．下列说法正确的是（）A．能够完全重合的两个图形成轴对称B．全等的两个图形成轴对称C．形状一样的两个图形成轴对称D．沿着一条直线对折能够重合的两个图形成轴对称15．已知AD//BC，AB⊥AD，点E点F分别在射线AD，射线BC上，若点E与点B关于 AC对称，点E点F关于BD对称，AC与BD相交于点G，则（）A．B．C．2BC=5CFD．9．（2003•黑龙江）将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为（）A．60l14．如图，将矩形ABCD沿DE折叠，使A点落在BC上F处，若∠EFB＝60°，则∠AED＝______________．16．如图，将矩形纸片的两只直角分别沿EF、DF翻折，点B恰好落在AD边上的点B′处，点C恰好落在边B′F上．若AE=3，BE=5，则FC=______________．19．如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为______________cm．22．在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称，请在备用图中画出4个这样的△DEF（不能重复）．21．（本题满分8分）如图，在Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，求线段BN的长．21．如图，在平面直角坐标系中完成下列各题：（不写作法，保留作图痕迹）（1）在图1中作出关于y轴对称的，并写出、、的坐标；（2）在图2中x轴上画出点，使的值最小．。