电路理论课后习题解答04
- 格式:doc
- 大小:2.54 MB
- 文档页数:10

电路理论习题库+参考答案一、判断题(共100题,每题1分,共100分)1.欧姆定律可表示成U=RI,也可表示成U=-RI,这与采用的参考方向有关。
()A、正确B、错误正确答案:A2.非正弦周期信号分解后的傅里叶级数不一定是一个收敛的无穷三角级数()A、正确B、错误正确答案:B3.由于假定各节点电压的参考极性总是由独立节点指向参考节点,所以,各节点电压在相连电阻中引起的电流总是流出该节点的。
因此,节点电压方程的等式左边是各节点电压引起的流出相应节点的电流,而右边则是电流源和等效电流源注入节点的电流。
()A、正确B、错误正确答案:A4.电阻混联是指电阻连接中,既有串联又有并联()A、正确B、错误正确答案:A5.理想变压器反映阻抗的性质与负载阻抗的性质相反。
()A、正确B、错误正确答案:B6.三相电路是一种特殊类型的复杂电路,因而仍可采用一般复杂电路的分析方法对其进行分析和计算。
()A、正确B、错误正确答案:A7.支路分析法适用于分析支路数较少的电路()A、正确B、错误正确答案:A8.正弦电路中,若串联电路的总电压超前电流(电压、电流取关联参考方向),则此电路一定呈感性。
()A、正确B、错误正确答案:A9.造成系统误差的原因主要是操作者粗心大意。
()A、正确B、错误正确答案:B10.一个线性含源二端网络和其外部负载所构成的电路无唯一解时,此二端网络就可能无等效电源电路()A、正确B、错误正确答案:A11.电工指示仪表准确度的数字越小,表示仪表的准确度越低。
(A、正确B、错误正确答案:B12.对称三相电路Y-Y系统中不管是否含有高次谐波分量,U1=√3U()A、正确B、错误正确答案:B13.工程上将同向耦合状态下的一对施感电流的入端或出端定义为耦合电感的同名端()A、正确B、错误正确答案:A14.三相电路中,对称负载Y接无中线时,发生一相断路故障后,非断开相的相电压降低到电源线电压的一半。
()A、正确B、错误正确答案:A15.RLC串联电路的谐振,电源提供的无功功率为0,电路中无能量交换。

第一章 电路模型和电路定律1.1 图示元件当时间t <2s 时电流为2A ,从a 流向b ;当t >2s 时为3A ,从b 流向a 。
根据图示参考方向,写出电流i 的数学表达式。
1.2图示元件电压u =(5-9e -t /τ)V ,τ >0。
分别求出 t =0 和 t →∞ 时电压u 的代数值及其真实方向。
babu +-图 题1.21.3 图示电路。
设元件A 消耗功率为10W ,求A u ;设元件B 消耗功率为-10W,求B i ;设元件C 发出功率为-10W ,求C u 。
Au +-10V+-Cu +-(a)(b)(c)图 题1.31.4求图示电路电流4321i i i i 、、、。
若只求2i ,能否一步求得?图 题1.41i 4i 3i 图 题1.51.5 图示电路,已知部分电流值和部分电压值。
(1) 试求其余未知电流1234,,,i i i i 。
若少已知一个电流,能否求出全部未知电流?(2) 试求其余未知电压 u 14、u 15、u 52、u 53。
若少已知一个电压,能否求出全部未知电压?1.6 图示电路,已知A 21=i ,A 33-=i ,V 101=u ,V 54-=u 。
求各元件消耗的功率。
图 题1.61uSu (a)(b)图 题1.71.7 图示电路,已知10cos()V S u t ω=,8cos()A S i t ω=。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压12,u u 。
1u +-2u +-图 题1.830u-+图 题1.91.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N 吸收的功率和电流源发出的功率。
10V0.5A8V1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路,已知电流源发出的功率是12W ,求r 的值。
1V图 题1.13图 题1.141V2V1.14 求图示电路受控源和独立源各自发出的功率。

电路理论教程答案陈希有【篇一:《电路理论基础》(第三版陈希有)习题答案第一章】电路电流的参考方向是从a指向b。
当时间t2s时电流从a流向b,与参考方向相同,电流为正值;当t2s时电流从b流向a,与参考方向相反,电流为负值。
所以电流i的数学表达式为2a t?2s? i??-3at?2s ?答案1.2解:当t?0时u(0)?(5?9e0)v??4v0其真实极性与参考方向相反,即b为高电位端,a为低电位端;当t??时u(?)?(5?9e??)v?5v0其真实极性与参考方向相同,即a为高电位端,b为低电位端。
答案1.3解:(a)元件a电压和电流为关联参考方向。
元件a消耗的功率为pa?uaia则ua?pa10w??5v ia2a真实方向与参考方向相同。
(b) 元件b电压和电流为关联参考方向。
元件b消耗的功率为pb?ubib则ib?pb?10w1a ub10v真实方向与参考方向相反。
(c) 元件c电压和电流为非关联参考方向。
元件c发出的功率为pc?ucic则uc?pc?10w10v ic1a真实方向与参考方向相反。
答案1.4解:对节点列kcl方程节点③: i4?2a?3a?0,得i4?2a?3a=5a节点④: ?i3?i4?8a?0,得i3??i4?8a?3a节点①: ?i2?i3?1a?0,得i2?i3?1a?4a节点⑤: ?i1?i2?3a?8a?0,得i1?i2?3a?8a??1a若只求i2,可做闭合面如图(b)所示,对其列kcl方程,得 i28a-3a+1a-2a0解得i2?8a?3a?1a?2a?4a答案1.5解:如下图所示(1)由kcl方程得节点①:i1??2a?1a??3a节点②:i4?i1?1a??2a节点③:i3?i4?1a??1a节点④:i2??1a?i3?0若已知电流减少一个,不能求出全部未知电流。
(2)由kvl方程得回路l1:u14?u12?u23?u34?19v回路l2:u15?u14?u45?19v-7v=12v回路l3:u52?u51?u12??12v+5v=-7v回路l4:u53?u54?u43?7v?8v??1v若已知支路电压减少一个,不能求出全部未知电压。

习题四1.用叠加定理求图题4-1所示电路中的电流i R 。
图题4-1解: A 2电流源单独作用时:A i R 12101010'−=×+−=V 80电压源单独作用时:i A i R 4101080''=+=原电路的解为:A i i i R R R 341'''=+−=+=2.用叠加定理求图题4-2所示电路中的电压u ab 。
4图题4-2解:V 24电压源单独作用时:Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时:Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为:V u u u ab ab ab 18612'''=+=+=3.用叠加定理求图题4-3所示电路中的电流i 。
6A图题4-3解: A 6电流源单独作用时:ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时:Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为:()()A i i i 624'''−=−+−=+=4.图题4-4所示电路中,R =6Ω,求R 消耗的功率。
图题4-4解: 将R 支路以外的部分看作一个二端电路。
可采用叠加原理求oc u :12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻:eqRΩ=++×=426363eq R 原电路简化为:Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5.图题4-5所示电路中, R 1=1.5Ω R 2=2Ω,求(a )从a、b 端看进去的等效电阻;(b )i 1与i s 的函数关系。

第一章电路的基础知识1-1电路及其主要物理量思考题解答P8 1-1-1 在图1-1-18所示电路中,已知R2=R4,UAD=15V,UCE=10V,试用电位差的概念计算UAB。
图1-1-18[答] 由R2=R4,有U CD=U EB,故UAB=U AC+U CD+U DE+U EB=(U AC+U CD)+(U DE+ U CD )=UAD+UCE=15+10=25V1-1-2 指出图1-1-19所示电路中A、B、C三点的电位。
图1-1-19[答] A、B、C三点的电位分别为:(a) 图:6V、3V、0V;(b)图:4V、0V、-2V;(c)图:开关S断开时6V、6V、0V;开关S闭合时6V、2V、2V;(d)图:12V、4V、0V;(e)图:6V、-2V、-6V。
1-1-3 在检修电子仪器时,说明书上附有线路图,其中某一局部线路如图1-1-20所示。
用电压表测量发现UAB=3V,UBC=1V,UCD=0,UDE=2V,UAE=6V。
试判断线路中可能出现的故障是什么?[答] 由UBC=1V,UDE=2V可知电阻R2、R4支路上有电流通过,而UCD=0,故判定电阻R3短路。
1-1-4 上题的线路故障可否用测量电位的方法进行判断?如何测量?[答] 可以用测量电位的方法进行判断。
只需测出B、C、D三点的电位,就可知R3支路上有电流,而R3电阻短路。
1-1-5 在图1-1-21所示电路中,已知U=-10V,I=2A,试问A、B两点,哪点电位高?元件P是电源还是负载?图1-1-20 图1-1-21 [答] 因U为负值,电压的实际方向与参考方向相反,故b点电位高。
又因P=UI=-10×2=-20W<0,产生功率,故元件P是电源。
1-2电路模型 思考题P191-2-1 以下说法中,哪些是正确的,哪些是错误的?(1)所谓线性电阻,是指该电阻的阻值不随时间的变化而变化。
(2)电阻元件在电路中总是消耗电能的,与电流的参考方向无关。

第1章习题解析一.填空题:1.电路通常由电源、负载和中间环节三个部分组成。
2.电力系统中,电路的功能是对发电厂发出的电能进行传输、分配和转换。
3. 电阻元件只具有单一耗能的电特性,电感元件只具有建立磁场储存磁能的电特性,电容元件只具有建立电场储存电能的电特性,它们都是理想电路元件。
4. 电路理论中,由理想电路元件构成的电路图称为与其相对应的实际电路的电路模型。
5. 电位的高低正负与参考点有关,是相对的量;电压是电路中产生电流的根本原因,其大小仅取决于电路中两点电位的差值,与参考点无关,是绝对的量6.串联电阻越多,串联等效电阻的数值越大,并联电阻越多,并联等效电阻的数值越小。
7.反映元件本身电压、电流约束关系的是欧姆定律;反映电路中任一结点上各电流之间约束关系的是KCL定律;反映电路中任一回路中各电压之间约束关系的是KVL定律。
8.负载上获得最大功率的条件是:负载电阻等于电源内阻。
9.电桥的平衡条件是:对臂电阻的乘积相等。
10.在没有独立源作用的电路中,受控源是无源元件;在受独立源产生的电量控制下,受控源是有源元件。
二.判断说法的正确与错误:1.电力系统的特点是高电压、大电流,电子技术电路的特点是低电压,小电流。
(错)2.理想电阻、理想电感和理想电容是电阻器、电感线圈和电容器的理想化和近似。
(对)3. 当实际电压源的内阻能视为零时,可按理想电压源处理。
(对)4.电压和电流都是既有大小又有方向的电量,因此它们都是矢量。
(错)5.压源模型处于开路状态时,其开路电压数值与它内部理想电压源的数值相等。
(对)6.电功率大的用电器,其消耗的电功也一定比电功率小的用电器多。
(错)7.两个电路等效,说明它们对其内部作用效果完全相同。
(错)8.对电路中的任意结点而言,流入结点的电流与流出该结点的电流必定相同。
(对)9.基尔霍夫电压定律仅适用于闭合回路中各电压之间的约束关系。
(错)10.当电桥电路中对臂电阻的乘积相等时,则该电桥电路的桥支路上电流必为零。


第四章单相交流电路4-1-1 已知i1=5sin314tA,i2=15sin(942t+90°)A。
你能说i2比i1超前90°吗?为什么?[答]两者频率不同,比较其相位是没有意义的,因此不能说i2超前i1 90°。
4-1-2 将通常在交流电路中使用的220V、100W白炽灯接在220V的直流电源上,试问发光亮度是否相同?为什么?[答]通常在交流电路中使用的220V、100W白炽灯,接在有效值为220V的交流电源上,其功率是100W,由于交流电有效值是从能量转换角度去考虑的等效直流值,如果将它接在220V的直流电源上,其功率也是100W,故发光亮度相同。
4-1-3 交流电的有效值就是它的均方根值,在什么条件下它的幅值与有效值之比是2?[答]必须是正弦交流电,它的幅值与有效值之比才是2。
4-1-4 有一耐压为220V的交、直流通用电容器,能否把它接在220V交流电源上使用?为什么?[答]电容器的耐压值是指它的绝缘物能承受的最高电压。
220V交流电压的最大值为2202V=380V,超过电容器的耐压值220V,会使电容器的绝缘击穿,故耐压为220V的交、直流通用电容器不能接在220V交流电源上使用。
4-2-1 正弦交流电压的有效值为220V,初相角ψ=30°,下列各式是否正确?(1) u =220 sin (ωt+30°)V(2) U=220 /30°V(3).U=220e j30°V(4).U=2220 sin (ωt+930°)V(5)u =220 /30°V(6)u =2220 /30°V[答]只有(3)是正确的。
(1)可改正为u =2220 sin (ωt+30°)V思考题解答(2) 可改正为 ·.U =220 /30°V (4) 可改正为 u =2220 sin (ωt +30°)V(5)可改正为 .U =220 /30°V(6) 可改正为 .U m =2220 /30°V4-2-2 已知İ=10/30°A,试将下列各相量用对应的时间函数来表示(角频率为ω):(1) İ(2) j İ(3) -j İ 。


答案4.1解:将非线性电阻左侧电路用戴维南定理进行等效化简,如图(b)所示。
1(b)列KVL 方程11V I U Ω⨯+= (1) 将非线性电阻特性2(1S )I U =⨯代入方程(1),得210U U +-= 解得0.618V U '=, 1.618V U ''=-(舍去) 2(1S )0.382A I U '=⨯=答案4.2解:将非线性电阻之外的电路等效化简,得图(b)所示电路。
1Ω(b)列KVL 方程1180I U Ω⨯+-= (1) 将I I U 22+=代入方程(1),得23180I I +-=解得:3A, 6A I I '''==-22()215V ()224VU I I U I I '''=+=''''''=+=答案4.3解:由非线性电阻的电压电流关系特性1I =2I = 得211100U I = ,222400U I = (1) 对回路列KVL 方程125V U U += (2) 将式(1)代入式(2)22121004005I I +=由非线性电阻串联可知 12I I =即215005I =解得10.1A I '= ,10.1A I ''=-(舍去) 即10.1A I =2111001V U I ==答案4.4解:对节点①、②列节点电压方程,其中非线性电阻电流设为未知量:121221112()n n s G G U G U GU I I +-=-- (1)21232S 2()n n G U G G U I I -++=+ (2)为消去12I I 、,须列补充方程11111222212S2()()(3)()()(4)n n n I f U f U I f U f U U U ==⎧⎨==--⎩将式(3)代入式(1)、(2),整理后得1212211212S11S121232212S2S ()()()()()n n n n n n n n n G G U G U f U f U U U G U G U G G U f U U U I +-++--=⎧⎨-++---=⎩答案4.5解:设回路电流方向如图所示。

答案10.1解:0<t时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A3)363685(V45)0(=Ω+⨯++=-i,A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得:V24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i由KVL 得开关电压:V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解:<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
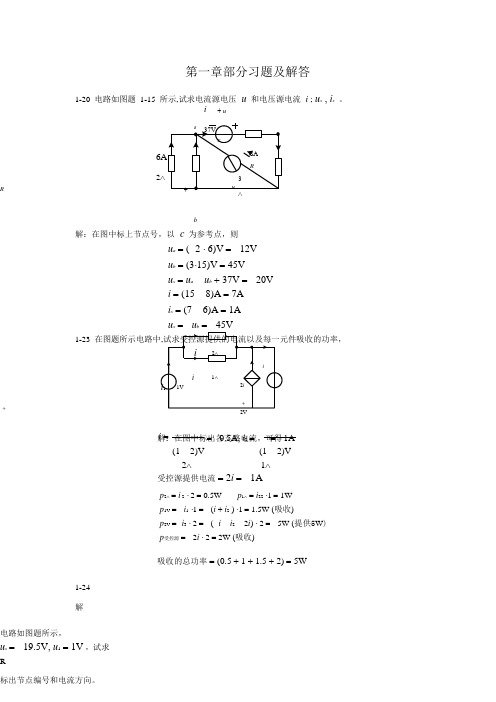
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。
i+ u2Rb解:在图中标上节点号,以 c 为参考点,则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解:在图中标出各支路电流,可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示,u s = 19.5V, u 1 = 1V ,试求R标出节点编号和电流方向。
ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R,需计算i4,u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。
a 1∧ci+6Vb解求解三个未知量需要三个独立方程。
由KCL可得其中之一,即i1 + i2 + i3 = 5对不含电流源的两个网孔,列写KVL方程,得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得: ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。

答案2.1解:本题练习分流、分压公式。
设电压、电流参考方向如图所示。
(a) 由分流公式得:23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得:3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解:电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得:220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯=再对图(a)使用分压公式得:13==30V 1+3U U ⨯答案2.3解:设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程:32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω再将3R 代入(1)式得210k 3R =Ω答案2.4解:由并联电路分流公式,得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解:首先将电路化简成图(b)。
图 题2.5120Ω(a)(b)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-=再由图(a)得321201A 360120I I =⨯=+由KVL 得,3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解:(a )设R 和r 为1级,则图题2.6(a)为2级再加x R 。


电路理论教程答案陈希有【篇一:《电路理论基础》(第三版陈希有)习题答案第一章】电路电流的参考方向是从a指向b。
当时间t2s时电流从a流向b,与参考方向相同,电流为正值;当t2s时电流从b流向a,与参考方向相反,电流为负值。
所以电流i的数学表达式为2a t?2s? i??-3at?2s ?答案1.2解:当t?0时u(0)?(5?9e0)v??4v0其真实极性与参考方向相反,即b为高电位端,a为低电位端;当t??时u(?)?(5?9e??)v?5v0其真实极性与参考方向相同,即a为高电位端,b为低电位端。
答案1.3解:(a)元件a电压和电流为关联参考方向。
元件a消耗的功率为pa?uaia则ua?pa10w??5v ia2a真实方向与参考方向相同。
(b) 元件b电压和电流为关联参考方向。
元件b消耗的功率为pb?ubib则ib?pb?10w1a ub10v真实方向与参考方向相反。
(c) 元件c电压和电流为非关联参考方向。
元件c发出的功率为pc?ucic则uc?pc?10w10v ic1a真实方向与参考方向相反。
答案1.4解:对节点列kcl方程节点③: i4?2a?3a?0,得i4?2a?3a=5a节点④: ?i3?i4?8a?0,得i3??i4?8a?3a节点①: ?i2?i3?1a?0,得i2?i3?1a?4a节点⑤: ?i1?i2?3a?8a?0,得i1?i2?3a?8a??1a若只求i2,可做闭合面如图(b)所示,对其列kcl方程,得 i28a-3a+1a-2a0解得i2?8a?3a?1a?2a?4a答案1.5解:如下图所示(1)由kcl方程得节点①:i1??2a?1a??3a节点②:i4?i1?1a??2a节点③:i3?i4?1a??1a节点④:i2??1a?i3?0若已知电流减少一个,不能求出全部未知电流。
(2)由kvl方程得回路l1:u14?u12?u23?u34?19v回路l2:u15?u14?u45?19v-7v=12v回路l3:u52?u51?u12??12v+5v=-7v回路l4:u53?u54?u43?7v?8v??1v若已知支路电压减少一个,不能求出全部未知电压。

电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ;(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –tV; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ;1-5.1-6. 0.1A. 1-7.1-8. 2F; 4C; 0; 4J. 1-9. 9.6V,0.192W, 1.152mJ; 16V, 0, 3.2mJ. 1-10. 1– e-106 tA , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W.1-14. –40V, –1mA; –50V, –1mA; 50V, 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W.1-16. 10V,50W;50V,250W;–3V,–15W;2V,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V, 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V, 18V. 1-21. K 打开:(a)0, 0, 0; (b)10V, 0, 10V; (c)10V,10V,0; K 闭合: (a)10V,4V,6V; (b)4V,4V,0; (c)4V,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V.1-25. –2.333V, 1.333A; 0.4V, 0.8A.1-26. 12V, 2A, –48W; –6V, 3A, –54W . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω. 2-2. 11.11Ω; 8Ω; 12.5Ω. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8. 10/3A,1.2Ω;–5V,3Ω; 8V,4Ω; 0.5A,30/11Ω. 2-9. 1A,2Ω; 5V,2Ω; 2A; 2A; 2A,6Ω. 2-10. –75mA; –0.5A. 2-11. 6Ω; 7.5Ω; 0; 2.1Ω. 2-12. 4Ω; 1.5Ω; 2k Ω. 2-13. 5.333A; 4.286A. 2-14. (a) –1 A ↓; (b) –2 A ↓, 吸20W. 2-16. 3A. 2-17. 7.33V. 2-18. 86.76W. 2-19. 1V, 4W. 2-20. 64W.2-21. 15A, 11A, 17A. 2-23. 7V, 3A; 8V,1A. 2-24. 4V, 2.5V, 2V. 2-26. 60V. 2-27. 4.5V. 2-28. –18V.2-29. 原构成无解的矛盾方程组; (改后)4V,10V. 2-30. 3.33 k , 50 k . 2-31. R 3 (R 1 +R 2 ) i S /R 1 . 2-32. 可证明 I L =- u S /R 3 . 2-33. –2 ; 4 .2-34. (u S1 + u S2 + u S3 )/3 . ※第三章3-1. –1+9=8V; 6+9=15V; sin t +0.2 e – t V. 3-2. 155V. 3-3. 190mA. 3-4. 1.8倍.3-5. 左供52W, 右供78W. 3-6. 1; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A.iA 0 s 1 12 3 1-e -t t 0 t ms imA 4 10 0 t ms p mW 4 100 2 25 i , A 0.4 .75 t 0 .25 1.25 ms -0.4 (d) u , V 80 0 10-20 t , ms(f ) u , V 1000 10 t , ms (e)p (W) 100 1 2 t (s) -10编辑版word3-8. 20V, –75.38V.3-9. –1A; 2A; –17.3mA. 3-10. 5V, 20; –2V, 4. 3-12. 4.6. 3-13. 2V; 0.5A. 3-14. 10V, 5k .3-15. 4/3, 75W; 4/3, 4.69W. 3-16. 1, 2.25W. 3-18. 50. 3-19. 0.2A. 3-20. 1A. 3-21. 1.6V. 3-22. 4A; –2A. 3-23. 23.6V; 5A,10V. 3-24. 52V. ※第四章4-1. 141.1V, 100V, 50Hz, 0.02s,0o , –120o ; 120 o.4-2. 7.07/0 o A, 1/–45 o A, 18.75/–40.9 oA. 4-3. 3mU , 7.75mA .4-4. 10/53.13oA, 10/126.87oA, 10/–126.87oA,10/–53.13oA ;各瞬时表达式略。

第四章 电路定理电路定理是电路理论的重要组成部分,为我们求解电路问题提供了另一种分析方法,这些方法具有比较灵活,变换形式多样,目的性强的特点。
因此相对来说比第三章中的方程式法较难掌握一些,但应用正确,将使一些看似复杂的问题的求解过程变得非常简单。
应用定理分析电路问题必须做到理解其内容,注意使用的范围、条件,熟练掌握使用的方法和步骤。
需要指出,在很多问题中定理和方程法往往又是结合使用的。
4-1 应用叠加定理求图示电路中电压ab u 。
解:首先画出两个电源单独作用式的分电路入题解4-1图(a )和(b )所示。
对(a )图应用结点电压法可得1sin 5)121311(1tu n =+++ 解得 15sin 3sin 53n tu t V == (1)111113sin sin 2133n ab n u u u t t V =⨯==⨯=+对(b )图,应用电阻的分流公式有1132111135tt e i e A --+=⨯=++所以 (2)110.25t t abu i e e V --=⨯== 故由叠加定理得 (1)(2)s i n 0.2ta b a b a b u u u t e V -=+=+4-2 应用叠加定理求图示电路中电压u 。
解:画出电源分别作用的分电路如题解(a )和(b )所示。
对(a )图应用结点电压法有105028136)101401281(1++=+++n u 解得 (1)113.650.10.0250.1n u u +==++18.624882.6670.2253V ===对(b )图,应用电阻串并联化简方法,可求得10402(8)32161040331040183(8)21040si u V ⨯⨯++=⨯=⨯=⨯+++ (2)16182323si u u V -==-⨯=- 所以,由叠加定理得原电路的u 为(1)(2)24888033u u u V =+=-= 4-3 应用叠加定理求图示电路中电压2u 。

电工学少学时1-4章课后习题答案第一章电路的基本概念和基本定律11 电路和电路模型(1)电路是电流的通路,是为了实现某种功能而将电气设备和元器件按照一定方式连接起来的整体。
(2)电路模型是由理想电路元件组成的,用于近似地描述实际电路的性能。
理想电路元件包括电阻、电感、电容、电源等。
12 电流和电压的参考方向(1)电流的参考方向是人为假定的电流流动的方向。
若实际电流方向与参考方向相同,电流为正值;反之,电流为负值。
(2)电压的参考方向也是假定的,通常规定从高电位指向低电位为电压的参考方向。
13 电源有载工作、开路与短路(1)电源有载工作时,电路中有电流通过,电源向外输出功率。
此时,电源的端电压等于电源电动势减去内阻上的压降。
(2)电源开路时,电路中没有电流,电源端电压等于电源电动势。
(3)电源短路时,电流很大,会损坏电源和电路。
14 基尔霍夫定律(1)基尔霍夫电流定律(KCL):在任一时刻,流入一个节点的电流之和等于流出该节点的电流之和。
(2)基尔霍夫电压定律(KVL):在任一时刻,沿任一闭合回路,各段电压的代数和为零。
课后习题答案:习题 11 一个手电筒电路,电池电动势为 3V,内阻为05Ω,灯泡电阻为5Ω。
求电路中的电流和灯泡两端的电压。
解:根据全电路欧姆定律,电路中的电流 I = E /(R + r) = 3 /(5 + 05) = 0545A灯泡两端的电压 U = IR = 0545 × 5 = 2725V习题 12 已知电路中某点的电位为 5V,若选择另一点为参考点,电位为 0V,两点之间的电压为 10V,求该点的电位。
解:因为两点之间的电压等于两点电位之差,所以该点的电位为 10 + 0 = 10V第二章电路的分析方法21 电阻串并联连接的等效变换(1)电阻串联时,总电阻等于各电阻之和。
(2)电阻并联时,总电阻的倒数等于各电阻倒数之和。
22 电源的两种模型及其等效变换(1)实际电源可以用电压源和电流源两种模型表示。
第四章 电路定理
4-1应用叠加定理求图示电路中电压ab u 。
2Ω
1Ω
+-
ab u a b 题4-1图
解:画出两个电源单独作用时的分电路如题解4-1图所示。
对(a)图应用结点电压法可得:
1
1
15sin 13211n t u ⎛⎫++= ⎪+⎝⎭
解得:
13sin n u tV =
()1
1
1sin 21
n ab u u tV =
⨯=+
题解4-1图
+-
(a)
()
1ab u +
-
(b)
()2ab u
对(b)图,应用电阻分流公式有
11
11351321
t t e i e A --=⨯=+++ 所以
()21
15
t ab u i e V -=⨯=
()()121
sin 5
t ab ab ab u u u t e V -=+=+
4-2应用叠加定理求图示电路中电压u 。
题4-2图
-
V
解:画出电源分别作用的分电路图
①(a)
(b)
题解4-2图
-
V u
对(a)图应用结点电压法有
1
111136508240108210n u ⎛⎫++=+ ⎪++⎝⎭
解得:
()1
182.667n u u V ==
对(b)图,应用电阻串并联化简方法,可得:
104028161040310403821040si u V ⨯⎛⎫
⨯+ ⎪
+⎝⎭=⨯=⨯⎛⎫
++ ⎪+⎝⎭
()28
23
si u u V -=
=- 所以,由叠加定理得原电路的u 为
()()1280u u u V =+=
4-3应用叠加定理求图示电路中电压2u 。
3Ω
题4-3图
+-
4Ω
1
2i 3A
2V
1i 2u
解:根据叠加定理,作出电压源和电流源单独作用时的分电路,受控源均保留在分电路中。
(a)
(b)
3Ω
题解4-3图
4Ω
2V
()
11
i ()11
2i
()
12u 3Ω
+-
4Ω
3A
()21i ()21
2i
(
)
22u
(a)图中
()112
0.54
i A =
= 所以根据KVL 有
()()1
1
213221u i V =-⨯+=-
(b)图中
()2
10i =
()2
2339u V =⨯=
故原电路电压
()()1
2
2228u u u V =+=
4-4图示电路中,当电流源1s i 和电压源1s u 反向时(2s u 不变),电压ab u 是原来的倍;
当电流源1s i 和电压源1s u 反向时(1s u 不变),电压ab u 是原来的倍。
问:仅1s i 反向时(1s u ,2s u 不变),电压ab u 应为原来的多少倍
题4-4图
解:根据叠加定理,设响应
()1121321ab s s s u K i K u k u =++
式中1K ,2K ,3k 为未知的比例常数,将已知条件代入上式,得
()11213220.5ab s s s u K i K u k u =--+ ()11213230.3ab s s s u K i K u k u =-+- ()1121324ab s s s xu K i K u k u =-++
将(1),(2),(3)式相加,得
()11213251.8ab s s s u K i K u k u =-++
因此求得
1.8x =
4-5图示电路110s U V =,215s U V =,当开关S 在位置1时,毫安表的读数为
40I mA '=;当开关S 在位置2时,毫安表的读数为60I mA ''=-。
如果把开关S 合向位置3,毫安表的读数为多少
题4-5图
解:设流过电流表的电流为I ,根据叠加定理:
12s s I K I K U =+
当开关S 在位置1时,相当于0s U =,当开关S 在位置2时,相当于1s s U U =,当开关S 在位置3时,相当于2s s U U =-把上述条件代入以上方程,可得关系式
140s K I = 12160s s K I K U -=+
从中解出
210K =-
所以S 在位置3时,有
12190s s I K I K U mA =+=
4-6图(a)所示含源一端口的外特性曲线画于(b)中,求其等效电源。
(a)
(b)
/
V
u 题4-6图
/i
解:根据戴维宁定理可知,图示含源一端口电路可以等效为题解4-6图,其端口电压
u 和电流i 满足关系式
oc eq u u R i =-
题解4-6图u
图(b )中所示的含源一端口的外特性曲线方程为
1
105
u i =-
比较以上两个方程式,可得等效电源电路参数
10,0.2oc eq u V R ==Ω
4-7求图示各电路的等效戴维宁电路和诺顿电路。
(a)
1'
1
(b)
8Ω
题4-7图
1'
1
(c)5Ω
解:(a)图中,应用网孔电压,设网孔电流1i ,2i ,其绕行方向如图所示。
列网孔电流方程为
(
)1122
10101050i i i =⎧⎪⎨
+++=⎪⎩ 得
20.8i A =-
故开路电压
210156515oc u i V =⨯-+-=
a
b
b
a (a1)
(a2)
将电流源断开,得(a1)所示电路,应用电阻串,并联等效求得等效电阻
()5//10101014eq R =++=Ω
戴维宁电路如图(a2)所示
(b)图中,根据KVL 求开路电压ab u 为
96236ab u V =-+⨯+=
把电压源短路,电流源断开,可以看出等效内阻为
61016eq R =+=Ω
a
b
(b1)
16Ω
戴维宁等效电路见题解图(b1)
(c)设开路电压参考方向图(c)所示。
显然oc u 等于受控源所在支路得电压,即
11220oc u i i =-=
由于电路中有受控源,求等效电阻时不能用电阻串,并联等效的方法,现采用求输入电阻的外加电源法。
将(c)图中4V 独立电压源短路,在ab 端子间加电压源u 如(c1)图所示。
b
8Ω(c1)
5Ωa u i
根据KVL 列方程
()1
1115810220
u i i i i i i =-⎧⎪⎨
++-=⎪⎩ 得
7u i =
故等效电阻为
7eq u
R i
=
=Ω 等效戴维宁电路图如(c2)
a
b
(c2)
4-8在图示电路中,试问:
(1)R 为多大时,它吸收的功率最大求此最大功率。
(2)若80R =Ω,欲使R 中电流为零,则a ,b 间应并接什么元件,其参数为多少画出电路图。
题4-8图V
解:(1)自a ,b 断开R 所在支路,应用电阻串,并联及电源等效互换将原图变为题解图解(a)由图解(a)可知:
()5025
10102537.5101010
oc u V -=⨯++=++
等效电阻
()1010//2010eq R =+=Ω
最后得等效电路如图解(b)所示,由最大功率传输定理可知,当10eq R R ==Ω时可获得最大功率。
此时
2max
35.1564oc eq
u P W R ==
题解4-8图
(a)
(b)
(c)
b
V R
(2)利用电源等效互换,图解(b)电路可以变化成图解(c),由KCL 可知,在a ,b 间并接一个理想电流源,其值 3.75s i A =,方向由a 指向b ,这样R 中的电流为零。
4-9图示电路的负载电阻L R 可变,试问L R 等于何值时可吸收最大的功率求此功率。
题4-9图
解:首先求出L R 以左部分的等效电路。
断开L R ,设oc u 如题解4-9图所示,并把受控电流源等效为受控电压源。
由KVL 可得
()112286i i ++=
10.5i A =
故开路电压
1112286oc u i i i V =++=
把端口短路,如题解图(b)所示应用网孔电流法求短路电流sc i ,网孔方程为
()()()111122286
224280
sc sc i i i i i i +-+=⎧⎪⎨
-++-+=⎪⎩ 解得
3
2
sc i A =
故一端口电路的等效电阻
4oc
eq sc
u R i =
=Ω 画出戴维宁等效电路,接上待求支路L R ,如题解图(c)所示。
由最大功率传输定理知4L eq R R ==Ω时获得最大功率。
L R 的最大功率为
2max
2.254oc eq
u P W R ==
(a)
(b)
(c)
题解4-9图。