下载文档原格式
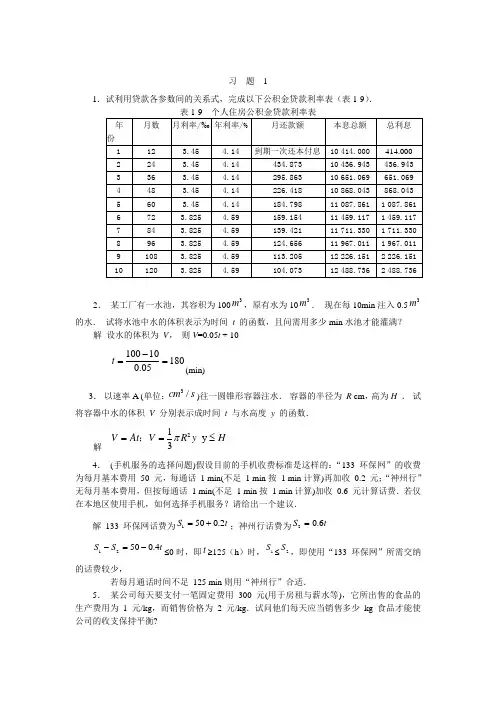
习 题 11．试利用贷款各参数间的关系式，完成以下公积金贷款利率表（表1-9）．2． 某工厂有一水池，其容积为1003m ，原有水为103m ． 现在每10min 注入0.53m 的水． 试将水池中水的体积表示为时间 t 的函数，且问需用多少min 水池才能灌满？解 设水的体积为 V ， 则V =0.05t + 10100101800.05t -==(min)3． 以速率A (单位：3/cm s )往一圆锥形容器注水． 容器的半径为 R cm ，高为H ． 试将容器中水的体积 V 分别表示成时间 t 与水高度 y 的函数．解 21y 3V At V R y Hπ==≤；4． (手机服务的选择问题)假设目前的手机收费标准是这样的：“133 环保网”的收费为每月基本费用 50 元，每通话 1 min(不足 1 min 按 1 min 计算)再加收 0.2 元；“神州行”无每月基本费用，但按每通话 1 min(不足 1 min 按 1 min 计算)加收 0.6 元计算话费．若仅在本地区使用手机，如何选择手机服务？请给出一个建议．解 133 环保网话费为1500.2S t =+；神州行话费为20.6S t =12500.4S S t -=-≤0时，即t ≥125（h ）时，1S ≤2S ，即使用“133 环保网”所需交纳的话费较少，若每月通话时间不足 125 min 则用“神州行”合适．5． 某公司每天要支付一笔固定费用 300 元(用于房租与薪水等)，它所出售的食品的生产费用为 1 元/kg ，而销售价格为 2 元/kg ．试问他们每天应当销售多少 kg 食品才能使公司的收支保持平衡?解 (21)300300x x -==，(kg)6． 设某商品的供给函数(即供给量作为价格的函数)为703)(2-+=x x x S ， 需求函数(即需求量作为价格的函数)为x x D -=410)(， 其中x 为价格．(1) (1)在同一坐标系中，画出)(),(x D x S 的图形； (2) (2)若该商品的需求量与供给量均衡，求其价格．解212()()3704102420 S x D x x x x x x =⇔+-=-⇒=-=，由实际意义取x =20 7． 有一物体作直线运动，已知物体所受阻力的大小与物体的运动速度成正比，但方向相反．当物体以4m/s 的速度运动时，阻力为 2 N ，试建立阻力与速度之间的函数关系．解 设20.5Ns/m 0.54N N kv k N vv=====，，即8． 一架飞机起飞用油是一个固定量，着陆用油是一个(不同的)固定量，空中飞行每km 用油也是一个固定量，所需的燃料总量是如何依赖于航程距离的？写出有关函数的表达式．解释表达式中常数的意义．解 设起飞用油为1s ，着陆用油2s ，空中飞行用油为3s ，则12s s ，为常量，其中3s kl =，其中k 为飞行每km 用油量，l 为航程，因此所需燃料总量12312S s s s s s kl =++=++9． 财产保险要估价财产，例如对小汽车或冰箱进行估价．财产的价值将随其使用时间的加长而降低，也就是会贬值．例如最初花 100 000 元购买的小汽车，几年后只值 50 000 元．计算财产值的最简单方法是利用“贬值直线”，它假定财产价值是时间的线性函数．如果一个 1 950 美元的冰箱 7 年后贬得一文不值，求出其价值作为时间函数的表达式． 解 设财产价值为V ，时间为t ，则此线性函数可设为V kt b =+；0t =时， 1 950V b ==；7 77 1 9500250t V k b k k ==+=+==-时，，； 所以250 1 950V t =-+10．(1) 利用表1-10中的数据确定一个形如 0e rt Q Q =的公式．该公式给出了时刻t (以月计)时，兔子的数量Q ．(2) 该兔子种群的近似倍增期是多少?(3) 利用你的方程预测该兔子种群何时达到1 000只．解 （1）解方程组：00002525e 0.5443e r Q Q r Q ⎧==⎧⇒⎨⎨==⎩⎩，所以公式为0.5425e tQ =（2）由0.542et=得到：28.1=t (月)（3）由0.54100025et=得到：83.6=t (月)注：求r 的时候可以选取任意两组数据进行计算，也可以用其他方式进行计算，比如用各相邻两组数据的差的平均值．结果略有差异．11． 旅客乘坐火车时，随身携带物品，不超过 20 kg 免费，超过 20 kg 部分，每kg 收费 0.20 元． 超过50 kg 部分再加收 50 %． 试列出收费与物品重量的函数关系式．解 设收费为P ，物重为W ，则当W ≤20时，0P =；20<W ≤50 0.2(20)P W =-时，50 0.2(20)0.5(50)W P W W >=-+-时，12． 某停车场收费标准为：凡停车不超过2 h 的，收费 2 元；以后每多停车 1 h(不到 1 h 仍以 1 h 计)增加收费 0.5 元．但停车时间最长不能超过 5 h ．试建立停车费用与停车时间之间的函数关系模型．解 设收费为P ，停车时间为T ，则当T ≤22P =时，；2<T ≤52(2)0.50.51P T T =+-⨯=+，13． 设仪器由于长期磨损，使用x 年后的价值是由下列模型0.040()e x Q x Q -=确定的．使用 20 年后，仪器的价值为 8 986.58 元．试问当初此仪器的价值为多少?解 由00.04()e xQ x Q -=，将20(20)8 986.58x Q ==，代入得到：000.04208 986.58e 20 000()Q Q -⨯=⇒=元14． 生物在稳定的理想状态下，细菌的繁殖按指数模型增长:()e kt Q t a = (表示 t min 后的细菌数)假设在一定的条件下，开始)0(=t 时有 2 000 个细菌，且 20 min 后已增加到 6 000 个，试问 1 h 后将有多少个细菌?解 2020602033(0) 2 000(20) 2 000e 6 000e 3(60) 2 000e2 000(e ) 2 000354 000()====⇒====⨯=k k kk Q a Q Q ；；个15． 大气压力P 随着离地球表面的高度h 的增加而呈指数减少：41.2100e--⨯=hP P其中0P 是海平面处的大气压力，h 以m 计．(1) 珠穆朗玛峰的顶峰海拔高 8 848.13 m ，那里的大气压力是多少？将其表示为海平面处大气压力的百分数；(2) 一架普通商用客机的最大飞行高度大约是 12 000 m ． 此高度的大气压力是多少？将其表示为海平面处大气压力的百分数．解441.2108 848.130001.21012 000000(1)0.345 834.58 %(2)0.236 923.69 %e e ---⨯⨯-⨯⨯======P P P P P P P P16． 某工厂的空气经过过滤使得污染数量P (单位：mg/L)正按照方程0e ktP P -=减少，其中t 表示时间（单位：h ）．如果在前 5 h 内消除了 10 % 的污染物： (1) 10 h 后还剩百分之几的污染物？ (2) 污染减少 50 % 需花多少时间？(3) 画出污染物关于时间的函数图象，在图象上表示出你的计算结果． (4) 解释污染量以这种方式减少的可能原因．解 000200000055105e 5 10 %)e e 0.90.021 (1) (10)e (e )0.8181 % (2) ()e50 %(e )0.533(h -------===========⇒=⇒=t kt k k k k ktk P P t P P k P P P P P P t P P t ，时，有(1-，，)(3) 图像略。
目录一、函数与极限 (2)1、集合的概念 (2)2、常量与变量 (3)2、函数 (4)3、函数的简单性态 (4)4、反函数 (5)5、复合函数 (6)6、初等函数 (6)7、双曲函数及反双曲函数 (7)8、数列的极限 (8)9、函数的极限 (10)10、函数极限的运算规则 (11)一、函数与极限1、集合的概念一般地我们把研究对象统称为元素，把一些元素组成的总体叫集合（简称集）。
集合具有确定性（给定集合的元素必须是确定的）和互异性（给定集合中的元素是互不相同的）。
比如“身材较高的人”不能构成集合，因为它的元素不是确定的。
我们通常用大字拉丁字母A、B、C、……表示集合，用小写拉丁字母a、b、c……表示集合中的元素。
如果a是集合A中的元素，就说a属于A，记作：a∈A，否则就说a不属于A，记作：a∉A。
⑴、全体非负整数组成的集合叫做非负整数集（或自然数集）。
记作N⑵、所有正整数组成的集合叫做正整数集。
记作N+或N+。
⑶、全体整数组成的集合叫做整数集。
记作Z。
⑷、全体有理数组成的集合叫做有理数集。
记作Q。
⑸、全体实数组成的集合叫做实数集。
记作R。
集合的表示方法⑴、列举法：把集合的元素一一列举出来，并用“｛｝”括起来表示集合⑵、描述法：用集合所有元素的共同特征来表示集合。
集合间的基本关系⑴、子集：一般地，对于两个集合A、B，如果集合A中的任意一个元素都是集合B的元素，我们就说A、B有包含关系，称集合A为集合B的子集，记作A⊆B（或B⊇A）。
⑵相等：如何集合A是集合B的子集，且集合B是集合A的子集，此时集合A中的元素与集合B中的元素完全一样，因此集合A与集合B相等，记作A＝B。
⑶、真子集：如何集合A是集合B的子集，但存在一个元素属于B但不属于A，我们称集合A是集合B的真子集。
⑷、空集：我们把不含任何元素的集合叫做空集。
记作∅，并规定，空集是任何集合的子集。
⑸、由上述集合之间的基本关系，可以得到下面的结论：①、任何一个集合是它本身的子集。
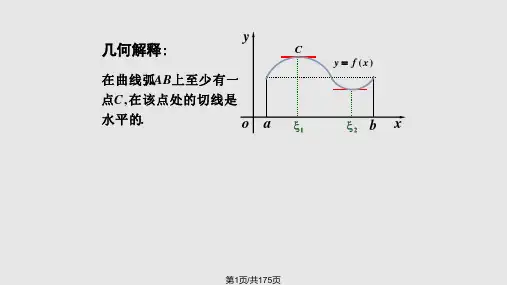
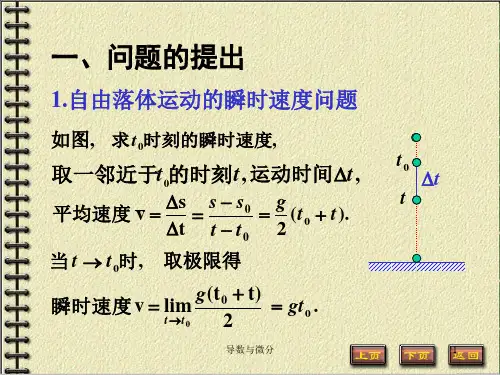
高等数学高职高专完整全套教学课件一、教学内容1. 第一章：函数与极限函数的概念、性质与图像极限的定义、性质及运算无穷小与无穷大的概念及其关系2. 第二章：导数与微分导数的定义、运算法则及求导公式微分的概念及其运算法则高阶导数的概念及其求法二、教学目标1. 理解并掌握函数、极限、导数与微分的基本概念及性质。
2. 能够运用求导公式和法则进行导数的计算，解决实际问题。
3. 培养学生的逻辑思维能力和解决复杂问题的能力。
三、教学难点与重点1. 教学难点：函数与极限的概念，导数的求法，微分的应用。
2. 教学重点：函数的性质与图像，导数的计算，微分的基本概念。
四、教具与学具准备1. 教具：多媒体教学设备、黑板、粉笔、直尺、圆规等。
2. 学具：教材、笔记本、文具等。
五、教学过程1. 引入：通过实际问题，引导学生了解函数在现实生活中的应用。
2. 知识讲解：讲解函数的定义、性质与图像，配合实例进行分析。
介绍极限的概念、性质及运算，通过例题进行讲解。
阐述导数与微分的定义、运算法则，配合求导公式进行讲解。
3. 随堂练习：针对每个知识点，设计相应的练习题，巩固所学内容。
六、板书设计1. 黑板左侧：列出本节课的主要知识点、公式及例题。
2. 黑板右侧：展示解题过程和答案，方便学生对照学习。
七、作业设计1. 作业题目：求下列函数的极限：lim(x→0) sin(x)/x，lim(x→∞)(1+1/x)^x。
求函数f(x) = x^3 3x^2 + 2x 1的导数。
求函数f(x) = e^x在x=1处的微分。
2. 答案：见附件。
八、课后反思及拓展延伸2. 拓展延伸：引导学生了解极限、导数与微分在物理学、工程学等领域的应用。
推荐相关学习资料，帮助学生深入理解高等数学的知识体系。
重点和难点解析1. 教学内容的选取与组织2. 教学目标的设定3. 教学难点与重点的区分4. 教学过程中的实践情景引入和例题讲解5. 板书设计的信息布局6. 作业设计的题目选取与答案提供7. 课后反思与拓展延伸的实际操作一、教学内容的选取与组织教学内容应紧密结合高职高专学生的学习基础和实际需求。
