布尔代数
- 格式:docx
- 大小:20.08 KB
- 文档页数:3

布尔代数化简布尔代数是一种逻辑代数,它使用了逻辑运算符和布尔变量来描述逻辑关系。
布尔代数化简是将复杂的布尔表达式简化为更简洁的形式的过程。
在计算机科学和电子工程中,布尔代数化简是非常重要的,因为它可以简化逻辑电路的设计和分析。
1. 布尔代数基础在布尔代数中,有三种基本的逻辑运算符:与(AND),或(OR)和非(NOT)。
它们的逻辑定义如下:•与运算:对于两个布尔变量A和B,当且仅当A和B都为真时,A与B的结果为真,否则为假。
•或运算:对于两个布尔变量A和B,当且仅当A和B中至少一个为真时,A 或B的结果为真,否则为假。
•非运算:对于一个布尔变量A,非A的结果为真当且仅当A为假,非A的结果为假当且仅当A为真。
这些逻辑运算符可以通过真值表来表示,真值表列出了所有可能的输入组合及其对应的输出结果。
2. 布尔代数化简的原理布尔代数化简的目标是通过应用布尔代数的规则和定律来简化复杂的布尔表达式。
以下是一些常用的布尔代数定律:•同一律:A OR 0 = A,A AND 1 = A•零律:A OR 1 = 1,A AND 0 = 0•吸收律:A OR (A AND B) = A,A AND (A OR B) = A•分配律:A AND (B OR C) = (A AND B) OR (A AND C),A OR (B AND C) =(A OR B) AND (A OR C)•德摩根定律:NOT (A AND B) = (NOT A) OR (NOT B),NOT (A OR B) = (NOT A) AND (NOT B)通过应用这些定律,我们可以将复杂的布尔表达式化简为更简单的形式。
3. 布尔代数化简的步骤布尔代数化简的步骤如下:步骤1:将布尔表达式写成标准形式将布尔表达式写成标准形式是化简的第一步。
标准形式是指将布尔表达式中的逻辑运算符按照优先级进行排列,并使用括号来明确运算的顺序。
例如,将表达式A AND (B OR C)写成(A AND B) OR (A AND C)的形式。


6-4 布尔代数一、复习分配格,有界格,有补格二、布尔格定义6-4.1 一个有补分配格称为布尔格。
三、布尔代数由于布尔格中,每个元素a都有唯一的补元a,因此可在A上定义一个一元运算—补运算“”。
这样,布尔格可看作具有两个二元运算和一个一元运算的代数结构,习惯上称它为布尔代数,记为<A, ∨,∧,>。
定义6-4.2 由布尔格<A,≤>,可以诱导一个代数系统<A, ∨,∧,>,这个代数系统称为布尔代数。
举例:253页例1布尔代数中补运算的性质定理6-4.1 对于布尔代数中任意两个元素a,b∈A,必定有①()a a=②a b a b∨=∧③a b a b∧=∨后两式称为格中德·摩根律。
四、布尔代数中运算的性质前已指出,布尔代数是有补分配格。
对任意a,b,c∈A,有① <A, ≤>是格,≤为A上的偏序关系,运算∨,∧满足(A-1) a∨b=lub{a,b}, a∧b=glb{a,b}(A-2) a≤b⇔a∨b=b⇔a∧b=a(A-3) a∨a=a, a∧a=a (等幂律)(A-4) a∨b=b∨a, a∧b=b∧a (交换律)(A-5) (a∨b) ∨c=a∨(b∨c),(a∧b)∧c=a∧(b∧c) (结合律)(A-6) a∨ (a∧b)=a,a∧ (a∨b)=a (吸收律)② <A, ≤>是分配格,满足(B-1) a∨ (b∧c)=(a∨b) ∧ (a∨c),a∧ (b∨c)=(a∧b) ∨ (a∧c) (分配律)(B-2) (a∨b=a∨c)∧(a∧b=a∧c)⇒b=c(B-3) (a∨b) ∧ (b∨c) ∧ (c∨a)=(a∧b) ∨ (b∧c) ∨ (c∧a)③ <A, ≤>是有界格,满足(C-1) 0≤a≤1(C-2) a∨0=a,a∧a=a (幺律)(C-3) a∨1=1,a∧0=0 (零律)④ <A, ≤>是有补格,满足(D-1) 1,0∨=∧=(互补律)a a a a(D-2) 10,01==⑤ <A, ≤>是有补分配格,满足 (E-1)()a a = (E-2) a b a b ∨=∧,a b a b ∧=∨ (德·摩根律)(E-3) a ≤b ⇔a’ ∨b=1⇔a ∧b’=0⇔b’≤a’注意,上述公式并非都是独立的,可从中选出一些公式作为基本公式,用它们推出其余的公式,而且可以用基本公式定义布尔代数。

第五章布尔代数布尔代数最初是作为对逻辑思维法则的研究出现的。
英国哲学家George Boole于1847年的论文“逻辑之数学分析”及“思维法则之研究”中引入了布尔代数。
本世纪30年代C.E. Shannon发表了“继电器和开关电路的符号分析”一文,为布尔代数在工艺技术中的应用开创了道路。
50年代苏联科学家把布尔代数发展成为接点网络实用中的通用理论,从而使布尔代数成为计算机科学中的重要基础理论。
从逻辑上讲,布尔代数是一个命题演算系统;从抽象代数观点讲,布尔代数是一个代数系统;从集合的观点讲,它是一个集合代数;从工程技术的观点讲,布尔代数是电路代数,电子线路的设计离不开它;5.1 布尔代数的基本定义和性质定义5.1.1给定一个具有三个运算的代数结构<S,⊕,⊙,′>,其中,⊕,⊙是S上的二元运算,′是S上的一元运算,0,1∈S。
若对于 x,y,z∈S(1) x⊕y=y⊕x,x⊙y=y⊙x (交换律)(2)x⊕(y⊕z)=(x⊕y)⊕z,x⊙(y⊙z)=(x⊙y)⊙z(结合律)(3)x⊕(y⊙z)=(x⊕y)⊙(x⊕z),x⊙(y⊕z)=(x⊙y)⊕(x⊙z)(分配律)(4)x⊕0=x,x⊙1=x (同一律)(5)x⊕x′=1,x⊙x′=0(有补律)则称<S,⊕,⊙,′>称为布尔代数(Boolean Algebra),⊕,⊙,′分别称为它的并(布尔和),交(布尔积)和补运算,0和1分别称为它的零元和么元。
一个布尔代数通常记为<S,⊕,⊙,′,0,1>。
例5.1.1二值(元)布尔代数<B,⊕,⊙,′,0,1>,其中B={0,1}1⊕1=1⊕0=0⊕1=1,0⊕0=0,1=0′1⊙1=1,1⊙0=0⊙1=0⊙0=0,0=1′例5.1.2集合代数<P(A),∪,∩,′,Φ,A>例5.1.3*命题代数定理5.1.1在一个布尔代数中,0和1 都是唯一的;定理5.1.2在一个布尔代数中,任一元素的补元是唯一的;证明(利用同一律,有补律和分配律)定理5.1.3在一个布尔代数中<S,⊕,⊙,′0,1>中,则对∀x∈S,(x′) ′=x定理5.1.4条件同上,则0′=1,1′=0;定理5.1.5条件同上,则对∀x∈S,x⊕x=x,x⊙x=x(幂等律)证明(利用同一律,有补律和分配律)定理5.1.6条件同上,则对∀x∈S,x⊕1=1,x⊙0=0(零一律)证明(同定理5.1.5)定理5.1.7条件同上,则对∀x,y∈S,x⊕(x⊙y)=x,x⊙(x⊕y)=x(吸收律)证明(同定理5.1.5)定理5.1.8条件同上,则对∀x,y∈S,(x⊙y)′=x′⊕y′,(x⊕y) ′=x′⊙y′(De morgan律)证明(同定理5.1.5)定理5.1.9条件同上,若对x,y,z∈S,x⊙y=x⊙z,x⊕y=x⊕z,则y=z (消去律)证明(利用集合中类似证明方法)定理5.1.10 条件同上,则对∀x,y∈S,x⊙y=x⇔x⊕y=y证明(利用吸收律)对偶原理: 在布尔代数<S,⊕,⊙,′,0,1>中,若P是某个已经得到证明的定理,将定理中的条件和结论(1)⊕与⊙互换; (2) 0与1 互换则由此而得的新定理仍然成立;5.2 格定理5.2.1设<S,⊕,⊙,′,0,1>为一个布尔代数,则集合≤={<x,y>| x⊙y=x∧x∈S∧y∈S}称为S上的偏序关系。

布尔代数基础和布尔函数的化简和实现布尔代数是分析和设计数字逻辑电路的数学工具。
因此这里从应用的角度向读者介绍布尔代数,而不是从数学的角度去研究布尔代数。
一、布尔代数的基本概念1、布尔代数的定义域和值域都只有“0”和“1”。
布尔代数的运算只有三种就是“或”(用+表示),“与”(用·表示)和“非”(用 ̄表示,以后用’表示)。
因此布尔代数是封闭的代数系统,可记为B=(k,+,·, ̄,0,1),其中k表示变量的集合。
2、布尔函数有三种表示方法。
其一是布尔表达式,用布尔变量和“或”、“与”和“非”三种运算符所构成的式子。
其二是用真值表,输入变量的所有可能取值组合及其对应的输出函数值所构成的表格。
其三是卡诺图,由表示逻辑变量所有可能取值组合的小方格所构成的图形。
3、布尔函数的相等可以有两种证明方法,一种是从布尔表达式经过演绎和归纳来证明。
另一种就是通过列出真值表来证明,如两个函数的真值表相同,则两个函数就相等。
二、布尔代数的公式、定理和规则1、基本公式有交换律、结合律、分配律、0—1律、互补律、重叠律、吸收律、对合律和德·摩根律。
值得注意的是分配律有两个是:A·(B+C)=A·B+A·C和A+B·C=(A+B)·(A+C),另外就是吸收律,A+AB=A;A+A’B=A+B它们是代数法化简的基本公式。
2、布尔代数的主要定理是展开定理(教材中称为附加公式)。
3、布尔代数的重要规则有对偶规则和反演规则。
三、基本逻辑电路1、与门F=A·B2、或门F=A+B3、非门F=A’(为了打字的方便,以后用单引号“’”表示非运算,不再用上划线表示非运算)4、与非门F=(A·B)’5、或非门F=(A+B)’6、与或非门F=(A·B+C·D)’7、异或门F=A’B+AB’=A⊕B8、同或门F=A’B’+AB=A⊙B四、布尔函数的公式法化简同一个布尔函数可以有许多种布尔表达式来表示它,一个布尔表达式就相应于一种逻辑电路。

数字通信原理实验布尔代数布尔代数作为一种表达逻辑关系的数学工具,在数字通信原理实验中扮演着重要的角色。
下面本文将从什么是布尔代数、布尔运算及其逻辑关系、布尔函数及其应用等几个方面来详细介绍布尔代数在数字通信原理实验中的应用。
一、什么是布尔代数?布尔代数是由英国数学家布尔(George Boole)在19世纪60年代提出的,它是处理逻辑关系的数学工具。
布尔代数是传统数学的一种扩展形式,将1和0的二进制数值,以及AND、OR、NOT三种基本的逻辑运算,用代数的方式加以表述。
它是逻辑代数的基础,适用于电子、电信、计算机等技术领域。
在数字通信原理实验中,布尔代数常用于电路的设计及数字信号的处理等领域。
二、布尔运算及其逻辑关系布尔运算是指布尔代数中的逻辑运算,包括AND、OR、NOT三种主要的逻辑运算。
下面逐一介绍:1.AND(与)运算:AND运算是指两个输入变量A、B,当它们都为1时,输出变量Y才为1,否则Y为0。
用符号表示为:Y=A·B。
2.OR(或)运算:OR运算是指两个输入变量A、B,当它们都为0时,输出变量Y 才为0,否则Y为1。
用符号表示为:Y=A+B。
3.NOT(非)运算:NOT运算是指一个输入变量A,当它为1时,输出变量Y为0,当它为0时,输出变量Y为1。
用符号表示为:Y=¬A。
布尔运算有一些重要的逻辑关系:1.结合律:结合律是指对于布尔代数中的AND和OR运算,无论括号怎样套用,结果都是相同的。
比如:(A·B)·C=A·(B·C);(A+B)+C=A+(B+C)。
2.分配律:分配律是指对于布尔代数中的AND和OR运算,无论括号怎样套用,结果都是相同的。
比如:A·(B+C)=A·B+A·C;A+(B·C)=(A+B)·(A+C)。
3.德摩根定理:德摩根定理是指NOT运算在布尔代数中的运用。


布尔代数pdf布尔代数(Boolean algebra)是数学中一种代数结构,由乔治·布尔(George Boole)于19世纪中叶提出。
它主要关注逻辑运算和关系,并在计算机科学、电子工程和信息技术等领域中得到广泛应用。
以下是一些基本概念:●布尔变量(Boolean Variables):布尔代数的基本单位是布尔变量,它只能取两个值,通常表示为0和1。
这两个值分别代表逻辑中的"假"和"真"。
●布尔运算(Boolean Operations):布尔代数包含一系列基本的逻辑运算,如与(AND)、或(OR)、非(NOT)等。
这些运算用于处理布尔变量,产生新的布尔值。
1.与运算(AND):如果所有输入都是1,结果为1;否则结果为0。
2.或运算(OR):如果至少有一个输入是1,结果为1;否则结果为0。
3.非运算(NOT):对输入取反,即1变为0,0变为1。
●布尔表达式(Boolean Expression):由布尔变量、常数和布尔运算符构成的代数表达式。
布尔表达式可用于描述逻辑函数。
●卡诺图(Karnaugh Map):一种图形工具,用于简化布尔表达式。
通过填写卡诺图中的1和0,可以直观地找到布尔表达式的最简形式。
逻辑门(Logic Gates):在电子和计算机领域,布尔代数被应用于设计逻辑电路。
逻辑门是实现布尔运算的电子元件,如与门、或门、非门等。
布尔代数在计算机科学中的应用是深远的,因为计算机内部的信息表示和处理都涉及到布尔逻辑。
逻辑电路和布尔代数的理论奠定了计算机硬件和软件设计的基础。


布尔代数化简一、布尔代数化简的概念与意义布尔代数化简,是指将一个复杂的布尔表达式通过一定的运算和规律,简化为一个更简单、易于理解和计算的布尔表达式。
它在数字电路设计、逻辑运算和计算机科学等领域具有重要的意义。
通过化简布尔表达式,可以降低电路的复杂度,提高运算速度和效率。
二、布尔代数的基本运算与定律1.布尔加法:两个布尔变量A、B的和为A·B。
2.布尔乘法:两个布尔变量A、B的积为A×B。
3.布尔减法:布尔变量A与B的差为A⊕B。
4.布尔非运算:布尔变量A的非为。
布尔代数的基本定律:1.分配律:A×(B+C) = (A×B) + (A×C)2.结合律:((A×B)×C) = (A×(B×C))3.吸收律:A×A = A,× =三、布尔代数化简的方法与步骤1.替换法:用简单的变量替换复杂的变量,使得表达式更易于化简。
2.分配律法:利用分配律对布尔表达式进行化简。
3.结合律法:利用结合律对布尔表达式进行化简。
4.吸收律法:利用吸收律对布尔表达式进行化简。
5.摩根定律:利用摩根定律对布尔表达式进行化简。
四、实例分析与解答例如,给定布尔表达式:A×(B+C) + D×(E+F)化简过程如下:1.使用分配律,将表达式拆分为两部分:A×B + A×C + D×E + D×F2.利用摩根定律,将乘法运算转化为加法运算:(A·B") + (A·C") + (D·E") + (D·F")3.继续化简,利用布尔加法、减法和非运算:A·B" + A·C" + D·E" + D·F"五、化简后的布尔表达式的应用化简后的布尔表达式在数字电路设计和计算机科学领域具有广泛的应用。
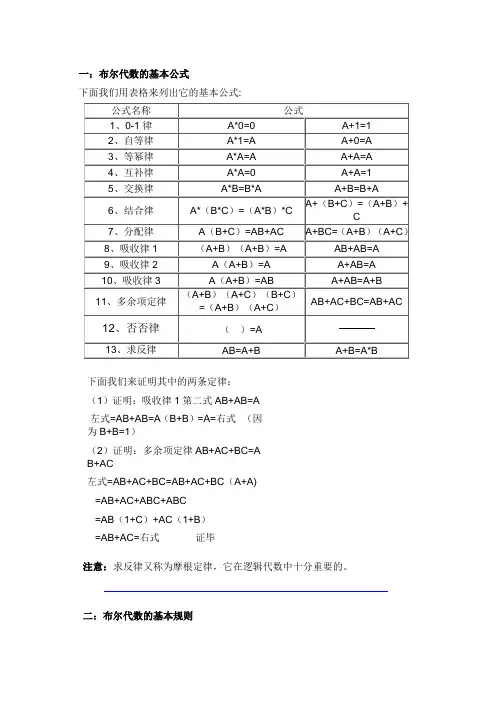
一:布尔代数的基本公式下面我们用表格来列出它的基本公式:下面我们来证明其中的两条定律:(1)证明:吸收律1第二式AB+AB=A左式=AB+AB=A(B+B)=A=右式(因为B+B=1)(2)证明:多余项定律AB+AC+BC=AB+AC左式=AB+AC+BC=AB+AC+BC(A+A)=AB+AC+ABC+ABC=AB(1+C)+AC(1+B)=AB+AC=右式证毕注意:求反律又称为摩根定律,它在逻辑代数中十分重要的。
二:布尔代数的基本规则代入法则它可描述为逻辑代数式中的任何变量A,都可用另一个函数Z 代替,等式仍然成立。
对偶法则它可描述为对任何一个逻辑表达式F,如果将其中的“+”换成“*”,“*”换成“+”“1”换成“0”,“0”换成“1”,仍保持原来的逻辑优先级,则可得到原函数F的对偶式G,而且F与G互为对偶式。
我们可以看出基本公式是成对出现的,二都互为对偶式。
反演法则有原函数求反函数就称为反演(利用摩根定律),我们可以把反演法则这样描述:将原函数F中的“*”换成“+”,“+”换成“*”,“0”换成“1”,“1”换成“0”;原变量换成反变量,反变量换成原变量,长非号即两个或两个以上变量的非号不变,就得到原函数的反函数。
的基本公式下面我们用表格来列出它的基本公式:下面我们来证明其中的两条定律:(1)证明:吸收律1第二式AB+AB=A左式=AB+AB=A(B+B)=A=右式(因为B+B=1)(2)证明:多余项定律AB+AC+BC=AB+AC左式=AB+AC+BC=AB+AC+BC(A+A)=AB+AC+ABC+ABC=AB(1+C)+AC(1+B)=AB+AC=右式证毕注意:求反律又称为摩根定律,它在逻辑代数中十分重要的。
二:布尔代数的基本规则代入法则它可描述为逻辑代数式中的任何变量A,都可用另一个函数Z 代替,等式仍然成立。
对偶法则它可描述为对任何一个逻辑表达式F,如果将其中的“+”换成“*”,“*”换成“+”“1”换成“0”,“0”换成“1”,仍保持原来的逻辑优先级,则可得到原函数F的对偶式G,而且F与G互为对偶式。
布尔代数法引言布尔代数法是一种逻辑思维工具,用于解决逻辑问题和设计数字电路。
它源于数学家乔治·布尔的研究,是20世纪发展起来的一种重要数学分支。
布尔代数法基于布尔变量和逻辑运算符,通过表达式的逻辑真值来描述和分析逻辑关系。
布尔代数基础布尔代数的基本元素是布尔变量,它的取值只能为真(1)或假(0)。
布尔变量通常用字母表示,如A、B、C等。
布尔代数包含以下逻辑运算符:1. 逻辑与运算逻辑与运算符表示两个布尔变量同时为真时的结果为真,否则为假。
逻辑与运算符用符号“∧”表示。
例如,A∧B表示A和B都为真时结果为真。
2. 逻辑或运算逻辑或运算符表示两个布尔变量至少一个为真时的结果为真,否则为假。
逻辑或运算符用符号“∨”表示。
例如,A∨B表示A和B中至少一个为真时结果为真。
3. 逻辑非运算逻辑非运算符表示对一个布尔变量取反,即真变假,假变真。
逻辑非运算符用符号“¬”表示。
例如,¬A表示A为假时结果为真。
布尔代数的运算法则布尔代数有一些运算法则,它们可以用于简化和分析逻辑表达式。
以下是常用的布尔代数运算法则:分配律是布尔代数中重要的法则之一。
它能够将逻辑和运算或逻辑或运算应用到一组布尔变量上。
分配律有两种形式:乘积和和的分配律。
乘积形式的分配律:A∧(B∨C) = (A∧B)∨(A∧C)和的形式的分配律:A∨(B∧C) = (A∨B)∧(A∨C)2. 吸收律吸收律能够用于减少逻辑表达式中的项,使其更加简洁。
吸收律有两种形式:乘积和和的吸收律。
乘积形式的吸收律:A∧(A∨B) = A和的形式的吸收律:A∨(A∧B) = A3. 交换律交换律适用于逻辑与运算和逻辑或运算。
它们允许交换布尔变量的位置,不影响结果。
逻辑与运算的交换律:A∧B = B∧A逻辑或运算的交换律:A∨B = B∨A布尔代数的应用布尔代数在逻辑设计和计算机科学等领域有广泛的应用。
以下是一些常见的布尔代数的应用:1. 逻辑电路设计布尔代数可以用来设计和分析数字电路,如门电路和寄存器。
布尔代数化简摘要:1.布尔代数的基本概念2.布尔代数的运算法则3.布尔代数的化简方法4.布尔代数化简的实际应用正文:1.布尔代数的基本概念布尔代数(Boolean algebra),又称为逻辑代数,是由英国数学家乔治·布尔(George Boole)在19 世纪创立的一种代数系统。
布尔代数主要用于研究逻辑关系,它的基本元素是逻辑变量,通常用p、q、r 等表示。
逻辑变量只有两种取值,即真(1)和假(0)。
布尔代数的基本运算有与(∧)、或(∨)、非()三种。
2.布尔代数的运算法则布尔代数的运算法则包括以下三个基本定律:(1)分配律:p ∧ (q ∨ r) = (p ∧ q) ∨ (p ∧ r),p ∨ (q ∧ r) = (p ∨ q) ∧ (p ∨ r)(2)结合律:(p ∧ q) ∧ r = p ∧ (q ∧ r),(p ∨ q) ∨ r = p∨ (q ∨ r)(3)交换律:p ∧ q = q ∧ p,p ∨ q = q ∨ p以及一个重言式:p ∧ p = p3.布尔代数的化简方法布尔代数化简的主要目的是将复杂的逻辑表达式简化为简单的逻辑表达式。
化简方法包括:(1)使用分配律将复杂的逻辑表达式拆分为简单的逻辑表达式。
(2)利用结合律和交换律改变逻辑表达式的结构,使其更易于理解。
(3)利用重言式p ∧ p = p 将复杂的逻辑表达式中的相同项合并。
4.布尔代数化简的实际应用布尔代数化简在实际应用中具有重要意义。
例如,在计算机科学中,逻辑电路的设计和分析需要用到布尔代数化简。
通过化简逻辑表达式,可以降低电路的复杂度,提高电路的运行效率。
布尔代数、∙目录∙发现者和发现过程Boolean algebra英国数学家G.布尔为了研究思维规律(逻辑学、数理逻辑)于1847和1854年提出的数学模型。
此后R.戴德金把它作为一种特殊的格。
所谓一个布尔代数,是指一个有序的四元组〈B,∨,∧,*〉,其中B是一个非空的集合,∨与∧是定义在B上的两个二元运算,*是定义在B上的一个一元运算,并且它们满足一定的条件。
布尔代数由于缺乏物理背景,所以研究缓慢,到了20世纪30~40年代才有了新的进展,大约在1935年,M.H.斯通首先指出布尔代数与环之间有明确的联系,他还得到了现在所谓的斯通表示定理:任意一个布尔代数一定同构于某个集上的一个集域;任意一个布尔代数也一定同构于某个拓扑空间的闭开代数等,这使布尔代数在理论上有了一定的发展。
布尔代数在代数学(代数结构)、逻辑演算、集合论、拓扑空间理论、测度论、概率论、泛函分析等数学分支中均有应用;1967年后,在数理逻辑的分支之一的公理化集合论以及模型论的理论研究中,也起着一定的作用。
近几十年来,布尔代数在自动化技术、电子计算机的逻辑设计等工程技术领域中有重要的应用。
1835年,20岁的乔治·布尔开办了一所私人授课学校。
为了给学生们开设必要的数学课程,他兴趣浓厚地读起了当时一些介绍数学知识的教科书。
不久,他就感到惊讶,这些东西就是数学吗?实在令人难以置信。
于是,这位只受过初步数学训练的青年自学了艰深的《天体力学》和很抽象的《分析力学》。
由于他对代数关系的对称和美有很强的感觉,在孤独的研究中,他首先发现了不变量,并把这一成果写成论文发表。
这篇高质量的论文发表后,布尔仍然留在小学教书,但是他开始和许多第一流的英国数学家交往或通信,其中有数学家、逻辑学家德·摩根。
摩根在19世纪前半叶卷入了一场著名的争论,布尔知道摩根是对的,于是在1848年出版了一本薄薄的小册子来为朋友辩护。
这本书是他6年后更伟大的东西的预告,它一问世,立即激起了摩根的赞扬,肯定他开辟了新的、棘手的研究科目。
一:布尔代数的基本公式
下面我们用表格来列出它的基本公式:
下面我们来证明其中的两条定律:
(1)证明:吸收律1第二式AB+AB=A
左式=AB+AB=A(B+B)=A=右式(因
为B+B=1)
(2)证明:多余项定律AB+AC+BC=A
B+AC
左式=AB+AC+BC=AB+AC+BC(A+A)
=AB+AC+ABC+ABC
=AB(1+C)+AC(1+B)
=AB+AC=右式证毕
注意:求反律又称为摩根定律,它在逻辑代数中十分重要的。
二:布尔代数的基本规则
代入法则它可描述为逻辑代数式中的任何变量A,都可用另一个函数Z 代替,等式仍然成立。
对偶法则它可描述为对任何一个逻辑表达式F,如果将其中的“+”换成“*”,“*”换成“+”“1”换成“0”,“0”换成“1”,仍保持原来的逻辑优先级,则可得到原函数F的对偶式G,而且F与G互为对偶式。
我们可以看出基本公式是成对出现的,二都互为对偶式。
反演法则有原函数求反函数就称为反演(利用摩根定律),
我们可以把反演法则这样描述:将原函数F中的“*”换成“+”,“+”换成“*”,“0”
换成“1”,“1”换成“0”;原变量换成反变量,反变量换成原变量,长非号即两个或两个以上变量的非号不变,就得到原函数的反函数。
的基本公式
下面我们用表格来列出它的基本公式:
下面我们来证明其中的两条定律:
(1)证明:吸收律1第二式AB+AB=A
左式=AB+AB=A(B+B)=A=右式(因
为B+B=1)
(2)证明:多余项定律AB+AC+BC=AB
+AC
左式=AB+AC+BC=AB+AC+BC(A+A)
=AB+AC+ABC+ABC
=AB(1+C)+AC(1+B)
=AB+AC=右式证毕
注意:求反律又称为摩根定律,它在逻辑代数中十分重要的。
二:布尔代数的基本规则
代入法则它可描述为逻辑代数式中的任何变量A,都可用另一个函数Z 代替,等式仍然成立。
对偶法则它可描述为对任何一个逻辑表达式F,如果将其中的“+”换成“*”,“*”换成“+”“1”换成“0”,“0”换成“1”,仍保持原来的逻辑优先级,则可得到原函数F的对偶式G,而且F与G互为对偶式。
我们可以看出基本公式是成对出现的,二都互为对偶式。
反演法则有原函数求反函数就称为反演(利用摩根定律),
我们可以把反演法则这样描述:将原函数F中的“*”换成“+”,“+”换成“*”,“0”换成“1”,“1”换成“0”;原变量换成反变量,反变量换成原变量,长非号即两个或两个以上变量的非号不变,就得到原函数的反函数。