当前位置：文档之家 › 第九章 玻色统计和费密统计理论

第九章 玻色统计和费密统计理论

  • 格式：pdf
  • 大小：298.44 KB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

玻色统计和费米统计+ppt

玻色统计和费米统计+ppt

f (ε) =
称为费米函数。在固体物理学中，化学势称为费 称为费 称为费米函数。在固体物理学中， 费米函数 米能级， 表示。 米能级，用ε F表示。 ），此时 当T→0 K时（费米能级ε F(0)），此时 → 时 ），此时1/kT→∞ ， →∞ 由上式得到
ωl
al
=
1 e
(ε -) kT
+1
f (ε ) = 1 , 当 ε ≤ ε F (0) 时; f (ε ) = 0 , 当 ε > ε F (0) 时.
U (ν , T ) 8πhν dν ρ ν ( T ) dν = dν = V c 3 e hν / kT 1
3
6
利用λν = c 和 dν = 上式化为
cdλ
λ
2
并考虑 ρν dν = ρλ dλ
ρ λ (T ) =
8 πhc
λ
5
(
1 e
hc / λ kT
1
)
将上式代入单色辐出度Mλ (T ) ，将Mλ (T) 改为 将上式代入单色辐出度 Mλ 0 (T)，得到 ，
f 1 1／2 ／
o
2
εF(0)
3 5π kT 2 U(T) = Nε F (0)[1 + ( ) ] 5 12 ε F (0)
19
N是系统内自由电子总数。 是系统内自由电子总数。 是系统内自由电子总数
18
处于ε F(0) 附近能态的电子和低能态的电子情 附近、 况不同 ，只有在εF(0)附近、数量级为 能量范 附近 数量级为kT 围内的能态占据情况才会发生变化 ， 其余绝大 多数能态的占据实际上并不改变，如图所示。 多数能态的占据实际上并不改变，如图所示。 对自由电子热容有贡献 的也是处于εF(0)附近能态 附近能态 的电子。 的电子。 自由电子气体系统的内 能用εF (0)可表示为 可表示为

凝聚态物理学中的玻色子与费米子

凝聚态物理学中的玻色子与费米子

凝聚态物理学中的玻色子与费米子凝聚态物理学是研究物质在集体行为中的性质和相变的学科。

在这个广阔的领域中，玻色子和费米子是两种基本的粒子，它们在物质中起着重要的角色。

本文将介绍玻色子和费米子的特性以及它们在凝聚态物理学中的应用。

一、玻色子的特性玻色子是一类自旋为整数的基本粒子，根据玻色–爱因斯坦统计，它们具有玻色统计性质。

最著名的玻色子是光子，它是电磁辐射的量子，没有质量和电荷，也是光的传播媒介。

除了光子以外，还有声子、准粒子等许多其他的玻色子存在。

玻色子的一个重要特性是它们可以聚集在同一个量子态，形成所谓的玻色-爱因斯坦凝聚。

这种凝聚态相当于一个巨大的共振态，所有玻色子将集体行为地维持在同一个基态。

这种凝聚态物质的行为在超导领域引起了广泛的研究，使得科学家们能够更好地理解新奇的物理现象。

二、费米子的特性费米子是一类自旋为半整数的基本粒子，根据费米–狄拉克统计，它们具有费米统计性质。

最著名的费米子是电子，它是构成物质的基本组成部分，具有质量和电荷。

费米子具有一种独特的特性，即不能聚集在同一个量子态，这就是所谓的泡利不相容原理。

泡利不相容原理导致费米子的排斥行为，通过排斥来形成精细结构，如原子的电子排布和分子的化学键。

正是由于费米子的排斥性质，物质才能够在一些极端条件下得到更加复杂的表现。

三、玻色子和费米子在凝聚态物理学中的应用1. 量子统计和超流体玻色子和费米子的量子统计性质对凝聚态物理学研究具有重要影响。

在低温下，玻色子可以表现出超流性，即在没有粘滞性的情况下流动。

超流体的研究不仅有助于我们理解基本粒子的行为，还在技术和应用领域有很多潜在的应用，如量子计算和超导材料等。

2. 凝聚态物质的相变凝聚态物质可以在不同的温度和压力下发生各种相变，包括固体-液体相变、超导-非超导相变等。

这些相变的理解和控制对于实现新的功能材料和技术具有重要意义。

玻色子和费米子在相变研究中的作用体现在它们的自旋、电荷等性质能够在相变过程中发生变化，导致物质的性质发生巨大的变化。

波色统计和费米统计

波色统计和费米统计
l
e l ( 1) l l 1 e l y l
e
l
l
l 1 y
al
l
l y
Y
Y
1 ln y
对比玻耳兹曼分布
1 ln Z1 Y N y
压强
p
1 ln V
al
l
1 x 2 x 1 e e x l l l e (1 e ) 1 e
13 热统
华中科技大学光学与电子信息学院
考虑平动
p2 2m
3 / 2 1/ 2 粒子微观状态数 D( )d g 2V ( 2 m ) d 3
e e
1 x 2 x 1 e e x 1 e
1 2 2 1 2
3 2 5
1 1 e x 1 x x 2 ( 1 e )( 1 e ) x 1 e 2
1 x 1 2 2 x 1 1 e e 1 5 e 2 2 2 2
e l ( 1) l 1 e l l

l
e l 1
ln
4
l
N
对比玻耳兹曼分布
N
N Z1e
热统
玻色统计和费米统计
华中科技大学光学与电子信息学院
2 内能
U l al
l l
e l 1
l al
al
))
k ln F .D
热统
玻色统计和费米统计
华中科技大学光学与电子信息学院
§8.2 弱简并玻色气体和费米气体
玻色统计与费米统计描述不可区分的粒子系统。主要是空间中不可 区分。但当粒子在空间可以区分时（稀薄气体），应该由描述可区分 粒子系统的理论－玻耳兹曼统计－描述。

凝聚态物理学中的玻色子与费米子

凝聚态物理学中的玻色子与费米子

凝聚态物理学中的玻色子与费米子凝聚态物理学是研究物质在宏观尺度上的性质和行为的领域。

在这个领域中，玻色子和费米子是两个重要的概念。

本文将探讨这两种粒子在凝聚态物理学中的重要性和应用。

玻色子和费米子是基本粒子的分类方式之一。

前者是具有整数自旋的粒子，如光子、声子、玻色-爱因斯坦凝聚（Bose-Einstein Condensate）中的粒子等；后者则是具有半整数自旋的粒子，如电子、质子和中子等。

这两种粒子的行为和性质有着显著的差异。

首先，玻色子和费米子的最显著区别之一是它们服从的统计分布。

根据玻色-爱因斯坦统计，多个玻色子可以占据同一个量子态，这就导致了Bose-Einstein凝聚的产生，其中所有粒子都处于同一个量子态，表现出量子相干性。

而根据费米-狄拉克统计，费米子不允许多个粒子处于同一个态，这也是为什么我们不能在同一时刻在同一个位置找到两个电子的原因。

这两种统计分布的不同给玻色子和费米子带来了截然不同的行为。

在凝聚态物理学中，玻色子和费米子有着不同的物理性质和相互作用。

作为最重要的实例之一，玻色-爱因斯坦凝聚是玻色子行为的一个突出例证。

在极低温度下，玻色子可以凝聚成一个巨大的波函数，而不再是彼此独立的实体。

这种凝聚体现了量子力学的特性，如相干性和波动性，是研究玻色子集体行为的有力工具。

与此相反，由于费米-狄拉克统计的限制，费米子之间的相互作用具有独特的属性。

著名的是，费米子统计下的电子导致了电子波函数的空间分布，进而导致了周期性的晶体结构。

这就是凝聚态物理学中晶体的形成原理之一。

费米子之间的排斥效应也导致了材料的稳定性，使得粒子之间不能靠得太近，从而形成凝聚态物质的基本结构。

除了上述的基本性质之外，玻色子和费米子在凝聚态物理学中还有广泛的应用。

玻色子激发态在超导体中扮演着重要的角色，通过与声子相互作用来传导电子。

费米子的行为则解释了诸如半导体和绝缘体等材料的电子结构，为材料的性质和行为提供了重要的基础。

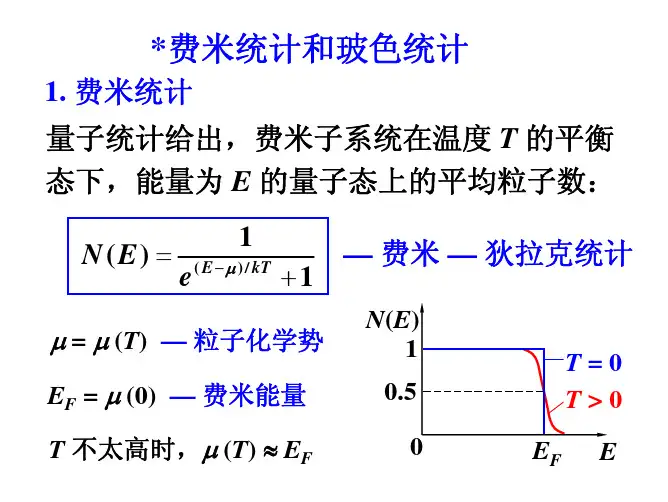
费米统计和玻色统计

费米统计和玻色统计
*费米统计和玻色统计
1. 费米统计 量子统计给出，费米子系统在温度 T 的平衡 态下，能量为 E 的量子态上的平均粒子数：
N (E) = 1 e
( E − μ ) / kT
+1
— 费米 — 狄拉克统计
N(E) 1 0.5 0 EF
μ = μ (T) — 粒子化学势
EF = μ (0) — 费米能量 T 不太高时，μ (T) ≈ EF
±1
≈e
− ( E − μ ) / kT
=e
μ / kT
⋅e
− E / kT
= A(T )e − E / kT
— 麦克斯韦 — 玻耳兹曼统计 所以高能态时，量子统计就过渡到经典的 麦克斯韦 — 玻耳兹曼统计。
Hale Waihona Puke 2. 玻色统计 量子统计给出，玻色子系统在温度 T 的平衡 态下，能量为 E 的量子态上的平均粒子数：
N (E) = 1 e ( E − μ ) / kT − 1
— 玻色 — 爱因斯坦统计 对所有温度 T ，N(E) 应满足 0 ≤ N(E) < ∞ ， 由此可引出玻色 — 爱因斯坦凝聚的概念。
设最低能级（基态）为能量零点：E0 = 0， 1 N 0 = N ( E 0 ) = − μ / kT e −1 T → 0K 时，要求 0 ≤ N0 < ∞ ， 则有 μ < 0 。
原子速度分布逐渐达到BEC的三维示意图 1995年实现了超冷原子的BEC，达到了宏观数量的 原子处于同一量子态（2001 Nobel）。 BEC实现了 原子相干，可做成原子干涉仪和量子频标等。
3. 量子统计到经典统计的过渡 当 E 很高时，(E−μ) >> kT
N (E) = 1 e

玻色子与费米子

玻色子与费米子

正确性？ 等概率原理是统计物理学中的一个合理的基本假设，该原理 不能从更基本的原理推出，也不能直接从实验上验证，它的正 确性在于从它推出的各种结论与客观实际相符而得到肯定。
四、分布与微观状态数
1. 分布
设有一个系统，由大量的近独立粒子构成，具有确定的N、U、V ，对于 确定的宏观状态下，如果系统的粒子按能级作如下排列：
形象描述：
一个粒子在某时刻的力学运动状态可以在μ空间中用一个点表示； 由N个全同粒子组成的系统在某时刻的微观运动状态可以在μ空间中用N 个点表示； 如果交换两个代表点在μ空间的位置，相应的系统的微观状态是不同的。
1
2





2. 系统微观运动状态的量子力学描述
•玻色子与费米子
a）费米子：自旋量子数为半整数的粒子。 如：电子、质子、中子等。 b）玻色子：自旋量子数为整数的粒子。 如：光子、介子等。
一个简单规则（几乎普遍适用）：
由玻色子构成的复合粒子是玻色子； 由偶数个费米子构成的复合粒子是玻色子； 由奇数个费米子构成的复合粒子是费米子。
例子： H原子， H原子， He原子为玻色子
2 3 3 H原子， H原子， He原子为费米子
1 2 4
费米子遵从泡利不相容原理: 在含有多个全同近独立费米子的系统，占据一个个体量子态的费米子不可 能超过一个。 玻色子构成的系统不受泡利不相容原理的约束。
3.玻耳兹曼系统、玻色系统、费米系统
玻耳兹曼系统: 由可分辨的全同近独立粒子组成； 特点：处在一个个体量子态上的粒子数不受限制。 玻色系统: 由不可分辨的全同近独立的玻色粒子组成； 特点：不受泡利不相容原理的约束，即处在同一个个体量子态上的粒子数 不受限制。 费米系统: 由不可分辨的全同近独立的费米粒子组成； 特点：受泡利不相容原理的约束，即处在同一个个体量子态上的粒子数 最多只能为1个粒子。 设系统由两个粒子组成，粒子的个体量子态有3个，如果这两个粒子分 属玻耳兹曼系统、玻色系统、费米系统时，试分别讨论系统各有那些可能的 微观状态？

费米狄拉克统计和玻色爱因斯坦统计

费米狄拉克统计和玻色爱因斯坦统计

费米狄拉克统计和玻色爱因斯坦统计费米狄拉克统计和玻色爱因斯坦统计是两种用于描述粒子统计行为的统计方法。

它们分别适用于费米子和玻色子，这两种粒子在量子力学中具有不同的交换行为和性质。

了解它们的差异对于研究粒子的行为以及理解宏观物理现象至关重要。

一、费米狄拉克统计费米狄拉克统计是描述费米子统计行为的一种统计方法。

费米子是一类具有半整数自旋的粒子，例如电子、质子和中子等。

狄拉克统计的主要特点是：每个量子态只能由一个费米子占据，不同费米子之间不能占据相同的量子态。

这种排斥行为称为泡利不相容原理，它导致了费米子在填充能级时的特殊性质。

对于费米子系统，它们的能级填充遵循费米-狄拉克分布函数。

费米-狄拉克分布函数表示了在温度为T的热平衡下，粒子占据能级的概率。

在零温下，费米子会填充最低的能级，而在有限温度下，费米子的填充受到波尔兹曼因子的影响。

二、玻色爱因斯坦统计玻色爱因斯坦统计是描述玻色子统计行为的统计方法。

玻色子是一类具有整数自旋的粒子，例如光子、声子和玻色凝聚中的声子等。

相比于费米子，玻色子具有不同的交换行为，允许多个玻色子占据相同的量子态。

玻色爱因斯坦统计的特点是，可以有多个玻色子处于同一能级上，而且他们之间的交换不会对系统的状态产生影响。

当玻色子系统处于热平衡时，玻色-爱因斯坦分布函数描述了粒子占据能级的概率分布。

在更低的温度下，玻色子会聚集在能级的基态上，形成玻色凝聚。

三、费米狄拉克统计和玻色爱因斯坦统计的应用费米狄拉克统计和玻色爱因斯坦统计在理论物理和实验物理研究中有广泛的应用。

它们被用来描述固体材料的电子结构、理解物质的热力学性质以及研究凝聚态物理中的相变和超流性等现象。

在固体物理学中，费米狄拉克统计用来解释电子在晶格中的分布，特别是在导体中的电子行为。

根据费米狄拉克统计，能带中的电子填充遵循泡利不相容原理，因此解释了为什么导体具有电流传导的性质。

而在玻色爱因斯坦统计方面，光子是一种典型的玻色子。

物理化学第九章 统计热力学初步

物理化学第九章 统计热力学初步

统计热力学的基本任务
根据对物质结构的某些基本假定，以及实 验所得的光谱数据，求得物质结构的一些基本常 数，如核间距、键角、振动频率等，从而计算分 子配分函数。再根据配分函数求出物质的热力学 性质，这就是统计热力学的基本任务。
定域子系统和离域子系统
粒子（子）（particles) ——聚集在气体、液体、固 体中的分子、原子、离子等。
t r v e n
同时，其简并度等于各独立运动形式的简并度之 积：
g gt gr gv ge gn
运动自由度
对于一个具有n个原子的分子，通常有3n个自 由度，分别为： 3个平动自由度（xyz轴方向的平动） 3个转动自由度（围绕三个轴的旋转） 3n-6个振动自由度 对于线型分子，转动自由度为2（围绕线轴的 旋转可忽略），振动自由度为3n-5
系统的可能的能级分布方式有：
能级分布数
能级分布 n0
n1
n2 n3
Σni
Σniεi =9hν/2
Ⅰ 0 3 0 0 3 3×3 hν/2=9hν/2
Ⅱ 2 0 0 1 3 2×hν/2+1×7hν/2=9hν/2
Ⅲ 1 1 1 0 3 1×hν/2+1×3hν/2 +1×5hν/2=9hν/2
2.状态分布
1.分子的平动
t
h2 8m
(
nx2 a2
n2y b2
nz2 c2
)
对立方容器a=b=c，V=a3
t
h2 8mV 3 / 2
( nx2
n2y
nz2
)
量子力学中把能级可能有的微观状态数称为该 能级的简并度(degeneration)，用符号g表示。 简并度亦称为退化度或统计权重。

热力学统计物理玻耳兹曼统计

热力学统计物理玻耳兹曼统计

义
粒子处在该
能级的几率
有效状 态数
al
N Z1
l
e
l
al
el l
N
Z1
el l el l
玻耳兹
曼因子 粒子总是优先占据较低能级；温度升高，占 据该能级的几率增大。
Z1——有效状态和 一个粒子所有可能达到的有效状态的总和。
热统 西华大学 理化学院
6
f e s
l 能量为εl的一个量子态s上的平均粒子数
p
3.粒子配分函数的经典表达式
处元于内能层的l 粒l内子，数运为动：状态处于相体积
al
l
h0r
fs
l h0r
e l
N Z1
l
h0r
el
l x
Z1
l
el l
h0r
al
N Z1
l
h0r
el
取 l 足够小，求和可化为积分：
Z1
el d
h0r
e ( p,q) dq1dq2 dqr dp1dp2 dpr h0r
l l
FD l l! BE
l
l
l
e l
ln
l l
l
对于满足非兼并条件的处
于平衡态（最可几分布） lnFD lnBE l ln l lnl !
的非定域（玻色、费米） 系统，通过对所对应的系 统微观状态数目取对数， 得到了微观状态数目的对 数ln与系统包含的粒子数
l
l
l ln l l ln l 1
玻尔兹曼、玻色、费米系统之间的关系
玻色粒子，玻色分布
＝
e＋
1
非兼并条件
e》1 l l
费密粒子，费密分布

量子理论的诞生和发展（13）：玻色统计和费米统计

量子理论的诞生和发展（13）：玻色统计和费米统计

量子理论的诞生和发展（13）：玻色统计和费米统计作者：张天蓉物理学中的统计规律是指粒子系统的宏观运动规律。

波尔兹曼研究的是经典粒子的统计行为，粒子系统的自由度用麦克斯韦-波尔兹曼统计方法来描述或计算。

不同于经典统计，量子力学的统计规律则有两种：玻色-爱因斯坦统计和费米-狄拉克统计。

图13-1：波色和费米提出量子统计理论的这四位物理学家，其中玻色可能是很多人不甚了解的一位。

玻色是印度人，他在一次有关光电效应的讲课中，因为犯了一个违反经典统计的“錯誤”却发现了玻色子的统计规律。

物理学中以他的名子命名玻色子，这使得他在物理学界还是挺有名的。

纳特·玻色（Nath Bose，1894年－1974年）出生于印度加尔各答，他的父亲是一名铁路工程师，他是七名孩子中的长子。

玻色在大学时曾得到几位优秀教师的赞赏和指点。

他获得数学硕士学位之后并未继续攻读博士，而是直接在加尔各答物理系担任讲师。

后来，他又到达卡大学物理系任讲师，并自学物理。

大约是在1921年，玻色讲授光电效应和黑体辐射引发的紫外灾难，他本来是想按照经典方法分析粒子的统计行为，结果犯了一个类似“掷两枚硬币，得到“正正”概率为三分之一”的错误。

然而没想到是，他的这个错误却得出了与实验相符合的结论，也就是不可区分的全同粒子所遵循的一种统计规律。

所谓“掷两枚硬币，‘正正’概率为三分之一”是错误的，意思是说当你掷两枚硬币的时候，因为每个硬币都有正反两面，实验结果就有四种情况：正正、正反、反正、反反。

也就是说，按照经典理论，这四种情况中的每一种发生的几率是一样的，即都是四分之一，但玻色所得到的结果却是三分之一。

玻色的这个“错误”之所以是“不可区分的全同粒子”的统计规律，是因为对于两个粒子而言，它们的统计行为是否可以区分或不可区分是有区别的。

假如两枚硬币不能区分谁正谁反，你掷两枚硬币所得到的正、反与反、正就是完全一样的结果。

“不可区分”的两个粒子如同“量子硬币”，它们在宏观系统中总是给我们完全一模一样的感觉。

玻色分布和费米分布

玻色分布和费米分布

玻色分布和费米分布现对费米分布推导如下 ： 对 ()∏-=Ωl l l l l D F a a !!!..ωω 取对数得：()[]∑---=Ωl l l l l D F a !ln !ln !ln ln ..εωω N>>1，若假设a l >>1 ， ωl >>1可得到：()()[]∑----=Ωll l l l l l l l D F a a a a ωωωωln ln ln ln ..约束条件：∑=llN a；∑=lll E a ε为求在此约束条件下的最大值，使用拉格朗日乘数法，取未定因子为α和β则拉格朗日函数为：l l l l l lD F a a aE N δβεαωβδαδδ∑⎪⎪⎭⎫ ⎝⎛++--=--Ωln ln .. 若令上式为零，则有：0ln=++-l l l l a a βεαω ， 即上式给出了费米系统粒子的最概然分布，称为费米——狄拉克分布。

玻色分布的推导作为练习，请同学们课后自己推导. 6．8 三种分布的关系 1 、由∑=llN a∑=lll E aε确定拉氏乘子a 和β的值.在许多实际问题中,也往往将β看作由实验确定的已知参量而由∑=l ll aεE 确定系统的内能.或将a 和β都当作由实验确定的已知参量,而由∑=llN a∑=lll E aε确定系统的平均总粒子数和内能.2 、能级的εl 有ωl 个量子态处在其中任何一个量子态上的平均粒子数应该是相同的,因此处在能量为εS 的量子态S 上的平均粒子数为: sss a f ω=即: sss a f ω=定域系统 ：seβεα--费米系统：11++se βεα 玻色系统：11++seβεα总粒子数和能量可分别表示为: N =∑ssf定域系统 =∑--sSe βεα“+”费米系统 “-”玻色系统 =∑±+sSe 11βεαE =∑sss f ε定域系统 =∑--ss Se βεαε“+”费米系统 “-”玻色系统 =∑±+ssSe 1βεαε(式中εs 为粒子的所有量子状态求和 )3 、若α满足 1>>αe ， 则 有: ss e e a lll βεαβεαωω++≈±=1这时玻色分布和费米分布都过渡到玻耳兹曼分布,由上式可知:11<<=+le a llβεαω（对所有l ）这时任一量子态上的平均粒子数都远小于1,这个式子就是前边提到的所谓的非简并性条件,当非简并条件满足时,费米分布和玻色分布都过渡到玻耳兹曼分布. 4 、在推导最概然分布时,应用了l >>1 ， ωl >>1, al -ωl >>1等条件,这些条件实际上是不满足的,这是推导过程的一个严重的缺点,我们将在后边的学习中用巨正则系统求平均分布的方法严格地导出这些分布.5 、定域系统和满足经典极限条件的玻色(费米)系统虽然遵从同样的分布,但它们的微观状态数是不同的.前者为ΩM.B.,后者为ΩM.B ./N!因此对那些直接由分布函数导出的热力学量,两者具有相同的统计表达式.然而,对于例如熵和自由能等与微观状态有关的热力学量,两者的统计表达式有差异.6最可几分布的推导也可以推广到含有多个组元的情况。

2023年大学_热力学统计物理第五版(汪志诚著)课后答案下载

2023年大学_热力学统计物理第五版(汪志诚著)课后答案下载

2023年热力学统计物理第五版(汪志诚著)课后答案下载热力学统计物理第五版(汪志诚著)内容简介导言第一章热力学的基本规律1.1 热力学系统的平衡状态及其描述1.2 热平衡定律和温度1.3 物态方程1.4 功1.5 热力学第一定律1.6 热容和焓1.7 理想气体的内能1.8 理想气体的绝热过程附录1.9 理想气体的卡诺循环1.10 热力学第二定律1.11 卡诺定理1.12 热力学温标1.13 克劳修斯等式和不等式1.14 熵和热力学基本方程1.15 理想气体的熵1.16 热力学第二定律的数学表述1.17 熵增加原理的简单应用1.18 自由能和吉布斯函数习题第二章均匀物质的热力学性质2.1 内能、焓、自由能和吉布斯函数的全微分 2.2 麦氏关系的简单应用2.3 气体的节流过程和绝热膨胀过程2.4 基本热力学函数的确定2.5 特性函数2.6 热辐射的热力学理论2.7 磁介质的.热力学2.8 获得低温的方法习题第三章单元系的相变3.1 热动平衡判据3.2 开系的热力学基本方程3.3 单元系的复相平衡条件3.4 单元复相系的平衡性质3.5 临界点和气液两相的转变3.6 液滴的形成3.7 相变的分类3.8 临界现象和临界指数3.9 朗道连续相变理论习题第四章多元系的复相平衡和化学平衡热力学第三定律 4.1 多元系的热力学函数和热力学方程4.2 多元系的复相平衡条件4.3 吉布斯相律4.4 二元系相图举例附录4.5 化学平衡条件4.6 混合理想气体的性质4.7 理想气体的化学平衡4.8 热力学第三定律习题第五章不可逆过程热力学简介5.1 局域平衡熵流密度与局域熵产生率 5.2 线性与非线性过程昂萨格关系5.3 温差电现象5.4 最小熵产生定理5.5 化学反应与扩散过程5.6 非平衡系统在非线性区的发展判据 5.7 三分子模型与耗散结构的概念习题第六章近独立粒子的最概然分布6.1 粒子运动状态的经典描述6.2 粒子运动状态的量子描述6.3 系统微观运动状态的描述6.4 等概率原理6.5 分布和微观状态6.6 玻耳兹曼分布6.7 玻色分布和费米分布……第七章玻耳兹曼统计第八章玻色统计和费米统计第九章系综理论第十章涨落理论第十一章非平衡态统计理论初步附录A 热力学常用的数学结果B 概率基础知识C 统计物理学常用的积分公式索引参考书目物理常量表热力学统计物理第五版(汪志诚著)图书目录《“十二五”普通高等教育本科国家级规划教材：热力学统计物理(第5版)》是“十二五”普通高等教育本科国家级规划教材，是作者在第四版的基础上全面修订而成的。

玻色统计研究玻色爱因斯坦凝聚

玻色统计研究玻色爱因斯坦凝聚

玻色统计研究玻色爱因斯坦凝聚
玻色爱因斯坦凝聚是一种奇特的量子现象，它描述了玻色子在低温条件下聚集到一个单一量子态的现象。

这种现象在实验室中已经被成功地观察到，并且已经被广泛应用于不同的领域，如超导性、光学和原子物理学等。

在理解玻色爱因斯坦凝聚的过程中，玻色统计发挥了重要的作用。

玻色子是一类不遵循泡利不相容原理的粒子，它们具有相同的量子态。

这意味着多个玻色子可以存在于同一个量子态中，形成一个大的集体。

在低温条件下，玻色子之间的相互作用将导致它们最终聚集在一个量子态中，形成玻色爱因斯坦凝聚。

这种凝聚现象在空间尺度上非常大，可以包含成千上万的玻色子。

玻色统计在理解玻色爱因斯坦凝聚的过程中起着至关重要的作用。

它提供了一种理论框架，描述了玻色子和凝聚态之间的相互作用。

同时，它也为实验研究和应用提供了丰富的思想和方法。

玻色统计和费米统计_热力学统计物理

玻色统计和费米统计_热力学统计物理

ln F.D l lnl al lnal (l al ) ln(l al )
l
l
l
S k ln F.D k( l lnl al lnal (l al ) ln(l al ))
ห้องสมุดไป่ตู้
l
l
l
S k(ln U N )
？ k ln F.D k( l lnl al lnal (l al ) ln(l al ))
l
l
e l (1) 1 e l
l
y
l
l l
e l 1 y
l
al
l
y
Y
Y 1 ln
y
对比玻耳兹曼分布 Y N 1 ln Z1 y
压强
p 1 ln
V
p N ln Z1
V
5
4 其它热力学函数：熵
由开系的热力学公式 dU Ydy dN TdS
S k(ln U N )
能否推导出 k ln B.E k( (l al ) ln(l al ) l lnl al lnal )
l
l
l
8
S k(ln U N )
al
l
e l
1
e l l al
al
l
ln l al
al
1 e l l l al
ln l ln(1 el ) (8.1.3)
l
ln
l ln(1 e l )
l
l
l
e l ( l )
1 e l
l
l l
e l 1
U
对比玻耳兹曼分布
U ln
U N ln Z1
4
3 广义力
Y
l

高二物理竞赛课件玻色统计与费米统计

高二物理竞赛课件玻色统计与费米统计

玻色统计与费米统计
当系统不满足非简并性条件，而且也不是定域系统时，需要采取玻色统计或费米统计的方法来处理。微观粒子全同性原理决定了二者与玻耳兹曼系统不同的宏观性质。
把玻色系统所遵循的玻色统计规律简称为玻色统计。把费米系统所遵循的费米统计规律简称为费米统计。
可以预期，由于玻耳兹曼系统与玻色系统和费米系统具有粒子可否分辨的差异，微观粒子全同性原理带来的量子统计关联对简并气体的宏观性质将产生决定性的影响；玻色系统和费米系统的差别也将使玻色气体和费米气体的内能和物态方程产生差异。
§8.1 热力学量的统计表达式
一.系统的平均粒子数
引入巨配分函数
的对数
其中：Βιβλιοθήκη 五. 巨热力学势玻尔兹曼关系式的证明
1.对于玻色子：
2. 费米子（略）：
二、 与基态粒子数

玻色子和费米子

玻色子和费米子

玻色子和费米子
粒子按其在高密度或低温度时集体行为的不同能够分成两大类：一类是费米子，得名于意大利物理学家费米，另一类是玻色子，得名于印度物理学家玻色。

区分这两类粒子的重要特点是自旋。

自旋是粒子的一种与其角动量（粒略地讲，确实是半径与转动速度的乘积）相联系的固有性质。

量子力学所揭示的一个重要之点是，自旋是量子化的，这确实是说，它只能取普朗克常数的整数倍（玻色子，如光子、介子等）或半整数倍（费米子，如电子、质子等）。

费米子和玻色子遵循完全不同的统计规律。

前者遵循的费米-狄拉克统计，其中一个显著和特点，确实是1925年瑞士科学家泡利发觉的“泡利不相容原理”，即在一个费米子系统中，绝不可能存在两个或两个以上在电荷、动量和自旋朝向等方面完全相同的费米子。

这就像电影院里的座位，每座只能容纳一个人。

而玻色子则完全不同，一个量子态能够容纳无穷多个玻色子。

因此，也只有玻色子才可能显现玻色－爱因斯坦凝聚现象。

例如，锂的两种同位素锂6和锂7分别为费米子和玻色子。

图片分别显示在810、510和240nk时锂6和锂7原子气和原子云照片。

我们能够看到，锂7（左），随着温度的降低所占的尺寸变小，也确实是发生了凝聚，而锂6（右）的尺寸则保持稳固，不发生凝聚。

这是因为泡利不相容原理的限制，使两个费米子不可能在同一时刻占据同一个空间。

正因如此，白矮星最终只能在引力作用下坍塌到一个极限尺寸而不再进一步缩小。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

β (du − Ydy ) = d ⎜ ⎜ ln Ξ − α
⎝
⎛
⎞ ∂ ∂ ˆ ln Ξ − β ln Ξ ⎟ ⎟ − αdN ∂α ∂β ⎠
(65.7)
对于闭系，系统与外界没有物质的交换， dN = 0 。这时（65.7）式简化为
β (dU − Ydy ) = d ⎜ ⎜ ln Ξ − α
⎝
⎛
⎞ ∂ ∂ ln Ξ − β ln Ξ ⎟ ⎟ ∂α ∂β ⎠
l
[
]
)
−ε l
（65.1）
Ξ 名为巨配分函数。巨配分函数的对数为
(
(65.2)
系统的平均总粒子数 N 可以表为
N =−
∂ ln Ξ ∂α
（65.3）
内能是系统所含粒子的无规运动的总能量
U = ∑ ε l βα l = ∑
l l
ε lω l
e
α + βε l
−1
通过 ln Ξ ，可以将 U 表为
U =−
ωl
e
α + βε l
−1
（64.5）
(64.5)式既是玻色系统中粒子的最可几分布，称为玻色分布。拉氏乘子 α 和 β 由条件(64.1) 即下式确定：
∑ eα
l
l + βε l
ω
−1
= N,
∑ eα
l
ε lω l
+ βε l
−1
= E,
（64.6）
现在导出费密系统的最可几分布。将(64.3)式取对数，得
ω = ck
P = hk
ε= ω
（66.4）
将(66.3)式代人(66.4)式，可以得到光子的能量动量关系 (66.5) ε = cp 光子是玻色子，达到平衡后遵从玻色分布。由于窑壁不断发射和吸收光子，在光于气体 中，光于数不是恒定的。在导出玻色分布时只存在 E 是常数的条件而不存在 N 是常数的条 件．因此我门只引进一个拉氏乘子 β 。这样光子的分布为
ε = ε 0 e i (k ⋅r −ωt )
（66.1）
其小中 ω 是圆频率，k 是波矢。k 的三个分量 k x , k y , k z 的可能值为
2π nx L 2π ky = ny L 2π kz = nz L kx =
n x = 0,±1,±2,
n y = 0,±1,±2,
（66.2）
n z = 0,±1,±2,
9.66 光子气体
在热力学部分我们曾经论证，空窖辐射的能量(内能)密度和能量密度按频率的分布只与 温度有关， 并证明能量密度与绝对温度的四次方成正比。 本节根据统计物理的理论研究空窖 辐射能量密度按频率的分布。 空窖内的辐射场可以分解为一系列单色平面波的叠加。 如果采用周期性边界条件， 单色 平面波的电场分量为
第九章
9.64
玻色统计和费密统计理论
玻色分布和费密分布
本节导出在玻色系统和费密系统中粒子的最可几分布。 考虑一个处在平衡状态的孤立系统具有确定的粒子数 N，体积 V 和能量 E（更精确地 况能量在 E 到 E+ ΔE 之间） 。我们以 ε l (l＝1，2，…)表示粒子的各个能级， ω l 表示能级 ε l 的简并度。以 { α l } 表示处在各能级上的粒子数。显然，分布 { α l } 必须满足条件
ε 0 有两个偏振方向。这两个偏振方向与 k 垂直，并相互垂直。单色平面波的磁场分量也有
相应的公式。将（66.1）式代入波动方程
∇ 2ε −
1 ∂2 ε =0 c 2 ∂t 2
可得， ω 与 k 之间存在以下关系 （66.3） 其小 c 是电磁波在真空的传播速度。 又有一定波矢 k 和一定偏振的单色平面波可以看作辐射场的一个自由度。 它以圆频率 ω 随时间作简谐变化，因此相当于一个振动自由度，通常称为辐射场的一个简正振动方式。 (66.2)式给出的 k 的可能假有无穷多个,相应于一个 k 又有两个偏振方向，所以整个辐射场是 具有无穷多个振动自由度的力学系统。根据统计物理理论可以研究这个系统的热力学性质， 求得其内能按频率的分布(习题 10.2)。 本节从粒子的观点研究空窖辐射问题。从粒子的观点可以把空窖内的辐射场看作光子 气体。在 S49 讲过，具有一定的波矢 k 和圆频率 ω 的单色平面波与具有一定的动量 p 和能 量 ε 的光子相应。动量 p 与波矢量 k，能量 ε 与圆频率 ω 之间遵从德布罗意关系
l
令 α l 有 δα l 的变化, ln Ω 将因而有 δ ln Ω 的变化,使 Ω 为极大的分布，必使 δ ln Ω =0：
δ ln Ω = ∑ [ln (ω l + α l ) − ln α l ] δα l = 0
l
但是各 δα l 不是任意的，必须满足条件：
δN = ∑ δα l = 0, δE = ∑ ε l δα l = 0
(64.3)
根据等几率原理， 对于处在平衡状态的孤立系统， 每一个可能的微观运动状态出现的几 率是相等的。因此，使 Ω 为极大的分布，出现的几率最大，是最可几分布。 先导出玻色系统的最可几分布。对(64.2)式取对数，得
ln Ω = ∑ [ln(ω l + α l − 1)!− ln α l !− ln(ω l − 1)!]
p=
1 ∂ ln Ξ β ∂V
(65.6)
由(65.4)式及(65.5)式得
β (dU − Ydy ) = − βd ⎜ ⎜
⎛ ∂ ln Ξ ⎞ ∂ ln Ξ ⎟ ⎟ + ∂y dy ⎝ ∂β ⎠
注意由(65.2)式引入的 ln Ξ 是 α , β , y 的函数，其全微分为
d ln Ξ =
故有
∂ ln Ξ ∂ ln Ξ ∂ ln Ξ dα + dβ + dy ∂α ∂β ∂y
积分得
⎛ ⎞ ∂ ∂ S = k⎜ ⎜ ln Ξ − α ∂α ln Ξ − β ∂β ln Ξ ⎟ ⎟ ⎝ ⎠
将(65.2)式代人(65.9)式，与(64.4)式比较，得
（65.9）
(65.10) (65.10)式就是玻耳兹曼关系。它给出熵函数 S 与微观状态数 Ω 的关系。 对于开系，将(65.7)式与开系的热力学基本方程
上式指出， β 是 (dU − Ydy ) 的积分因子。在热力学知道， (dU − Ydy ) 有积分因子去，使
1 (dU − Ydy ) = ds T
比较可知
β=
所以
1 kT
（65.8）
⎛ ⎞ ∂ ∂ dS = kd ⎜ ⎜ ln Ξ − α ∂α ln Ξ − β ∂β ln Ξ ⎟ ⎟ ⎝ ⎠
9.65
热力学公式
本节推导玻色系统和费密系统的热力学公式。 首先考虑玻色系统。我们把 α , β 和 y 看作由实验确定的参量。系统的平均总粒子数为
N = ∑α l = ∑
l l
ω
e
l
α + βε l
−1
对于玻色系统，引入函数
l l
Ξ = ∏ Ξ l = ∏ 1 − e −α − βε l ln Ξ = −∑ σ l ln 1 − e −α − βε l
fs =
1 e
α + βε l
∓1
（64.10）
(64.6)或(64.9)式也可表为
N =∑
E=∑
s
1
e
α + βε l
±1
（64.11）
εs
e
α + βε s
±1
其中
∑
s
对粒子的所有量子状态求和。
由于玻色分布(64.5)和费密分布(64.8)可以看出，如果 α 满足条件
e α >> 1
（64.12）
ln Ω = ∑ [ln ω l !− ln α l !− ln(ω l − α l )!]
假设 ω l >> 1, α l >> 1, ω l − α l >> 1 ，上式可近似为
ln Ω = ∑ [ω l ln ω l − α l ln α l − (ω l − α l ) ln (ω l − α l )]
l l
[
]
ωl
（65.13）
其对数
l
ln Ξ = ∑ ω l ln 1 + e −α − βω l
(
)
（65.14）
前面的讨论和有关公式完全适用。 如果要根据(65.2)式或(65.14)式求巨配分函数的对数，必须知道粒子的能级和能级的简 并度，并将求和计算出来。这是玻色统计理论和费密统计理论中求热力学函数的一般程序。 节中我们将讨论具体的例子。
J = −kT ln Ξ
（65.12）
当给定的参量是 N,T,V 时，可在(65.3)式中令 N = N ，解出 α = α ( N , T , V ) ，再代入 (65.4)，(65.5)和(65.9)式，而求得系统的基本热力学函数。 对于费密系统，只要将巨配分函数改为
Ξ = ∏ Ξ l = ∏ 1 + e −α − βε l
(64.5)式和(64.8)式分母中 ± 1 这一项就可以忽略。这时玻色分布和费密分布都过渡到玻耳兹 曼分布
α l = ω l e −α − βε
当(64.12)式满足时，显然有
l
（64.13）
αl << 1 (对所有 l) ωl
(64.14)
这时任一量子态上的平均粒于数都远小于 1(64.14)式就是 S50 所说的非简并性条件。当非简 并性条件满足时，玻色分布与费密分布都过渡到玻耳兹曼分布，这跟 S64 的有关结论是一 致的。 最后应当说明，在前面导出玻色分布和费密分布时，应用了诸如 α l >> 1, ω l >> 1 等条 件，这些条件实际不满足。因此以上的推导是有严重缺点的。我们在 S77 将用巨正则系综 求平均分布的方=