下载文档原格式
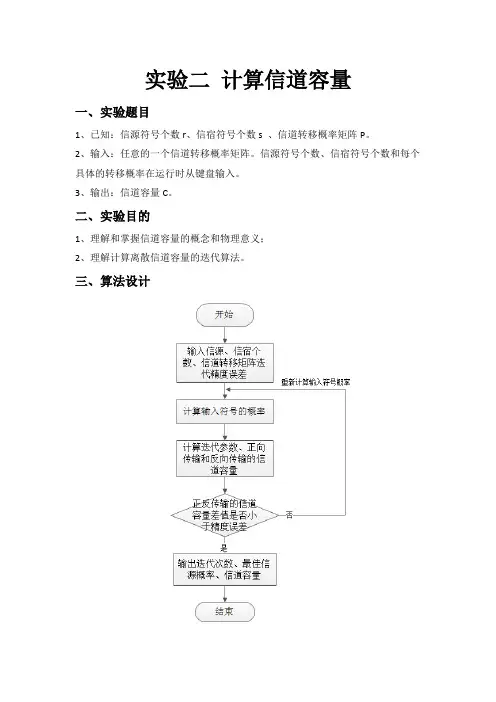
计算离散信源熵、离散信道容量1 实验任务和目的实验任务：（1）简要总结信源的熵、信道容量的物理意义，概念；（2）写出离散信源熵、离散信道容量计算的基本步骤，画出实现离散信源熵、离散信道容量计算的程序流程图；（3）讨论信源的熵的大小与前后符号之间相关性的关系，讨论信道容量与信源先验概率及信道转移概率的关系。
实验目的：掌握信源的熵、信道容量的物理意义，概念；熟练掌握离散信源熵、离散信道容量的计算方法步骤；利用Matlab 编写离散信源熵、离散信道容量的计算程序；验证程序的正确性。
2 实验过程和结果 2.1 实验过程1、简要总结信源的熵、信道容量的物理意义，概念。
信源熵的物理意义是指信源中的各个符号的平均不确定性；熵是信源符号的平均信息量，是信源符号的平均不确定度。
信道容量 概念：在信道可以传输的基本前提下，对信源的一切可能的概率分布而言，信道能够传输的最大（接收）熵速率称为信道容量。
意义：求出了某个信道的信道容量，也就找到了信源的最佳概率分布。
从而指导人们改造信源，使之最大可能地利用信道的传输能力。
2、写出离散信源熵、离散信道容量计算的基本步骤，画出实现离散信源熵、离散信道容量计算的程序流程图；离散信源熵的计算步骤：()()()11log log ()qr r r i i i i H X E p a a p a =⎛⎫==- ⎪⎝⎭∑信道容量的计算步骤：()(){}()符号/;max bit Y X I C XP =3、（1）讨论信源的熵的大小与前后符号之间相关性的关系，讨论信道容量与信源先验概率及信道转移概率的关系。
信源的相关性是信源符号间的依赖程度的度量。
由于信源输出符号间的依赖关系也就是 信源的相关性使信源的实际熵减小。
信源输出符号间统计约束关系越长，信源的实际熵越小。
当信源输出符号间彼此不存在依赖关系且为等概率分布时，信源的实际熵等于最大熵。
（2）信道容量与信源先验概率及信道转移概率的关系。
实验二 离散信道容量一、实验目的1. 掌握离散信道容量的计算。
2. 理解离散信道容量的物理意义。
3. 练习应用matlab 软件进行二元对称离散信道容量的函数曲线的绘制，并从曲线上理解其物理意义。
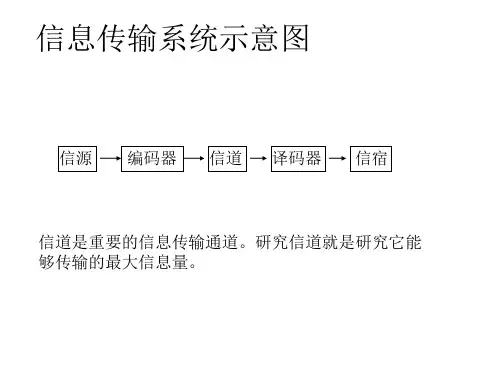
二、实验原理信道是传送信息的载体—信号所通过的通道。
信息是抽象的，而信道则是具体的。
比如二人对话，二人间的空气就是信道；打电话，电话线就是信道；看电视，听收音机，收、发间的空间就是信道。
研究信道的目的：在通信系统中研究信道，主要是为了描述、度量、分析不同类型信道，计算其容量，即极限传输能力，并分析其特性。
二元对称信道BSC （Binary Symmetric Channel ）二进制离散信道模型有一个允许输入值的集合X={0，1}和可能输出值的集合Y={0，1}，以及一组表示输入和输出关系的条件概率（转移概率）组成。
如果信道噪声和其他干扰导致传输的二进序列发生统计独立的差错，且条件概率对称，即(0/1)(1/0)(1/1)(0/0)1p Y X p Y X p p Y X p Y X p ======⎧⎨======-⎩这种对称的二进制输入、二进制输出信道称做二元对称信道（或二进制对称信道，简称BSC 信道），如下图所示：信道容量公式：{()}max p x C I(X,Y)=三、实验内容BSC信道是DMC信道对称信道的特例，对于转移概率为P(0/1)=P(1/0)=p，P(0/0)=P(1/01)=1-p，求出其信道容量公式，并在matlab上绘制信道容量C与p 的曲线。
根据曲线说明其物理意义。
四、实验要求1.提前预习实验，认真阅读实验原理以及相应的参考书。
2.认真高效的完成实验，实验中服从实验室管理人员以及实验指导老师的管理。
3.认真填写实验报告。
实验二 离散信道及其容量
一、[实验目的]
1、理解离散信道容量的内涵；
2、掌握求二元对称信道（BSC ）互信息量和容量的设计方法；
3、掌握二元扩展信道的设计方法并会求其平均互信息量。
二、[实验环境]
windows XP,MATLAB 7
三、[实验原理]
若某信道输入的是N 维序列x ，其概率分布为q(x ),输出是N 维序列y ,则平均互信息量记为I(X ;Y )，该信道的信道容量C 定义为()
max (X;Y)q x C I =。
四、[实验内容]
1、给定BSC 信道，信源概率空间为
信道矩阵 0.990.010.010.99P ⎡⎤=⎢⎥⎣⎦
求该信道的I(X;Y)和容量，画出I(X;Y)和ω、C 和p 的关系曲线。
2 、编写一M 脚本文件t03.m ，实现如下功能：
在任意输入一信道矩阵P 后，能够判断是否离散对称信道，若是，求出信道容量C 。
3、已知X=(0,1,2);Y=(0,1,2,3),信源概率空间和信道矩阵分别为
求： 平均互信息量；
4、 对题(1)求其二次扩展信道的平均互信息I(X;Y)。
五、[实验过程
] X
P ０ １
0.6 0.4
= X
Px ０ １ ２ 0.3 0.5 0.2
= 0.1 0.3 0 0.6 0.3 0.5 0.2 0 0.1 0.7 0.1 0.1
P=
每个实验项目包括：1)设计思路2)实验中出现的问题及解决方法；
1)设计思路
1、信道容量( )
max (X; Y)
q x
C = I
，因此要求给定信道的信道容量，只要知道该信道
的最大互信息量，即求信道容量就是求信道互信息量的过程。
程序代码：
clear all,clc;
w=0.6;
w1=1-w;
p=0.01;
X
P
０１
= 0.6 0.4
p1=1-p;
save data1 p p1;
I_XY=(w*p1+w1*p)*log2(1/(w*p1+w1*p))+(w*p+w1*p1)*log2(1/(w*p+w1*p1))- ...
(p*log2(1/p)+p1*log2(1/p1));
C=1-(p*log2(1/p)+p1*log2(1/p1));
fprintf('互信息量:%6.3f\n信道容量:%6.3f',I_XY,C);
p=eps:0.001:1-eps;
p1=1-p;
C=1-(p.*log2(1./p)+p1.*log2(1./p1));
subplot(1,2,1),plot(p,C),xlabel('p'),ylabel('C');
load data1;
w=eps:0.001:1-eps;
w1=1-w;
I_XY=(w.*p1+w1.*p).*log2(1./(w.*p1+w1.*p))+(w.*p+w1.*p1).*log2(1./(w.*p+w1.*p1))- . .
.(p.*log2(1./p)+p1.*log2(1./p1));
subplot(1,2,2),plot(w,I_XY)
xlabel('w'),ylabel('I_XY');
实验结果：
互信息量:0.891
信道容量:0.919
I(X;Y)和ω、C和p的关系曲线图：
0 0.5 1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
p
C
0 0.5 1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
w
I X Y
2、离散对称信道：当离散准对称信道划分的子集只有一个时，信道关于输入和输出对称。
离散准对称信道：若一个离散无记忆信道的信道矩阵中，按照信道的输出集Y 可以将信道划分成n个子集，每个子矩阵中的每一行都是其他行同一组元素的不同排列。
实验代码：
clc;clear;
P=input('输入信道转移概率矩阵：');
[r,c]=size(P);
if sum(P,2)-1~=zeros(1,r)';
error('输入的信道矩阵不合法！');%矩阵行和一定要为1
end
l=1;
Sum=0;
for j=2:c
for i=1:r%i是行变量
for k=1:r
if P(k,j)==P(i,1)
Sum=Sum+1;
break;
end
end
end
end
if Sum==r*(c-1)
fprintf('是离散输出对称信道!\n',j);
else fprintf('不是对称信道!');
end
实验结果:
输入信道转移概率矩阵：[0.01 0.99;0.99 0.01]
是离散输出对称信道!
输入信道转移概率矩阵：[0.4 0.6;0.3 0.7]
不是对称信道!
3、二次扩展信道的互信息量I(X;Y)=H(Y)-H(Y|X).
实验代码：
clc,clear;
p=0.01;
P_X1=[0.6,0.4];
p1=1-p;
X2=[0,0;0,1;1,0;1,1];%二次扩展输入符号阵
Y2=X2;%二次扩展输出符号
P_X2=[P_X1(1)^2,P_X1(1)*P_X1(2),P_X1(2)*P_X1(1),P_X1(2)^2];
%求二次扩展后信道矩阵N
N=zeros(4);
for i=1:4
for j=1:4
l=length(find(xor(X2(i,:),Y2(j,:))==0));%比较得正确传递元素个数
N(i,j)=p1^l*p^(2-l);
end
end
%下面求I
P_Y2=P_X2*N;
P_XY2=[P_X2(1)*N(1,:);P_X2(2)*N(2,:);P_X2(3)*N(3,:);P_X2(4)*N(4,:)];%联合分布H_Y2=sum(-P_Y2.*log2(P_Y2));
H_Y_X2=sum(sum(-P_XY2.*log2(N)));
I_XY2=H_Y2-H_Y_X2;
fprintf('2次扩展信道的平均互信息为:%5.3f',I_XY2);
实验结果：
2次扩展信道的平均互信息为:1.783
2)实验中出现的问题及解决方法；
1、信道容量与互信息量有关，而互信息量又与信源熵相关，所以要求得信道容量就必须知道信道传递概率，然后根据公式一步一步计算。
2、对于判断离散对称信道，不需要弄清楚的是它的概念，根据定义来判断。
3、对于扩展信道，分有记忆的和无记忆的，在不确定的情况下计算扩展信源的熵，我们要根据定义来计算。
六、[实验总结]
通过本次实验，我对于信道的分类，各种信道的特点有了一定的认识和了解。
实验中涉及的主要是二元对称信道，而它的最佳分布是输入和输出均对称。
实验中最主要的部分还是关于信道容量的计算，此次实验，让我们验证了课
本上的定理，也让我们更好地理解和掌握了课堂上所学的知识。
__。
