06平面立体及其截切体的投影

单元四基本体及其截断体的投影项目描述：任何机体，不管其形状多么复杂，都可以看成是由圆柱、圆锥、圆球、棱柱、棱锥等单一几何形体(基本体)按一定方式组合而成，它们是构成形体的基本单元。

本项目中通过介绍各种基本几何体及截断体的投影特征，学习基本几何体的画法及表面取点方法；学习基本几何体及截断体尺寸标注方法。

项目目标：1、掌握平面立体和曲面立体的种类及其三视图画法。

2、掌握平面立体和圆柱体表面取点、取线的作图方法。

3、能正确、完整的标注基本及其切口穿孔的尺寸。

4、掌握截切基本体交线的画法。

能力目标：1、学会运用投影原理分析基本体及其三视图。

2、培养运用投影原理绘制基本体三视图的能力。

3、掌握基本几何体表面求点方法。

任务一平面立体根据表面性质的不同，基本体分为平面立体和曲面立体两类。

立体表面全部由平面所围成的立体，称为平面立体。

如棱柱和棱锥等。

图4-1 基本体组成的机体一、六棱柱三视图及斜截六棱柱的三视图画法棱柱由两个底面和棱面组成，棱面与棱面的交线称为棱线，棱线互相平行。

棱线与底面垂直的棱柱称为正棱柱。

图4-2a所示为一正六棱柱。

由上、下两个底面（正六边形）和六个棱面（长方形）组成。

设将其放置成上、下底面与水平投影面平行，并有两个棱面平行于正投影面面。

(a) (b) 立体图 (c)投影图图4-2 正六棱柱投影及表面上的点的三视图1．六棱柱的三视图分析上、下两底面均为水平面，它们的水平投影重合并反映实形，正面及侧面投影积聚为两条相互平行的直线。

六个棱面中的前、后两个为正平面，它们的正面投影反映实形，水平投影及侧面投影积聚为一直线。

其他四个棱面均为铅垂面，其水平投影均积聚为直线，正面投影和侧面投影均为类似形。

(1)俯视图六棱柱的俯视图是正六边形，是六棱柱顶面和底面的重合投影，反映顶、底面的实形。

正六边形的六条边是六个侧面垂直于顶、底面的积聚性投影。

(2)主视图六棱柱的主视图由三个矩形线框组成。

中间的矩形线框为前、后侧面的重合投影，反映实形。

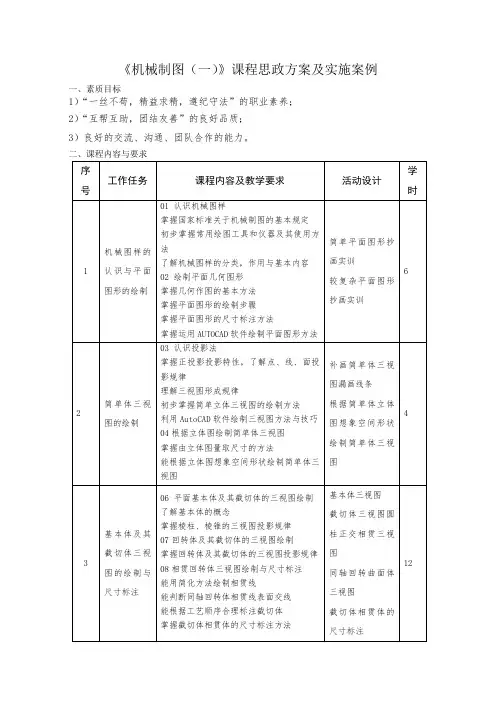
《机械制图（一）》课程思政方案及实施案例
一、素质目标
1）“一丝不苟，精益求精，遵纪守法”的职业素养；
2）“互帮互助，团结友善”的良好品质；
3）良好的交流、沟通、团队合作的能力。

二、课程内容与要求
案例1
工匠精神：培养学生树立新时代的设计思想；爱岗敬业的工匠精神；认真负责的工作态度和一丝不苟的工作作风。

爱护每一台教具产品，按规矩拆卸、组装；按次序摆放各类零件；按规定摆放各类工具、量具。

及时清理工作场地。

离开测绘现场时，必须做到关闭窗户、关闭电源。

杜绝一切安全事故的发生。

案例2
法制、诚信:在授课过程中，适时灌输中外知识产权保护法律法规，使学生认识到严格遵守相关法律的重要性，培养尊重知识产权的诚信精神。

严格遵守日常的行为准则、职业规范与职业道德。

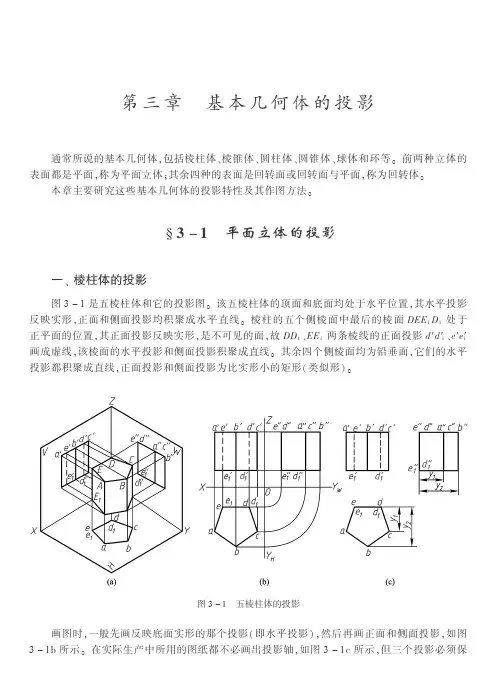
第三章　基本几何体的投影通常所说的基本几何体，包括棱柱体、棱锥体、圆柱体、圆锥体、球体和环等。

前两种立体的表面都是平面，称为平面立体；其余四种的表面是回转面或回转面与平面，称为回转体。

本章主要研究这些基本几何体的投影特性及其作图方法。

§3－1　平面立体的投影一、棱柱体的投影图３－１是五棱柱体和它的投影图。

该五棱柱体的顶面和底面均处于水平位置，其水平投影反映实形，正面和侧面投影均积聚成水平直线。

棱柱的五个侧棱面中最后的棱面DEE１D１处于正平面的位置，其正面投影反映实形，是不可见的面，故DD１、EE１两条棱线的正面投影d′d′１、e′e′１画成虚线，该棱面的水平投影和侧面投影积聚成直线。

其余四个侧棱面均为铅垂面，它们的水平投影都积聚成直线，正面投影和侧面投影为比实形小的矩形（类似形）。

图３－１　五棱柱体的投影画图时，一般先画反映底面实形的那个投影（即水平投影），然后再画正面和侧面投影，如图３－１ｂ所示。

在实际生产中所用的图纸都不必画出投影轴，如图３－１ｃ所示，但三个投影必须保持左右、上下、前后的对应关系，即V 、H 两面投影左右对正，V 、W 两面投影上下平齐，H 、W 两面投影前后相等。

二、棱锥体的投影图３－２是正三棱锥体和它的投影图。

该三棱锥体的底面处于水平位置，其水平面投影反映实形，正面和侧面投影积聚成水平直线。

三棱锥的右侧棱面SBC 为正垂面，其正面投影s ′b ′c ′积聚成直线，水平面投影sbc 和侧面投影s ″b ″c ″为类似形。

前棱面SAB 和后棱面SAC 均为一般位置平面，因而，它们的三面投影均为类似形（正面投影两个三角形重合）。

图３－２　正三棱锥体的投影画图时，先画出底面三角形ABC 和锥顶S 的投影，然后顺次连接各棱线SA 、SB 、SC 的同面投影，如图３－２ｂ所示。

通过棱柱和棱锥体的投影分析，可归纳如下几点：１）由于平面立体的棱线是直线，所以画平面立体的投影图就是先画出各棱线交点的投影，然后顺次连线，并注意区分可见性。

《机械制图（一）》课程思政方案及实施案例
一、素质目标
1）“一丝不苟，精益求精，遵纪守法”的职业素养；
2）“互帮互助，团结友善”的良好品质；
3）良好的交流、沟通、团队合作的能力。

二、课程内容与要求
案例1
工匠精神：培养学生树立新时代的设计思想；爱岗敬业的工匠精神；认真负责的工作态度和一丝不苟的工作作风。

爱护每一台教具产品，按规矩拆卸、组装；按次序摆放各类零件；按规定摆放各类工具、量具。

及时清理工作场地。

离开测绘现场时，必须做到关闭窗户、关闭电源。

杜绝一切安全事故的发生。

案例2
法制、诚信:在授课过程中，适时灌输中外知识产权保护法律法规，使学生认识到严格遵守相关法律的重要性，培养尊重知识产权的诚信精神。

严格遵守日常的行为准则、职业规范与职业道德。

平面几何体的投影与截面平面几何体是我们日常生活中常见的三维物体，如长方体、球体等。

投影和截面是研究这些几何体的重要概念，它们在工程设计、建筑规划、计算机图形学等领域具有广泛的应用。

本文将说明平面几何体的投影和截面的概念、方法和应用。

一、投影的概念与方法投影是指将三维物体在某个方向上的投射到一个二维平面上得到的图形。

平面几何体的投影可以分为正射投影和斜投影两种。

正射投影是指投影线与投影平面垂直的投影方式，主要用于工程制图等需要几何精确性的场合。

它的投影方法很简单，只需要将物体上的点沿着投影方向画垂线，然后将垂线与投影平面相交的点连接起来即可得到投影图形。

斜投影是指投影线与投影平面不垂直的投影方式，主要用于美术设计等需要艺术表现性的场合。

斜投影可以按照一定比例将物体在相应方向上的尺寸缩小，使得整个图形更为立体感。

二、截面的概念与应用截面是指在某个平面上与物体相交所得到的图形。

通过截面可以更加清晰地观察物体的内部结构和形状特征。

截面可以有多种方式，常见的有平行截面和垂直截面。

平行截面是指在与物体平行的平面上进行截面操作，常用于分析物体的层次结构和交叉部分。

例如，在工程设计中，通过平行截面可以更加清楚地了解建筑物的内部布局和管线走向。

垂直截面是指在与物体垂直的平面上进行截面操作，常用于观察物体的形状特征和截面积。

例如，在医学影像学中，通过垂直截面可以获得人体器官的具体结构，有助于诊断和治疗。

三、投影与截面的应用举例1. 工程设计中的投影应用：在建筑设计中，工程师常常使用正射投影来绘制平面图和立面图。

通过投影，可以清晰地展示建筑物的外观和内部结构，为施工提供准确的参考。

2. 计算机图形学中的截面应用：在计算机图形学中，截面常常用于三维物体的可视化和模拟。

利用截面，可以实现真实感渲染和光线追踪等高级图形算法，提供逼真的视觉效果。

3. 艺术设计中的截面应用：在雕塑和景观设计中，设计师常常使用截面来展示作品的内部结构和形态特征。

平面立体图形的投影与展开在我们的日常生活和学习中，平面立体图形无处不在。

从简单的正方体、长方体，到复杂的棱柱、棱锥，这些图形的投影与展开是理解其结构和性质的重要途径。

首先，让我们来了解一下什么是平面立体图形的投影。

投影可以简单地理解为光线照射在物体上，在某个平面上所形成的影子。

在数学中，我们通常考虑正投影，也就是光线垂直于投影面的情况。

比如说，一个正方体，当光线从它的正前方垂直照射时，在后面的平面上形成的投影就是一个正方形。

但如果光线从上方垂直照射，投影就变成了一个正方形的框。

不同的平面立体图形，其投影的形状和大小会有所不同。

对于长方体来说，如果它的长、宽、高各不相同，那么从不同的方向进行正投影，可能会得到长方形或者正方形。

而对于三棱柱，如果它的底面是等边三角形，且侧棱与底面垂直，那么从侧面投影就是一个长方形，从上下底面投影就是等边三角形。

接下来，我们说一说平面立体图形的展开。

展开图就像是把一个立体图形的表面“拆开”，平铺在一个平面上所得到的图形。

通过研究展开图，我们可以更直观地看到立体图形的各个面之间的关系。

以正方体为例，它有 11 种不同的展开图。

常见的有“1-4-1”型，就像“一”字排开；“2-3-1”型，像楼梯一样；还有“2-2-2”型，三个“2”并排。

通过观察这些展开图，我们可以清晰地看到正方体的 6 个面是如何相互连接的。

再比如长方体，它的展开图相对来说要复杂一些，因为长方体的长、宽、高可能不同。

但总的来说，也是由 6 个长方形（特殊情况下可能有两个正方形）组成，并且相对的面在展开图中是相同的。

平面立体图形的投影和展开在实际生活中有很多应用。

比如在制造业中，工程师们需要根据零件的投影图来设计和制造产品；在包装设计中，要考虑如何将立体的物品展开成平面，以节省材料和方便包装。

在学习数学的过程中，理解平面立体图形的投影和展开对于培养我们的空间想象力和逻辑思维能力非常重要。

当我们能够在脑海中想象出一个立体图形的投影和展开图时，就能够更好地解决与立体几何相关的问题。