高考理科数学模拟试卷(附答案)

高考理科数学模拟试卷（含答案）本试卷分选择题和非选择题两部分. 第Ⅰ卷(选择题)1至2页,第Ⅱ卷 (非选择题)3至4页,共4页,满分150分,考试时间120分钟. 注意事项：1.答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号.3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定位置上.4.所有题目必须在答题卡上作答,在试题卷上答题无效.5.考试结束后,只将答题卡交回.第Ⅰ卷 (选择题,共60分)一、选择题：本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合2{1,0,1,2,3,4},{|,}A B y y x x A =-==∈,则AB =(A){0,1,2} (B){0,1,4} (C){1,0,1,2}- (D){1,0,1,4}- 2. 已知复数11iz =+,则||z =(A)2(B)1 (D)2 3. 设函数()f x 为奇函数,当0x >时,2()2,f x x =-则((1))f f = (A)1- (B)2- (C)1 (D)24. 已知单位向量12,e e 的夹角为2π3,则122e e -=(A)3 (B)75. 已知双曲线22221(0,0)x y a b a b-=>>的渐近线方程为3y x =±,则双曲线的离心率是(B)3 (C)10 (D)1096. 在等比数列{}n a 中,10,a >则“41a a <”是“53a a <”的(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件7. 如图所示的程序框图,当其运行结果为31时,则图中判断框①处应填入的是(A)6?i ≤ (B)5?i ≤ (C)4?i ≤ (D)3?i ≤8. 已知,a b 为两条不同直线,,,αβγ为三个不同平面,下列命题：①若///,,/ααγβ则//βγ；②若//,//,a a αβ则//αβ；③若,,αγγβ⊥⊥则αβ⊥；④若,,a b αα⊥⊥则//a b .其中正确命题序号为 (A)②③(B)②③④(C)①④(D)①②③9. 南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,5,11,21,37,61,95,则该数列的第8项为 (A)99(B)131(C)139(D)14110. 已知πlog e,a =πln ,eb =2e ln ,πc =则(A)a b c << (B)b c a <<(C)b a c <<(D)c b a <<11. 过正方形1111ABCD A B C D -的顶点A 作直线l ,使得l 与直线11,B C C D 所成的角均为60︒,则这样的直线l 的条数为(A)1 (B)2 (C) 3 (D) 412. 已知P 是椭圆2214x y +=上一动点,(2,1),(2,1)A B -,则cos ,PA PB 的最大值是第Ⅱ卷 (非选择题,共90分)二、填空题：本大题共4小题,每小题5分,共20分.把答案填在答题卡上. 13.已知数列{}n a 的前n 项和为,n S 且111,1(2),n n a a S n -==+≥则4a =14. 已知实数,x y 满足线性约束条件117x y x y ≥⎧⎪≥-⎨⎪+≤⎩,则目标函数2z x y =+的最大值是15. 如图是一种圆内接六边形ABCDEF ,其中BC CD DE EF FA ====且.AB BC ⊥则在圆内随机取一点,则此点取自六边形ABCDEF 内的概率是16. 若指数函数x y a =(0a >且1)a ≠与三次函数3y x =的图象恰好有两个不同的交点,则实数a 的取值范围是三、解答题：本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)在ABC ∆中,内角,,A B C 的对边分别为,,.a b c 已知2.tan sin a bA B= (1)求角A 的大小； (2)若2,a b ==求ABC ∆的面积.18.(本小题满分12分)成都七中为了解班级卫生教育系列活动的成效,对全校40个班级进行了一次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果：得分在[80,100]评定为“优”,奖励3面小红旗；得分在[60,80)评定为“良”,奖励2面小红旗；得分在[40,60)评定为 “中”,奖励1面小红旗；得分在[20,40)评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如下图：(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数；(2)学校用分层抽样的方法,从评定等级为“优”、“良”、“中”、“差”的班级中抽取10个班级,再从这10个班级中随机抽取2个班级进行抽样复核,记抽样复核的2个班级获得的奖励小红旗面数和为X ,求X 的分布列与数学期望()E X .19.(本小题满分12分)如图,在四棱锥M ABCD -中,2,2.,,3AB AM AD MB MD AB AD =====⊥ (1)证明：AB ⊥平面ADM ； (2)若//CD AB 且23CD AB =,E 为线段BM 上一点,且2BE EM =,求直线EC 与平面BDM 所成角的正弦值.20.(本小题满分12分)已知函数22e (),(e,).ln x xf x x x x++=∈+∞ (1)证明：当(e,)x ∈+∞时,3eln ex x x ->+； (2)若存在*0[,1)()x n n n N ∈+∈使得对任意的(e,)x ∈+∞都有0()()f x f x ≥成立. 求n 的值.(其中e 2.71828=是自然对数的底数).21.(本小题满分12分)已知点P 是抛物线21:2C y x =上的一点,其焦点为点,F 且抛物线C 在点P 处的切线l 交圆:O 221x y +=于不同的两点,A B .(1)若点(2,2),P 求||AB 的值；(2)设点M 为弦AB 的中点,焦点F 关于圆心O 的对称点为,F '求||F M '的取值范围.请考生在第22,23题中任选择一题作答,如果多做,则按所做的第一题记分.作答时,用2B 铅笔在答题卡上将所选题目对应的标号涂黑.22.(本小题满分10分)选修44-：坐标系与参数方程在平面直角坐标系xOy 中,曲线C 的参数方程为233x y αα⎧=⎪⎨=⎪⎩(α为参数,0πα≤≤).在以坐标原点为极点,x 轴的非负半轴为极轴的极坐标系中,射线l 的极坐标方程是π6θ=.(1)求曲线C 的极坐标方程；(2)若射线l 与曲线C 相交于,A B 两点,求||||OA OB ⋅的值.23.(本小题满分10分)选修45-：不等式选讲已知0,0,a b >>且24,a b +=函数()2f x x a x b =++-在R 上的最小值为.m (1)求m 的值；(2)若22a mb tab +≥恒成立,求实数t 的最大值.参考答案及评分意见第Ⅰ卷 (选择题,共60分)一、选择题(每小题5分,共60分)1.B ；2.A ；3.C ；4.D ；5.A ；6.A ；7.B ；8.C ；9.D ； 10.B ； 11.C ； 12.A.第Ⅱ卷 (非选择题,共90分)二、填空题(每小题5分,共20分)13.8； 14.15；； 16.3e (1,e ).三、解答题(共70分)17. 解：(1)由正弦定理知sin sin a b A B =,又2,tan sin a b A B =所以2.sin tan a aA A=于是1cos ,2A =因为0π,A <<所以π.3A =6分(2)因为π2,,3a b A ===22π222cos ,3c c =+-⨯⨯即2230.c c --=又0,c >所以 3.c =故ABC ∆的面积为11πsin 23sin 223bc A =⨯⨯⨯=12分18.解：(1)得分[20,40)的频率为0.005200.1⨯=；得分[40,60)的频率为0.010200.2⨯=； 得分[80,100]的频率为0.015200.3⨯=；所以得分[60,80)的频率为1(0.10.20.3)0.4.-++=设班级得分的中位数为x 分,于是600.10.20.40.520x -++⨯=,解得70.x = 所以班级卫生量化打分检查得分的中位数为70分.5分 (2)由(1)知题意“优”、“良”、“中”、“差”的频率分别为0.3,0.4,0.2,0.1.又班级总数为40.于是“优”、“良”、“中”、“差”的班级个数分别为12,16,8,4．分层抽样的方法抽取的“优”、“良”、“中”、“差”的班级个数分别为3,4,2,1. 由题意可得X 的所有可能取值为1,2,3,4,5,6.211214410101111111324221120211(1),(2),(3,145945)C C C C C C P X P X P C C C X C C C +=======+== 2432111123101021304224(4),(5),(6)41151515.C C C C P X P X P X C C C C C ========+=9分 所以X459451512()123456515.455E X =⨯+⨯+⨯+⨯+⨯+⨯==所以X 的数学期望19().5E X = 12分 19.解：(1)因为2AB AM ==,MB =所以222.AM AB MB +=于是.AB AM ⊥又,AB AD ⊥且,AM AD A AM =⊂平面,ADM AD ⊂平面ADM ,所以AB ⊥平面.ADM5分(2)因为2,23AM AD MD ===所以120.MAD ∠=︒如图所示,在平面ADM 内过点A 作x 轴垂直于AM ,又由(1)知AB ⊥平面ADM ,于是分别以,AM AB 所在直线为,y z 轴建 立空间直角坐标系.A xyz -于是4(3,1,0),(3,1,),(0,0,2),(0,2,0).3D C B M --因为2BE EM =,于是42(0,,).33E 所以72(3,,),(0,2,2),(3,1,2).33EC BM BD =-=-=--设平面BDM 的法向量为,n 于是00BM n BD n ⎧⋅=⎪⎨⋅=⎪⎩即220.320y z x y z -=⎧⎪--=取1z =得(3,1,1).n = 设直线EC 与平面BDM 所成角为θ,则413sin cos ,.54553EC n EC n EC nθ⋅====⨯ 所以直线EC 与平面BDM 所成角的正弦值为1.512分20.解：(1)令3e ()ln ,(e,).e x g x x x x -=-∈+∞+则22214e (e)()0.(e)(e)x g x x x x x -'=-=>++于是()g x 在(e,)+∞单调递增,所以()(e)0,g x g >=即3eln ,(e,).exx x x ->∈+∞+ 5分 (2)22222222(21)ln (e )(ln 1)(e )ln (e )().(ln )(ln )x x x x x x x x x x f x x x x x +-+++--++'== 令2222()(e )ln (e ),(e,).h x x x x x x =--++∈+∞当(e,)x ∈+∞时,由(1)知3e ln .e x x x ->+则222223e 4e 1()(e )(e )2(4e 1)2(),e 2x h x x x x x x x x x -+>--++=-+=-+ (i)当4e 1[,)2x +∈+∞时,于是()0h x>,从而()0.f x '> 故()f x 在4e 1[,)2++∞严格单调递增.其中4e 15.936562+=9分 (ii)当(e,5]x ∈时,则2222222222()(e )ln 5(e )2(e )(e )3e h x x x x x x x x x ≤--++<--++=-- 2203e 0.≤-<(用到了223e x x --在(e,5]单调递增与2e 7>)于是()0f x '<,故()f x 在(e,5]严格单调递减.11分综上所述,()f x 在(e,5]严格单调递减,在4e 1[,)2++∞严格单调递增. 因为4e 16,2+<所以0[5,6).x ∈所以 5.n =12分21.解：设点00(,)P x y ,其中2001.2y x =因为,y x '=所以切线l 的斜率为0,x 于是切线2001:.2l y x x x =-(1)因为(2,2),P 于是切线:2 2.l y x =-故圆心O 到切线l的距离为d =于是||5AB ===5分(2)联立22200112x y y x x x ⎧+=⎪⎨=-⎪⎩得22340001(1)10.4x x x x x +-+-= 设1122(,),(,),(,).A x y B x y M x y 则301220,1x x x x +=+32240001()4(1)(1)0.4x x x ∆=--+-> 又200,x ≥于是2002x ≤<+于是32200120022001,.22(1)22(1)x x x x x y x x x x x +===-=-++ 又C 的焦点1(0,),F 于是1(0,).F '-故||F M'===9分令201,t x =+则13t ≤<+于是||F M'==因为3t t+在单调递减,在+单调递增.又当1t =时,1||2F M '=；当t =时,||F M '=； 当3t =+时,11||.2F M'=> 所以||F M '的取值范围为1).212分 22.解：(1)消去参数α得22(2)3(0)x y y -+=≥将cos ,sin x y ρθρθ==代入得 22(cos 2)(sin )3,ρθρθ-+=即24cos 10.ρρθ-+=所以曲线C 的极坐标方程为2π4cos 10(0).3ρρθθ-+=≤≤ 5分(2)法1：将π6θ=代入2π4cos 10(0)3ρρθθ-+=≤≤得210ρ-+=,设12ππ(,),(,),66A B ρρ则12 1.ρρ=于是12|||| 1.OA OB ρρ⋅==10分法2：π3θ=与曲线C 相切于点,M π||2sin 1,3OM == 由切割线定理知2|||||| 1.OA OB OM ⋅==10分23.解：(1)3, (,),2()2, [,],23, (,).a x a b x a f x x a x b x a b x b x a b x b ⎧--+∈-∞-⎪⎪⎪=++-=++∈-⎨⎪+-∈+∞⎪⎪⎩.当(,)2ax ∈-∞-时,函数()f x 单调递减；当(,)x b ∈+∞时,函数()f x 单调递增.所以m 只能在[,]2a b -上取到.当[,]2ax b ∈-时,函数()f x 单调递增.所以2() 2.222a a a bm f a b +=-=-++==5分(2)因为22a mb tab +≥恒成立,且0,0a b >>,所以22a mb t ab +≤恒成立即mina b mb t a ⎛⎫≤+ ⎪⎝⎭.由(1)知2m =,于是a b a mb +≥== 当且仅当2aab =时等号成立即1)0,2(20.a b =>=> 所以t ≤,故实数t 的最大值为10分。

2023届高考理科数学模拟试题一(含答案及解析)本卷分选择题和非选择题两部分，满分150分，考试时间120分钟。

注意事项：1． 考生务必将自己的姓名、准考证号用黑墨水钢笔、签字笔写在答题卷上；2． 选择题、填空题每小题得出答案后，请将答案填写在答题卷相应指定位置上，答在试题卷上不得分；3． 考试结束，考生只需将答题卷交回。

参考公式：锥体的体积公式13V Sh =，其中S 是锥体的底面积，h 是锥体的高 如果事件A 、B 互斥，那么()()()P A B P A P B +=+ 如果事件A 、B 相互独立，那么()()()P A B P A P B *=*第一部分 选择题(共40分)一、选择题（本大题共8小题，每小题5分，满分40分。

在每小题给出的四个选项中，只有一项是符合题目要求的） 1. 已知复数1z i =+，则2z= A ． i 2-B ．i 2C ．i -1D ．i +12. 设全集,U R =且{}|12A x x =->,{}2|680B x x x =-+<,则()U C A B =A ．[1,4)-B ．(2,3)C ．(2,3]D ．(1,4)-3. 椭圆221x my +=的焦点在y 轴上，长轴长是短轴长的两倍，则m 的值为（ ） A ．14B ．12C ． 2D ．4 4. ABC ∆中，3A π∠=，3BC =，AB =，则C ∠=A ．6πB ．4π C ．34π D ．4π或34π5. 已知等差数列{}n a 的前n 项和为n S ，且2510,55S S ，则过点(,)n P n a 和2(2,)n Q n a(n N ＋)的直线的斜率是A ．4B ．3C ．2D ．16.已知函数),2[)(+∞-的定义域为x f ,且1)2()4(=-=f f )()(x f x f 为'的导函数，函数)(x f y '=的图象如图所示， 则平面区域⎪⎩⎪⎨⎧<+≥≥1)2(00b a f b a 所围成的面积是A ．2B ．4C ．5D ．87. 一台机床有13的时间加工零件A ，其余时间加工零件B ， 加工A 时,停机的概率是310，加工B 时，停机的概率是25，则这台机床停机的概率为( )A ． 1130B ．307 C ．107 D ．1018. 在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点，如果函数()f x 的图象恰好通过()n n N +∈个整点，则称函数()f x 为n 阶整点函数。

第三轮数学综合复习高考模拟试题及答案考试注意1.本试卷总分150分；2.答题时间120分钟，请在规定时间内完成。

一、选择题（每题5分，共50分）1、已知集合A={x|−3＜x＜3}，B={x|−1＜x＜4}，则A∩B=（）A、（-3，-1〕B、（-1，4〕C、（-3，-4〕D、（-1，3〕2、设复数满足：z + z·（1-i）= 3+i，那么z = （）A、1+ iB、2+ iC、2+ 2iD、1+ 2i3、已知θ是向量x，x的夹角，若θ =150°，且丨x丨=1，丨x丨=√3则|x+2x|=（）A、√2B、√3C、√7D、√114、函数f（x）=Asin（ωx+φ）+k其中A＞0，ω＞0，丨φ丨＜x2若f（x）的部分图像如图所示，则（）A、f（x）= sin（x + π）+1B、f（x）= 2sin（2x + x6）+1C、f（x）= 3sin（3x + x3）+1 D、f（x）= 4sin（4x + x4）+15、如图，在立方体ABCD-A/B/C/D/中，已知点E，F，G，H分别是棱AD，BB/，B/C/，DD/的中点，从这些中点任意选取两点所形成的直线与平面AB/D/平行的条数是（）A、2B、4C、6D、86、函数f（x）= 14x2+cosx，已知f/（x）是f（x）的导函数，则f/（x）的大致图像是（）A、 B、C、 D、7、已知2sin（x2+ a）- 13=√3sin（2x3- a），则sin（2a+ 31x6）=（）A、79 B、89C、 - 79 D、 - 898、已知点（3，-2）在椭圆x2a2 + y2b2=1（a＞b＞0）上，若椭圆与双曲线x 23 + y 22 =1有相同的焦点，则椭圆的离心率为（ ） A 、 √33B 、 √64C 、 √56D 、 √789、已知a ＞0，b ＞0，且1a + 1b = 2，则2a + b a + 4ab 的值是（ ）A 、4B 、5C 、6D 、710、已知数列{x x }的前n 项和x x = x 2 -5n ，数列{x x }的首项为1若x x +1 −x x =x x ，则x 12=（ ）A 、65B 、66C 、67D 、68二、填空题（每题8分，共40分）11、（3x −1x ）8展开式的常数项是 。

第1页，共20页2023年陕西省安康市高考数学二模试卷（理科）

1. 已知，则( )

A. iB. C. 1D. 2. 若集合，，则( )

A. B. C. D. 3. 如图，在矩形ABCD中，M是CD的中点，若

，则( )A. B. 1

C. D. 2

4. 已知x，y满足约束条件，则的最大值为( )

A. B. C. 2D. 5. 已知函数的最小正周期为，则下列说法不正

确的是( )A.

B. 的单调递增区间为，

C. 将的图象向左平移个单位长度后所得图象关于y轴对称

D. 6. 已知四面体的四个面均为直角三角形如图所示，则该四面体中异面直线AB与CD所

成角的余弦值为( )第2页，共20页

A. B. C. D. 7. ，，，，则a，b，c，d的大小关系为( )

A. B. C. D. 8. 下列命题正确的是( )

A. “，”的否定为假命题

B. 若“，”为真命题，则

C. 若，，且，则

D. 的必要不充分条件是

9. 设抛物线C：的焦点是F，直线l与抛物线C相交于A，B两点，且

，过弦AB的中点P作的垂线，垂足为Q，则的最小值为( )A. B. 3C. D. 10. 宋代理学家周敦颐的《太极图》和《太极图说》是象数和义

理结合的表达.《朱子语类》卷七五：“太极只是一个混沦底道理，里面包含阴阳、刚柔、奇偶，无所不有”.太极图如下图将平衡美、对称美体现的淋漓尽致.定义：对于函数，若存在圆C，使得的图象能将圆C的周长和面积同时平分，则称是圆C的太极函数.下列说法正确的是( )①对于任意一个圆，其太极函数有无数个

②是的太极函数③太极函数的图象必是中心对称图形④存在一个圆C，是它的太极函数A. ①④B. ③④C. ①③D. ②③第3页，共20页

11. 已知…，则

的值为( )A. 0B. C. D. 12. 已知，恒成立，则的取值范围是( )

A. B. C. D. 13. 某服装公司对月份的服装销量进行了统计，结果如下：

月份编号x12345

人教版高三数学高考模拟测试题(理科）含答案、选择题：（1)设全集U为实数集R ，A X12 X 5 ，B x｜1 X 4 ，贝U AI （C U B)A. B. x｜4 X 5 C.x 14 X 5 D。

X|x 4(2）i为虚数单位，复数（111i 1 i)（1 ) A. 0i 1 iB.2C。

2i D。

2i（3）数列a n、b n满足b n 2*（n N），则“数列耳是等差数列”是“数列 g是等比数列"的A .充分但不必要条件B .必要但不充分条件 C。

充要条件 D 。

既不充分也不必要条件(4）设0 X 1 ，则下列叙述正确的是A。

X2、。

X X B。

Ig、X Ig(x2) Ig XC. Ig X log？＊lg（x2）2D. I0g2（x ）Ig（x2） I0g2∖χ（5)已知函数 f （x） Sin X -(0)的最小正周期为,则该函数的图象( )IlJU IlJU IlJU满足OP （2 ）OA QB ，则点P的轨迹是 ()A与I平行的直线B。

与I垂直的直线 C.与I相交但不垂直的直线（7）—个几何体的主视图、左视图和俯视图如图所示,第7题图E、F，其中A、B、C为右手持拍的选手,选手，而F为左右手皆可持拍的选手•现在要派出两名选手参加双打，规定由一名可以右手持拍的选手与一名可以左手持拍的选手搭配,则可能的搭配有 A.9种 B.11种 C.13种 D.15种(9）三棱锥P ABC四个顶点都在半径为 2的球面上,若PA ，PB ，PC两两垂直，则三棱锥P ABC的侧面积A关于点—,0对称B .关于直线X—对称C关于点—,0对称D .关于直线X—对称(6)已知代B是直线I上任意不同两点, O是I外一点，点PD.以上都有可能则这个几何体的体积是( )A. 20 B. 64 16 C. 64 4 D. 64 16D、E为左手持拍的(8) —乒乓球队共有6位选手，编号为:的最大值为 A 。

高三数学（理科）模拟试卷及答案3套模拟试卷一一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{|2,}xA y y x ==∈R ，{|lg(2)}B x y x ==-，则A B =I （ ） A ．(0,2)B ．(,2]-∞C ．(,2)-∞D ．(0,2]2．若复数z 满足(i 1)2i z -=（i 为虚数单位），则z 为（ ） A ．1i +B ．1i -C ．1i -+D ．1i --3．AQI 即空气质量指数，AQI 越小，表明空气质量越好，当AQI 不大于100时称空气质量为“优良”，如图是某市3月1日到12日AQI 的统计数据，则下列叙述正确的是（ ）A ．这12天的AQI 的中位数是90B ．12天中超过7天空气质量为“优良”C ．从3月4日到9日，空气质量越来越好D ．这12天的AQI 的平均值为1004．已知平面向量(2,3)=a ，(,4)x =b ，若()⊥-a a b ，则x =（ ） A ．1B ．12C ．2D ．35．某围棋俱乐部有队员5人，其中女队员2人，现随机选派2人参加围棋比赛，则选出的2人中有女队员的概率为（ ） A ．103 B ．35C ．45D ．7106．已知m ，n 表示两条不同的直线，α表示平面，下列说法正确的是（ ） A ．若m α∥，n α∥，则m n ∥B ．若m α⊥，n α⊥，则m n ∥C ．若m α⊥，m n ⊥，则n α∥D ．若m α∥，m n ⊥，则n α⊥7．函数π()3sin(2)(||)2f x x ϕϕ=+<的图象向左平移π6个单位长度后，所得到的图象 关于原点对称，则ϕ等于（ ） A ．π6B ．π6-C ．π3D ．π3-8．下图是某实心机械零件的三视图，则该机械零件的表面积为（ ）A ．662π+B ．664π+C ．662π-D ．664π-9．函数2()ln(1)f x x x =+-的图象大致是（ ）A ．B ．C ．D ．10．正三角形ABC 的边长为2，将它沿高AD 折叠，使点B 与点C 3， 则四面体ABCD 外接球的表面积为（ ） A ．6πB ．7πC ．8πD ．9π11．有如下命题：①函数sin y x =与y x =的图象恰有三个交点；②函数sin y x =与y x =一个交点；③函数sin y x =与2y x =的图象恰有两个交点；④函数sin y x =与3y x =的图象恰有三个交点，其中真命题的个数为（ ）A ．1B ．2C ．3D ．412．若函数2(1)()f x x x ax b =-++（）的图象关于点(2,0)-对称，1x ，2x 分别是()f x 的 极大值点与极小值点，则21x x -=（ ） A ．3- B ．23C ．23-D ．3二、填空题：本大题共4小题，每小题5分．13．在ABC △中，若13AB =，3BC =，120C ∠=︒，则AC =_____．14．如图，圆C （圆心为C ）的一条弦AB 的长为2，则AB AC ⋅=u u u r u u u r_____．15．在4(1)x x ++的展开式中，2x 项的系数为________（结果用数值表示）． 16．定义在正实数上的函数(){{}}f x x x =⋅，其中{}x 表示不小于x 的最小整数，如{0.2}1=，{1.6}2=，当(0,]x n ∈，n ∈*N 时，函数()f x 的值域为n A ，记集合n A 中元素的个数为n a ，则n a =________．三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤． 17．（12分）如图，在平面四边形ABCD 中，23AB =，2AC =，90ADC CAB ∠=∠=︒，设DAC θ∠=． （1）若60θ=︒，求BD 的长度； （2）若30ADB ∠=︒，求tan θ．18．（12分）为了解全市统考情况，从所有参加考试的考生中抽取4000名考生的成绩，频率分布直方图如下图所示．（1）求这4000名考生的平均成绩x （同一组中数据用该组区间中点值作代表）；（2）由直方图可认为考生考试成绩z 服从正态分布2(,)N μσ，其中μ，2σ分别取考生的平均成绩x 和考生成绩的方差2s ，那么抽取的4000名考生成绩超过84.81分（含84.81分）的人数估计有多少人？ （3）如果用抽取的考生成绩的情况来估计全市考生的成绩情况，现从全市考生中随机抽取4名考生，记成绩不超过84.81分的考生人数为ξ，求(3)P ξ≤．（精确到0.001）附：①2204.75s =，204.7514.31≈；②2~(,)z N μσ，则()0.6826P z μσμσ-<<+=，(22)0.9544P z μσμσ-<<+=；③40.84130.501≈．19．（12分）如图，三棱柱111ABC A B C -中，111160B A A C A A ∠=∠=︒，14AA AC ==，2AB =，P ，Q 分别为棱1AA ，AC 的中点．（1）在BC 上确定点M ，使AM ∥平面1PQB ，并说明理由； （2）若侧面11ACC A ⊥侧面11ABB A ，求直线11C A 与平面1PQB 所成角的正弦值．20．（12分）已知两直线方程1:l y x =与2:2l y x =-，点A 在1l 上运动，点B 在2l 上运动，且线段AB 的长为定值．（1）求线段AB 的中点C 的轨迹方程；（2）设直线:l y kx m =+与点C 的轨迹相交于M ，N 两点，O 为坐标原点， 若54OM ON k k ⋅=，求原点O 到直线l 的距离的取值范围．21．（12分）已知函数2(1)211()()22x f x e x e f x -'=-+⋅． （1）求()f x 的单调区间；（2）若存在1x ，212()x x x <，使得12()()1f x f x +=，求证：122x x +<．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（10分）【选修4-4：坐标系与参数方程】在平面直角坐标系xOy 中，曲线1C 的参数方程为2cos 22sin x y αα⎧=⎪⎨=+⎪⎩（α为参数），直线2C 的方程为y x =，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系． （1）求曲线1C 的极坐标方程；（2）若直线2C 与曲线1C 交于P ，Q 两点，求||||OP OQ ⋅的值．23．（10分）【选修4-5：不等式选讲】 已知函数()|||22|(0)f x x m x m m =--+>． （1）当1m =时，求不等式()1f x ≥的解集；（2）若x ∀∈R ，t ∃∈R ，使得()|1||1|f x t t +-<+，求实数m 的取值范围．答案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．【答案】A2．【答案】A3．【答案】C4．【答案】B5．【答案】D6．【答案】B7．【答案】D8．【答案】B9．【答案】B10．【答案】B11．【答案】C12．【答案】C二、填空题：本大题共4小题，每小题5分．13．【答案】114．【答案】215．【答案】1916．【答案】(1)2n n+三、解答题：本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．17．【答案】（1）19；（2）233．【解析】（1）由题意可知，1AD=，在ABD△中，150DAB∠=︒，23AB=，1AD=，由余弦定理可知，2223(23)12231()19BD=+-⨯⨯⨯-=，19BD=．（2）由题意可知，2cosADθ=，60ABDθ∠=︒-，在ABD△中，由正弦定理可知，sin sinAD ABABD ADB=∠∠，∴2cos43sin(60)θθ=-，∴2tan33θ=．18．【答案】（1）70.5x=分；（2）约635人；（3）0.499．【解析】（1）由题意知：∴450.1550.15650.2750.3850.15950.170.5x=⨯+⨯+⨯+⨯+⨯+⨯=，∴4000名考生的竞赛平均成绩x为70.5分．（2）依题意z服从正态分布2(,)Nμσ，其中70.5xμ==，2204.75Dσξ==，14.31σ≈，∴z服从正态分布22(,)(70.5,14.31)N Nμσ=，而()(56.1984.81)0.6826P z P zμσμσ-<<+=<<=，∴10.6826(84.81)0.15872P z -≥==． ∴竞赛成绩超过84.81分（含84.81分）的人数估计为0.158********.8⨯=人635≈人． （3）全市竞赛考生成绩不超过84.81分的概率10.15870.8413-=．而(4,0.8413)B ξ~，∴444(3)1(4)1C 0.841310.5010.499P P ξξ≤=-==-⋅≈-=．19．【答案】（1）详见解析；（2． 【解析】（1）取1BB 中点E ，连结AE ，BQ ，在1BB Q △中，取H 为BQ 中点，连接,EH AH ，则1EH B Q ∥， 延长AH 与BC 交于点M ，则M 即为所求点，11ABB A 为平行四边形，点E ，P 为中点，则1AE PB ∥，由线面平行的判定定理可得AE ∥平面1PQB ， 同理可得，EH ∥平面1PQB ， 又AE EH E =I ，111B P B Q B =I ，据此可得平面AME ∥平面1PQB ，故AM ∥平面1PQB ． （2）作QO ⊥平面11ABB A ，与1A A 延长线交于O ，则1AO =，QO =1OB ==1QB =，∵12B P =，PQ =1cos QPB ∠==，∴1sin QPB ∠=，∴112242PQB S ⨯==⨯△．作11PN C A ∥，则直线11AC 与平面1PQB 所成角即直线PN 与平面1PQB 所成角，∵142PQN S =⨯=△1123B PQN V -=⨯=．设N 到平面1PQB 的距离为h ，则1232h ⨯=，∴h =，∴直线11A C 与平面1PQB 所成角的正弦值为39413h =．20．【答案】（1）2214x y +=；（2）214[0,7． 【解析】（1）∵点A 在12:2l y x =上运动，点B 在22:2l y x =-上运动， ∴设112()A x x ，222(,)B x x ， 线段AB 的中点(,)C x y ，则有122x x x +=，1222222x x y =，∴122x x x +=，1222x x -=， ∵线段AB 的长为定值2222121222()()822x x x x -++=， 即22(22)2)8x +=，化简得2214x y +=， ∴线段AB 的中点C 的轨迹方程为2214x y +=． （2）设33(,)M x y ，44(,)N x y ，联立2214x y y kx m ⎧+=⎪⎨⎪=+⎩，得222(41)8440k x kmx m +++-=，222(8)4(41)(44)0Δkm k m =-+->，化简得2241m k <+①，则342841kmx x k +=-+，23424441m x x k -=+， 2234343434()()()y y kx m kx m k x x km x x m =++=+++，若54OM ON k k ⋅=，则343454y y x x =，即343445y y x x =，所以2234343444()45k x x km x x m x x +++=，即22222448(45)4()404141m km k km m k k --+-+=++，化简得2254m k +=②， 由①②得2605m ≤<，215204k <≤， 因为O 到直线l的距离d =，所以2222225941114(1)km d k k k -===-++++， 又因为215204k <≤，所以2807d ≤<， 所以O 到直线l的距离的取值范围是[0,7． 21．【答案】（1）函数()f x 在R 上单调递增；（2）证明见解析． 【解析】（1）2(1)1()2()2x f x e x e f -''=-+⋅， 令12x =，则111()1()22f e f e ''=-+⋅，解得11()2f e'=，∴2(1)()21x f x ex -'=-+， 令2(1)()21x h x ex -=-+，2(1)11()222(1)(1)x x x h x e e e ---'=-=+-，∴1x =时，函数()f x '取得极小值即最小值，∴()(1)0f x f ''≥=， ∴函数()f x 在R 上单调递增． （2）由（1）可得：函数2(1)21()2x f x e x x -=-+在R 上单调递增． 要证明：12121222()(2)x x x x f x f x +<⇔<-⇔<-，又12()()1f x f x +=，因此1222()(2)1()(2)f x f x f x f x <-⇔-<-，即22()(2)10f x f x +-->，11(1)1122f =-+=，则121x x <<， 令2(1)22(1)211()(2)()1(2)2122x x g x f x f x e x x e x x --=-+-=--+-+-+-2(1)2(1)21124322x x e e x x --=+-+-， 1x >，(1)0g =，2(1)2(1)()44x x g x e e x --'=-+-+，令2(1)2(1)()44x x x ee x ϕ--'=-+-+，2(1)2(1)()2240x x x e e ϕ--'=+-≥，∴()g x '在(1,)+∞上单调递增．∴()(1)0g x g ''>=，∴函数()g x 在(1,)+∞上单调递增． ∴()(1)0g x g >=，因此结论122x x +<成立．22．【答案】（1）2cos 4sin 30ρθρθ--+=；（2）3． 【解析】（1）曲线1C的普通方程为22((2)4x y +-=， 则1C的极坐标方程为2cos 4sin 30ρθρθ--+=．（2）设1(,)P ρθ，2(,)Q ρθ， 将π6θ=代入2cos 4sin 30ρθρθ--+=，得2530ρρ-+=， 所以123ρρ=，所以||||3OP OQ ⋅=． 23．【答案】（1）2[2,]3--；（2）01m <<．【解析】（1）当1m =时，1|1||22|131x x x x ≤-⎧--+≥⇔⎨+≥⎩或11311x x -<<⎧⎨--≥⎩或131x x ≥⎧⎨--≥⎩，解得223x -≤≤-，所以原不等式的解集为2[2,]3--． （2）()|1||1|()|1||1|f x t t f x t t +-<+⇔<+--对任意x ∈R 恒成立，对实数t 有解．∵3,()3,3,x m x m f x x m m x m x m x m +≤-⎧⎪=---<<⎨⎪--≥⎩，根据分段函数的单调性可知：x m =-时，()f x 取得最大值()2f m m -=， ∵||1||1|||(1)(1)|2t t t t +--≤+--=，∴2|1||1|2t t -≤+--≤，即|1||1|t t +--的最大值为2， 所以问题转化为22m <，解得01m <<．模拟试卷二考试时量：120分钟 试卷满分：150分一、选择题（本大题共12小题，每小题5分，共60分． 在每小题给出的四个选项中，只有一项是符合题目要求的） 1．设集合{}{}22|log (2),|320A x y x B x x x ==-=-+<，则A C B =A ．(,1)-∞B ．(,1]-∞C ．(2,)+∞D ．[2,)+∞2. 设i 为虚数单位，若()2a iz a R i-=∈+是纯虚数，则a = A ．12 B ． 12- C ．1 D ．1- 3. 已知某超市2019年12个月的收入与支出数据的折线图如图所示：根据该折线图可知，下列说法错误的是A ．该超市2019年的12个月中的7月份的收益最高B ．该超市2019年的12个月中的4月份的收益最低C ．该超市2019年1~6月份的总收益低于2019年7~12月份的总收益D ．该超市2019年7~12月份的总收益比2019年1~6月份的总收益增长了90万元 4．已知3sin()32πα-=2020cos()3πα+= A 23．23．12D ．12-5. 已知12121ln ,2x x e -==，3x 满足33ln x e x -=，则A ．123x x x <<B ．132x x x <<C ．213x x x <<D ．312x x x <<6. 函数2()1sin 1xf x x e ⎛⎫=-⎪+⎝⎭图象的大致形状是A B C D7.公元前5世纪，古希腊哲学家芝诺发表了著名的阿基里斯悖论：他提出让乌龟在阿基里斯前面1000米处开始与阿基里斯赛跑，并且假定阿基里斯的速度是乌龟的10倍.当比赛开始后，若阿基里斯跑了1000米，此时乌龟便领先他100米，当阿基里斯跑完下一个100米时，乌龟先他10米，当阿基里斯跑完下一个10米时，乌龟先他1米，……所以，阿基里斯永远追不上乌龟.按照这样的规律，若阿基里斯和乌龟的距离恰好为210-米时，乌龟爬行的总距离为A ．410190-米B ．5101900-米C ．510990-米D ．4109900-米8.已知函数()2sin()(0,0),()2,()082f x x f f ππωϕωϕπ=+><<==，且()f x 在(0,)π上单调.则下列说法正确的是 A ．12ω=B ．62()82f π-= C ．函数()f x 在[,]2ππ--上单调递增 D ．函数()f x 的图象关于点3(,0)4π对称 9.在AOB ∆中，OA a OB b ==u u u r r u u u r r ，，满足||2a b a b ⋅=-=r r r r，则AOB ∆的面积的最大值为3 B. 2C. 232210．已知双曲线C ：22221(0,0)x y a b a b-=>>，12,F F 分别为其左、右焦点，O 为坐标原点，若点2F 关于渐近线的对称点恰好落在以1F 为圆心，1OF 为半径的圆上，则C 的离心率是 A 2 B 3．2 D ．311. 在正方体1111ABCD A B C D -中，P ，Q 分别为1AD ，1B C 上的动点，且满足1AP B Q =，则下列4个命题中： ①存在P ，Q某一位置，使AB PQ ∥； ②BPQ V 的面积为定值；③当0PA >时，直线1PB 与直线AQ 一定异面；④无论P ，Q 运动到何位置，均有BC PQ ⊥. 其中所有正确命题的序号是A. ①②④B. ①③④C. ①③D. ②④12．若函数12()2log (0)x x f x ex a a -=+->在区间(0,2)内有两个不同的零点，则实数a的取值范围是A. 22)e B. (0,2]C. 222)e + D. 3424(2,2)e +二、填空题（本大题共4小题，每小题5分，共20分． 把答案填在答题卡中的横线上） 13．若25(ax 的展开式中5x 的系数为80-，则实数a =__ __． 14．在菱形ABCD 中，060DAB ∠=，将这个菱形沿对角线BD 折起，使得平面DAB ⊥平 面BDC ，若此时三棱锥A BCD -的外接球的表面积为5π，则AB 的长为 ． 15.已知数列{}n a 满足11a =，135n n a a n ++=+，*n N ∈，则(1)21n a -= ， (2)2111(1)i i ni i a a +=+-=∑ .16．如图，衡阳市有相交于点O 的一条东西走向的公路l 与一条南北走向的公路m ，有一商城A 的部分边界是椭圆的四分之一，这两条公路为椭圆的对称轴，椭圆的长半轴长为2，短半轴长为1(单位:千米). 根据市民建议，欲新建一条公路PQ ，点,P Q 分别在公路,l m 上，且要求PQ 与椭圆形商城A 相切，当公路PQ 长最短时，OQ 的长为________千米.Q三、解答题（本大题共6小题，共70分． 解答应写出文字说明，证明过程或演算步骤） （一）必考题：60分．17．(本小题满分12分) 已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且tan(sin 2cos )cos 2222A C A C a b a+=． （1）求角B 的值；（2）若△ABC 的面积为D 为边AC 的中点，求线段BD 长的最小值．18．(本小题满分12分) 已知正方形ABCD ，E ，F 分别为AB ，CD 的中点，将△ADE 沿DE 折起，使△ACD 为等边三角形，如图所示，记二面角A-DE-C 的大小为(0)θθπ<<.（1）证明：点A 在平面BCDE 内的射影G 在直线EF 上； （2）求角θ的正弦值.EE19．(本小题满分12分) 如图，已知椭圆2222:1(0)x y C a b a b+=>>的长轴12A A 长为4，过椭圆的右焦点为F 作斜率为(0)k k ¹的直线交椭圆于B ，C 两点，直线12,BA BA 的斜率之积为34-.1）求椭圆C 的方程；2）已知直线:4l x =，直线11,A B A C 分别与l 相交于,N 两点，设E 为线段MN 的中点，求证：BC EF ^20．(本小题满分12分)已知函数()e sin )(2()2xf x x a R ax π=--∈+．（1）当1a =时，求函数()f x 在区间[,]ππ-上的值域； （2）对于任意120x x π<<<，都有2121()()22x x f x f x a e e π->---，求实数a 的取值范围.21. (本小题满分12分) 随着科学技术的飞速发展，网络也已经逐渐融入了人们的日常生活，网购作为一种新的消费方式，因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数，得到如下的相关数据(其中“x =1”表示2015年，“x =2”表示2016年，依次类推；y 表示人数)：(1)300万人； (2)该公司为了吸引网购者，特别推出“玩网络游戏，送免费购物券”活动，网购者可根据抛掷骰子的结果，操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”，则网购者可获得免费购物券500元；若遥控车最终停在“失败大本营”，则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是12，方格图上标有第0格、第1格、第2格、…、第20格。

2023届高考理科数学模拟试卷四十一（含参考答案）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若集合，，则“”是“”的( )（A ）充分不必要条件 （B ）必要不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件 2．下列函数中，在区间(0，+∞)上是增函数的是（ ）.（A ） y = - x 2（B ）2y=2x - （C ） x1y=2⎛⎫⎪⎝⎭（D ）21y=log x3．如果直线l 与直线3x -4y +5=0关于x 轴对称，那么直线l 的方程为（ ）. （A ）（B ）（C ）（D ）4．定积分220dx π⎰（x -sinx ）的值为（ ）（A ）38π （B ）318π+（C ）3124π- （D ）3124π+5．已知函数f (x)的定义域为[–2，+∞)，部分对应值如下表；f ′(x)为f (x)的导函数，函数y = f ′(x)的图象如下图所示．若实数a 满足f (2a + 1)＜1，则a 的取值范围是（ ） （A ）（B ） （C ）（D ） 6．若满足条件60,C AB BC a =︒==的ABC ∆有两个，那么a 的取值范围是（ ）(A)(B)(C)2) (D)(1,,2)7．若函数f （x ）＝2x 2－lnx 在其定义域内的一个子区间（k －1，k ＋1）内不是．．单调函数，则实数k 的取值范围是( ))23,23(-13(,)22-3(0,)217(,)22x –2 0 4f (x) 1 –1 1x y \O -2A ．[1，＋∞）B ．[1，32）C ．[1,2）D ．[32，2）8. 设等比数列的前项和为，若，则下列式子中数值不能确定的是（ ）A.B. C. D.9．已知函数()c os ()(f x A x x R ωϕ=+∈的图象的一部分如右图所示，其中0,0,2A πωϕ>><，为了得到函数()f x 的图象，只要将函数22()2cos 2sin ()22x xg x x R =-∈的图象上所有的点( )(A)向右平移6π个单位长度，再把所得各点的横坐标变为原来的12倍，纵坐标不变；(B)向右平移6π个单位长度，再把所得各点的横坐标变为原来的2倍；纵坐标不变；(C)向左平移3π个单位长度，再把得所各点的横坐标变为原来的12倍；纵坐标不变； (D)向左平移3π个单位长度，再把所得各点的横坐标变为原来的2倍，纵坐标不变.10．在△中，是边中点，角的对边分别是，若c 0AC aPA bPB ++=，则△的形状为( )A ．直角三角形B ．钝角三角形C ．等边三角形D ．等腰三角形但不是等边三角形11．已知函数是等差数列，的值（ ）A ．恒为正数B ．恒为负数C ．恒为OD ．可正可负12．已知11)(1+-=x x x f ，对任意*N n ∈，恒有)]([)(11x f f x f n n =+，则=)2013(2014f （ ） A.10071006 B.10061007- C.2013 D. 20131- 二、填空题.(共4小题，每小题5分，共20分) 13. 已知幂函数223()(1)m m f x m m x+-=--在0=x 处有定义，则实数m ＝14. “函数在上存在零点”的充要条件是{}n a n n S 0852=+a a 35a a 35S S nn a a 1+n n S S 1+ABC P B C AB C 、、a b c 、、ABC 531()4(),{}5n f x x x x x a =++∈R 数列31350,()()()a f a f a f a >++则()3+=ax x f []2,1-15已知函数f (x )＝x 3＋ax 2＋bx ＋a 2在x ＝1处取得极值10，则f (2)＝_________16.已知集合123{,,}n A a a a a =…，，记和中所有不同值的个数为．如当时，由，，，，，得．对于集合123{,,}n B b b b b =…，，若实数123,,n b b b b …，成等差数列，则= ．三、解答题：本大题共6小题，满分70分。

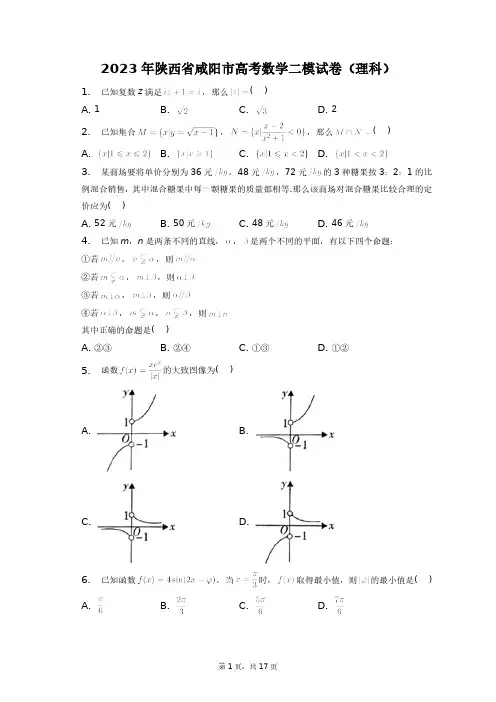
2023年陕西省咸阳市高考数学二模试卷（理科）1. 已知复数z满足，那么( )A. 1B.C.D. 22. 已知集合，，那么( )A. B. C. D.3. 某商场要将单价分别为36元，48元，72元的3种糖果按3：2：1的比例混合销售，其中混合糖果中每一颗糖果的质量都相等.那么该商场对混合糖果比较合理的定价应为( )A. 52元B. 50元C. 48元D. 46元4. 已知m，n是两条不同的直线，，是两个不同的平面，有以下四个命题：①若，，则②若，，则③若，，则④若，，，则其中正确的命题是( )A. ②③B. ②④C. ①③D. ①②5. 函数的大致图像为( )A. B.C. D.6. 已知函数，当时，取得最小值，则的最小值是( )A. B. C. D.7. 数列的前n项和为，对一切正整数n，点在函数的图象上，且，则数列的前n项和为( )A. B.C. D.8. 已知直角三角形ABC，，，，现将该三角形沿斜边AB旋转一周，则旋转形成的几何体的体积为( )A. B. C. D.9. 巴塞尔问题是一个著名的级数问题，这个问题首先由皮耶特罗门戈利在1644年提出，由莱昂哈德欧拉在1735年解决.欧拉通过推导得出：某同学为了验证欧拉的结论，设计了如图的算法，计算的值来估算，则判断框填入的是( )A.B.C.D.10. 2022年卡塔尔世界杯足球赛落幕，这是历史上首次在卡塔尔和中东国家境内举行、也是第二次在亚洲举行的世界杯足球赛.有甲，乙，丙，丁四个人相互之间进行传球，从甲开始传球，甲等可能地把球传给乙，丙，丁中的任何一个人，以此类推，则经过三次传球后乙只接到一次球的概率为( )A. B. C. D.11. 已知双曲线C：，c是双曲线的半焦距，则当取得最大值时，双曲线的离心率为( )A. B. C. D.12. 已知实数，…，对任意，不等式恒成立，则实数a的取值范围是( )A. B. C. D.13. 二项式的展开式中的系数为______.14. 过抛物线的焦点F的直线l与抛物线交于A，B两点，若l的倾斜角为，则线段AB的中点到x轴的距离是______ .15.已知非零向量，，满足，，的夹角为，且，则向量，的数量积为______ .16. 如图，已知在扇形OAB中，半径，，圆内切于扇形圆和OA、OB、弧AB均相切，作圆与圆、OA、OB相切，再作圆与圆、OA、OB相切，以此类推.设圆、圆…的面积依次为，…，那么…______ .17. 的内角A，B，C的对边分别为a，b，c，已知，求；若，求的周长.18. 如图，直四棱柱的底面是菱形，，，E，M，N分别是BC，，的中点.证明：平面；求二面角的正弦值.19. 2023年1月26日，世界乒乓球职业大联盟支线赛多哈站结束，中国队包揽了五个单项冠军，乒乓球单打规则是首先由发球员发球2次，再由接发球员发球2次，两者交替，胜者得1分.在一局比赛中，先得11分的一方为胜方，10平后，先多得2分的一方为胜方，甲、乙两位同学进行乒乓球单打比赛，甲在一次发球中，得1分的概率为，乙在一次发球中，得1分的概率为，如果在一局比赛中，由乙队员先发球.甲、乙的比分暂时为8：8，求最终甲以11：9赢得比赛的概率；求发球3次后，甲的累计得分的分布列及数学期望.20. 椭圆C：的左、右焦点分别为、，且椭圆C过点，离心率为求椭圆C的方程；若点是椭圆上任一点，那么椭圆在点M处的切线方程为已知是中椭圆C上除顶点之外的任一点，椭圆C在N点处的切线和过N点垂直于切线的直线分别与y轴交于点P、求证：点P、N、Q、、在同一圆上.21. 已知函数当时，求函数的零点；对于任意的，恒有，求实数a的取值范围.22. 在平面直角坐标系xOy中，曲线C的参数方程为为参数，以坐标原点O 为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为求曲线C的普通方程和直线l的直角坐标方程；若直线l与曲线C交于P，Q两点，且点，求的值.23. 已知：，若，求不等式的解集；，若图像与两坐标轴围成的三角形面积不大于2，求正数m 的取值范围.答案和解析1.【答案】B【解析】解：因为，所以，所以，即，所以，所以故选：根据复数的四则运算求出复数z，即可得的值．本题主要考查复数的四则运算，以及复数模公式，属于基础题．2.【答案】C【解析】解：由，得，所以，由及，得，解得，解得，所有，故选：根据偶次根式要求被开方式大于等于零，求得集合，解分式不等式求得集合，然后求交集得到结果．本题主要考查了集合交集运算，属于基础题．3.【答案】D【解析】解：定价元故选：本质上是求3种糖果单价的加权平均值，只需将三种糖果的单价加权平均即可．本题主要考查加权平均值的求法，考查运算求解能力，属于基础题．4.【答案】A【解析】解：m，n是两条不同的直线，，是两个不同的平面，①若，，则或，故①错误；②若，，则，故②正确；③若，，则，故③正确；④若，，，则m，n平行、相交或异面，故④错误．故选：由线面的位置关系可判断①；由面面垂直的判定定理可判断②；由线面垂直的性质可判断③；由线线的位置关系可判断④．本题考查空间中线线、线面和面面的位置关系，考查转化思想和推理能力，属于基础题．5.【答案】B【解析】解：因为，，当时，，单调递增，当时，，单调递减且，所以只有B选项才满足，故选：求出当和的解析式，再根据指数函数的单调性及值域即可得答案．本题考查了指数函数的性质、值域，属于基础题．6.【答案】C【解析】解：因为当时，取得最小值，即，所以，即，解得：，当时，，当时，，所以的最小值是故选：根据时，取得最小值，列出等式后解出，取k为连续的整数时，刚好正负发生变化，即可得出的最小值．本题主要考查三角函数的最值，正弦函数的性质，考查运算求解能力，属于中档题．7.【答案】D【解析】解：由题意知①，当时，，当时，②，①-②得，又，，符合题意，，，故选：根据与的关系求得，进而求出，利用裂项相消求和法即可求解．本题考查根据数列的前n项和求通项公式，裂项求和法的应用，属中档题．8.【答案】C【解析】解：将直角三角形ABC沿斜边AB旋转一周，旋转形成的几何体的如图所示，，，故选：由题意作出旋转体由两个圆锥构成，利用等面积法求出底面圆的半径，即可根据圆锥的体积公式求出旋转体的体积．本题主要考查了圆锥的结构特征，属于基础题．9.【答案】D【解析】解：若，时，当判断框填入的是，或时，则直接输出，错误，由题意得，，，，，，，，，，当时，则直接输出，若时，则满足，则还需要再循环1次，则输出的结果为，则需要，故选：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，属于中档题．10.【答案】D【解析】解：传球的结果可以分为：分别传给3人时：乙丙丁，乙丁丙，丙乙丁，丙丁乙，丁乙丙，丁丙乙，共6种；若传给2人时：乙丙乙，丙乙丙，乙丁乙，丁乙丁，丁丙丁，丙丁丙，共6种；再传给甲的：乙甲乙，丙甲丙，丁甲丁，乙丙甲，乙甲丙，乙丁甲，乙甲丁，丙乙甲，丙甲乙，丁乙甲，丁甲乙，丙丁甲，丙甲丁，丁甲丙，丁丙甲，共15种；共27种，只传乙一次的有16种，所以所求概率为故选：将所有传球的结果列出，再利用古典概型求结果．本题主要考查了古典概型的概率公式，属于基础题．11.【答案】A【解析】解：是双曲线C：的半焦距，，设，，则，令，则，当时，有最大值，，，故选：由题意得，利用三角换元，用c表示a，b，利用三角函数求得最值，结合离心率公式，即可得出答案．本题考查双曲线的性质，考查转化思想和换元法，考查逻辑推理能力和运算能力，属于中档题．12.【答案】A【解析】解：因为，所以，即，即，所以，令，，易知在上单调递增，又因为，所以，所以，，所以，，令，，则，所以当时，，单调递减；当时，，单调递增；所以，所以，解得故选：将原不等式变化为，令，，则在上单调递增，故有，即有，，，，令，，求出的最小值即可得答案．本题考查利用导数研究函数的单调性及最值，考查不等式的恒成立问题，查逻辑推理能力及运算求解能力，属于中档题．13.【答案】80【解析】解：二项式的展开式的通项公式为，令，，故展开式中的系数为，故答案为在二项展开式的通项公式中，令x的幂指数等于3，求出r的值，即可求得展开式中的系数．本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．14.【答案】3【解析】解：由题意得抛物线的标准方程为，则，即直线l为，联立，整理得，设，，则，故线段AB的中点的横坐标为，代入直线l得，线段AB的中点到x轴的距离是3，故答案为：由题意可设直线l的方程为，联立抛物线方程，利用韦达定理可得AB的中点横坐标，即可得出答案．本题考查抛物线的性质，考查方程思想和转化思想，考查逻辑推理能力和运算能力，属于基础题．15.【答案】0【解析】解：，，又，的夹角为，且，向量，的数量积，故答案为：由题意得，根据向量数量积的性质，即可得出答案．本题考查平面向量数量积的性质及其运算，考查转化思想，考查运算能力，属于基础题．16.【答案】【解析】解：如图，设圆圆，与OA分别切于点C，E，则，，圆，，，⋯⋯的半径为，，，⋯⋯，，因为，所以，在中，，则，即，解得，在中，，则，即，解得，同理可得，所以，，，⋯⋯，是以为首项，为公比的等比数列，因为，所以面积，，，⋯⋯，构成一个以为首项，以为公比的等比数列，则故答案为：分别设圆，，，⋯⋯的半径为，，，⋯⋯，根据题意可得，，，⋯⋯，是以为首项，为公比的等比数列，然后结合圆的面积公式和等比数列求和公式计算即可求解．本题考查数列的求和，考查运算求解能力，属中档题．17.【答案】解：在中，，，，，；在中，，由正弦定理可得，，又，，由余弦定理可得，，，解得，故的周长为【解析】根据已知条件，结合余弦函数的两角和公式，即可求解；根据已知条件，结合正弦定理，以及余弦定理，即可求解．本题主要考查解三角形，考查转化能力，属于中档题．18.【答案】解：证明：连接ME，，，E分别为，BC中点，且，又且，四边形为平行四边形，且，又N为中点，且，，，四边形MNDE为平行四边形，，又平面，平面，平面；连接AC，BD，，，设，，则由直四棱柱性质可知平面ABCD，四边形ABCD为菱形，，以O为原点，可建立如图所示的空间直角坐标系，则根据题意可得：，，，，，取AB中点F，连接DF，则，，，四边形ABCD为菱形且，为等边三角形，，又平面ABCD，平面ABCD，，又，，平面，平面，即平面，为平面的一个法向量，且，设平面的一个法向量为，则，取，，，二面角的正弦值为【解析】连接ME，，证明四边形MNDE为平行四边形，可得，再根据线面平行的判定定理即可得证；连接AC，BD，，，设，，以O为原点，可建立如图所示的空间直角坐标系，利用向量法求解即可．本题考查线面平行的证明，线面平行的判定定理，向量法求解二面角问题，向量夹角公式的应用，属中档题．19.【答案】解：甲以11：9赢得比赛，共计20次发球，在后4次发球中，需甲在最后一次获胜，最终甲以11：9赢得比赛的概率为：；设甲累计得分为随机变量X，X的可能取值为0，1，2，3，，，，，随机变量X的分布列为：X0123P【解析】根据题意可得甲以11：9赢得比赛，则甲再得到3分，乙得到1分，且甲得到最后一分，再根据独立事件的乘法公式求概率即可；根据题意可得X的可能取值为0，1，2，3，求出相应的概率列出分布列，再求其数学期望即可．本题主要考查了独立事件的概率乘法公式，考查了离散型随机变量的分布列和期望，属于中档题．20.【答案】解：由题意得，解得，，所以椭圆C的标准方程为证明：由题意知：过点的椭圆的切线方程为，令，则；且，则设直线NQ方程为，令，则；又，，则；，即，，，即点N、P、Q、、在以PQ为直径的圆上．【解析】根据离心率和椭圆所过点及得到方程组，求出答案；根据题意得到过点的椭圆的切线方程及直线NQ方程，得到P、Q两点坐标，从而得到，得到，，得到证明．本题主要考查椭圆的性质及标准方程，直线与椭圆的综合，考查运算求解能力，属于中档题．21.【答案】解：当时，，得，令，则，，即，所以在R上单调递增，注意到，故有唯一的零点注意到，只要即可，，，令，则，当时，，有，即，符合题意；当时，，若，即时，，此时，即，符合题意；若，即时，在上单调递减，在上单调递增知，，不合题意，综上，即实数a的取值范围为【解析】的正负不明显时，对其再次求导判断值域，即可得出的正负，从而得出的单调性，再结合函数值即可判断零点个数．注意到，可考虑让在单调递增求出a的范围即可符合题意，然后再检验不单调递增时a的范围即可，此法为端点效应．本题考查利用导数研究函数的单调性，考查函数的零点以及不等式的恒成立问题，本题第二问的关键在于分类讨论，首先讨论时的情况，然后讨论时，利用端点效应代入求出a的范围，并检验是否符合题意，考查逻辑推理能力及运算求解能力，属于中档题．22.【答案】解：由曲线为参数，消去t得，曲线C的普通方程为，由直线l：，，，可得其直角坐标方程为直线l：化为参数式为为参数，将直线l的参数方程代入，可得，即由根与系数的关系可得，，，【解析】消去参数t，可得曲线C的普通方程，由极坐标和直角坐标间的转化关系可得直线l 的直角坐标方程；写出直线l的参数方程，与曲线C的方程联立，利用参数的几何意义即可得解．本题主要考查极坐标方程与直角坐标方程的互化，参数方程与普通方程的互化，参数方程的几何意义及其应用等知识，属于中等题．23.【答案】解：当时，，所以当时，，即，解得，当时，，即，解得，当时，，即，解得，综上，或，所以不等式的解集为，如图所示，图像与两坐标轴交于点，，则，依题意，即，所以实数m的取值范围为【解析】将代入函数，并将函数化为分段函数的形式，再分类讨论解不等式即可；作出函数图象，结合图象得到点A，B的坐标，进而表示出的面积，由此可得解．本题考查分段函数及其运用，考查分类讨论思想，数形结合思想以及运算求解能力，属于中档题．。

俯视图侧视图正视图2023届高考理科数学模拟试卷四(含参考答案)一、选择题：（本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.） 1．设全集U = R ，A =10xx ⎧⎫<⎨⎬⎩⎭，则U C A =（ ） A .｛x | x ≥0｝ B.｛x | x > 0｝ C. 10x x ⎧⎫>⎨⎬⎩⎭ D.1x x ⎧⎨⎩≥0⎭⎬⎫2．"1''=a 是“函数ax ax y 22sin cos -=的最小正周期为π”的 ( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．设0x 是方程ln 4x x +=的解，则0x 属于区间A. （0，1）B. （1，2）C. （2，3）D.（3，4） 4．按向量)2,6(π=a 平移函数()2sin()3f x x π=-的图象，得到函数()y g x =的图象，则 A. ()2cos 2g x x =-+ B. ()2cos 2g x x =-- C. ()2sin 2g x x =-+ D. ()2sin 2g x x =--5．已知实数x 、y 满足约束条件⎪⎩⎪⎨⎧≤+≥≥622y x y x ,则y x z 42+=的最大值为 ( )A. 24B. 20C. 16D. 126．.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示，则这个棱柱的体积为A.B. C.2 D. 67．一水池有2个进水口，1 个出水口，进出水速度如图甲、乙所示. 某天0点到6点，该水池的蓄水量如图丙所示.（至少打开一个水口）（第15小题）给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③ 4点到6点不进水不出水.则一定能确定正确的论断是A ．①②③B ．①② C.②③ D.①③ 8.定义在(－∞,＋∞)上的偶函数f(x)满足f(x ＋1)=－f(x), 且f(x)在[－1,0]上是增函数, 下面五个关于f(x)的命题中: ① f(x)是周期函数 ② f(x) 的图象关于x=1对称 ③ f(x)在[0,1]上是增函数, ④f(x)在[1,2]上为减函数 ⑤ f(2)=f(0) 正确命题的个数是( ) A. 1个 B. 2个 C.3个 D.4个二、填空题：（本大题共6个小题，每小题5分，共30分，其中9-12题必做,在13,14,15题中选做两题,多选以前两题计分,把答案写在答题卷上）． 9.已知0t >，若()021d 6tx x -=⎰，则t =10．sin168sin 72sin102sin198︒︒︒︒+= ． 11.函数2234log ()y x x =--的单调增区间是______________;12.符号[]x 表示不超过x 的最大整数，如[][]208.1,3-=-=π，定义函数()[]f x x x =-， 那么下列命题中正确的序号是 ．（1）函数()f x 的定义域为R ，值域为[]1,0； （2）方程()12f x =，有无数解； （3）函数()f x 是周期函数； （4）函数()f x 是增函数. 13、极坐标方程sin 2cos ρθθ=+所表示的曲线的直角坐标方程是 . 14、已知c b a ,,都是正数，且,12=++c b a 则cb a 111++15．已知圆O 的半径为3，从圆O 外一点A 引切线AD 和割线ABC ，圆心O 到AC 的距离为22，3AB =，则切线AD 的长为 _______.三、解答题：本大题共6小题，满分80分，解答应写出文字说明，证明过程或演算步骤． 16．（本题满分12分）已知02cos 22sin =-xx ， （Ⅰ）求x tan 的值；（Ⅱ）求xx xsin )4cos(22cos ⋅+π的值．17．（本题满分12分）已知函数()f x 是定义在[]1,1-上的奇函数,在[0,1]上()()2ln 11xf x x =++-（Ⅰ）求函数()f x 的解析式;并判断()f x 在[]1,1-上的单调性(不要求证明) （Ⅱ）解不等式()()22110f x f x ++-≥.18．（本题满分14分）某“帆板”集训队在一海滨区域进行集训，该海滨区域的海浪高度y （米）随着时间(024,)t t ≤≤单位小时而周期性变化，每天各时刻t 的浪高数据的平均值如下表：（Ⅰ）试画出散点图；（Ⅱ）观察散点图，从,sin(),cos()y ax b y A t b y A t ωϕωϕ=+=++=+中选择一个合适的函数模型，并求出该拟合模型的解析式；（Ⅲ）如果确定在白天7时~19时当浪高不低于0.8米时才进行训练，试安排恰当的训练时间。

2023年陕西省西安市周至县高考数学二模试卷（理科）1. 已知全集，，，则集合( )A. B. C. D.2. 设复数z满足，则复数z的虚部是( )A. B. 5 C. D.3.若非零向量满足，则必有( )A. B.C. D.4. 已知数据，，…，是某市个普通职工的年收入，如果再加上世界首富的年收入，组成个数据，则下列说法正确的是( )A. 年收入的平均数可能不变，中位数可能不变，方差可能不变B. 年收入的平均数大大增加，中位数可能不变，方差变大C. 年收入的平均数大大增加，中位数可能不变，方差变小D. 年收入的平均数大大增加，中位数一定变大，方差可能不变5. “双碳”战略倡导绿色、环保、低碳的生活方式年9月中国明确提出2030年实现“碳达峰”，2060年实现“碳中和”，为了实现这一目标，中国持续推进产业结构和能源结构调整，大力发展可再生能源，新型动力电池随之也迎来了蓬勃发展机遇于1898年提出蓄电池的容量单位：，放电时间单位：与放电电流单位：之间关系的经验公式，其中为Peukert常数.在电池容量不变的条件下，当放电电流时，放电时间，则当放电电流时，放电时间为( ) A. 14h B. C. 29h D. 56h6. 是的( )A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件7. 已知函数的部分图象如图所示，其中，，则( )A. 1B.C.D.8. 折扇是我国传统文化的延续，在我国已有四千年左右的历史，“扇”与“善”谐音，折扇也寓意“善良”“善行”．它常以字画的形式体现我国的传统文化，也是运筹帷幄、决胜千里、大智大勇的象征如图，图2为其结构简化图，设扇面A，B间的圆弧长为l，AB间的弦长为d，圆弧所对的圆心角为为弧度角，则l、d和所满足的恒等关系为( )A. B. C. D.9. 如图，在正方体中，F为线段的中点，E为线段上的动点，下列四个结论中，正确的是( )A. 平面B. 存在点E，使平面C. 存在点E，使D.10. 某学生在“捡起树叶树枝，净化校园环境”的志愿活动中拾到了三支小树枝视为三条线段，想要用它们作为三角形的三条高线制作一个三角形，经测量，其长度分别为3cm，4cm，6cm，则( )A. 能作出一个锐角三角形B. 能作出一个直角三角形C. 能作出一个钝角三角形D. 不能作出这样的三角形11. 已知是抛物线C：上一点，点M到抛物线C的焦点F的距离为若过点向抛物线C作两条切线，切点分别为A，B，则( )A. 18B. 17C. 16D. 1512. 已知，，，则( )A. B. C. D.13. 双曲线的实轴长为4，则其渐近线方程为______ .14. 若满足约束条件，则的最小值为______ .15. 《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有阳马，广五尺，褒七尺，高八尺，问积几何？”其意思为：“现在有底面为矩形，一条侧棱垂直于底面的四棱锥，它的底面长、宽分别为7尺和5尺，高为8尺，问它的体积是多少？”若以上的条件不变，则这个四棱锥的外接球的表面积为______平方尺．16. 函数是计算机程序中一个重要函数，它表示不超过x的最大整数，例如，已知函数且，若的图象上恰有3对点关于原点对称，则实数a的最小值为______ .17. 在①；②，；③，这三个条件中任选一个，补充在下面问题中，并作答.已知为等差数列的前n项和，若_____.求数列的通项公式；设，求数列的前n项和注：如果选择多个条件分别解答，按第一个解答计分.18. 某学校在假期安排了“垃圾分类知识普及实践活动”，为了解学生的学习成果，该校对全校学生进行了测试，并随机抽取50名学生的成绩进行统计，将其分成以下6组：整理得到如图所示的频率分布直方图.求图中a的值；若将频率视为概率，从全校成绩在80分及以上的学生中随机抽取3人，用X表示这3人中成绩在中的人数，求随机变量X的分布列及数学期望.19. 在如图所示的多面体中，，，平面ABCD，四边形ACFE为矩形.求证：平面平面CDF；若，，求直线AD与平面BEF所成角的正弦值.20. 如图，已知椭圆E：的一个焦点为，离心率为求椭圆E的方程；过点作斜率为k的直线交椭圆E于A，B两点，AB的中点为设O为原点，射线OM 交椭圆E于点当四边形OACB为平行四边形时，求k的值.21. 已知函数讨论的零点个数；若有两个零点，，求证：22. 已知圆C的极坐标方程为，直线l的方程为以极点为坐标原点，极轴为x轴正半轴建立直角坐标系求圆C的圆心坐标及半径；直线l与圆C的交点为A，B，求三角形ABC的面积.23. 已知函数求不等式的解集；若的最小值为k，且实数a，b，c满足，求证：答案和解析1.【答案】C【解析】解：全集，，，，则集合故选：利用补集定义先求出，再由交集定义能求出集合本题考查集合的运算，考查交集、补集定义、不等式的性质等基础知识，考查运算求解能力，是基础题．2.【答案】C【解析】解：，则，故复数z的虚部是故选：根据已知条件，结合复数模公式，以及复数的运算，求出z，再结合虚部的定义，即可求解．本题主要考查复数的运算，属于基础题．3.【答案】B【解析】解：若非零向量满足，则，即，，故选：把已知向量等式变形，可得，由此得到本题考查平面向量数量积的性质及运算，考查向量垂直与数量积的关系，是基础题．4.【答案】B【解析】解：数据，，…，是某市个普通职工的年收入，而为世界首富的年收入，则会远远大于，，…，，故这个数据中，年收入平均数大大增大，中位数可能不变，也可能变大，又数据的集中程度也更加离散，则方差变大．故选：根据平均数，中位数及方差的意义判断即可．本题主要考查了数据的平均数及中位数，方差的特征，属于基础题．5.【答案】D【解析】解：，因为电池容量不变，则有，即有，所以当放电电流时，放电时间为故选：根据给定的条件，列出方程，结合指数、对数运算计算作答．本题考查函数模型的选择及其应用，考查对数的运算，属基础题．6.【答案】C【解析】解：由，可得或，由，一定可以推出，所以是的必要不充分条件，故选：根据充分条件和必要条件的定义分别进行判断即可．本题主要考查充分条件和必要条件的判断，根据充分条件和必要条件的定义是解决本题的关键，属于基础题．7.【答案】C【解析】【分析】本题考查由部分图像求三角函数解析式，考查计算能力，是基础题．利用函数的图象求解，结合五点法作图求解即可．【解答】解：由题意可知：，解得，则，解得，由五点法作图可得，，且，解得，所以，可得故选：8.【答案】A【解析】解：由题意，如图，可得，，设，则在中，，①又，②所以由①②可得：，即故选：由题意，设，在中，解三角形可得，又，联立方程即可求解．本题考查了扇形的弧长公式的应用，考查了数形结合思想，属于基础题．9.【答案】D【解析】解：如图，当E为线段的中点时，，则平面，当E不为线段的中点时，EF 与平面相交，故A错误；若存在点E，使平面，而平面，则平面平面，而平面与平面所成角的正切值为，矛盾，故B错误；当E与重合时，EF与相交，当E不与重合时，又异面直线所成角的定义可知，EF与异面，故C错误；由正方体的结构特征可知，平面，而平面，则，故D正确．故选：由空间中直线与平面的位置关系判定A；利用反证法思想判断B；由异面直线的定义判断C；直接证明D正确．本题考查空间中直线与直线、直线与平面、平面与平面位置关系的判定，考查空间想象能力与思维能力，是中档题．10.【答案】C【解析】解：设高分别为3cm、4cm、6cm对应的底边长分别为a、b、单位：，则，设，则，，由三角形三边关系可知，这样的三角形存在，设该三角形的最大内角为，则，则为钝角，故能作出一个钝角三角形．故选：计算出三角形三边的比值，并计算出三角形中最大角的余弦值，可得出结论．本题考查余弦定理的应用，是中档题．11.【答案】B【解析】解：抛物线C：，则抛物线的焦点，准线方程为，是抛物线C：上一点，点M到抛物线C的焦点F的距离为6，，解得，抛物线的方程为，显然不在抛物线C上，，则，设切点，，抛物线在切点A处的切线方程为，将代入得，又，则，同理可得抛物线C在点B处的切线方程为，直线AB的方程为，联立，整理得，，，故选：由题意得抛物线的焦点，准线方程为，求出p，求出在切点A、B的切线方程，可得直线AB的方程为，联立，利用韦达定理，即可得出答案．本题考查抛物线的性质，考查转化思想和方程思想，考查逻辑推理能力和运算能力，属于中档题．12.【答案】A【解析】解：设，则恒成立，所以在R上单调递增，所以，所以，即，所以，设，则，当时，，所以在上单调递增，所以，所以，即，所以，综上，故选：设，，利用导数可证在R上单调递增，在上单调递增，再代入运算，得解．本题考查利用导数研究函数的单调性，构造新函数是解题的关键，考查逻辑推理能力和运算能力，属于中档题．13.【答案】【解析】解：双曲线的实轴长为4，，解得，即双曲线的渐近线为，即故答案为：由题意得，可得，即可得出答案．本题考查双曲线的性质，考查转化思想，考查运算能力，属于基础题．14.【答案】【解析】解：因为变量x，y满足约束条件，目标函数，画出图形：点，平移直线可得：z在点A处有最小值：故答案为：线性约束条件画出可行域，然后求出目标函数的最小值．本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．15.【答案】【解析】解：将该四棱锥补全成以底面长、宽分别为7尺和5尺，高为8尺的长方体，则此四棱锥的外接球为该长方体的外接球，长方体的体对角线即为外接球的直径2R，由长方体的体对角线公式得，，所求球的表面积为，故答案为：先将该四棱锥补全成长方体，则长方体的为接球即为该四棱锥的外接球，长方体的体对角线即为外接球的直径，再利用长方体的体对角线公式求出外接球半径，最后代入球的表面积公式即可求解．本题考查四棱锥的外接球问题，分割补形法，长方体的体对角线公式，球的表面积公式，属基础题．16.【答案】【解析】解：根据新定义，作出的图象如下：要使的图象上恰有3对点关于原点对称，则与的图象恰有3个交点，由图象可得，解得，即实数a的取值范围是故答案为：根据新定义，作出的图象，结合图象即可求解．本题主要考查分段函数及其应用，考查数形结合思想与运算求解能力，属于中档题．17.【答案】解：方案一：选择条件①由题意，当时，，当时，，当时，也满足上式，，方案二：选择条件②由题意，设等差数列的公差为d，则，解得，，方案三：选择条件③由题意，设等差数列的公差为d，则，解得，，由可得，，故【解析】在选择条件①的情况下根据题干已知条件并结合公式即可计算出数列的通项公式；在选择条件②的情况下先设等差数列的公差为d，再结合等差数列的通项公式列出关于公差d的方程，解出d的值，即可计算出数列的通项公式；在选择条件③的情况下先设等差数列的公差为d，再结合等差数列的前n项和公式列出关于公差d的方程，解出d的值，即可计算出数列的通项公式．先根据第题的结果计算出数列的通项公式，再运用裂项相消法即可计算出前n项和本题主要考查数列求通项公式，以及运用裂项相消法求前n项和问题．考查了方程思想，转化与化归思想，分类讨论，等差数列通项公式与求和公式的运用，以及逻辑推理能力和数学运算能力，属中档题．18.【答案】解：由频率分布直方图可得，，解得由图可知，成绩在与的学生比例为2：1，所以从全校成绩在80分及以上的学生中抽取1人，成绩在的概率为，抽取3人，成绩在中的人数为X，，则，的分布列如下：X0123P【解析】根据频率分布直方图中各矩形面积之和等于1，即可求得a的值；确定随机变量X服从于二项分布，根据二项分布的概率计算以及期望公式，即可求得答案．本题主要考查离散型随机变量的分布列及期望，是中档题．19.【答案】解：证明：，平面CDF，平面CDF，平面CDF，四边形ACFE为矩形，，平面CDF，平面CDF，平面CDF，，平面ABE，平面ABE，平面平面易知AB，AD，AE两两相互垂直，以点A为原点，AB，AD，AE所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，则，，，，，，，，设平面BEF的法向量为，，且，，取，可得，直线AD与平面BEF所成角的正弦值为【解析】可知，，从而得出平面CDF，平面CDF，从而根据面面平行的判定定理即可得出平面平面CDF；可以A为原点，AB，AD，AE所在的直线分别为x，y，z轴，建立空间直角坐标系，然后可得出，，的坐标，然后设平面BEF的法向量，根据即可求出的坐标，然后根据向量夹角的余弦公式可求出，然后即可得出直线AD 与平面BEF所成角的正弦值．本题考查了线面平行和面面平行的判定定理，通过建立坐标系，利用向量求线面角的正弦值的方法，向量垂直的充要条件，向量坐标的数量积运算，考查了计算能力，属于基础题．20.【答案】解：由椭圆E：的一个焦点为，可得半焦距，又椭圆的离心率为，，则，，椭圆E的方程为由得椭圆E的方程为，由题意得直线AB的方程为，即，联立消去y得，设，，则四边形OACB是平行四边形，设，则，即，，又，即，解得【解析】由题意易求c，a，从而可求椭圆E的方程；联立直线与椭圆方程可得进而可得，求解即可．本题考查椭圆方程的求法，直线与椭圆的位置关系的综合应用，考查转化思想以及计算能力，属中档题．21.【答案】解：，因为，所以当时，，单调递减；当时，，单调递增，所以，当，即时，的零点个数为0，当，即时，的零点个数为1，当，即时，注意到，因为，所以，因此，，使得，所以此时的零点个数为2，综上，当时，的零点个数为0；当时，的零点个数为1；当时，的零点个数为2；证明：由可知，当时，函数有两个零点，且，令，则，当时，，所以在区间上单调递增，所以，所以，因为，所以，又由可知，在区间上单调递增，所以，故【解析】由题意当时，单调递减；当时，单调递增，得，分，，三种情况，讨论得到的零点个数；由可知，当时，函数有两个零点，且，令，求导后利用单调性即可得证．本题考查了导数的综合应用，属于中档题．22.【答案】解：圆C的极坐标方程为，所以，根据得直角坐标方程为所以圆的半径为直线l的极坐标方程为所以，整理得，所以，所以由于为等腰三角形．所以弦AB上的高，所以【解析】利用极坐标与直角坐标的互化，转化求解即可．利用弦长公式求解，然后求解圆的圆心到直线的距离，即可求解三角形的面积．本题考查极坐标与坐标坐标的互化，直线与圆的位置关系的应用，考查分析问题解决问题的能力，是中档题．23.【答案】解：因为函数，所以不等式可化为或或，解得或或，即或，所以不等式的解集为证明：由知时，，时，，时，，所以，所以所以，所以，所以，当且仅当时取等号，所以【解析】利用分段讨论法去掉绝对值，再求不等式的解集．求出，化简，利用基本不等式求出的最小值即可．本题考查了含有绝对值的不等式解法与应用问题，也考查了基本不等式的应用问题，是中档题．。

2023届高考理科数学模拟试卷六十二（含参考答案）一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、 已知全集是U ，集合M 和N 满足，则下列结论中不成立的是（ ）A ．=MN M B ．=MN N C. =N C M U )=∅U M N D ．=M C N U )=∅U M N2、设x R ∈则“1x =”是“复数()()211z x x i =-++为纯虚数”的（ ）A ．充分必要条件B ．必要不充分条件 C.充分不必要条件 D ．既不充分也不必要条件3、 已知数列{}n a 是1为首项、2为公差的等差数列，{b n }是1为首项、2为公比的等比数列．设nb n ac =，T n =c 1+c 2+…+c n （n ∈N*），则当T n ＞2013时，n 的最小值是（ ）4、将函数)32sin(2)(-=x x f 的图像向左平移4个单位，得到函数)(x g 的图像，则函 数)(x g 的一个单调递增区间是 ( ) A ． ]0,125[π-B ．]0,3[π-C ． ]3,0[πD ．]2,6[ππ- 5、已知函数)3(log )(25.0a ax x x f +-=在),2[+∞单调递减，则的取值范围( ) A.]4,(-∞ B.),4[+∞ C. ]4,4[-D. ]4,4(-6、已知函数f （x ）是定义在R 上的增函数，则函数y ＝f （｜x －1｜）－1的图象可能是 ( )7、若是两个非零向量，且，则与的夹角的取值范围是( )N M ⊆a主视图俯视图 (第16题)NMD C BA(第12题)输出S是否 结束开始 S =0 i > i =1i =2i +1S =S +2 A ．⎥⎦⎤⎢⎣⎡65,32ππ B. ⎥⎦⎤⎢⎣⎡32,3ππ C. ⎥⎦⎤⎢⎣⎡2,3ππ D. ⎥⎦⎤⎢⎣⎡3,6ππ 8、设a 、b 是两条不同的直线，α、β是两个不同的平面，则下列四个命题①若αα//,,b a b a 则⊥⊥ ②若ββαα⊥⊥a a 则,,// ③αβαβ//,,a a 则⊥⊥④βαβα⊥⊥⊥⊥则若,,,b a b a其中正确的命题的个数是（ ）A ．0个B ．1个C ．2个D ．3个9、公差不为0的等差数列{n a }的前21项的和等于前8项的和．若80k a a ＋＝，则k ＝( ) A ．20 B ．21 C ．22 D ．2310、记函数()ln 1f x x =-的零点为a ，函数()ln xg x x e -=-的零点为b ，函数12()x h x e x -=-的零点为c ，则三个函数的零点大小关系为（ ）A ．a ＜b ＜cB ．c ＜b ＜aC ．c ＜a ＜bD ．b ＜a ＜二、 填空题：本大题共7小题, 每小题4分, 共28分。

2023届高考理科数学模拟试卷六十（含参考答案）考生须知：1. 全卷分试卷和答卷。

试卷2页，答卷4页。

考试时间120分钟，满分150分。

2. 本卷的答案必须做在答卷的相应位置上，做在试卷上无效。

3. 请用钢笔或圆珠笔将班级、准考证号、姓名、座位号分别填写在答卷的相应位置上。

一、选择题：本大题共10小题，每小题5分，共50分. 1．全集{0,1,2,3}U =，{2}U C M =，则集合M =（ ）A ．{0，1，3}B ．{1，3}C ．{0，3}D ．{2}2．若函数()f x （x R ∈）是奇函数，函数()g x （x R ∈）是偶函数，则（ ）A ．函数()()f x g x +是奇函数B ．函数()()f x g x ⋅是奇函数C ．函数[()]f g x 是奇函数D ． 函数[()]g f x 是奇函数 3. 下列函数中，图像的一部分如右图所示的是（ ） A ．sin()6y x π=+B ．sin(2)6y x π=-C ．cos(2)6y x π=-D ．cos(4)3y x π=-4．等比数列{a n }的前n 项和为S n ，若S 2n ＝3(a 1＋a 3＋…＋a 2n －1)，a 1a 2a 3＝8，则a 10等于（ ）A ．－1024B ．1024C ．－512D ．5125．已知函数2()f x x bx =+的图象在点A (1，f (1))处的切线的斜率为3，数列1()f n ⎧⎫⎨⎬⎩⎭的前n 项和为n S ，则2013S 的值为（ ）A ．20102011B ．20112012 C ．20122013D ．201320146．若实数x ，y 满足不等式组2402300x y x y x y +-≥--≥-≥⎧⎪⎨⎪⎩， 则x ＋y 的最小值是（ ）A ．4B．3 C ． 4 D ． 6第3题图8．命题p ：“1≠x 或3y ≠”是命题q ：“4≠+y x ”的（ ）条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要9．如图，半圆的直径6AB =，O 为圆心，C 为半圆上不同于A 、B 的任意一点，若P 为半径OC 上的动点，则()PA PB PC +的最小值为（ ） A ．92 B ．9 C ．92- D ．－910．若函数32()f x x ax bx c =+++有两个极值点12,x x ,且11()f x x =,则关于x 的方程23(())2()0f x af x b ++=的不同实根个数是（ ）A ．3B ．4C ．5D ．6二、填空题：本大题共7小题，每小题4分，共28分. 11. 不等式2(2)211x x -≤+的解集为 ____.12. 已知数列{}n a 满足11a =，12n n n a a +=+，则10a =_________. 13．在ABC ∆中，,,a b c 分别是内角,,A B C 的对边，已知16,4,cos 3a c B ===，则____b =.14. 已知， ，则的值为________．15. 若是偶函数，则 .16. 函数21()2ln 2f x x x x a =+-+在区间(0,2)上恰有一个零点，则实数a 的取值范围是_____.17. 已知函数2()|21|f x x x =+-，若1a b <<-且()()f a f b =，则a b a b ++的取值范围_____.41)4sin(=+πθ),23(ππθ--∈)127cos(πθ+)4sin(3)4sin()(ππ-++=x x a x f =a OP CBA三、解答题：第18、19、20题每题14分，第21、22每题15分，共72分．18．已知 且； :q 集合{}2(2)10,A x x a x x R =+++=∈，{}0B x x =>且A B =∅.若∨为真命题，∧为假命题，求实数a 的取值范围.19．已知函数. （1）写出如何由函数sin y x =的图像变换得到的图像；（2）在中，角所对的边分别是，若，求的取值范围.20．已知函数R ，， （1）求函数f (x )的值域；1:(),3xp f x -=|()|2f a <p q p q 2()sin2cos 24x x f x =+()f x ABC ∆AB C 、、a b c 、、C b B c a cos cos )2(=-)(A f 2()(xxf x a x a =+∈1)a >（2）记函数()(),[2,)g x f x x =-∈-+∞，若的最小值与无关，求的取值范围； （3）若，直接写出（不需给出演算步骤）关于的方程的解集．21.已知数列的前n 项和（n 为正整数）．（1）令，求证数列是等差数列，并求数列的通项公式； （2）令，12n n T c c c =+++，试比较与的大小，并予以证明．()g x aa m >x ()f x m ={}n a 11()22n n n S a -=--+2nn n b a ={}n b {}n a 1n n n c a n+=n T 521nn +22．已知实数a 满足02a <≤，1a ≠，设函数3211()32a f x x x ax +=-+． （1）当2a =时，求()f x 的极小值；（2）若函数32()(24)ln g x x bx b x x =+-++（b R ∈）的极小值点与()f x 的极小值点相同．求证：()g x 的极大值小于等于54．参考答案一、选择题：本大题共10小题，每小题5分，共50分.二、填空题：本大题共7小题，每小题4分，共28分.11___[1,7]-_______ 12____1023______ 13___________6_____14___8-____ 15____3-_____ 16____2ln 24a ≤-或32a =-__17_______(1,1)-____三、解答题：第18、19、20题每题14分，第21、22每题15分，共72分．18．已知 且； :q 集合{}2(2)10,A x x a x x R =+++=∈，{}0B x x =>且A B =∅.若∨为真命题，∧为假命题，求实数a 的取值范围. 解：对p ：所以．若命题p 为真，则有；...........2分 对q ：∵且∴若命题q 为真，则方程无解或只有非正根．∴或, ∴...........................5分∵p, q 中有且只有一个为真命题∴ (1) p 真，q 假：则有；......................8分 (2) p 假，q 真：则有； ∴或． ........................14分19．已知函数. （1）写出如何由函数sin y x =的图像变换得到的图像；1:(),3xp f x -=|()|2f a <p q p q 1|()| ||23af a -=<75<<-a }0x |x {B >=∅=⋂B A 01x )2a (x )x (g 2=+++=04)2a (2<-+=∆0(0)0202g a ⎧⎪∆≥⎪≥⎨⎪+⎪-<⎩4a ->4a 54a 7a 5-≤<-⎩⎨⎧-≤<<-，即有7a 4a 5a 7a ≥⎩⎨⎧->-≤≥，即有或4a 5-≤<-7a ≥2()sin2cos 24x x f x =+()f x（2）在中，角所对的边分别是，若，求的取值范围. 解：……………………3分 （Ⅰ） 24sin sin()sin()424x y x y x y πππ=−−−−→=+−−−−−→=+左移横坐标伸长为原来的倍个单位1sin()sin()12424x x y y ππ→=+−−−→=++上移个单位 ……7分 （Ⅱ）由，利用三角形中的正弦定理知： ∵，∴……………………10分，∵，∴，……………………12分 ∴……………………14分20．已知函数R ，， （1）求函数f (x )的值域；（2）记函数()(),[2,)g x f x x =-∈-+∞，若的最小值与无关，求的取值范围； （3）若，直接写出（不需给出演算步骤）关于的方程的解集．解：(1)①时，， ABC ∆AB C 、、a b c 、、C b B c a cos cos )2(=-)(A f ()142sin 212cos 2sin+⎪⎭⎫⎝⎛+=++=πx x x x f ()C b B c a cos cos 2=-1cos 2=B π<<B 03π=B ()142sin 2+⎪⎭⎫⎝⎛+=πA A f 320π<<A 127424πππ<+<A 142sin 22≤⎪⎭⎫⎝⎛+<πA ()122+≤<A f 2()(xx f x a x a=+∈1)a >()g x aa m >x ()f x m =0x≥221,()x xxx x a f x a a a a≥=+=+≥·········································· ·········································· 试场·········································· ·········································· --------------------线-------------------当且仅当，即时等号成立； ②，，由①②知函数的值域为．(2)，①，，②时，，令，则，记，，时等号成立，(i)，即时，结合①知与无关； (ii)，即时，， 在上是增函数，，结合①知与有关；综上，若的最小值与无关，则实数的取值范围是．(3)①时，关于的方程的解集为；②m >3时，关于x 的方程的解集为或．21.已知数列的前n项和（n 为正整数）．（1）令，求证数列是等差数列，并求数列的通项公式； （2）令，12n n T c c c=+++，试比较与的大小，并予以证明． 解（I ）在中，令n=1，可得，即 当时，，2xx a a=1x a =>0x <31,01,()3xx a a f x a>∴<<∴=>()f x )+∞()()2,[2,)x xg x f x a a x =-=+∈-+∞0x ≥1,1,()3,()3x xa a g x a g x >∴≥=∴≥20x -≤<211,1,()2x x xa a gx a a a->≤<=+xt a =1()2g x t t=+1()2.h t t t =+21(1)t a ≤<1()2h t t t =+≥12t t=2t =21a ≤a ≥min ()g x =a 212a >1a <<421()220h t a t'=-≥->()h t ∴21[,1)a 2min min 2212()()()3g x h t h a a a===+<2min 22()g x a a=+a ()g x a a a ≥3m <≤x ()f x m =|log 2a m x x ⎧⎪=⎨⎪⎪⎩⎭()f x m =|log 2a m x x ⎧+⎪=⎨⎪⎩3log a x m ⎫=⎬⎭{}n a 11()22n n n S a -=--+2nn n b a ={}n b {}n a 1n n n c a n+=n T 521nn +11()22n n nS a -=--+1112n S a a =--+=112a =2n ≥21111111()2()22n n n n n n n n n S a a S S a a ------=--+∴=-=-++，..又数列是首项和公差均为1的等差数列. 于是. (II)由（I ）得，所以由①-②得于是确定的大小关系等价于比较的大小 由可猜想当证明如下： 证法1：（1）当n=3时，由上验算显示成立。

2023届高考理科数学模拟试卷五十三（含参考答案）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的.）1．已知集合{}{}|1,|20,A x x B x x =>-=-≤≤则AB = （ ）A.{}|0x x ≥B. {}|2x x ≥-C. {}|10x x -<≤D. {}|10x x -≤< 2．下列各式中值为的是 （ ）A ．B ．C ．D ．3．已知1a >，22()x xf x a +=，则()1f x <成立的充要条件是 （ ）A ． 0＜x ＜1B ． ﹣1＜x ＜0C ． ﹣2＜x ＜0D ． ﹣2＜x ＜14．下列结论错误的．．．是 （ ）A ．命题“若，则”与命题“若则”互为逆否命题;B ．命题，命题则为真;C ．若为假命题，则、均为假命题．D ．“若则”的逆命题为真命题;5．若11(2)ax x+⎰d x = 3 + ln 2，则 a 的值为 （ ） A ．6B ．4C ．3D ．26．设函数22()sin ()cos ()44f x x x ππ=+-+（x ∈R ），则函数()f x 是 （ ）． 最小正周期为的奇函数D ． 最小正周期为的偶函数函数()f x 在定义域R 内可导，若()(2)f x f x =-，且（x ﹣1）f ′（x ）＜0，若(0)a f =，1()2b f =，(3)c f =，则,,a b c 的大小关系是 （ ）A ．B ．C ．D ． 9．设函数，则下列结论正确的是 （ ）A ．的图像关于直线对称B ．的图像关于点对称23o o 15cos 15sin 2o2o 215sin 15cos -115sin 2o2-o2o 215cos 15sin +p q ,q ⌝p ⌝:[0,1],1x p x e ∀∈≥2:,10,q x R x x ∃∈++<p q ∨q p ∨p q 22,am bm <a b <()sin(2)3f x x π=+()f x 3x π=()f x (,0)4πC ．的最小正周期为，且在上为增函数D ．把的图像向左平移个单位，得到一个偶函数的图像10．若α是锐角，且cos （）=﹣，则sin α的值等于 （ ）A ．B ．C ．D ．．()f x 是定义在R 上的以3为周期的奇函数，(2)f =0，则方程()f x =0在区间（0，6）内解的个数 （ ） 12. 已知函数()y f x =是定义在R 上的奇函数，且当x ∈（﹣∞，0）时不等式()f x +x f ′（x ）＜0成立，若0.30.33(3)a f =⋅，(log 3)(log 3)b f ππ=⋅，3311(log )(log )99c f =．则,,a b c 的大小关系是 （ ）A. a b c >>B. c a b >>C. a b c >>D. a c b >> 二、填空题（本大题共4小题，每小题5分，共20分）. 13. 函数的定义域是___ ___ .14．曲线34y x x =-在点()1,3--处的切线方程是 ． 15．已知函数()f x =，若函数g （x ）=f （x ）﹣m 有3个零点，则实数m 的取值范围是 ． 16. 给出下列四个命题：①函教()f x ＝lnx －2＋x 在区间（1，e ）上存在零点： ②若＝0，则函数y ＝f （x ）在处取得极值： ③若m≥一1，则函数.的值城为R;④‘“a＝1”是“函数()f x ＝在定义域上是奇函数”的充分不必要条件。

【冲锋号·考场模拟】赢战2023年高考数学模拟仿真卷02卷（理科）（全国卷专用）（解析版）（考试时间：120分钟试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．写在本试卷上无效．3．回答第Ⅱ卷时，将答案写在答题卡上．写在本试卷上无效．4．测试范围：高考全部内容5．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}2|2A x x x =<+，{}1,0,1,2,3B =-，则A B = （）A ．{}1,0,1-B ．{}0,1,2C ．{}0,1D ．{}1,2【答案】C【分析】解不等式得到{}|12A x x =-<<，求出交集.【详解】22x x <+，即220x x --<，解得：12x -<<，故{}|12A x x =-<<，所以{}{}{}1,0,1,1|122,30,A x B x =--<=< .故选：C 2．若复数z 满足2iz+为纯虚数，且1z =，则z 的虚部为（）A ．5±B C ．D①命题“x ∃∈R ，210x x ++≥”的否定是“x ∀∈R ，210x x ++<”；②0a b +=的充要条件是1ba=-；③若函数()y f x =为奇函数，则()0f x =；④0ab ≥是222a b ab +≥的必要条件.A ．1个B ．2个C ．3个D ．4个能是（）A ．1()f x x=-B ．2()f x x =-C ．()e e x x f x -=+D ．1()ln1x f x x-=+111中，11分別是1111的中点，1，则1BD 与1AF 所成角的正弦值是（）A 10B ．12C ．10D ．3015位女生中安排3人到三个场馆做志愿者，每个场馆各位男生入选，则不同安排方法有（）种.A ．16B ．20C ．96D ．120【答案】C【分析】分一男两女与两男一女两类讨论.【详解】若选一男两女共有：123243C C A 72=；若选两男一女共有：213243C C A 24=；因此共有96种，故选：C7．函数()()f x x ωϕ=+其中π0,||2ωϕ><，的图象的一部分如图所示，()g x x ω=，要想得到()g x 的图象，只需将()f x 的图象（）A ．向右平移π4个单位长度B ．向右平移2个单位长度C ．向左平移π4个单位长度D ．向左平移2个单位长度中，每场比赛甲队获胜的概率为23，乙队获胜的概率为13，则在这场“五局三胜制”的排球赛中乙队获胜的概率为（）A．1481B．13C．1781D．1681的锐角组成的对称多边形纹样，具有组合性强、结构稳定等特点．有的八角星纹中间镂空出一个正方形，有的由八个菱形组成，内部呈现米字形线条．八角星纹目前仍流行在中国南方的挑花和织锦中．在图2所示的八角星纹中，各个最小的三角形均为全等的等腰直角三角形，中间的四边形是边长为2的正方形，在图2的基础上连接线段，得到角α，β，如图3所示，则αβ+=（）A．30°B．45°C．60°D．75°【答案】B则Rt ABC △中，2BC =，AC 在Rt DEF△中，2EF =，DE =所以()tan tan tan 1tan tan αβαβαβ++=-(),0,45αβ∈10．函数()e e cos 2x xf x x -=-在区间ππ,22⎡⎤-⎢⎥⎣⎦大致图像可能为（）A ．B ．C ．D ．【答案】B【分析】利用定义判断()f x 的奇偶性，再结合函数值的符号分析判断，即可得答案.【详解】∵()()()()()()e e cos 2e e cos 2e e e e cos 20x x x xx x x x f x f x x x x ----+-=-+--=-+-=，即()()f x f x =--，11．若双曲线()2210,0x y a b a b-=>>的渐近线与圆C ：22420x y x +-+=相交，则此双曲线的离心率的取值范围是（）A ．(B ．()1,2C ．)2D ．)+∞12A ．2121e e ln ln x xx x ->-B ．2121e e ln ln x xx x -<-C ．1221e e x xx x >D ．1221e e x xx x <13．双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12,F F ，已知焦距为8，离心率为2，过右焦点2F 作垂直于x 轴的直线l 与双曲线C 的右支交于,A B 两点，则||AB =_____．故||6(6)12AB =--=，故答案为：12.14．已知O 为坐标原点，且(1,),(4,4)A m B m -，若,,O A B 三点共线，则实数m =_____．【答案】45##0.8的面积为___________.绕AD 顺时针旋转π2，则线段AP 扫过的区域面积为____________．故答案为：5π4.三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．某商场计划按月订购一种酸奶，每天进货量相同，进货成本每瓶8元，售价每瓶10元，未售出的酸奶降价处理，以每瓶4元的价格当天全部处理完.根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关.如果最高气温不低于25，需求量为600瓶；如果最高气温位于区间[20,25)，需求量为400瓶；如果最高气温低于20，需求量为300瓶.为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：最高气温[10，15）[15，20）[20，25）[25，30）[30，35）[35，40）天数117382275以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)估计六月份这种酸奶一天的需求量不超过400瓶的概率，并求出前三年六月份这种酸奶每天平均的需求量；(2)设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量为550瓶时，写出Y的所有可能值，并估计Y大于零的概率.38；②7；③2，4，5成等比数列.从中任选1个，补充到下面的问题中并解答问题：设数列{}n a 的前n 项和为n S ，已知()*12N n n n S S a n +=++∈，.(1)求数列{}n a 的通项公式；(2)n S 的最小值并指明相应的n 的值．【答案】(1)212n a n =-；(2)n =5或者6时，n S 取到最小值30-.【分析】（1）由已知可得12n n a a +-=，则{}n a 是公差为2的等差数列，若选①，则由382a a +=-列方程可求出1a ，从而可求出通项公式；若选②，则由728S =-列方程可求出1a ，从而可求111的底面为正三角形，1，点D ，E 分别在AB ，1BB 上，且AD DB =，113BE EB =．(1)证明：平面1A DC ⊥平面EDC ；(2)求二面角1A EC D --的余弦值．由题意得()1,0,0B ，()1,0,0C -，(A 因为AD DB =，113BE EB =，所以D 所以113,,222DE ⎛⎫=- ⎪ ⎪⎝⎭ ，3,0,2DC ⎛=- ⎝）AD DB =，113BE EB =，所以1,0,2D ⎛⎝12,,02CE ⎫ ⎪⎭=⎛⎝，()11,2,3CA = ，1DA 设平面1A EC 的法向量为(),,n x y z =，20．已知椭圆C ：221x y a b+=()0a b >>的下顶点为点D ，右焦点为()21,0F .延长2DF 交椭圆C 于点E ，且满足223DF F E =.(1)试求椭圆C 的标准方程；(2)A ，B 分别是椭圆长轴的左右两个端点，M ，N 是椭圆上与A ，B 均不重合的相异两点，设直线AM ，AN 的斜率分别是1k ，2k .若直线MN 过点2⎫⎪⎪⎝⎭，则12k k ⋅是否为定值，若是求出定值，若不是请说明理由.联立222212x my x y ⎧=+⎪⎪⎨⎪+=⎪⎩，消去x ，得则12222m y y m +=-+，122y y =-y y，ln x a a g x =+（0a >，是自然对数的底数）．(1)若直线y kx =与曲线()y f x =，()y g x =都相切，求a 的值；(2)若()()f x g x ≥恒成立，求实数a 的取值范围．按所做的第一题计分．选修4-4：坐标系与参数方程22．在平面直角坐标系中，曲线1C 的参数方程为3cos 2sin x y ϕϕ=⎧⎨=⎩（ϕ为参数），以O 为极点，x轴的正半轴为极轴建立极坐标系，曲线2C 是圆心在极轴上且经过极点的圆，射线6πθ=与曲线2C交于点6D π⎛⎫ ⎪⎝⎭．(1)求曲线1C ，2C 的普通方程；(2)()1,A ρθ，2,2B πρθ⎛⎫- ⎪⎝⎭是曲线1C 上的两点，求221211ρρ+的值．选修4-5：不等式选讲23．（1）已知0a >，0b >，412a b+=，求a b +的最小值；（2）已知a ，b ，c ，为任意实数，求证：222a b c ab bc ca ++≥++.。