红对勾理科数学选4-4-1
- 格式:ppt
- 大小:4.24 MB
- 文档页数:48
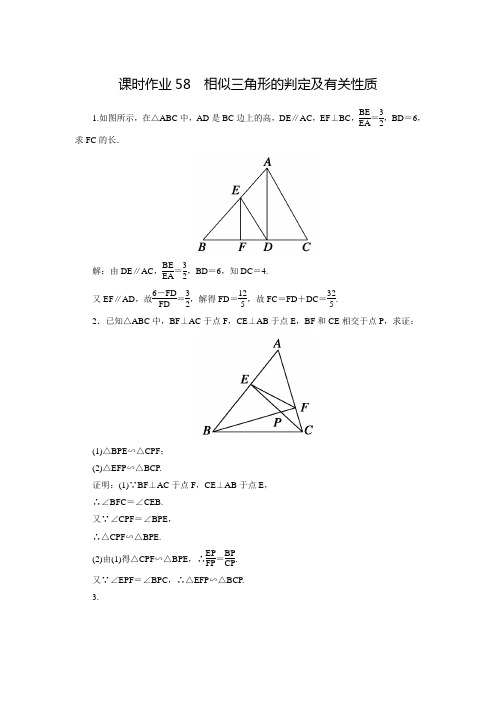
课时作业58 相似三角形的判定及有关性质1.如图所示,在△ABC 中,AD 是BC 边上的高,DE ∥AC ,EF ⊥BC ,BE EA =32,BD =6,求FC 的长.解:由DE ∥AC ,BE EA =32,BD =6,知DC =4. 又EF ∥AD ,故6-FD FD =32,解得FD =125,故FC =FD +DC =325. 2.已知△ABC 中,BF ⊥AC 于点F ,CE ⊥AB 于点E ,BF 和CE 相交于点P ,求证:(1)△BPE ∽△CPF ;(2)△EFP ∽△BCP.证明:(1)∵BF ⊥AC 于点F ,CE ⊥AB 于点E ,∴∠BFC =∠CEB.又∵∠CPF =∠BPE ,∴△CPF ∽△BPE.(2)由(1)得△CPF ∽△BPE ,∴EP FP =BP CP. 又∵∠EPF =∠BPC ,∴△EFP ∽△BCP.3.如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于D ,DF ⊥AC 于F ,DE ⊥AB 于E ,求证:(1)AB·AC =BC·AD ;(2)AD 3=BC·CF·BE.证明:(1)在Rt △ABC 中,AD ⊥BC ,∴S △ABC =12AB·AC =12BC·AD. ∴AB·AC =BC·AD.(2)Rt △ADB 中,DE ⊥AB ,由射影定理可得BD 2=BE·AB ,同理CD 2=CF·AC ,∴BD 2·CD 2=BE·AB·CF·AC.又在Rt △BAC 中,AD ⊥BC ,∴AD 2=BD·DC ,∴AD 4=BE·AB·CF·AC ,又AB·AC =BC·AD.即AD 3=BC·CF·BE.4.(2016·南阳模拟)如图,△ABC 中,AB =AC ,∠BAC =90°,AE =13AC ,BD =13AB ,点F 在BC 上,且CF =13BC. 求证:(1)EF ⊥BC ;(2)∠ADE =∠EBC.证明:设AB =AC =3a ,则AE =BD =a ,CF =2a.(1)CE CB =2a 32a =23,CF CA =2a 3a =23. 又∠C 为公共角,故△BAC ∽△EFC ,由∠BAC =90°,∴∠EFC =90°,∴EF ⊥BC.(2)由(1)得EF =2a ,故AE EF =a 2a =22,AD FB =2a 22a =22, ∴AE EF =AD FB,∵∠DAE =∠BFE =90°, ∴△ADE ∽△FBE ,∴∠ADE =∠EBC.5.(2016·银川模拟)如图,在△ABC 中,D 是AC 的中点,E 是BD 的中点,AE 的延长线交BC 于F.(1)求BF FC的值. (2)若△BEF 的面积为S 1,四边形CDEF 的面积为S 2,求S 1S 2的值.解:(1)过点D 作DG ∥BC ,并交AF 于G 点,因为E 是BD 的中点,所以BE =DE.又因为∠EBF =∠EDG ,∠BEF =∠DEG ,所以△BEF ≌△DEG ,则BF =DG ,所以BF FC =DG FC.又因为D 是AC 的中点,则DGFC =12, 则BF FC =12,即BF FC =12. (2)若△BEF 以BF 为底,△BDC 以BC 为底,则由(1)知BFBC =13, 又由BE BD =12可知h 1h 2=12, 其中h 1,h 2分别为△BEF 和△BDC 的高,则S △BEF S △BDC =13×12=16, 则S 1S 2=1 5.6.如图,在梯形ABCD 中,点E ,F 分别在AB ,CD 上,EF ∥AD ,假设EF 做上下平行移动.(1)若AE EB =12,求证:3EF =BC +2AD ; (2)请你探究一般结论,即若AE EB =m n,那么你可以得到什么结论?解:过点A 作AH ∥CD 分别交EF ,BC 于点G ,H.(1)证明:因为AE EB =12, 所以AE AB =13. 又EG ∥BH ,所以EG BH =AE AB =13,即3EG =BH.又EG +GF =EG +AD =EF , 从而EF =13(BC -HC)+AD , 所以EF =13BC +23AD ,即3EF =BC +2AD. (2)因为AE EB =m n ,所以AE AB =m n +m. 又EG ∥BH ,所以EG BH =AE AB ,即EG =m m +nBH. 所以EF =EG +GF =EG +AD =m m +n(BC -AD)+AD , 所以EF =m m +n BC +n m +n AD ,即(m +n)EF =mBC +nAD.。




课时作业4 函数及其表示一、选择题(每小题5分,共40分)1.(2022·江西理,2)下列函数中,与函数y =13x定义域相同的函数为( )A .y =1sin x B .y =ln xx C .y =x e xD .y =sin xx解析:本题考查函数的定义域,由于y =13x的定义域为{x |x ≠0},满足条件的函数只有D ,故选D.答案:D2.(2022·北京海淀)假如f (1x )=x1-x ,则当x ≠0且x ≠1时,f (x )=________.( )A.1xB.1x -1C.11-xD.1x -1解析:令1x =t ,得x =1t . ∴f (t )=1t1-1t =1t -1∴f (x )=1x -1.答案:B3.设函数f (x )=⎩⎪⎨⎪⎧-x ,x ≤0x 2,x >0,若f (α)=4,则实数α=( )A. -4或-2B. -4或2 C .-2或4D .-2或2解析:本题主要考查分段函数求函数值等基础学问. 当α≤0时,f (α)=-α=4,∴α=-4; 当α>0时,f (α)=α2=4,∴α=2. 综之:α=-4或2,选B. 答案:B4.下列对应法则f 为A 上的函数的个数是( ) ①A =Z ,B =N +,f :x →y =x 2 ②A =Z ,B =Z ,f :x →y =x ③A =[-1,1],B ={0},f :x →y =0 A .0 B .1 C .2D .3解析:对于①,当0∈A 时,y =0∉B ,故①所给的对应法则不是A 到B 的映射,当然它不是A 上的函数关系;对于②,当2∈A 时,y =2∉B ,故②所给的对应法则不是A 到B 的映射,当然它不是A 上的函数关系;对于③,对于A 中的任一个数,依据对应法则,在B 中都有唯一元素0和它对应,故③所给的对应法则是A 到B 的映射,这两个数集之间的关系是集合A 上的函数关系.答案:B5.(2022·福建厦门3月模拟)已知函数f (x )=⎩⎪⎨⎪⎧3-x 2,x ∈[-1,2],x -3,x ∈(2,5],则方程f (x )。

高考解答题专项训练(四) 空间向量与立体几何1.如图,正方形AMDE 的边长为2,B ,C 分别为AM ,MD 的中点.在五棱锥P -ABCDE 中,F 为棱PE 的中点,平面ABF 与棱PD ,PC 分别交于点G ,H .(1)求证:AB ∥FG ;(2)若P A ⊥底面ABCDE ,且P A =AE ,求直线BC 与平面ABF 所成角的大小,并求线段PH 的长.解:(1)证明:在正方形AMDE 中,因为B 是AM 的中点,所以AB ∥DE . 又因为AB ⊄平面PDE , 所以AB ∥平面PDE .因为AB ⊂平面ABF ,且平面ABF ∩平面PDE =FG , 所以AB ∥FG .(2)因为P A ⊥底面ABCDE , 所以P A ⊥AB ,P A ⊥AE .如图建立空间直角坐标系A -xyz ,则A (0,0,0),B (1,0,0),C (2,1,0),P (0,0,2),F (0,1,1),BC →=(1,1,0).设平面ABF 的法向量为n =(x ,y ,z ),则⎩⎨⎧n ·AB →=0,n ·AF →=0,即⎩⎪⎨⎪⎧x =0,y +z =0.令z =1,则y =-1.所以n =(0,-1,1). 设直线BC 与平面ABF 所成角为α,则 sin α=|cos 〈n ,BC →〉|=⎪⎪⎪⎪⎪⎪⎪⎪n ·BC →|n ||BC →|=12.因此直线BC 与平面ABF 所成角的大小为π6. 设点H 的坐标为(u ,v ,w ). 因为点H 在棱PC 上, 所以可设PH →=λPC →(0<λ<1), 即(u ,v ,w -2)=λ(2,1,-2). 所以u =2λ,v =λ,w =2-2λ. 因为n 是平面ABF 的法向量, 所以n ·AH →=0,即(0,-1,1)·(2λ,λ,2-2λ)=0.解得λ=23,所以点H 的坐标为⎝ ⎛⎭⎪⎫43,23,23.所以PH =⎝ ⎛⎭⎪⎫432+⎝ ⎛⎭⎪⎫232+⎝ ⎛⎭⎪⎫-432=2. 2.如图,在三棱台DEF -ABC 中,AB =2DE ,G ,H 分别为AC ,BC 的中点.(1)求证:BD ∥平面FGH ;(2)若CF ⊥平面ABC ,AB ⊥BC ,CF =DE ,∠BAC =45°,求平面FGH 与平面ACFD 所成的角(锐角)的大小.解:(1)证法一:连接DG ,CD ,设CD ∩GF =O ,连接OH .在三棱台DEF -ABC 中, AB =2DE ,G 为AC 的中点, 可得DF ∥GC ,DF =GC , 所以四边形DFCG 为平行四边形. 则O 为CD 的中点, 又H 为BC 的中点, 所以OH ∥BD ,又OH ⊂平面FGH ,BD ⊄平面FGH , 所以BD ∥平面FGH .证法二:在三棱台DEF -ABC 中, 由BC =2EF ,H 为BC 的中点, 可得BH ∥EF ,BH =EF , 所以四边形BHFE 为平行四边形, 可得BE ∥HF .在△ABC 中,G 为AC 的中点,H 为BC 的中点, 所以GH ∥AB . 又GH ∩HF =H ,所以平面FGH ∥平面ABED . 因为BD ⊂平面ABED , 所以BD ∥平面FGH . (2)设AB =2,则CF =1.在三棱台DEF -ABC 中,G 为AC 的中点, 由DF =12AC =GC ,可得四边形DGCF 为平行四边形, 因此DG ∥FC .又FC ⊥平面ABC ,所以DG ⊥平面ABC .在△ABC 中,由AB ⊥BC ,∠BAC =45°,G 是AC 中点, 所以AB =BC ,GB ⊥GC , 因此GB ,GC ,GD 两两垂直.以G 为坐标原点,建立如图所示的空间直角坐标系G -xyz .所以G (0,0,0),B (2,0,0),C (0,2,0),D (0,0,1).可得H ⎝ ⎛⎭⎪⎫22,22,0,F (0,2,1). 故GH →=⎝ ⎛⎭⎪⎫22,22,0,GF →=(0,2,1).设n =(x ,y ,z )是平面FGH 的法向量,则由⎩⎨⎧n ·GH →=0,n ·GF →=0,可得⎩⎪⎨⎪⎧x +y =0,2y +z =0.可得平面FGH 的一个法向量n =(1,-1,2). 因为GB →是平面ACFD 的一个法向量,GB →=(2,0,0), 所以cos 〈GB →,n 〉=GB →·n |GB →|·|n |=222=12.所以平面FGH 与平面ACFD 所成角(锐角)的大小为60°.3.(2019·湖北重点中学协作体联考)等边△ABC 的边长为3,点D ,E 分别是AB ,AC 上的点,且满足AD DB =CE EA =12(如图①),将△ADE 沿DE 折起到△A 1DE 的位置,使二面角A 1-DE -B 成直二面角,连接A 1B ,A 1C (如图②).(1)求证:A 1D ⊥平面BCED ;(2)在线段BC 上是否存在点P ,使直线P A 1与平面A 1BD 所成的角为60°?若存在,求出PB 的长;若不存在,请说明理由.解:(1)证明:题图①中,由已知可得:AE=2,AD=1,A=60°.从而DE=12+22-2×1×2×cos60°= 3.故得AD2+DE2=AE2,∴AD⊥DE,BD⊥DE.∴题图②中,A1D⊥DE,BD⊥DE,∴∠A1DB为二面角A1-DE-B的平面角,又二面角A1-DE-B为直二面角,∴∠A1DB=90°,即A1D⊥DB.∵DE∩DB=D且DE,DB⊂平面BCED,∴A1D⊥平面BCED.(2)存在.由(1)知ED⊥DB,A1D⊥平面BCED.以D为坐标原点,以射线DB、DE、DA1分别为x轴、y轴、z轴的正半轴建立空间直角坐标系D-xyz,如图,过P 作PH ∥DE 交BD 于点H , 设PB =2a (0≤2a ≤3),则BH =a ,PH =3a ,DH =2-a ,易知A 1(0,0,1),P (2-a ,3a,0),E (0,3,0), 所以P A 1→=(a -2,-3a,1). 因为ED ⊥平面A 1BD ,所以平面A 1BD 的一个法向量为DE →=(0,3,0). 因为直线P A 1与平面A 1BD 所成的角为60°,所以sin60°=|P A 1→·DE →||P A 1→||DE →|=3a 4a 2-4a +5×3=32,解得a =54. ∴PB =2a =52,满足0≤2a ≤3,符合题意.所以在线段BC 上存在点P ,使直线P A 1与平面A 1BD 所成的角为60°,此时PB =52.4.(2019·河北衡水中学、河南顶级名校联考)如图,在三棱柱ABC -A 1B 1C 1中,AC =BC =AB =AA 1,过AA 1的平面分别交BC ,B 1C 1于点D ,D 1.(1)求证:四边形ADD 1A 1为平行四边形;(2)若AA 1⊥平面ABC ,D 为BC 的中点,E 为DD 1的中点,求二面角A -C 1E -C 的余弦值.解:(1)证明:因为AA 1∥BB 1,AA 1⊄平面BCC 1B 1,BB 1⊂平面BCC 1B 1,所以AA 1∥平面BCC 1B 1.又因为AA 1⊂平面ADD 1A 1,平面ADD 1A 1∩平面BCC 1B 1=DD 1, 所以AA 1∥DD 1.因为平面ABC ∥平面A 1B 1C 1,平面ABC ∩平面ADD 1A 1=AD ,平面A 1B 1C 1∩平面ADD 1A 1=A 1D 1,所以AD ∥A 1D 1.所以四边形ADD 1A 1为平行四边形. (2)因为D 为BC 的中点,AC =AB , 所以AD ⊥BC .因为AA 1∥DD 1,AA 1⊥平面ABC , 所以DD 1⊥平面ABC ,从而DD 1⊥AD . 又DD 1∩BC =D ,所以AD ⊥平面BCC 1B 1.分别以DA ,DB ,DD 1所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示.设AC =BC =AB =AA 1=2,则A (3,0,0),E (0,0,1),C 1(0,-1,2),AE →=(-3,0,1),C 1E →=(0,1,-1). 设平面AC 1E 的法向量为n =(a ,b ,c ),由⎩⎨⎧AE →·n =0,C 1E →·n =0,得⎩⎪⎨⎪⎧-3a +c =0,b -c =0,取c =3,得n =(1,3,3).由AD ⊥平面BCC 1B 1,得平面CC 1E 的一个法向量为DA →=(3,0,0), 所以cos 〈DA →,n 〉=DA →·n |DA →|·|n |=37×3=77,又易知二面角A -C 1E -C 为锐二面角, 故二面角A -C 1E -C 的余弦值为77.5.(2019·天津十二校联考)如图,ABCD 是边长为3的正方形,平面ADEF ⊥平面ABCD ,AF ∥DE ,AD ⊥DE ,AF =26,DE =3 6.(1)求证:面ACE ⊥面BED ;(2)求直线CA 与平面BEF 所成角的正弦值;(3)在线段AF 上是否存在点M ,使得二面角M -BE -D 的大小为60°?若存在,求出AMAF 的值;若不存在,说明理由.解:(1)证明:因为平面ADEF ⊥平面ABCD ,平面ADEF ∩平面ABCD =AD ,DE ⊂平面ADEF ,DE ⊥AD ,所以DE ⊥平面ABCD .又因为AC ⊂平面ABCD ,所以DE ⊥AC . 因为ABCD 是正方形,所以AC ⊥BD ,又因为DE ∩BD =D ,DE ⊂平面BED ,BD ⊂平面BED , 所以AC ⊥平面BDE .又因为AC ⊂平面ACE ,所以平面ACE ⊥平面BED .(2)因为DE ⊥DC ,DE ⊥AD ,AD ⊥DC , 所以建立空间直角坐标系D -xyz 如图所示.则A (3,0,0),F (3,0,26),E (0,0,36),B (3,3,0),C (0,3,0), 所以CA →=(3,-3,0),BE →=(-3,-3,36),EF →=(3,0,-6). 设平面BEF 的法向量为n =(x 1,y 1,z 1).则⎩⎨⎧n ·BE →=0,n ·EF →=0,即⎩⎪⎨⎪⎧-3x 1-3y 1+36z 1=0,3x 1-6z 1=0,令x 1=6,则y 1=26,z 1=3, 则n =(6,26,3).所以cos 〈CA →,n 〉=CA →·n |CA →|·|n |=-3632×39=-1313.所以直线CA 与平面BEF 所成角的正弦值为1313. (3)存在.点M 在线段AF 上,设M (3,0,t ),0≤t ≤2 6. 则BM →=(0,-3,t ),BE →=(-3,-3,36), 设平面MBE 的法向量为m =(x 2,y 2,z 2),则⎩⎨⎧m ·BM →=-3y 2+tz 2=0,m ·BE →=-3x 2-3y 2+36z 2=0,令y 2=t ,得m =(36-t ,t,3),|cos 〈m ,CA →〉|=|m ·CA →||m |·|CA →|=|96-6t |32×(36-t )2+t 2+9=12, 整理得:2t 2-66t +15=0,解得t =62或t =562(舍),故在线段AF 上存在点M ,使得二面角M -BE -D 的大小为60°,此时AM AF =14.6.(2019·广州模拟)如图1,在正方形ABCD 中,点E ,F 分别是AB ,BC 的中点,BD 与EF 交于点H ,G 为BD 的中点,点R 在线段BH 上,且BR RH =λ(λ>0).现将△AED ,△CFD ,△DEF 分别沿DE ,DF ,EF 折起,使点A ,C 重合于点B (该点记为P ),如图2所示.(1)若λ=2,求证:GR ⊥平面PEF ;(2)是否存在正实数λ,使得直线FR 与平面DEF 所成角的正弦值为225?若存在,求出λ的值;若不存在,请说明理由.解:(1)证明:由题意,可知PE ,PF ,PD 三条直线两两垂直.∴PD ⊥平面PEF .在图1中,E ,F 分别是AB ,BC 的中点,G 为BD 的中点,则EF ∥AC ,GD =GB =2GH .在图2中,∵PR RH =BR RH =2,且DG GH =2,∴在△PDH 中,GR ∥PD .∴GR ⊥平面PEF .(2)存在.由题意,分别以PF ,PE ,PD 所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系P -xyz .设PD =4,则P (0,0,0),F (2,0,0),E (0,2,0),D (0,0,4),∴H (1,1,0).∴BR RH =PR RH =λ,∴PR →=λ1+λPH →,∴R ⎝ ⎛⎭⎪⎫λ1+λ,λ1+λ,0. ∴RF →=⎝ ⎛⎭⎪⎫2-λ1+λ,-λ1+λ,0 =⎝ ⎛⎭⎪⎫2+λ1+λ,-λ1+λ,0.EF →=(2,-2,0),DE →=(0,2,-4),设平面DEF 的法向量为m =(x ,y ,z ),由⎩⎨⎧EF →·m =0,DE →·m =0,得⎩⎪⎨⎪⎧2x -2y =0,2y -4z =0. 取z =1,则m =(2,2,1).∵直线FR 与平面DEF 所成角的正弦值为225,∴|cos 〈m ,RF →〉|=|m ·RF →||m ||RF →| =41+λ3⎝ ⎛⎭⎪⎫2+λ1+λ2+⎝ ⎛⎭⎪⎫-λ1+λ2=223λ2+2λ+2=225,∴9λ2+18λ-7=0,解得λ=13或λ=-73(不合题意,舍去).故存在正实数λ=13,使得直线FR 与平面DEF 所成角的正弦值为225.。