泵与风机的性能计算
- 格式:doc
- 大小:68.50 KB
- 文档页数:3

2.5离心式泵与风机的理论性能曲线本节研究泵或风机所具备的技术性能的表达方式。
泵与风机的扬程、流量、功率、效率和转速等性能是互相影响的,当一个参数变化时,其他的都随之变化,这种函数关系用曲线表示,就是泵与风机的性能曲线。
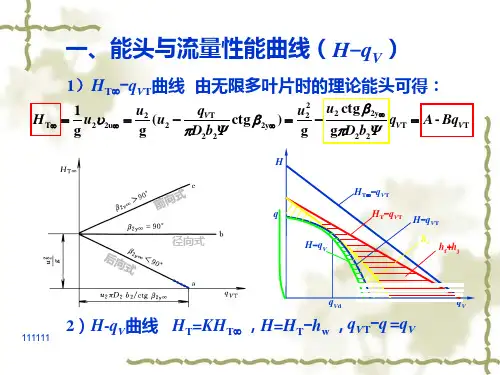
通常用以下三种形式来表示这些性能之间的关系:(1)泵或风机所提供的流量和扬程之间的关系,用)(Q H 1f =来表示:(2)泵或风机所提供的流量和所需外加轴功率之间的关系,用)(Q N 2f =来表示;(3)泵或风机所提供的流量与设备本身效率之间的关系,用)(T T Q H 1f =及)(T T Q N 2f =来表示。
理论性能曲线是从欧拉方程出发,研究无损失流动这一理想条件下及的关系。
如叶轮出口前盘与后盘之间的轮宽为b 2,则叶轮在工作时所排出的理论流量应为:222r T v b D Q επ=(2-15)式中符号同前。
将式(2-15)变换后代入(2-13)可得:对于大小一定的泵或风机来说,转速不变时,上式中u 2,g ,ε,D 2及B 2均为定值,故上式可改写为:(2-16)式中gu 22=A ,222b επD 1g u B ∙=均为常数,而cot β2代表叶型种类,也是常量。
此时说明在固定转速下,不论叶型如何,泵或风机理论上的流量与扬程关系是线形的。
同时还可以看出,当Q T =0时,H T =gu 22=A 。
图2-8为3种不同叶型的泵和风机理论上的流量-扬程曲线。
显然由所代表的曲线斜率是不同的,因而3种叶型具有各自的曲线倾向。
下面研究理论上的流量与外加功率的关系。
在无损失流动条件下,理论上的有效功率就是轴功率,可按式(1-4)计算,即:当输送某种流体时=常数。
用式(2-16)代人此式可得:(2-17)可见对于不同的值具有不同形状的曲线。
但当Q T =0时,3种叶型的理论轴功率都等于零,3条曲线同相交于原点(见图2-9)。
图2-83种不同叶型的泵图2-93种不同叶型的泵和风机理论上的流量-扬程曲线和风机理论上的流量-功率曲线对于具有径向叶型的叶轮来说=90°,,功率曲线为一条直线。
![流体力学泵与风机[总结]](https://uimg.taocdn.com/f88c2b0afd4ffe4733687e21af45b307e871f9ac.webp)
流体力学泵与风机方程式(Z+p/γ)=C 从物理学:Z项是单位重量液体质点相对于基准面的位置势能,p/γ项是单位重量液体质点的压力势能,Z+p/γ项是单位重量液体的总势能,(Z+p/γ)=C表明在静止液体中,各液体质点单位重量的总势能均相等。
从水力学:Z为该点的位置相对于基准面的高度,称位置水头,p/γ是该点在压强作用下沿测压管所能上升的高度,称压强水头,Z+p/γ称测压管水头,它表示测压管液面相对于基准面的高度,(Z+p/γ)=C表示同一容器的静止液体中,所有各点的测压管液头均相等。
——————————————等压面:①在连通的同种静止液体中,水平面必然是等压面②静止液体的自由液面是水平面,该自由液面上各点压强均为大气压钱,所以自由液面是等压面③两种不同液体的分界面是水平面,故该面也是等压面——————————————绝对压强=相对压强+真空压强——————————————压强的量度单位:①用单位面积上所受的压力来表示,单位N/m2,或Pa②用液柱的高度来表示,mH2O、mmHg、mmH2O,h=p/γ③用大气压的倍数来表示,单位为工程大气压和标准大气压,1atm=101.325kPa。
——————————————流线:同一时刻流场中一系列流体质点的流动方向线,即在流场中画出的一条曲线,在某一瞬时,该曲线上的任意一点的流速矢量总是在该点与曲线相切。
迹线:某一流体质点在连续时间内的运动轨迹。
——————————————能量方程式的意义(物理意义):z表示单位重量流体的位置势能,简称位能,简称位能,p/γ表示单位重量流体的压力势能,简称压能,av2/2g表示单位重量流体的平均势能,简称动能,hw表示克服阻力所引起的单位能量损失,简称能量损失,z+p/γ表示单位势能,z+p/γ+av2/2g表示单位总机械能。
(几何意义)方程式中各项的单位都是米,具有长度量纲[L]表示某种高度,可以用几何线段来表示,流体力学上称为水头,z称为位置水头,p/γ称为压强水头,av2/2g 称为流速水头,hw称为水头损失,z+p/γ称为测压管水头(Hp),z+p/γ+av2/2g称为总水头(H)——————————————沿程水头损失:在管路中单位水流的沿程能量损失。


《泵与风机实验》实验指导书及实验报告工程热物理教研室编泵与风机实验室华北电力大学(北京)二OO八年五月前言⒈实验总体目标通过学生亲自实践《泵与风机》课程的三个实验,增强学生综合分析能力、实验动手能力、数据处理及查阅资料能力,培养学生的实践与创新能力。
⒉适用专业热能与动力工程专业、核能与动力工程专业、建筑环境与设备工程专业。
⒊先修课程泵与风机、热工测量、工程流体力学。
⒋实验课时分配⒌实验环境(对实验室、机房、服务器、打印机、投影机、网络设备等配置及数量要求)泵与风机实验对实验环境有如下要求:①实验室最好安排在一层,要求实验室离教室和办公室有一定距离,以防止实验时的噪声影响正常的教学和办公。
②风机实验室安排在窗户较多的屋子,做实验时室外最好风力不要太大。
③离心泵实验室要求有自来水或离取水位置较近。
④实验室内要求有黑板。
⒍实验总体要求对于泵与风机实验,有以下几点总体要求:①在做实验前,要求学生认真学习实验指导书,并复习所学《泵与风机》、《热工测量》、《工程流体力学》等课程的相关知识。
②实验前,要求实验室向学生开放,以便学生了解实验设备和测量设备,以及对整个实验有感性认识。
③对于验证性实验,要求学生在实验前就已很好地掌握了测量设备的工作原理、使用方法以及实验步骤。
④对于综合性、设计性实验,应适当提前向学生布置任务。
学生应根据实验任务,查阅资料,进行理论分析和研究,确定实验方案,或根据规定的实验方案,确定实验步骤。
学生拟定的实验方案或实验步骤,应经过指导教师审查同意后方可进行实验。
实验后,要求学生按要求整理实验数据,撰写实验报告,并提出或回答相关问题。
⒎本实验的重点、难点及教学方法建议①本实验的重点:是对教材所讲科学规律进行验证,掌握相关参数的测量方法。
②本实验的难点:综合性设计性实验的实验方案确定、实验步骤的确定。
③教学方法建议:采用多媒体手段对实验进行必要的讲解和布置实验任务;综合性设计性实验分组进行方案论证;实验现场更多发挥学生的主动性,教师只做必要的辅导。


(红色字是需要删除的内容,绿色字是改动过的内容,仅做参考!)第十一章 相似理论在泵与风机中的应用【本章重点】泵与风机的相似条件与相似定律,比转数与无因次性能参数。
【本章难点】相似定律的应用【学习目标】理解泵与风机几何、运动、动力相似的内容;掌握流量、扬程和功率(相似)定律的具体内容,理解比转数对风机的分类方法(,掌握风机性能曲线与无因次性能曲线的换算方法)。
泵与风机的相似理论(定律)是研究几何相似的泵或风机在相似工况之间性能参数的关系。
(它应用于)泵与风机的研制、选用与运行中(性能参数的换算),可以解决以下三方面问题。
首先,研制新的泵与风机尤其大型机,需要通过模型试验,原型与模型之间性能参数按相似律进行换算。
第二,泵与风机的设计与制造按系列进行,同一系列的泵与风机是几何相似的,它们的性能参数符合相似律。
第三,同一台泵与风机,当转数(速)改变或流体密度改变时,性能参数随之变化,需要用相似律进行换算。
工程上使用的泵与风机有不同的尺寸,并且可以在不同的转速下运行。
对于不同尺寸的和转速的泵与风机,其工作参数各不相同,但存在内部流动彼此相似的泵与风机。
根据流动的相似性,相似的泵和风机相应的运行参数(之)间必(然)存在着一定的关系,这种关系正是相似理论所描述的。
第一节 相似条件根据流体力学中的相似理论我们可以知道,要使泵与风机内部流体流动相似,必须满足几何相似、运动相似和动力相似三个相似条件。
在下面的讨论中,以下标“m”表示模型的各参数,和以“p”表示原型的各参数。
一、 几何相似几何相似是指模型和原型各对应的线性尺寸成比例且比值为一常数,对应的角度相等,叶片数相等。
图11-1表示满足几何相似的两个叶轮,其参数满足:pm p m p m p m p m D Db b b b D D D D ==== 22112211 (11-1)p m 11ββ=,p m 22ββ=(图中实型中的参数无下标)图11-1 几何相似和运动相似的叶轮二、 运动相似运动相似是指几何相似的泵与风机的流场中,流体对应点对应的速度大小成同一比值为一常数,且夹角相等,方向相同。


1、测得一台模型泵设计工况的性能参数为:n=2900r/min,Q=0.17m3/s,H=104m,N=214Kw。
现有一台与该泵相似而尺寸大一倍的原型泵,求原型泵转速为n=1450r/min时的性能参数。
2、一台双吸泵,设计工况下的流量Q=2016m3/h,扬程H=12.8m,转速n=970r/min,求该泵的比转数。
一台多级泵的比转数n s=150,流量Q=5l/s,扬程H=52m,转速n=2950r/min,求该泵的级数。
3、一台单级离心泵,转速n=1800 r/min,设计工况下Q=570 m3/h,H=60m,现需选用一台与该泵相似,但Q=980 m3/h ,H=26m的泵,试问选用哪种比转数的泵?其转数应为多少?4、已知某水泵的工作参数:n=1470 r/min ,q v=130 l/s,H=54m,P sh=92kW。
如果机械损失△P m=5kW,漏损流量q=4 l/s,试求:(1)由于流量损失和水力损失所损耗的功率;(2)水泵的容积效率和水力效率。
5、某泵站安装24SH-19型水泵,水泵叶轮直径为540mm,水泵设计点的扬程为32m,流量为880l/s,轴功率为314KW。
该泵站净扬程19m,总管路阻力参数为4.24s2/m5,该水泵长期低效率运行。
为了减少能耗,希望水泵在高效点工作,拟采用车削调节。
试求车削后的叶轮直径和相应的工作参数Ha、Qa、Na、ηa 6、已知参数同第2题,如果该泵的设计转速为1450r/min,拟采用变速调节,试求水泵的转速和相应的工作参数。
7、一台水泵的进口直径为200mm,,Q=77.8l/s,[Hs]=3.6m。
估算进水管路损失为0.5m,请分别计算标准状况下及在拉萨地区(海拔3958m),从开敞进水池抽送40℃清水时,水泵的最大安装高度。
8、一台轴流泵抽水装置,叶片中心线在进水池自由水面以下0.5m处,进水池水面海拔高程80m,抽送常温清水,水泵转速750r/min,泵的允许汽蚀余量[Δh]=8.4m,泵进口部分较短,水力损失忽略不计。

第三章 泵与风机的性能(1)泵与风机实际H-Q 特性曲线及其主要影响因素 ①叶轮叶片出口角β2∞变化时的影响。
②叶轮叶片出口外径 D 2 变化时的影响。
③叶轮叶片出口宽度 b 2 变化时的影响。
④叶轮转速n 变化时的影响。
⑤实际叶轮为有限叶片数(Z ≠∞)的影响。
⑥实际流体具有粘性而产生摩擦损失的影响。
⑦偏离额定工况而产生冲击损失的影响。
⑧实际流道的泄露而产生容积损失的影响。
⑨泵与风机的实际H-Q特性曲线的形式。
首先,根据Euler 方程讨论泵与风机实际性能曲线的主要影响因素为提高理论扬程通常取叶片入口角α1=90°,则额定工况下,流体沿径向进入叶轮,即V 1u ∞=0,代入Euler 方程:又由出口速度三角形得到:式中:显然对于已给定参数的叶轮来说,理论扬程 H T ∞ 与理论流量 Q T 之间呈线性关系。
直线的斜率为: ,直线的截距为:由上述Euler 方程,我们可以讨论各个因素的影响。
① 叶轮叶片出口角β2∞的影响根据前面所得到的结果可知:叶轮叶片出口角β2∞的变化只影响斜率,而不影响其截矩。
我们可对以下三种情况讨论:a) β2∞< 90°(后向))(11122V u V u H u u T g ∞∞∞-=β∞∞∞-=222,2ctgVu V m u FQ b D Q VTTm 2222==∞πb D u g ctg 2222πβ∞-g u 2202222<-∞bD u g ctgπβb) β2∞=90°(径向)c) β2∞> 90°(前向)②叶轮外径D 2的影响∵斜率:∴斜率与叶轮外径D 2无关。
又∵截矩:∴截矩与叶轮外径D 2的平方成正比。
③叶轮出口宽度b 2的影响∵斜率:∴斜率的绝对值与叶轮出口宽度 b 2 的大小成反比。
又∵截矩:∴截矩与叶轮出口宽度 b 2 无关。
④转速 n 的影响 ∵斜率:∴斜率的绝对值与叶轮转速 n 的大小成正比。
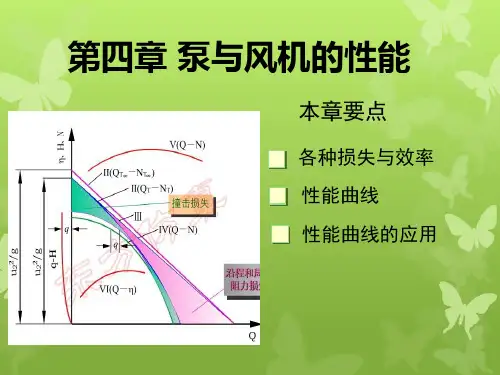
泵与风机的性能
1、某台IR125-100-315型热水离心泵的流量为240m3/h,扬程为120m,泵效率为77%,热水温度为80℃,密度为970kg/m3,试计算该泵有效功率和轴功率的大小。
解:
(m3/s)
该泵有效功率为:(kW)该泵轴功率为:(kW)
2、某台离心通风机的额定参数为:流量44090 m3/h,全压105mmH2O,风机效率0.88。
采用联轴器直联传动,ηtm=0.98,取电动机容量富余系数k=1.15,问该风机应选用多大容量的电动机?
解:
(m3/s)
(Pa)
电动机的容量应为:
(kW)
说明:电动机的容量一般是指电动机的铭牌额定输出功率,在工程实际中,进行了上述计算后,应查阅有关电动机产品系列,选用容量等级等于或略大于16.8kW的电动机,对于本题可选用容量为18.5 kW的电动机。
风机全压单位换算是1 mmH2O等于9.797Pa,工程计算时可取10Pa。
3、某电厂循环水泵的电动机输入功率为1720 kW,电动机效率为0.90,直联传动效率为0.98,泵的扬程为20m,循环水的密度为1000 kg/m3,问该循环水泵的流量为多少立方米/小时(取泵的效率为0.78)?
解:
由公式得:
(m3/s)
(m3/h)
4、若水泵流量qV为25L/s,泵出口压力表读数p B为32×104Pa,入
口处真空表读数p m为4×104Pa,吸入管直径d1为100cm,出水管直径
d2为75cm,电动机功率表读数p g为12.6kW,电动机效率η1为0.9,传
动效率η2为0.97。
试求泵的轴功率、有效功率及泵的总效率。
解:d1=100cm=1m,d2=75cm=0.75m
泵入口的流速w1=qV/A1=4qV/πd21=4×25×10-3(3.14×12)=
0.032(m/s)
泵出口的流速w2=qV/A2=4qV/πd22=4×25×10-3/
(3.14×0.752)=0.057(m/s)
水获得的能量H=(p B+p m)/ρg+(w22-w21)/2g=(32×104+
4×104)/1000×9.81+(0.0572-0.0322)/(2×9.81)=36.69(m)
所以泵的有效功率P e=ρg qVH/1000=1000×9.81×25×10-3×36.69/1000=8.998(kW)
所以泵的总效率η=P e/(P gη1η2)×100%=8.998/
(12.6×0.9×0.97)×100%=81.8%
泵的轴功率P sh=P e/η=8.998/0.818=11(kW)
答:泵的轴功率为11kW,有效功率为8.998kW,泵的总效率为
81.8%。
5、某水泵把温度为50℃的水提高到Hz=30 m的地方,吸水面压力为大气压p a,出水面的表压力为499000P a,水的密度为998kg/m3,管路的全部流动损失为h w=5m,试计算泵的扬程。
分析:题目中没有明确给出泵进、出口处的水密度,而只是笼统地指出了水的密度,说明本题可忽略泵进、出口的密度差别。
同样,题目中没有指出水泵进、出口的高度差,也没有给出进、出口的水速或用于计算该水速的其它条件,因此,本题可忽略泵进、出口处的高度差和流速差。
所以,本题计算可用泵扬程定义式
中的公式(2-7e),即,式中p2、p1为泵进、出口处的绝对压力。
假设泵的吸水高度为H1、排水高度为H2,由题意知:H1+H2=30m;设吸水管道的流动损失为h w1、排水管道的流动损失为h w2,由题意知:h w1+h w2=5m。
吸水面压力为大气压力p a,根据题意,出水面的绝对压力则为p02= p a+499000(P a)。
由伯努利方程可得:
代入公式(2-7e)得:
解:泵的扬程为:
(m)
6、某锅炉给水泵进口压力表读数为0.7MP a,该压力表的安装高度为1m;出口压力表读数为17.7MP a,该压力表的安装高度为9m,给水的密度取950kg/m3。
试计算给水泵的扬程。
分析:根据题意,本题可以忽略泵进、出口的高度差、给水密度差和速度差,但应考虑进出口压力表的表位差。
解:该给水泵的扬程为:
(m)
7、有一装有进风管道和出风管道的送风机,用U形管在风机进口处测得空气静压p1b和动压p d1分别为-37.5mmH2O和6.5 mmH2O;风机出口处的静压p2b和动压p d2分别为19mmH2O和12.5 mmH2O,试计算风机的全压为多少?。