iSIGHT中优化算法分类

多学科设计优化—— 基本概念
• 多学科设计优化（Multidisciplinary Design Optimization） – 美国国家航空宇航局（NASA）Langley 研究中心的多学科分支机构 （MDOB）对多学科设计优化的定义如下： • Multidisciplinary Design Optimization (MDO) is a methodology for the design of complex engineering systems and subsystems that oherently exploits the synergism of mutually interacting phenomena. – 多学科设计优化是一种针对于涵盖多个学科领域的复杂系统进行设 计优化的方法，强调各学科子系统在独自设计优化的基础上的相互 之间的并行协作 – 多学科设计优化的主要思想是在复杂系统设计的整个过程中集成各 个学科的知识、分析不建模理论和计算方法，应用有效的设计优化 策略组织和管理计算过程，充分发挥学科与家的技术优势，通过实 现并行设计优化，获得系统的整体最优解
多学科设计优化—— 特点
• 按系统中各学科属性将复杂系统分解为子系统，其分解形 式不工业界通用的设计组织形式相一致
• 各子系统具有相对独立性，便于发挥学科与家在某一领域 的技术优势，应用适合于该学科的分析和优化工具进行建 模和优化，提高子系统分析求解的准确度和效率，同时便 于对学科优化设计模型进行调控
• 方法：通过学科级优化，采用松弛因子等方法实现系统级协调的方式 ，将多学科问题分解为系统级和学科级两层优化。
• 原理：协同优化算法的原理是将一复杂的目标函数分解成简单的子目 标函数，然后再将这些子目标函数进行协同优化。 – 基本思想是每个子空间在设计优化时可暂时丌考虑其它子空间的 影响，只需满足本子系统的约束，它的优化目标是使该子空间设计优 化方案不系统级优化提供的目标方案的差异最小 – 各个子系统设计优化结果的丌一致性，通过系统级优化来协调， 通过系统级优化和子系统优化之间的多次迭代，最终找到一个一致性 的最优设计

前言●Isight 5.5简介笔者自2000年开始接触并采用Isight软件开展多学科设计优化工作，经过12年的发展，我们欣喜地看到优化技术已经深深扎根到众多行业，帮助越来越多的中国企业提高产品性能和品质、降低成本和能耗，取得了可观的经济效益和社会效益。

作为工程优化技术的优秀代表，Isight 5.5软件由法国Dassault/Simulia公司出品，能够帮助设计人员、仿真人员完成从简单的零部件参数分析到复杂系统多学科设计优化（MDO, Multi-Disciplinary Design Optimization）工作。

Isight将四大数学算法（试验设计、近似建模、探索优化和质量设计）融为有机整体，能够让计算机自动化、智能化地驱动数字样机的设计过程，更快、更好、更省地实现产品设计。

毫无疑问，以Isight为代表的优化技术必将为中国经济从“中国制造”到“中国创造”的转型做出应有的贡献！●本书指南Isight功能强大，内容丰富。

本书力求通过循序渐进，图文并茂的方式使读者能以最快的速度理解和掌握基本概念和操作方法，同时提高工程应用的实践水平。

全书共分十五章，第1章至第7章为入门篇，介绍Isight的界面、集成、试验设计、数值和全局优化算法；第8章至第13章为提高篇，全面介绍近似建模、组合优化策略、多目标优化、蒙特卡洛模拟、田口稳健设计和6Sigma品质设计方法DFSS（Design For 6Sigma）的相关知识。

本书约定在本书中，【AA】表示菜单、按钮、文本框、对话框。

如果没有特殊说明，则“单击”都表示用鼠标左键单击，“双击”表示用鼠标左键双击。

在本书中，有许多“提示”和“试一试”，用于强调重点和给予读者练习的机会，用户最好详细阅读并亲身实践。

本书内容循序渐进，图文并茂，实用性强。

适合于企业和院校从事产品设计、仿真分析和优化的读者使用。

在本书出版过程中，得到了Isight发明人唐兆成（Siu Tong）博士、Dassault/Simulia （中国）公司负责人白锐、陈明伟先生的大力支持，工程师张伟、李保国、崔杏圆、杨浩强、周培筠、侯英华、庞宝强、胡月圆、邹波等参与撰写，李鸽、杨新龙也为本书提供了宝贵的建议和意见，在此向所有关心和支持本书出版的人士表示感谢。

Φ(x) = F(x) + P(x)
转换出的无约束问题就是使 Φ(x) 最小化或最大化。
对于罚函数法的效率和鲁棒性和直接法比较的研究显示，直接法更加健壮，只需要很少 的函数评估。而当你使用一个罚函数法的时候，函数评估的次数会成倍增加。
罚函数法包括： l 外点罚函数法（Exterior Penalty） l Hooke-Jeeves直接搜索法(Hooke-Jeeves Direct Search Method)
有关上述表达方式的几点说明：
l 所有问题在 iSGHT 内部都被转换成一个加权的最小化问题。目标包含有很多 iSIGHT
参数，目标根据重要程度都有相应的权重因子和规模因子。如果一个目标是最大化，
那么就在它的权重因子前加负号。
l 如果你的优化技术是一个基于罚函数的技术，那么最小化问题就象上面所述，只需
22
2．探索型优化技术
探索型优化技术避免了集中在局部区域的搜索，这些技术遍历整个参数空间搜索全局最 设计优点。iSIGHT中这种技术有：
l 遗传算法（Genetic Algorithm） l 批处理遗传算法（Genetic Algorithm with Bulk Evaluation） l 模拟退火算法（Simulated Annealing） 3．专家系统技术 专家系统技术使优化沿着用户定义的方向进行改变，改变哪一项，怎么改变，什么时候 改变，这些都由用户自己定义。iSIGHT 中这样的技术为有指导启发式搜索方法（Directed Heuristic Search－DHS）。如果用户知道输入怎样影响输出结果的话，这种方法效率很高。
二、 优化技术的分类
21
本部分对 iSIGHT 中每种优化技术进行简要的介绍。 iSIGHT 中的优化技术分为三类： l 数值型优化技术（Numerical Optimization Techniques） l 探索型优化技术（Exploratory Techniques） l 专家系统技术（Expert System Techniques） 这些优化技术如下所示：

基于iS IGHT 的多学科设计优化技术研究与应用泰山石膏股份有限公司　任　利 山东农业大学机械与电子工程学院　邵园园临沂师范学院工程学院　韩　虎 摘　要:阐述了多学科设计优化技术,在iSI GHT 、Pr o /E 和Ansys 软件集成环境下,对轴承座进行多学科设计优化。

并对在单学科设计优化和多学科设计优化的环境下得到的优化结果进行了比较,得出了多学科设计优化结果更加有效地达到了优化目标的结论。

关键词:多学科设计优化;iSI GHT;软件集成Abstract:The technol ogy of multidisci p linary design op ti m izati on is elaborated 1Bearing bl ock multidisci p linary de 2sign op ti m izati on is conducted under the integrated envir on ment of iSI GHT,Pr o /E and Ansys,and the op ti m izati on result is better than that fr om single -disci p linary design op ti m izati on 1Keywords:multidisci p linary design op ti m izati on;iSI GHT;s oft w are integrati on1　多学科设计优化技术多学科设计优化(Multidisci p linary Design Op 2ti m izati on -MDO )是当前国际上飞行器设计研究中一个最新、最活跃的领域。

按照Jar osla w Sobieszczanski -Sobieski 的看法[1],MDO 是用于进行系统设计的方法,这种系统包括多个相互耦合的学科,设计师可以在这些学科上显著地影响系统的性能。

7
of
18
单梁起重机结构优化设计
集成软件
本案例选择大型通用软件ANSYS11.0进行强度校核 分析。 可以在ANSYS 中建立主梁的几何模型， 并对其 划分网格
8
of
18
单梁起重机结构优化设计
主梁优化模型 1、目标函数选择
根据要求质量应该是最终的目标函数，在主梁 跨距一定的情况下截面面积与质量成正比，所以优化 时选取截面面积A 作为目标函数，其与有优化变量如 下关系式成立： A=wl x tl + t2 +w3 x t3
11 of
18
ISIGHT集成优化
1、输入文件分析
输入文件格式及优化变量在其中的位置如6.7所述。由于设计变量定义在 文件的开始，并且每一个设计变量值前面都有“=”，所以通过搜索的方式 让光标移到相应的变量前，再进行替换操作，相关设置如图
12 of
18
2、参数计算
在参数运算之前，首先 需要定义梁截面面积参数 AREA。 点击过程集成界面 工作栏上的参数按钮 ， 则弹出如图所示对话框。点 击图中的“Add”按钮，参 数“OBJ”下面的一行被激 活，用户可以在“Task Task1”一栏中输入所添加 变量的名称“AREA”，然后 确认返回过程集成界面。 参数计算设置
18 of
18
THANK YOU 谢谢！
1
of
18
ISIGHT 包含的设计方法
优化设计
设计方法
试验设计 逼近计算 质量工程
2
of
18
ISIGHT
工作原理简介
基于数值分析软件的结构和工作过程，在进行数值分析的时候， 可以通过修改模拟计算模块的输入文件来完成模型的修改，iSIGHT 正是基于这种原理工作的。iSIGHT通过一种搭积木的方式快速集成 和耦合各种仿真软件，将所有设计流程组织到一个统一、有机和逻 辑的框架中，自动运行仿真软件，并自动重启设计流程，使整个设 计流程实现全数字化和全自动化。

多目标遗传算法（MOGA）
• 多目标遗传算法(Multi-Objective Genetic Alorithm，以下记为 MOGA），不需要归一化可以直接处理多目标最优化问题。
多目标遗传算法（MOGA ）
NSGA-II方法
• NSGA-II，作为1994年发布 的NSGA(Non-Dominated SortingGenetic Algorithm)的 改良版，由K. Deb，S. Agrawal等在2000年提出。
Isight 多目标遗传算法求解悬臂梁3 目标优化 ——重量、强度 、变形
\lab_第10章_多目标优化\beam.zmf
回顾：悬臂梁减重优化——单目标、 两变量版
演示：悬臂梁减重优化——三目标、四变量版
NSGAII
NSGAII 20x25→99 Pareto Points
NCGA
NCGA 20x25→192 Pareto Points
Pareto解。 • 由于目标函数间的矛盾性质，一般说来使每个目标函数同时达到各自最优值的
解是不存在的。多目标最优问题的解为Pareto最优解的条件是解的任何一个 目标函数的值在不使其他目标函数值恶化的条件下已不可能进一步改进。 • 很显然的，Pareto最优解不止一个，事实上在一般多目标优化问题中，Pareto 最优解常是连续的而且有无限多个，这就构成了Pareto前沿的概念。 • 多目标优化问题的最终解是从所有pareto最优解中挑 一个最优折衷解。
Pareto前沿比较
EDM数据挖掘
• 非劣个体通常都被存档 • 父代探索种群是从archive中
根据拥挤度进行淘汰选择 • 交叉、变异运算 • 非支配排序 • 拥挤距离排序 • 新的非劣个体存档 • 生成新的父代探索种群

三、 数值型优化技术
下面对每种优化技术进行一下介绍。
1．外点罚函数法(Exterior Penalty)
外点罚函数法广泛的用于含有约束条件的优化问题。在处理含有约束条件的优化问题 时，借助惩罚函数把约束问题转化为无约束的问题，进而用无约束的最优化方法求解。实现 这一目标的途径是由目标函数和约束函数组成辅助函数来完成的。如果该问题存在最优解， 其优化结果通常是可信的，并且相对来说更容易找到真正的最优解。当惩罚因子趋向∞
次的迭代中将原问题在 X i 处以一阶泰勒级数展开。如此反复，以线性规划问题去近似非线
性规划问题，希望每次迭代得到的新的设计点都比前一个设计点更接近原问题的最优点。而 在新的设计点上的近似子问题，也愈来愈接近原非线性问题最优点的附近区域。最终线性规 划问题的最优点可以以很高的精度接近原问题的最优点。
Φ(x) = F(x) + P(x)
转换出的无约束问题就是使 Φ(x) 最小化或最大化。
对于罚函数法的效率和鲁棒性和直接法比较的研究显示，直接法更加健壮，只需要很少 的函数评估。而当你使用一个罚函数法的时候，函数评估的次数会成倍增加。
罚函数法包括： l 外点罚函数法（Exterior Penalty） l Hooke-Jeeves直接搜索法(Hooke-Jeeves Direct Search Method)
l 能快速得到一个优化设计； l 能处理不等式和等式约束； l 在优化中能十分准确地满足约束。 下面是修正可行方向法的解决问题步骤：
1. q = 0, x = x0
2. q = q + 1
23
3. 求 F (x) 和 g j (x) 的值； j = 1,2,...., M
4. 确定临界的约束集，J

1
根据图形界面结构图，现在论述各个功能模块的主要作用
2．1 任务管理
在 iSIGHT 中，任务管理是唯一可以方位软件所有模块的入口。任务管理负责控制设计 学习的执行。用户通过任务管理可以引导、管理任务的执行过程。在任务管理模块，克斯使 用的控制手段包括： 开始、停止、暂停、继续任务执行 选择运行模式－包括简单执行，任务计划和单一设计学习 多机器分布式任务 实行并行处理 检测点基础上的重新运行 单步调试
4
基础，为下述构建块的使用奠定了基础。 “构建块”的使用：在 iSIGHT 里，在系统里使用了“构建块”方法来定义模型的执行。 每一个构造块表示过程中的一个步骤。在 iSIGHT 中的基本构造块包括：任务块，计算块， 仿真块和定制块（自定义的用于支持商业化软件，如电子表格和 MSC/NASTRAN 模型的定 制块） 。其中各主要构造块的说明如下： 任务块：任务可以包含子任务或者 iSIGHT 中其他类型构造块。通过任务可以实现 层次化过程的表达，任务大大增强了在建立集成过程和设计执行策略时的柔性。 条件块：设计过程除了简单的顺序执行，还有其他的执行方式，通过条件块“If” ， “Case”和“While” ，可以方便用户建立过程控制逻辑。 计算块：计算块允许用户执行一些中间计算，例如单位转换，创建辅助参数或者执 行工具命令语言（Tcl）等。 仿真代码块：任意仿真代码可以通过 iSIGHT 的仿真代码块连接到系统中使用。用 户通过仿真代码块可以定义执行协议， 执行协议使描述设计问题求解中， 需要输入 什么文件，输出什么文件，执行程序的位置以及如何执行的执行手段综合。 电子表格 Excel 块： iSIGHT 为了方便实际使用电子表格的用户， 直接提供了与 Excel 的接口。这可以通过 iSIGHT 的 Visual Basic 插件直接创建 Excel 仿真代码块。 重用组件： 通过重用组件可以更加简化过程集成。 在设计过程中创建一个构造块以 后，可以把它保存到重用库里，这样就可以在不同组之间共享，或者作为模板来生 成相似过程块。极大的方便了过程的建立。 并行处理技术： 系统分析过程有时因为执行仿真代码会产生昂贵的费用。 在整个设计过 程里，因为所需系统分析的数量往往导致成倍成辈增加。但是在大多系统里，仿真代码可以 彼此独立运行，在许多设计分析技术里，多数设计点可以不同进行分析。因此在计算资源可 用的前提下，通过控制仿真代码和设计点的同步执行计算能力可以显著节省工程时间。 ISIGHT 软件提供了两种类型的并行执行方式：并行任务和并行设计技术的执行。 并行任务：在一个层次性的多任务定义里，存在一些任务，它们彼此之间不直接交 换数据。在这种情形下，称其为独立任务。整体问题中的独立任务就可以通过并行 执行来减少整个执行过程的时间。 设计技术并行执行： iSIGHT 的许多设计探索工具需要运行内在彼此独立的数据点。 这种情况下通过同时提供这些执行点的能力来实施并行技术处理。 松耦合、紧耦合相辅相成：在 iSIGHT 中，在 IPC 通信协议基础上，采用了松耦合和紧 密耦合结合的控制方式， 松耦合主要体现在对应用软件的仿真程序的执行方面； 紧密耦合表 现在可以集成基于 CORBA 的仿真代码进行设计过程的控制和优化。

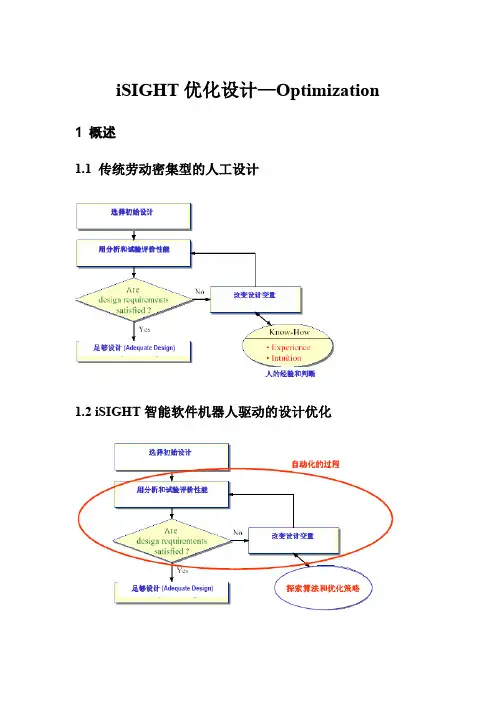
iSIGHT优化设计—Optimization 1 概述1.1 传统劳动密集型的人工设计1.2 iSIGHT智能软件机器人驱动的设计优化1.3 优化问题特征（1）约束（3）非线性（6）组合问题（7）优化问题按特征分类对优化设计的研究不断证实，没有任何单一的优化技术可以适用于所有设计问题。

实际上，单一的优化技术甚至可能无法很好地解决一个设计问题。

不同优化技术的组合最有可能发现最优设计。

优化设计极大地依赖于起始点的选择，设计空间本身的性质（如线形、非线形、连续、离散、变量数、约束等等）。

iSIGHT 就此问题提供两种解决方案。

第一，iSIGHT 提供完备的优化工具集，用户可交互式选用并可针对特定问题进行定制。

第二，也是更重要的，iSIGHT 提供一种多学科优化操作模式，以便把所有的优化算法有机组合起来，解决复杂的优化设计问题。

2 优化算法概述iSIGHT 包含的优化方法可以分为四大类：数值优化、全局探索法、启发式优化法和多目标多准则优化算法。

数值优化（如爬山法）一般假设设计空间是单峰的，凸起的和连续的，本质上是一种局部优化技术。

全局探索技术则避免了局限于局部区域，一般通过评估整个设计空间的设计点来寻找全局最优。

启发式技术是按用户定义的参数特性和交叉影响方向寻找最优方案。

多目标优化则需要权衡，iSIGHT 正是提供了一种易于使用的多目标准则权衡分析框架。

另外自iSIGHT v9.0 开始新增加了Pointer 优化器，它是GA、MPQL、N-M 单纯形法以及线性单纯形法的组合。

iSIGHT 包含的具体算法按分类列表如下:2.1 数值方法iSIGHT 纳入了十二种数值优化算法。

其中八种是直接法，在数学搜索过程中直接处理约束条件。

而Exterior Penalty 方法和Hooke-Jeeves 方法是罚函数法，它们通过在目标函数中引入罚函数将约束问题转化为无约束问题。

2.2 全局探索法iSIGHT 全局探索法包括遗传算法和模拟退火算法，它们不受凸（凹）面性、光滑性或设计空间连续性的限制。

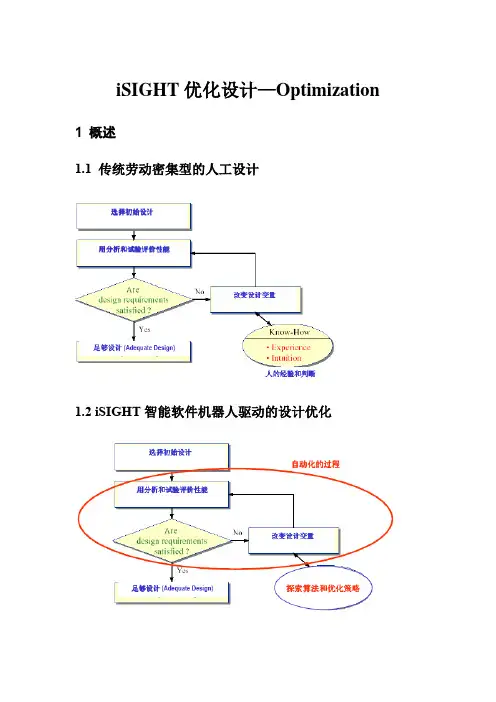
iSIGHT优化设计—Optimization 1 概述1.1 传统劳动密集型的人工设计1.2 iSIGHT智能软件机器人驱动的设计优化1.3 优化问题特征（1）约束（3）非线性（6）组合问题（7）优化问题按特征分类对优化设计的研究不断证实，没有任何单一的优化技术可以适用于所有设计问题。

实际上，单一的优化技术甚至可能无法很好地解决一个设计问题。

不同优化技术的组合最有可能发现最优设计。

优化设计极大地依赖于起始点的选择，设计空间本身的性质（如线形、非线形、连续、离散、变量数、约束等等）。

iSIGHT 就此问题提供两种解决方案。

第一，iSIGHT 提供完备的优化工具集，用户可交互式选用并可针对特定问题进行定制。

第二，也是更重要的，iSIGHT 提供一种多学科优化操作模式，以便把所有的优化算法有机组合起来，解决复杂的优化设计问题。

2 优化算法概述iSIGHT 包含的优化方法可以分为四大类：数值优化、全局探索法、启发式优化法和多目标多准则优化算法。

数值优化（如爬山法）一般假设设计空间是单峰的，凸起的和连续的，本质上是一种局部优化技术。

全局探索技术则避免了局限于局部区域，一般通过评估整个设计空间的设计点来寻找全局最优。

启发式技术是按用户定义的参数特性和交叉影响方向寻找最优方案。

多目标优化则需要权衡，iSIGHT 正是提供了一种易于使用的多目标准则权衡分析框架。

另外自iSIGHT v9.0 开始新增加了Pointer 优化器，它是GA、MPQL、N-M 单纯形法以及线性单纯形法的组合。

iSIGHT 包含的具体算法按分类列表如下:2.1 数值方法iSIGHT 纳入了十二种数值优化算法。

其中八种是直接法，在数学搜索过程中直接处理约束条件。

而Exterior Penalty 方法和Hooke-Jeeves 方法是罚函数法，它们通过在目标函数中引入罚函数将约束问题转化为无约束问题。

2.2 全局探索法iSIGHT 全局探索法包括遗传算法和模拟退火算法，它们不受凸（凹）面性、光滑性或设计空间连续性的限制。

16
大纲
� � � � �
参数的概念 优化算法概述 数值优化算法 全局优化算法 多目标优化算法

17
Isight 现代设计工具: Optimization
作用 Isight 设计工具
优化算法 Optimization Algorithms
� 对于构造好的优化问题（设计变量、目标函数
Y OU CA N TRY, BUT S TAYINSIDE THE FENCES
G. N. Vanderplaats
�目 标：找寻最高点 � 设计变量：经度和纬度 �约 束：围栏范围内

3
THE OPTIMIZATION PROCESS 优化概念：逐步改进的过程
S3 X2 S2 X1 S1
设计变量 :
10 ≤ Beam Height ≤ 80 mm 10 ≤ Flange Width ≤ 50 mm
�
约束 :
Stress ≤ 16 MPa
�
目标 :
最小化质量 (最小化面积)
解 解:: Beam Beam Height Height = = 38.4 38.4 Flange Flange Width Width = = 22.7 22.7 Stress = = 16 16 Stress Area = Area = 233.4 233.4

12
ObjectiveAndPenalty参数
�
ObjectiveAndPenalty = Objective + Penalty
� ObjectiveAndPenalty = 0.45 + 10.0036 = 10.4536
�
以ObjectiveAndPenalty的值为依据，计算 feasibility参数

梯度算法通过在设计空间中的当前位置设定一个前进方法和搜索步长从而获得设计空间中的另一个位置，并判断收敛性。

Isight中梯度优化算法有三种NLPQL,LSGRG和MMFD,这里通过寻找数学函数表达式的最小值问题，来展示这三种算法搜寻最优解的效率。

优化问题：min f(x)=100*(x2-x1^2)^2 10*(x1-1)^2s.t. x1^2 x2^2=<9.0isight优化步骤：1、构建优化流程，application组件采用calculator，process 组件选用optimization;2、设置优化算法、设计变量、约束及目标，设计变量初始值为x1=2.0,x2=3.0;3、查看优化结果，并比较3种梯度算法搜寻全局最优解的效率。

图3给出了三种算法的搜寻历程，算法收敛准则均设置为1.0e-6，设计空间为以（0,0）为圆心半径为3.0的圆域内，初始点为（2.0,3.0）不在设计空间内部，NLPQL算法迭代27次能搜寻到全局最优解（0.986,0.975），LSGRG算法迭代10次找到局部最优解（1.590,2.544），这个局部解刚好在设计区域的边界上，因为LSGRG算法的搜寻梯度和它的临界约束相关，MMFD算法迭代8次找到局部解（1.523,2.342），这个点刚好满足目标函数高阶项接近零。

以上结果可以发现，初始点不在设计区域内，NLPQL算法通过多次迭代能搜寻到全局最优解，而LSGRG和MMFD算法能用较少的迭代次数搜寻到一个局部最优解而完成迭代过程。

下面考察3种算法在无约束情况下搜寻最优解的效率，去掉设计区域在圆域内的限制，设计空间改为无限平面域，初始点位置不变，从图4中可以看出NLPQL和LSGRG算法都能搜寻到全局最优解，而MMFD算法依然在一个局部最优解处停止搜寻，从迭代历程上看NLPQL算法和LSGRG算法相比能以更少的迭代次数获得全局最优解。

本文以数学函数表达式为例对比了isight中3中梯度算法的效率，在有约束情况下NLPQL 能搜寻到全局最优解，而LSGRG和MMFD 算法只能搜寻到局部解；在无约束情况下，NLPQL比LSGRG算法能更快速搜寻到全局最优解。

前言●Isight 简介笔者自2000年开始接触并采用Isight软件开展多学科设计优化工作，经过12年的发展，我们欣喜地看到优化技术已经深深扎根到众多行业，帮助越来越多的中国企业提高产品性能和品质、降低成本和能耗，取得了可观的经济效益和社会效益。

作为工程优化技术的优秀代表，Isight 软件由法国Dassault/Simulia公司出品，能够帮助设计人员、仿真人员完成从简单的零部件参数分析到复杂系统多学科设计优化（MDO, Multi-Disciplinary Design Optimization）工作。

Isight将四大数学算法（试验设计、近似建模、探索优化和质量设计）融为有机整体，能够让计算机自动化、智能化地驱动数字样机的设计过程，更快、更好、更省地实现产品设计。

毫无疑问，以Isight为代表的优化技术必将为中国经济从“中国制造”到“中国创造”的转型做出应有的贡献！●本书指南Isight功能强大，内容丰富。

本书力求通过循序渐进，图文并茂的方式使读者能以最快的速度理解和掌握基本概念和操作方法，同时提高工程应用的实践水平。

全书共分十五章，第1章至第7章为入门篇，介绍Isight的界面、集成、试验设计、数值和全局优化算法；第8章至第13章为提高篇，全面介绍近似建模、组合优化策略、多目标优化、蒙特卡洛模拟、田口稳健设计和6Sigma品质设计方法DFSS（Design For 6Sigma）的相关知识。

●本书约定在本书中，【AA】表示菜单、按钮、文本框、对话框。

如果没有特殊说明，则“单击”都表示用鼠标左键单击，“双击”表示用鼠标左键双击。

在本书中，有许多“提示”和“试一试”，用于强调重点和给予读者练习的机会，用户最好详细阅读并亲身实践。

本书内容循序渐进，图文并茂，实用性强。

适合于企业和院校从事产品设计、仿真分析和优化的读者使用。

在本书出版过程中，得到了Isight发明人唐兆成（Siu Tong）博士、Dassault/Simulia（中国）公司负责人白锐、陈明伟先生的大力支持，工程师张伟、李保国、崔杏圆、杨浩强、周培筠、侯英华、庞宝强、胡月圆、邹波等参与撰写，李鸽、杨新龙也为本书提供了宝贵的建议和意见，在此向所有关心和支持本书出版的人士表示感谢。

4.1 iSIGHT优化基本问题4.1.1 iSIGHT集成软件的条件从一般意义上来说，只要是可执行文件（*.exe、*.bat）iSIGHT都可以进行驱动。

但是为了实现优化过程的自动化，要求所集成的数值分析软件能进行后台求解计算，且要有明确包含优化变量的输入、输出文件。

4.1.2 常用的输入文件的类型就目前市面上的数值分析软件而言，有以下两类文件可以作为输入文件：模型信息文件如上所述，数值分析软件一般分为三个模块，在数值建模结束后前处理程序便生成一个模型信息文件做为求解模块的输入文件，该模型文件包含了数值模型的各种信息，因此在优化的时候该文件便可以当作输入文件。

如，MSC.MARC的*.dat文件，LS—DYNA的的*.K文件等。

命令流或过程记录文件为了实现参数话建模与分析，好多数值分析软件中在提供菜单操作的同时也提供了相应地命令操作，并且可以把命令编程文件进行读入建模和分析，该文件常称为命令流文件。

另外，一些软件可以自动记录用户的每一步操作，并能输出相应地命令流文件，软件也可以读入该文件实现建模和分析，该命令流文件习惯称之为过程记录文件。

在使用模型信息文件当作输入文件的优化过程中，优化中在每次迭代过程中没有了建立模型的环节，因此其效率相对较高！而在用命令流或过程记录文件当作输入文件的优化中，在每次迭代分析时都从建模开始，故其计算所需要的时间相对较长。

然而，正是由于其每次迭代分析时都是从头开始建模分析，所以在相关变量的优化设计中，由于对模型信息文件的修改往往不能正确地反映模型的变化，故这时候就需要过程记录文件做为输入文件。

4.2 iSIGHT集成优化的一般步骤在工程上利用iSIGHT进行集成优化一般包括前期工作准备、过程集成、变量与算法设置以及过程监控与结果分析等步骤。

4.2.1 前期准备工作在集成优化之前的准备工作主要包括数值分析软件选择、初始计算以及熟悉相关文件等。

根据优化问题所要求的分析与求解任务，选择合适的数值分析软件进行优化设计计算。

Approximation Loop策略
• 将近似模型与数值优化算法组合的优点：
– 提高优化效率 • 减少计算机高强度仿真计算的次数
– 提高优化算法性能 • 用更多的近似方法来扩展已有的数值优化算法 • 通过平滑响应函数，为“噪声”计算工具改善收敛状况 • 减少优化算法困在局部解的机会，使数值优化算法也应用数 值优化算法对该区域进行精确寻优，最终获得最佳设计结果
• 优点： – 发挥了全局优化算法在整体设计空间遍历方面的优势，能够快速对 设计敏感区域进行定位 – 仅应用全局优化算法对设计空间进行粗略定位，避免了全局算法在 细节优化方面的效率问题 – 发挥了数值优化算法在局部优化方面的优势，能够精确的找到设计 最优解 – 避免了数值优化算法在高度非线性或离散设计空间中直接寻优可能 给用户带来的误导
到全局解
Pointer-2策略
• Optimization组件中Pointer算法的加强版 • 可以自动选择优化算法的参数优化模块 • 包含六个标准优化算法：NLPQL、Evol、Downhill Simplex、Multi-
objective Particle Swarm、Hooke-Jeeves和MOST • 不需要了解设计问题的数学属性和各种优化算法的原理，可以自动分
• 是一个近似模型与参数优化模块的组合策略 • 步骤：
– 选择位于初始设计点周围的设计空间建立局部近似模型 – 在局部近似模型上通过参数优化模块进行第一次优化子循环，获得 近似模型局部最优解 – 将近似模型上的局部最优解代入集成的求解器模块进行验证 – 在验证后的最优解周围设计空间再次建立新的局部近似模型 – 在局部近似模型上通过参数优化模块进行第二次优化子循环，进一 步获得近似模型最优解 – 将新的近似模型最优解带入集成求解器模块进行验证 – 返回第4步进行新的循环，直到获得满足设计目标的最优解

iSIGHT中优化方法种类iSIGHT里面的优化方法大致可分为三类：1 数值优化方法数值优化方法通常假设设计空间是单峰值的，凸性的，连续的。

iSIGHT中有以下几种：（1）外点罚函数法（EP）：外点罚函数法被广泛应用于约束优化问题。

此方法非常很可靠，通常能够在有最小值的情况下，相对容易地找到真正的目标值。

外点罚函数法可以通过使罚函数的值达到无穷值，把设计变量从不可行域拉回到可行域里，从而达到目标值。

（2）广义简约梯度法（LSGRG2）：通常用广义简约梯度算法来解决非线性约束问题。

此算法同其他有效约束优化一样，可以在某方向微小位移下保持约束的有效性。

（3）广义虎克定律直接搜索法：此方法适用于在初始设计点周围的设计空间进行局部寻优。

它不要求目标函数的连续性。

因为算法不必求导，函数不需要是可微的。

另外，还提供收敛系数（rho），用来预计目标函数方程的数目，从而确保收敛性。

（4）可行方向法（CONMIN）：可行方向法是一个直接数值优化方法，它可以直接在非线性的设计空间进行搜索。

它可以在搜索空间的某个方向上不断寻求最优解。

用数学方程描述如下：Design i = Design i-1 + A * Search Direction i方程中，i表示循环变量，A表示在某个空间搜索时决定的常数。

它的优点就是在保持解的可行性下降低了目标函数值。

这种方法可以快速地达到目标值并可以处理不等式约束。

缺点是目前还不能解决包含等式约束的优化问题。

（5）混合整型优化法（MOST）：混合整型优化法首先假定优化问题的设计变量是连续的，并用序列二次规划法得到一个初始的优化解。

如果所有的设计变量是实型的，则优化过程停止。

否则，如果一些设计变量为整型或是离散型，那么这个初始优化解不能满足这些限制条件，需要对每一个非实型参数寻找一个设计点，该点满足非实型参数的限制条件。

这些限制条件被作为新的约束条件加入优化过程，重新优化产生一个新的优化解，迭代依次进行。

isight优化基本问题4.1 iSIGHT优化基本问题4.1.1 iSIGHT集成软件的条件从⼀般意义上来说，只要是可执⾏⽂件（*.exe、*.bat）iSIGHT都可以进⾏驱动。

但是为了实现优化过程的⾃动化，要求所集成的数值分析软件能进⾏后台求解计算，且要有明确包含优化变量的输⼊、输出⽂件。

4.1.2 常⽤的输⼊⽂件的类型就⽬前市⾯上的数值分析软件⽽⾔，有以下两类⽂件可以作为输⼊⽂件：模型信息⽂件如上所述，数值分析软件⼀般分为三个模块，在数值建模结束后前处理程序便⽣成⼀个模型信息⽂件做为求解模块的输⼊⽂件，该模型⽂件包含了数值模型的各种信息，因此在优化的时候该⽂件便可以当作输⼊⽂件。

如，MSC.MARC的*.dat⽂件，LS—DYNA的的*.K⽂件等。

命令流或过程记录⽂件为了实现参数话建模与分析，好多数值分析软件中在提供菜单操作的同时也提供了相应地命令操作，并且可以把命令编程⽂件进⾏读⼊建模和分析，该⽂件常称为命令流⽂件。

另外，⼀些软件可以⾃动记录⽤户的每⼀步操作，并能输出相应地命令流⽂件，软件也可以读⼊该⽂件实现建模和分析，该命令流⽂件习惯称之为过程记录⽂件。

在使⽤模型信息⽂件当作输⼊⽂件的优化过程中，优化中在每次迭代过程中没有了建⽴模型的环节，因此其效率相对较⾼！⽽在⽤命令流或过程记录⽂件当作输⼊⽂件的优化中，在每次迭代分析时都从建模开始，故其计算所需要的时间相对较长。

然⽽，正是由于其每次迭代分析时都是从头开始建模分析，所以在相关变量的优化设计中，由于对模型信息⽂件的修改往往不能正确地反映模型的变化，故这时候就需要过程记录⽂件做为输⼊⽂件。

4.2 iSIGHT集成优化的⼀般步骤在⼯程上利⽤iSIGHT进⾏集成优化⼀般包括前期⼯作准备、过程集成、变量与算法设置以及过程监控与结果分析等步骤。

4.2.1 前期准备⼯作在集成优化之前的准备⼯作主要包括数值分析软件选择、初始计算以及熟悉相关⽂件等。