由平方差公式的几何证明谈代数

数学简便计算方法之平方差公式证明推导及运用详解平方差公式是小学奥数计算中的常用公式。

通常写为：a²-b²=(a+b)x(a-b)它的几何方法推导过程是这样的：如下图所示，四边形ABCD和四边形DEFG为正方形，边长分别为a和b，求阴影部分面积。

显然，阴影部分面积有2种求法。

第一种方法阴影面积=大正方形面积-小正方形面积即，阴影面积=a²-b²（G老师讲奥数）第二种方法作两条辅助线，延长FG、EG，分别交线段AB、BC与点H、J。

阴影面积=四边形AEGH面积+四边形HBJG面积+四边形GFCJ面积跟G老师一起分别计算下上述三个四边形的边长吧。

分别计算出三个四边形的边长后，我们发现四边形GFCJ=四边形AEGH面积。

接下来，我们将四边形GFCJ旋转后挪到四边形HBJG右侧。

即如下图所示，将③移到④后，纯手绘，就认为和上边的图一样吧此刻，阴影部分的面积=①+②+④组成的大矩形面积。

阴影部分面积=(a-b)x[b+(a-b)+b]=(a-b)x(a+b)。

因为第一种和第二种方法都是计算阴影部分面积，所以它们的结果是相等的。

a²-b²=(a+b)x(a-b)当然，代数方法也可以证明。

令A=(a+b)，(a+b)x(a-b)=Ax(a-b)=Axa-Axb (乘法分配律)=(a+b)xa-(a+b)xb（代入A=a+b）=a²+ab-ab-b²=a²-b²【例题】计算：48x52+37x43分析：48和52刚好都与50相差2，37和43刚好与40相差3。

48x52+37x43=(50-2)x(50+2)+(40-3)x(40+3)=50²-2²+40²-3²=2500-4+1600-9=4087这类题目往往不会明确告知你需要用什么技巧简化计算，关键在于自己要熟练掌握，牢记于心，灵活运用。

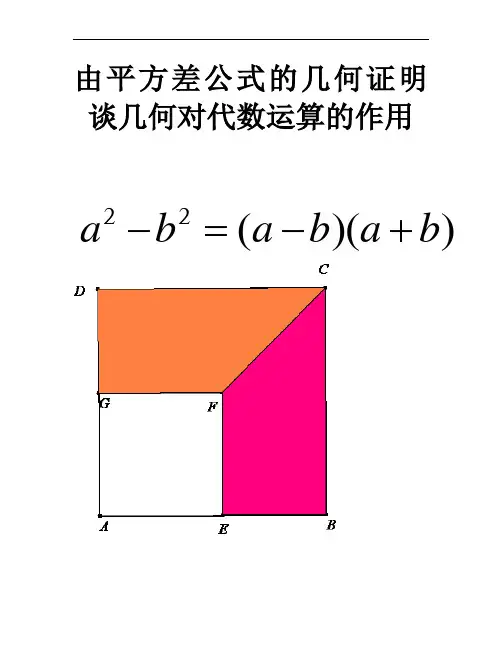
由平方差公式的几何证明谈几何对代数运算的作用22()() a b a b a b-=-+↓把四边形EBCF 移动跟四边形CFGD 构成长方形DEBG↓求证：22()()a b a b a b -=-+ 证明：设|AD|=a , |AG| =b 则S AEFG =2a ,S ABCD =2bS AEFG –S ABCD ==S EBFC +S CFGD而 S EBFC +S CFGD =|DG| .|DE|=(|AD| -|AG| ).(|DC| +|CE| )=(a-b)(a+b)(就是把四边形EBCF 移动跟四边形CFGD 构成长方形DEBG 算面积）这种用几何的方法证明平方差公式很容易理解，也让人容易接受，可以把抽象的代数运算用几何的方法具体化。

我们知道代数主要研究的是数字与数字之间的逻辑联系,是代数式与代数式的运算。

而几何是图形中各种边角面积之间的必然联系。

有些代数运算可以用几何图形表示而还有些代数运算不能用几何图形表示。

我在上面用几何的方法证明了我们常用的，也是最简单的平方差公式，同样的方法也可以证明单项式和多项式的相乘，多项式和多项式相乘公式等等。

用几何方法可以解决很多复杂的难题。

每个函数有它相对应的几何图形，有图形我们就可以看出函数的很多性质，特征。

例如：上面这个心形的函为2/1sin *cos 1617/(a ）θθρ-=我们用代数式能画出各种各样漂亮的图形，且解决很多问题。

抽象的代数式可以用具体的几何图像来表示。

对学数学的专业人士代数和几何都一样，但是对不是专业人理解几何图形比理解代数式容易很多，所以我们要让别人看懂我们做的成果就要用一些几何图形来表示。

用几何图形表示的时候可以看出这个函数的定义域，值域，最大最小值等等一些性质。

总之几何在代数运算中有何大的作用，几何使代数运算简单化，具体化。

我这个图像是用超级画板做出来的，下面 谈谈我个人学超级画板的感受，对超级画板的看法以及超级画板对代数和几何中的作用。

平方差公式几何证明6种平方差公式是数学中的一个重要公式，在几何中也有广泛的应用。

本文将从几何的角度出发，通过六种不同的例子，来证明平方差公式的几何意义。

1. 两点间距离的平方差设平面上有两个点A(x1, y1)和B(x2, y2)，我们要证明点A和点B 之间的距离的平方等于x坐标之差的平方加上y坐标之差的平方。

我们可以画出以A和B为顶点的直角三角形ABC，其中C点的坐标为(x2, y1)。

根据勾股定理，我们有AB的平方等于AC的平方加上CB的平方，即AB^2 = AC^2 + CB^2。

将AC和CB的长度代入，即可得到平方差公式的几何证明。

2. 线段中点连线的平方差假设平面上有一条线段AB，其中A和B分别为端点。

我们要证明线段中点M到A点和B点的距离的平方之差等于线段的长度的四分之一。

我们可以通过连接AM和BM，得到两个直角三角形AMC 和BMC。

根据勾股定理，我们有AM的平方等于AC的平方加上CM的平方，BM的平方等于BC的平方加上CM的平方。

将这两个等式相减，即可得到平方差公式的几何证明。

3. 直角三角形斜边上某点到两直角边的平方差考虑一个直角三角形ABC，其中∠C为直角，AC为斜边。

我们要证明任意一点D在斜边AC上，D点到直角边AB的距离的平方减去D点到直角边BC的距离的平方等于线段AD和CD的长度之差。

我们可以通过连接AD和CD，得到两个直角三角形ADC和BDC。

根据勾股定理，我们有AD的平方等于AC的平方减去CD的平方，CD的平方等于BC的平方减去BD的平方。

将这两个等式相减，即可得到平方差公式的几何证明。

4. 三角形边长平方差设平面上有一个三角形ABC，其中AB、BC、AC分别为三边的长度。

我们要证明三角形的三条边长的平方之差等于三条边上的三角形面积的四倍。

我们可以通过求三角形的面积，利用海伦公式得到三角形面积的表达式。

然后将三边长的平方代入表达式，即可得到平方差公式的几何证明。

5. 矩形对角线平方差考虑一个矩形ABCD，其中AB和CD为矩形的对边。

用面积法验证平方差公式平方差公式是高中数学中重要的公式之一，它用于求两个数的平方差。

在学习该公式时，我们可以通过几何的方法来验证它，即面积法。

我们来看平方差公式的表达式：$(a+b)(a-b)=a^2-b^2$。

为了验证该公式，我们可以构造一个正方形，其边长为$a+b$，并在该正方形内部构造两个矩形。

一个矩形的长为$a$，宽为$b$，另一个矩形的长为$b$，宽为$a$。

如下图所示：[图1：正方形及两个矩形的示意图]我们先计算正方形的面积。

根据正方形的面积公式，正方形的面积等于边长的平方，即$(a+b)^2$。

然后，我们计算两个矩形的面积。

第一个矩形的面积为$a \times b$，第二个矩形的面积为$b \times a$。

接下来，我们将两个矩形的面积相加。

根据面积的加法性质，我们可以得到两个矩形面积之和为$(a \times b) + (b \times a)$。

现在，我们来比较正方形的面积和两个矩形面积之和。

根据构造的图形，我们可以看出正方形的面积应该等于两个矩形面积之和，即$(a+b)^2 = (a \times b) + (b \times a)$。

继续化简等式，我们可以得到$(a+b)^2 = 2ab$。

接下来，我们再来比较正方形的面积和平方差的表达式$a^2-b^2$。

根据构造的图形，我们可以看出正方形的面积应该等于平方差的表达式，即$(a+b)^2 = a^2-b^2$。

将上述两个等式进行对比，我们可以发现它们是相等的，即$(a+b)^2 = 2ab = a^2-b^2$。

因此，我们通过面积法验证了平方差公式$(a+b)(a-b)=a^2-b^2$。

总结一下，通过构造正方形和两个矩形，并利用面积的加法性质，我们可以得到平方差公式的几何验证。

这种方法相对直观且易于理解，帮助我们更好地掌握平方差公式的本质。

同时，这也展示了数学中几何和代数之间的联系和应用。

在学习数学过程中，我们经常会遇到需要验证公式或定理的情况。

8.3 完全平方公式与平方差公式1．了解乘法公式的几何背景，掌握公式的结构特征，并能熟练运用公式进行简单的计算．2．感受生活中两个乘法公式存在的意义，养成“观察—归纳—概括”的数学能力，体会数形结合的思想方法，提高学习数学的兴趣和运用知识解决问题的能力，进一步增强符号感和推理能力．1．完全平方公式(1)完全平方公式：(a＋b)2＝a2＋2ab＋b2，(a－b)2＝a2－2ab＋b2.上式用语言叙述为：两个数的和(或差)的平方，等于这两个数的平方和加(或减)这两个数乘积的2倍．(2)完全平方公式的证明：(a±b)2＝(a±b)(a±b)＝a2±ab±ab＋b2(多项式乘多项式)＝a2±2ab＋b2(合并同类项)．(3)完全平方公式的特点：①左边是一个二项式的完全平方，右边是一个二次三项式，其中有两项是公式左边二项式中每一项的平方，另一项是左边二项式中两项乘积的2倍．可简单概括为“首平方，尾平方，积的2倍夹中央”．②公式中的a，b可以是单项式，也可以是多项式．③对于符合两数和(或差)的平方的乘法，均可用上述公式计算．【例1－1】用完全平方公式计算(1)(x＋2y)2；(2)(2a－5)2；(3)(－2s＋t)2；(4)(－3x－4y)2；(5)(2x＋y－3z)2.分析：第(1)、(2)两题可直接用和、差平方公式计算；第(3)题可先把它变成(t－2s)2，然后再计算，也可以把－2s看成一项，用和平方公式计算；第(4)题可看成－3x与4y差的平方，也可以看成－3x与－4y和的平方；(5)可把2x＋y看成一项，用差平方公式计算，然后再用和平方公式计算，也可以把它看成2x与y－3z的和平方，再用差平方公式计算．解：(1)(x＋2y)2＝x2＋2·x·2y＋(2y)2＝x2＋4xy＋4y2；(2)(2a－5)2＝(2a)2－2·2a·5＋52＝4a2－20a＋25；(3)(－2s ＋t )2＝(t －2s )2＝t 2－2·t ·2s ＋(2s )2＝t 2－4ts ＋4s 2；(4)(－3x －4y )2＝(－3x )2－2·(－3x )·4y ＋(4y )2＝9x 2＋24xy ＋16y 2；(5)(2x ＋y －3z )2＝[2x ＋(y －3z )]2＝(2x )2＋2·2x ·(y －3z )＋(y －3z )2＝4x 2＋4xy －12xz ＋y 2－2·y ·3z ＋(3z )2＝4x 2＋y 2＋9z 2＋4xy －12xz －6yz .(1)千万不要与公式(ab )2＝a 2b 2混淆，发生类似(a ±b )2＝a 2±b 2的错误；(2)切勿把“乘积项”2ab 中的2漏掉；(3)计算时，应先观察所给题目的特点是否符合公式的条件，如符合，则可以直接套用公式进行计算；如不符合，应先变形，使其具备公式的结构特点，再利用公式进行计算，如变形后仍不具备公式的结构特点，则应运用乘法法则进行计算．此外，在运用公式时要灵活，如第(4)题，由于(－3x －4y )2与(3x ＋4y )2是相等关系，故可以把(－3x －4y )2转化为(3x ＋4y )2，再进行计算，再如(5)题，也有许多不同的方法．(4)完全平方公式的几何解释．如图是对(a ＋b )2＝a 2＋2ab ＋b 2几何意义的阐释．大正方形的面积可以表示为(a ＋b )2，也可以表示为S ＝S Ⅰ＋S Ⅱ＋S Ⅲ＋S Ⅳ，又S Ⅲ，S Ⅰ，S Ⅳ，S Ⅱ分别等于a 2，ab ，ab ，b 2，所以S ＝a 2＋ab ＋ab ＋b 2＝a 2＋2ab ＋b 2.从而验证了完全平方公式(a ＋b )2＝a 2＋2ab ＋b 2.如图是对(a －b )2＝a 2－2ab ＋b 2几何意义的阐释．正方形Ⅰ的面积可以表示为(a －b )2，也可以表示为S Ⅰ＝S 大－S Ⅱ－S Ⅳ＋S Ⅲ，又S 大，S Ⅱ，S Ⅲ，S Ⅳ分别等于a 2，ab ，b 2，ab ，所以SⅠ＝a 2－ab －ab ＋b 2＝a 2－2ab ＋b 2.从而验证了完全平方公式(a －b )2＝a 2－2ab ＋b 2.【例1－2】下图是四张全等的矩形纸片拼成的图形，请利用图中的空白部分面积的不同表示方法，写出一个关于a ，b 的恒等式：__________________.解析：根据图中的面积写一个恒等式，需要用两种方法表示空白正方形的面积．首先观察大正方形是由四个矩形和一个空白正方形组成，所以空白正方形的面积等于大正方形的面积减去四个矩形的面积，即(a ＋b )2－4ab ，空白正方形的面积也等于它的边长的平方，即(a－b )2，根据面积相等有(a ＋b )2－4ab ＝(a －b )2.答案：(a ＋b )2－4ab ＝(a －b )22．平方差公式(1)平方差公式：(a＋b)(a－b)＝a2－b2.上式用语言叙述为：两个数的和与这两个数的差的积，等于这两个数的平方差．(2)平方差公式的证明：(a＋b)(a－b)＝a2－ab＋ab＋b2(多项式乘多项式)＝a2－b2(合并同类项)．(3)平方差公式的特点：①左边是两个二项式相乘，这两项中有一项完全相同，另一项互为相反数；②右边是乘式中两项的平方差(相同项的平方减去互为相反数项的平方)；③公式中的a和b可以是具体的数，也可以是单项式或多项式．利用此公式进行乘法计算时，应仔细辨认题目是否符合公式特点，不符合平方差公式形式的两个二项式相乘，不能用平方差公式．如(a＋b)(a－2b)不能用平方差公式计算．【例2－1】计算：(1)(3x＋2y)(3x－2y)；(2)(－m＋n)(－m－n)；(3)(－2x－3)(2x－3)．分析：(1)本题符合平方差公式的结构特征，其中3x对应“a”，2y对应“b”；(2)题中相同项为－m，互为相反数的项为n与－n，故本题也符合平方差公式的结构特征；(3)利用加法交换律将原式变形为(－3＋2x)(－3－2x)，然后运用平方差公式计算．解：(1)(3x＋2y)(3x－2y)＝(3x)2－(2y)2＝9x2－4y2.(2)(－m＋n)(－m－n)＝(－m)2－n2.(3)(－2x－3)(2x－3)＝(－3＋2x)(－3－2x)＝(－3)2－(2x)2＝9－4x2.利用公式计算，关键是分清哪一项相当于公式中的a，哪一项相当于公式中的b，通常情况下，为防止出错，利用公式前把相同项放在前面，互为相反数的项放在后面，然后套用公式．(4)平方差公式的几何解释如图，阴影部分的面积可以看成是大正方形的面积减去小正方形的面积，即a2－b2；若把小长方形Ⅲ旋转到小长方形Ⅳ的位置，则此时的阴影部分的面积又可以看成SⅠ＋SⅢ＝SⅠ＋SⅣ＝(a＋b)(a－b)．从而验证了平方差公式(a＋b)(a－b)＝a2－b2.【例2－2】下图由边长为a和b的两个正方形组成，通过用不同的方法，计算图中阴影部分的面积，可以验证的一个乘法公式是____________________．分析：要表示阴影部分的面积，可以从两个方面出发：一是观察阴影部分是由边长为a的正方形除去边长为b 的正方形得到的，所以它的面积等于a 2－b 2；二是阴影部分是由两个直角梯形构成的，所以它的面积又等于两个梯形的面积之和．这两个梯形的面积都等于12(b＋a )(a －b )，所以梯形的面积和是(a ＋b )(a －b )，根据阴影部分的面积不变，得(a ＋b )(a－b )＝a 2－b 2.因此验证的一个乘法公式是(a ＋b )(a －b )＝a 2－b 2.答案：(a ＋b )(a －b )＝a 2－b23．运用乘法公式简便计算平方差公式、完全平方公式不但是研究整式运算的基础，而且在许多的数字运算中也有广泛地运用．不少数字计算题看似与平方差公式、完全平方公式无关，但若根据数字的结构特点，灵活巧妙地运用平方差公式、完全平方公式，常可以使运算变繁为简，化难为易．解答此类题，关键是分析数的特点，看能否将数改写成两数和的形式及两数差的形式，若改写成两数和的形式乘以两数差的形式，则用平方差公式；若改写成两数和的平方形式或两数差的平方形式，则用完全平方公式．【例3】计算：(1)2 0132－2 014×2 012；(2)1032；(3)1982.分析：(1)2 014＝2 013＋1,2 012＝2 013－1，正好符合平方差公式，可利用平方差公式进行简便运算；(2)可将1032改写为(100＋3)2，利用两数和的平方公式进行简便运算；(3)可将1982改写为(200－2)2，利用两数差的平方公式进行简便运算．解：(1)2 0132－2 014×2 012＝2 0132－(2 013＋1)×(2 013－1)＝2 0132－(2 0132－12)＝2 0132－2 0132＋1＝1.(2)1032＝(100＋3)2＝1002＋2×100×3＋32＝10 000＋600＋9＝10 613.(3)1982＝(200－2)2＝2002－2×200×2＋22＝40 000－800＋4＝39 204. 4．利用乘法公式化简求值求代数式的值时，一般情况是先化简，再把字母的值代入化简后的式子中求值．在化简的过程中，合理地利用乘法公式能使整式的运算过程变得简单．在代数式化简过程中，用到平方差公式及完全平方公式时，要特别注意应用公式的准确性．【例4】先化简，再求值：5(m ＋n )(m －n )－2(m ＋n )2－3(m －n )2，其中m ＝－2，n ＝15.解：5(m ＋n )(m －n )－2(m ＋n )2－3(m －n )2＝5(m 2－n 2)－2(m 2＋2mn ＋n 2)－3(m 2－2mn ＋n 2)＝5m 2－5n 2－2m 2－4mn －2n 2－3m 2＋6mn －3n 2＝－10n 2＋2mn .当m ＝－2，n ＝15时，原式＝－10n2＋2mn ＝－10×⎝ ⎛⎭⎪⎫152＋2×(－2)×15＝－65.5．乘法公式的运用技巧一些多项式的乘法或计算几个有理数的积时，表面上看起来不能利用乘法公式，实际上经过简单的变形后，就能直接运用乘法公式进行计算了．有些题目往往可用不同的公式来解，此时要选择最恰当的公式以使计算更简便．在运用平方差公式时，注意以下几种常见的变化形式：①位置变化：(b＋a)(－b＋a)＝a2－b2.②符号变化：(－a＋b)(－a－b)＝(－a)2－b2＝a2－b2.③系数变化：(0.5a＋3b)(0.5a－3b)＝(0.5a)2－(3b)2.④指数变化：(a2＋b2)(a2－b2)＝(a2)2－(b2)2＝a4－b4.⑤增项变化：(a－b－c)(a－b＋c)＝(a－b)2－c2，(a＋b－c)(a－b＋c)＝a2－(b－c)2.⑥增因式变化：(a＋b)(a－b)(－a－b)(－a＋b)＝(a2－b2)(a2－b2)＝(a2－b2)2.⑦连用公式变化：(a－b)(a＋b)(a2＋b2)(a4＋b4)＝a8－b8.【例5－1】计算：(1)(a＋b＋1)(a＋b－1)；(2)(m－2n＋p)2；(3)(2x－3y)2(2x＋3y)2.解：(1)(a＋b＋1)(a＋b－1)＝[(a＋b)＋1][(a＋b)－1]＝(a＋b)2－1＝a2＋2ab＋b2－1.(2)(m－2n＋p)2＝[(m－2n)＋p]2＝(m－2n)2＋2·(m－2n)·p＋p2＝m2－4mn＋4n2＋2mp－4np＋p2.(3)(2x－3y)2(2x＋3y)2＝[(2x－3y)(2x＋3y)]2＝(4x2－9y2)2＝(4x2)2－2×4x2×9y2＋(9y2)2＝16x4－72x2y2＋81y4.在运用平方差公式时，应分清两个因式是否是两项之和与差的形式，符合形式才可以用平方差公式，否则不能用；完全平方公式就是求一个二项式的平方，其结果是一个三项式，在计算时不要发生：(a＋b)2＝a2＋b2或(a－b)2＝a2－b2这样的错误；当因式中含有三项或三项以上时，要适当的分组，看成是两项，从而应用平方差公式或完全平方公式．【例5－2】计算：(2＋1)(22＋1)(24＋1)(28＋1)…(22n＋1)的值．分析：为了能便于运用平方差公式，观察到待求式中都是和的形式，没有差的形式，可设法构造出差的因数，于是可乘以(2－1)，这样就可巧妙地运用平方差公式了．解：(2＋1)(22＋1)(24＋1)(28＋1)…(22n＋1)＝(2－1)(2＋1)(22＋1)(24＋1)(28＋1)…(22n＋1)＝(22－1)(22＋1)(24＋1)(28＋1)…(22n＋1)＝(24－1)(24＋1)(28＋1)…(22n＋1)＝…＝(22n－1)(22n＋1)＝24n－1.6．乘法公式的实际应用 在解决生活中的实际问题时，经常把其中的一个量或几个量先用字母表示，然后列出相关式子，进而化简，这往往涉及到整式的运算．解题时，灵活运用乘法公式，往往能事半功倍，使问题得到快速解答．【例6】一个正方形的边长增加3 cm ，它的面积就增加39 cm 2，这个正方形的边长是多少？分析：如果设原正方形的边长为x cm ，根据题意和正方形的面积公式可列出方程(x ＋3)2＝x 2＋39，求解即可．解：设原正方形的边长为x cm ，则(x ＋3)2＝x 2＋39，即x 2＋6x ＋9＝x 2＋39，解得x ＝5(cm)． 故这个正方形的边长是5 cm. 7．完全平方公式的综合运用学习乘法公式应注意掌握公式的特征，认清公式中的“两数”，注意为使用公式创造条件．(1)完全平方公式变形后可得到以下一些新公式： ①a 2＋b 2＝(a ＋b )2－2ab ； ②a 2＋b 2＝(a －b )2＋2ab ；③(a ＋b )2＝(a －b )2＋4ab ；④(a －b )2＝(a ＋b )2－4ab ；⑤(a ＋b )2＋(a －b )2＝2(a 2＋b 2)；⑥(a ＋b )2－(a －b )2＝4ab 等．在公式(a ±b )2＝a 2±2ab ＋b 2中，如果把a ＋b ，ab 和a 2＋b 2分别看做一个整体，则知道了其中两个就可以求第三个．(2)注意公式的逆用不仅会熟练地正用公式，而且也要求会逆用公式，乘法公式均可逆用，特别是完全平方公式的逆用——a 2＋2ab ＋b 2＝(a ＋b )2，a 2－2ab ＋b 2＝(a －b )2.【例7－1】已知a 2＋b 2＋4a －2b ＋5＝0，则a ＋b a －b的值是__________．解析：原等式可化为(a 2＋4a ＋4)＋(b 2－2b ＋1)＝0，即(a ＋2)2＋(b －1)2＝0，根据非负数的特点知a ＋2＝0且b －1＝0，从而可知a ＝－2且b ＝1.然后将其代入求a ＋ba －b的值即可．答案：13【例7－2】已知a ＋b ＝2，ab ＝1，求a 2＋b 2的值．分析：利用完全平方公式有(a ＋b )2＝a 2＋2ab ＋b 2，把2ab 移到等式的左边，可得(a ＋b )2－2ab ＝a 2＋b 2，然后代入求值即可．解：∵(a ＋b )2＝a 2＋2ab ＋b 2，∴a 2＋b 2＝(a ＋b )2－2aB ．∵a ＋b ＝2，ab ＝1，∴a 2＋b 2＝22－2×1＝2.涉及两数和或两数差及其乘积的问题，就要联想到完全平方公式．本题也可从条件出发解答，如因为a ＋b ＝2，所以(a ＋b )2＝22，即a 2＋2ab ＋b 2＝4.把ab ＝1代入，得a 2＋2×1＋b 2＝4，于是可得a 2＋b 2＝4－2＝2.。

平方差公式的几何解释师：刚才，我们大家运用多项式乘法法则证明了平方差公式。

那么，我们能否用图形来证明平方差公式呢，这可是我们从来没有做过的，我们可以大胆的试一试，看看从中你们能发现是吗。

师：大家拿起课前发的那张纸卡，同学观察一下纸卡是适马图形？生：正方形。

师：阴影部分呢？ a生：也是正方形。

b师：请你动手吧阴影部分剪掉，然后求出所剩面积是多少？同学先自己独立思考，然后在与小组同学交流。

（学生个人开始动手剪纸卡，并思考，之后与小组成员交流，5分钟）师：那个组先来在说说？生：我们组这样做：先设:大正方形的边长为a，再设小正方形的边长是b，然后用大正方形的面积减去小正方形的面积就是剩余面积。

先出计算式是：a2-b2.师：其他组还有其它方法吗？生：没有。

师：同学在动手做一做，用适马方法能证明我们求得的面积是正确的，然后总结一下从中你发现了适马。

这个问题有一定的难度，请小组合作完成。

（学生们开始合作学习，教师深入各组巡视指导。

大约15分钟，只剩下一个小组在还在讨论，其余小组都做好了交流准备。

）师：那个小组先来交流？生：我们小组把纸卡剩余部分剪成两个长方形，大家看，再把这两个长方形拼成一个长方形，求得的长方形的面积与剩余面积正好相等。

师：很好，请继续说出你们小组的字母表达式。

生：(a+b)(a-b)师：其他小组也是这么做的吗？生：这两种方法构成的式子正好是平方差公式，说明平方差公式是正确的。

师：你们还发现了适马呢？生：代数问题也可以用几何方法来证明。

师：同学们的这一方法太重要了。

这就是数形结合思想。

你们今天的表现太棒了。

初中代数定理公式证明由于您没有给出具体的初中代数定理公式，以下为您提供一些常见的初中代数定理公式及其证明资料（人教版）：一、一元二次方程的求根公式。

1. 定理内容。

对于一元二次方程ax^2+bx + c = 0(a≠0)，其求根公式为x=frac{-b±√(b^2)-4ac}{2a}。

2. 证明过程。

- 对于一元二次方程ax^2+bx + c = 0(a≠0)，我们首先进行配方。

- 方程两边同时除以a，得到x^2+(b)/(a)x+(c)/(a)=0。

- 移项可得x^2+(b)/(a)x =-(c)/(a)。

- 在等式左边加上((b)/(2a))^2进行配方，得到x^2+(b)/(a)x+((b)/(2a))^2=((b)/(2a))^2-(c)/(a)。

- 左边可以写成(x +(b)/(2a))^2，则(x+(b)/(2a))^2=frac{b^2}{4a^2}-(c)/(a)=frac{b^2-4ac}{4a^2}。

- 当b^2-4ac≥slant0时，两边开平方得x+(b)/(2a)=±frac{√(b^2)-4ac}{2a}。

- 移项可得x=frac{-b±√(b^2)-4ac}{2a}。

二、完全平方公式。

1. 定理内容。

(a + b)^2=a^2+2ab + b^2，(a - b)^2=a^2-2ab + b^2。

2. 证明过程。

- 对于(a + b)^2：- 根据乘法分配律(a + b)^2=(a + b)(a + b)=a(a + b)+b(a + b)。

- 展开得a^2+ab+ba + b^2=a^2+2ab + b^2。

- 对于(a - b)^2：- (a - b)^2=(a - b)(a - b)=a(a - b)-b(a - b)。

- 展开得a^2-ab - ba+b^2=a^2-2ab + b^2。

三、平方差公式。

1. 定理内容。

(a + b)(a - b)=a^2-b^2。

知识点060 平方差公式的几何背景（解答）1. 乘法公式的探究及应用（1）如图1，可以求出阴影部分的面积是a2-b2（写成两数平方差的形式）；（2）如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是a-b，长是a+b，面积是（a+b）（a-b）（写成多项式乘法的形式）；（3）比较图1、图2阴影部分的面积，可以得到公式（a+b）（a-b）=a2-b2；（4）运用你所得到的公式，计算下列各题：①10.2×9.8，②（2m+n-p）（2m-n+p）．考点：平方差公式的几何背景．专题：计算题．分析：（1）利用正方形的面积公式就可求出；（2）仔细观察图形就会知道长，宽由面积公式就可求出面积；（3）建立等式就可得出；（4）利用平方差公式就可方便简单的计算．解答：解：（1）利用正方形的面积公式可知：阴影部分的面积=a2-b2；（2）a-b，a+b，（a+b）（a-b）；（3）（a+b）（a-b）=a2-b2（等式两边交换位置也可）；（4）①解：原式=（10+0.2）×（10-0.2），=102-0.22，=100-0.04，=99.96；②解：原式=[2m+（n-p）]•[2m-（n-p）]，=（2m）2-（n-p）2，=4m2-n2+2np-p2．点评：此题主要考查了平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差，这个公式就叫做平方差公式．对于有图形的题同学们注意利用数形结合求解更形象直观．2. 如图是边长为a+2b的正方形（1）边长为a的正方形有1个（2）边长为b的正方形有4个（3）两边分别为a和b的矩形有4个（4）用不同的形式表示边长为a+2b的正方形面积，并进行比较写出你的结论．考点：平方差公式的几何背景；列代数式；完全平方式．分析：（1）（2）（3）根据图直接可以看出，（4）根据正方形的面积公式=边长×边长=（a+2b）（a+2b）=（a+2b）2，然后利用平方差公式把它展开又是另一种表现形式．解答：解：（1）由图可知边长为a的正方形只有一个；（2）由图可知边长为b的正方形有4个；（3）由图可知两边长分别为a和b的矩形有4个；（4）∵S边长为a+2b的正方形=（a+2b）2S边长为a+2b的正方形=a2+4b2+4ab；∴结论是（a+2b）2=a2+4b2+4ab．点评：本题主要考查了同学们的观察能力以及运用面积公式求正方形的面积．3. 如图1所示，边长为a的大正方形中有一个边长为b的小正方形，如图2是由图1中阴影部分拼成的一个长方形．（1）请你分别表示出这两个图形中阴影部分的面积：a2-b2、（a+b）（a-b）；（2）请问以上结果可以验证哪个乘法公式？平方差公式；（3）试利用这个公式计算：20092-2010×2008．考点：平方差公式的几何背景．分析：本题通过（1）中的面积=a2-b2，（2）中矩形的面积=（a+b）（a-b），并且两图形阴影面积相等，据此即可得出平方差公式，即a2-b2=（a+b）（a-b）．解答：解：（1）a2-b2（1分）；（a+b）（a-b）．（1分）（2）平方差公式．（2分）（3）20092-2010×2008，=20092-（2009+1）（2009-1），=20092-20092+1，=1．（4分）点评：本题主要考查了利用面积公式证明平方差公式，熟记公式结构是利用平方差公式解决实际问题．4. 乘法公式的探究及应用：（1）如图1所示，可以求出阴影部分的面积是a2-b2（写成两数平方差的形式）．（2）若将图1中的阴影部分裁剪下来，重新拼成一个如图2的矩形，此矩形的面积是（a+b）（a-b）（写成多项式乘法的形式）．（3）比较两图的阴影部分面积，可以得到乘法公式a2-b2=（a+b）（a-b）．（4）应用所得的公式计算：(1-1/22)(1-1/32)(1-1/42)…(1-1/992)(1-1/1002)．考点：平方差公式的几何背景．专题：探究型．分析：（1）利用面积公式：大正方形的面积-小正方形的面积=阴影面积；（2）利用矩形公式即可求解；（3）利用面积相等列出等式即可；（4）利用平方差公式简便计算．解答：解：（1）a2-b2；（2）（a+b）（a-b）；（3）a2-b2=（a+b）（a-b）；（4）原式=(1-1/2)(1+1/2)(1-1/3)(1+1/3)…(1-1/99)(1+1/99)(1-1/100)(1+1/100)，=1/2×3/2×2/3×4/3×…×98/99×100/99×99/100×101/100，=101/200．点评：本题综合考查了证明平方差公式和使用平方差公式的能力．5. 如图：大正方形的边长为a，小正方形的边长为b，利用此图证明平方差公式．考点：平方差公式的几何背景．专题：证明题．分析：由大正方形的面积-小正方形的面积=四个等腰梯形的面积，进而证得平方差公式．解答：解：根据题意大正方形的面积-小正方形的面积=a2-b2，四个等腰梯形的面积=1/2（a+b）（1/2a-1/2b）×4=（a+b）（a-b），故a2-b2=（a+b）（a-b）．点评：本题主要考查平方差公式的几何背景，不是很难．6. （1）如图1，可以求出阴影部分的面积是a2-b2（写成两数平方差的形式）；（2）如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是a-b，长是a+b，面积是（a-b）（a+b）（写成多项式乘法的形式）；（3）比较左、右两图的阴影部分面积，可以得到乘法公式（a+b）（a-b）=a2-b2（用式子表达）．考点：平方差公式的几何背景．分析：（1）中的面积=大正方形的面积-小正方形的面积=a2-b2；（2）中的长方形，宽为a-b，长为a+b，面积=长×宽=（a+b）（a-b）；（3）中的答案可以由（1）、（2）得到，（a+b）（a-b）=a2-b2．解答：解：（1）阴影部分的面积=大正方形的面积-小正方形的面积=a2-b2；（2）长方形的宽为a-b，长为a+b，面积=长×宽=（a+b）（a-b）；（3）由（1）、（2）得到，（a+b）（a-b）=a2-b2．点评：本题考查了平方差公式的几何表示，利用不同的方法表示图形的面积是解题的关键．7. 会说话的图形．如下图，把正方形的方块，按不同的方式划分，计算其面积，便可得到不同的数学公式．按图1所示划分，计算面积，便得到一个公式：（x+y）2=x2+2xy+y2．若按图2那样划分，大正方形则被划分成一个小正方形和两个梯形，通过计算图中的面积，请你完成下面的填空．（1）图2正方形的面积为x2；（2）图2中两个梯形的面积为1/2(x+y)(x-y)；（3）根据（1）和（2），你得到的一个数学公式为x2-y2=（x+y）（x-y）．考点：平方差公式的几何背景；完全平方公式的几何背景．专题：图表型．分析：本题的关键是仔细观察图形从图形中找到规律，按正方形，梯形的面积公式进行计算即可．解答：解：（1）图正方形的面积为x2；（2）两个梯形的面积分别为1/2（x+y）（x-y）；（3）则有x2-y2=2×1/2（x+y）（x-y）；即x2-y2=（x+y）（x-y）．故答案为：x2；1/2（x+y）（x-y）；x2-y2=（x+y）（x-y）．点评：本题考查了平方差公式的几何表示，通过数形结合，推导并验证了平方差公式．8. 请大家阅读下面两段材料，并解答问题：材料1：我们知道在数轴上表示4和1的两点之间的距离为3，（如图）而|4-1|=3，所以在数轴上表示4和1的两点之间的距离为|4-1|．再如在数轴上表示4和-2的两点之间的距离为6，（如图）而|4-（-2）|=6，所以数轴上表示数4和-2的两点之间的距离为|4-（-2）|．根据上述规律，我们可以得出结论：在数轴上表示数a 和数b 两点之间的距离等于|a-b|（如图）材料2：如下左图所示大正方形的边长为a ，小正方形的边长为b ，则阴影部分的面积可表示为：a2-b2．将上图中的左图重新拼接成右图，则阴影部分的面积可表示为（a+b ）（a-b ），由此可以得到等式：a2-b2=（a+b ）（a-b ），阅读后思考：（1）试一试，求在数轴上表示的数532与-441的两点之间的距离为91211； （2）请用材料2公式计算：（4998）2-（4991）2=77； （3）上述两段材料中，主要体现了数学中数形结合的数学思想．考点：平方差公式的几何背景；数轴．专题：阅读型；数形结合．分析：（1）首先理解材料1的题意，利用它的公式即可求结果；（2）利用平方差公式把题目展开成平方差公式的形式，然后根据有理数的加法法则计算，并且这样计算比较简便；（3）此题把图形和数的计算结合起来，所以容易知道利用的数学思想．解答：解：（1）数532与-441的两点之间的距离为|532+441|=91211； （2）（4998）2-（4991）2=(4998+4991)(4998-4991)=77； （3）数形相结合．故答案为：91211，77，数形结合． 点评：本题考查了平方差公式的几何表示，关键是理解题意，才能根据题目的公式进行计算，此题还考查了数形结合的思想．9. 如图1所示大正方形的边长为a ，小正方形的边长为b ，则阴影部分的面积可表示为：a2-b2，将图1中的图形重新拼接成图2，则阴影部分的面积可表示为（a-b ）（a+b ），这样可以得到等式：a2-b2=（a-b ）（a+b ）．请用此公式计算：（99998）2-（99991）2考点：平方差公式的几何背景．分析：图1阴影部分的面积=大正方形的面积-小正方形的面积，图2阴影部分的面积根据矩形面积公式即可得出，根据阴影部分的面积相等可得等式．计算题直接利用公式即可． 解答：解：a2-b2，（a-b ）（a+b ），a2-b2=（a-b ）（a+b ）；（99998）2-（99991）2 =（99998+99991）（99998-99991）， =1000×99997， =98998000． 点评：本题利用组合图形考查平方差公式，计算题较为简单，直接利用公式即可．做题时认真观察图形，找到各部分的面积及两面积相等是解决本题的关键．10. 如图，在边长为a 的正方形中剪去一个边长为b 的小正方形（ ），把剩下部分拼成一个梯形，通过计算这两个图形阴影部分的面积，可验证公式为？考点：平方差公式的几何背景．分析：要求可验证的公式，可分别求出两个图形的面积，令其相等，即可得出所验证的公式． 解答：解：在边长为a 的正方形中剪去一个边长为b 的小正方形，剩余面积为a •a-b •b=a2-b2图中梯形的上底为2b ，下底为2a ，高为a-b ，∴梯形的面积为1/2(2a+2b)(a-b)=（a+b ）（a-b ），∴可验证的公式为a2-b2=（a+b ）（a-b ）．点评：本题考查了平方差公式的几何意义，用不同的方法求阴影部分的面积是解题的关键，考法较新颖．11. 如图，小刚家有一块“L ”形的菜地，要把这块菜地按图示那样分成面积相等的梯形，种上不同的蔬菜，这两个梯形的上底都是xm，下底都是ym，高都是（y-x）m，请你帮小刚家算一算菜地的面积是y2-x2平方米．当x=20m，y=30m时，面积是500平方米．考点：平方差公式的几何背景．分析：本题结合图形，根据梯形的面积公式=1/2（上底+下底）×高，列出菜地的面积，再运用平方差公式计算．解答：解：由题意得菜地的面积为2×1/2（x+y）（y-x）=y2-x2．当x=20，y=30时，y2-x2=302-202=900-400=500m2．故答案为：y2-x2；500．点评：本题考查了平方差公式的几何表示，计算菜地的面积时，也可运用边长为y的正方形的面积减去边长为x的正方形的面积求得，这样更为简单．12. 如图，有一位狡猾的地主，把一块边长为a的正方形的土地，租给老汉种植，他对老汉说：“我把你这块地的一边减少4m，另一边增加4m，继续租给你，你也没有吃亏，你看如何”．老汉一听，觉得自己好像没有吃亏，就答应了．同学们，你们觉得老汉有没有吃亏？请说明理由．考点：平方差公式的几何背景．分析：本题只要利用面积公式，再利用平方差公式计算就可知．解答：解：老汉吃亏了．理由：原来的种植面积为a2，变化后的种植面积为（a+4）（a-4）=a2-16，因为a2＞a2-16，所以老汉吃亏了．点评：本题考查了平方差公式在实际生活中的运用，只有利用平方差公式计算后才能做出正确的判断．13. （1）通过观察比较左、右两图的阴影部分面积，可以得到乘法公式为（a-b）（a+b）．（用式子表达）（2）运用你所学到的公式，计算下列各题：①1022②103×97．考点：平方差公式的几何背景；完全平方公式；平方差公式．分析：（1）本题需先根据图中所给的数据，再根据面积公式进行计算，再与两边的图形进行比较，即可求出答案．（2）本题需先根据平方差公式的求法，分别进行计算，即可求出答案．解答：解：（1）根据题意得：S=a2-b2=（a-b）（a+b）．（2）①1022=（100+2）2=1002+400+4=10404，②103×97=（100+3）（100-3）=1002-32=9991．点评：本题主要考查了平方差公式的几何表示，表示出图形阴影部分面积是解题的关键．14. 我们已经知道利用图形中面积的等量关系可以得到某些数学公式，如图一，我们可以得到两数差的完全平方公式：（a-b）2=a2-2ab+b2（1）请你在图二中，标上相应的字母，使其能够得到两数和的完全平方公式（a+b）2=a2+2ab+b2，（2）图三是边长为a的正方形中剪去一个边长为b的小正方形，剩下部分拼成图四的形状，利用这两幅图形中面积的等量关系，能验证公式a2-b2=（a+b）（a-b）；（3）除了拼成图四的图形外还能拼成其他的图形能验证公式成立，请试画出一个这样的图形，并标上相应的字母．考点：平方差公式的几何背景；完全平方公式的几何背景．专题：作图题．分析：（1）此题只需将大正方形的边长表示为a，小正方形的边长表示为b即可，（2）此题只需将两个图形的面积表示出来写成等式即可；（3）此题还可以拼成一个矩形来验证公式的成立．解答：解：（1）．（2）根据两图形求得两图形的面积分别为：S1=a2-b2；S2=12（2a+2b）（a-b）=（a+b）（a-b）（3）拼成的图形如下图所示：点评：本题考查了平方差公式及完全平方式的几何背景，考查的围比较广．15. 如图，在边长为a的正方形的一角是一个边长为b的正方形，请用这个图形验证公式：a2-b2=（a+b）（a-b）．考点：平方差公式的几何背景．专题：计算题．分析：利用正方形的面积减去小正方形的面积，即为所剩部分的面积．解答：解：由图可知：大正方形的面积-小正方形的面积=剩余部分的面积，∴a2-b2=（a-b）b+（a-b）a=（a+b）（a-b），即a2-b2=（a+b）（a-b）．点评：此题主要考查了乘法的平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差，这个公式就叫做平方差公式．16. （1）如图甲所示，可得阴影部分的面积是a2-b2（写成多项式的形式）；（2）如图乙所示，若将阴影部分裁剪下来重新拼成一个长方形，它的长是a+b，宽是a-b ，面积是（a+b）（a-b）（写成两式乘积形式）；（3）比较图甲和图乙中阴影部分的面积，可得乘法公式（a+b）（a-b）=a2-b2；（4）利用公式计算（-2x+y）（2x+y）=y2-4x2．考点：平方差公式的几何背景．专题：计算题．分析：（1）利用正方形的面积公式就可求出；（2）仔细观察图形就会知道长，宽由面积公式就可求出面积；（3）建立等式就可得出；（4）利用平方差公式就可方便简单的计算．解答：解：（1）利用正方形的面积公式可知：阴影部分的面积=a2-b2；（2）a+b，a-b，（a+b）（a-b）；（3）（a+b）（a-b）=a2-b2（等式两边交换位置也可）；（4）①原式=（10+0.2）×（10-0.2），=102-0.22，=100-0.04，=99.96；②原式=（y+2x）（y-2x）=（y）2-（2x）2，=y2-4x2．故答案是：（1）a2-b2（2）a-b，a+b，（a+b）（a-b）；（3）（a+b）（a-b）=a2-b2（4）y2-4x2．点评：此题主要考查了平方差公式．即两个数的和与这两个数的差的积等于这两个数的平方差，这个公式就叫做平方差公式．对于有图形的题同学们注意利用数形结合求解更形象直观．17. 乘法公式的探究及应用．（1）如左图，可以求出阴影部分的面积是a2-b2（写成两数平方差的形式）；（2）如右图，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是a-b，长是a+b，面积是（a+b）（a-b）．（写成多项式乘法的形式）（3）比较左、右两图的阴影部分面积，可以得到乘法公式（a+b）（a-b）=a2-b2．（用式子表达）（4）运用你所得到的公式，计算下列各题：①10.3×9.7②（2m+n-p）（2m-n+p）考点：平方差公式的几何背景．分析：（1）利用大正方形面积减去小正方形面积即可求出；（2）根据图形中长方形长与宽求出即可；（3）结合（1）（2）即可得出（a+b）（a-b）=a2-b2；（4）利用平方差公式进行运算即可，注意符合（a+b）（a-b）=a2-b2的形式才能运算．解答：解：（1）利用大正方形面积减去小正方形面积即可求出：a2-b2；（2）它的宽是a-b，长是a+b，面积是（a+b）（a-b）；（3）根据题意得出：（a+b）（a-b）=a2-b2；（4）①10.3×9.7=（10+0.3）（10-0.3）=100-0.09=99.91；②（2m+n-p）（2m-n+p）=[2m+（n-p）][2m-（n-p）]=4m2-（n-p）2=4m2-n2-p2+2np．点评：此题主要考查了平方差公式的几何背景，利用图形面积得出公式是近几年中考中考查重点，同学们应重点掌握．18. 如图所示，有一位狡猾的老账主，把一块边长为a米（a＞30）的正方形土地给老汉种植．隔了一年，他对老汉说：“我把你这块地的一边减少5米，另一边增加5米，继续租给你，你也没有吃亏，你看如何？”老汉一听，觉得好像没有吃亏，就答应了．你觉得老汉有没有吃亏呢？请说明理由．考点：平方差公式的几何背景．专题：几何图形问题．分析：本题只要利用面积公式，再利用平方差公式计算就可知．解答：解：老汉吃亏了．因为他原来所租地的面积为a2平方米，而后经过割补，面积变为（a+5）（a-5）=a2-25（平方米）所以，他实际是少25平方米．因此，他吃亏了．点评：本题考查了平方差公式在实际生活中的运用，只有利用平方差公式计算后才能做出正确的判断．19. 如图：边长为a的大正方形中有一个边长为b的小正方形．（1）通过观察①、②两图的阴影部分面积，可以得到的乘法公式为a2-b2=（a-b）（a+b）；（用式子表达）（2）运用你所得到的公式，计算：102×98（不用公式计算不得分）考点：平方差公式的几何背景．专题：计算题．分析：（1）图1阴影部分的面积=大正方形的面积-小正方形的面积，图2阴影部分的面积根据矩形面积公式即可得出，根据阴影部分的面积相等可得等式．（2）计算题直接利用平方差公式即可．解答：解：（1）图1阴影部分的面积a2-b2，图2阴影部分的面积（a-b）（a+b），则a2-b2=（a-b）（a+b）．故答案为：a2-b2=（a-b）（a+b）；（2）102×98=（100+2）（100-2）=1002-22=10000-4=9996．点评：本题利用组合图形考查平方差公式，计算题较为简单，直接利用公式即可．做题时认真观察图形，找到各部分的面积及两面积相等是解决本题的关键．20. 如图阴影部分，是边长为4cm的正方形纸片，在它的中心剪去一个边长为2.5cm的正方形小纸片得到的，请尝试用最简便方法作一个长方形使其面积等于图中阴影部分的面积．考点：平方差公式的几何背景．专题：计算题．分析：如图，将阴影部分沿虚线剪开，以4+2.5=6.4cm为长，4-2.51.5cm为宽，作出与阴影部分面积相等的长方形．解答：解：如图，作长为6.5cm，宽为1.5cm的长方形；理由：42-2.52=（4+2.5）（4-2.5）=6.5×1.5．点评：本题考查了平方差公式的几何背景．关键是通过将面积合理的分割，解释平方差公式．21. 如图：边长为a，b的两个正方形的中心重合，边保持平行，如果从大正方形中剪去小正方形，剩下的图形可以分割成4个大小相等的等腰梯形．请你用a，b表示出梯形的高和面积，并由此说明a2-b2=（a+b）（a-b）的几何意义．考点：平方差公式的几何背景．分析：根据图形可得等腰梯形的高为1/2（a-b），根据大正方形的面积减去小正方形的面积可作出说明．解答：解：梯形的高=1/2（a-b），面积=1/4（a+b）（a-b），∴a2-b2=（a+b）（a-b）的几何意义是大正方形的面积减去小正方形的面积．点评：本题考查平方差公式的几何背景，属于比较简单的题目，解答本题的关键是正确的求出等腰梯形的高．22. 如图，边长为a的大正方形有一个边长为b的小正方形．（1）阴影部分面积是a2-b2．（2）小欣把阴影部分的两个四边形拼成如图6所示的长方形，则这个长方形的宽是a-b面积是（a+b）（a-b）．（3）由此可验证出的结论是（a+b）（a-b）=a2-b2．考点：平方差公式的几何背景．专题：计算题．分析：（1）边长为a的正方形的面积减去边长为b的正方形的面积即可；（2）根据图形求出长方形的长和宽，根据面积公式求出即可；（3）根据阴影部分的面积相等求出即可．解答：解：（1）图中阴影部分的面积是：a2-b2，故答案为：a2-b2．（2）由图象可知：这个长方形的宽是：a-b，长方形的面积是：（a+b）（a-b），故答案为：a-b，（a+b）（a-b）．（3）根据阴影部分的面积相等，∴（a+b）（a-b）=a2-b2，故答案为：（a+b）（a-b）=a2-b2．点评：本题考查了平方差公式的应用，解此题的关键是能根据面积公式求出各个部分的面积，题型较好，难度适中，是一道不错的题目，通过此题能培养学生的观察能力.23. 用四块长为acm、宽为bcm的矩形材料（如图1）拼成一个大矩形（如图2）或大正方形（如图3），中间分别空出一个小矩形A和一个小正方形B．（1）求（如图1）矩形材料的面积；（用含a，b的代数式表示）（2）通过计算说明A、B的面积哪一个比较大；（3）根据（如图4），利用面积的不同表示方法写出一个代数恒等式．考点：平方差公式的几何背景．专题：几何图形问题．分析：（1）根据矩形的面积公式可得出答案．（2）分别求出矩形的长和宽，求出正方形的边长，从而计算出面积即可作出比较．（3）求出新形成的矩形的长和宽，根据面积相等即可得出答案．解答：解：（1）S=长×宽=ab；（2）根据图形可得：矩形的长=（2b+a），宽=a；正方形的边长=a+b，矩形的面积=2ab+a2，正方形的面积=a2+2ab+b2，正方形面积-矩形的面积=b2，∴矩形的面积大；（3）根据图形可得：a2-b2=（a-b）（a+b）．点评：本题考查平方差公式的背景，难度不大，运用几何直观理解、解决平方差公式的推导过程，通过几何图形之间的数量关系对平方差公式做出几何解释．24. （1）比较左、右两图的阴影部分面积，可以得到乘法公式（a+b）（a-b）=a2-b2（用式子表达）．（2）运用你所得到的公式，计算（a+2b-c）（a-2b-c）．考点：平方差公式的几何背景；完全平方公式的几何背景．分析：（1）首先利用平行四边形与正方形面积求解方法表示出两个图形中的阴影部分的面积，又由两图形阴影面积相等，即可得到答案．（2）利用平方差公式就可简单的计算．注意将a-c看作一个整体．解答：解：（1）（a+b）（a-b）=a2-b2（2分）；故答案为：（a+b）（a-b）=a2-b2．（2）（a+2b-c）（a-2b-c），=[（a-c）+2b][（a-c）-2b]，=（a-c）2-（2b）2，=a2-2ac+c2-4b2．（8分）点评：本题主要考查了平方差公式的几何表示，表示出图形阴影部分面积是解题的关键．注意可以从第2个图形得出平行四边形的高．25. （1）小思同学用如图所示的A、B、C三类卡片若干，拼出了一个长为2a+b宽为a+b长方形图形．请你求出小思同学拼这个长方形所用A、B、C三类卡片各几（要求：所拼图形中，卡片之间不能重叠，不能有空隙）．（2）小明同学用四长为x、宽为y的长方形卡片，拼出如图所示的包含两个正方形的图形（任两相邻的卡片之间没有重叠，没有空隙）．①图中小正方形的边长是x-y②通过计算小正方形面积，可推出（x+y）2，xy，（x-y）2三者的等量关系式为：（x+y）2-（x-y）2=4xy③参用②中的结论，试求：当a+b=6，ab=7时（a-b）2的值．考点：平方差公式的几何背景；完全平方公式；矩形的性质；正方形的性质．专题：计算题；图表型．分析：（1）根据长方形的面积公式求出拼接后的长方形的面积，再利用多项式的乘法运算法则进行计算，然后根据系数即可得解；（2）①根据图形中正方形的大正方形的边长解答；②根据大正方形的面积减去小正方形的面积等于四个长方形的面积解答；③代入②的结论进行计算即可．解答：解：（1）（2a+b）（a+b）=2a2+2ab+ab+b2=2a2+3ab+b2；∵A、B、C三类卡片的面积分别为ab、b2、a2，∴所以A、B、C三类卡片分别为3，1，2；（2）①小正方形的边长是x-y；②大正方形的面积为（x+y）2，四周四个小长方形的面积为4xy，中间小正方形的面积为（x-y）2，∴（x+y）2-（x-y）2=4xy；③根据②，∵a+b=6，ab=7，∴（a-b）2=（a+b）2-4ab=62-4×7=36-28=8．点评：本题考查了平方差公式的几何背景以及完全平方公式，矩形的面积公式，利用面积的不同表示求解进行解答是解题的关键，也是此类题目常用的方法之一．。

平方差公式的证明平方差公式，这可是数学里的一个重要小宝贝！它的表达式是：(a+ b)(a - b) = a² - b²。

那咱们就来好好唠唠这个公式是咋被证明的。

咱先从简单的乘法运算入手哈。

比如说，（3 + 2）×（3 - 2），按照正常的乘法规则，咱们一步一步来。

先算第一个括号里的 3 + 2 ，那就是 5 。

再算第二个括号里的 3 - 2 ，结果是 1 。

最后 5 乘以 1 ，得出 5 。

那咱们再按照平方差公式来算算。

这里的 a 就是 3 ，b 就是 2 。

公式说（a + b）（a - b） = a² - b²，那就是 3² - 2²，3 的平方是 9 ，2 的平方是 4 ，9 - 4 ，可不就是 5 嘛！你看，这两种算法结果一样，这就初步验证了平方差公式的正确性。

咱们再深入点儿，用代数的方法来证明。

（a + b）（a - b），展开这个式子，就是 a×a - a×b + a×b - b×b 。

中间的 - a×b 和 + a×b 一抵消，可不就剩下 a² - b²了嘛！这就好比你去超市买东西，你买了 a 元的苹果和 b 元的香蕉，然后超市搞活动，买苹果送 b 元，买香蕉减 a 元。

最后你实际花的钱，就是买苹果的钱减去买香蕉优惠的钱，也就是 a² - b²。

我还记得有一次给学生讲这个平方差公式，有个小家伙特别较真儿，非说不相信这个公式能在所有情况下都成立。

我就笑着跟他说：“那咱们来多做几道题试试呗！”结果做了好几道，每一道用平方差公式一算，答案都对得死死的。

这小家伙最后服气啦，还说：“老师，这公式真厉害！”其实啊，平方差公式在我们生活中也有不少用处呢。

比如说，你要给一个长方形的花坛铺地砖，长是 a 米，宽是 b 米，如果要把宽增加一点变成（b + x）米，长减少一点变成（a - x）米，那面积的变化就可以用平方差公式来算啦。

平方差公式的推导过程用代数法
假设我们要求解两个数的平方之差，假设这两个数分别为a和b，即我们要求a^2-b^2
首先，我们可以将a^2-b^2进一步分解成(a+b)(a-b)。

这是平方差公式的核心思想之一
我们来证明一下：
展开(a+b)(a-b)得到 a^2 - ab + ab - b^2，简化后得到 a^2 - b^2所以，我们证明了a^2-b^2可以分解成(a+b)(a-b)。

接下来，我们将对上述证明进行代数推导，具体如下：
1.已知a^2-b^2=(a+b)(a-b)。

2.先展开右边的乘法：
(a+b)(a-b)=a(a-b)+b(a-b)。

= a^2 - ab + ab - b^2
=a^2-b^2
所以，(a+b)(a-b)=a^2-b^2
通过上述代数推导过程，我们证明了平方差公式的正确性。

即a^2-b^2可以分解成(a+b)(a-b)。

总结起来，平方差公式的推导过程可以通过代数法来完成，将a^2-b^2分解为(a+b)(a-b)。

通过代数推导可以证明平方差公式的正确性。

平方差公式证明过程
嘿，咱今天来聊聊平方差公式的证明过程啊！平方差公式，那可是数学里超级重要的家伙呢！就像一把神奇的钥匙，能打开好多难题的大门。

咱先从代数角度来看。

(a+b)(a-b)，这就是平方差公式的样子啦。

把它展开，哇塞，就得到了a²-b²。

这感觉就像是变魔术一样，一下子就出来了。

你说神奇不神奇？
再想象一下，这就好比搭积木，(a+b)和(a-b)就是两块特别的积木，它们一组合，就搭出了a²-b² 这个漂亮的造型。

这可不是随便就能做到的哦，这里面蕴含着深深的数学智慧呢！
然后咱从几何角度来瞧瞧。

画一个边长为 a 的正方形，然后在一边减去一个边长为 b 的小正方形。

这时候，剩下的部分不就是(a+b)(a-b)嘛。

再仔细看看，那大块的面积不就是a²，小块的面积不就是b²，两者一减，不就是平方差公式嘛！是不是恍然大悟？
哎呀，这平方差公式的证明过程，真的是太有意思啦！它就像一个隐藏在数学世界里的宝藏，等着我们去发现和挖掘。

所以啊，平方差公式真的是超级厉害的，它在数学中有着广泛的应用，能帮我们解决好多问题呢！这证明过程不就是数学之美的体现吗？我们一定要好好掌握它呀！。

数形结合平方差公式
我们要证明平方差公式：a^2 - b^2 = (a + b)(a - b)。

首先，我们可以通过数形结合的方法来理解这个公式。

假设我们有一个正方形，边长为a。

如果我们从正方形中减去一个边长为b的小正方形，那么剩余的部分可以表示为：a^2 - b^2。

现在，如果我们把剩余的部分重新组合，它实际上是一个大的矩形，这个矩形的长度是a+b，宽度是a-b。

所以，这个大矩形的面积是：(a + b)(a - b)。

由于这两个面积是相等的（一个是正方形减去小正方形，另一个是大矩形），我们可以得出：
a^2 - b^2 = (a + b)(a - b)。

这样，我们就通过数形结合的方法证明了平方差公式。

浅谈平方差公式和应用比例的推广平方差公式和应用比例是数学中非常重要的概念和工具，它们在各种数学问题和实际应用中起着重要作用。

本文将从浅显的角度对平方差公式和应用比例进行讨论，并探讨其在实际问题中的推广和应用。

一、平方差公式平方差公式是数学中常见的一个重要公式，它描述了两个数的平方之差与它们的和的关系。

具体表达式如下：(a+b)² = a² + 2ab + b²这两个公式分别描述了两个数的和的平方和差的平方与它们自身的关系。

平方差公式在代数中有着广泛的应用，可以用来简化计算，化简公式，求解各种方程和不等式等。

平方差公式还有一个重要的应用，就是在几何中计算点的坐标之间的距离。

通过平方差公式，我们可以求解两点之间的距离，为几何问题的解决提供了便利。

平方差公式还可以应用在物理学中。

比如在力学中，可以通过平方差公式来进行速度、加速度等问题的求解，提高问题的求解效率。

二、应用比例比例是一个很基础的数学概念，它描述了两个量之间的关系。

应用比例在很多实际问题中都有着广泛的应用，在商业、工程、科学等领域都起着重要作用。

在商业中，比例常常用来描述产品的成本和售价之间的关系，通过比例可以计算利润率、成本占比等问题。

比例在市场调研、商品定价等领域有着非常重要的应用。

在工程中，比例也是一个重要的工具。

在建筑设计中，比例可以用来确定建筑物的尺寸、比例尺相关的问题。

在机械设计中，比例可以用来计算零部件之间的比例关系，保证装配的准确性。

在科学中，比例也有广泛的应用。

在实验中，比例可以用来描述实验数据之间的关系，通过分析比例可以得出很多实验规律和结论。

在地理学、生物学等学科中，比例也有着广泛的应用，比如地图的比例尺、生物种群的比例关系等问题。

平方差公式和应用比例虽然是数学中的基础概念和工具，但是它们在实际问题中的应用是非常广泛的。

我们可以通过推广和拓展它们的应用，进一步提高它们的实际价值。

对于平方差公式，我们可以考虑将它应用到更多的实际问题中。

平方差公式的结构特征平方差公式是高中数学中一个十分重要的公式，它是用来计算两个数的平方和与平方差之间的关系的。

在本文中，将从几何角度、代数角度和推广角度三个方面来探讨平方差公式的结构特征。

从几何角度来看，平方差公式的结构特征主要表现为以下三个方面：一，平方和可以表示为从原点到各点的距离的平方之和。

假设有两个点A(x1,y1)和B(x2,y2)，它们之间的距离可以表示为d=√[(x2-x1)²+(y2-y1)²]。

那么，如果有三个点A(x1,y1)、B(x2,y2)和C(x3,y3)，则它们之间的距离的平方和为d(A,B)²+d(B,C)²+d(A,C)²=2(x1²+x2²+x3²+y1²+y2²+y3²)-(x1x2+x2x3+x1x3+y1y2+y2y3+y1y3)。

可见，平方和的结构特征是用坐标表示为每个点到原点的距离的平方和。

二，平方差可以表示为两点到原点的距离之差和它们之间的距离的平方。

如果有两个点A(x1,y1)和B(x2,y2)，则它们之间的距离可以表示为d=√[(x2-x1)²+(y2-y1)²]，它们到原点的距离分别为r1=√(x1²+y1²)和r2=√(x2²+y2²)，则它们的平方差为(r1-r2)²+d²/2-[(r1+r2)²-d²/2]/2=x1x2+y1y2。

由此可见，平方差的结构特征是将两个向量的点乘作为一个几何量。

三，平方和与平方差之间的关系可以通过勾股定理来解释。

如果三角形ABC为直角三角形，其中∠ACB=90°，则有AB²=AC²+BC²。

同样，如果有两个向量a和b，则有(a+b)²=(a-b)²+4ab，即平方和等于平方差加上两倍的点乘。

平方差公式起源一、引言平方差公式是数学中的一个重要定理，用于计算两个数的平方差。

它被广泛应用于代数、几何和物理等领域，在解决实际问题中起着重要作用。

本文将从历史的角度出发，探讨平方差公式的起源及其相关背景。

二、古希腊数学的发展古希腊是数学发展的重要时期，许多数学定理和公式都起源于那个时代。

在古希腊，数学被认为是一种哲学的表达方式，受到了许多思想家的重视。

其中，毕达哥拉斯学派对平方差公式的发展起到了重要的推动作用。

三、毕达哥拉斯学派的贡献毕达哥拉斯学派是古希腊数学的重要学派之一，将数学与几何相结合，提出了许多重要的数学理论。

其中，平方差公式就是毕达哥拉斯学派的一项重要贡献。

四、平方差公式的推导平方差公式的推导主要是通过几何方法进行的。

我们可以从一个正方形开始，然后将其分割成若干个小正方形和矩形，再进行面积计算，最终得到平方差公式的表达式。

五、平方差公式在代数中的应用平方差公式在代数中有许多应用，特别是在因式分解和方程求解中。

通过平方差公式，我们可以将一个二次方程转化为一个一次方程，从而简化计算过程。

六、平方差公式在几何中的应用除了代数，平方差公式在几何中也有广泛的应用。

例如，在计算正方形的对角线长度时，我们可以利用平方差公式进行计算，从而简化问题的求解过程。

七、平方差公式在物理中的应用在物理学中，平方差公式也有许多应用。

例如，在计算速度的平方差时，我们可以利用平方差公式进行计算，从而得到更精确的结果。

八、结语通过对平方差公式的起源和应用进行探讨，我们可以看到它在数学、几何和物理等领域的重要性。

它不仅简化了计算过程，而且为解决实际问题提供了有效的方法。

相信通过深入研究和应用，平方差公式将发挥更大的作用，促进各个领域的发展。

九、参考文献[1] 陈红. 数学分析与应用[M]. 科学出版社, 2008.[2] 高亚峰, 赵士军. 数学分析教程[M]. 高等教育出版社, 2007.[3] 黄依梅. 数学分析(第三版)[M]. 高等教育出版社, 2007.。