《有限元基础教程》_【MATLAB算例】3.3.7(2)__三梁平面框架结构的有限元分析(Beam2D2Node)

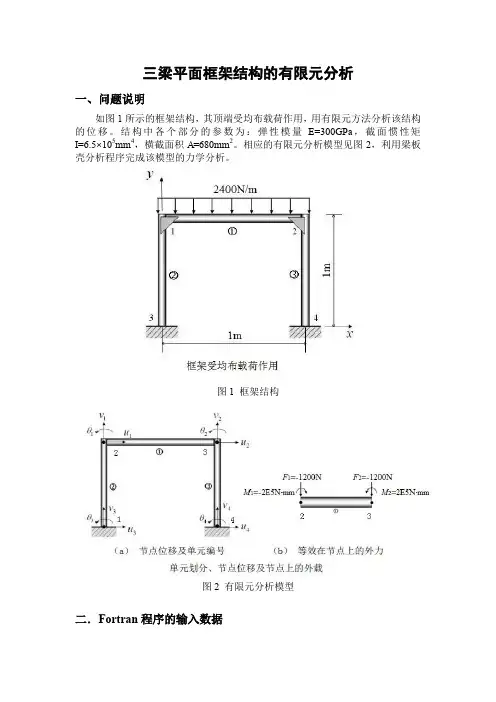
三梁平面框架结构的有限元分析一、问题说明如图1所示的框架结构，其顶端受均布载荷作用，用有限元方法分析该结构的位移。

结构中各个部分的参数为：弹性模量E=300GPa，截面惯性矩I=6.5×105mm4，横截面积A=680mm2。

相应的有限元分析模型见图2，利用梁板壳分析程序完成该模型的力学分析。

图1框架结构图2有限元分析模型二．Fortran程序的输入数据（1）Facile.11 4 3 6 0 12 42 1 11 1 11 3 51 2 2 3 3 40 0 0 0 1000 01000 1000 0 1000 0 0（2）Facile.2111 211 1111 0 0 0 1 03E5 1.6E5680 6.5E5 6.5E5 6.5E50 0（3）Facile.312 41 02 03 04 05 06 0 19 0 20 0 21 0 22 023 0 24 08 -1200 12 -200000 14 -1200 18 200000输出的数据文件为：Facile7和Facile8，其中各节点位移结果在文件Facile8中。

三．计算结果各节点的位移计算结果见表1。

四．Ansys分析结果Ansys计算结果如下图所示，图3为节点x方向的位移云图，图4为节点y 方向的位移云图，图5为节点转角云图。

图3 节点x方向的位移图4 节点y方向的位移图5 节点转角各节点的位移值见表2。

五．结果对比通过对比表1和表2中的数据可以发现，Fortran程序与Ansys分析的结果十分接近。

matlab有限元三单元编程MATLAB是一种功能强大的编程语言和环境，广泛用于工程和科学领域的数值计算、数据分析和可视化。

在有限元分析中，MATLAB的强大功能和直观的语法使其成为一个理想的选择。

在本文中，我们将讨论MATLAB中有限元三单元的编程方法和实践。

有限元分析是一种数值方法，用于解决连续介质的力学问题。

它将一个复杂的结构分解成更简单的有限元单元，然后通过求解线性代数方程组来得到结构的应力和位移解。

在有限元分析中，三角形和四边形单元是最常用的有限元单元之一。

本文将重点讨论三角形单元的编程实现。

首先，我们需要定义一个三角形单元的几何信息。

在三角形单元中，我们有三个顶点，每个顶点有两个坐标。

我们可以使用一个3x2的矩阵来表示这些坐标。

例如，定义三角形ABC的顶点坐标矩阵为P：P = [x_A, y_A;x_B, y_B;x_C, y_C];接下来，我们需要定义三角形单元的连接性信息。

在MATLAB中，我们可以使用一个3x1的向量来表示三个顶点的连接性。

例如，定义三角形ABC的连接性向量为E：E = [1;2;3];然后，我们可以定义三角形单元材料属性和载荷信息。

这些信息包括杨氏模量、泊松比和外力向量。

我们可以将这些信息存储在一个结构体中，例如：properties.E = 210e9; % 杨氏模量properties.v = 0.3; % 泊松比properties.f = [0; -1000; 0]; % 外力向量接下来，我们可以使用这些信息来计算三角形单元的刚度矩阵和力向量。

刚度矩阵是一个3x3的矩阵，力向量是一个3x1的向量。

我们可以使用以下公式来计算它们：K = (E/(1-v^2)) * [1 v 0;v 1 0;0 0 (1-v)/2] * A;f = (A/3) * [1; 1; 1] * properties.f;其中，A是三角形的面积。

我们可以使用以下公式来计算它：A = abs(det([1, 1, 1;x_A, x_B, x_C;y_A, y_B, y_C])) / 2;最后，我们可以使用这些信息来求解三角形单元的位移解。

有限元分析基础教程前言有限元分析已经在教学、科研以及工程应用中成为重要而又普及的数值分析方法和工具；该基础教程力求提供具备现代特色的实用教程。

在教材的内容体系上综合考虑有限元方法的力学分析原理、建模技巧、应用领域、软件平台、实例分析这几个方面，按照教科书的方式深入浅出地叙述有限元方法，并体现出有限元原理“在使用中学习，在学习中使用”的交互式特点，在介绍每一种单元的同时，提供完整的典型推导实例、MATLAB实际编程以及ANSYS应用数值算例，并且给出的各种类型的算例都具有较好的前后对应性，使学员在学习分析原理的同时，也进行实际编程和有限元分析软件的操作，经历实例建模、求解、分析和结果评判的全过程，在实践的基础上深刻理解和掌握有限元分析方法。

一本基础教材应该在培养学员掌握坚实的基础理论、系统的专业知识方面发挥作用，因此，教材不但要提供系统的、具有一定深度的基础理论，还要介绍相关的应用领域，以给学员进一步学习提供扩展空间，本教程正是按照这一思路进行设计的；全书的内容包括两个部分，共分9章；第一部分为有限元分析基本原理，包括第1章至第5章，内容有：绪论、有限元分析过程的概要、杆梁结构分析的有限元方法、连续体结构分析的有限元方法、有限元分析中的若干问题讨论；第二部分为有限元分析的典型应用领域，包括第6章至第9章，内容有：静力结构的有限元分析、结构振动的有限元分析、传热过程的有限元分析、弹塑性材料的有限元分析。

在基本原理方面，以基本变量、基本方程、求解原理、单元构建等一系列规范的方式进行介绍；在阐述有限元分析与应用方面，采用典型例题、MATLAB程序及算例、ANSYS算例的方式，以体现出分析建模的不同阶段和层次，引导学员领会有限元方法的实质，还提供有大量的练习题。

本教程的重点是强调有限元方法的实质理解和融会贯通，力求精而透，强调学员综合能力(掌握和应用有限元方法)的培养，为学员亲自参与建模、以及使用先进的有限元软件平台提供较好的素材；同时，给学员进一步学习提供新的空间。

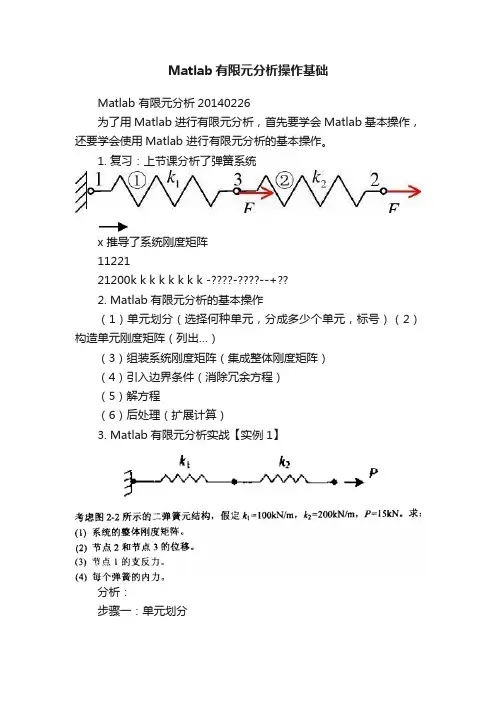
Matlab有限元分析操作基础Matlab 有限元分析20140226为了用Matlab 进行有限元分析，首先要学会Matlab 基本操作，还要学会使用Matlab 进行有限元分析的基本操作。

1. 复习：上节课分析了弹簧系统x 推导了系统刚度矩阵1122121200k k k k k k k k ----+??2. Matlab有限元分析的基本操作（1）单元划分（选择何种单元，分成多少个单元，标号）（2）构造单元刚度矩阵（列出…）（3）组装系统刚度矩阵（集成整体刚度矩阵）（4）引入边界条件（消除冗余方程）（5）解方程（6）后处理（扩展计算）3. Matlab有限元分析实战【实例1】分析：步骤一：单元划分步骤二：构造单元刚度矩阵>>k1=SpringElementStiffness(100) >>…?步骤三：构造系统刚度矩阵a) 分析SpringAssemble库函数function y = SpringAssemble(K,k,i,j)% This function assembles the element stiffness% matrix k of the spring with nodes i and j into the % global stiffness matrix K.% function returns the global stiffness matrix K% after the element stiffness matrix k is assembled. K(i,i) = K(i,i) + k(1,1);K(i,j) = K(i,j) + k(1,2);K(j,i) = K(j,i) + k(2,1);K(j,j) = K(j,j) + k(2,2);y = K;b) K是多大矩阵？今天的系统刚度矩阵是什么？因为11221212k kk kk k k k----+所以10001000200200 100200300----c) K=SpringAssemble(K,k1,1,2) function y = SpringAssemble(K,k,i,j) K(i,i) = K(i,i) + k(1,1);K(i,j) = K(i,j) + k(1,2);K(j,i) = K(j,i) + k(2,1);K(j,j) = K(j,j) + k(2,2); 1100100100100k -??=??-??10010001001000000K -??=-??K=SpringAssemble(K,k2,2,3) 1200200200200k -??10010001003002000200200K -??=---??1001000100010010030020002002000200200100200300----≠----步骤四：引入边界条件，消除冗余方程>>k=K(2:3,2:3)%构造不含冗余的方程>>f=[0;15]%构造外力列阵步骤五：解方程引例：已知1212u 31u u u +=??-=?，求 12u u 和解：类似求解KU=F ，输入下列Matlab 命令：>> K=[1 1;1,-1]>> F=[3;1]>> U=inv(K)*F>> U=K \F（继续弹簧系统求解）>>u=k \f %使用高斯消去法求解>>U=[0 ; u]%构造原方程组>>F=K*U %求出所有外力，含多余计算步骤六：后处理、扩展计算>>u1=[0;U(2)]%构造单元位移>>f1=SpringElementForces(k1,u1)%求单元1内力>>u2=[U(2) ; U(3)]%构造单元2位移>>f2=SpringElementForces(k2,u2)%求单元2内力4. 总结clck1=SpringElementStiffness(100)%创建单元刚度矩阵 1 k2=SpringElementStiffness(200)%创建单元刚度矩阵 2 K=zeros(3,3)%创建空白整体刚度矩阵K=SpringAssemble(K,k1,1,2)%按节点装入单元矩阵 1 K=SpringAssemble(K,k2,2,3)%按节点装入单元矩阵2 k=K(2:3,2:3)%构造不含冗余的方程f=[0;15]%构造外力列阵u=k\f%使用高斯消去法求解U=[0 ; u]%构造系统节点位移列阵F=K*U%求出所有外力，含多余计算u1=[0;U(2)]%构造单元位移f1=SpringElementForces(k1,u1)%求单元1内力u2=[U(2) ; U(3)]%构造单元2位移f2=SpringElementForces(k2,u2)%求单元2内力5. 练习1 Danyi 132 dan 34 3dan 35 4dan 35 dan5 54 dan6 42。

matlab 有限元基础一、什么是有限元分析？有限元分析（Finite Element Analysis，FEA）是一种数值计算方法，用于解决复杂的工程和科学问题。

它将连续的物理系统分解成离散的有限元素，通过求解线性或非线性方程组来计算系统的行为。

有限元分析可以用于求解结构、流体力学、热传导等领域中的问题。

二、Matlab 有限元基础1. Matlab 基础知识Matlab 是一个数值计算软件，它提供了强大的矩阵运算能力和丰富的绘图功能。

在进行有限元分析时，Matlab 可以用于构建模型、求解方程组和可视化结果。

2. 有限元模型构建在进行有限元分析之前，需要先构建模型。

通常情况下，模型可以通过 CAD 软件进行建模，并导出为 STL 格式。

然后使用 Matlab 中的importGeometry 函数将 STL 文件导入到 Matlab 中，并使用pdegeometry 函数创建几何体对象。

3. 生成网格生成网格是指将几何体对象分割成小块的过程。

在 Matlab 中，可以使用 generateMesh 函数生成简单形状网格或使用 PDE 工具箱中的自动网格生成器生成更复杂形状的网格。

4. 定义边界条件在进行有限元分析时，需要定义边界条件。

边界条件包括约束和载荷。

约束是指物体的运动被限制的方式，载荷是施加在物体上的力或压力。

5. 求解方程组在定义好模型、网格和边界条件后，可以使用 Matlab 中的 pdepe 函数求解偏微分方程组。

pdepe 函数使用有限元方法求解偏微分方程组，并返回解向量。

6. 可视化结果最后一步是可视化结果。

Matlab 提供了丰富的绘图函数，可以用于绘制网格、位移、应力等结果。

三、有限元分析中常用的 Matlab 工具箱1. PDE 工具箱PDE 工具箱是一个专门用于求解偏微分方程问题的工具箱。

它提供了自动网格生成器、求解器和可视化工具，可以用于求解结构、流体力学和热传导等问题。

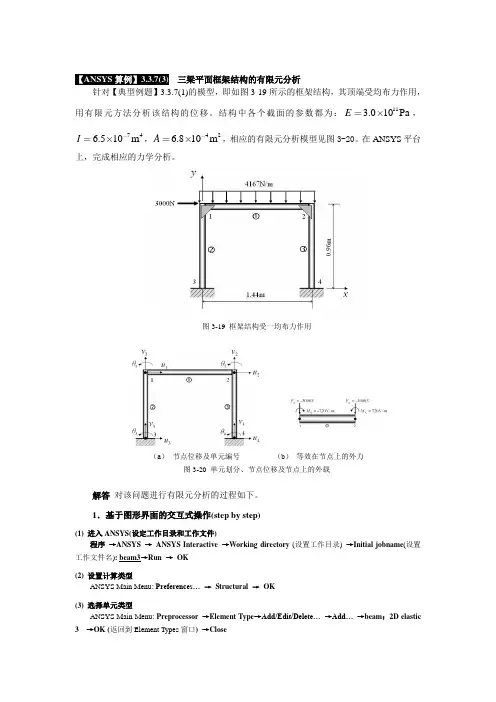
【ANSYS 算例】3.3.7(3) 三梁平面框架结构的有限元分析针对【典型例题】3.3.7(1)的模型，即如图3-19所示的框架结构，其顶端受均布力作用，用有限元方法分析该结构的位移。

结构中各个截面的参数都为：113.010Pa E ，746.510m I ，426.810m A ，相应的有限元分析模型见图3-20。

在ANSYS 平台上，完成相应的力学分析。

图3-19 框架结构受一均布力作用（a ） 节点位移及单元编号 （b ） 等效在节点上的外力图3-20 单元划分、节点位移及节点上的外载解答 对该问题进行有限元分析的过程如下。

1．基于图形界面的交互式操作(step by step)(1) 进入ANSYS(设定工作目录和工作文件)程序 →ANSYS → ANSYS Interactive →Working directory (设置工作目录) →Initial jobname (设置工作文件名): beam3→Run → OK(2) 设置计算类型ANSYS Main Menu: Preferences… → Structural → OK(3) 选择单元类型ANSYS Main Menu: Preprocessor →Element Type →Add/Edit/Delete… →Add… →beam ：2D elastic 3 →OK (返回到Element Types 窗口) →Close(4) 定义材料参数ANSYS Main Menu:Preprocessor →Material Props →Material Models→Structural →Linear →Elastic→Isotropic: EX:3e11 (弹性模量) →OK →鼠标点击该窗口右上角的“ ”来关闭该窗口(5) 定义实常数以确定平面问题的厚度ANSYS Main Menu: Preprocessor →Real Constant s… →Add/Edit/Delete →Add →Type 1 Beam3→OK→Real Constant Set No: 1 (第1号实常数), Cross-sectional area:6.8e-4 (梁的横截面积) →OK →Close(6) 生成几何模型生成节点ANSYS Main Menu: Preprocessor →Modeling →Creat→Nodes→In Active CS→Node number 1 →X:0,Y:0.96,Z:0 →Apply→Node number 2 →X:1.44,Y:0.96,Z:0 →Apply→Node number 3 →X:0,Y:0,Z:0→Apply→Node number 4 →X:1.44,Y:0,Z:0→OK生成单元ANSYS Main Menu: Preprocessor →Modeling →Create →Element →Auto Numbered →Thru Nodes →选择节点1，2(生成单元1)→apply →选择节点1，3(生成单元2)→apply →选择节点2，4(生成单元3)→OK(7)模型施加约束和外载左边加X方向的受力ANSYS Main Menu:Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择节点1→apply →Direction of force: FX →V ALUE：3000 →OK→上方施加Y方向的均布载荷ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Beams →选取单元1(节点1和节点2之间)→apply →V ALI：4167→V ALJ：4167→OK左、右下角节点加约束ANSYS Main Menu:Solution →Define Loads →Apply →Structural →Displacement →On Nodes →选取节点3和节点4 →Apply →Lab:ALL DOF →OK(8) 分析计算ANSYS Main Menu:Solution →Solve →Current LS →OK →Should the Solve Command be Executed? Y→Close (Solution is done! ) →关闭文字窗口(9) 结果显示ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape … →Def + Undeformed →OK (返回到Plot Results)(10) 退出系统ANSYS Utility Menu: File→Exit …→Save Everything→OK(11) 计算结果的验证与MA TLAB支反力计算结果一致。

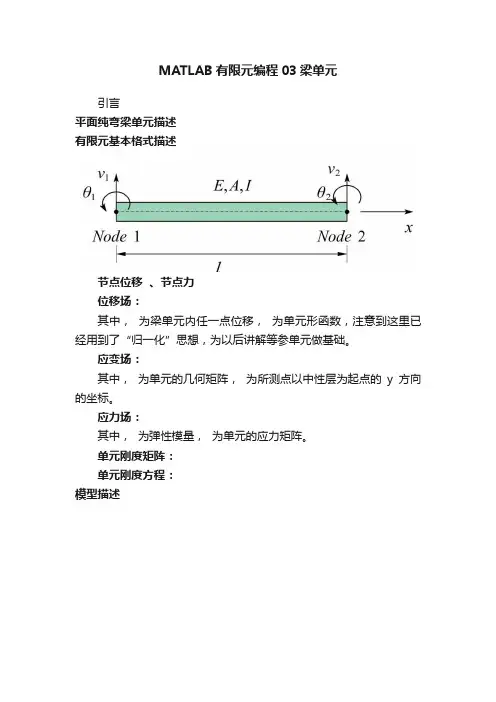
MATLAB有限元编程03梁单元引言平面纯弯梁单元描述有限元基本格式描述节点位移、节点力位移场：其中，为梁单元内任一点位移，为单元形函数，注意到这里已经用到了“归一化”思想，为以后讲解等参单元做基础。

应变场：其中，为单元的几何矩阵，为所测点以中性层为起点的y方向的坐标。

应力场：其中，为弹性模量，为单元的应力矩阵。

单元刚度矩阵：单元刚度方程：模型描述Matlab编程：% 公众号：易木木响叮当，回复梁单元，即可自动获取。

function k =Beam1D2Node_Stiffness(E,I,L)% 直接组装梁单元刚度k = E*I/(L*L*L)*[12 6*L -12 6*L6*L 4*L*L -6*L 2*L*L-12 -6*L 12 -6*L6*L 2*L*L -6*L 4*L*L];function z = Beam1D2Node_Assembly(KK,k,i,j)% 该函数进行整体刚度矩阵的组装% 输入单元刚度矩阵k，单元的节点编号i、j% 输出整体刚度矩阵KKDOF(1)=2*i-1;DOF(2)=2*i;DOF(3)=2*j-1;DOF(4)=2*j;for n1=1:4for n2=1:4KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2); endendz=KK;function v = Beam1D2Node_Deflection(x,L,u)% 该函数计算单元内某点的挠度% 输入所测点距梁单元左节点的水平距离x% 输入梁单元的长度L，节点位移列阵ue=x/L;N1=1-3*e*e+2*e*e*e;N2=L(e-2*e*e+e*e*e);N3=3*e*e-2*e*e*e;N4=L(e*e*e-e*e);N=[N1,N2,N3,N4];v=N*u% -----------主程序----------------format compactE = 200*10^9;I = 118.6*10^-6;L1 = 5;L2 = 2.5;% cal element stiffnessk1 = Beam1D2Node_Stiffness(E,I,L1);k2 = Beam1D2Node_Stiffness(E,I,L2);% stiffness assemblyKK = zeros(6,6);KK = Beam1D2Node_Assembly(KK,k1,1,2);KK = Beam1D2Node_Assembly(KK,k2,2,3)% cal displacementk = KK(4:6,4:6);p = [39062;-31250;13021];u = k\p% cal node forceU = [0;0;0;u];P = KK*U% cal RFF = [-62500;-52083;-93750;39062;-31250;13021];RF = P-F最终计算得到的支反力、节点位移值与书中解析解一致，可自行验证。

有限元刚架结构matlab程序clcclearformat compactformat shortGjd=input('请输⼊节点数：');dy=input('请输⼊单元数：');E=input('请输⼊杨⽒模量E：');I=input('请输⼊惯性矩I：');L=input('请输⼊单元长度L：');A=input('请输⼊单元截⾯积：');FAI=input('请输⼊单元相对旋转⾓度：');%输⼊对应关系时，⼩节点放前⾯[单元节点1 节点2]dy_jd=input('请输⼊单元与节点对应关系：');%输⼊⼒与扭矩约束[值作⽤节点作⽤类型]（转矩为3 x⽅向为1 y⽅向为2）lys=input('⼒与转矩约束矩阵：');%输⼊结构约束[作⽤节点作⽤类型]（转⾓为3 x⽅向为1 y⽅向为2）wys=input('结构约束矩阵：');%原始数据% L=1;% E=3*10^10;% P=1000;% A=0.05;% dy=2;jd=3;LL=[L 2*L];I=20*A;% dy_jd=[1 1 2;2 2 3];% FAI=[pi/2 0];% q=P/L;M=P*L/10;% lys=[44/125*P 1 1;-12*P*L/125 1 3;81/125*P 2 1;-P 2 2;-67/750*P*L 2 3;-P 3 2;P*L/3 3 3]; % wys=[1 1;1 2;1 3;3 1;3 2;3 3];%对⼒约束与位移约束式⼦分别进⾏编号处理wys(:,3)=(wys(:,1)-1)*3+wys(:,2);lys(:,4)=(lys(:,2)-1)*3+lys(:,3);%对⼒约束与位移约束式⼦进⾏排序lys=sortrows(lys,4);wys=sortrows(wys,3);%单元刚度矩阵syms fai e a i l realk=[e*a/l 0 0 -e*a/l 0 0;0 12*e*i/l^3 6*e*i/l^2 0 -12*e*i/l^3 6*e*i/l^2;0 6*e*i/l^2 4*e*i/l 0 -6*e*i/l^2 2*e*i/l;-e*a/l 0 0 e*a/l 0 0;0 -12*e*i/l^3 -6*e*i/l^2 0 12*e*i/l^3 -6*e*i/l^2;0 6*e*i/l^2 2*e*i/l 0 -6*e*i/l^2 4*e*i/l];t=[ cos(fai), sin(fai), 0;-sin(fai), cos(fai), 0;0, 0, 1];%坐标变换矩阵T=blkdiag(t,t);%总体坐标系下的单元刚度矩阵K=T'*k*T;%带⼊每个单元的数，⽣成单元刚度矩阵kk，其每⼀页对应相应页数的单元的刚度矩阵for j=1:dy; e=E;i=I;l=LL(j);a=A;fai=FAI(j);kk(:,:,j)=eval(K);end%⽣成总体刚度矩阵KK%采⽤元胞数组的⽅式对各项进⾏保存%⽣成空元胞数组，元胞数组的⾏列⼤⼩与节点数相同for j=1:jd;for jj=1:jd;ling1{j,jj}=zeros(3);endendling2=ling1;%将对单元刚度矩阵部分分成4分加⼊元胞数组中for j=1:dy;kk1=kk(1:3,1:3,j);kk2=kk(1:3,4:6,j);kk3=kk(4:6,1:3,j);kk4=kk(4:6,4:6,j);ling2{dy_jd(j,2),dy_jd(j,2)}=kk1+ling2{dy_jd(j,2),dy_jd(j,2)}; ling2{dy_jd(j,2),dy_jd(j,3)}=kk2+ling2{dy_jd(j,2),dy_jd(j,3)}; ling2{dy_jd(j,3),dy_jd(j,2)}=kk3+ling2{dy_jd(j,3),dy_jd(j,2)}; ling2{dy_jd(j,3),dy_jd(j,3)}=kk4+ling2{dy_jd(j,3),dy_jd(j,3)}; end %将元胞数组进⾏拼接，形成总体刚度矩阵for j=1:jd;ling3(:,:,j)=cat(2,ling2{j,:});endKK=ling3(:,:,1);for j=2:jd;KK=[KK;ling3(:,:,j)];end%消去有已知位移的⾏与列b=KK;b(:,wys(:,3))=[];b(wys(:,3),:)=[];kjiejuzhen=inv(b);%提取对应外⼒lyss=lys;for j=1:size(wys,1);for jj=1:size(lys,1);if lyss(jj,4)==wys(j,3);lyss(jj,:)=0;endif jj==size(lyss,1);breakendendendlyss(all(lyss==0,2),:)=[];%求解weiyijie=[作⽤值作⽤节点作⽤类型（转⾓为3 x⽅向为1 y⽅向为2）序列] weiyijie=kjiejuzhen*lyss(:,1);weiyijie(:,1)=weiyijie;weiyijie(:,2)=lyss(:,2);weiyijie(:,3)=lyss(:,3);weiyijie(:,4)=lyss(:,4);%计算不计作⽤在约束⽅向上时的⽀反⼒lysjiee=[作⽤值作⽤节点作⽤类型（转⾓为3 x⽅向为1 y⽅向为2）序列] lysjie(:,1)=KK(wys(:,3),lyss(:,4))*weiyijie(:,1);lysjie(:,2:4)=wys(:,1:3);%将作⽤在约束⽅向上时的⽀反⼒加在上⾯的求解结果上for j=1:size(lysjie,1)for jj=1:size(lys,1);if lysjie(j,4)==lys(jj,4);lysjie(j,1)=lysjie(j,1)-lys(jj,1);endendend%答案weiyijielysjie。

matlab编译平面有限元计算编译平面有限元计算是一种常用的数值计算方法，可以用于求解各种复杂的工程问题。

在本文中，我们将介绍如何使用MATLAB编写平面有限元计算程序，并通过一个实例来说明其应用。

让我们了解一下有限元方法的基本原理。

有限元方法是一种将连续体划分为有限个单元，根据物理方程和边界条件，在每个单元上建立离散方程组，最终求解得到整个连续体的近似解的方法。

在平面问题中，连续体被划分为三角形或四边形单元。

MATLAB是一种功能强大的数值计算软件，它提供了丰富的工具箱和函数，可以方便地进行有限元计算。

下面我们将以求解平面弹性力学问题为例，介绍如何使用MATLAB编写平面有限元计算程序。

我们需要定义问题的几何信息、边界条件和材料参数。

在MATLAB中，可以通过定义节点坐标、单元连接关系、边界条件和材料参数来描述问题。

节点坐标可以用一个矩阵表示，其中每一行代表一个节点的坐标。

单元连接关系可以用一个矩阵表示，其中每一行代表一个单元的节点编号。

边界条件可以用一个向量表示，其中每个元素代表一个节点的边界条件。

材料参数可以用一个矩阵表示，其中每一行代表一个单元的材料参数。

接下来，我们需要建立有限元离散方程组。

在平面弹性力学问题中，离散方程组可以通过组装单元刚度矩阵和外力向量得到。

单元刚度矩阵可以通过单元的几何信息和材料参数计算得到。

外力向量可以根据边界条件和载荷信息计算得到。

最终，我们可以通过求解离散方程组得到节点的位移解。

我们可以根据节点的位移解计算出单元的应力和应变。

在平面弹性力学问题中，应力可以通过单元的几何信息和位移解计算得到。

应变可以通过应力和材料参数计算得到。

通过计算应力和应变，我们可以评估结构的稳定性和性能。

MATLAB编译平面有限元计算程序是一种强大的工具，可以用于求解各种复杂的工程问题。

通过定义几何信息、边界条件和材料参数，建立有限元离散方程组，求解得到节点的位移解，最终计算出单元的应力和应变。

Matlab 有限元基础什么是有限元法有限元法（Finite Element Method，FEM）是一种数值计算方法，常被用于工程和科学领域中的结构力学、流体力学、热传导等问题的求解。

有限元法通过将复杂的实际问题离散化为有限个简单的单元，利用数学模型和计算方法来近似求解问题。

有限元法的基本思想是将计算域划分为有限个小单元，每个小单元的物理性质通过节点上的数学函数进行近似描述。

通过对这些小单元的数学模型进行积分计算，得到整个计算域的方程，并通过求解这些方程来得到问题的近似解。

Matlab 在有限元分析中的应用Matlab作为一种功能强大的数值计算和编程软件，被广泛应用于有限元分析中。

它提供了丰富的数学和计算工具，能够方便地实现有限元法的建模、求解和分析。

有限元法的建模在Matlab中，有限元法的建模主要包括以下几个步骤：1.创建几何模型：通过定义节点和单元来描述计算域的几何形状。

可以使用Matlab提供的图形界面工具或者编程方式来创建几何模型。

2.定义边界条件：根据实际问题的边界条件，为模型的节点或单元指定相应的约束条件。

这些条件通常包括位移、力和温度等。

3.定义材料性质：根据实际问题的材料性质，为模型的节点或单元定义相应的材料参数。

这些参数包括弹性模量、泊松比和热导率等。

4.网格划分：将计算域划分为有限个小单元，形成离散化的网格结构。

在Matlab中，可以使用自带的网格划分工具或者自定义的算法进行网格划分。

5.构建刚度矩阵和载荷向量：根据节点的约束条件和单元的材料性质，利用数学公式和计算方法构建刚度矩阵和载荷向量。

有限元法的求解有限元法的求解主要包括以下几个步骤：1.组装系统方程：根据刚度矩阵和载荷向量，将节点的位移和载荷进行组合，形成整个系统的方程。

2.施加边界条件：将已知的位移和载荷应用于系统方程中的相应位置，形成含有未知位移的方程。

3.求解方程：使用Matlab提供的线性代数求解函数，求解含有未知位移的系统方程，得到位移的近似解。

有限元课程设计matlab一、课程目标知识目标：1. 学生能理解有限元分析的基本原理，掌握运用MATLAB进行有限元建模和求解的基本步骤。

2. 学生能够运用MATLAB软件进行简单物理场的有限元模拟，并解释模拟结果。

3. 学生掌握如何将实际问题抽象为有限元模型，并能够运用MATLAB进行模型参数的设定和调整。

技能目标：1. 学生能够独立操作MATLAB软件，进行有限元模型的构建和求解。

2. 学生能够通过MATLAB编程实现有限元模型的自动化处理，包括前处理、求解和后处理。

3. 学生通过解决实际问题，提高数值分析能力和计算机应用能力。

情感态度价值观目标：1. 学生培养对科学研究的兴趣，特别是在工程计算和仿真领域。

2. 学生通过解决实际问题，体会数学和工程结合的美，增强对工程问题的探究欲望。

3. 学生通过团队合作解决问题，培养协作精神和解决问题的能力。

本课程针对高年级本科生或研究生，他们具备一定的数学基础和编程能力。

课程性质偏重实践，旨在通过MATLAB这一工具将有限元理论应用于具体问题的求解。

课程目标旨在使学生不仅掌握理论知识，而且能够实际操作，将理论知识转化为解决实际问题的技能。

通过课程学习，学生应能够将所学知识应用于未来的学术研究或工程实践中。

二、教学内容1. 有限元方法基本原理回顾：包括有限元离散化、单元划分、形函数、刚度矩阵和载荷向量等概念。

- 教材章节：第二章 有限元方法基础2. MATLAB编程基础：介绍MATLAB的基本操作、数据结构、流程控制、函数编写等。

- 教材章节：第三章 MATLAB编程基础3. MATLAB中的有限元工具箱使用：学习如何使用MATLAB内置的有限元工具箱进行建模和求解。

- 教材章节：第四章 MATLAB有限元工具箱介绍4. 有限元模型构建与求解：结合实际问题，学习如何构建有限元模型，并进行求解。

- 教材章节：第五章 有限元模型构建与求解5. 实例分析与上机操作：通过案例分析，让学生实际操作MATLAB软件，解决具体的有限元问题。

有限元分析基础教程Fundamentals of Finite Element Analysis(ANSYS算例)曾攀清华大学2008-12有限元分析基础教程曾攀有限元分析基础教程Fundamentals of Finite Element Analysis曾攀(清华大学)内容简介全教程包括两大部分，共分9章；第一部分为有限元分析基本原理，包括第1章至第5章，内容有：绪论、有限元分析过程的概要、杆梁结构分析的有限元方法、连续体结构分析的有限元方法、有限元分析中的若干问题讨论；第二部分为有限元分析的典型应用领域，包括第6章至第9章，内容有：静力结构的有限元分析、结构振动的有限元分析、传热过程的有限元分析、弹塑性材料的有限元分析。

本书以基本变量、基本方程、求解原理、单元构建、典型例题、MATLAB程序及算例、ANSYS算例等一系列规范性方式来描述有限元分析的力学原理、程序编制以及实例应用；给出的典型实例都详细提供有完整的数学推演过程以及ANSYS实现过程。

本教程的基本理论阐述简明扼要，重点突出，实例丰富，教程中的二部分内容相互衔接，也可独立使用，适合于具有大学高年级学生程度的人员作为培训教材，也适合于不同程度的读者进行自学；对于希望在MATLAB程序以及ANSYS平台进行建模分析的读者，本教程更值得参考。

本基础教程的读者对象：机械、力学、土木、水利、航空航天等专业的工程技术人员、科研工作者。

- 1 -标准分享网 免费下载目录[[[[[[\\\\\\【ANSYS算例】3.3.7(3) 三梁平面框架结构的有限元分析 1 【ANSYS算例】4.3.2(4) 三角形单元与矩形单元的精细网格的计算比较 3 【ANSYS算例】5.3(8) 平面问题斜支座的处理 6 【ANSYS算例】6.2(2) 受均匀载荷方形板的有限元分析9 【ANSYS算例】6.4.2(1) 8万吨模锻液压机主牌坊的分析(GUI) 15 【ANSYS算例】6.4.2(2) 8万吨模锻液压机主牌坊的参数化建模与分析(命令流) 17 【ANSYS算例】7.2(1) 汽车悬挂系统的振动模态分析(GUI) 20 【ANSYS算例】7.2(2) 汽车悬挂系统的振动模态分析(命令流) 23 【ANSYS算例】7.3(1) 带有张拉的绳索的振动模态分析(GUI) 24 【ANSYS算例】7.3(2) 带有张拉的绳索的振动模态分析(命令流) 27 【ANSYS算例】7.4(1) 机翼模型的振动模态分析(GUI) 28 【ANSYS算例】7.4(2) 机翼模型的振动模态分析(命令流) 30 【ANSYS算例】8.2(1) 2D矩形板的稳态热对流的自适应分析(GUI) 31 【ANSYS算例】8.2(2) 2D矩形板的稳态热对流的自适应分析(命令流) 33 【ANSYS算例】8.3(1) 金属材料凝固过程的瞬态传热分析(GUI) 34 【ANSYS算例】8.3(2) 金属材料凝固过程的瞬态传热分析(命令流) 38 【ANSYS算例】8.4(1) 升温条件下杆件支撑结构的热应力分析(GUI) 39 【ANSYS算例】8.4(2) 升温条件下杆件支撑结构的热应力分析(命令流) 42 【ANSYS算例】9.2(2) 三杆结构塑性卸载后的残余应力计算(命令流) 45 【ANSYS算例】9.3(1) 悬臂梁在循环加载作用下的弹塑性计算(GUI) 46 【ANSYS算例】9.3(2) 悬臂梁在循环加载作用下的弹塑性计算(命令流) 49 附录 B ANSYS软件的基本操作52 B.1 基于图形界面(GUI)的交互式操作(step by step) 53 B.2 log命令流文件的调入操作(可由GUI环境下生成log文件) 56 B.3 完全的直接命令输入方式操作56 B.4 APDL参数化编程的初步操作57i【ANSYS 算例】3.3.7(3) 三梁平面框架结构的有限元分析如图3-19所示的框架结构，其顶端受均布力作用，用有限元方法分析该结构的位移。

基于3节点三角形单元的矩形薄板分析(Triangle2D3Node)如图4-20所示为一矩形薄平板，在右端部受集中力100 000F N =作用，材料常数为：弹性模量7110E Pa =⨯，泊松比13μ=，板的厚度0.1t m =。

基于MA TLAB 平台求解该结构的节点位移、支反力以及单元应力。

图4-20解答：对该问题进行有限元分析的过程如下。

（1）结构的离散化与编号将结构离散为二个3节点三角形单元，单元编号及节点编号如图4-20(b)所示。

（2）计算各单元的刚度矩阵(以国际标准单位)首先在MA TLAB 环境下，输入弹性模量E 、泊松比NU 、薄板厚度t 和平面应力问题性质指示参数ID ，然后针对单元1和单元2，分别两次调用函数Triangle2D3Node_Stiffness ，就可以得到单元的刚度矩阵k1(6×6)和k2(6×6)。

>> E=1e7;>> NU=1/3;>> t=0.1;>> ID=1;>> k1=Triangle2D3Node_Stiffness(E,NU,t,2,0,0,1,0,0,ID)k1 = 1.0e+006 *0.2813 0 0 0.1875 -0.2813 -0.18750 0.0938 0.1875 0 -0.1875 -0.09380 0.1875 0.3750 0 -0.3750 -0.18750.1875 0 0 1.1250 -0.1875 -1.1250-0.2813 -0.1875 -0.3750 -0.1875 0.6563 0.3750-0.1875 -0.0938 -0.1875 -1.1250 0.3750 1.2188>>k2=Triangle2D3Node_Stiffness(E,NU,t,0,1,2,0,2,1,ID)k2 = 1.0e+006 *0.2813 0 0 0.1875 -0.2813 -0.18750 0.0938 0.1875 0 -0.1875 -0.09380 0.1875 0.3750 0 -0.3750 -0.18750.1875 0 0 1.1250 -0.1875 -1.1250-0.2813 -0.1875 -0.3750 -0.1875 0.6563 0.3750-0.1875 -0.0938 -0.1875 -1.1250 0.3750 1.2188（3） 建立整体刚度方程由于该结构共有4个节点，则总共的自由度数为8，因此，结构总的刚度矩阵为KK (8×8)，先对KK 清零，然后两次调用函数Triangle2D3Node_Assembly 进行刚度矩阵的组装。