第六章 因子分析.

第五章主成分分析clearset more offcd"C:\Users\zhou\OneDrive\Lectures_ebook\multivariate_statistics\labora tory\03principal"use data*定义变量的标签label var area "省份"label var x1 "GDP(亿元）"label var x2 "居民消费水平(元）"label var x3 "固定资产投资(亿元)"label var x4 "职工平均工资（元）"label var x5 "货物周转量(亿吨公里)"label var x6 "居民消费价格指数(上年100)"label var x7 "商品零售价格指数(上年100)"label var x8 "工业总产值(亿元)"describesumcorr//findit factortest//ssc install factortest//check the datafactortest x1-x8pca x1-x8, correlation /*主成分估计*/pca x1-x8, covariance component(3) /*主成分估计*///testestat kmo /*KMO检验，越高越好*/estat smc /*SMC检验，值越高越好*/screeplot /* 碎石图（特征值等于1处的水平线标示保留主成分的分界点）*/ loadingplot , yline(0) xline(0)/*载荷图 */loadingplot , combined factors(3) yline(0) xline(0)/*载荷图 */predict f1 f2 f3 /*预测变量得分*/scoreplot,mlabel(area) yline(0) xline(0) /*得分图*/scoreplot,xtitle("经济社会总量") ytitle("人民生活水平") mlabel(area) yline(0) xline(0) /*得分图*/scatter f2 f3,xtitle("人民生活水平") ytitle("物价水平") mlabel(area) yline(0) xline(0) /*得分图*/scoreplot, factors(3) mlabel(area) /*得分图*/scoreplot,combined factors(3) mlabel(area) yline(0) xline(0) /*得分图*///ranking by scoredescribe f1-f3sort f1 //sortinggen rank_nature=_n //rankingbrowse area f1 rank_nature // show datgsort -f1 //generalized sortinggen rank_nature1=_n //rankingbrowse area f1 rank_nature rank_nature1 // show datcor x1-x8matrix CM=r(C) //define covariance matrixpcamat CM, comp(3) n(1000) names(a1 a2 a3 a4 a5 a6 a7 a8)//rotate /*旋转*/。

第六章因子分析第六章因子分析§6.1因子分析的基本原理与模型一、因子分析的基本思想基本思想：根据相关性的大小将变量分组，使得同组内变量间的相关性较高，不同组间的相关性较低。

每组变量代表一个基本结构，并用一个不可观测的综合变量形式表示，这个基本结构成为公共因子。

此时的原始变量就可以分解成两部分之和的形式，一部分是少数几个不可测的所谓公共因子的线性函数，另一部分是与公共因子无关的特殊因子。

目的：从一些有错综复杂的问题中找出几个主要因子，每个主要因子代表原始变量间相互依赖的一种作用。

二、因子分析的基本模型常用的因子分析模型：R型因子分析和Q 型因子分析（一）R型因子分析模型R型因子分析是对变量作因子分析。

R型因子分析中的公共因子是不可直接观测但又客观存在的共同影响因素，每一个变量都可以表示成公共因子的线性函数与特殊因子之和，即:其中：称为公共因子，称为的特殊因子矩阵表达式：且满足：（1）（2），即公共因子与特殊因子是不相关的（3），即各公共因子不相关且方差为1（4），即各个特殊因子不相关，方差不要求相等模型中称为因子载荷，是第个变量在第个因子上的负荷，如果把变量看成维空间中的一个点，则表示它在坐标轴上的投影，因此矩阵称为因子载荷矩阵。

（二）Q型因子分析Q型因子分析是对样品作因子分析。

模型同上注：主成分分析与因子分析的区别主成分分析的数学模型本质上是一种线性变换，是将原始坐标变换到变异程度大的方向上去，相当于从空间上转换观看数据的的角度，突出数据变异的方向，归纳重要信息。

因子分析与主成分分析一样都属降低变量维数的方法。

但因子分析的本质是从显在变量去“提炼”潜在因子的过程。

模型中应注意的问题：（1）变量的协方差阵的分解式为即（2）因子载荷不是唯一的。

三、因子载荷阵的统计意义（一）因子载荷的统计意义对于因子模型可知的协方差若对作标准化处理，的标准差为1，且的标准差为1则（相关系数）综上可知：对于标准化后的，是的相关系数，一方面表示的依赖程度，绝对值越大，密切程度越高；另一方面也反映了变量对公共因子的相对重要性。

第五讲 因子分析在许多实际问题中，涉及的变量众多，各变量间还存在错综复杂的相关关系，这时最好能从中提取少数综合变量，这些综合变量彼此不相关，而且包含原变量提供的大部分信息。

因子分析就是为解决这一问题提供的统计分析方法。

以后，如无特别说明，都假定总体是一个p 维变量：),...,,(21'=p X X X x它的均值向量μ=)(x E ，协方差矩阵V =(σij )p ⨯p 都存在。

第一节 正交因子模型1．1 公共因子与特殊因子从总体中提取的综合变量：F 1, F 2, … , F m (m <p )称为（总体的）公共因子。

一般来说，公共因子不可能包含总体的所有信息，每个变量X i 除了可以由公共因子解释的那部分外，总还有一些公共因子解释不了的部分，称这部分为变量X i 的特殊因子，记为：εi 。

于是，我们有：变量X i 的信息＝公共因子可以表达部分+公共因子不可表达部分这就是所谓因子模型。

目前，公共因子可以表达的部分由公共因子的线性组合表示。

即上面的因子模型可以写成以下的形式：p i F a F a F a X i m im i i i i ,...,2,1,2211=++++=-εμ1．2 正交因子模型设总体),...,,(21'=pX X X x ，均值向量μ=)(x E ，协方差矩阵p p V x Va r ⨯=)( 。

因子模型有形式：其中m<p ，F 1,F 2,…,F m 称为所有变量的公共因子；εi 称为变量X i 的特殊因子。

如果引入以下向量与矩阵：),...,,(,),...,,(2121'='=p m F F F F εεεε⎪⎪⎪⎪⎪⎭⎫⎝⎛=pm p p m m a a a a a a a a a A212222111211则因子模型的矩阵形式为：εμ+=-F A x 对于正交的因子模型，还要进一步要求：z 1. m m I F Var F E ⨯==)(,0)(。

第六章 因子分析一．基本原理因子分析（Factor anslysis ）是用来分析隐藏在表象背后的因子作用的一类统计模型与方法。

起源于心理度量学（Phsycholometrics ），在方法上与主成分分析有密切联系。

因子分析一般有两个用途，一是通过寻求变量的基本结构，对变量进行简化；二是通过因子得分，在因子轴构成的空间中将变量或者样品进行分类。

1．正交因子模型设x 为一个p 维可观测随机向量，假定x 受到m 个不可观测的随机因子的控制，称这m 个影响x 的因子为公共因子，若m 维随机向量f 对x 的影响是线性的，则x 与f 之间的关系可用下述模型来表述：x Lf με=++其中μ为P 维常向量，表示X 的均值；L 为p m ⨯维常数阵，L 的第I 行表示公共因子f 对X 第I 个分量i x 的影响系数；ε为P 维随机变量，表示X 中与f 无关的那一部分，称为特殊因子。

其中f 和ε都是不可观测的，假定它们满足下列条件 （1）f 和ε相互独立 （2）()0,()m E f V f I ==（3）()0,()E V εε==ψ，其中ψ(psai)为对角阵。

由于()m V f I =，即各因子之间不相关，这样的模型便称为正交因子模型。

在正交因子模型中，公共因子f 对X 的各分量都起作用，而特殊因子ε的第I 个分量只对X 的第I 个分量起作用。

L 称为载荷阵（Loading Matrix ）。

如果对X 进行标准化处理，则μ为0，原式化为x Af ε=+。

A 为载荷阵。

X 的方差是由载荷阵和特殊因子的方差构成的。

即()Var X AA '=+ψ。

2．因子分析与其他多元分析方法的区别与多元回归的区别：因子分析中，各个公共因子是虚拟的，本身是未知量。

与主成分分析的区别：主成分分析本质上是一种变量变换，而因子分析则是构造出一组新的因子来对原变量进行解释。

二．计算模型1．因子载荷的含义假定在因子分析模型中，对各变量及公共因子、特殊因子均进行了标准化处理。

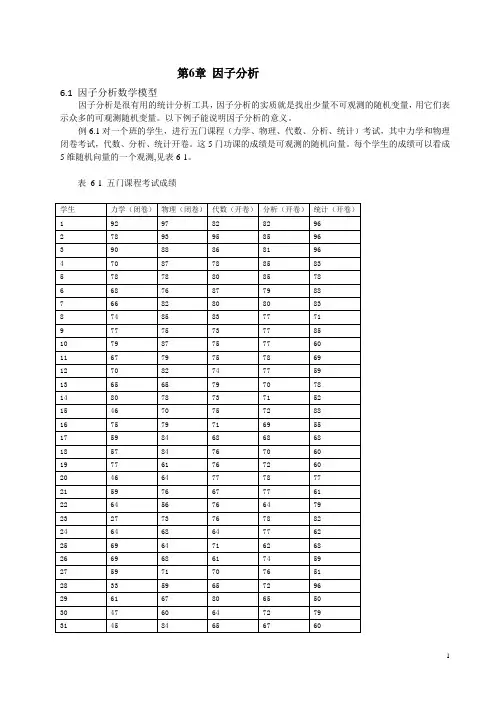
第6章因子分析6.1 因子分析数学模型因子分析是很有用的统计分析工具，因子分析的实质就是找出少量不可观测的随机变量，用它们表示众多的可观测随机变量。

以下例子能说明因子分析的意义。

例6.1对一个班的学生，进行五门课程（力学、物理、代数、分析、统计）考试，其中力学和物理闭卷考试，代数、分析、统计开卷。

这5门功课的成绩是可观测的随机向量。

每个学生的成绩可以看成5维随机向量的一个观测,见表6-1。

表6-1 五门课程考试成绩经过一定计算（因子分析）后发现存在不可观测的随机变量：1f 、2f ，它们和51,...x x 间有关系 521542143213221212116377.1091469.9750.678264.162258.5364.721559.013358.6909.720269.564838.7523.721220.864570.8409.62v f f x v f f x v f f x v f f x v f f x +-+=+-+=+-+=+++=+++= （6.1） 其中1f 、2f 是不可观测的随机变量。

我们认为它们分别表示学生的学习能力和适应开闭卷能力，所以可分别称为学习因子和适应开闭卷因子。

（6.1）揭示了这两个因子如何影响5门功课的成绩，也揭示5门课成绩的实质：每门课的成绩由学习因子和适应开闭卷因子的线性组合，加上常数，再加上随机变量而得。

这是是很有意义的。

象例6.1那样，找出少量不可观测因子（例如1f 、2f ），并给出它们影响可观测随机变量（例如51,...x x ）方式的统计分析，就是因子分析。

因子分析与主成分分析不同：主成分分析是寻求若干个可观测随机变量的少量线性组合，说明其含义；因子分析主要的目的是找出不一定可观测的潜在变量作为公共因子，并解释公共因子的意义，及如何用不可观测随机变量，计算可观测随机变量。

因子分析方法在心理学，经济，医学，生物学，教育学等方面有重要用途。

因子分析方法范文一、引言因子分析是一种主成分分析方法，用于解释观测变量之间的关系和降低变量的维度。

在社会科学和心理学领域，因子分析被广泛应用于问卷调查和测量工具的开发中。

本文将详细介绍因子分析的基本概念、原理、步骤和应用。

二、因子分析的基本概念1.因子因子指的是解释观测变量之间的共同变异的一组变量。

在因子分析中，我们希望找到一组“潜在因子”，这些因子无法直接观测到，但它们通过观测变量的共同变异来解释数据。

2.因子载荷因子载荷是指变量与因子之间的相关系数，表示变量与因子之间的相关程度。

因子载荷的绝对值越大，表示变量与因子之间的相关性越高。

3.因子旋转因子旋转是调整因子载荷和使因子解释变量之间的关系更为清晰和简单的一种方法。

常见的因子旋转方法有正交旋转和斜交旋转两种。

三、因子分析的原理因子分析的核心原理是通过计算观测变量之间的协方差矩阵，并找到一组“最佳”因子，使得这些因子能够解释尽可能多的变异。

最常用的因子提取方法有主成分分析法和极大似然估计法。

四、因子分析的步骤1.数据准备将需要进行因子分析的数据进行标准化处理，确保所有变量的均值为0，标准差为1，以消除不同变量之间的度量单位差异。

2.因子提取使用主成分分析法或极大似然估计法提取因子。

主成分分析法假设所有因子是非相关的，适用于变量间具有明显线性关系的情况。

极大似然估计法则更加强调因子与变量之间的相关性。

3.因子旋转选择适当的因子旋转方法进行旋转，常用的方法有方差最大化旋转、直角旋转和斜向旋转等。

通过旋转可以使得因子与变量之间的相关性更简明清晰。

4.因子命名和解释根据因子载荷矩阵，为每个因子命名，并解释因子与变量之间的关系。

通过因子载荷，可以判断每个变量在每个因子上的贡献程度。

五、因子分析的应用因子分析广泛应用于心理学、教育学、经济学、市场调研等领域。

以心理学领域为例，因子分析可用于测量心理特征和人格特征。

例如，通过问卷调查，可以使用因子分析识别不同人格特征的因子，并进行心理特征分析。

第6章--因子分析第六章因子分析一、填空题1. 因子分析常用的两种类型为 ____________ 和 ___________ 。

2. 因子分析是将具有错综复杂关系的变量（或样品）综合为数量较少的几个因子，以再现______________ 与____________ 间的相互关系。

3•因子分析就是通过寻找众多变量的______________ 来简化变量中存在的复杂关系的一种方法。

4 •因子分析是把每个原始变量分解成两个部分即____________ 、。

5 •变量共同度是指因子载荷矩阵中__________________________ 。

6 •公共因子方差与特殊因子方差之和为________ 。

7.求解因子载荷矩阵常用的方法有______________________ 和________________ &常用的因子旋转方法有 ____________________ 和__________________ 。

9. Spss中因子分析采用__________________ 命令过程。

10•变量X i的方差由两部分组成，一部分为 ___________ ，另一部分为__________二、判断题1. 在因子分析中，因子载荷阵不是唯一的。

（）2. 因子载荷阵经过正交旋转后，各变量的共性方差和各个因子的贡献都发生了变化。

（）3. 因子分析和主成分分析的核心思想都是降维。

（）4.因子分析有两大类，R型因子分析和Q型因子分析；其中R型因子分析是从变量的相似矩阵出发，而Q型因子分析是从样品的相关矩阵出发。

（）5. 特殊因子与公共因子之间是相互独立的。

（）6. 变量共同度是因子载荷矩阵列元素的平方和。

（）7. 公共因子的方差贡献是衡量公共因子相对重要性指标。

（）8. 对因子载荷阵进行旋转的目的是使结构简化。

（）三、简答题1.因子分析的基本思想是什么，它与主成分分析有什么区别和联系？2 •因子模型的矩阵形式UF ，其中:F F1, ,F m 1, , P U U ij pm请解释式中F、、U的统计意义。

第六章因子分析分解
首先，让我们了解因子分析分解的背后原理。

当我们有多个相关的变量时，通常会遇到数据中的冗余信息。

这些冗余信息可能使分析和解释数据变得困难。

因子分析分解可以帮助我们找到这些变量之间的共同维度，并将其归纳为更少的因子。

这些因子代表了原始变量中的共享信息。

下面，我将介绍因子分析分解的步骤。

首先，我们需要准备多个变量的数据集。

然后，我们将对这些变量进行主成分分析。

主成分分析是一种将多个变量转化为少数几个无关主成分的方法。

在主成分分析中，我们通过计算协方差矩阵来确定主成分。

接下来，我们选择解释变量方差的主成分，并按主成分的大小对它们进行排列。

最后，我们可以从这些主成分中选择最相关的因子，作为我们的最终结论。

那么，因子分析分解有什么实际应用呢？因子分析分解可以在许多领域中使用，例如心理学、市场调研和人社科学。

在心理学中，因子分析分解可以用于理解人们的个性特征和行为模式。

在市场调研中，因子分析分解可以用于确定消费者的购买偏好和行为倾向。

在人社科学中，因子分析分解可以用于研究人口统计学数据中的潜在因素。

总结一下，因子分析分解是一种用于理解多个变量之间关系的方法。

它通过检测数据中的共同变异性，将复杂的数据结构简化为更容易解释和理解的形式。

在进行因子分析分解时，我们需要按照特定步骤进行，包括数据准备、主成分分析和因子选择。

因子分析分解在心理学、市场调研和人社科学中有广泛的应用。

希望通过这篇文章的介绍，可以让读者对因子分析分解有一个初步的了解。